目前,针对复杂武器系统的发射动力学响应研究,多数基于ADAMS等多体动力学软件,建立了发射系统的动力学模型[2],解决发射装备设计或试验中遇到的问题。为了提高仿真的精度,综合应用ANSYS等有限元软件得到柔性体模态信息,进行联合仿真[3-5],或开发外接子程序以弥补ADAMS等软件的不足[6-7],或完全基于ABAQUS非线性有限元软件建立发射系统的有限元模型,研究发射动力学响应。以上方法在进行方案优化时,其效率低下的特点就成为制约车载冷发射方案优化设计的主要因素,甚至不可能采用此类方法开展方案设计。因此,用简化的动力学模型模拟车载冷发射系统的动力学特性,研究发射动力学快速模拟方法,是工程应用的迫切需求[8]。
多刚体动力学方法在发射动力学中应用较多,主要解决火炮武器精度的问题,一般采用第二类拉格朗日方程[9]、传递矩阵法[8]、Kane法[10]等快速多体动力学方法进行研究,但针对车载冷发射系统的动力学研究并不多见。本文旨在研究车载冷发射系统的快速动力学分析方法,为发射系统优化设计提供支撑。对发射过程中弹射载荷在系统内部的扩散形式、分配关系、衰减过程等物理现象分析的基础上,采用多刚体动力学的绝对坐标方法[11],解决发射车约束复杂和变拓扑结构[12]的问题。在此基础上,建立车载冷发射多刚体动力学快速仿真模型(简称快速仿真模型),并与ADAMS和ABAQUS 2种商用软件的仿真结果进行比较,以验证快速仿真模型的有效性和快速性,同时深入研究底座支腿载荷比的动态特性和附加载荷分配因子对底座支腿载荷比均值和发射管口最大位移的影响,为车载冷发射系统的设计提供参考。
1 车载冷发射系统物理模型 根据典型车载冷发射系统的结构特点,建立如图 1所示的多刚体物理模型。该模型将车架、发射管、弹体3个独立部分简化为刚体。车架用4个支腿支撑在地面上,车架和发射管用旋转铰连接于O点,各刚体之间用弹簧、阻尼器连接,以模拟相互间的弹性连接关系,并保持平衡状态。车架支腿与地面的连接关系用4个弹簧K1~K4和4个阻尼器C1~C4模拟(K2、C2、K4、C4未在图 1中示出),其中,K1和K2模拟后支腿,K3和K4模拟前支腿。发射管和车架之间的起竖油缸用弹簧K5和阻尼器C5模拟。发射管和弹体之间的导向带用若干组弹簧、阻尼器模拟,将其中一道导向带放大示于图 1中,由一组相互垂直的弹簧、阻尼器K6、C6和K7、C7模拟,其中K6、C6垂直于纸面。
弹体发射前竖立在弹体支撑面上。发射过程中,燃气发生器产生的管内弹道载荷在弹体底部产生推力Ft,使其加速滑离发射管。在此过程中,弹体和发射管的约束条件会发生变化。同时,底座将管内弹道载荷分散传递到地面,使底座受力Fd,并产生影响发射系统稳定的附加于发射管底部的载荷Fa(即附加载荷)。
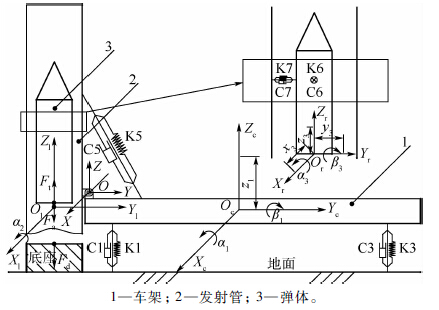 |
| 图 1 车载冷发射动力学模型示意图 Fig. 1 Schematic of vehicular cold launch dynamics model |
| 图选项 |
2 多刚体动力学仿真模型 2.1 模型简化及假设 根据车载发射结构和发射物理过程,建立多刚体动力学仿真模型,主要假设如下:
1) 所有铰约束均为理想完整约束。
2) 忽略地面的柔性影响。
3) 导弹在发射管内滑动而不跳动。
4) 考虑车架横向偏心的影响。经简化后的快速仿真模型共有9个自由度,如图 1所示。其中车架有3个自由度,为沿Zc轴的平动位移z1,绕Xc轴的转动角α1和绕Yc轴的转动角β1;发射管有1个自由度,为绕Xl轴的转动角α2;弹体有5个自由度,分别为沿Xr、Yr和Zr轴的3个平动位移x3、y3和z3,以及绕Xr的转动角α3和绕Yr的转动角β3。
5) 管内弹道载荷简化为作用在弹体底部的推力Ft、作用在底座上的力Fd和作用在发射管底部的附加载荷Fa。
2.2 多刚体动力学方程 在车架、发射管和弹体上分别建立随体坐标系OcXcYcZc、OlXlYlZl和OrXrYrZr。全局坐标系为OXYZ,刚体运动采用笛卡儿坐标方法描述,则系统的广义坐标可表示为
 | (1) |
式中:Ri=[xi,yi,zi]T(i=1,2,3)分别为随体坐标系原点Oc、Ol和Or在全局坐标系中的位置;θi=[αi,βi,γi]Τ(i=1,2,3)为卡尔丹角表示的随体坐标系姿态角。
根据第一类拉格朗日方程可以得到多刚体动力学方程为
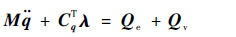 | (2) |
式中:M为质量矩阵;CqT为系统约束的雅可比矩阵的转置,文中广义坐标或时间在下标位置表示对其求偏导数;λ为拉格朗日乘子;Qe为广义力列阵;Qv为耦合惯性力列阵,具体表达式可参考文献[11]。
2.3 约束方程 在图 1所示的系统中,铰约束有3个,分别为车架与地面之间的车架铰、车架和发射管之间的旋转铰、发射管和弹体之间的接触约束,它们可以用图 2中所示的5个向量表示。
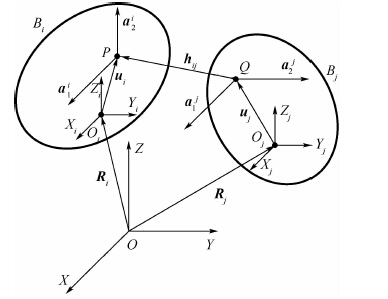 |
| 图 2 铰约束示意图 Fig. 2 Schematic of constraint joint |
| 图选项 |
如图 2所示,定义全局坐标系OXYZ,体Bi、Bj的随体坐标系分别为OiXiYiZi和OjXjYjZj,铰在体Bi、Bj上的安装点分别为P、Q,位置坐标分别为ui和uj,不失一般性,分别在铰点建立铰坐标系,使其与随体坐标系平行。在以P、Q为原点的铰坐标系中分别定义相互垂直的单位向量a1i和a2i固连在体Bi上,a1j和a2j固连在体Bj上,且a1i和a1j平行,向量hij表示PQ间的位移。利用上述5个向量可以构造出车载冷发射系统中的3个铰约束方程。
2.3.1 车架铰 在发射过程中,车架沿Xc、Yc向的位移较小,而且不会绕Zc轴转动,定义a2i为沿Zc轴的单位向量,因此车架和地面之间的车架铰约束方程为
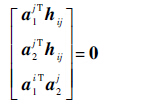 | (3) |
第1个和第2个式子表示刚体间相对平动在a1j和a2j方向的投影为0,限制沿Xc、Yc向的平动,第3个式子表示限制刚体间绕Zc轴的转动。
2.3.2 旋转铰 采用式(3)中的描述方法,定义a2i为沿Xl轴的单位向量,则车架和发射管之间的旋转铰约束方程为
 | (4) |
第1个式子表明车架和发射管相对平动位移为0,第2个和第3个式子限制绕Yl轴和Zl轴的转动。
2.3.3 接触约束 发射管和弹体之间的接触约束有2个方面:一是导向带接触约束;二是弹体和弹体支撑面之间的接触约束。前者可以将导向带的接触约束分解为沿导向带轴线方向的切向摩擦力、垂直轴线的法向力以及限制弹体转动的周向摩擦力,法向力简化为相互垂直的几组弹簧、阻尼器模型,切向摩擦力根据库仑摩擦定律计算。
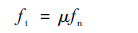 | (5) |
式中:ft为切向摩擦力;fn为法向弹簧力;μ为动摩擦因数。
发射管和弹体之间的接触约束为变拓扑约束,根据发射过程可简化为3种铰约束关系,定义a2i为沿Zr轴的单位向量,则约束方程如下:
1) 在弹体克服最大摩擦力和重力起动之前,限制沿Zr向的位移和绕Zr轴转动,约束方程为
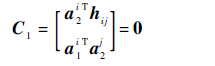 | (6) |
2) 弹体在发射管内滑动到出管之前,限制绕Zr轴的转动,约束方程为
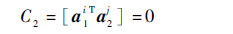 | (7) |
3) 弹体出管后,解除弹体和发射管之间的约束,即
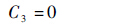 | (8) |
2.3.4 变拓扑约束识别方程 对于变拓扑系统,还需要建立系统识别方程[12],确定约束关系改变的时刻。识别方程通常可以是接触约束的运动学或动力学方程。
C1和C2的约束识别方程为
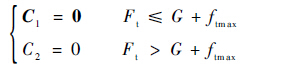 | (9) |
式中:G为弹体重力;ftmax为最大静摩擦力。
C2和C3的约束识别方程为
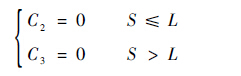 | (10) |
式中:S为弹体偏离静平衡位置的距离;L为发射管导向段长度。
2.4 多刚体动力学方程的数值求解 把系统的约束方程与式(2)联立可得
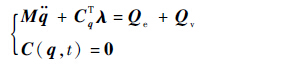 | (11) |
式(11)为指标3的微分代数方程组[13],求解此类方程的数值方法分为两大类:分离坐标法和增广法。为了便于求解系统中各铰处的约束反力,本文采用增广法。在数值积分中,通常对约束方程求时间的2阶导数为
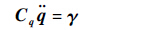 | (12) |
式中:
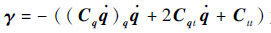
式(12)在数值积分过程中,由于截断误差影响,导致速度约束和位移约束违约。1972年,Baumgarte[14]提出了约束违约稳定法,利用反馈控制理论,通过在式(12)右端加入控制项
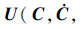
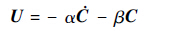 | (13) |
将式(11)第1行和式(12)写成矩阵形式,即
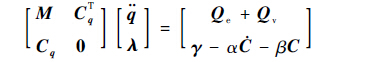 | (14) |
式中:α和β为稳定参数。
由于式(14)系数矩阵含有大量非零元素且为对称矩阵,为了提高方程组的求解效率,本文采用稀疏矩阵LU分解法进行计算,得到加速度响应后,采用4阶显式龙格库塔法积分,即可得到系统的动态速度和位移响应。同时,式(14)也求得了拉格朗日乘子λ,通过式(15)可得到对应于系统广义坐标的约束反力Qc,为发射车结构设计提供载荷输入。
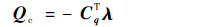 | (15) |
2.5 静平衡分析 发射系统动力学响应分析一般都是从系统平衡状态开始计算,因此在进行动态分析之前,还必须通过静平衡分析得到系统的平衡位置。静平衡分析通常有3种方法:动力安定法、迭代求解法以及最小势能法[15]。本文采用动力安定法,首先移除系统外力,在系统仅受重力的条件下进行时间积分。为了缩短平衡时间,利用附加阻尼动力安定法,通过在广义运动自由度上附加人工阻尼和改变系统弹簧-阻尼器的阻尼为临界阻尼,以达到快速平衡的目的。构建如下新的动力学方程[15]:
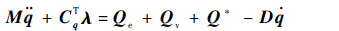 | (16) |
式中:D为人工阻尼系数矩阵;Q*为改变原系统阻尼为临界阻尼得到的系统广义外力。这样做并不会改变系统的平衡位置,但却可以减少静平衡分析的时间。
2.6 发射动力学分析 发射过程主要载荷为冷发射过程管内弹道载荷,简化为3个力后,可分别表示为
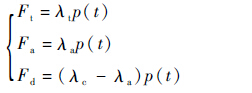 | (17) |
式中:p为管内弹道载荷;λt为弹体底面面积;λa为附加载荷分配因子;λc为与发射管结构相关的常数。
由式(17)可知,任意时刻底座受力与附加载荷的比值是常数,其大小表明了管内弹道载荷通过底座分散到地面和发射车的分配关系,定义底座载荷与附加载荷的比值(简称底座附加载荷比)Rda描述这种分配关系:
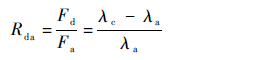 | (18) |
3 计算流程与程序实现 冷发射动力学计算流程如图 3所示。在静平衡分析部分,当系统各刚体广义位移变化量Δq<1 μm时,说明发射系统达到平衡位置。在动力学分析部分,当计算时间t大于设定的结束时间tend时,终止计算,并且输出需要的参数。
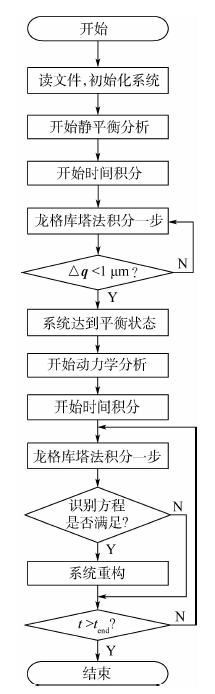 |
| 图 3 冷发射动力学计算流程 Fig. 3 Calculational flowchart of cold launch dynamics |
| 图选项 |
本文程序基于Fortran语言,利用定义派生数据类型的方法定义了体、铰和外力等数据类型,并通过链表将数据集成,这样变拓扑系统分析时可快速添加和删除约束。
4 动力学仿真分析 4.1 仿真模型验证 为了从时间和精度上验证本文方法的有效性,分别在ADAMS和ABAQUS中建立如图 1所示的仿真模型。以某型车载冷发射系统为例进行仿真对比,发射过程持续时间为2 s。本文和ADAMS的静平衡分析均采用动力安定法,持续时间为3 s;在ABAQUS静平衡分析中,重力采用线性加载,加载时间为3 s。本文和ADAMS仿真的积分时间间隔设置为0.001 s,仿真耗时分别为3 s和42 s,ABAQUS有限元仿真耗时约为23 h。本文的程序耗时分别是ADAMS的7.1%和ABAQUS的0.004%,显然,本文方法将为系统级方案设计大大节省仿真时间。
图 4为车架4个支腿载荷随时间变化曲线。由于实际发射过程在0.52 s左右已经结束,因此本文截取0.6 s的计算数据进行研究。可以看出,车架横向偏心引起的左侧两支腿和右侧两支腿的载荷偏差均不超过3%,本文选取左侧前后支腿载荷进行分析。除非特殊说明,下文中出现的后支腿均指左后支腿,而前支腿均指左前支腿。
 |
| 图 4 支腿载荷随时间变化曲线 Fig. 4 Variation curves of load of outrigger with time |
| 图选项 |
图 5为3种方法计算的后支腿载荷随时间变化曲线。可以看出,本文计算结果与ADAMS和ABAQUS 2种软件仿真结果的最大载荷偏差都小于4%。载荷偏差的主要原因为:①在ABAQUS中采用柔性体模型,而本文和ADAMS仿真模型均采用刚体假设;②本文和ADAMS仿真模型忽略了导向带的质量,而ABAQUS仿真模型中考虑了导向带的质量,由此引起后支腿静态载荷不同;③ADAMS中车架铰采用bushing力元模型实现式(3)中的约束关系。图 5说明了本文所建立的仿真模型是有效的,可用于分析系统的动态特性。
 |
| 图 5 后支腿载荷仿真结果对比 Fig. 5 Simulation results comparison of load of rear outrigger |
| 图选项 |
4.2 底座支腿载荷比动态特性 设任意时刻t的后支腿载荷为F1前支腿载荷为F3定义底座支腿载荷比分别为
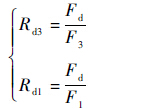 | (19) |
式中:Rd3为底座前支腿载荷比;Rd1为底座后支腿载荷比。
本文仿真模型计算所得底座支腿载荷比的动态特性如图 6所示。可以看出,初始时刻,底座所受载荷为零,前后支腿承受静平衡载荷,Rd1=Rd3=0。随着管内弹道载荷的增大,Rd1和Rd3逐渐增大并达到稳定。在稳定段,Rd1波动较小且为常数,Rd3基本保持常数但有较大波动。
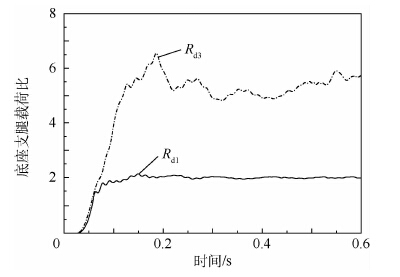 |
| 图 6 底座支腿载荷比动态特性 Fig. 6 Dynamic characteristics of load ratio of transmitting tube base-chassis outrigger |
| 图选项 |
底座前后支腿载荷比首次达到最大值的时刻分别用t3max和t1max表示,定义底座前后支腿载荷比均值为
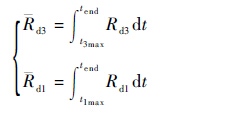 | (20) |
这样做是为了研究附加载荷通过车架分散传递到前后支腿上的载荷分配关系。
4.3 附加载荷分配因子对底座支腿载荷比均值的影响 对底座支腿载荷比的分析表明,当设计确定附加载荷分配因子后,就可以计算确定发射过程中底座支腿载荷比均值Rd3和Rd1,说明附加载荷分配因子λa与Rd3和Rd1有函数关系。
图 7为Rd3、Rd1和Rda随λa的变化规律。其中Rda随λa增大而减小,说明管内弹道载荷分配到发射车的载荷逐渐增大而通过底座传递到地面的载荷减小。当λa≥0.02时,Rd1与Rda的变化规律基本一致,与附加载荷分配因子成反比。Rd3与λa则成线性递减规律。以上2个规律表明了附加载荷分配因子与底座前后支腿载荷比均值之间的定量关系。当Rd3和Rd1随λa减小而逐渐增大到相等(λa=0.013时),底座前后支腿载荷比均值相等,前后支腿承受大致相等的力。在发射过程中,当λa<0.013时,前支腿分配载荷较大;当λa>0.013时,后支腿分配载荷较大。
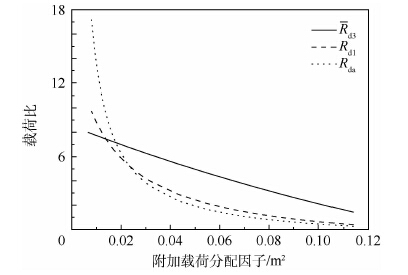 |
| 图 7 底座支腿载荷比均值随附加载荷分配因子的变化规律 Fig. 7 Variation of load ratio mean of transmitting tube base-chassis outrigger with adjunctive load distribution factor |
| 图选项 |
在设计发射管时,当根据发射管结构确定λa后,由式(18)计算得到Rda,即可确定管内弹道载荷通过底座分散到地面和发射车的分配关系。由图 7能够得到传递到发射车上的那部分附加载荷通过前后支腿分散传递到地面的分配关系,最终可以为优化管内弹道压力载荷的传递路径提供设计依据。
4.4 附加载荷分配因子对管口位移的影响 管口位移定义为发射管口中心偏离其静平衡位置的位移在管口平面上的投影。管口位移用u表示:
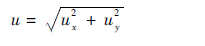 | (21) |
式中:uijx和uijy分别为u的X和Y向分量。
图 8为发射管口最大位移随λa变化曲线。随着λa的增大,管口最大位移先减小后增大,存在极小值,表明存在最佳附加载荷分配因子,能使发射系统对弹体初始扰动的影响最小。
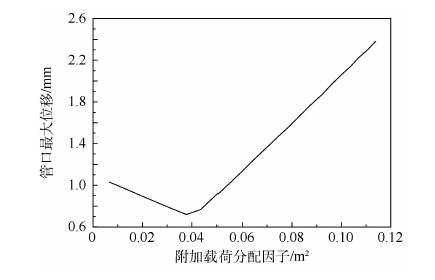 |
| 图 8 发射管口最大位移随附加载荷分配因子变化曲线 Fig. 8 Variation curve of maximum displacement of transmitting tube nozzle with adjunctive load distribution factor |
| 图选项 |
5 结 论 通过对车载冷发射系统的动力学研究,可以得出以下结论:
1) 9自由度快速仿真模型得到的支腿载荷与ADAMS和ABAQUS仿真结果对比,最大载荷偏差都小于4%,而仿真时间只有ADAMS软件的7.1%,可快速有效地分析车载冷发射系统的动态特性。
2) 底座支腿载荷比在发射过程中逐渐增大,并趋于稳定值。
3) 当附加载荷分配因子大于等于0.02时,底座后支腿载荷比均值与底座附加载荷比的变化规律基本一致,与附加载荷分配因子成反比。底座前支腿载荷比均值与附加载荷分配因子成线性递减规律。
4) 存在最佳附加载荷分配因子,能使发射系统对弹体初始扰动的影响最小。
参考文献
| [1] | 刘琥, 倪晓琛, 白静. 自适应底座悬垂弹射过程附加载荷分析[J].导弹与航天运载技术, 2012(3): 23–25.LIU H, NI X C, BAI J. Additional load study during the drape launch of adapting base[J].Missiles and Space Vehicles, 2012(3): 23–25.(in Chinese) |
| [2] | 郑利, 张萍, 贺卫东. 某型车载导弹垂直发射系统动力学仿真研究[J].导弹与航天运载技术, 2012(5): 22–26.ZHENG L, ZHANG P, HE W D. Simulation calculation and dynamic analysis of a vehicular missile launching system[J].Missiles and Space Vehicles, 2012(5): 22–26.(in Chinese) |
| [3] | 殷增振, 毕世华. 车载导弹多柔体发射动力学仿真研究[J].弹箭与制导学报, 2009, 29(2): 183–190.YIN Z Z, BI S H. Simulation study on multi-flexible-body launching dynamics for a vehicular missile launche[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(2): 183–190.(in Chinese) |
| [4] | 张涛, 刘相新, 郑斌. 基于模态综合法的发射过程刚柔耦合动力学研究[J].导弹与航天运载技术, 2009(6): 51–54.ZHANG T, LIU X X, ZHENG B. Rigid-flexible coupling dynamic analysis during launching based on component model synthesis[J].Missiles and Space Vehicles, 2009(6): 51–54.(in Chinese) |
| [5] | 冯勇, 马大为, 薛畅, 等. 多管火箭炮刚柔耦合多体发射动力学仿真研究[J].兵工学报, 2006, 27(3): 545–548.FENG Y, MA D W, XUE C, et al. Simulation dtudies of coupled rigid and flexible multi-body dynamics for multiple launch rocket system[J].Acta Armamentarii, 2006, 27(3): 545–548.(in Chinese) |
| [6] | 张志勇, 王毅, 南宫自军. 包含随机间隙的导弹发射系统动力学仿真[J].导弹与航天运载技术, 2013(2): 36–40.ZHANG Z Y, WANG Y, NANGONG Z J. Dynamic analysis of launching system with stochastic backlash[J].Missiles and Space Vehicles, 2013(2): 36–40.(in Chinese) |
| [7] | 刘浩, 李军. 高低压发射系统动力学特性仿真分析[J].弹箭与制导学报, 2009, 29(2): 199–202.LIU H, LI J. Simulation of dynamic characteristic of high-low pressure launching system[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(2): 199–202.(in Chinese) |
| [8] | 芮筱亭. 多体系统发射动力学及其应用[J].中国工程科学, 2011(10): 76–82.RUI X T. Launch dynamics of multibody system and its applications[J].Engineering Sciences, 2011(10): 76–82.(in Chinese) |
| [9] | 闵建平, 杨国来, 杨伯忠, 等. 自行火炮多体发射动力学仿真研究[J].兵工学报, 2001, 22(1): 34–36.MIN J P, YANG G L, YANG B Z, et al. Simulation and analysis of the launching dynamics of a self-propelled gun[J].Acta Armamentarii, 2001, 22(1): 34–36.(in Chinese) |
| [10] | 洛刚. 车载类火炮发射动力学仿真计算研究[J].装备指挥技术学院学报, 2002, 13(6): 47–50.LUO G. Study on dynamic simulation calculation for launching of vehicle-gun[J].Journal of the Academy of Equipment Command & Technology, 2002, 13(6): 47–50.(in Chinese) |
| [11] | 张雄, 王天舒. 计算动力学[M].北京: 清华大学出版社, 2007.ZHANG X, WANG T S. Computational dynamics[M].Beijing: Tsinghua University Press, 2007.(in Chinese) |
| [12] | 张永, 吴德隆, 黄铁球, 等. 机动导弹系统变拓扑多体系统动力学建模方法研究[J].导弹与航天运载技术, 1999(1): 34–38.ZHANG Y, WU D L, HUANG T Q, et al. Study on dynamic modeling method of multibody systems with changing topologies for mobile missile system[J].Missiles and Space Vehicles, 1999(1): 34–38.(in Chinese) |
| [13] | 刘延柱, 潘振宽, 戈新生. 多体系统动力学[M].2版.北京: 高等教育出版社, 2014.LIU Y Z, PAN Z K, GE X S. Dynamics of multibody systems[M].Dynamics of multibody systems[M].2nd ed.Beijing: Higher Education Publisher, 2014.(in Chinese) |
| [14] | BAUMGARTE J. Stabilization of constraints and integrals of motion in dynamical systems[J].Computer Methods in Applied Mechanics and Engineering, 1972, 1(1): 1–16.DOI:10.1016/0045-7825(72)90018-7 |
| [15] | 陆佑方. 柔性多体系统动力学[M].北京: 高等教育出版社, 1996.LU Y F. Dynamics of flexible multibody systems[M].Beijing: Higher Education Publisher, 1996.(in Chinese) |
