在综合模块化航电软件中,传统的位于分布式节点的应用以分区应用方式集成到综合模块化计算平台上[2]。针对于此,ARINC 653规范规定系统采用分区内调度和分区间调度双层调度机制。分区内调度一般采用传统嵌入式的实时调度策略,由分区应用的开发者决定;分区之间按照静态主时间框架进行确定性的周期调度,在系统集成层次确定。航电系统作为一类强实时系统,需要研究双层调度机制下的2个方面问题:①给定主时间框架分析系统的可调度性;②生成主时间框架对系统进行调度。关于ARINC 653系统的可调度性问题已经存在一些研究结果[3-5]。本文研究ARINC 653实时操作系统背景下可调度性分析的对立问题:给定若干分区应用,如何生成主时间框架在系统层进行分区间调度。
从分区应用生成主时间框架面临如何从分区应用设计分区以及进一步分区间调度这2个阶段问题。何锋等[6]以分区任务执行系数和轮转调度周期作为参数考察分区能力和系统集成问题,给出了关键参数的设计方法。文献[7]推导出了分区内任务集合在单调速率[8](Rate Monotonic,RM)调度下的分区利用率最小上界。
Shin和Lee[9]提出了分区的周期资源模型,在该模型中,分区参数包含分区周期和分区执行时间。类似于周期资源模型,Lee等[10]给出了分区周期和分区利用率满足的关系。借助将其他分区视作当前分区的堵塞,文献[11]同样给出了分区周期和利用率的可行域,并提出了系统低耗能优化算法。Lipari和Bini[12]对分区内部采用固定优先级(Fixed Priority,FP)调度的分区应用,从分区内任务集合导出了分区的有界延迟模型[13]参数。对于文献[12]中的问题,文献[14]利用最坏情况分析方法导出了分区参数,该方法较文献[12]中的算法较大幅度提升了运算速度,但仅能给出近似解。
不同于以上介绍的关于分区内任务对分区能力需求的研究,Mok和Austin[15]给出了有界延迟分区之间集成的相关结论并且考虑了原子时间片的问题。文献[15]属于分区间集成问题的工作,但是没有涉及分区间调度生成静态主时间窗口框架的问题。
在已有分区参数选择工作的基础上,本文的工作在于考虑分区之间影响的因素下将分区的有界延迟模型参数转化为分区周期和分区执行时间参数,提出了基于这2个参数生成主时间框架的算法,从而给出了从若干分区应用生成主时间框架的完整流程。
1 系统模型 1.1 ARINC 653系统调度模型 ARINC 653分区实时操作系统规范采用层次调度机制,分为分区间调度和分区内调度。其中分区内调度由分区应用的设计者指定,分区之间按照主时间框架周期地静态调度。主时间窗口框架详细规定了每个分区拥有的时间窗口的起始时间和持续时间。图 1所示的即是一个主时间窗口框架[1],该图显示了一个共存在4个分区的计算模块,主时间框架总长度为200 ms。在200 ms的主时间框架内,P1分区获得了2个时间窗口,P2分区获得了2个时间窗口,P3分区共获得了4个时间窗口,P4分区仅有1个时间窗口。
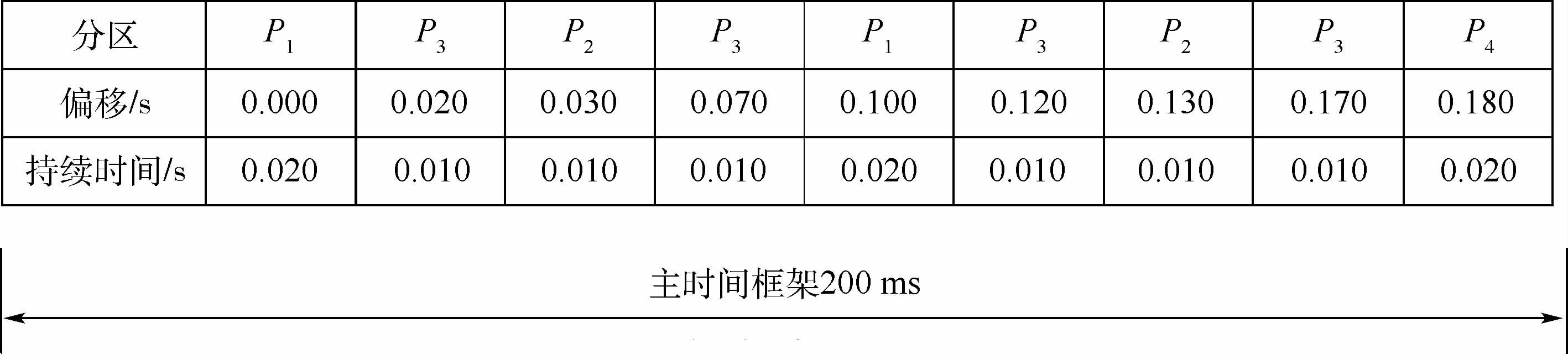 |
| 图 1 主时间窗口框架中的分区窗口[1] Fig. 1 Partition windows within a major time frame[1] |
| 图选项 |
1.2 相关概念定义 ARINC 653 规范限定的适应对象是单核处理器,所以本文下面的探讨范围适用于多个分区在单核处理器上集成的情况。对于多核处理器,在限制应用不可核间迁移情况下,可将其视作单核情况[16]。
一个计算任务表征为一个三元组〈C,D,T〉,其中:C表示周期任务在一个周期内的最坏情况下执行时间(Worst Case Execute Time,WCET),D表示相对截止时间,如果周期任务在就绪后D时间内没有执行结束意味着超时,T表示周期任务的周期。
一个应用程序Γ是一个计算任务集合{τ1,τ2,…,τn},其中:τi为三元组模型〈C,D,T〉描述的任务,该集合内的计算任务被加载于某一ARINC 653分区上。一个ARINC 653资源分区Φ是一个二元组〈W,P〉[13]。其中:W表示一个n个时间区间(窗口)集合{(s1,e1),(s2,e2),…,(sn,en)},P表示分区的周期,并且满足:0≤s1 <e1<s2<e2<…<sn<en≤P。分区在时间区间(si,ei)内获得资源用于执行分区内任务(ei和si为第i个时间区间的起点和终点),因此对于一个周期分区,其获得资源的时间区间为(si+j·P,ei+j·P),1≤i≤n,j为自然数。
定义1?分区利用率[13]
分区Φ的分区利用率为
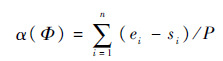 | (1) |
定义2?匀速等效执行[13]
假设分区Φ所在的处理器的执行速度是r,它的分区利用率为α,则它的匀速等效执行是指以独占非打断方式在执行速度α·r的处理器上的执行。
定义3?服务时间函数[13]
服务时间函数S(t)是0~t时间间隔内分区获得的计算时间总和。
定义4?分区延迟[15]
分区延迟λ是满足不等式(2)的Δ最小值。
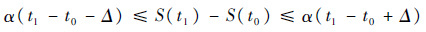 | (2) |
定义5?有界延迟分区[13, 15]
有界延迟分区Φ是一个二元组〈α,λ〉。
对于周期为P、分区利用率为α的分区容易得出分区执行时间O=P·α,最坏情况下分区执行窗口延迟λmax=2P·(1-α)[12]。
定义6?Harmonic集合
一个整数集合是Harmonic集合当且仅当集合中的任意2个元素e1和e2满足式(3)约束关系:
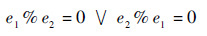 | (3) |
式中:e1%e2表示e1对e2进行取余运算。
在综合模块化航电软件系统中,被调度元素的周期通常被建议配置成具有Harmonic关系[4, 10, 17],以减少分析复杂度。
2 分区参数设计 本节将从分区内的计算任务集合导出分区参数,保证分区内实时任务的可调度性。分区参数的设计过程如图 2所示,首先利用可调度分析从分区内任务集合参数导出分区有界延迟模型参数:分区利用率α、最大延迟λ;然后将参数转化为可实际用于分区配置的分区周期P、周期内执行时间参数O,用于分区间调度。需要指出的是,2.1节中从分区任务集合导出参数 <α,λ >的方法是已有工作[12-13],本文仍将其简要归纳、扩展讨论从而完整给出基于若干分区任务集合设计系统主时间框架的全部过程。本文基于已有工作,在2.2节分析讨论了当分区周期满足Harmonic关系、分区遵循严格周期调度情况下,模型参数转化的问题。
 |
| 图 2 分区参数设计过程 Fig. 2 Process of partition parameter design |
| 图选项 |
2.1 有界延迟模型参数的可行域 定理1?[13] 给定一个任务集合Γ={τ1,τ2,…,τn}和一个有界延迟分区Φ=(α,λn),设Sn是任务集合Γ在有界延迟分区Φ的等价匀速执行处理器上的一个调度,Sp是Γ在有界延迟分区Φ=(α,λn)上和Sn的调度次序和资源分配量都相同的一个调度。设λ是保证Sn中所有任务都能够在截止期前λ时间完成计算时取得的最大值,那么Sp可调度当且仅当λ >λn。
该定理指出了有界延迟分区参数的可调度条件,以此可以推导出相应的参数计算公式:
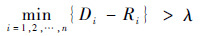 | (4) |
式中:Di为任务τi的截止期;Ri为响应时间。
对于采用最早截止时间优先(Earliest Deadline First,EDF)调度的分区,计算某一任务的最大响应时间比较复杂[18]。文献[13]指出可以采用将所有计算任务的截止期提前λ后验证可调度性的方法确定延迟分区的最大延迟参数是否能够取值为λ。例如,借助文献[19]中提出的快速收敛分算法(Quick convergence Processor-demans Analysis,QPA),可以二分搜索得出最大允许的延迟λmax。
对于采用FP调度的分区,Lipari和Bini[12]给出了分区延迟的计算公式(5)。给定分区利用率,借助式(5)可计算出能够保证分区内任务集合可调度时分区服务器允许的最大延迟。
 | (5) |
例1 设分区内的计算任务参数如表 1所示,分区内部采用RM调度算法调度。图 3显示出当分区利用率取不同值时,各个任务可调度时允许的最大分区延迟。例如,当分区利用率为0.6时,任务T1具有最高的优先级,任务T3具有最低的优先级。按照优先级从高至低顺序,对于任务T1,首先将D1=6代入计算得出集合P0(6)={6},进一步可以根据λi计算公式计算出分区允许延迟时间λ1 = 4.33;类似地,对于任务T2和任务T3,分别可以计算出其允许延迟时间λ2=5,λ3=5。最终,根据计算公式(5)可以计算该分区服务器在分区利用率为0.6时允许的最大延迟:
 |
表 1 任务参数 Table 1 Parameters of tasks
| 任务编号 | 最坏执行时间/ms | 截止期/ms | 周期/ms |
| T1 | 1 | 6 | 6 |
| T2 | 1 | 10 | 10 |
| T3 | 3 | 20 | 20 |
表选项
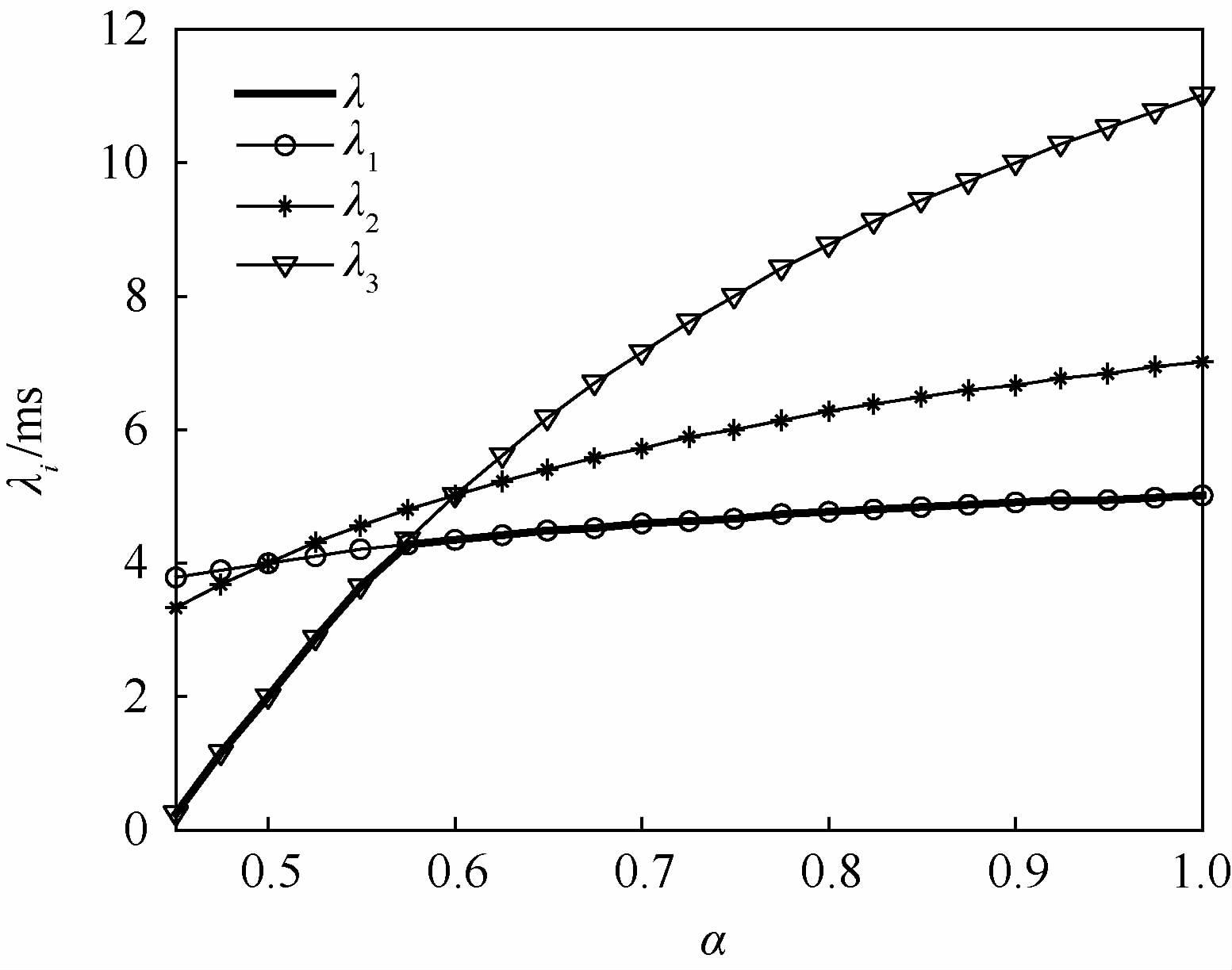 |
| 图 3 不同分区利用率下允许的最大延迟 Fig. 3 Maximum feasible delay with differentpartition utilizations |
| 图选项 |
图 3显示出当选择分区利用率α为自变量时,在能够保证分区内任务集合可调度条件下,分区允许的最大延迟可以表征为分区利用率α的函数[20],即λmax=f(α)。因此,有界延迟分区参数可行域可以表征为区域集合{(α,λ)|bl≤α≤br,0≤λ≤f(α)},其中br、bl表征分区利用率上下界。下面的推论说明函数λmax=f(α)具有单调递增性。
推论1 设λmax=f(α)是分区允许的最大延迟关于分区利用率α的函数,则该函数在可行区间内单调递增。
证明 设原分区利用率为α0,现将分区利用率提升至α1>α0,其匀速等效执行速度增大α1/α0倍。考察分区的匀速等效执行系统。
假设分区内采用EDF调度,所有任务周期的最小公倍数为L,考察[0,L]区间内各个任务的各次周期执行的结束时刻组成的有穷集合{f1,f2,…,fi,…,fn}。对于第一个时刻f1,其对应某个任务τi的第一次执行结束,执行区间为[s1,f1],且Ci=f1-s1,其中s1是执行开始时间。当处理器速度增大α1/α0倍时,在EDF调度下,因为所有任务的周期和截止期不变,所以任务τi在[s1,f1]内仍是最高优先级任务,容易得出其执行结束时刻
f ′1=s1+Ci/(α1/α0) <f1=s1+Ci
假设对于前k个结束时刻结束执行的任务,当处理器速度变大α1/α0倍时响应时间缩短,现考察第k+1个执行结束时刻。
设fk+1对应任务τx的第j次执行,设其释放至截止期区间(rx,j,dx,j]内的执行时间区间为
[s1,e1]∪[s2,e2]∪…∪[sn,en]
并且满足:
| ${{C}_{x}}=\sum\limits_{l=1}^{n}{{{e}_{l}}-{{s}_{l}}}$ |
其中:Cx为τx的执行时间,出现多个执行区间是因为可能被更高优先级任务抢占。处理器速度增大α1/α0倍后,因为所有任务周期的周期和截止期不变,所以任务τx在原执行时间区间[s1,e1]∪[s2,e2]∪…∪[sn,en]内仍是最高优先级任务。此时,在en时刻,处理器至少已经分配了Cx时间用于τx的第j次执行,由于Cx/(α1/α0) <Cx,所以τx的第j次执行在en时刻前已经结束,即响应时间缩短。结论对于第k+1个时刻结束执行的任务仍然成立。
由于所有任务的响应时间缩短,由定理1,可以得出保证分区内部可调度的最大分区延迟增大。采用FP调度策略的系统类似可证。
该性质的证明过程表明,在单核情况下,当任务集合被限制在分区服务器提供的时间片内执行时,增大分区服务器的分区利用率有助于缩短分区内计算任务的响应时间,进而能够容许更大的分区服务器延迟。
2.2 参数变换与参数选择 有界延迟模型参数能够描述分区内任务对分区的能力需求,但无法用于分区间调度。本节基于分析参数的可行域性质,将有界延迟模型参数〈α,λ〉转化为分区服务器的调度参数〈O,P〉。
2.2.1 固定偏移执行的分区服务器 引理1 设分区服务器集合的调度参数为{〈O1,P1〉,〈O2,P2〉,…,〈On,Pn〉},其中周期参数{P1≤P2≤…≤Pn}满足Harmonic关系。若采用RM调度算法进行分区间调度,每个分区将固定偏移执行,分区窗口具有周期性。
证明 由于不同的分区周期满足Harmonic关系,Pi%Pj=0∨ Pj%Pi = 0,当Pi≤Pj时,易得Pj%Pi = 0。即第i+1个分区的周期是前i个分区周期的公倍数。
根据RM调度算法,周期更小的分区有更高的优先级。第1个分区被调度时,处理器空闲,容易得知其将固定偏移执行,分区窗口具有周期性。
假设前i个分区的执行时间具有周期性。对于第i+1个分区,由于Pi+1是前i个分区周期的公倍数,且前i个分区周期执行,所以它也将在前i个分区执行后形成的空闲时间区间内被固定偏移执行,分区窗口具有周期性执行特征。所以,前i+1个分区组合成以Pi+1为周期的调度。根据数学归纳法,易得所有分区的将固定偏移执行,分区窗口具有周期性。
由于每个分区将被固定偏移执行,分区窗口具有周期性,记S(t)为分区资源服务时间函数,由该引理容易得出如下关系:
| $S\left( t+kP \right)=S\left( t \right)+kO$ |
其中:k∈N。
2.2.2 分区周期的可行区间 文献[12]指出,若干周期分区服务器被调度时,因调度引起的延迟最大为λserver=2P(1-α)。实际上,对于严格周期执行的分区服务器,由于分区间调度引起的延迟可以通过更精确的分析限制为λserver=P(1-α)。通过更小的分区延迟,分区服务器可以在更小的分区利用率情况下使得分区内的任务可调度。该结论优化自文献[12],因其对于后续的分区周期参数选择有重要作用,将其作为定理2列出,并给出证明。
定理2 分区周期满足Harmonic关系的若干分区在采用RM调度算法调度时,分区由于调度引起的延迟λserver≤P(1-α)。
证明 假设某个分区在t时刻获得的执行时间为S(t),当分区在某种调度下的分布窗口使得区间[t0,t1](t1>t0)内获得的资源S(t1)-S(t0)最少,不等式α(t1-t0-λ)≤S(t1)-S(t0)两侧取等号时,资源分区延迟λ取最大值,即
| $\alpha ({{t}_{1}}-{{t}_{0}}-\lambda )=S({{t}_{1}})-S({{t}_{0}})$ |
设t1-t0=d+kP,d∈N∧d∈[0,P),k∈N,由S(t+kP)=S(t)+kO得
 | (6) |
假设λ>P(1-α)成立,则
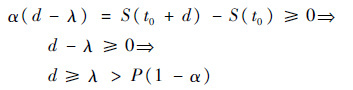 | (7) |
即d>P(1-α)。
又由P>d >P(1-α),S(t+P)=Pα+S(t),利用鸽巢原理得
 | (8) |
进一步联合式(6)的结论α(d-λ)=S(t0+d)-S(t0)容易得出
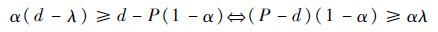 | (9) |
由假设λ>P(1-α),从式(9)容易得出
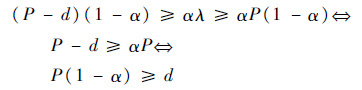 | (10) |
式(10)结论P(1-α)≥d与式(7)已推出的结论d>P(1-α)矛盾,所以假设错误,即分区延迟参数λ不可能超过P(1-α)。
对于优先级最高的分区,当t1=P,t0=Pα时,α(P-Pα-λ)=S(P)-S(Pα)=Pα-Pα=0。此时分区延迟参数λ取得最大值P(1-α)。
该定理指出在分区服务器被固定偏移执行、分区窗口具有周期性时,分区服务器能够保证提供的资源延迟λserver不超过P(1-α)。
由推论1,当分区的利用率为α时,能够保证分区内任务集合可调度的分区服务器最大延迟为λmax=f(α)。为使分区服务器满足分区内任务集合的可调度要求,应保证分区服务器的供给能力不小于需求能力,即
λserver≤P(1-α)≤f(α)=λmax
变换可得
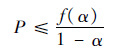 | (11) |
式(11)给出了分区周期P的上界。推论1指出λmax=f(α)具有单调递增性,1/(1-α)在(0,1)区间内也单调递增,所以式(11)右侧在区间(0,1)内单调递增。因此,分区周期的最大值与分区的利用率最大值相关,当分区利用率取最大值αmax时,分区周期取得最大值Pmax。
对于存在多个分区的系统,单个分区利用率的上界是能够保证其他分区内的任务可调度,因此,对于某个分区i,它的利用率取值范围至多为
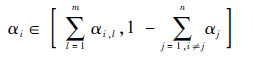 | (12) |
式中:m为分区i内的任务个数;αi,l为分区内任务l的利用率;n为系统内分区个数;αj为分区j的分区利用率。此时,分区周期最大值Pmax可由式(11)和式(12)计算:
 |
分区周期与分区的切换次数正相关,在文献[21]中,通过增大分区利用率的方式获得更大的分区周期参数,以实现减少分区切换次数的目的。将该结论应用于本文时,可以限制分区周期不小于某一最小值Pmin,从而限制分区的切换次数。此时可以确定单个分区周期的可能取值区间至多为[Pmin,Pmax]。
2.2.3 分区调度参数选择 已知分区周期P,若分区执行时间O能够使得分区内的任务集合可调度,则对于相同的周期和执行时间O′>O,同样能够使得任务集合可调度。这一性质使得在分区周期固定时,可以利用二分搜索算法搜索出使得分区内部任务集合可调度的最小分区执行时间参数O∈[0,P]。借助式(12)给出的分区利用率约束,可以进一步缩小参数O的搜索范围。
在周期资源模型参数选择时,可依据不同的系统设计目标进行相应的周期参数、执行时间参数选择。如果选择分区利用率之和最小使得系统具有更强的可扩展能力为优化目标,可通过遍历方法搜索出最优的分区周期和执行时间参数,分区参数选择伪代码如下:
Pseudocode 1 Parameter Selection
1:O=[]
2:P=[]//O and P are target parameters
3:Umin=+∞
4:for each v∈Ps do
5:?U=0
6:? for each Pi∈v do
7:??Ol=Omin,Or=Omax
8:??while Ol<Or do
9:??? Omid=(Ol+Or)/2
10:??? if<Omid,Pi>is schedulable then
11:????Or=Omid
12:??? else
13:????Ol=Omid
14:??? end if
15:???end while
16:??U=U+Ol/Pi
17:? end for
18:?if U<Umin∧U<1 then
19:?? update (O,P,Umin)
20:? end if
21:end for
根据2.2.2 节得出的分区周期取值范围,利用搜索算法可以得出所有分区周期满足Harmonic关系的分区周期向量集合。记所有可能的Harmonic分区向量组成的集合(代码第4行)为
Ps={〈P1,P2,…,Pi,…,Pn〉Pi%Pj=0∨Pj%Pi=0}
算法第4~21行的循环用于搜索所有可能的分区周期取值,其中第6~17行的代码对一个分区进行二分搜索最小执行时间。第18~20行更新搜索出的最新结果。
对于某个分区服务器的周期P,需二分搜索一次最小执行时间,对应的时间复杂度为O(Plb P)·O(SchTest),其中O(SchTest)为用于检测分区是否可调度的某种算法的复杂度(如QPA[19])。对于所有可能的周期取值,共需要搜索Ps次,因此对于n个分区的系统,该算法的最终复杂度为:O(nPsPlbP)·O(SchTest)。
3 主时间窗口框架设计 确定每个分区的周期和执行时间后,分区间调度问题可以转化为传统实时任务调度问题。引理1表明,当分区周期满足Harmonic关系且采用RM调度算法进行分区间调度时,每个分区将被固定偏移执行,分区窗口具有严格周期性。为了减少分区切换次数,本文提出最少窗口数目匹配-最佳匹配(Minimum number of windows Fit-Best Fit,MFBF)算法分配调度时间片。
MFBF算法按照分区优先级顺序进行分区调度,首先根据RM算法指定的分区优先级对所有分区进行由高到低排序。其中优先级相同的分区按照执行时间由小到大排列优先级,对于此时优先级仍相同的分区,按照出现顺序赋值优先级。
对于第i个分区,在一个分区周期内,分区所需要的执行时间是O,分区所能获得的空闲处理器时间是一个区间或者多个区间的并集。现需要将O分配在这若干个区间上。如果不存在一个区间能够满足执行时间O,依次从这多个区间中按照区间长度由大到小顺序依次将O分配在这多个区间中(对应伪代码9~15行)。在选择最后一个的区间时,选择能够满足剩余执行时间且区间长度最小的区间(对应伪代码16~18行),即最匹配的区间。MFBF匹配算法伪代码如下所示:
Pseudocode 2 MFBF
1: Sp={Sp1,Sp2,…,Spn}
//partition set,priority desc
2:? for each i=1: n do
3:?Pi=period of Spi
4: Oi=capacity of Spi
??//scheduling parameters of partition Spi
5: Sf={[l1,r1],[l2,r2],….[lm,rm]}
6:?L=[r1+1-l1,r2+1-l2,…,rm+1-lm]
??//free intervals in [0,Pi)
7:?sort Sf,L as length of intervals desc
8:?index=1
9:?while Oi>L (index) do
10:?? Oi=Oi-L (index)
11:?? allocate Sf (index) to partition Spi
12:?? delete L (index) from L
13:?? delete Sf (index) from Sf
14:?? index=index+1
15: ?end while
16: ?[l,r]=available interval with minimum length in Sf
17: ?allocate[r+1-Oi,r] to partition Spi
18: ?delete[r+1-Oi,r] from Sf
19: end for
因为分配时间片时按照优先级由高到低进行,所以该算法能够保证分区周期执行。除此以外,由于每次分配时间片时使用尽可能少的分区窗口完成一次分区服务,该算法能在一定程度上减少分区切换次数。下文4.2节中的实验结果表明,算法能够减少分区的切换次数,提升系统效率。
对于一组周期升序排列且满足Harmonic关系的周期资源模型分区{〈O1,P1〉,〈O2,P2〉,…,〈On,Pn〉},可利用MFBF调度算法进行调度形成一个以Pn为周期长度的离线调度结果。该离线调度结果可用于生成静态的主时间框架。
离线调度结果保存了处理器的时间片分配信息。一个分区获得的一个连续时间片对应该分区服务器的一个时间窗口。遍历长度为Pn的时间片分配方案,可以得出每个时间窗口所属的分区、开始时间和持续时间信息。这些信息可以组成类似于图 1所示的ARINC 653分区实时系统的主时间框架。进一步地,可将主时间窗口框架按照规定格式记录在XML文件中[1],用于平台部署,最终完成ARINC 653分区实时系统主时间窗口配置的全部过程。
4 案例与实验分析 4.1 案例分析 本节通过一个案例分析演示从分区应用集合出发生成系统的主时间框架的完整过程。设系统中的分区以及分区内的任务参数如表 2所示。任务的调度参数表示为〈C,D,T〉三元组,且每个分区内部按照RM调度算法调度。
表 2 系统中的分区及分区内任务参数 Table 2 Partitions within system and task parameterswithin partitions
| ms | ||
| 分区P1中任务 〈C,D,T〉 | 分区P2中任务 〈C,D,T〉 | 分区P3中任务 〈C,D,T〉 |
| 〈2,20,20〉 | 〈4,40,40〉 | 〈5,40,40〉 |
| 〈4,25,25〉 | 〈4,50,50〉 | 〈6,100,100〉 |
| 〈1,50,50〉 | 〈5,200,200〉 | |
表选项
首先,根据式(12),可以计算得出分区P1的利用率最小值为分区内任务利用率之和αmin= 2/20+4/25+1/50 = 0.28,分区P2和P3分区利用率最小值为0.18和0.21。为保证分区P2和P3可调度,分区P1的分区利用率至多为1-0.18-0.21=0.61。同理,最终可计算得3个分区的利用率取值范围分别是[0.28,0.61],[0.18,0.51],[0.21,0.54]。
对于每个分区,当分区利用率取最大值时,分区内任务集合可以承受的最大分区服务器延迟λmax=f(αmax)。类似于例1计算过程,当分区利用率取最大值[0.61,0.51,0.54]时,可计算得出分区内任务集合能够承受的最大分区服务器延迟:[11.89,26.47,30.74] ms。进一步将分区利用率取值上界代入式(11)得
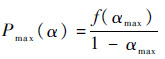 |
计算得出的分区周期的上界是[30, 54, 66] ms。如果为控制分区切换次数,依次选择3个分区的周期不小于[10, 10, 20] ms,此时可以得出3个分区服务器的周期取值范围I=[[10,34],[10, 54],[20, 66]]。
在3个分区允许的周期范围内,存在[10, 10, 20]~[30, 30, 60]共113个满足Harmonic关系的周期选择方案。当选择系统利用率最小作为优化目标时,利用2.2.3 节中搜索算法且结果保留1位小数精度,最终得出的分区执行时间-分区周期参数为:〈4.2,10〉,〈2.5,10〉和〈5.0,20〉,此时对应的系统利用率为0.92。将分区调度参数代入第3节给出的MFBF调度算法后,得出如图 4所示的主周期长度为20 ms的分区调度结果。
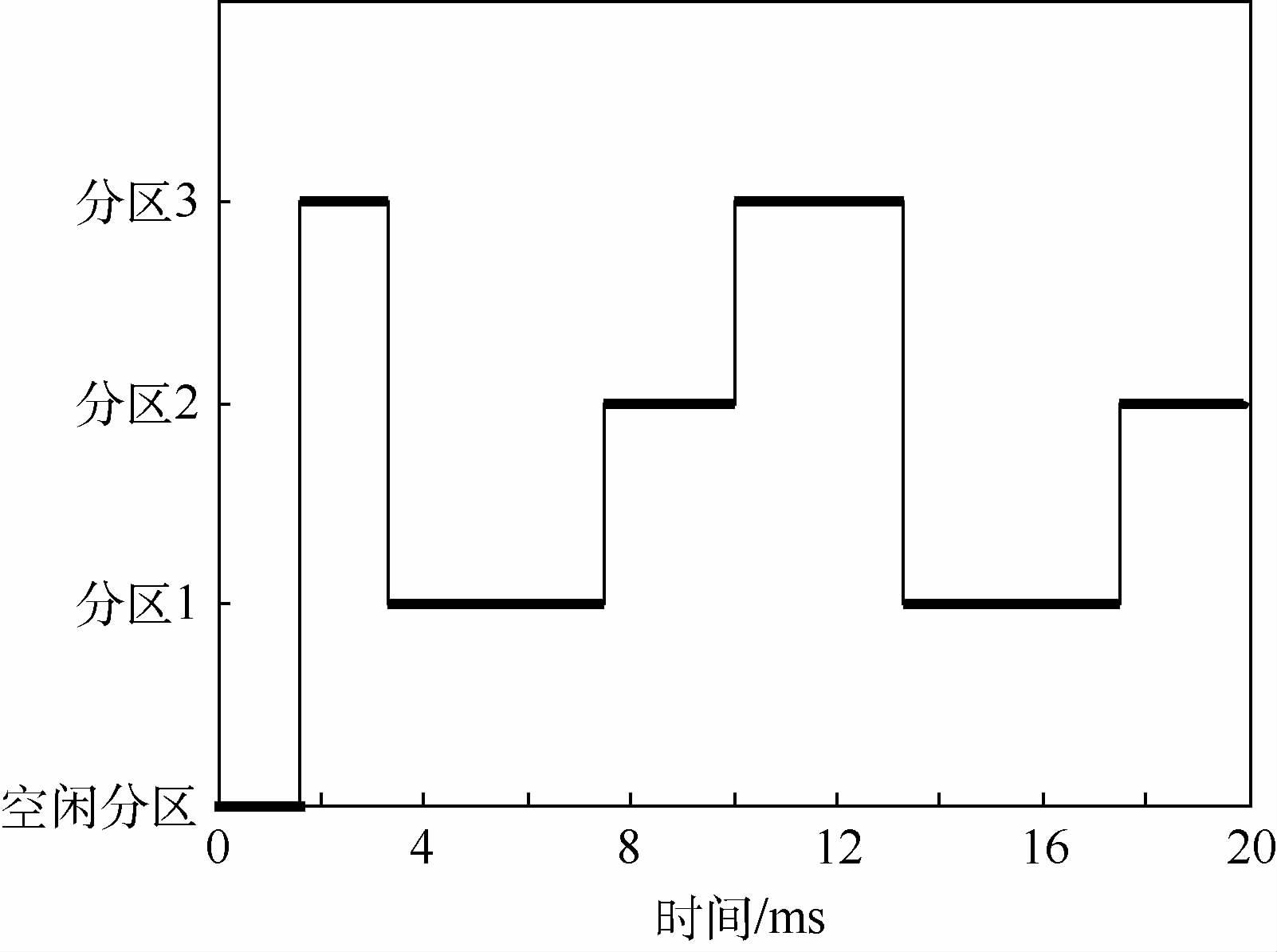 |
| 图 4 案例系统的分区调度结果 Fig. 4 Scheduling result of partitions within example system |
| 图选项 |
将调度结果统一偏移调度开始的空闲分区后得出主时间框架如表 3所示。
表 3 案例系统的主时间框架 Table 3 Major time frame of example system
| 窗口id | 窗口起始时间/ms | 窗口持续时间/ms |
| 3.1 | 0 | 1.7 |
| 1.1 | 1.7 | 4.2 |
| 2.1 | 5.9 | 2.5 |
| 3.2 | 8.4 | 3.3 |
| 1.2 | 11.7 | 4.2 |
| 2.2 | 15.9 | 2.5 |
表选项
4.2 窗口微调算法的性能试验 为了对第3节中提出的分区窗口匹配算法MFBF进行实验测试,按照UUFast[22]算法随机产生分区的利用率,并随机选择分区周期进行实验。为避免分区利用率过小导致在分区最小执行时间为1(原子时间)时周期特别大的情况,对于分区利用率小于0.005的分区重新随机生成分区利用率。
由于分区的周期需要满足Harmonic关系,实验采用如下算法随机生成一组满足Harmonic关系的分区周期。
1) 从[2, 10] 区间内的正整数中,等概率随机选择一个整数B作为基数。
2) 对于每个待生成的分区周期,首先从[10,10 000]区间内的正整数中,等概率随机选择一个正整数P作为分区周期。
3) 按照文献[23]中Harmonic关系调整计算公式进行分区周期Harmonic调整,作为最后的分区周期,同样记作P。计算公式为
 | (13) |
式中:等号右侧的B和P参数分别为步骤1)和步骤2)随机生成的基数与周期。
4) 将调整后的周期P乘以UUFast算法生成的该分区的分区利用率能够生成该分区的执行时间O,如果O小于1(原子时间),即出现了最小执行时间不足1的情况,转步骤2),重新随机生成周期。
由于UUFast算法能够保证分区的利用率等概率均匀分布,上述的分区周期生成算法用到的基数B和初始周期P也都是等概率随机选择生成,所以经过式(13)进行Harmonic关系调整后最终的分区执行时间-周期参数能够保持一定的随机特征。
产生的执行时间-周期参数作为MFBF算法输入,将其调度结果与RM算法调度结果进行比较。为考察算法在不同系统负载情况下的运行效果,实验测试了分区数为3、6和9,分区利用率之和为0.3~1.0之间的系统。在每次实验中,对于给定的分区数目和系统所有分区利用率之和,随机生成调度参数,实验100次取平均结果。MFBF算法的分区切换次数优化效果如图 5所示,其中横坐标U为所有分区利用率之和,纵坐标R为MFBF算法的分区切换次数与RM算法分区切换次数的比值。如图 5中所示,MFBF算法在系统不同负载的情况下均能减少分区切换次数,提升系统效率。
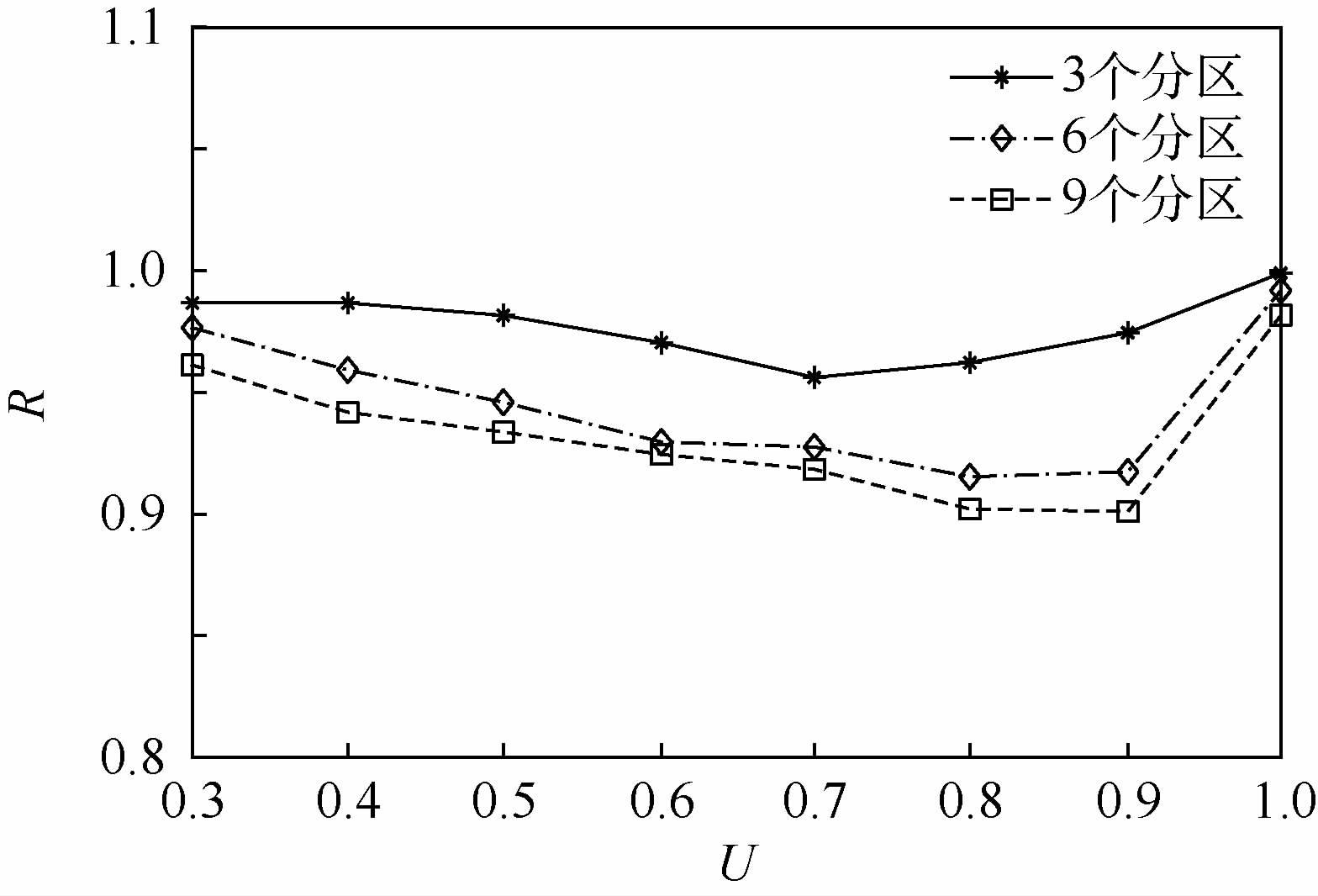 |
| 图 5 MFBF算法和RM算法的分区切换次数比率 Fig. 5 Ratio of partition switch times between MFBFalgorithm and RM algorithm |
| 图选项 |
5 结 论 1) 本文中描述的主时间框架设计流程能够从分区任务集合的调度参数出发生成系统主时间框架。在最终生成的主时间框架中,各分区服务器周期执行,分区的周期满足Harmonic关系。分区服务器提供的计算时间资源能够保证分区内的任务集合可调度。
2) MFBF算法的调度结果能够使得分区服务器周期执行。算法通过对分区时间窗口进行优化配置减少时间窗口切换次数,实验结果表明,MFBF算法能够在不同的系统负载情况下减少分区时间窗口切换次数,提升系统效率。
参考文献
| [1] | Airlines Electronic Engineering Committee.ARINC specification, avionics application software standard interface:ARINC 653-2[S].Annapolis,MA:Aeronautical Radio,Inc.,2006:1-205. |
| [2] | 褚文奎, 张凤鸣, 樊晓光. 综合模块化航空电子系统软件体系结构综述[J].航空学报, 2009, 30(10): 1912–1917.CHU W K, ZHANG F M, FAN X G. Overview on software architecture of integrated modular avionic systems[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1912–1917.(in Chinese) |
| [3] | 高晓光, 薛亚勇, 温增葵. IMA双层调度算法中的任务可调度性分析方法[J].航空学报, 2015, 36(2): 585–595.GAO X G, XUE Y Y, WEN Z K. Task schedulability analyzing method of two-level hierarchical scheduling algorithm in integrated modular avionics[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 585–595.(in Chinese) |
| [4] | ARVIND E,INSUP L,OLEG S,et al.A compositional framework for avionics (ARINC-653) systems:MS-CIS-09-04[R].Philadelphia:Department of Computer & Information Science,University of Pennsylvania,2009.http://cn.bing.com/academic/profile?id=369313234&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | CHANG Y,DAVIS R,WELLINGS A.Schedulability analysis for a real-time multiprocessor system based on service contracts and resource partitioning:YCS-432[R].York:Department of Computer Science,University of York,2008. |
| [6] | 何锋, 宋丽茹, 熊华钢. 航空电子双层任务分区调度设计[J].北京航空航天大学学报, 2008, 34(11): 1364–1368.HE F, SONG L R, XIONG H G. Two-level task partition scheduling design in integrated modular avionics[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(11): 1364–1368.(in Chinese) |
| [7] | 李昕颖, 顾健, 何锋, 等. 硬实时系统在强分区约束下的双层分区调度[J].计算机学报, 2010, 33(6): 1032–1039.LI X Y, GU J, HE F, et al. Two-level partition scheduling in hard real time system under strong partition constraints[J].Chinese Journal of Computers, 2010, 33(6): 1032–1039.DOI:10.3724/SP.J.1016.2010.01032(in Chinese) |
| [8] | LIU C L, LAYLAND J W. Scheduling algorithms for multiprogramming in a hard-real-time environment[J].Journal of the ACM, 1973, 20(1): 46–61.DOI:10.1145/321738.321743 |
| [9] | SHIN I,LEE I.Periodic resource model for compositional real-time guarantees[C]//Proceedings of 24th IEEE Real-Time Systems Symposium. Piscataway,NJ:IEEE Press,2003:2-13.http://cn.bing.com/academic/profile?id=2167972204&encoded=0&v=paper_preview&mkt=zh-cn |
| [10] | LEE Y H,KIM D,YOUNIS M,et al.Partition scheduling in APEX runtime environment for embedded avionics software[C]//Proceedings of 5th International Conference on Real-Time Computing Systems and Applications. Piscataway,NJ:IEEE Press,1998:103-109.http://cn.bing.com/academic/profile?id=1899851850&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | ZHOU T, XIONG H. Design of energy-efficient hierarchical scheduling for integrated modular avionics systems[J].Chinese Journal of Aeronautics, 2012, 25(1): 109–114.DOI:10.1016/S1000-9361(11)60368-3 |
| [12] | LIPARI G,BINI E.Resource partitioning among real-time applications[C]//Proceedings of 15th Euromicro Conference on Real-Time Systems. Piscataway,NJ:IEEE Press,2003:151-158.http://cn.bing.com/academic/profile?id=2135297309&encoded=0&v=paper_preview&mkt=zh-cn |
| [13] | MOK A K,FENG X,CHEN D.Resource partition for real-time systems[C]//Proceedings of Real-Time Technology and Applications Symposium. Piscataway,NJ:IEEE Press,2001:75-84.http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=929867 |
| [14] | ALMEIDA L,PEDREIRAS P.Scheduling within temporal partitions:Response-time analysis and server design[C]//Proceedings of 4th ACM International Conference on Embedded Software. New York:ACM Press,2004:95-103. |
| [15] | MOK A K,AUSTIN U O T A.A model of hierarchical real-time virtual resources[C]//Proceedings of 23rd Real-Time Systems Symposium. Piscataway,NJ:IEEE Press,2002:26-35.http://cn.bing.com/academic/profile?id=2129593667&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | DAVIS R I, BURNS A. A survey of hard real-time scheduling for multiprocessor systems[J].ACM Computing Surveys(CSUR), 2011, 43(4): 1–35. |
| [17] | LEE Y H,KIM D,YOUNIS M,et al.Resource scheduling in dependable integrated modular avionics[C]//Proceedings of International Conference on Dependable Systems and Networks. Piscataway,NJ:IEEE Press,2000:14-23.http://cn.bing.com/academic/profile?id=2149272340&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] | MARCO S.Analysis of deadline scheduled real-time systems:Technical report RR-2772[R].Pairs:INRIA,1996. |
| [19] | ZHANG F, BURNS A. Schedulability analysis for real-time systems with EDF scheduling[J].IEEE Transactions on Computers, 2009, 58(9): 1250–1258.DOI:10.1109/TC.2009.58 |
| [20] | BUTTAZZO G, BINI E, WU Y F. Partitioning real-time applications over multicore reservations[J].IEEE Transactions on Industrial Informatics, 2011, 7(2): 302–315.DOI:10.1109/TII.2011.2123902 |
| [21] | PATHAN R M,STENSTROM P,GREEN L G,et al. Overhead-aware temporal partitioning on multicore processors[C]//Proceedings of the IEEE 20th Real-Time and Embedded Technology and Applications Symposium. Piscataway,NJ:IEEE Press,2014:251-262.http://cn.bing.com/academic/profile?id=1979474236&encoded=0&v=paper_preview&mkt=zh-cn |
| [22] | BINI E,BUTTAZZO G.Biasing effects in schedulability measures[C]//Proceedings of 16th Euromicro Conference on Real-Time Systems. Piscataway,NJ:IEEE Press,2004:196-203.http://cn.bing.com/academic/profile?id=2119477620&encoded=0&v=paper_preview&mkt=zh-cn |
| [23] | CHAN M Y, CHIN F. Schedulers for larger classes of pinwheel instances[J].Algorithmica, 1993, 9(5): 425–462.DOI:10.1007/BF01187034 |
