航空航天上为了实现隔热、隐身、防辐射等目的，需要对一些三维产品做表面材料贴层。例如，为了减少雷达散射截面积(RCS)和过滤电磁波以实现导弹隐身的目的，通常在常规介质雷达罩上应用频率选择表面(FSS)进行表面贴层^[1-3]。当导弹雷达罩外形为三维不可展开曲面时(如抛物形头罩、哈克形头罩、指数形头罩以及非旋成体曲面等)，刚性贴层材料在曲面变形较大的位置会产生较大应变甚至破裂，柔性材料则可能产生褶皱，这都影响贴层的预期性能。因此需要将雷达罩三维曲面近似分片展开，映射到二维平面上，按照分片投影后的二维形状对贴层材料进行切割加工，再分别对每块分片进行贴层。
通常，不可展开曲面近似展开分为2个步骤：首先把不可展开曲面分成若干较小部分，在一定阈值范围内将这些较小部分看作是可展开表面，此为曲面分片；然后将分割后的各个部分投影为二维平面形状，此为曲面展开。在曲面分片的步骤中，李旭惠等^[4]应用了高斯曲率对面积的积分与曲面面积的比值作为分片系数对曲面进行分片，这种方法能够综合考虑曲面的空间双向弯曲程度与曲面面积的影响；王红艳^[5]研究了提高曲面可展性与曲面沿网格边的剪口算法，但对不规整的网格划分效果有待提高。在曲面展开投影步骤中，陈动人和王国瑾^[6]提出了基于伪直母线的复杂曲面的展开算法，其缺点是复杂曲面展开后会产生很多小碎面。蒋威^[7]使用了保形的三角网格细分方法，对弯曲幅度不大的曲面具有较好的展开效果；王纪清^[8]基于能量法的曲面展开算法对钣金不可展曲面进行近似展开，这种方法适合一些结构简单、弯曲程度小的曲面；李占利等^[9]针对三角形网格提出了一种基于弹簧-质点模型的不规则曲面纹理映射，能够使用于任意三角形网格表示的不规则曲面。另外，考虑到一些导弹雷达罩曲面会出现曲率不连续的情况(如类F22战斗机头罩外形的导弹雷达罩曲面)，则首先应提取出雷达罩曲面上的特征线(曲率不连续处)，这些特征线应处于贴层材料的剪口路径上。然后根据这些特征线将雷达罩曲面分割为C²连续曲面再进行分片展开工作。Ito^[10]、Baker^[11]和Borouchaki^[12]等采用基于网格二面角(相邻网格法矢的夹角)进行了特征线提取方法，杨晟院等^[13]通过对网格二面角进行统计分析，认为仅通过一个单一的阈值就能完整地提取出基本外形(如圆柱、圆锥、圆环等)的特征线。
鉴于当前研究现状及工业部门的迫切需要，本文研究发展了一种通用的导弹雷达罩曲面分片与展开算法，并开发了相应的应用程序软件。算法能针对任意导弹雷达罩曲面，首先识别曲面上的特征线，将雷达罩曲面分割为C²连续曲面；然后对这些C²连续曲面自动判别其是否为可展开曲面。对于可展曲面，直接应用展开算法进行展开为二维平面形状；对于不可展曲面，则首先对其近似分片再对其展开。为了尽量减小贴层分片对雷达隐身性能的影响，曲面分片遵循分片数量最少、剪口路径之和最短的原则；同时兼顾雷达罩曲面的空间双向弯曲程度和面积对分片大小的影响，以高斯曲率的绝对值对面积的积分作为曲面分片系数，在给定分片系数阈值后对雷达罩曲面进行离散、分片；构造十字基带进行映射为二维平面图形，以保证分片外形和控制展开误差的积累。
为了使本次开发的雷达罩曲面分片与展开系统具有良好的操作性和可视化特性，本文在上述雷达罩曲面分片数据操作的基础上，使用MFC开发应用程序框架，使用OpenGL进行雷达罩曲面的显示，最后输出AutoCAD格式以方便贴层材料的切割加工。
1 雷达罩曲面的离散化和分片 通常，对旋转对称外形的雷达罩曲面分片，纵向剪口应限制在同一条母线上。本文采用四边形结构网格来离散雷达罩曲面，这样可以使分片沿着网格的边进行，保证纵向剪口在同一条母线上，同时也能使得剪口路径之和尽量减小。并且，结构网格以I、J的数据格式来管理离散后的面元节点，这样极大地方便了分片位置的查找。对于四边形网格离散后的曲面，本文通过如下方法确定特征线阈值α的大小：首先找出所有二面角中小于10°的最大二面角值θ，再找出所有二面角中大于10°的最小二面角值φ，然后将(θ+φ)/2的值作为阈值α用于提取特征线^[13]，将雷达罩曲面划分为C²连续的空间曲面。
空间曲面可展的充要条件是其各处的高斯曲率是否恒等于零。相应地，其高斯曲率对面积的积分也应为零。对于C²连续的空间曲面进行网格离散后，求曲面的高斯曲率就变为求离散后各节点的高斯曲率。
假设曲面上曲线方程为r=r(u(t), v(t))，则曲线上节点的高斯曲率K可按式(1)计算^[14]：

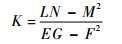(1)

式中:L、N、M和E、F、G分别为曲面的第一基本量和第二基本量。其计算方式分别为

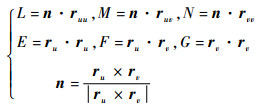(2)

在雷达罩曲面分片前，首先应判断曲面是否可展。将节点的高斯曲率加权平均到每个面元上，设K_i和S_i分别为第i个四边形网格的高斯曲率和面积(可由网格节点坐标和海伦公式的拓展公式求出)，则高斯曲率的绝对值对面积的积分为

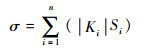(3)

当σ=0时，曲面可展：否则为不可展曲面。图 1为几种常见的导弹雷达罩外形的表面高斯曲率(无量纲)。其中哈克形、尖拱形、指数形头罩不满足曲面可展条件，而锥形头罩为可展开曲面。对于可展外形，不须进行分片工作，可直接对曲面进行等距映射，并且映射结果在理论上是唯一的。

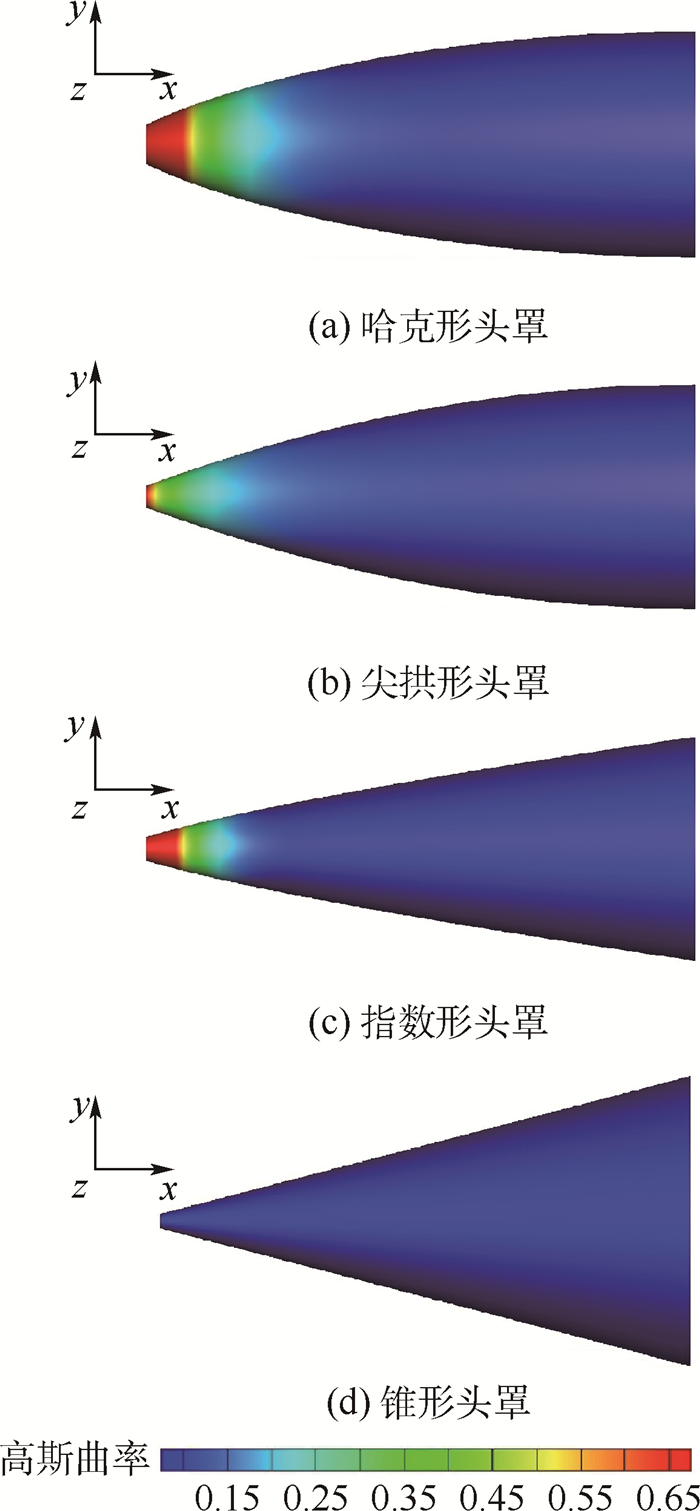图 1 不同雷达罩的高斯曲率 Fig. 1 Gaussian curvature of different radomes

图选项

2 分片展开映射算法 在对雷达罩三维曲面分片后，可通过展开算法和内部结构映射算法对其展开为二维平面图形。鉴于雷达罩材料贴层间允许少量重叠但不得有裂缝的要求，本文采用十字基带展开法对四边形网格离散的雷达罩曲面分片进行展开^[15]。即首先在分片上确定一个展开基点，再由相交于基点(并且一直延伸到边界)的网格边作为十字基带首先展开，最后根据映射算法展开剩余节点。分片展开中，以相对面积误差作为曲面展开质量的参考标准。其具体步骤如下。
步骤1 ??展开基点的确定
对雷达罩曲面分片后，可认为每块分片的曲率变化平缓。因此，可选取分片中心作为展开基点。当然，如果曲面某处曲率变化较大，则应选择该处作为展开基点。如图 2所示，指定点O作为展开基点，并指定展开后的二维坐标为(0，0)。

图 2 曲面展开基点的选取 Fig. 2 Selection of base point of surface projection

图选项

步骤2??展开基点相邻四点的映射
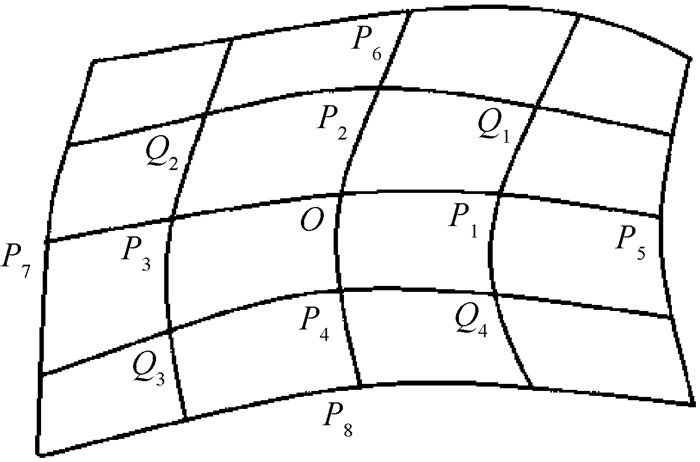
假设展开基点O附近4个点为P₁、P₂、P₃、P₄，对应展开到二维平面后的点为O′、P′₁、P′₂、P′₃、P′₄。基点及附近4个点展开前后的角度变化如图 3所示，投影后的夹角β′_i可由式(4)及式(5)得出：

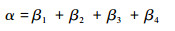(4)

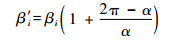(5)

图 3 展开前后基点周围的角度变化 Fig. 3 Angles around base point change before and after projection

图选项

规定点P′₁位于x轴正方向，再根据投影前各节点到基点的距离，可求出基点相邻4个点展开后的二维坐标。
步骤3??四边形单元待定节点的确定
在确定一个四边形单元内3个节点的映射后，可通过如下确定最后一个节点的映射：如图 4所示，设空间四边形单元IPJK，在该四边形单元中，假设点I、J、K已经映射到二维平面，现在要求点P在二维平面上的映射坐标。令A_I、A_J、A_K、A_P分别为△PJK、△IPK、△IPJ和△IJK的面积，则根据几何关系可以推导出P点坐标^[12]：

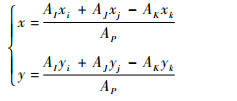(6)

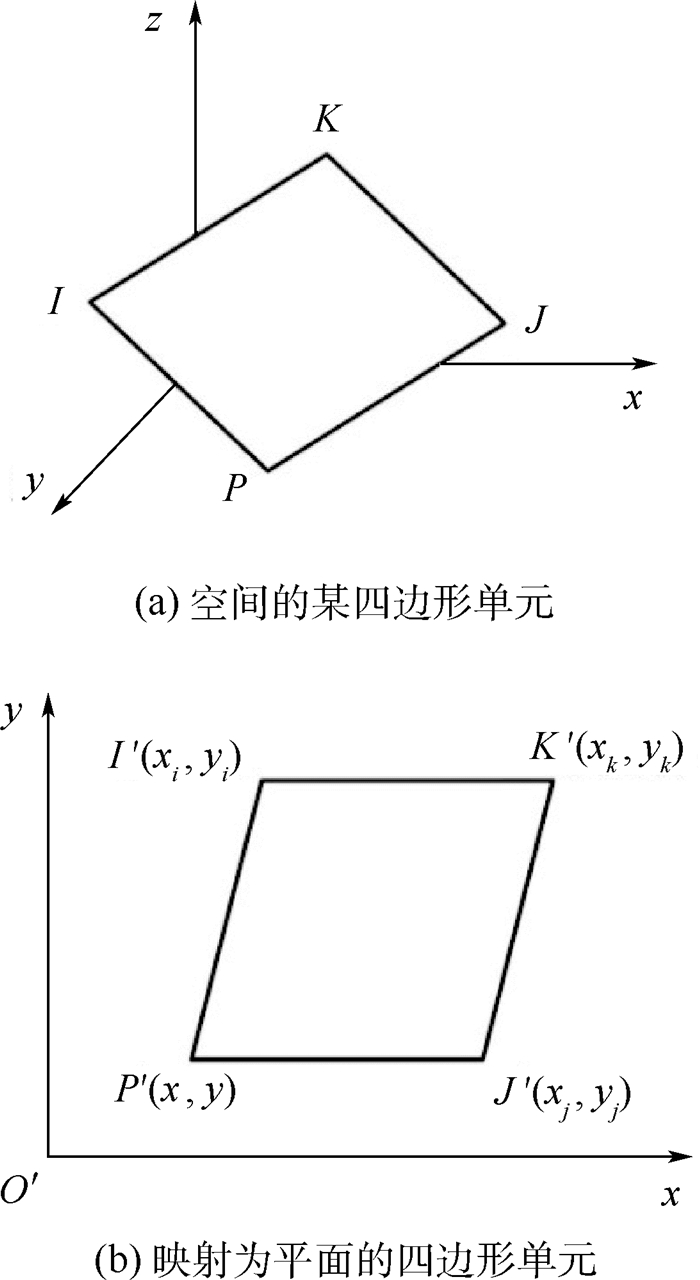图 4 四边形单元待定节点的确定 Fig. 4 Determination of quadrilateral cell nodes

图选项

步骤4??分片上剩余节点的确定
上述步骤1、2、3可以确定展开基点以及基点周围8个节点的映射。分别向分片有限元网格的I、J的正、负方向移动，以下一个节点作为基点，不断重复步骤2和3，直到分片边界结束，可以确定一个十字展开基带的映射；再从展开基带出发，对分片上未映射的节点采用步骤3，可以确定剩余节点的映射。到此，一个分片节点的映射工作完毕。
3 分片展开的可视化与输出 3.1 应用软件总体设计思路 为了使雷达罩曲面分片与展开应用软件具有良好的交互性，本文使用MFC开发应用程序框架，包括曲面外形参数化、管理实现数据操作以及创建图形用户界面框架。
基于MFC和OpenGL的曲面分片与展开应用软件的总体设计思路是：使用MFC中的文档/视图结构(Document/View Architecture)实现模型数据与显示交互的相互分离。如图 5所示，文档类CDocument负责管理模型(CDocument Object)，视图类CView负责显示模型(CView Object)以及与用户交互操作，视图类与文档类则通过函数指针进行中间操作，实现对模型数据的修改。

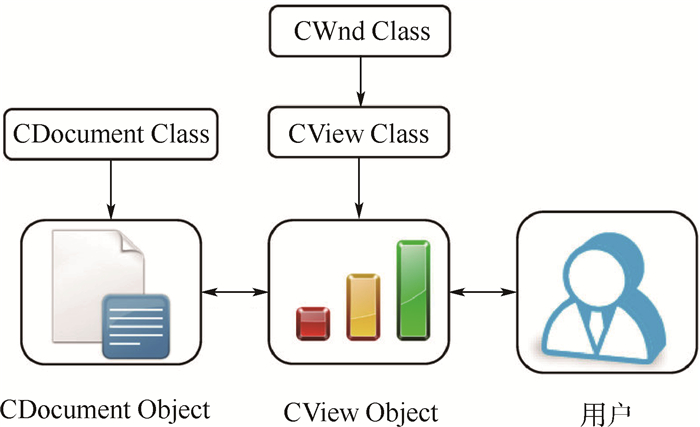图 5 文档、视图与用户的关系 Fig. 5 Relationship among document, view and user

图选项

在曲面分片数据可视化方面，本文采用基于OpenGL的CAD模型显示技术^[16]。OpenGL图形系统是一个连接图形硬件的软件接口。本文首先使用三角形面元或四边形面元绘制离散后的三维曲面，使用双面光照和材料属性来较为真实地模拟出光滑表面的三维实体，最后使用32位RGB颜色系统来区别不同分片，并且标明了分片与映射图形之间的对应关系。图 6(a)为OpenGL绘制的某雷达罩曲面CAD模型，图 6(b)生成三维曲面分片与映射后对比的渲染图形。

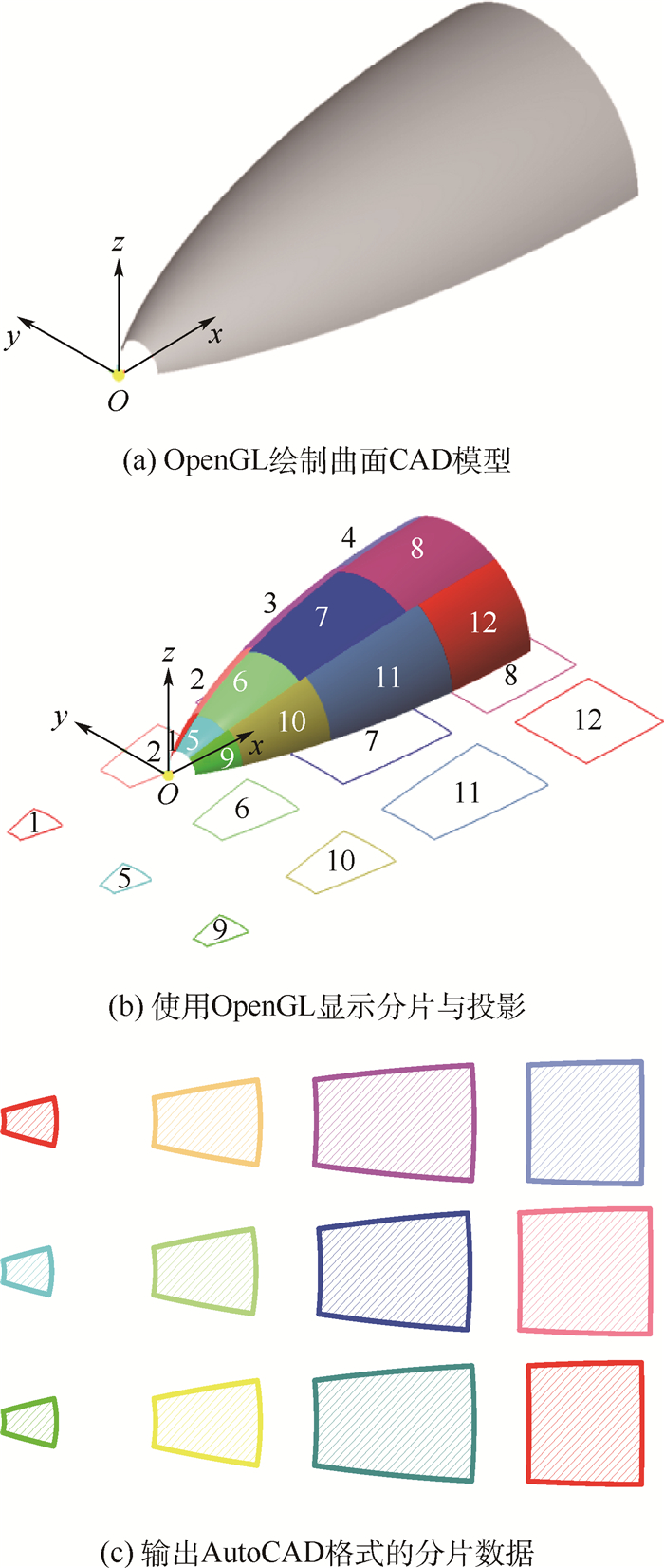图 6 曲面分片展开的可视化过程 Fig. 6 Visualization of surface partition and projection

图选项

为了在Windows环境下使用OpenGL进行三维绘图，一般在MFC环境下创建一个OpenGL Windows程序，即在MFC视图类CView的基础上派上一个封装了OpenGL的类CGLView。图 7所示为CGLView类中的函数调用关系。图中：m_hRC和m_hDC分别为渲染场景句柄和设备场景句柄；PreCreateWindow ()为创建窗口和定义窗口类型；GLInit ()为OpenGL的初始化函数；OnDestroy ()的作用为调用GLRelease ()函数，释放所创建的渲染场景；OnSize ()则处理视图窗口尺寸变化；完成以上工作后，就可以使用OpenGL调用OnDraw ()函数进行绘图，其中，三维图形的绘制是在RenderScence ()里完成的；OnEraseBkgnd ()用于窗口背景的擦除。

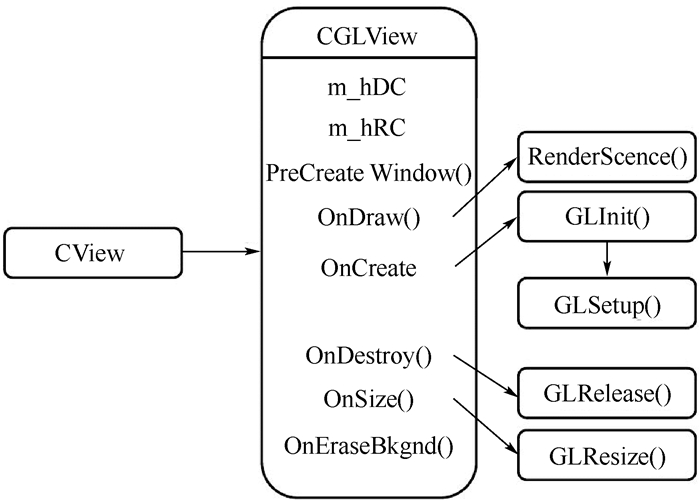图 7 CGLView类中的函数调用关系 Fig. 7 Functions call relationship in CGLView class

图选项

3.2 分片数据的几何变换 通过OpenGL绘制的三维图形显示在屏幕上，用户要清楚地看到所绘制对象的形态、大小、颜色及各对象的空间位置，就涉及到一个视点观察与图形变换问题。图形变换是CAD系统中的最基本内容之一，物体的平移、缩放、旋转等都要靠图形变换来实现。对几何对象的变换，实际上是对几何模型中点的齐次坐标通过矩阵运算进行坐标变换，也就是通过n+1维矩阵的乘法来表示n维几何体的坐标改变形式^[17]。
三维物体齐次坐标变换矩阵的形式如下：

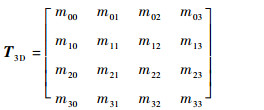(7)

将T_3D划分为4个子矩阵，每个矩阵负责不同的变换任务。其中：用于产生缩放、旋转、剪切等几何变换；[m₃₀ m₃₁ m₃₂]用于产生平移变换；[m₀₃ m₁₃ m₂₃]^T用于产生投影变换；[m₃₃]用于产生整体缩放变换。
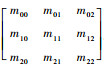
3.3 分片数据的输出 在输出分片数据方面，由于AutoCAD在零件或板材中切割加工应用十分广泛^[18]，因此本文选择将分片数据输出为AutoCAD格式。DXF类型文件是AutoCAD的一种数据格式。由于DXF文件内部为ASCII码，可读性好，用户可以很方便地对它进行编程处理，实现从外部图形进行编辑的目的，因此DXF文件被广泛用于AutoCAD与其CAD软件之间进行数据交换^[19]。本文采用开源C++库dxflib对展开后的数据进行输出。图 6(c)为分片展开数据输出的AutoCAD格式图形。
4 雷达罩曲面分片展开算例 为了验证本文导弹雷达罩曲面分片程序的通用性与分片精度，本文选取了某型头罩为非旋成体的导弹作为分片算例。图 8为该型导弹的CAD模型，其中蓝色部分为要展开的雷达罩曲面外形。

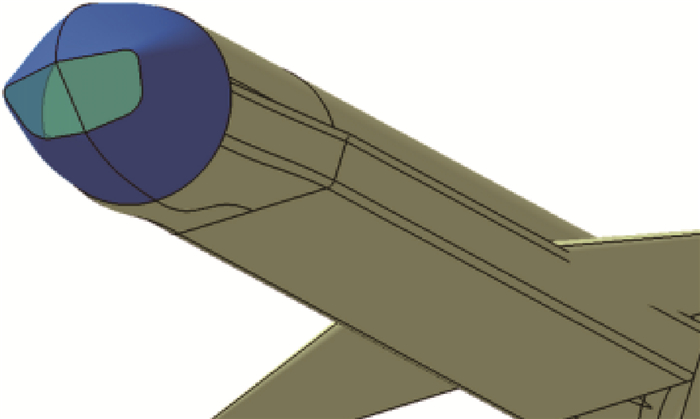图 8 某型导弹CAD模型 Fig. 8 CAD model of a missile

图选项

根据导弹头罩贴层的要求，对于平面对称外形，剪口应在对称面上。因此，将头罩外形的一半进行分片、映射。在周向布置两条剪口，最终输出分片的平面映射AutoCAD图形如图 9所示。

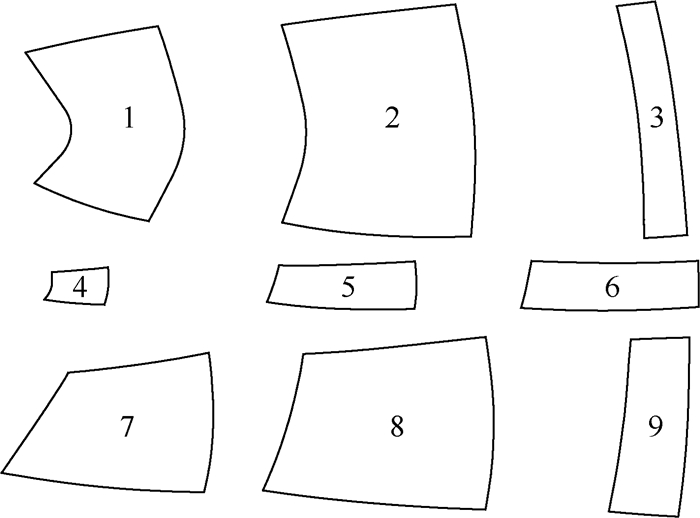图 9 半块头罩外形分片投影 Fig. 9 Shape partition projection of a half radome

图选项

本文的误差精度判定方法为相对面积误差法。展开前后的误差用相对面积误差S_error和相对边长误差L_error来衡量，其定义分别如下：

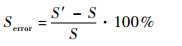(8)

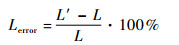(9)

式中:S为被展分片面积; L为被展分片的边长；S′为展开图形面积; L′为展开图形的边长。
本文算例分片的相对面积误差如表 1所示。相对误差均为正，且最大分片误差小于10%，表示分片能够逼近还原成曲面。并且，算例中分片展开后图形的相对边长差非常小，所有展开分片的边，相对边长误差最大不超过2%，表明分片贴层中有少量重叠、没有间隙。这证明了本文雷达罩曲面分片算法的有效性。
表 1 分片展开后的面积误差 Table 1 Area error after projection of partitions

曲面编号	1	2	3	4	5	6	7	8	9
Serror/%	2.513 64	2.394 64	6.031 60	9.512 05	7.533 31	6.413 17	2.121 63	2.659 73	5.509 07

表选项






5 结论 本文开发的导弹雷达罩曲面的分片与展开系统，能够对旋成体和非旋成体曲面进行自适应分片、展开。
1)分片展开算法误差较小：在曲面曲率较大的分片处，展开后的相对面积误差小于10%，且相对边长误差最大不超过2%。
2)使用MFC+OpenGL开发的应用程序框架，实现了雷达罩曲面分片映射操作的可视化，操作人员能够方便地找出分片与投影图形之间的对应关系。
3)分片数据输出AutoCAD通用格式，方便材料的切割加工。

参考文献

[1]	张建.有限大频率选择表面及其在雷达罩上的应用研究[D].北京:中国科学院研究生院, 2015:3-8.ZHANG J.Research on finite frequency selective surface and its application on radome[D].Beijing:Graduate University of Chinese Academy of Sciences, 2015:3-8(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-80139-1015345958.htm
[2]	王秀芝, 高劲松, 徐念喜. Ku/Ka波段双通带频率选择表面雷达罩设计研究[J].物理学报, 2013, 62(23): 324–330.WANG X Z, GAO J S, XU N X. Design and study on the dual-band radome with FSS operation at Ku-/Ku-band[J].Acta Physica Sinica, 2013, 62(23): 324–330.(in Chinese)
[3]	侯新宇, 张澎, 卢俊, 等. 一种双曲率雷达罩的频率选择表面分片设计[J].弹箭与制导学报, 2006, 26(1): 123–125.HOU X Y, ZHANG P, LU J, et al. A novel frequency selective surfaces path design for double curved radome[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 123–125.(in Chinese)
[4]	李旭惠, 王俊彪, 张贤杰. 应用高斯曲率积分的曲面可展化分片方法研究[J].计算机工程与应用, 2011, 47(6): 202–204.LI X H, WANG J B, ZHANG X J. Developable surface partition algorithm based on Gaussian curvature integration[J].Computer Engineering and Applications, 2011, 47(6): 202–204.(in Chinese)
[5]	王红艳.三角网格曲面优化展开技术研究[D].哈尔滨:哈尔滨工业大学, 2013:25-30.WANG H Y.Research on optimization for triangular mesh surface flattening technology[D].Harbin:Harbin Institute of Technology, 2013:25-30(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10213-1014003552.htm
[6]	陈动人, 王国瑾. 基于伪直母线的复杂曲面自适应分片与展开[J].软件学报, 2003, 14(3): 660–665.CHENG D R, WANG G J. A complex surface adaptive segment and development algorithm based on its quasi-rulings[J].Journal of Software, 2003, 14(3): 660–665.(in Chinese)
[7]	蒋威.不可展曲面的近似展开及其应用[D].上海:复旦大学, 2013:11-14.JIANG W.Approximation algorithms for undevelopable surfaces and its application[D].Shanghai:Fudan University, 2013:11-14(in Chinese).
[8]	王纪清.三维钣金展开与工艺规划的研究[D].西安:西安工业大学, 2012:23-35.WANG J Q.Research on the 3D sheet metal flattening and process planning[D].Xi'an:Xi'an Technological University, 2012:23-35(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10702-1012325499.htm
[9]	李占利, 刘小靖, 孙瑜. 基于弹簧-质点模型的不规则曲面纹理映射[J].计算机工程与设计, 2014, 35(10): 3545–3548.LI Z L, LIU X J, SUN Y. Texture mapping for irregular surface based on spring-mass model[J].Computer Engineering and Design, 2014, 35(10): 3545–3548.(in Chinese)
[10]	ITO Y, NAKAHASHI K. Direct surface triangulation using stereolithography data[J].AIAA Journal, 2002, 40(3): 490–496.DOI:10.2514/2.1672
[11]	BAKER T J.Identification and preservation of surface features[C]//Proceedings of 13th International Meshing Roundtable.Williamburg:Sandia National Laboratories, 2004:299-310.
[12]	BOROUCHAKI H, VILLARD J, LAUG P, et al. Surface mesh enhancement with geometric singularities identification[J].Computer Methods in Applied Mechanics and Engineering, 2005, 194(48): 4885–4894.
[13]	杨晟院, 舒适, 朱少茗. 基于STL文件的三角形表面网格的特征线提取[J].计算机工程与应用, 2008, 44(4): 14–19.YANG S Y, SHU S, ZHU S M. Feature line extraction from triangular meshes based on STL files[J].Computer Engineering and Applications, 2008, 44(4): 14–19.(in Chinese)
[14]	毛昕, 马明旭. 曲面映射与展开中的几何分析[M].北京: 清华大学出版社, 2013: 7-17.MAO X, MA M X. Geometric analysis of surface mapping and deployed[M].Beijing: Tsinghua University Press, 2013: 7-17.(in Chinese)
[15]	孙新申.不可展曲面近似展开和内部结构映射方法研究[D].西安:西北工业大学, 2004:13-21.SUN X S.Study on approximate expansion and internal structure mapping method of non-developable surface[D].Xi'an:Northwestern Polytechnical University, 2004:13-21(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10699-2004062976.htm
[16]	SHREINER D, SELLERS G, KESSENICH J M, et al. OpenGL programming guide:The official guide to learning OpenGL, Version 4.3[J].Upper Saddle River:Addison-Wesley, 2013: 31–115.
[17]	王浩然, 梁彦刚, 陈磊. 空间态势场景中OpenGL视点控制策略与实现[J].太赫兹科学与电子信息学报, 2015, 13(2): 302–307.WANG H R, LIANG Y G, CHEN L. OpenGL viewpoint control strategy and implementation in space situation scene[J].Journal of Terahertz Science and Electronic Information Technology, 2015, 13(2): 302–307.(in Chinese)
[18]	邢海蛟.基于AutoCAD图形数控切割的应用研究[D].哈尔滨:哈尔滨理工大学, 2015:18-30.XING H J.The application study of graphic CNC cutting system based on AutoCAD[D].Harbin:Harbin University of Science and Technology, 2015:18-30(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10214-1015576304.htm
[19]	石鑫.AutoCAD环境下DXF文件格式分析与处理[D].沈阳:沈阳航空航天大学, 2015:14-16.SHI X.File format analysis and process of AutoCAD DXF[D].Shenyang:Shenyang Aerospace University, 2015:14-16(in Chinese).