在生物界,同样存在着类似复合材料结构的连接问题。以骨制结构为例,其由钙质与胶原纤维按照特定排布规律构成,同样具备高比刚度、比强度等优异力学性能。当2块骨质结构相连接时,并未采用工业复合材料结构的“硬”连接方法,而是通过生物结构中的骨缝齿接界面[2-4]这样特殊的几何齿接构型进行连接,从而获得了良好的连接与承载特性。
该类连接结构在生物力学层面所表现出的优异性能,引起了包括力学界在内的研究人员广泛关注。研究表明,对于骨缝连接机制,其齿接构件的几何、材料性能,齿间界面的承载、破坏特性以及层级数量等参数都会影响连接结构自身的力学性能[5-10]。Jasinoski等[11]从工程应用方面研究了胶层界面属性及齿顶角度对齿接结构应力分布的影响;Boyce和Li[12-14]等则对自然齿接结构胶层界面几何外形与基本力学性能的相互作用机理进行了一系列研究。然而对于结构参数与其力学性能间的联系及其在复合材料连接上的应用鲜有文献报道。
仿生齿接结构模型的参数化表述是研究该类连接结构失效机制的基础,由于结构层级、几何结构参数的复杂性,传统手工建模手段已不再适应。本文以几种典型骨缝齿接构型为研究对象,基于分形几何理论,构建骨缝齿接构型参数化表述方法;通过Python语言对ABAQUS进行二次开发,完成骨缝齿接结构的数值模型建立,并对复合材料齿接结构在拉伸条件下的力学特性进行了研究。
1 骨缝齿接结构参数化建模 1.1 几何外形参数描述 典型三角骨缝齿接结构如图 1(a)所示,齿顶角度与齿高等参数决定了其几何构型;对于单级多齿结构,如图 1(b)~图 1(d)所示,齿接基线(直线、正弦曲线)也会影响几何构型;图 1(e)为多层级齿接结构。由此可见,对于齿接结构的几何外形可以由齿顶角θ、齿高h、齿数n、间隔d、层级D和基线类型6个关键参数确定,而当齿接基线为正弦曲线时,关键参数还应包括幅值和周期,由泰勒级数可知,以上典型齿接结构可以扩展表达不同基线条件下的齿接结构类型,因此对自然齿接结构的表述具有普适性。
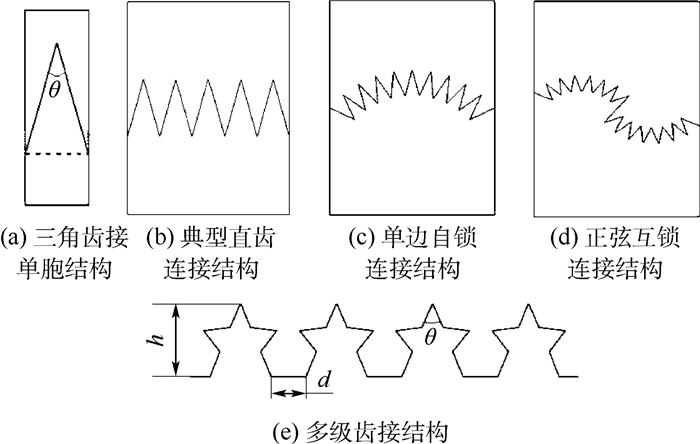 |
| 图 1 典型骨缝齿接结构示意图 Fig. 1 Schematic diagram of typical suture joint structure |
| 图选项 |
1.2 基于分形原理与MATLAB的齿接结构几何构型表述 为了对齿接结构特别是层级齿接结构的几何构型进行参数化表述,本文采用了基于Koch曲线的分形原理,并结合MATLAB编制了控制模型参数的图形用户界面(Graphical User Interface,GUI)。
由齿接结构参数分析可知,对于齿顶角θ、齿高h、齿数n、间隔d和基线类型参数,可以基于MATLAB编制程序进行表达,而如何表述齿接结构的层级特性则是该类模型构建的难点。
由Koch曲线分形原理可知:设一个边长为1的等边三角形,取每边中间的三分之一,连接一个形状完全相似的但边长为其三分之一的三角形,结果是一个六角形。现在取六角形的每个边做同样的变换,即在中间三分之一位置连接更小的三角形,以此重复,直至无穷。外界的变得原来越细微曲折,形状接近理想化的雪花。本文借鉴该原理并加以改动,改为齿顶角为θ的等腰三角形,且只取两腰进行变换:取每边中间的三分之一,连接一个形状相似的但边长为其三分之一的无底边的三角形,以此重复,直至达到所需齿接层级。所以齿接层级即是该分形过程的分形维度。
因此,齿接结构几何构型表述的关键是确定控制点的坐标,当基线类型为直线时,可以通过解析方法求解控制点坐标,而当基线类型为正弦曲线时,则需要求解超越方程。齿顶角、齿高确定后,等腰三角形底边长度便确定,该底边左端点坐标已知,右端点坐标既满足底边长度一定,又满足在正弦曲线上,这是一个超越方程组,可由MATLAB进行方程求解。
几何构型表述程序流程如图 2所示。基线类型为直线且D=1时,调用子程序line_function1;基线类型为直线且D≥2时,调用子程序line_function2;基线类型为正弦曲线且D=1时,调用子程序sin_function1;基线类型为正弦曲线且D≥2时,调用子程序sin_function2。
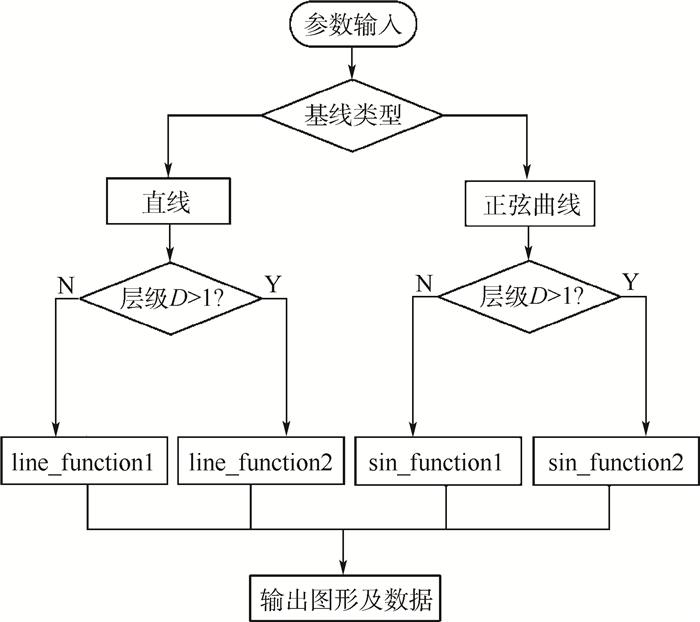 |
| 图 2 几何构型表述程序流程图 Fig. 2 Program flowchart of geometric shape generation |
| 图选项 |
为了方便后续输入参数,创建MATLAB的GUI。首先选择基线类型(直线或正弦曲线),基线类型为直线且D=1时,控制参数为齿数、齿顶角和齿高;直线且D≥2时,控制参数为层级、齿数、齿顶角、齿高和间隔;基线为正弦曲线且D=1时,控制参数为齿数、齿顶角、齿高和幅值和周期;为正弦曲线且D≥2时,控制参数为层级、齿数、齿顶角、间隔、幅值和周期。
GUI生成的几种不同分形结果如图 3所示,其中图 3(a)展示了基线类型为直线、层级为4、齿数为4的齿接结构示意图。
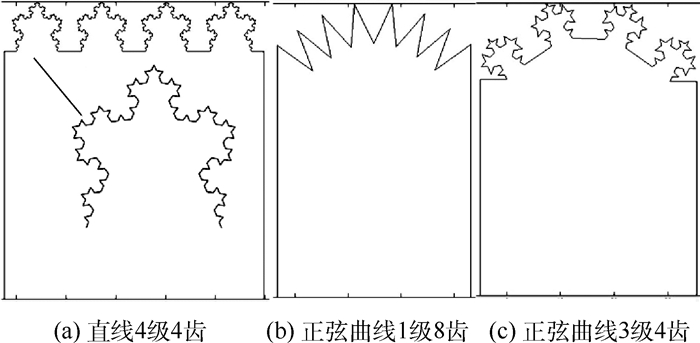 |
| 图 3 GUI界面生成分形结果 Fig. 3 Fractal outline generated through GUI |
| 图选项 |
通过GUI输入齿接结构几何外形的关键参数,就可以输出平面外形图,并将齿接结构的几何关键点导出到inp文件,为ABAQUS参数化建模提供数据,并为后续分析不同参数对齿接结构力学性能的影响奠定基础。
1.3 基于Python语言的齿接结构参数化建模 Python是一种面向对象的脚本语言,它功能强大,既可以独立运行,也可以用作脚本语言,特别适用快速的应用程序开发[15]。本文对ABAQUS前处理进行二次开发,综合运用了MATLAB和Python语言控制ABAQUS的建模与装配过程。利用GUI,让用户方便地输入有关参数,得到各种所需的齿接结构并输出几何关键点坐标,然后通过Python语言编写前处理程序自动读取这些数据点坐标进行建模和装配,有效地解决了建模时的繁琐、易错等问题,提高了建模效率与精度。图 4所示为基于ABAQUS有限元分析软件构建的几种齿接结构有限元模型(FEM)。
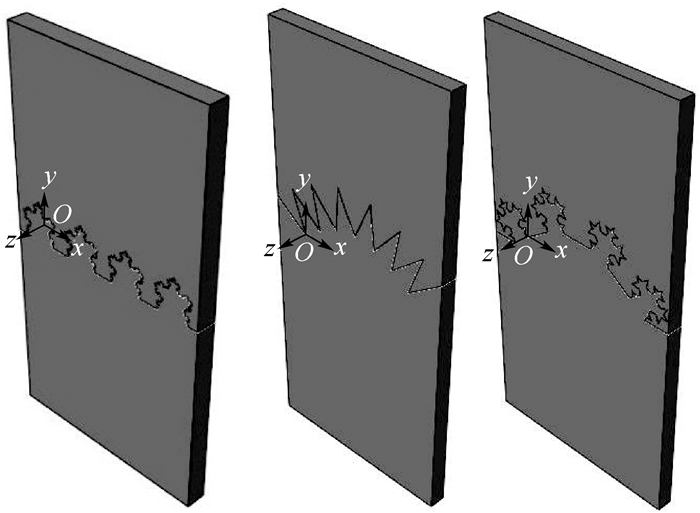 |
| 图 4 GUI生成的骨缝齿接结构有限元模型 Fig. 4 FEM of suture joint structure generated by GUI |
| 图选项 |
2 复合材料齿接结构力学行为 2.1 齿接结构几何外形 为了比较研究,共设计7个齿接结构,长、宽、厚均相同(长96mm,宽40mm,厚度5mm),关键参数如表 1所示。
表 1 骨缝齿接结构关键参数 Table 1 Key parameters of suture joint structure
| 齿数 | 齿顶角/(°) | 基线类型 | 层级 |
| 9 | 30 | 直线 | 1 |
| 9 | 45 | 直线 | 1 |
| 9 | 60 | 直线 | 1 |
| 15 | 45 | 直线 | 1 |
| 15 | 45 | 正弦曲线 | 1 |
| 5 | 45 | 直线 | 2 |
| 5 | 45 | 直线 | 3 |
表选项
2.2 有限元模型 为了研究齿接结构的拉伸响应过程,选取短纤维增强光固化环氧树脂基复合材料作为齿接结构材料,该材料各向同性且线弹性较好,便于分析拉伸过程中结构自身几何特性对其连接、承载机制的影响,其材料参数见表 2。齿接结构结合处通过环氧树脂胶黏剂胶接,此处采用零厚度内聚力(cohesive)单元模拟齿接界面,其材料参数见表 3[16]。
表 2 骨缝齿接结构材料参数 Table 2 Material parameters of suture joint structure
| 材料参数 | 弹性模量/MPa | 泊松比 |
| 数值 | 116 000 | 0.3 |
表选项
表 3 内聚力材料参数[16] Table 3 Material parameters of cohesive element[16]
| MPa | |||
| 材料参数 | Knn | Kss | Ktt |
| 数值 | 491 000 | 264 500 | 264 500 |
| 注:Knn-法向刚度;Kss-1方向刚度;Ktt-2方向刚度。 | |||
表选项
齿接结构界面由于复杂的几何形貌导致其应力分布和失效机理复杂化。为了准确表达这种连接结构的渐进损伤行为,使用混合模式(mixed-mode)内聚力单元来描述界面力学行为。式(1)为初始损伤控制方程,式(2)为损伤扩展控制方程。
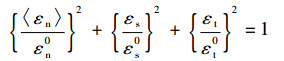 | (1) |
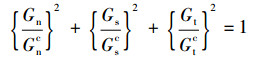 | (2) |
式中:〈εn〉为法向平均应变;εn0为弹性变形段法向峰值应变;εs为1方向应变;εs0为弹性变形段1方向峰值应变;εt为2方向应变;εt0为弹性变形段2方向峰值应变;Gn为法向能量释放率;Gnc为法向能量释放率临界值;Gs为1方向能量释放率;Gsc为1方向能量释放率临界值;Gt为2方向能量释放率;Gtc为2方向能量释放率临界值。
对于双剪拉伸-分离准则,内聚力界面失效应力见表 4;各方向的临界失效位移假设为0.2 mm。
表 4 内聚力界面失效应力 Table 4 Failure stress for cohesive interface
| 名义应力 | 法向 | 1方向 | 2方向 |
| 数值/MPa | 55 | 30 | 30 |
表选项
本节的有限元模型用ABAQUS/Standard求解。复合材料齿接结构单元类型采用三维实体八节点减缩积分单元C3D8R、结合处采用三维八节点内聚力单元COH3D8。同时,内聚力单元与实体单元之间使用面面接触来模拟理想黏结及胶层失效。
2.3 结果分析及讨论
2.3.1 齿顶角的影响 不同齿顶角齿接结构的载荷-位移曲线如图 5(a)所示。各结构载荷-位移曲线在初始阶段重合,随着界面损伤的产生,曲线开始分离,载荷达到峰值后部件承载能力下降。其中,30°齿顶角的最大载荷较其他结构高出近30%。这是由于较小的齿顶角会使得界面接触面积增大;而当考虑界面等效应力(载荷/接触面积)与结构位移的关系时(如图 5(b)所示),可见小齿顶角结构的等效应力较其他较大角度的等效应力小。这解释了为什么自然界中的齿接结构通常有较小的齿顶角。
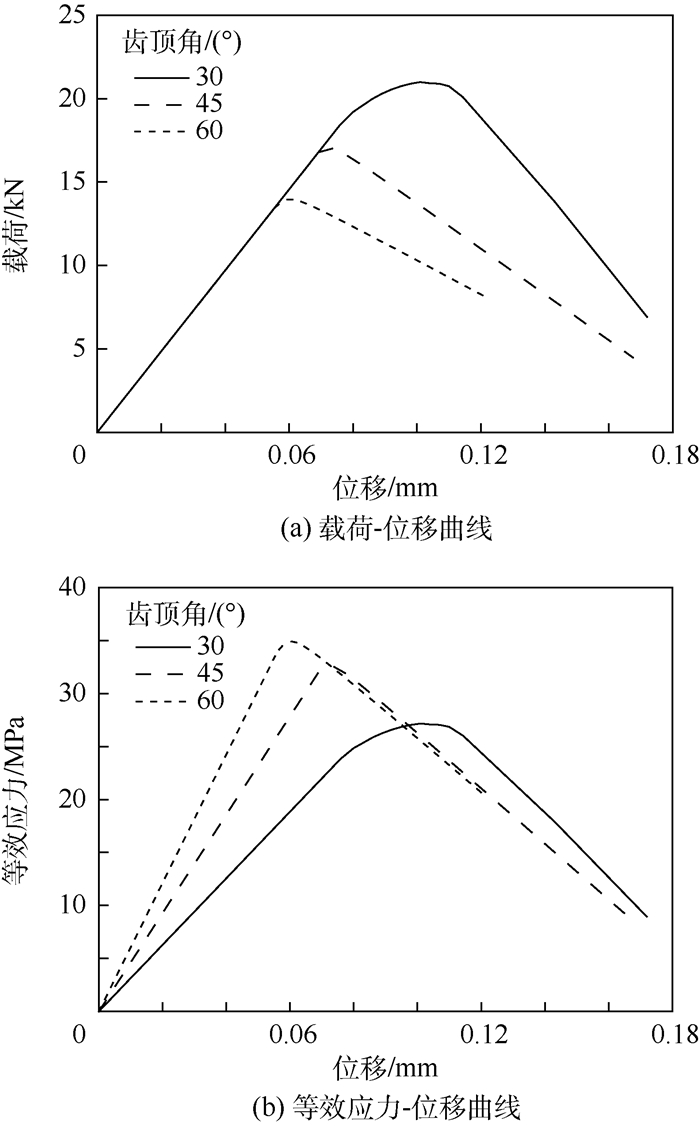 |
| 图 5 齿顶角不同的骨缝齿接结构载荷-位移曲线、等效应力-位移曲线 Fig. 5 Curves of load-displacement and equivalent stress-displacement for suture joint structure with different tooth angles |
| 图选项 |
2.3.2 基线类型的影响 不同基线类型齿接结构的载荷-位移曲线、等效应力-位移曲线如图 6所示。基线类型采用正弦曲线的齿接结构,其最大载荷比直线结构的高出近60%,最大等效应力却只高出不到20%。这是因为基线类型是正弦曲线时,齿接结构具有互锁能力,同时接触面积也更大。
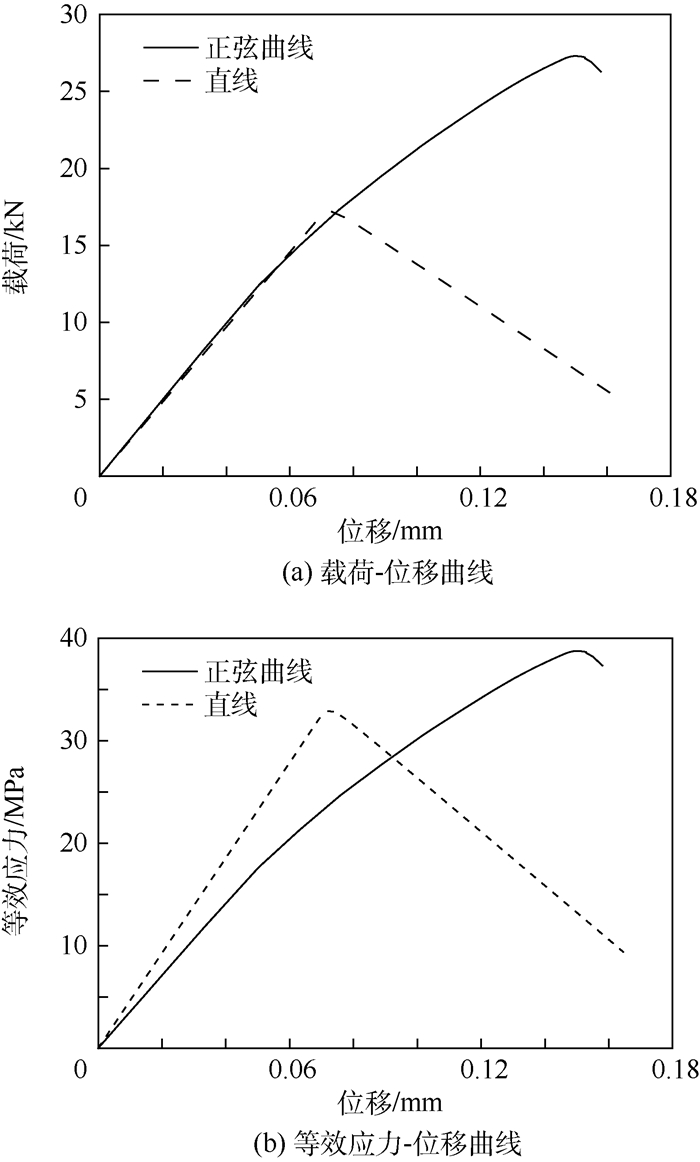 |
| 图 6 不同基线类型骨缝齿接结构载荷-位移曲线、等效应力-位移曲线 Fig. 6 Curves of load-displacement and equivalent stress-displacement for suture joint structure with different baseline types |
| 图选项 |
此外,不同基线类型齿接结构内聚力单元损伤(SDEG)过程如图 7所示。当结构界面基线类型为直线时,界面各处损伤同步产生与扩展;而采用正弦曲线基线时,界面各处破坏程度出现差别,从而避免了界面瞬时破坏所带来的结构承载能力突降,也使得结构具有了更好的损伤容限特性,这也解释了自然界齿接结构基线以曲线为主的原因。
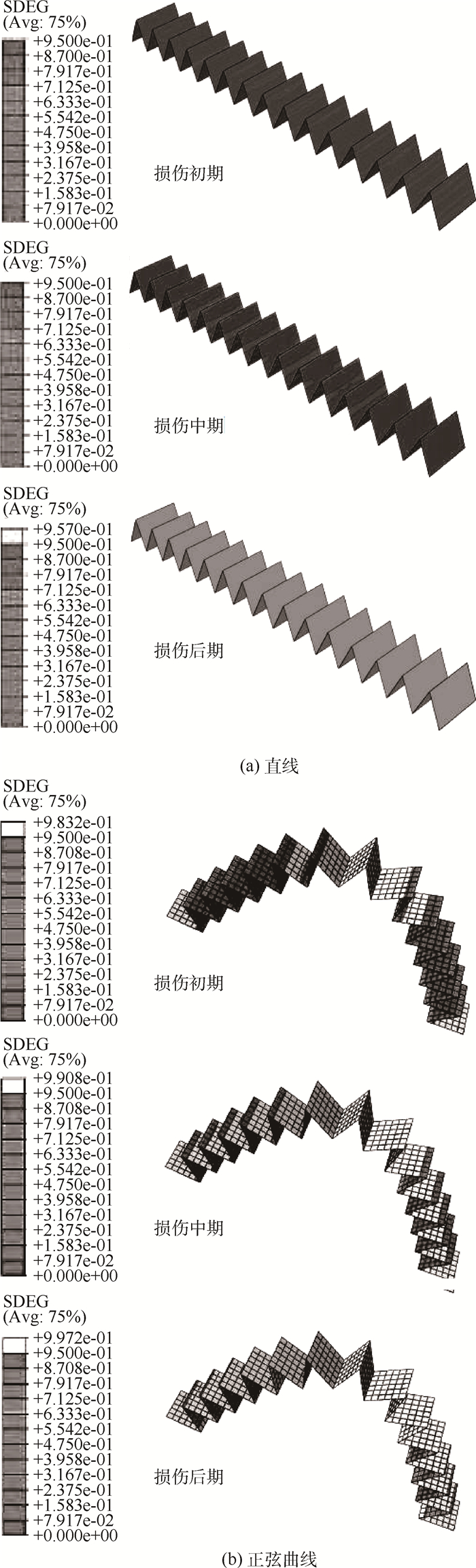 |
| 图 7 不同基线类型骨缝齿接结构内聚力单元损伤过程 Fig. 7 Damage evolution of cohesive element for suture joint structure with different baseline types |
| 图选项 |
2.3.3 层级的影响 不同层级齿接结构的应力(SMises)分布如图 8(a)所示,可以看出,结构最大应力与平均应力的比值均小于2,但1级结构出现了沿着自由端的应力集中,这将导致齿接结构可能出现初始损伤。另一方面,高层级齿接结构内聚力单元界面处的应力集中表明结构初始破坏主要由界面几何属性决定。
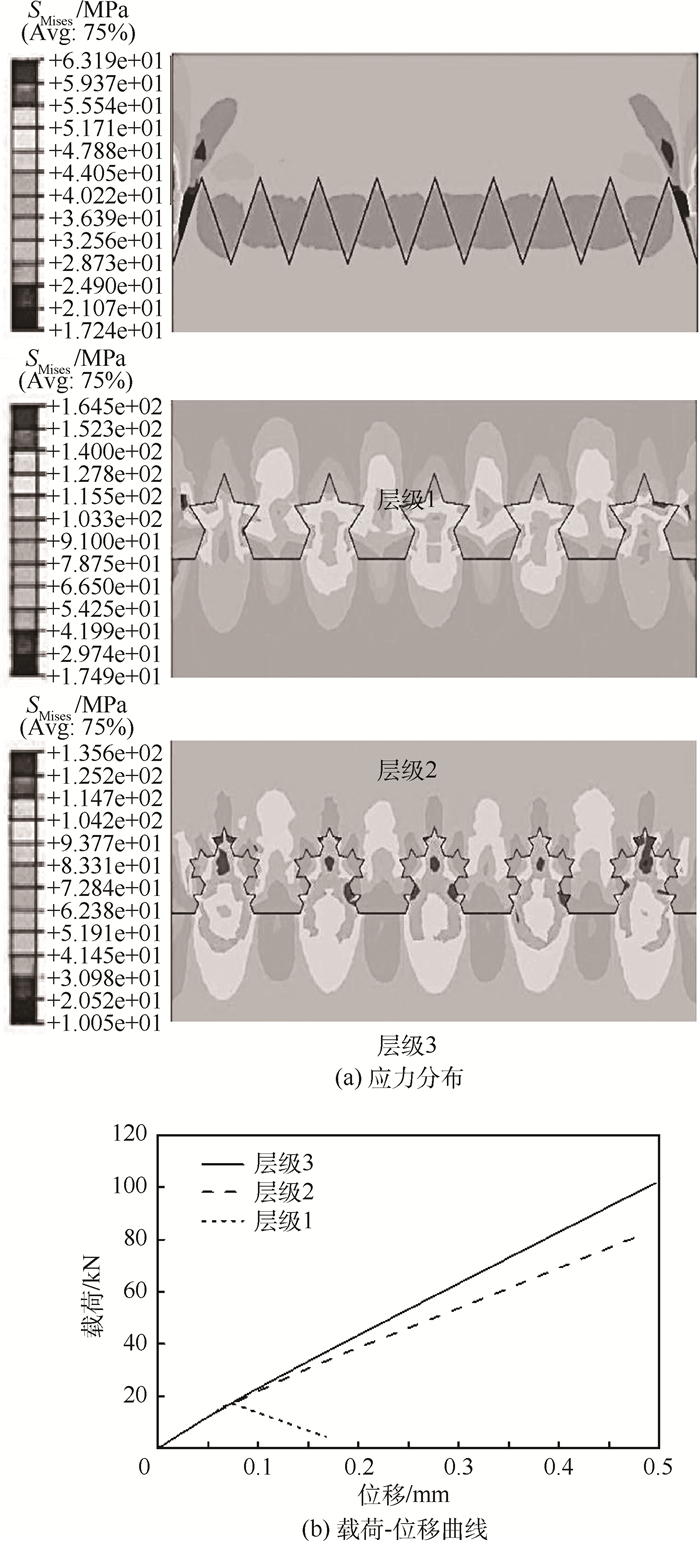 |
| 图 8 不同层级骨缝齿接结构应力分布、载荷-位移曲线 Fig. 8 Stress distribution and load-displacement curves for suture joint structure with different hierarchies |
| 图选项 |
不同层级齿接结构的载荷-位移曲线如图 8(b)所示,发现1级齿接结构的最大载荷较其他2种结构都低。这是因为1级齿接结构缺少自锁能力,载荷全部由内聚力单元界面承受,但由于界面强度相对较低,因此结构整体承载能力较低。
高层级的齿接结构由于具有界面自锁能力,载荷通过挤压、剪切转移到其他部位,延迟了界面损伤,提升了结构的完整性,使得其最大承载能力有显著提升。
3 结论 本文构建了齿接结构参数化数值分析模型,并采用该模型研究了复合材料齿接结构在拉伸载荷作用下的力学特性,数值模型研究结果表明:
1)低层级齿接结构的承载能力随着齿顶角度减小而增大,且齿间界面初始损伤首先发生在自由边位置。
2)当齿基线类型为正弦曲线时,结构由于自锁特性,使得承载能力明显提高。
3)对于高层级齿接结构,其结构强度及损伤容限由于界面自锁能力的提高而显著提升。
本文研究结果初步揭示了自然进化过程中齿接结构的演化规律所对应的力学性能提高过程,并为进一步研究复合材料仿生齿接结构的复杂力学行为与结构优化提供了研究基础。
参考文献
| [1] | 赵美英.复合材料机械连接失效分析及强度影响因素研究[D].西安:西北工业大学, 2006:4-6.ZHAO M Y.Failure analysis of composite mechanically fastened joints and study of effects on failure strength[D].Xi'an:Northwestern Polytechnical University, 2006:4-6(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10699-2007035477.htm |
| [2] | SAUNDERS W B, WORK D M. Shell morphology and suture complexity in upper carboniferous ammonoids[J].Paleobiology, 1996, 22(2): 189–218.DOI:10.1017/S0094837300016171 |
| [3] | SONG J H, REICHERT S, KALLAI L, et al. Quantitative microstructural studies of the armor of the marine threespine stickleback (gasterosteus aculeatus)[J].Journal of Structural Biology, 2010, 171(3): 318–331.DOI:10.1016/j.jsb.2010.04.009 |
| [4] | JASLOW C R, BIEWENER A A. Strain patterns in the horncores, cranial bones and sutures of goats (capra hircus) during impact loading[J].Journal of Zoology, 1995, 235(2): 193–210. |
| [5] | LI Y, ORTIZ C, BOYCE M C. Stiffness and strength of suture joints in nature[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 84(6Pt1): 2184–2188. |
| [6] | HARTWIG C W. Fractal analysis of sagittal suture morphology[J].Journal of Morphology, 1991, 210(3): 289–298.DOI:10.1002/(ISSN)1097-4687 |
| [7] | JASLOW C R. Mechanical properties of cranial sutures[J].Journal of Biomechanics, 1990, 23(4): 313–321.DOI:10.1016/0021-9290(90)90059-C |
| [8] | MEHRAN M, NEIL C, PAUL O, et al. Assessment of the role of sutures in a lizard skull:A computer modelling study[J].Proceedings Biological Sciences, 2009, 276(1654): 39–46.DOI:10.1098/rspb.2008.0863 |
| [9] | DE BLASIO VITTORIO F. The role of suture complexity in diminishing strain and stress in ammonoid phragmocones[J].Lethaia, 2007, 41(1): 15–24. |
| [10] | GAO H J. Application of fracture mechanics concepts to hierarchical biomechanics of bone and bone-like materials[J].International Journal of Fracture, 2006, 138(1-4): 101–137.DOI:10.1007/s10704-006-7156-4 |
| [11] | JASINOSKI S C, REDDY B D, LOUW K K, et al. Mechanics of cranial sutures using the finite element method[J].Journal of Biomechanics, 2010, 43(16): 3104–3111.DOI:10.1016/j.jbiomech.2010.08.007 |
| [12] | ORTIZ C, BOYCE M C. Materials science-Bioinspired structural materials[J].Science, 2008, 319(5866): 1053–1054.DOI:10.1126/science.1154295 |
| [13] | LI Y, ORTIZ C, BOYCE M C. Bioinspired, mechanical, deterministic fractal model for hierarchical suture joints[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2012, 85(3): 922–938. |
| [14] | LI Y, ORTIZ C, BOYCE M C. A generalized mechanical model for suture interfaces of arbitrary geometry[J].Journal of Mechanics Physics of Solids, 2013, 61(4): 1144–1167.DOI:10.1016/j.jmps.2012.10.004 |
| [15] | 曹金凤. Python语言在Abaqus中的应用[M].北京: 机械工业出版社, 2011: 2-3.CAO J F. The application of Python language in Abaqus[M].Beijing: China Machine Press, 2011: 2-3.(in Chinese) |
| [16] | BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J].Composites Science & Technology, 1996, 56(4): 439–449. |
