输出排队(Output Queueing,OQ)结构由于其work-conserving的特性,具有良好的吞吐率和时延性能,但由于其需要与端口数N等量的加速比,可扩展性不足。而输入排队(Input Queueing,IQ)结构的加速比为1,具有良好的可扩展性[1],但存在信头 (Head-of-Line,HoL)堵塞问题[2]。虚拟输出排队(Virtual Output Queuing,VOQ)结构[3]克服了HoL堵塞问题[4],但VOQ在调度控制过程中较为复杂,根本原因是输入输出竞争的密切耦合。联合输入交叉点排队(Combined Input-Crosspoint-Queued,CICQ)结构[5]通过在所有交叉节点(crosspoint)上配置一定容量(单个或多个信元)的缓存(crossbuffer)来解耦输入竞争和输出竞争,使得分组调度更有效地进行。本文讨论交叉缓存容量为单个信元(cell)的情况。
到目前为止,人们对CICQ结构的调度进行了大量研究,经典算法有输入端采用Round-Robin(RR)或其改进算法的RR-RR[6]、Differential Round-Robin(DRR)[7]、 Tracking Fair Quota Allocation(TFQA)[8]及Round-Robin with Longest Queue Detecting(RR-LQD)[9]等;以及以队长、交叉缓存占用率、阻塞时间为权重的最大权重匹配法例如Longest Queue First and RR(LQF-RR)[10]、Most Critical Buffer First(MCBF)[11]、 Shortest Crosspoint Buffer First(SCBF)[12]、the Shortest Buffer First and the Greatest Weigh buffer First(SBF-GWF) [13]、Hybrid Optimization Packet Scheduling(HOPS)[14]和Most Critical Queue First(MCQF)[15]等。RR及其改进算法实现简单,复杂度一般为O(1),且大多数算法对可接入业务的吞吐率可接近100%,但分组平均时延较大。最大权重匹配法以提高复杂度的代价来获取分组时延的下降。例如代表性的MCBF算法以特定输出和输入端口对应的crossbar中缓存的分组数目为权重,充分利用crossbar资源,但没有考虑VOQ的队列长度。而近来提出的SBF-GWF算法,在MCBF的基础上,进一步地,输出调度采用VOQ队长为权重,相比MCBF及其他算法,时延性能有显著的提高。
在已有的CICQ调度算法的研究中,即使是性能突出的SBF-GWF算法,相比采用最简单的First In First Out(FIFO)算法的OQ结构,其时延性能依然有较大差距。其根本原因是OQ结构能够使交换机工作于work-conserving状态,实现100%的吞吐率,从而使得时延下降。基于这个思路,不同于已有的算法,本文以实现或最大程度使得交换机工作于work-conserving状态为核心,研究提出了CICQ结构中的一种新算法,即交叉缓存队列均衡(Crossbuffer Queue Balance,CQB)算法,尽量均衡所有输出端口的crossbuffer分组占用。仿真结果显示其时延性能优于SBF-GWF算法。
首先,本文通过证明给出了CICQ结构crossbuffer容量为单个cell条件下可能实现work-conserving的前提,以及充分必要条件,并以此为基础,具体给出了CQB调度算法;其次,给出了CQB算法性能的数值仿真结果,并和现有的代表性算法进行了分析比较;最后,进行了小结并给出了今后研究工作。
1 Work-conserving的充要条件 图 1给出了CICQ交换结构。在本文讨论中,假设在同一个时隙,输入调度和输出调度同时进行,那么当前时隙通过输入调度进入crossbar的分组,最早只能在下个时隙进行输出调度。本文将一次的输入调度和其下个时隙的输出调度合称为一次调度。在CICQ结构中work-conserving的含义为:在任意一次调度中,若输入端有去往某个输出端口的分组,那么输出调度中该端口必有分组被调度离开交换机。本节将通过提出一些定理并给出证明,讨论CICQ结构中,在输入调度前后VOQ与crossbar的状态与work-conserving的关系。
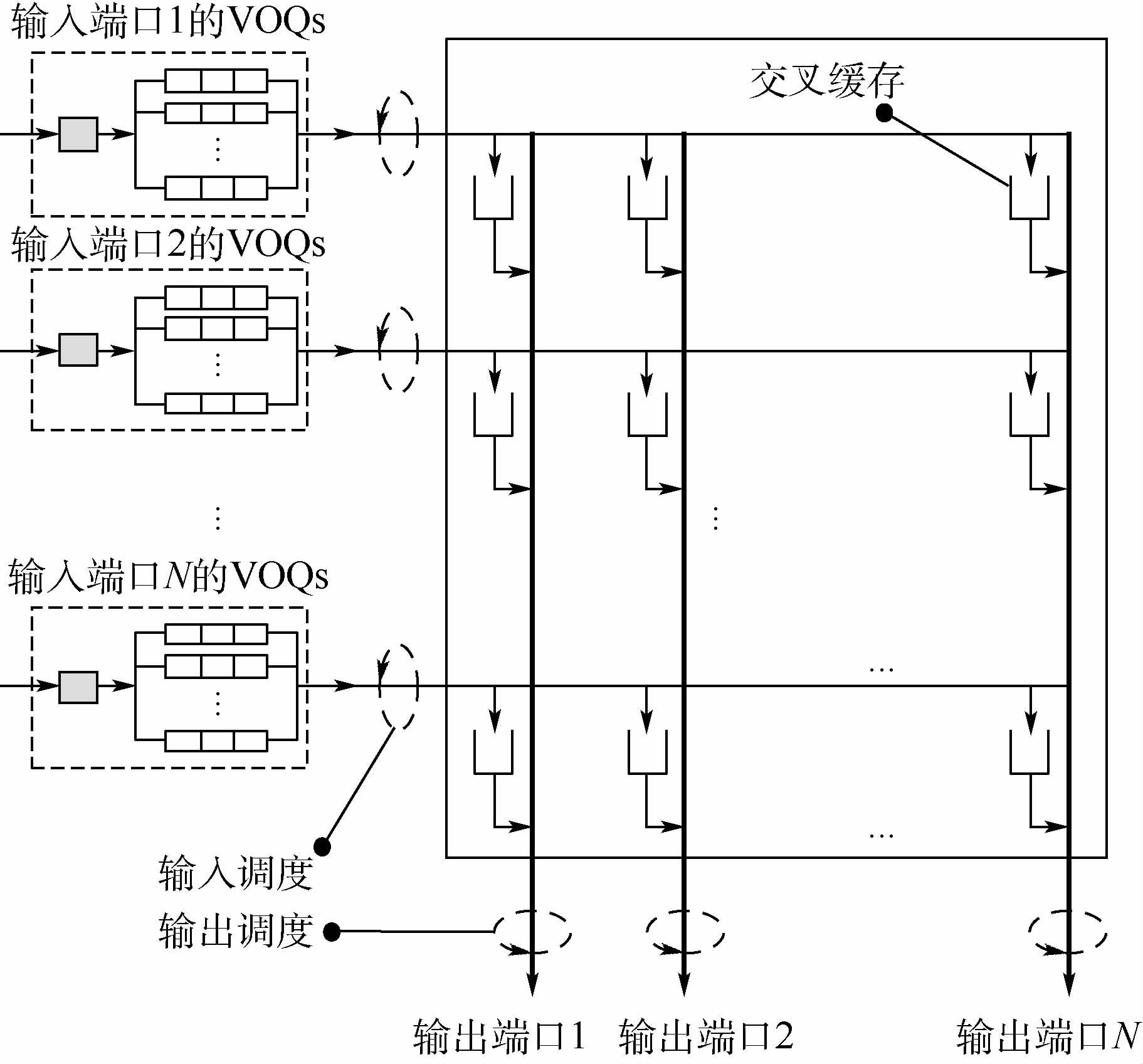 |
| 图 1 CICQ交换结构 Fig. 1 CICQ switch architecture |
| 图选项 |
符号说明:Vij为输入端口i和输出端口j对应的VOQ;N为交换机端口数;Cij为输入端口i和输出端口j对应的交叉缓存(crossbuffer);fij为Cij的状态标识,若Cij为空,则 fij=0,否则,fij=1;Bj为所有去往输出端口j的crossbuffer中排队分组的队列长度之和,即$Bj = \sum\limits_{i = 1}^N {{f_{ij}}} $;矩阵PN×N= {pij}N×N ,若Vij不为空且Cij 为空,则pij=1,否则pij=0;E为输出端口j的集合,E={1≤j≤N一次调度的开始时刻,VOQ中有去往输出端口j的分组,且Bj=0};M为集合E中的端口数目;QN×M为在矩阵P中取集合E中的全部输出端口对应的M列,组成新的矩阵QN×M。
定理1?在一次调度中,可以实现work-conserving的充要条件是,在输入调度后、输出调度前,任一j∈E,都有Bj > 0。
证明 充分性。对于该次调度没有分组传出的任一输出端口k,由work-conserving的定义可知,则在输入调度后、输出调度前必有Bk=0。因为在输入调度后、输出调度前,对所有的j∈E,都有Bj>0,而Bk=0,则k∈E。由集合E的条件可知,在该次调度的开始时刻(即输入调度前),由k∈E可以说明输出端口k至少不满足以下2个条件之一:①输入端VOQ中有去往输出端口k的分组。②Bk=0。
由于输入调度后Bk=0,而输入调度不会使Bk减小,又Bk恒非负,则该次调度开始时刻也有Bk=0。即输出端口k满足上述条件②,则必然不满足条件①。
即在该次调度中对于没有分组传出的任一输出端口k,证得在输入端没有去往该端口的分组。此为work-conserving的逆否命题,则该次调度可以实现work-conserving,充分性得证。
必要性。若在输入调度后、输出调度前,?j∈E,有Bj=0,那么本次调度输出端口j将没有分组传出。
而又因为j∈E,可知VOQ中有去往输出端口j的分组,但本次调度中输出端口j却无分组传出,则不满足work-conserving定义,即本次调度是非work-conserving的。必要性得证。??证毕
定理1给出了实现work-conserving,输入调度所要实现的目标,即对于有分组传输需求的输出端口,需要在输入调度后,其所对应的交叉节点缓存队列非空。例如在一次调度开始时刻,输入端VOQ和crossbar的状态分别为
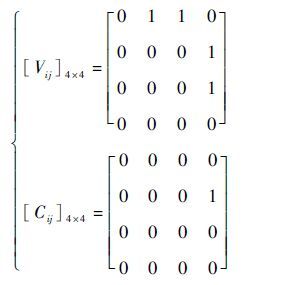 | (1) |
式中:0代表Vij或Cij为空;1代表非空。
此时只有B4=1非零,E={2,3}。输出端口1由于无传输需求,故不会影响work-conserving的实现与否;而输出端口4由于在输入调度前就有B4> 0,输入调度不会使Bj减小,则在输出调度前也必有B4> 0,可以保证本时隙有分组传出,也不会对实现work-conserving造成影响。故影响work-conserving实现的关键就在于集合E中的输出端口2和3,所以输入调度的目标是使得B2和B3在输出调度前均大于零,即定理1所阐述的work-conserving的充要条件。
而是否存在一种输入调度满足以上条件,这取决于输入调度前VOQ与crossbar的状态。
定理2?在一次调度中,时隙开始时刻存在一种输入调度可以完成work-conserving的充要条件是,矩阵Q对应的二分图最大匹配数可以达到M。
证明 充分性。若矩阵Q的列数为M,其对应二分图最大匹配数也可达到M,那么任取一种最大匹配,则该匹配矩阵UN×M每一列均有一个元素为1。
由于矩阵Q中的M列与集合E中的M个输出端口一一对应,则按照上述矩阵Q的最大匹配矩阵U进行输入调度,即调度匹配矩阵中对应位置元素为1的VOQ中的分组进入相应的crossbuffer,完成之后,对所有的j∈E,都有Bj=1>0。
则根据定理1,该次调度可以实现work-conserving。
必要性。若存在一种输入调度可以完成work-conserving,取其调度矩阵中集合E中的输出端口对应的M列组成新的矩阵SN×M。
对于所有j∈E,有输入调度前Bj=0,由定理1,有输入调度后Bj>0,则S中任一列均至少有一个元素非零为1,将这些每列中的一个非零元素取出组成新的矩阵UN×M,则其即为矩阵Q的匹配数为M的最大匹配矩阵。??证毕
定理2给出了通过合适的输入调度实现work-conserving的前提条件。这说明在理论上work-conserving并不能仅通过输入调度算法100%实现。例如图 2所示状态,有M=2,
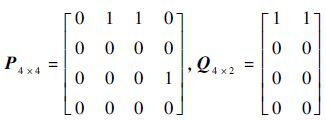
现就一次调度考虑,在输出调度完成后,对输出端口给出如下定义:
non-work-conserving端口为VOQ队列中有去往该输出端口的分组,但本次调度无分组传出的输出端口;work-conserving端口为non-work-conserving端口的补集。
推论1 在一次调度中,令通过调度能达到的最大work-conserving端口数为L,矩阵Q对应的二分图最大匹配数为K,则有
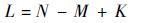 | (2) |
证明 最大work-conserving端口数为L,则最小non-work-conserving端口数为N-L,由定理2可得N-L=M-K,则有L=N-M+K。??证毕
由定理2可以看出,存在类似于图 2所示的某些业务状态,使得无论通过何种输入调度,均无法在该时隙实现work-conserving。
因此要尽可能实现交换机的work-conserving状态,调度算法除了要保证当前时隙实现work -conserving外,还需要尽量保证后续时隙不出现上述的不可能实现work-conserving的情况。
2 CQB算法 根据定理1,可以看出在当前时隙内,是否可以实现work-conserving的关键在于集合E中的输出端口所对应的crossbuffer队列,这些队列在输入调度前为空,而实现work-conserving的充要条件就是在输入调度后将其均变为非空。故在输入调度时,优先处理这些空的输出crossbuffer队列,为其寻找合适的输入端口使其建立匹配,并将相应分组调度进来。之所以称其为CQB算法,就是因为该算法优先处理Bj最小(一般为0)的输出crossbuffer队列,通过调度使其Bj提高,然后继续这个过程直至调度结束。至于输入端口的选择,根据传输需求来进行,传输需求说明如式(3)所示。当为输出端口1的crossbuffer队列选择匹配时,输入端口1和输入端口2均可供选择,但由于输入端口2只有去往输出端口1的分组,而输入端口1除此之外还有去往输出端口2的分组,则认为对于输出端口1,输入端口2的传输需求比输入端口1大,故选择输入端口2与输出端口1进行匹配。
 | (3) |
需要说明的是,CQB算法是一种输入调度的算法。在输出端,本文采用权重匹配的方式,如最大队长优先(Longest Queue First,LQF)、 Oldest Cell First(OCF)等,并根据输出调度的算法不同,将整个算法称为CQB-LQF算法、CQB-OCF算法等。
本文具体讨论CQB-LQF算法。方便起见,算法中的符号含义如下:ti为输入端口i包含的非空VOQ队列数目;Rj为满足Vij 不为空且Cij 为空的所有输入端口的集合;O为输出端口的集合;I为输入端口的集合;Wj为Rj与I的交集;pp为输入端口的优先级指针;pp为输出端口的优先级指针。
调度开始时令pi指向输入端口1,po指向输出端口1。CQB-LQF算法的具体步骤如下。
输入调度算法:
1) 每个时隙开始时,令O包含所有输出端口,I包含所有输入端口。
2) 如果O为空,则该时隙输入竞争裁决结束。
3) 从pp指向的输出端口开始,在O中选择第一个Bj最小的输出端口j,并将pp指向其下一个输出端口的位置。
4) 如果Wj为空,从O中剔除输出端口j,回到第2)步。
5) 从pp指向的输入端口开始,在Wj中选择第一个ti最小的输入端口i,并将pp指向其下一个输入端口的位置,将Vij的头信元发送到Cij 中。
6) 将Bj加1,从I中剔除输入端口i,更新Rj和所有的W,回到第3)步。
输出调度算法:
每个时隙中,对于每个输出端口j,选择满足Cij不为空且Vij队长最大的i,将Cij中的分组调度输出。同样仿照输入调度使用优先级指针裁决VOQ队长相等的情况。
3 性能仿真与比较 文献[13]将SBF-GWF算法与一些经典的算法(iSLIP、RR-RR、LQF-RR、 OCF-OCF、MCBF等)做了平均时延的仿真比较,可以看出在各种不同的业务以及不同的负载下,SBF-GWF算法的时延性能均优于其他经典算法。在本节,将用本文提出的CQB-LQF算法,与SBF-GWF算法同样在各种业务各个负载下进行仿真比较,并以OQ结构FIFO算法的结果作为参照。比较的性能除了吞吐率和平均时延外,还涉及到一个新的性能参数:non-work-conserving比率:
 | (4) |
式中:Tnwc为non-work-conserving的时隙数;TS为总仿真时隙数。Rnwc可以表征逼近work-conserving的程度,以此来观察work-conserving 对交换机性能的影响。
本文仿真时间为50万个时隙,交换机端口数为32×32。其中ON-OFF业务的平均突发长度(mean burst length)为120。仿真结果如下。
3.1 去向分布均匀业务的结果 由于在低负载下各算法的吞吐率基本为1,故观察归一化负载(下文简称“负载”)较高(0.90、0.95、0.99)时的吞吐率。
为区别吞吐率的细小差别,吞吐率数据以表格的形式呈现。均匀业务的吞吐率数据如表 1、表 2所示,可以看出在均匀业务下,2种算法的吞吐率几乎一致,并极接近于OQ。
表 1 均匀Bernoulli业务吞吐率 Table 1 Throughput under uniform Bernoulli traffic
| 算法 | 业务吞吐率 | ||
| l=0.90 | l=0.95 | l=0.99 | |
| SBF-GWF | 0.999 989 6 | 0.999 980 8 | 0.999 782 9 |
| CQB-LQF | 0.999 989 6 | 0.999 980 8 | 0.999 782 9 |
| OQ | 0.999 991 7 | 0.999 982 8 | 0.999 785 0 |
表选项
表 2 均匀ON-OFF业务吞吐率 Table 2 Throughput under uniform ON-OFF traffic
| 算法 | 业务吞吐率 | ||
| l=0.90 | l=0.95 | l=0.99 | |
| SBF-GWF | 0.997 505 7 | 0.986 224 8 | 0.975 294 1 |
| CQB-LQF | 0.997 505 5 | 0.986 229 5 | 0.975 294 4 |
| OQ | 0.997 508 2 | 0.986 232 2 | 0.975 298 2 |
表选项
图 2和图 3分别给出了2种均匀业务下的分组平均时延的对比结果。其中l为归一化负载,d为平均时延/时隙。可以看出在均匀业务下,2种算法的性能几乎相同,并且均与OQ基本一致,进一步改进幅度相当有限。
 |
| 图 2 均匀Bernoulli业务平均时延 Fig. 2 Average delay under uniform Bernoulli traffic |
| 图选项 |
 |
| 图 3 均匀ON-OFF业务平均时延 Fig. 3 Average delay under uniform ON-OFF traffic |
| 图选项 |
3.2 非均匀去向分布业务的结果 非均匀业务采用经典的Diagonal模型,其表达式为
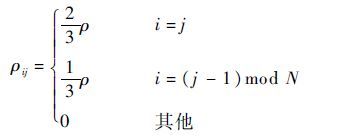 | (5) |
式中:ρij为Vij的负载;ρ为交换机输入负载。
非均匀业务的吞吐率如表 3、表 4所示,可以看出在与OQ的接近程度上,CQB-LQF算法明显优于SBF-GWF。
表 3 非均匀Bernoulli业务吞吐率 Table 3 Throughput under unbalanced Bernoulli traffic
| 算法 | 业务吞吐率 | ||
| l=0.90 | l=0.95 | l=0.99 | |
| SBF-GWF | 0.999 993 3 | 0.999 986 6 | 0.999 920 3 |
| CQB-LQF | 0.999 993 5 | 0.999 989 8 | 0.999 942 7 |
| OQ | 0.999 996 0 | 0.999 992 8 | 0.999 958 8 |
表选项
表 4 非均匀ON-OFF业务吞吐率 Table 4 Throughput under unbalanced ON-OFF traffic
| 算法 | 业务吞吐率 | ||
| l=0.90 | l=0.95 | l=0.99 | |
| SBF-GWF | 0.998 737 2 | 0.996 882 0 | 0.991 328 3 |
| CQB-LQF | 0.998 817 8 | 0.997 234 8 | 0.992 578 5 |
| OQ | 0.999 052 4 | 0.997 835 2 | 0.995 108 1 |
表选项
图 4、图 5给出了在非均匀业务高负载条件下分组平均时延的结果对比。从中可以看出,CQB-LQF算法的平均时延也明显优于SBF-GWF算法,并且与OQ的接近程度几乎是SBF-GWF算法的2倍。
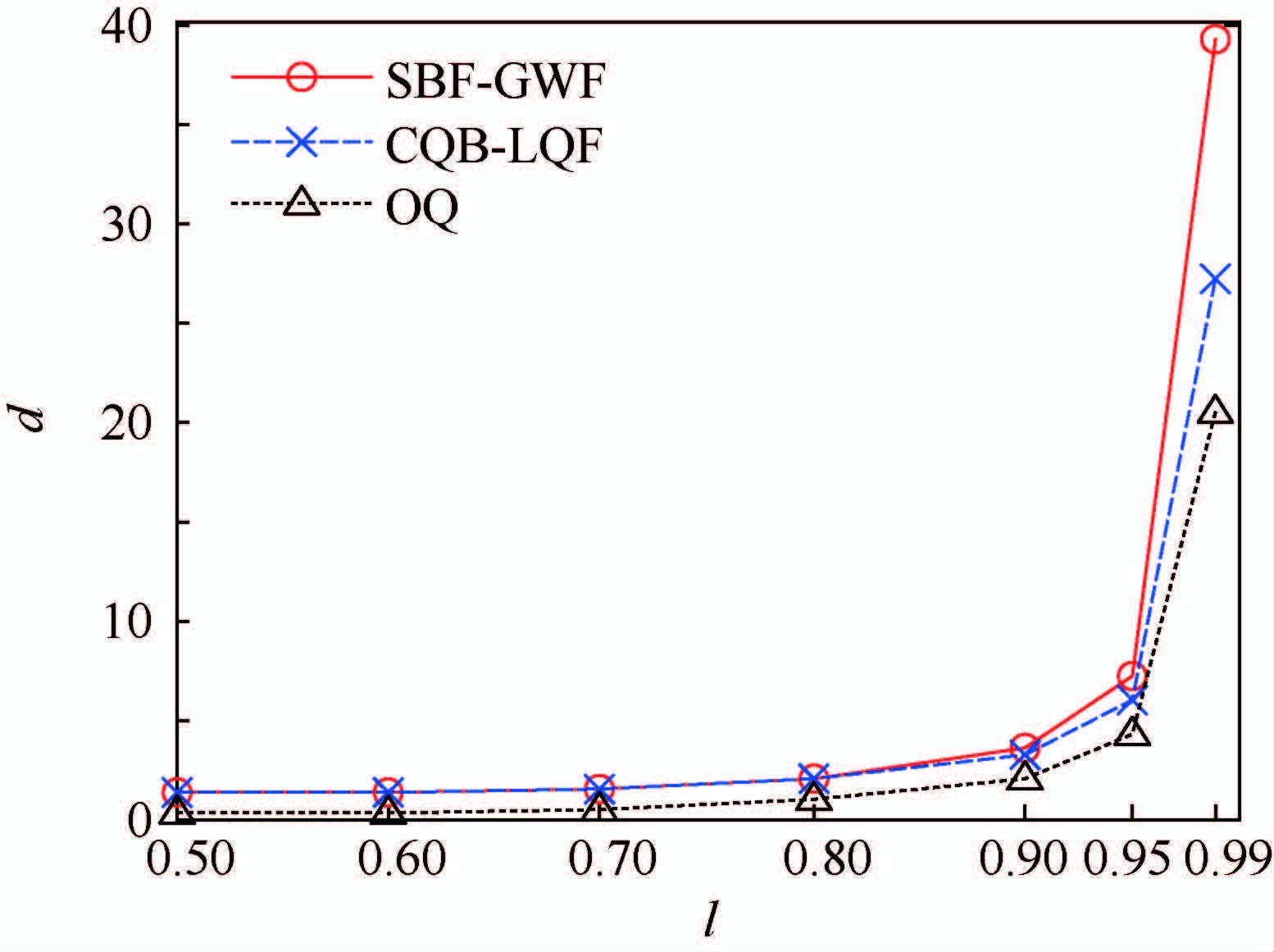 |
| 图 4 非均匀Bernoulli业务平均时延 Fig. 4 Average delay under unbalanced Bernoulli traffic |
| 图选项 |
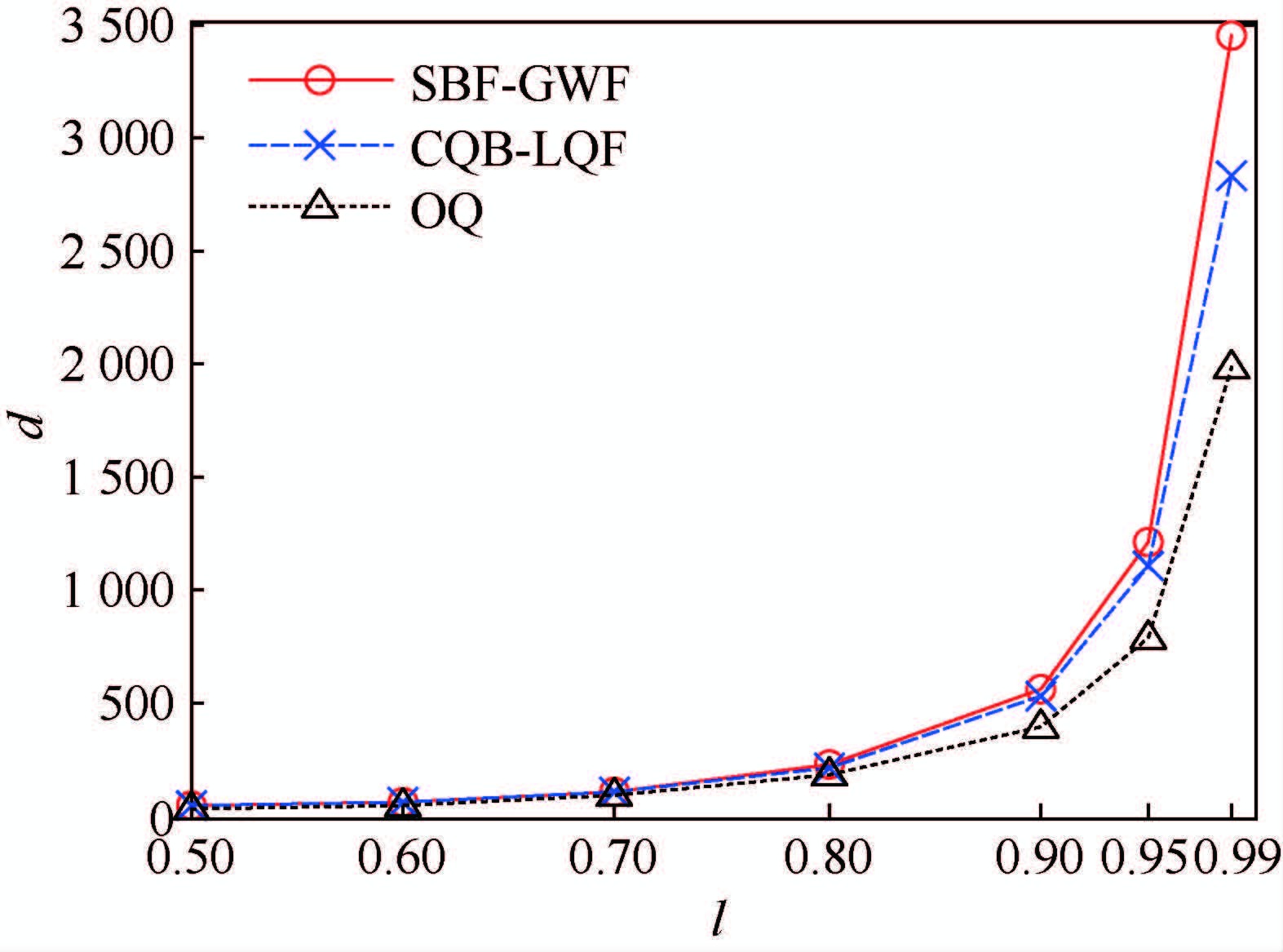 |
| 图 5 非均匀ON-OFF业务平均时延 Fig. 5 Average delay under unbalanced ON-OFF traffic |
| 图选项 |
CQB-LQF在非均匀业务下吞吐率和平均时延性能的优势,体现了追求尽可能逼近work-conserving这一算法设计思路的作用。这一点可以由图 6、图 7看出,在大部分情况下,尤其是负载较高时,CQB-LQF算法的Rnwc值显著低于SBF-GWF算法,即CQB-LQF算法更逼近work-conserving。
 |
| 图 6 非均匀Bernoulli业务Rnwc Fig. 6 Rnwc under unbalanced Bernoulli traffic |
| 图选项 |
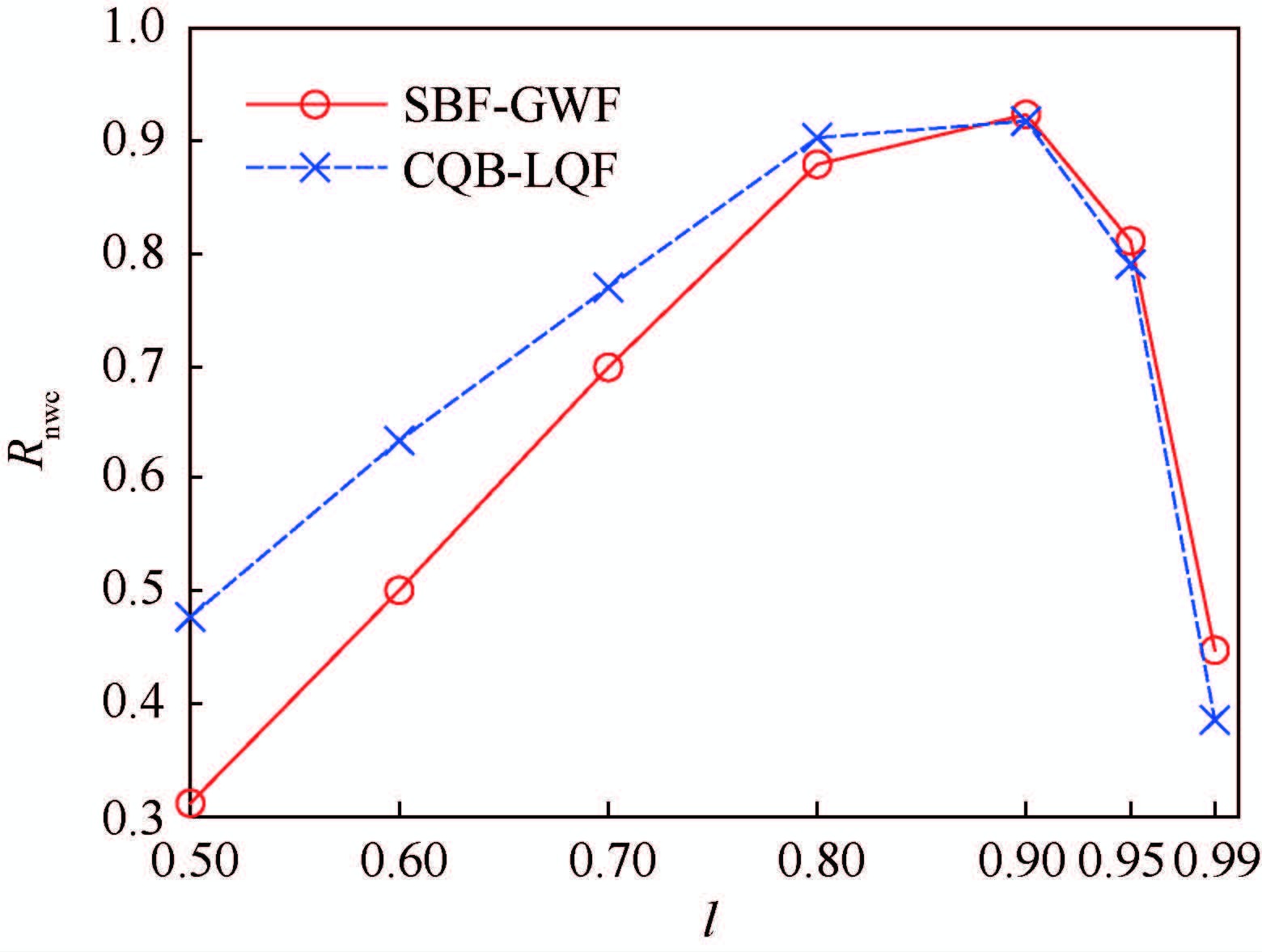 |
| 图 7 非均匀ON-OFF业务Rnwc Fig. 7 Rnwc under unbalanced ON-OFF traffic |
| 图选项 |
对于图 7所示的非均匀ON-OFF业务负载较低的情况下,CQB-LQF算法与SBF-GWF相比,致力于实现work-conserving,但Rnwc反而较高的现象,其原因可以由定理2进行解释。定理2表明了输入调度算法实现work-conserving有前提条件,这个前提条件的满足与否受VOQ的状态影响,更进一步受业务到达的影响。而CQB-LQF算法着重考虑当前时隙的work-conserving实现,没有更多地考虑业务到达情况,这样做是考虑了算法的简单。而ON-OFF业务和Bernoulli业务相比,业务到达的因素对调度的影响前者更明显,对调度算法的要求更大,使得出现了上述现象。这一点由图 5中ON-OFF业务和图 6中Bernoulli业务两种算法对比结果的差异可以说明。
上述现象为今后对CQB算法进一步的改进提出了方向,即可以加入一些关于业务特性和状态的考虑,以进一步提升work-conserving实现比率和时延性能。但在高速网络中算法的简单也是同样重要的,同时CQB-LQF算法的时延性能比SBF-GWF更好,因此可以说CQB-LQF算法是一种性能更优的调度算法。而work-conserving实现比率与负载大小、业务状态等因素更详细具体的关系,有待于进一步地深入研究。
4 结 论 1) 不同于已有基于轮询以及以队长或时延等为权重实现最大权重匹配的研究,本文以交换机最大程度工作于work-conserving状态为目标,讨论并证明交叉节点容量为单个cell的CICQ结构实现work-conserving的充分且必要条件。
2) 以上述条件为基础,研究提出了一种新的输入调度算法——CQB算法。通过仿真与现有研究中性能突出的SBF-GWF算法进行对比,结果显示在均匀业务中,CQB-LQF算法与SBF-GWF性能相近,而在非均匀业务中,CQB-LQF算法性能更优。
由于CQB算法是一种输入调度算法,在未来的研究中也可进一步研究相应的输出调度算法,使之更为逼近work-conserving。
参考文献
| [1] | 熊庆旭. 输入排队结构交换机分组调度研究[J].通信学报, 2005, 26(6): 118–129.XIONG Q X. Research on packet scheduling in input-queued switches[J].Journal on Communications, 2005, 26(6): 118–129.(in Chinese) |
| [2] | KAROL M J, HLUCHYJ M G, MORGAN S P. Input versus output queueing on a space-division packet switch[J].IEEE Transactions on Communications, 1987, 35(12): 1347–1356.DOI:10.1109/TCOM.1987.1096719 |
| [3] | NONG G, HAMDI M. On the provision of quality-of-service guarantees for input queued switches[J].IEEE Communications Magazine, 2000, 38(12): 62–69.DOI:10.1109/35.888259 |
| [4] | MCKEOWN N, MEKKITTIKUL A, ANANTHARAM V, et al. Ach-ieving 100% throughput in an input-queued switch[J].IEEE Transactions on Communications, 1999, 47(8): 1260–1267.DOI:10.1109/26.780463 |
| [5] | NABESHIMA M. Performance evaluation of a combined input-and crosspoint-queued switch[J].IEICE Transactions on Communications, 2000, 83(3): 737–741. |
| [6] | ROJAS-CESSA R,OKI E,JING Z,et al.CIXB-1:Combined input-one-cell-crosspoint buffered switch[C]//2001 IEEE Workshop on High Performance Switching and Routing.Piscataway,NJ:IEEE Press,2001:324-329. |
| [7] | LUO J,LEE Y,WU J.DRR a fast high-throughput scheduling algorithm for combined input crosspoint-queued cicq switches[C]//IEEE 20th IEEE International Symposium on Modeling,Analysis and Simulation of Computer and Telecommunication Systems.Piscataway,NJ:IEEE Press,2005:329-332. |
| [8] | HUA N,WANG P,JIN D,et al.Simple and fair scheduling algorithm for combined input-crosspoint-queued switch[C]//IEEE International Conference on Communications,ICC' 2007.Piscataway,NJ:IEEE Press,2007:6305-6310. |
| [9] | YUN Z,PENG L,ZHAO W,et al.RR-LQD:A novel scheduling algorithm for CICQ switching fabrics[C]//Proceedings of the 15th Asia-Pacific Conference on Communications,APCC 09.Piscataway,NJ:IEEE Press,2009:846-849. |
| [10] | JAVIDI T,MAGILL R,HRABIK T.A high-throughput scheduling algorithm for a buffered crossbar switch fabric[C]//IEEE International Conference on Connmunications,ICC' 2001.Piscataway,NJ:IEEE Press,2001:1586-1591. |
| [11] | MHAMDI L,HAMDI M.CBF:A high-performance scheduling algorithm for buffered crossbar switches[C]//Workshop on High Performance Switching and Routing,2003,HPSR.Piscataway,NJ:IEEE Press,2003:67-72. |
| [12] | ZHANG X,BHUYAN L N.An efficient scheduling algorithm for combined input-crosspoint-queued (CICQ) switches[C]//IEEE Global Telecommunications Conference,2004.GLOBECOM'04.Piscataway,NJ:IEEE Press,2004,2:1168-1173. |
| [13] | GAO Z,ZENG H,XIA Y,et al.SBF-GWF scheduling for combined input-crosspoint-queued (CICQ) switches[C]//2011 6th International Conference on Computer Sciences and Convergence Information Technoloy(ICCIT).Piscataway,NJ:IEEE Press,2011:404-408. |
| [14] | 高志江, 曾华燊, 申志军. 混合优化的 CICQ 交换结构调度算法[J].计算机应用, 2012, 32(7): 1791–1795.GAO Z J, ZENG H Y, SHEN Z J. Hybrid optimization packet scheduling algorithm for CICQ switches[J].Journal of Computer Applications, 2012, 32(7): 1791–1795.(in Chinese) |
| [15] | WANG X T,WANG Y W,LI S C,et al.A novel high performance scheduling algorithm for crosspoint buffered crossbar switches[C]//International Conference on Computer Information Systems and Industrial Applications.Paris:Atlantis Press,2015:59-62. |
