在目标跟踪的实际过程中,量测数据是由雷达在极坐标下观测得到,而系统模型是在直角坐标系下建立的,二者需要进行非线性转换。针对非线性估计问题,****们提出了扩展卡尔曼滤波(Extend Kalman Filter,EKF)、基于无迹变换(Unscented Transformation,UT)的不敏卡尔曼滤波(Unscented Kalman Filter,UKF)等多种非线性滤波方法,但这些滤波方法自身都存在一些缺陷。2009年,Arasaratnam和Haykin[8]首次提出基于Cubature变换的容积卡尔曼滤波(Cubature Kalman filter,CKF),CKF是一种基于对非线性概率密度函数进行近似的高斯滤波算法,无需对非线性模型线性化,比EKF、UKF具有更好的非线性逼近能力;孙枫和唐李军[9]经过证明指出当系统维数n>3时,CKF比UKF的滤波精度更高;对强非线性问题,CKF克服了EKF和UKF的应用局限性,数值稳定性更强[10];从滤波器结构来看,CKF无需设置滤波参数,而UKF需要合理选择滤波参数[11];为了提高CKF的滤波性能,Arasaratnam等[12]又进一步提出了平方根容积卡尔曼滤波(Square Root Cubature Kalman Filter,SRCKF)。但是当系统模型不准确或状态突变导致出现不良量测时,CKF和SRCKF的滤波性能都可能恶化。
考虑上述问题,****们将强跟踪滤波(Strong Tracking Filter,STF)的思想与容积卡尔曼滤波相结合,董鑫等[13]提出ST-CKF算法用于解决非线性故障诊断问题;徐树生等[14-15]给出ST-SRCKF并应用到动力定位系统中,但这些强跟踪算法引入的均是单一的渐消因子,难以对系统状态的每个变量都准确估计。此外,为了对超高速强机动目标的机动过程准确建模,****们先后提出了Jerk模型、CS-Jerk模型及其改进方法[7, 16-18],然而这些模型仍存在自适应性不足的问题。
本文针对超高速强机动目标运动模型难以准确建立以及超高速强机动运动阶段量测噪声增大的问题,选择ST-SRCKF算法进行滤波,并在文献[15]的ST-SRCKF算法中引入多重渐消因子,借鉴文献[19]中ST-UKF的推导过程,分析直接在状态预测协方差矩阵中引入渐消因子对滤波结果的不良影响,重新确定了渐消因子的作用位置和求解方法;其次,针对CS-Jerk模型的缺陷进行改进,根据新息的统计学特性,即新息协方差矩阵的迹服从卡方分布[20],由卡方检验原理构造活化函数并得到活化因子,在线更新模型参数,从而实时调整状态噪声协方差矩阵和滤波增益矩阵,减小了目标状态估计误差,改进CS-Jerk模型与本文滤波算法的结合实现了对超高速强机动目标的高精度跟踪,仿真实验验证了本文算法的可行性。
1 平方根容积卡尔曼滤波 CKF算法本质上是一种求积近似高斯滤波,考虑如下积分:
 | (1) |
式中:I为关于f的积分;f为关于X的求积非线性函数;X为系统的状态向量;Rn为n维实向量,n为系统状态的维数。
利用一组2n个等权值分布的Cubature点{χi, ωi}对式(1)实现非线性逼近,即
 | (2) |
式中:N(·)为正态分布函数;

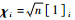
 | (3) |
假设式(1)中的状态向量
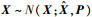
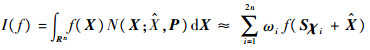 | (4) |
式中:

标准的CKF滤波算法见文献[8],然而在CKF算法中,滤波器的每一步递推计算都需要进行矩阵开方,使得误差协方差阵可能会失去对称性和正定性,造成滤波中断,滤波器数值稳定性变差。SRCKF在CKF中引入正交三角分解,不需要对状态协方差矩阵进行开方运算,保证了滤波器的稳定性,SRCKF步骤见文献[12]。
2 多重渐消因子强跟踪SRCKF 2.1 多重渐消因子的引入 假设非线性系统描述如下:
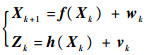 | (5) |
式中:f(·)和h(·)分别为系统的非线性状态转移函数和量测函数;Xk、Xk+1分别为k时刻和k+1时刻系统的n维状态向量;Zk为k时刻系统的m维量测向量;wk为协方差矩阵为Qk的状态噪声;vk为协方差矩阵为Rk的量测噪声。
通常情况下,系统状态噪声wk和量测噪声vk都是零均值的高斯白噪声,滤波器正常工作,且根据新息(残差)理论可知,滤波输出满足[21]:
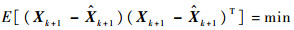 | (6) |
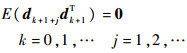 | (7) |
式中:min为等式左边期望的最小值;

式(6)表示滤波输出为最小方差估计,而式(7)要求不同时刻的残差序列保持正交,对于E(dk+1+jdk+1T),文献[19]证明存在定理1:
定理1????在式(5)中,令εk=Xk-

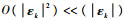
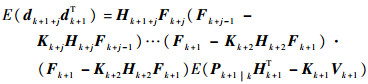 | (8) |
式中:
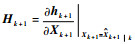

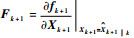
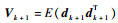
超高速强机动目标在高速运动或发生突变机动时,模型准确性更差,传感器的观测精度降低,量测噪声增大,此时的观测量可看作不良量测,由定理1可知,当模型不确定性增大或系统出现不良量测,将造成k+1时刻残差向量协方差阵偏差过大,又因为k+1时刻的增益矩阵Kk+1已经确定,故很难保证式(8)成立,导致不同时刻的残差向量失去正交性,即式(7)不成立。
为了满足条件式(7),基于EKF的STF在状态预测协方差矩阵中引入渐消因子,实时在线调整滤波增益矩阵,使不同时刻的滤波残差保持相互正交,抑制了滤波发散和鲁棒性差的问题。ST-SRCKF算法结合了STF和SRCKF的优点,其核心思想也是引入渐消因子λ′k+1修正状态预测协方差矩阵,当未引入渐消因子时,状态预测协方差矩阵为Pk+1|k(l),上标(l)表示未引入渐消因子,引入渐消因子后,状态预测协方差矩阵为Pk+1|k。
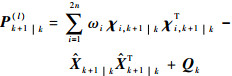 | (9) |
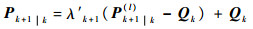 | (10) |
式中:χik+1|k, 为SRCKF算法中第j个容积点经函数f(·)传播后的一步预测值。
与STF不同的是,文献[15]中的ST-SRCKF算法精度更高,且无需计算雅可比矩阵,但该ST-SRCKF算法与之前的ST-CKF算法采用的都是单一渐消因子,对于低维系统,一般可以实现状态量的准确估计,而对于超高速强机动目标这样的高维系统,系统状态中的变量多,模型不确定性和不良量测对不同变量的影响程度也不同,采用单一的渐消因子难以保证对每个变量都能很好地跟踪。文献[22]将多重渐消因子引入ST-UKF,改善了ST-UKF的滤波性能,多重渐消因子实际上是一种变尺度调节方法,其原理是:考虑到目标机动对目标状态各分量的影响不同,因此针对各分量分别设计渐消因子,并由各渐消因子构成渐消因子矩阵,各状态分量对应不同的调节速率,从而改善算法的滤波性能。
因此本文在ST-SRCKF算法中采用多重渐消因子,对各状态变量分别调整,进而提高ST-SRCKF算法的滤波稳定性和滤波精度。
2.2 ST-SRCKF结构改进 文献[19]根据正交性原理重新推导并提出了一种改进的ST-UKF算法,指出已有的ST-UKF算法均如式(11)所示引入渐消因子λ′k+1对状态预测重新定义,即
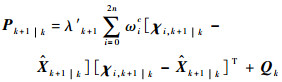 | (11) |
式中:ωic为χik+1|k对应的权值,上标c为协方差。
文献[19]分析并证明,对于引入渐消因子前后的残差d′k+1和dk+1,当按照式(11)在Pk+1|k中引入渐消因子λ′k+1,若滤波器使用d′k+1得到系统状态估计,则不能确保式(6)成立;若使用dk+1得到系统状态估计,则不能确保式(7)成立。改进的ST-UKF算法未使用渐消因子修正状态预测协方差矩阵,而是引入渐消因子重新定义量测预测协方差矩阵PZZ, k+1和互协方差矩阵PXZ, k+1。借鉴这一思想,因式(10)与式(11)结构相同,故同样可以证明,若按照式(10)在SRCKF算法中引入渐消因子,则很难保证强STF算法的2个条件(式(6)和式(7))均成立。经上述讨论,针对非线性系统式(5),本文提出改进的ST-SRCKF算法,其步骤如下:
初始化:给定X的初始值为X1,初始预测值和协方差矩阵分别为

时间更新:
1)计算容积点(i=1, 2, …, 2n)
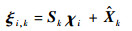 | (12) |
2)计算经非线性函数传播后的容积点
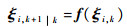 | (13) |
3)计算状态一步预测值

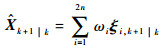 | (14) |
4)状态误差方差矩阵平方根的一步预测为
 | (15) |
式中:Tria(·)为矩阵正交三角分解;SQ为状态噪声协方差矩阵的平方根;ξk+1k定义为
 | (16) |
式中:
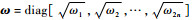
渐消因子的计算及量测更新:
1)计算容积点
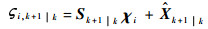 | (17) |
2)计算经量测方程传播后的容积点
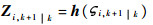 | (18) |
3)量测量一步预测为
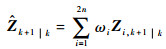 | (19) |
4)计算新息及新息协方差矩阵的平方根
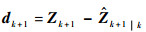 | (20) |
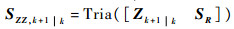 | (21) |
式中:SR为量测噪声协方差矩阵的平方根;Zk+1k表达式为
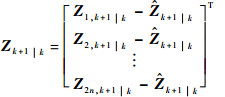 | (22) |
可得未引入渐消因子的新息协方差矩阵为
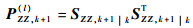 | (23) |
5)计算未引入渐消因子的互协方差矩阵
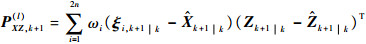 | (24) |
6)根据2.3节(式(30)~式(40))可得多重渐消因子矩阵λk+1,并分别计算引入渐消因子后的PZZ, k+1和PXZ, k+1,即
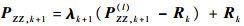 | (25) |
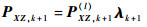 | (26) |
式中:矩阵λk+1为与PZZ, k+1(l)同维的对角阵。
7)计算卡尔曼滤波增益,即
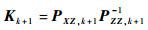 | (27) |
8)状态及状态协方差矩阵平方根更新分别为
 | (28) |
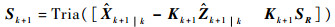 | (29) |
分析上述算法可知,与文献[15]中ST-SRCKF相比,本文的算法借鉴了文献[22]中采用多重渐消因子的ST-UKF算法,考虑了目标机动对目标状态各变量的不同影响,用多重渐消因子代替ST-SRCKF算法中的单一渐消因子;同时,改进的ST-SRCKF没有将渐消因子引入到状态预测协方差矩阵Pk+1k(l)中,而是将其引入到新息协方差PZZ, k+1(l)和互协方差更新式PZZ, k+1(l)中,因此多重渐消因子矩阵的结构也不同于文献[22]。
2.3 多重渐消因子的确定 根据定理1,ST-SRCKF保持残差序列正交化的充分条件为
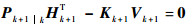 | (30) |
文献[14]中推导了SRCKF中互协方差矩阵的表达式为
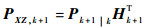 | (31) |
则式(30)可以改写为
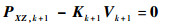 | (32) |
又根据式(27)可得
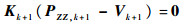 | (33) |
Kk+1为非零矩阵,故式(30)成立的充分条件可等效为
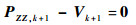 | (34) |
将式(25)代入式(34),得
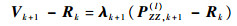 | (35) |
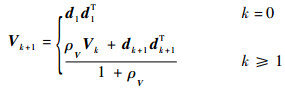 | (36) |
式中:0 < ρV≤1为遗忘因子,下标V为新息的方差矩阵。
多重渐消因子矩阵λk+1的次优解法如下:令多重渐消因子矩阵
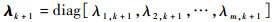 |
其中:m为观测向量维数;λi, k+1为对应每个量测量的渐消因子,且
 | (37) |
式中:ai为由先验信息确定的常数,当量测量误差很大或变化很快时,选择较大的ai,否则ai可均取为1;ck+1为待求因子。
考虑式(35),令
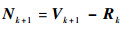 | (38) |
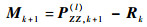 | (39) |
对等式(35)两边矩阵同时求迹,得待求因子ck+1的表达式为
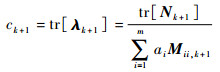 | (40) |
式中:tr[·]为矩阵求迹。
将ck+1代入式(37),可得多重渐消因子矩阵λk+1,由推导过程可知,矩阵λk+1与量测向量的维数相同,且能够更直接地反映量测数据的变化。
3 改进的CS-Jerk模型 CS-Jerk模型借鉴“当前”统计模型的结构,用修正的瑞利分布描述加加速度的统计特性,将加加速度j的一步预测值
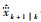
3.1 CS-Jerk模型的缺陷 在CS-Jerk模型中,目标的机动频率α和j的最大值jmax、j-max等参数决定了模型的结构,若目标进行突变的强机动,CS-Jerk模型将从2个方面制约目标的跟踪精度:
1) 在目标运动的实际过程中,目标为了实现战术目的或躲避对方防御系统的跟踪和锁定,需要进行强机动等运动,其运动状态将发生突变,机动频率α必然是不断变化的,但CS-Jerk模型中机动频率α取为固定值,影响目标跟踪精度。
2) CS-Jerk模型中机动加加速度的最大值jmax、j-max取为定值,当目标发生机动时,若
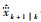
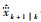
为了克服CS-Jerk模型的上述缺陷,需对算法的结构进行改进。
3.2 改进的CS-Jerk模型算法 根据CS-Jerk模型算法,在直角坐标系中建立系统的状态方程并离散化,得
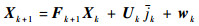 | (41) |
式中:jk为加加速度均值;Uk为输入矩阵。
量测方程为
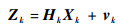 | (42) |
通常通过观察滤波残差的变化来判断目标的机动情况,
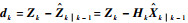
文献[20]指出,若n维随机向量服从零均值的高斯分布,则该向量的协方差矩阵亦为随机矩阵,且矩阵的迹服从自由度为n的χ2分布。在目标跟踪的滤波过程中,滤波残差是m维的随机向量,当目标未发生机动时,滤波残差序列服从零均值的高斯分布,且残差协方差阵的迹服从自由度为m的χ2分布,故可以通过检验残差协方差矩阵迹的统计学分布来判断目标的机动情况。
目标的机动通过量测值的变化直接体现出来,量测值的变化又在残差的变化中体现,而残差协方差矩阵的迹tr[PZZ, k]反映了残差序列的统计学特性,于是可得活化因子fk的计算步骤如下:
1) 通过上述分析并由卡方检验原理,可确定目标机动的判断函数,即
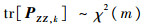 | (43) |
2) 由统计学中的Neyman-Pearson定理,可提出假设检验如下:
H0:tr[PZZ, k]≤ε;H1:tr[PZZ, k]>ε,取ε为指标来判断目标的机动情况,当目标未进行机动,H0成立;当目标进行机动,H1成立。
根据P=P{tr[PZZ, k]≥ε|H0}=ρ,可求得指标ε。若给定显著水平ρ=0.01,由P=P{tr[PZZ, k]≥ε|H0}=ρ,查卡方分布表可确定ε=9.21,此时漏警率P{tr[PZZ, k] < ε|H1}值最小。
3) 定义归一化残差的平方d=dkTPZZ, k-1dk。
4) 进一步通过活化函数引入活化因子,即
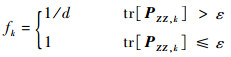 | (44) |
为了提高加加速度估计的鲁棒性,采用移动平均法确定当前时刻机动加加速度的均值,令
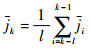 | (45) |
式中:l为步长,通常根据目标的类型取3~10之间的整数;ji为i时刻机动加加速度的均值,i的范围为k-l~k-1;jk为当前时刻前l个时刻加加速度的平均值,在算法中将它作为当前时刻机动加加速度的均值。
与CS-Jerk模型同理,机动加加速度j的预测值方差为
 | (46) |
图 1为改进的CS-Jerk模型算法结构,jmax、j-max为最大机动加加速度的初始值,初始机动频率为α0,将活化因子fk代入即可对机动频率和jmax、j-max进行实时更新,并根据j的修正瑞利分布假设得到改进算法中j的方差为
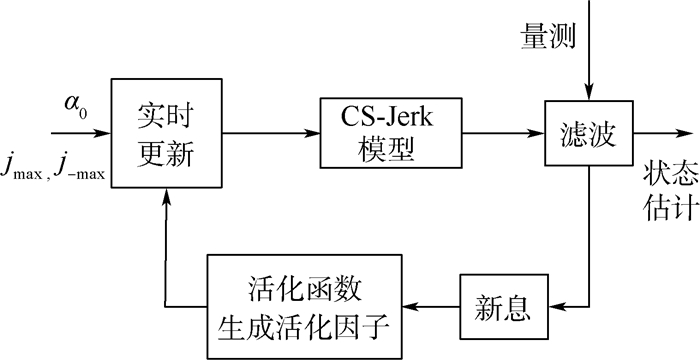 |
| 图 1 改进CS-Jerk模型结构 Fig. 1 Structure of modified CS-Jerk model |
| 图选项 |
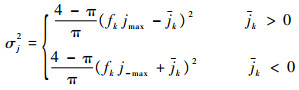 | (47) |
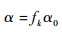 | (48) |
由图 1可知,改进的CS-Jerk模型通过自适应调整α和jmax、j-max,使得矩阵Fk+1、Uk和Qk能够根据目标的机动情况实时更新,提高了目标的建模准确度。
将式(47)和式(48)代入文献[17]的CS-Jerk模型中,目标状态方程仍为式(41),状态转移矩阵Fk+1的表达式为
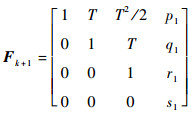 | (49) |
式中:T为采样间隔,其余变量定义为
 | (50) |
输入控制矩阵Uk表达式为
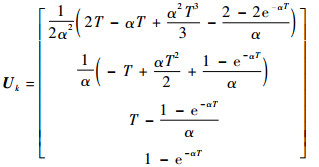 | (51) |
状态噪声协方差Qk如式(52)所示,矩阵各元素表达式与CS-Jerk模型相同。
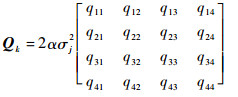 | (52) |
4 仿真验证 以单雷达单机动目标为研究对象,系统状态方程在直角坐标系下建立,量测数据为雷达观测到的二维极坐标数据。本文所研究的超高速强机动目标以美军HTV-2为实际背景,同时为了验证算法的可行性,通常都是在更为严苛的环境下进行仿真实验,因此本文假设目标的最大速度将达到20 Ma,最大加速度达到40 g,最大加加速度达到6 g/s,设置仿真条件:仿真时长为200 s,采样时间间隔为T=1 s,目标的真实运动轨迹为:
x轴,即高度方向,目标做强机动运动,目标的初始位置、速度、加速度和加加速度分别为10 000 m、-300 m/s、0 m/s2和0 m/s3。0~20 s,目标匀速运动,20~30 s、30~40 s分别做加速度为150 m/s2、-120 m/s2的匀加速度运动,40~60 s匀速运动,60~80 s做加速度为300 m/s2的匀加速度运动,80~90 s做加加速度为-60 m/s3的匀加加速度运动,90~110 s之间做20 s的匀加速运动,110~120 s做10 m/s3的匀加加速度运动,120~140 s匀加速运动,之后10 s进行60 m/s3的匀加加速度运动,150~160 s做匀加速运动,160~200 s保持匀速运动。
y轴为水平方向,目标初始位置为0 m,目标进行200 s速度为200 m/s的匀速运动。
假设观测雷达位于坐标原点,k时刻目标状态向量为
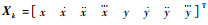
 | (53) |
式中:vk~N(0, Rk),Rk=diag[σr2, σθ2]为噪声协方差矩阵,σr=100 m,σθ=0.1°。
仿真实验中目标的初始状态设定为
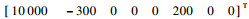
在上述条件下完成2个仿真,每个仿真进行100次蒙特卡罗实验,仿真1验证改进CS-Jerk模型对目标跟踪精度的提高作用,仿真2验证本文ST-SRCKF算法对滤波性能的改善作用。机动目标跟踪算法的性能指标主要包括跟踪精度和处理时间等,而跟踪精度是算法的核心指标[23],所以提高目标的跟踪精度是本文算法的主要任务,以目标状态估计值的均方根误差(ERMSE)、均值误差(EME)以及100次蒙特卡罗仿真的平均耗时作为统计指标来衡量改进算法的性能。状态估计值的均方根误差和均值误差分别定义为
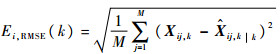 | (54) |
 | (55) |
式中:Xij, k和

仿真1 ????分别以Jerk模型、CS-Jerk模型和本文提出的改进CS-Jerk模型建立系统状态方程,采用文献[15]中ST-SRCKF进行滤波,比较3种模型算法的跟踪结果。图 2给出了目标运动真实轨迹及采用改进CS-Jerk模型建模时目标的跟踪轨迹,图 3给出了x轴方向目标的实际速度和加速度曲线,y轴方向目标匀速运动,速度和加速度曲线不必给出。
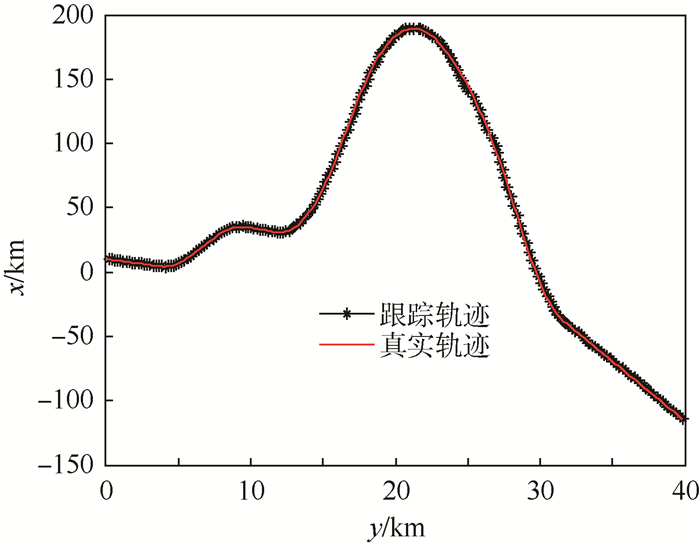 |
| 图 2 目标跟踪轨迹与真实轨迹 Fig. 2 Target tracking track and real track |
| 图选项 |
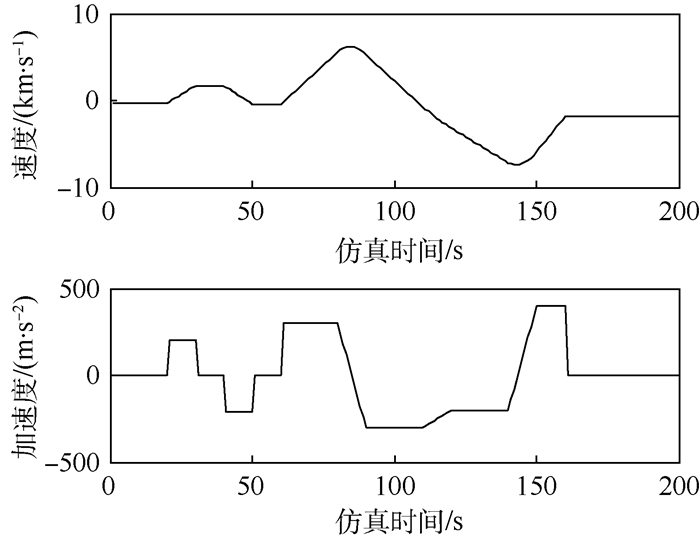 |
| 图 3 x轴目标的实际速度和加速度曲线 Fig. 3 Real velocity and acceleration curves of target in axis x |
| 图选项 |
图 4和图 5分别为x、y轴方向上,3种不同模型算法目标跟踪的位置、速度的均方根误差,表 1为x、y轴方向上目标状态的平均误差。
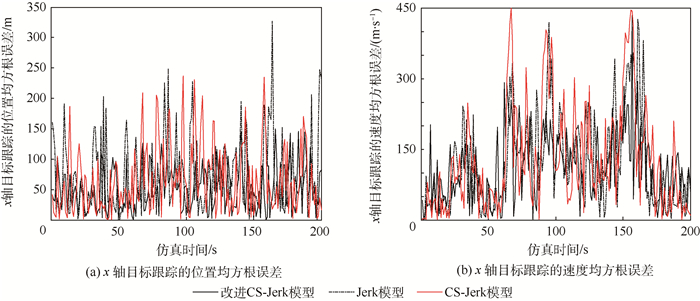 |
| 图 4 仿真1 x轴目标跟踪的位置和速度均方根误差 Fig. 4 Target tracking location and velocity root mean square errors of axis x in simulation one |
| 图选项 |
 |
| 图 5 仿真1 y轴目标跟踪的位置和速度均方根误差 Fig. 5 Target tracking location and velocity root mean square errors of axis y in simulation one |
| 图选项 |
表 1 仿真1各状态分量的平均误差 Table 1 Each state component average error in simulation one
| 模型 | x方向 | y方向 | 平均耗时/s | ||||
| 位置/m | 速度/(m·s-1) | 加速度/(m·s-2) | 位置/m | 速度/(m·s-1) | 加速度(m·s-2) | ||
| 改进CS-Jerk模型 | 47.41 | 111.69 | 45.51 | 55.52 | 8.09 | 1.39 | 0.952 8 |
| CS-Jerk模型 | 66.54 | 129.57 | 50.31 | 73.11 | 22.23 | 4.37 | 0.930 9 |
| Jerk模型 | 74.02 | 129.74 | 51.12 | 73.23 | 27.39 | 4.74 | 0.895 4 |
表选项
图 4和图 5表明,在x轴方向上,与Jerk模型和CS-Jerk模型相比,改进CS-Jerk模型算法减小了对目标位置和速度的跟踪误差,且对0~60 s、160~200 s目标弱机动和60~160 s目标强机动,位置的跟踪误差相差不大,而3种算法在60~160 s的速度跟踪误差均高于0~60 s、160~200 s;y轴方向上目标匀速运动,由于x轴方向的耦合作用,3种算法在60~160 s位置和速度的跟踪误差均比其他时刻要高,而改进CS-Jerk模型的跟踪误差显然更低。
表 1中数据表明,相比Jerk模型,x轴方向上改进CS-Jerk模型对位置、速度和加速度估计的平均误差分别减小35.95%、9.00%和10.97%,y轴方向上位置、速度和加速度估计的平均误差分别减小24.18%、70.46%和70.67%;而相比CS-Jerk模型,x轴方向上位置、速度和加速度估计的平均误差分别减小28.75%、13.79%和9.54%,y轴方向上位置、速度和加速度估计的平均误差分别减小24.05%、63.61%和68.19%。从算法的平均耗时来看,改进CS-Jerk模型耗时最长,但仅比CS-Jerk模型和Jerk模型分别增加了2.35%和6.41%,因此以时间为代价换取跟踪精度的提高是可取的。
可以发现,由于目标在x轴方向上做强机动而在y轴方向做弱机动,而改进算法对目标强机动和弱机动跟踪性能的提高作用不同,所以y轴方向的改善更明显。
仿真2 ????在仿真1的基础上,根据改进的CS-Jerk模型对系统建模,采用本文ST-SRCKF算法实现滤波计算,与文献[15]中ST-SRCKF算法的滤波结果进行对比。x、y轴方向上目标位置和速度的均方根误差分别如图 6和图 7所示,表 2给出了目标状态的平均误差。
 |
| 图 6 仿真2 x轴目标跟踪的位置和速度均方根误差 Fig. 6 Target tracking location and velocity root mean square errors of axis x in simulation two |
| 图选项 |
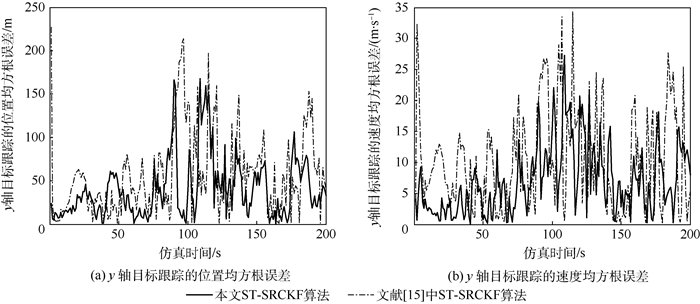 |
| 图 7 仿真2 y轴目标跟踪的位置和速度均方根误差 Fig. 7 Target tracking location and velocity root mean square errors of axis y in simulation two |
| 图选项 |
表 2 仿真2各状态分量的平均误差 Table 2 Each state component average error in simulation two
| 算法 | x方向 | y方向 | 平均耗时/s | ||||
| 位置/m | 速度/(m·s-1) | 加速度/(m·s-2) | 位置/m | 速度/(m·s-1) | 加速度/(m·s-2) | ||
| 本文ST-SRCKF算法 | 42.31 | 102.41 | 39.61 | 36.98 | 6.01 | 1.12 | 0.965 8 |
| 文献[15]中ST-SRCKF算法 | 47.41 | 111.69 | 45.51 | 55.52 | 8.09 | 1.39 | 0.952 8 |
表选项
图 6和图 7表明,本文提出的ST-SRCKF算法在保持原有ST-SRCKF算法良好的鲁棒性和数值稳定性的同时,提高了目标状态的估计精度。表 2的数据表明,与原有ST-SRCKF算法相比,本文算法对x轴方向上目标位置、速度和加速度的估计精度分别提高了10.76%、8.31%和12.96%,对y轴方向上目标位置、速度和加速度的估计精度分别提高了33.39%、25.71%和19.42%,同时改进ST-SRCKF算法的平均耗时仅增加了1.36%。
5 结论 超高速强机动目标的机动运动具有复杂性和强非线性等特点,对这类目标的跟踪存在两方面问题:一是目标高速强机动运动阶段易出现不良量测;二是系统建模的准确度不够,导致目标状态估计误差较大甚至出现滤波发散。
本文将一种新的强跟踪平方根容积卡尔曼滤波应用到超高速强机动目标跟踪中:
1) 在ST-SRCKF中引入多重渐消因子矩阵代替单一渐消因子,同时改进滤波器的结构,提高了原有算法的滤波精度且能够对每个状态变量都能很好地估计。
2) 根据新息理论提出一种自适应CS-Jerk模型,使得系统建模准确度更高,这两者的结合克服了模型不准确和不良量测影响滤波精度和滤波稳定性的问题,改善了现有算法的跟踪性能。
3) 实验数据表明,本文算法既保证了滤波的稳定性,又保证了目标的跟踪精度,具有良好的跟踪性能,从算法的平均耗时来看,这是以牺牲时间为代价的,但由于平均耗时增加的并不多,且跟踪精度是主要考虑因素,因此这样的代价是可以允许的,对于低速弱机动目标则不必采用本文的跟踪算法。
参考文献
| [1] | 黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J].宇航学报, 2014, 35(4): 369–379.HUANG C Q, GUO H F, DING D L. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J].Journal of Astronautics, 2014, 35(4): 369–379.(in Chinese) |
| [2] | 唐志共, 许晓斌, 杨彦广, 等. 高超声速风洞气动力试验技术进展[J].航空学报, 2015, 36(1): 86–97.TANG Z G, XU X B, YANG Y G, et al. Research progress on hypersonic wind tunnel aerodynamic testing techniques[J].Acta Aeronautics et Astronautics Sinica, 2015, 36(1): 86–97.(in Chinese) |
| [3] | 张翔宇, 王国宏, 李俊杰, 等. 临近空间高超声速滑跃式轨迹目标跟踪技术[J].航空学报, 2015, 36(6): 1983–1994.ZHANG X Y, WANG G H, LI J J, et al. Tracking of hypersonic sliding target in near-space[J].Acta Aeronautics et Astronautics Sinica, 2015, 36(6): 1983–1994.(in Chinese) |
| [4] | XU B. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity[J].Nonlinear Dynamics, 2015, 80(3): 1509–1520.DOI:10.1007/s11071-015-1958-8 |
| [5] | XU B, YANG C G, PAN Y P. Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle[J].IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(10): 2563–2575.DOI:10.1109/TNNLS.2015.2456972 |
| [6] | XU B, WANG D W, SUN F C, et al. Direct neural discrete control of hypersonic flight vehicle[J].Nonlinear Dynamics, 2012, 70(1): 269–278.DOI:10.1007/s11071-012-0451-x |
| [7] | 周政, 刘进忙, 谭西江. 基于Jerk输入估计的MCS模型及非线性跟踪算法[J].北京航空航天大学学报, 2013, 39(10): 1397–1402.ZHOU Z, LIU J M, TAN X J. MCS model based on Jerk input estimation and nonlinear tracking algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1397–1402.(in Chinese) |
| [8] | ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J].IEEE Transactions on Automatic Control, 2009, 54(6): 1254–1269.DOI:10.1109/TAC.2009.2019800 |
| [9] | 孙枫, 唐李军. Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策, 2013, 28(2): 303–308.SUN F, TANG L J. Estimation precision comparison of Cubature Kalman filter and Unscented Kalman filter[J].Control and Decision, 2013, 28(2): 303–308.(in Chinese) |
| [10] | 郭志, 董春云, 蔡远利, 等. 时变转移概率IMM-SRCKF机动目标跟踪算法[J].系统工程与电子技术, 2015, 37(1): 24–30.GUO Z, DONG C Y, CAI Y L, et al. Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking[J].Systems Engineering and Electronics, 2015, 37(1): 24–30.(in Chinese) |
| [11] | 王小旭, 潘泉, 黄鹤, 等. 非线性系统确定采样型滤波算法综述[J].控制与决策, 2012, 27(6): 801–812.WANG X X, PAN Q, HUANG H, et al. Overview of deterministic sampling filtering algorithms for nonlinear system[J].Control and Decision, 2012, 27(6): 801–812.(in Chinese) |
| [12] | ARASARATNAM I, HAYKIN S, HURD T R. Cubature Kalman filtering for continuous-discrete systems:Theory and simulations[J].IEEE Transactions on Signal Processing, 2010, 58(10): 4977–4993.DOI:10.1109/TSP.2010.2056923 |
| [13] | 董鑫, 欧阳高翔, 韩威华, 等. 强跟踪CKF算法及其在非线性系统故障诊断中的应用[J].信息与控制, 2014, 43(4): 451–456.DONG X, OUYANG G X, HAN W H, et al. Strong tracking CKF and its application to fault diagnosis of nonlinear systems[J].Information and Control, 2014, 43(4): 451–456.(in Chinese) |
| [14] | 徐树生, 林孝工, 赵大威, 等. 强跟踪SRCKF及其在船舶动力定位中的应用[J].仪器仪表学报, 2013, 34(6): 67–73.XU S S, LIN X G, ZHAO D W, et al. Strong tracking SRCKF and its application in vessel dynamic positioning[J].Chinese Journal of Scientific Instrument, 2013, 34(6): 67–73.(in Chinese) |
| [15] | 徐树生, 林孝工, 李新飞. 强跟踪自适应平方根容积卡尔曼滤波算法[J].电子学报, 2014, 42(12): 2394–2400.XU S S, LIN X G, LI X F. Strong tracking adaptive square-root cubature Kalman filter algorithm[J].Acta Electronica Sinica, 2014, 42(12): 2394–2400.(in Chinese) |
| [16] | MEHROTRA K, MAHAPATRA P R. A Jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Aeropace and Electronics Systems, 1997, 33(4): 1094–1105.DOI:10.1109/7.624345 |
| [17] | QIAO X D, WANG B S, LI T. A motion modle for tracking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 6(3): 493–499. |
| [18] | QIAN H M, CHEN L, YANG J W.A nonlinear tracking algorithm of maneuvering target tracking based on MEP-Jerk model[C]//2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE).Piscataway, NJ:IEEE Press, 2011:1673-1677. |
| [19] | 郭泽, 缪玲娟, 赵洪松. 一种改进的强跟踪UKF算法及其在SINS大方位失准角初始对准中的应用[J].航空学报, 2014, 35(1): 203–214.GUO Z, MIAO L J, ZHAO H S. An improved strong tracking UKF algorithm and its application in SINS initial alignment under large azimuth misalignment angles[J].Acta Aeronautics et Astronautics Sinica, 2014, 35(1): 203–214.(in Chinese) |
| [20] | GADZHIEV C M. Checking multivariate model fit from the generalized wishart statistic variance[J].Measurement Techniques, 1993, 30(12): 103–110. |
| [21] | 黄伟平, 徐毓, 王杰. 基于改进"当前"统计模型的非线性机动目标跟踪算法[J].控制理论与应用, 2011, 28(12): 1723–1728.HUANG W P, XU Y, WANG J. A nonlinear maneuver-tracking algorithm based on modified current statistical model[J].Control Theory & Applications, 2011, 28(12): 1723–1728.(in Chinese) |
| [22] | 杜占龙, 李小民. 基于多渐消因子强跟踪UKF和约束AR模型的故障估计与预测[J].控制与决策, 2014, 29(9): 1667–1672.DU Z L, LI X M. Fault estimation and prediction based on multiple fading factors strong tracking UKF and constrained AR model[J].Control and Decision, 2014, 29(9): 1667–1672.(in Chinese) |
| [23] | 何友, 修建娟, 关欣. 雷达数据处理及应用[M].3版北京: 电子工业出版社, 2013: 10.HE Y, XIU J J, GUAN X. Radar data processing with application[M].3rd edBeijing: Electronic Industry Publishing House, 2013: 10.(in Chinese) |
