对入水问题的早期研究多采用试验方法,最早可以追溯到19世纪初,Worthington[4]首次借助于高速摄像技术观察记录了液滴和球型结构体入水全过程,记录并描述了入水喷溅、空泡演化等现象;近年来,Duclaux[5]、Truscott[6-7]以及何春涛[8]等众多国内外****依然延续摄影试验方法对结构体入水问题开展了研究,对入水运动规律、入水空泡演化、流体动力特征以及影响因素进行了分析。随着计算机技术和计算流体力学的发展,数值方法在入水问题研究中得到了广泛应用,可以获得更加丰富、更加精细的流场结构信息。Lee等[9]针对射弹入水空泡的闭合方式和闭合点特征开展了理论和数值计算,其基于能量守恒原理建立了空泡演化的理论模型,分析了影响闭合方式的因素,以及深闭合方式下空泡的几何、运动特征参数;何春涛等[10]对锥头圆柱体入水流场特征进行数值计算,获得了不同入水速度条件下泡内压力变化规律,以及空泡内压力场、速度场分布情况;陈晨等[11]对高速射弹入水过程开展了数值计算研究,分析了空气域压力对入水喷溅形态、空泡闭合时间及内部空化效应的影响;赵蛟龙等[12]对底部带空腔的圆柱体不同俯仰角入水载荷进行计算,分析了空腔结构在入水冲击载荷作用下的结构响应,以及与俯仰角间的关系;潘龙等[13]针对圆柱体头部喷气入水缓冲特征开展研究,建立了顶部喷气平头圆柱体入水模型;杨衡等[14]开展了横流作用下圆柱体入水数值仿真,分析了在波、流作用下入水弹道和姿态响应。目前,对开放空腔结构入水问题的研究尚处于探索阶段,公开发表的文献资料相对较少,空腔内部流场结构以及对外部流场的扰动均是十分复杂的流动过程,具有较广泛的研究空间和应用前景。
针对含开放空腔的壳体结构在入水过程中内外流场耦合作用特点,忽略壳体结构变形,本文对下方完全敞开的开放空腔壳体垂直入水过程开展了数值模拟,结合腔内气体运动情况,分析了气体涨缩对流场结构和空泡形态的周期性扰动规律;空泡内气体漩涡的运动特征和其对空泡闭合的影响;以及扰动情况下壳体流体动力特征及分布情况。
1 数值计算理论 1.1 基本控制方程 入水运动是一个非定常问题,流动参数均随空间和时间变化,在宏观上,表现为质量的扩散、动量的黏滞耗散、能量的传导等现象,流体流动将受到物理基本定律的支配,包括连续性方程、动量方程和能量方程。
连续性方程:
 | (1) |
式中:ρ为流体密度;t为时间;ui为i方向速度;xi为i方向位置。
动量方程:
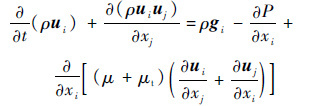 | (2) |
式中:gi为i方向重力加速度分量;P为压强;μ为动力黏度;μt为湍动黏度。
能量方程:
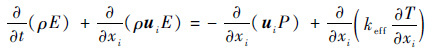 | (3) |
式中:E为流体能量;keff为有效热导率系数;T为流体温度。
1.2 多相流模型 低速入水问题是一种典型的多相流问题,通常形成具有明确气液界面的泡状流动,气液两相介质互不掺混,并且空泡壁面处气液两相流动速度基本一致,因此,对于此问题可应用均相流(homogeneous flow)模型,以一等效可压缩流体代替气液两相流。
本文选用流体体积 (Volume of Fluid,VOF)均相流模型对入水过程中气液两相流体的流动进行描述,且不考虑气液相变影响。VOF模型将气液两相流看作单一介质的混合流体,各相共享同一压力场和速度场,共用一套动量方程,通过求解单独的动量方程和处理穿过区域的每一流体的容积比来描述各相流体。混合流体的混合密度ρm、混合动力黏度系数μm和混合能量Em分别如下:
 | (4) |
 | (5) |
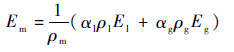 | (6) |
式中:αl和αg分别为液体和气体所占体积分数,αl+αg=1,下标m表示气液混合物,l表示液体,g表示气体。
1.3 湍流模型 在壳体入水过程中,开放空腔内气体将对外部流场产生扰动,引起空泡壁面波动流动,是开放腔体结构体入水过程的主要特征之一,波动强度具有周期性,存在黏性流动和湍动流动交替出现,导致空泡壁面流动复杂多变。另一方面,对于低速入水条件,空腔气体对流场的扰动微弱,雷诺数相对较小,因此对此问题的模拟需要考虑低雷诺数模型。
本文选用SST k-ω低雷诺数湍流模型,其通过湍动能(turbulence kinetic energy)k和比耗散率(specific dissipation rate)ω来描述湍动黏度,并以湍动黏度修正系数γ实现在黏性流动区域和湍动流动区域均具有适合的湍动黏度,表达式如下:
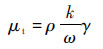 | (7) |
式中:$k=\frac{1}{2}\left( {{u}^{'2}}+{{v}^{'2}}+{{w}^{'2}} \right)$为湍动能;$w=\frac{\varepsilon }{{{C}_{\mu }}k}$为比耗散率,ε为湍动耗散率;常数Cμ=0.09;γ=min$\left[ {{a}^{*}},\frac{{{a}_{1}}w}{SF} \right]$为湍动黏度修正系数,a*=a∞$\left( \frac{a_{0}^{*}{{R}_{k}}+{{\operatorname{Re}}_{1}}}{{{R}_{k}}+{{\operatorname{Re}}_{1}}} \right)$为低雷诺数修正系数,Ret=$\frac{\rho k}{\mu w}$,Rk=6、a∞*=1、a0*=0.024及a1=0.31为经验系数,S为应变率不变测度,F为调和函数。
湍动能输运方程和比耗散率输运方程:
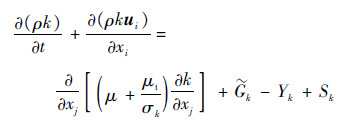 | (8) |
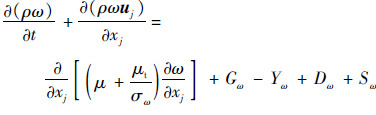 | (9) |
式中:σk、σω为普朗特数;${\tilde{G}}$k=min(Gk,10ρβ*kω)为湍动能生成项,Gk为标准k-ω模型湍动能生成项,β*为系数;Yk=ρβ*kω为湍动能耗散项;Sk为湍动能源项;Gω=$\frac{a}{{{v}_{1}}}{{{\tilde{G}}}_{k}}$为比耗散率产生项;Yω=ρβω2为比耗散率耗散项,β为系数;Sω为比耗散率源项;Dω=$\frac{2}{{{\sigma }_{w,2}}}\left( 1-{{F}_{1}} \right)\frac{\rho }{w}\cdot \frac{\partial k}{\partial {{x}_{i}}}\cdot \frac{\partial w}{\partial {{x}_{j}}}$为交叉扩散项,F1为调和函数,σω,2=1.168。
1.4 数值方法 基于Fluent软件平台,采用有限体积法(Finite Volume Method,FVM)[15]对控制方程离散化求解,时间离散为一阶精度,空间离散均为二阶精度,瞬态项采用时间显式积分离散方式;对流项采用二阶迎风格式;扩散项中梯度离散采用基于单元体的最小二乘法插值(least-quares cell based)格式;压力插值采用基于体积力(body force weighted)离散格式;体积率插值采用Geo-Reconstruct离散格式;其他均采用二阶迎风格式(second order upwind)。选用基于压力的分离式求解器(segregation solver),压力场、速度场采用Coupled耦合算法,联立求解离散化连续性方程和离散化动量方程。
2 计算模型 2.1 几何模型 开放空腔壳体模型选用一端具有完全开放的全腔体刚性结构,图 1给出模型示意图,为方便后续分析,对模型各面进行定义。模型几何参数及属性见表 1。
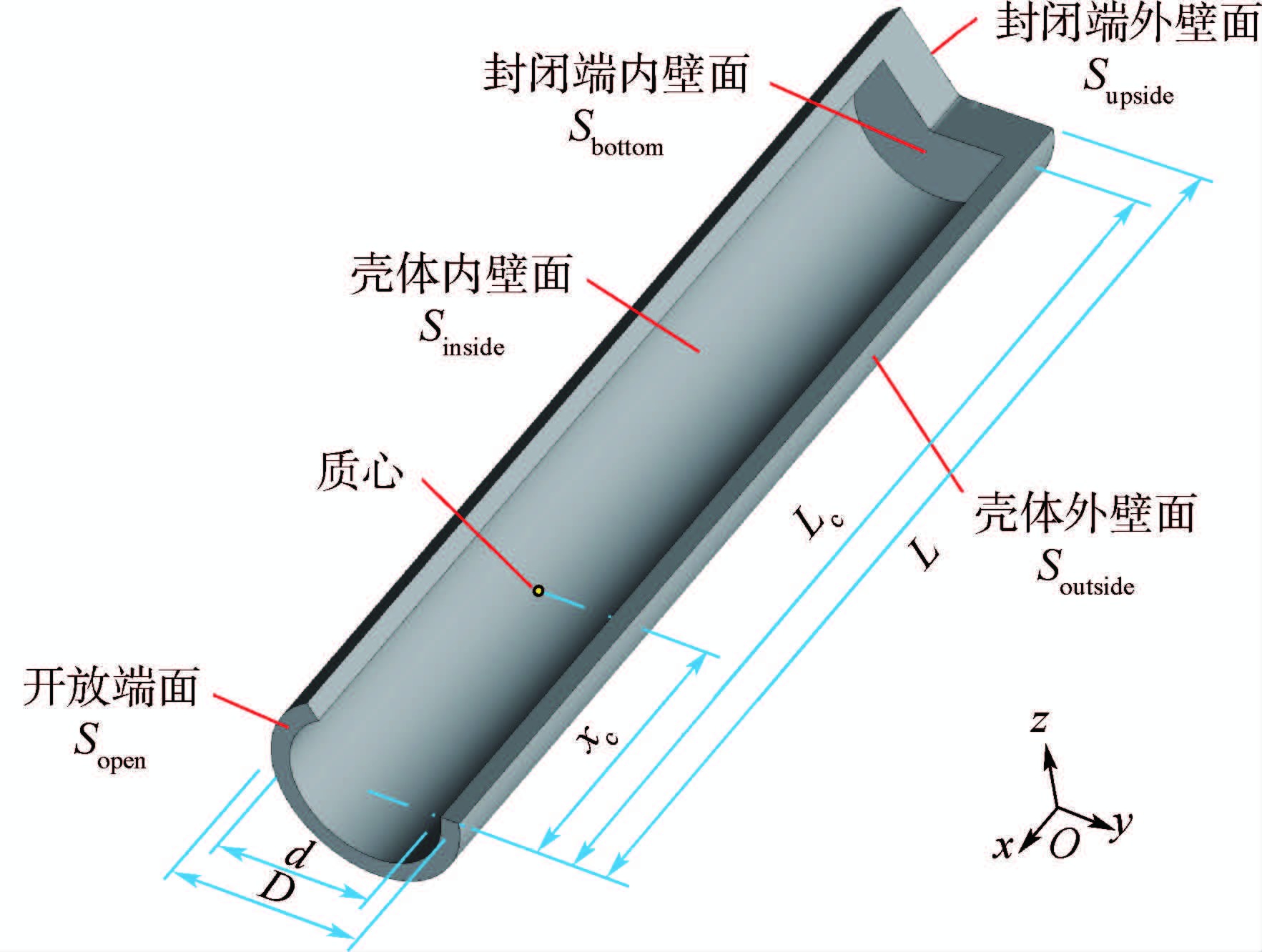 |
| 图 1 开放空腔壳体模型示意图 Fig. 1 Schematic of model of semi-closed cylinder |
| 图选项 |
表 1 模型几何参数及属性 Table 1 Geometric parameters and properties of model
| 参数 | L/m | LL/m | D/m | d/m | M/kg | xx/m |
| 数值 | 0.20 | 0.19 | 0.04 | 0.032 | 0.35 | 0.08 |
表选项
2.2 计算流域及边界条件 图 2给出了模型入水过程的计算流域和边界条件设置,选用圆柱型计算域,流域尺度参照试算结果,考虑计算效率和计算精度,设定边界区域为压力、速度和温度等流动参数输运现象较为微弱的最小计算流域尺度。计算应用动网格技术,采用动计算域方式,即计算域整体随壳体同步运动,实现沿重力方向单自由度运动。另一方面,动计算域方式导致流域边界不固定,要求在边界上给出时变的压力、体积分数参数分布,通过设定边界压力、液面位置与惯性坐标间的关系,依据壳体运动反馈的位置参数,确定动态边界条件,使边界条件与运动参数匹配,实现网格和数据的更新。通过给定的初始条件,流体动力与弹道参数耦合计算,得到壳体入水的运动规律和流体动力情况。
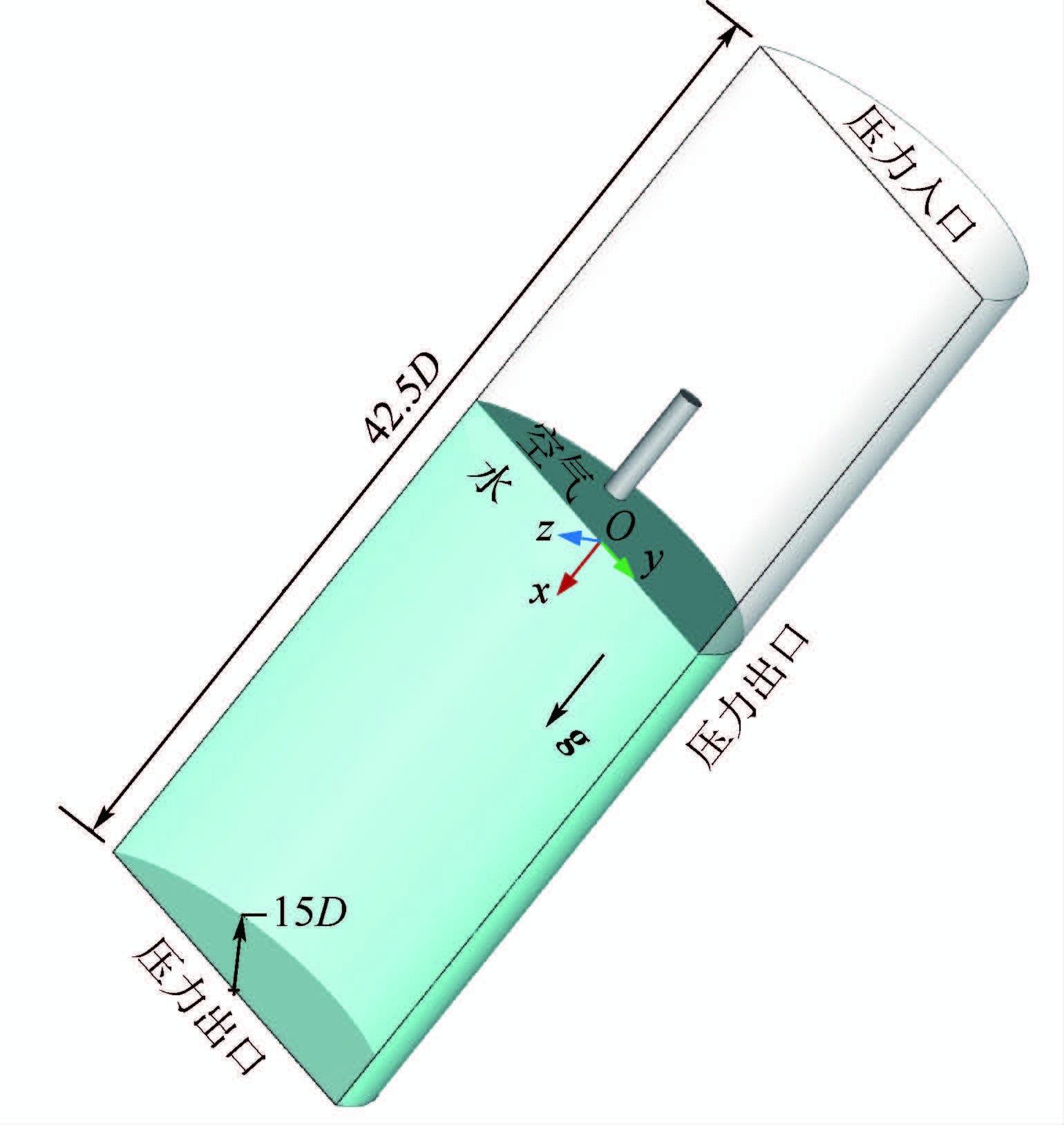 |
| 图 2 计算流域及边界条件 Fig. 2 Computational domain and boundary conditions |
| 图选项 |
为方便对计算结果分析,设定坐标系如下:以开放端撞击自由液面时刻为时间零点,自由液面位置为坐标原点,重力方向为运动正方向,如图 2所示。计算初始条件:壳体开放端面距自由液面垂向距离为1.25D,即-0.05 m;初始运动速度2.50 m/s;对应计算开始时间为-0.02 s。气相流体采用理想气体,液相流体采用常温下不可压缩的水。具体计算条件和流体属性参数如表 2所示。
表 2 计算条件及流体属性 Table 2 Computational conditions and fluid properties
| 入水 速度v0/(m·s-1) | 重力 加速度g/ (m·s-2) | 环境 压力 P∞/Pa | 液体属性 | 气体属性 | |
| ρl/ (kg·m-3) | μl/ (kg·ms-1) | 比热cp/(J· (kg·K)-1) | |||
| 2.55 | 9.8 | 101 325 | 998.2 | 0.001 003 | 1 006.43 |
表选项
2.3 计算网格划分 图 3给出了壳体模型表面网格和流域空间网格的划分方式,均采用了正六面体结构化网格,可以较好控制网格质量和数量。为了保证计算结果的有效性和提高计算精度,更好地捕捉开放空腔壳体入水过程中的流动特征,对壳体开放端附近扰动区域的网格、开放端下方和腔体内部流场参数畸变区域的网格以及尾缘涡区域的网格进行了加密处理。
 |
| 图 3 计算网格 Fig. 3 Computational grid |
| 图选项 |
根据SST k-ω湍流模型对近壁面网格距壁面无量纲长度y+的要求,同时避免网格出现较大的横纵比,对近壁面网格细化,图 4给出空泡闭合时刻的开放空腔壳体壁面y+分布,高速回射流使壁面黏性层厚度达到极小值,其值均小于11。全域网格最大横纵比网格均出现在远场,比例大于0.006;最小网格出现在壳体开放端,尺度为0.00 002 m,最大网格出现在远场,尺度为0.015 m;网格总量为648万。
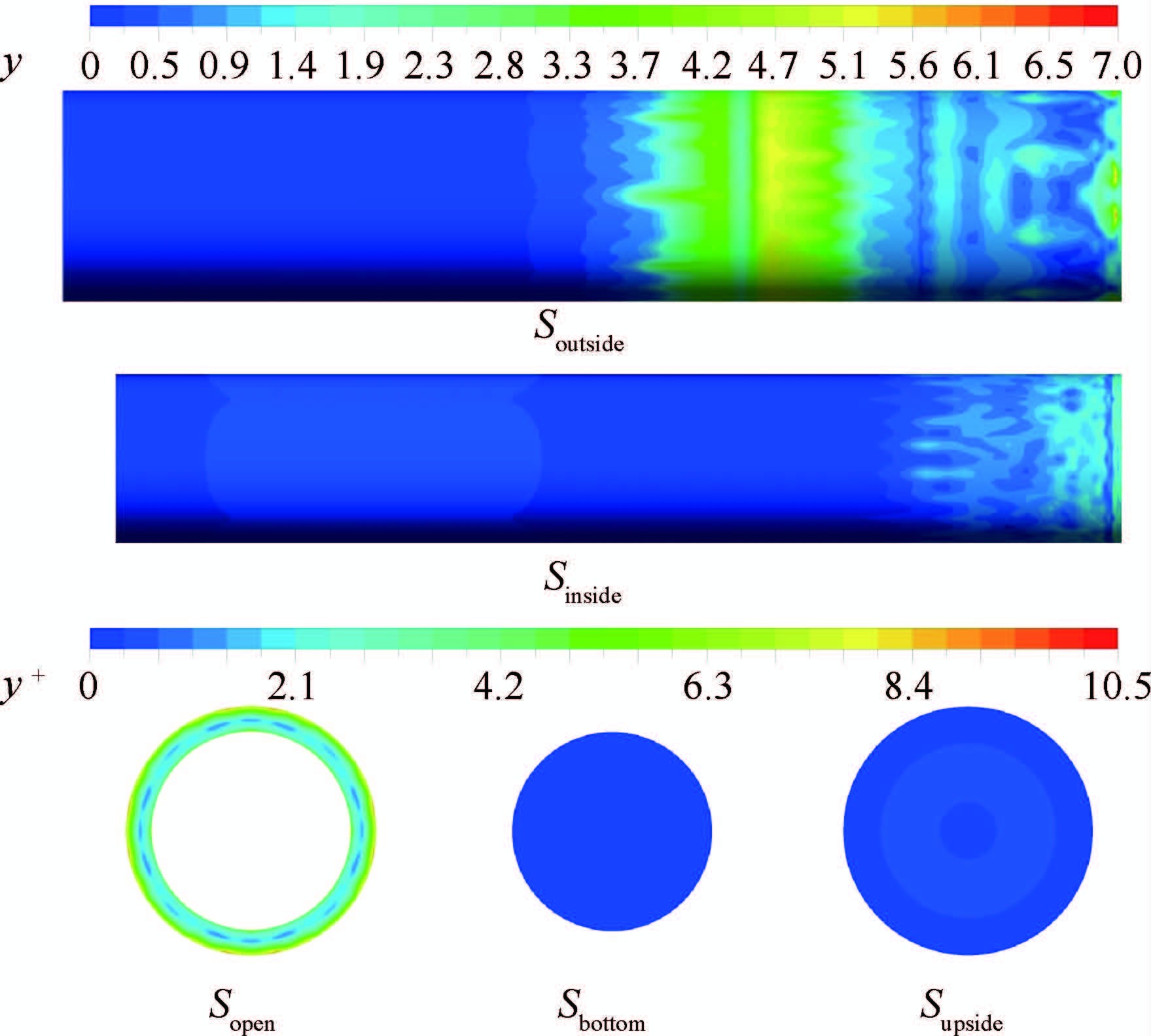 |
| 图 4 圆柱壳体外表面y+分布 Fig. 4 Distribution of y+ on external surface ofcylinder shell |
| 图选项 |
3 结果分析 入水过程中,开放空腔内气体在流体动力作用下将发生周期涨缩现象,是开放空腔壳体入水问题的主要特点之一,一方面其运动对液体流域产生扰动,改变流场结构,形成特殊流动现象;另一方面气体涨缩作用于壳体,改变流体动力特征。下面依次对流场结构、空泡特征和流体动力3个问题进行分析。
3.1 流场结构特征分析 入水后空腔内气体涨缩将引起液体流域受到周期性扰动,流场结构特征也表现出周期性变化,图 5分别给出了开放端液体排出阶段和吸入阶段流线图和等压线图。
 |
| 图 5 流线及等压线 Fig. 5 Streamlines and pressure isobars |
| 图选项 |
对于液体排出阶段,空腔内气体压缩到极大值后,腔内压力到达极值,开放端流域形成局部高压,由于作用范围较小,使压力梯度较大,液面开始下降,但初始流速较小,外部流域未产生明显流动现象。排出的液体逐渐加速,压力作用范围扩展,在动压的作用下,开放端流域继续处于高压状态,但腔内气体静压减弱,压力梯度略有减小,随流速增加空泡区域环流形成,促进了局部空泡扩展。空腔持续性排出液体导致压力急剧下降,开放端逐渐形成相对低压区域,出现逆向压力梯度,液体流动速度减缓,特别是横向流动开始衰减,环流减弱,空泡扩展阶段结束。
对于液体吸入阶段,空腔内气体过度膨胀导致压力小于环境压力,开放端附近流域形成指向空腔内部的压力梯度,外部液体回流,腔内液面上升。随着流入液体的加速,空腔内气体压缩、开放端下方向外侧排开的液体流量减小,空泡扩展程度受到抑制,开始进入局部收缩阶段。空腔压缩程度进一步增加,流入的液体开始减速,开放端再次形成高压区,并形成以开放端向外辐射的压力梯度,直至腔内压缩至最大值,然后再一次进入到液体排出阶段,同时空泡收缩阶段结束,完成一次周期运动。
考虑入水空泡结构特征,开放端的这种扰动使空泡区域的局部流场产生压力梯度,导致沿轴线不同位置处空泡的扩展程度出现差异,由于扰动是周期性的,因此空泡在整体上表现出波动现象。可见,这种空泡的波动流动是开放空腔对流场扰动的一种传播形式,其可以反映出空腔内气体涨缩的频率及强度,同时又将反作用于流场,特别对于空泡内易压缩的气体介质,空泡的波动影响到形成气体环流。闭合前,在空泡与大气连接的开口处形成明显的气体漩涡,并受空泡波动影响而出现移动;闭合后,形成附着于壳体运动的独立空泡,其完全处于液面以下,此阶段空腔内气体涨缩极度衰减,空泡波动程度减弱。同时由于液体密度、黏度均较大,液体漩涡耗散十分迅速,难以形成大尺度涡,对于液体流场主要为势流流动,空腔形成的谐振腔在开放端产生周期性压力源,形成沿径向扩展的速度势,沿深度出现周期性的压力场和速度场分布。
3.2 空腔气体扰动对入水空泡的影响 入水空泡是入水运动的重要特征之一,是气液两相流动相互作用的结果,对近壁面流场结构和流体动力具有较大影响。对于开放空腔壳体而言,开放空腔结构对入水空泡具有一定的扰动影响,为得到较为直观的空泡流动特征,针对开放腔体和封闭腔体2种壳体模型入水空泡形态开展了入水试验,图 6给出具有封闭腔体和开放腔体的2种模型入水空泡试验照片,为方便对入水空泡扰动分析,试验采用与文中数值计算1∶1模型和一致的运动初始条件,见表 1、表 2,可以发现2种模型的入水空泡特征及形态具有明显差异,在开放空腔气体扰动作用下,入水空泡出现波动,并抑制、推迟空泡的闭合,空泡闭合时刻照片在图中用方框标记。
 |
| 图 6 入水空泡演化试验照片 Fig. 6 Test photographs of development ofwater-entry cavities |
| 图选项 |
通过3.1节对入水流场结构特征的分析,知道空腔内气体涨缩将引起空泡形态周期性变化,在空泡内形成气体漩涡流动,漩涡运动又将对空泡波动、闭合特征和闭合时间产生影响,下面针对空泡内的气体漩涡流动情况开展分析。
漩涡强度通常可以采用速度梯度张量第二不变量(the second invariant of the velocity gradient tensor)[16]来描述,其表达式为
 | (10) |
式中:δij为Kronecker符号;Q为正值表示流体微元旋转运动强于轴向变形,为负值表示流体微元旋转运动弱于轴向变形,可以有效地对漩涡强度进行描述。
图 7给出了开放端液体排出阶段和吸入阶段空泡内气体涡旋分布及演化规律。在液体排出阶段,由于空泡未闭合,泡内空间与外界大气形成气体环流,在空泡开口处产生气体漩涡,随着排出液体流速的增加,涡旋强度也逐渐增强,并通过空泡与大气连接的开口处向空泡外部移动。另一方面对于空腔内部,液体沿空腔内壁面流速相对较高,特别在开放端首次射流阶段,部分气体将由开放端外缘泻出,在空泡内部形成一个反向旋转的气体漩涡。随着开放端排出液体速率开始减小,大气中气旋运动方向改变,通过空泡与大气连接的开口处再次进入空泡内部,并与空泡内部的气体漩涡融合、耗散,涡旋强度不断减弱。在液体吸入阶段,开放端射流形成的气体漩涡迅速耗散消失,空泡内气体漩涡再次向上方运动,此时空泡出现闭合,形成独立的空泡,其内部气体运动相对平稳,最终完全耗散。
 |
| 图 7 入水空泡内Q值分布 Fig. 7 Distribution of Q value in water-entry cavity |
| 图选项 |
空腔周期性涨缩引起的流场扰动使空泡处流场出现扰动,导致泡内空间局部气体出现压力梯度,根据开尔文定理(Kelwin’s theorem):
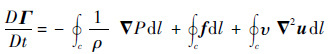 | (11) |
式中:Γ为速度环量,Γ=Δ×v,表征涡旋流动强度,v为流体速度; f为体积力;υ为运动黏度。压力梯度导致泡内出现速度环量,形成气体涡旋。涡旋沿压力梯度作用方向移动,导致气体漩涡通过空泡与大气连通的开口位置往复进出空泡,再次影响空泡界面上的压力分布,阻碍空泡开口收缩,推迟空泡闭合时间。
3.3 流体动力特征分析 入水后壳体受到重力和流体动力的共同作用,其中流体动力主要由压差阻力和黏滞阻力构成,前者表现为流体动压和静压,垂向作用于运动体表面,后者是由流体黏性产生,切向作用于运动体表面,并与相对流速反向。本文中开放空腔壳体垂直入水过程仅存在沿重力方向的单自由度运动,且运动无攻角,具有轴对称特征,因此,轴向作用力是问题研究的重点。
空腔内气体涨缩引起开放端液体往复吸入、排出,对流场结构产生扰动,在一定程度上会影响流体动力特征,图 8给出了流入空腔的液体质量流量(q)规律,根据腔内液体的运动规律,可将壳体运动过程分为A空气域运动阶段,B液体吸入阶段,C液体排出阶段。开放端撞水后,液体周期性往返通过,使B、C阶段交替出现,在开放端液体排出末期,即C-B过程,质量流量曲线出现波动拐点,特别是首次液体射流末期,由于气体部分外泄,导致出现流入空腔内的液体出现一次波动。与射流过程不同,在液体吸入过程,即B-C过程,曲线则相对光滑。
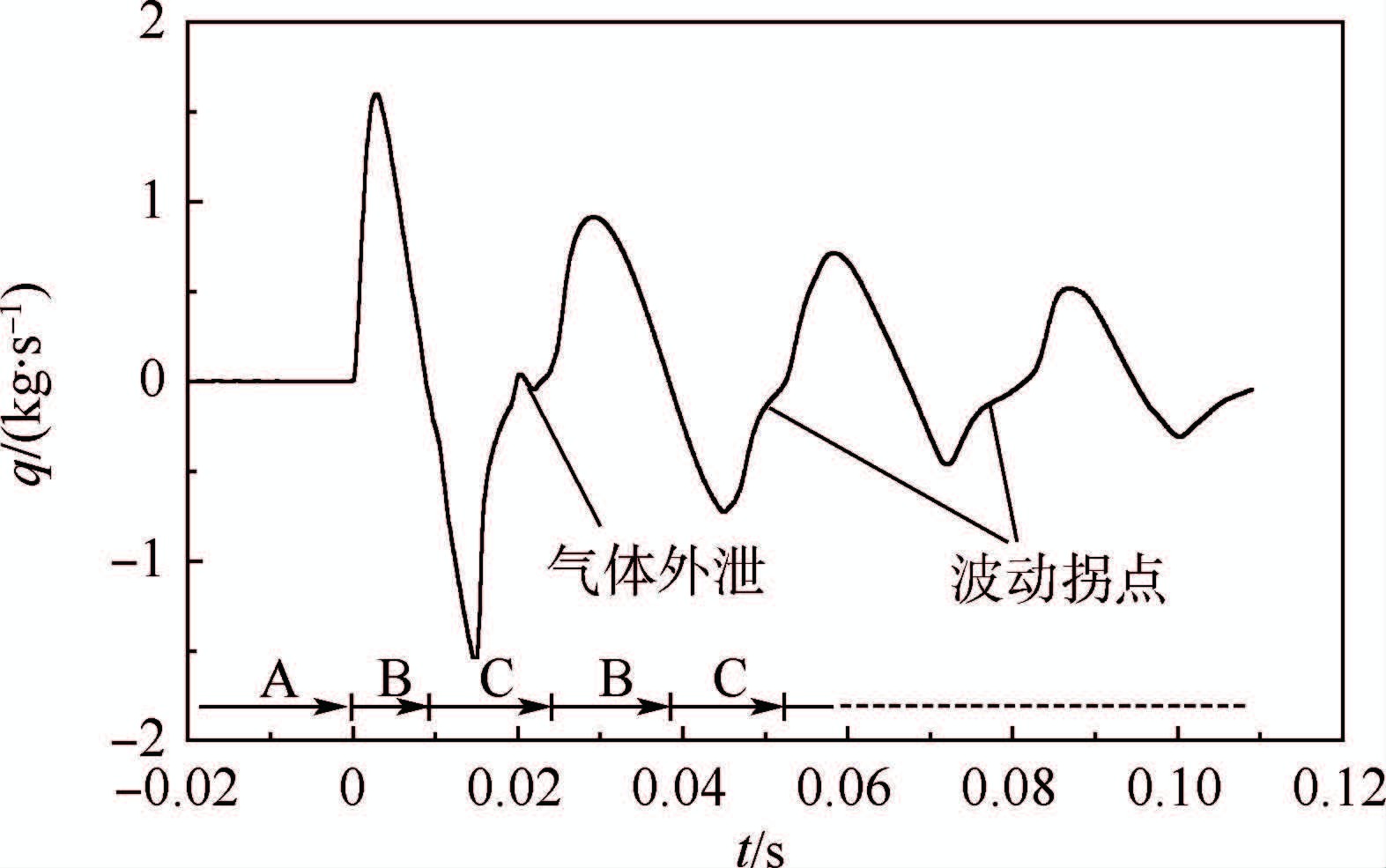 |
| 图 8 流入空腔的液体质量流量时程曲线 Fig. 8 Time history of water mass flow rate into cell |
| 图选项 |
图 9给出了开放端面Sopen和封闭端内壁面Sbottom上的压力(F)变化规律,具有以下3个典型特征:压力出现明显波动规律,2个面上压力波动具有一定相位差,以及在液体排放阶段出现压力波动反常现象。
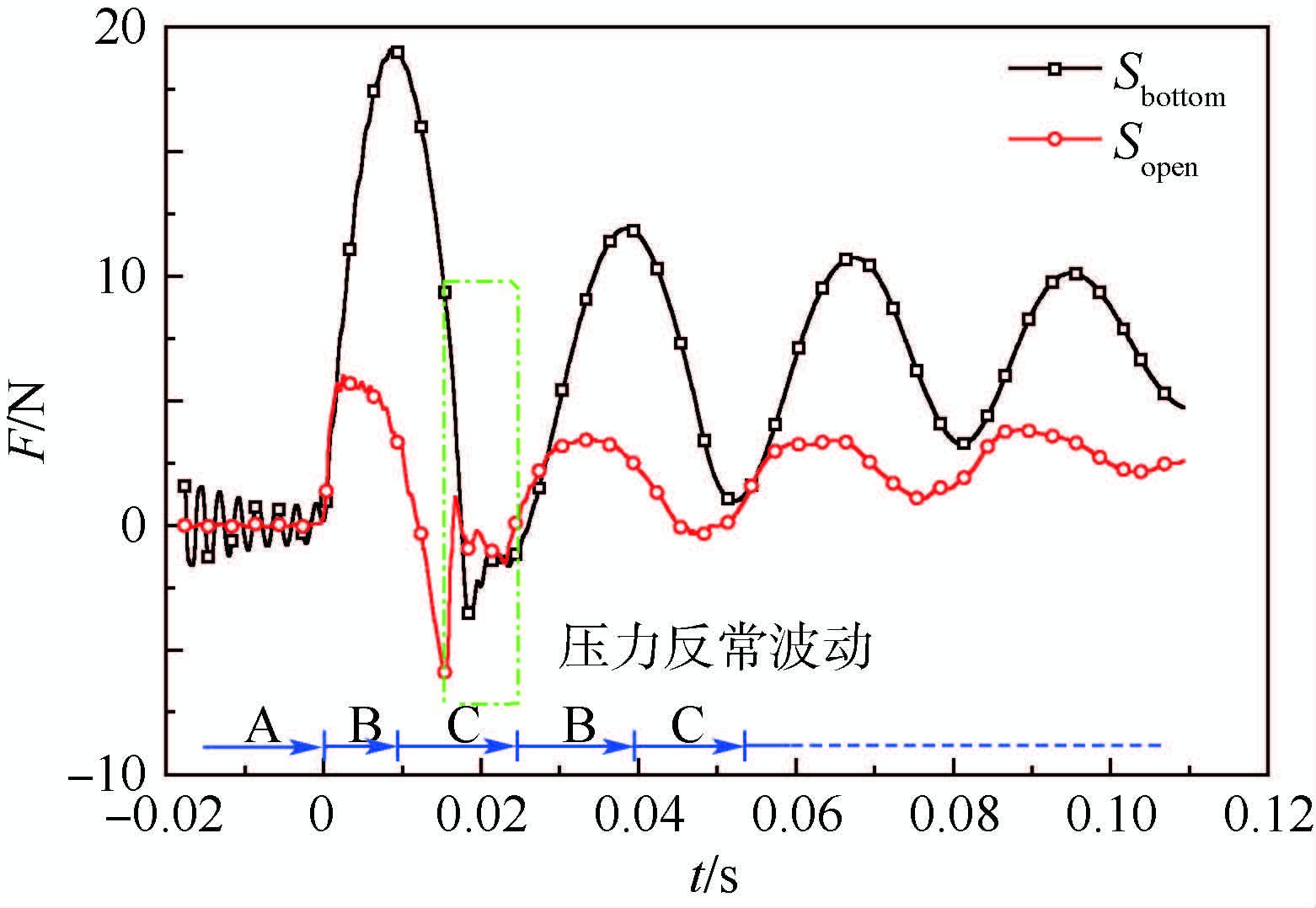 |
| 图 9 Sbottom面和Sopen面上压力变化时程曲线 Fig. 9 Time history of pressure on the surface of Sbottom and Sopen |
| 图选项 |
压力波动主要是由于气液两相流体相互作用,引起腔体内气体周期性涨缩和开放端周期性流动,改变了流场结构,使流体动力出现相应的周期性变化。在入水前(t<0 s),空腔内气体同样伴随涨缩现象,Sbottom上压差阻力出现波动,由于气体惯性较小,压差阻力表现为高频率、低幅值特征,对后续入水阶段的影响微弱;Sopen则仅受到恒定的气体动压作用,压差阻力表现平稳。入水后(t>0 s),由于气体的易压缩性,液体流入空腔内部,相对于气体,液体惯性明显,导致封闭气体涨缩现象更为明显,幅值增加、频率降低。由于Sopen的面积相对于Sbottom较小,因此作用在Sopen上的力在量值上较小。
波动不同步是由于作用流体介质属性导致,Sbottom仅受气体作用,气体惯性较小,压力主要表现为气体静压,其与气体压缩程度呈正比关系,即Sbottom压力由空腔压缩量决定;Sopen则主要受液体作用,液体惯性较大,压力主要表现为液体动压,其数值大小与流入腔体的液体流速有关,即Sopen压力由空腔压缩速度决定。根据开放端流入液体质量流量的波动变化特征,可知空腔内气体涨缩形成谐振腔,气体压缩速度为气体压缩量的时间导数,压缩速度与压缩量之间具有π/2相位差。因此,Sopen上的压力波动提前于Sbottom 1/4周期。
在开放端首次射流末期(C阶段),壁面压力出现反常波动,如图 9中虚线框所示,参照图 8中流入空腔液体质量流量,此阶段部分气体外泄,一方面引起空腔内液体涌动,出现压力梯度(图 5(a)),使Sbottom上的压力突增,且伴随高频波动;另一方面,溢出的气体改变开放端流场结构,开放端再次封闭后,Sopen上将受到液体抨击作用,导致压力突增,表现出压力的反常波动。
图 10给出了壳体内壁面Sinside和外壁面Soutside上的黏滞阻力变化规律。入水前(t<0 s),近壁面附近的气体流动将引起黏滞作用,腔内气体周期性涨缩形成Sinside上的波动黏滞阻力。入水后(t>0 s),液体流入空腔,出现沾湿区域,在液体高黏度作用下黏滞阻力明显增大,由于腔内液面波动、气体环流、外泄等作用,在前2个涨缩周期内Sinside上的黏滞阻力波动规律性较差,此后才表现出明显的周期性,阻力值与开放端流入液体的质量流量成正比关系。Soutside的黏滞阻力受到入水空泡的影响,特别是入水初始阶段(0~0.016 s),空泡将液体与壳体外壁面隔离,泡内形成低压区域,气体流入产生负向的黏滞力;当腔内气体外泄后,在空泡内形成较为强烈的气体环流,黏滞阻力负向增长,并随气体漩涡的分离、融合运动而出现同步波动;空泡闭合后(0.026 s),外壁面被水沾湿,由于液体黏度远远大于气体,液体的黏滞作用占据主导,但在空泡回流作用下黏滞阻力仍处于负值;空泡持续性增长,并出现多次脱落,导致空泡覆盖面积出现周期性变化,Soutside上黏滞阻力将随其沾湿面积的变化出现波动;当空泡逐渐稳定,覆盖面积相对较小,回射流强度减弱,黏滞阻力出现正值。
 |
| 图 10 黏滞阻力变化规律时程图 Fig. 10 Time history of viscous resistance |
| 图选项 |
通常采用无量纲化阻力系数来描述流体动力情况,分别定义压差阻力系数Cp和黏滞阻力系数Cν如下:
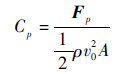 | (12) |
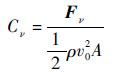 | (13) |
式中: Fp和Fν分别为压差阻力和黏滞阻力;本文ρ=998.2 kg/m3;v0为特征速度,选取入水速度作为特征速度;A为特征面积,选取壳体最大截面积A=0.25πD2。
图 11和图 12分别给出开放空腔壳体入水过程中压差阻力系数和黏滞阻力系数的时程曲线。压差阻力作为流体动力的主导部分受到空腔气体扰动影响,呈现出周期性变化趋势,特别是气体首次涨缩过程的压力波动幅值尤为明显,并在首次射流末段压差阻力系数出现瞬时负值。黏滞阻力在入水初始阶段主要受到空泡形态、运动等特征的影响,扰动的流场导致空泡产生特殊的演化过程,黏滞阻力系数出现图中较为复杂的规律。在空泡闭合后,黏滞阻力出现波动增加趋势。对比压差阻力系数和黏滞阻力系数,发现在入水过程中压差阻力始终占据主导,黏滞阻力几乎不决定壳体运动及姿态特征。
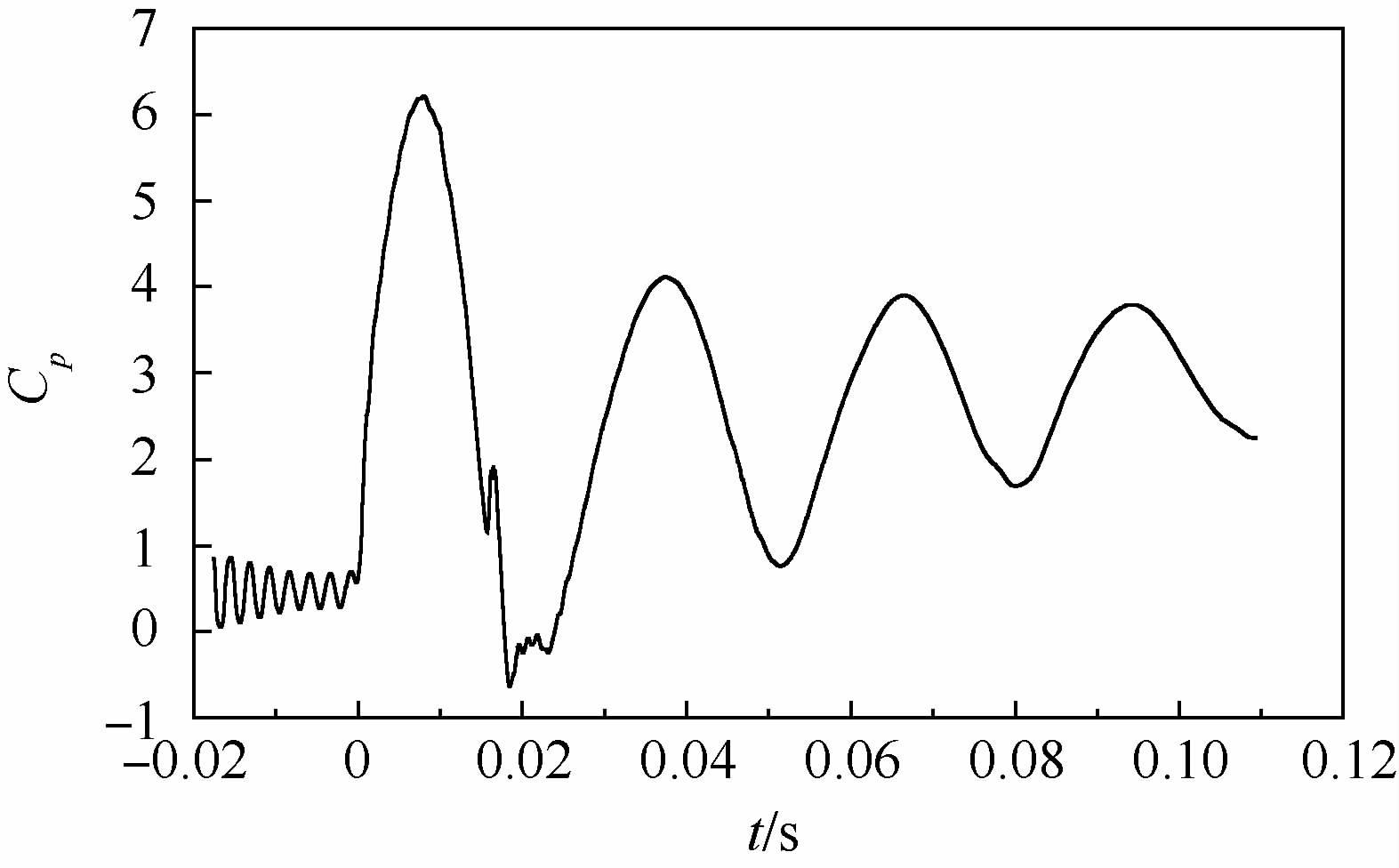 |
| 图 11 入水过程压差阻力系数 Fig. 11 Pressure drag coefficients during water-entry |
| 图选项 |
 |
| 图 12 入水过程黏滞阻力系数 Fig. 12 Viscous drag coefficients during water-entry |
| 图选项 |
4 结 论 本文针对撞水端敞开的开放空腔壳体垂直入水过程开展了数值仿真,分析了开放空腔壳体入水对流场结构的扰动和壳体流体动力变化规律,获得了压力场、流线和涡量场分布及变化情况,以及壳体各部分受力及整体的阻力特征等规律。具体结论如下:
1) 入水前空腔气体便出现了涨缩现象,但扰动极其微弱;入水后液体流入空腔与气体同步运动,在液体惯性作用下空腔涨缩幅度明显增强,在开放端形成压力源,对压力场、速度场产生周期性扰动。
2) 空泡受到流场扰动影响沿轴线出现扩展尺度差异,形成空泡波动现象;空泡波动使泡内气体流场结构变化显著,产生速度环量,形成气体漩涡,并随空腔涨缩反复通过空泡与大气连接处进出空泡内部,阻碍、推迟了空泡闭合的发生。
3) 扰动的流场产生附加流体动力,使流体动力均呈现波动变化,波动频率与空腔涨缩频率一致,压差阻力远大于黏滞阻力,占据主导作用。封闭端静压波动幅值与压缩量成正比,撞水面动压波动幅值与液体流入速度成正比,两者波动相差1/4周期;受空泡和空腔液体流动影响,入水初期内壁面黏滞阻力表现明显,空泡溃灭后外壁面表现明显。
参考文献
| [1] | DE BACKER G, VANTORRE M, BEELS C, et al. Experimental investigation of water impact on axisymmetric bodies[J].Applied Ocean Research, 2009, 31(3): 143–156.DOI:10.1016/j.apor.2009.07.003 |
| [2] | MASON D,FOLKMAN S,BEHRING M.Thrust oscillations of the space shuttle solid rocket booster motor during static tests[C]//15th Joint Propulsion Conference.Reston:AIAA,1979.http://cn.bing.com/academic/profile?id=2004033879&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | 刘若辰, 王英民. 声呐浮标空投入水受力特性仿真研究[J].水声工程, 2011, 35(10): 59–62.LIU R C, WANG Y M. Reserch of water-entry mechanical property of Sonobuoy[J].Underwater Acoustic Engineering, 2011, 35(10): 59–62.(in Chinese) |
| [4] | WORTHINGTON A M. Impact with a liquid surface studied with aid of instantaneous photography[J].Philosophical Transactions of the Royal Society of London, 1900, 194. |
| [5] | DUCLAUX V, CAILLé F, DUEZ C, et al. Dynamics of transient cavities[J].Journal of Fluid Mechanics, 2007, 591: 1–19. |
| [6] | TRUSCOTT T T, TECHET A H. Water-entry of spinning spheres[J].Journal of Fluid Mechanics, 2009, 625: 135–165.DOI:10.1017/S0022112008005533 |
| [7] | ARISTOFF J M, TRUSCOTT T T, TECHET A H, et al. The water entry of decelerating spheres[J].Physics of Fluids, 2010, 22(3): 417–422. |
| [8] | 何春涛, 王聪, 何乾坤, 等. 圆柱体低速入水空泡试验研究[J].物理学报, 2012, 61(13): 134701–8.HE C T, WANG C, HE Q K, et al. Low speed water-entry of cylindrical projectile[J].Acta physica Sinica, 2012, 61(13): 134701–8.(in Chinese) |
| [9] | LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J].Physics of Fluids, 1997, 9(3): 540–550.DOI:10.1063/1.869472 |
| [10] | HE C T, WANG C, WEI Y J, et al. Numerical simulation of pressure distribution in vertical water-entry cavity[J].Journal of Ship Mechanics, 2011, 15(9): 960–968. |
| [11] | 陈晨, 马庆鹏, 魏英杰, 等. 空气域压力对高速射弹入水流场影响[J].北京航空航天大学学报, 2015, 41(8): 1443–1450.CHEN C, MA Q P, WEI Y J, et al. Effects of operating pressure on high-speed projectile's water-entry flow[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1443–1450.(in Chinese) |
| [12] | 赵蛟龙, 孙龙泉, 张忠宇, 等. 柱形空腔结构落水载荷及冲击响应研究[J].振动与冲击, 2013, 32(20): 113–118.ZHAO J L, SUN L Q, ZHANG Z Y, et al. Hydrodynamic loads and impact response for a water entry of a cylindrical cavitary structure[J].Journal of Vibration and Shock, 2013, 32(20): 113–118.(in Chinese) |
| [13] | 潘龙, 王焕然, 姚尔人, 等. 头部喷气平头圆柱体入水缓冲机制研究[J].工程热物理学报, 2015, 36(8): 1691–1695.PAN L, WANG H R, YAO E R, et al. Mechanism reserch on the water-entry impact of the head-jetting flat cylinder[J].Journal of Engineering Thermophysics, 2015, 36(8): 1691–1695.(in Chinese) |
| [14] | 杨衡, 孙龙泉, 刘莹, 等. 波流作用下圆柱体入水特性的三维数值模拟研究[J].船舶力学, 2015, 19(10): 1186–1196.YANG H, SUN L Q, LIU Y, et al. 3D numerical simulation on water entry of cylindrical under wave and stream action[J].Journal of Ship Mechanics, 2015, 19(10): 1186–1196.(in Chinese) |
| [15] | HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics, 1981, 39(1): 201–225.DOI:10.1016/0021-9991(81)90145-5 |
| [16] | JEONG J, HUSSAIN F. On the identification of a vortex[J].Journal of Fluid Mechanics, 1995, 285(4): 69–94. |
