在工业机器人领域，多机器人协调工作以代替人类完成诸如抓取、装配、搬运等重复繁重的动作正在成为一种不可逆转的趋势，而双臂协调机械手则是多机器人领域的典型代表。与成熟的运动学模型相比，动力学模型——尤其对于双臂协调机械手的动力学建模问题，如何将约束关系融入动力学建模的过程中，是获得精确动力学模型的关键所在，也是实现高品质协调运动控制的重要基础。
当前，大多数****的关注点几乎都集中在协调机械手的控制算法上，少有****关注协调机械手的动力学建模问题。在众多研究协调机器人控制问题的著作与文献中，基本上都采用了传统的拉格朗日方程建立动力学模型^[1-2]，而且其控制算法的仿真算例基本上都采用了平面双臂机械手。这是因为在应用拉格朗日方法进行动力学建模时，当机械手臂的数目超过3时，计算量就会变得非常巨大，而表达式也会相当繁琐。对于双臂协调机械手而言，利用传统拉格朗日方程建立的动力学模型，其约束关系得不到很好地体现。即无法用系统的物理变量表达出解析的系统模型。
双臂协调机械手属于典型的闭链系统。对于闭链系统的动力学建模，Tarn^[3]、Nakamura^[4]和Luh^[5]等提出一套系统的方法，并基于此，创建了双臂协调机械手的动力学模型，然而建模的过程却极其复杂，同时寻找递推关系也非常困难，计算的时间也相当冗长。Smith^[6]将闭链系统划分为几个部分，转化为开链系统，利用达朗贝尔原则和拉格朗日算子计算未知力矩。然而，拉格朗日算子的计算却是非常困难的。Nakamura 和Ghoudoussi^[4]提出了一种计算闭链系统动力学逆动力学模型的方法，该方法并未采用拉格朗日算子。与传统的方法相比尽管有一定的进步，但能否获得解析形式的动力学方程，则取决于给定的系统初始条件，也就是说，该方法也不能用系统的物理变量表达出解析的系统模型^[7]。
众所周知，“协调”的本质是“约束”，协调运动的实现就是在运动过程中保持一定物理约束关系，反过来保持机器人运动中的各种物理学约束关系就是协调的表现形式。早在1996年，美国南加州大学Udwadia提出了一种崭新的多体动力学建模方法，即Udwadia-Kalaba方程,并取得了许多研究成果。该方法的最大特点就是将系统的约束关系融入动力学方程中，并且在不出现拉格朗日乘子的条件下，得出约束力的解析表达式，成为分析动力学领域的一个重要突破^[8-12]。非常可惜的是，在此后至今近20年时间里，该方法并未得到太多的关注，其主要应用领域集中在卫星系统的动力学建模及控制研究^[13-14]。而在机器人领域的应用寥寥无几。只有黄晋等^[15]利用该法建立了并联机器人的动力学模型，赵函等^[16]建立了一种机器鱼的动力学模型。
Udwadia-Kalaba方程的建模过程分为3个步骤：第一，建立系统在未受约束时的动力学方程；第二，寻找并建立系统所受约束的解析表达式；第三，利用Udwadia-Kalaba方程建立系统的动力学方程。为此，本文基于Udwadia-Kalaba方程的建模思想，针对平面协调搬运机械手动力学建模存在的问题，给出平面多杆机械手动力学方程的一般表达式，将系统的固有几何约束和预定轨迹均视为系统所受的外在约束关系，并将其应用到协调机械手动力学建模过程中，最终获得双臂协调机械手的解析动力学模型。
1 Udwadia-Kalaba方程 对于未受轨迹约束的工业机械手，其动力学方程的一般形式可表示为

(1)

式中: q =[q₁?q₂?…?q_n]^T为描述系统的n维广义坐标； M(q) 为n×n维的质量矩阵，n表示所研究的机械手为n杆；和 分别为n×1的离心力和哥氏力向量； G(q) 为n×1的重力矢量； τ 为n×1关节力矩矩阵。
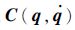
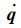
假设该系统受到m个约束为

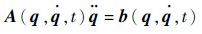(2)

式中： 为m×n维矩阵，t为时间变量；为m维列阵。
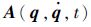
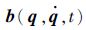
由于该组约束的存在，系统除要受到重力作用外，还要受约束力距 Q _c的作用，系统在它们共同作用下，其运动将发生变化。也就是说，由于该组约束的存在，使得系统运动方程变为

(3)

式中： 。根据Udwadia-Kalaba方程^[10]，有

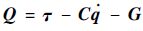
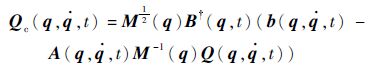(4)

式中： ；“?”表示矩阵的广义逆。
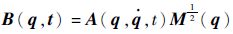
也就是说，对于约束多体机械系统而言，其动力学方程可表示为如下的一般形式：

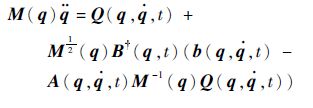(5)

2 平面 n 杆机械手的动力学方程 利用Udwadia-Kalaba方程建立平面协调搬运机械手动力学模型的第1步就是建立系统未受约束的动力学方程。然而由于平面协调搬运机械手属于多杆系统，因此利用传统的拉格朗日方程建立协调搬运机械手未受约束时的动力学方程将是非常复杂的。为此，本文给出平面多杆机械手动力学方程的一般表达式。
图 1为平面n杆机械手示意图。xOy为系统全局坐标系，位于机械手基座位置；l_i为杆长，i=1,2,…,n；q_i为系统的广义坐标变量。

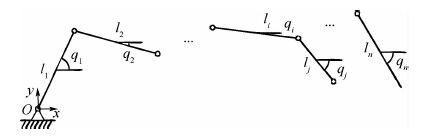图 1 平面n杆机械手示意图 Fig. 1 Sketch map of n-link planar manipulators

图选项

将方程式(1)重新表示为方程式(6)的形式：

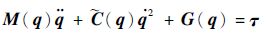(6)

式中：和g_iⁿ分别表示矩阵 M(q) 、和 G(q) 中各元素。

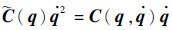
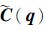
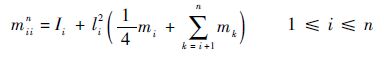(7)

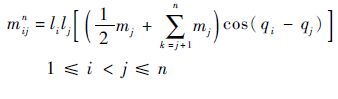(8)

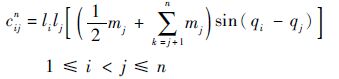(9)

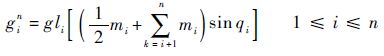(10)

式中：g为重力加速度；m_i为杆的质量，i=1,2,…,n；I_i为杆的转动惯量。
证明 假设对于n杆和n+1杆机械手，式(7)~式(10)成立，那么有

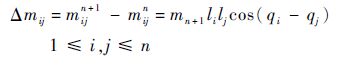(11)

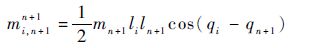(12)

(13)

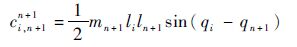(14)

(15)

根据数学归纳法，假设对于n杆机械手式(7)~式(10)成立，那么对于n+1杆机械手式(7)~式(10)也应同样成立。也就是说，由于增加了第n+1杆而导致的各矩阵的变化应满足式(11)~式(15)。而各矩阵的变化均来自第n+1杆的拉格朗日方程。
如图 1所示，第n+1杆的质心坐标为

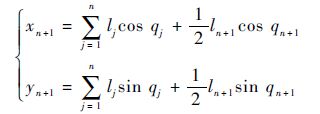(16)

第n+1杆的拉格朗日函数为

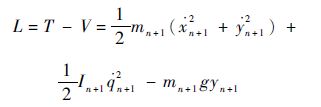(17)

式中：T为系统的动能；V为系统的势能。
进一步可得拉格朗日方程为

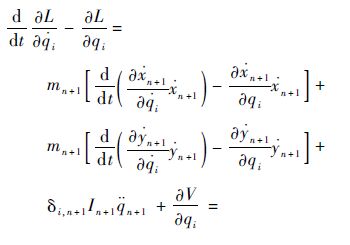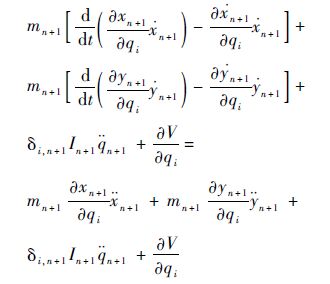(18)

式中：δ_i,n+1为克罗内克符号。
对约束条件式(16)两次求导得

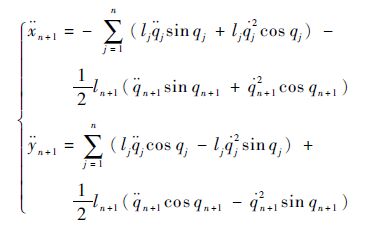(19)

将式(19)代入式(18)得

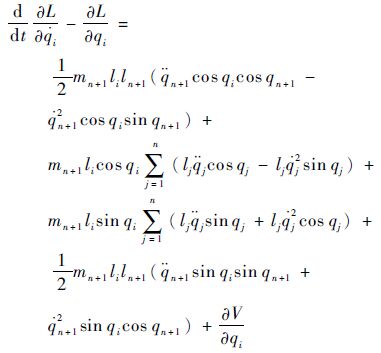(20)

进一步可简化得

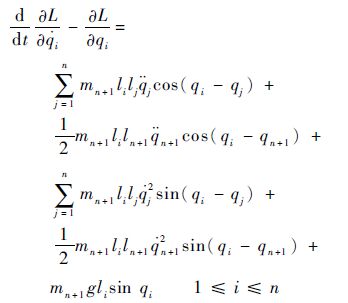(21)

式(21)表明，对于n+1杆机械手动力学方程的质量和哥式矩阵的非对角元素，应该对n杆机械手动力学方程的质量和哥氏矩阵相对应位置元素添加式(21)右侧前4项。对于n+1杆机械手动力学方程的重力矩阵，应该对n杆机械手动力学方程的重力矩阵添加式(21)右侧的最后一项。而对于质量矩阵的对角元素m_n+1,n+1ⁿ⁺¹，重力矩阵的f_n+1ⁿ⁺¹可通过类似的方法获得，这里不再赘述。
3 动力学建模与数值仿真 3.1 动力学建模 图 2为由两个平面三自由度机械臂组成的双臂协调机械手搬运木棒的示意图。xO₁y为系统的全局坐标系，位于左侧机械手基座位置。O₁O₂=L为两个机械手基座间的距离。AB为木棒。系统的广义坐标为 θ =[q₁ q₂ q₃ q₄ q₅]^T。假设木棒与两个末端机械手之间没有相对滑动与转动，即紧抓持，这样图 2中矩形部分所包括的木棒与两侧末端机械手就可以看作一个杆件处理，如图 3所示。这样系统就转化为一个闭环平面五杆机构。

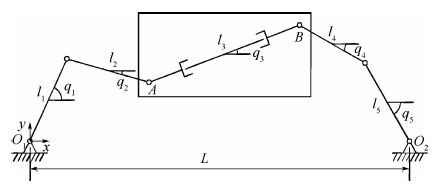图 2 双臂协调搬运机械手示意图 Fig. 2 Sketch map of dual-arm cooperating manipulatorscarrying a bar

图选项

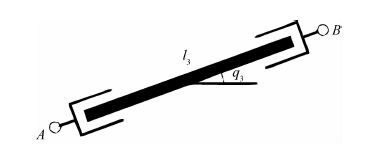图 3 木棒与末端执行器关系示意图 Fig. 3 Sketch map of relationship between bar andend-effectors

图选项

根据Udwadia-Kalaba方程的建模思想，首先建立系统未受约束时的动力学方程。假设系统未受到右侧基座的约束。此时系统相当于一个平面五杆机构，由式(6)可得系统此时动力学方程为

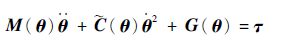(22)

根据式(7)~式(10)可得式(22)中矩阵 M 、 和 G 的元素为


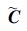
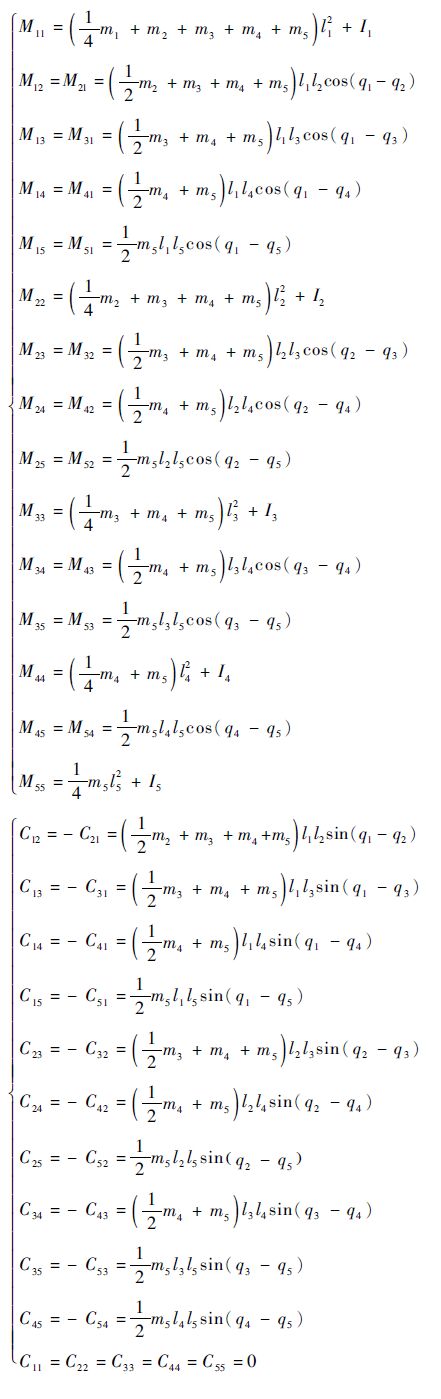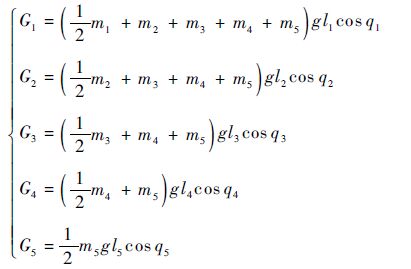由于此时系统还没有考虑其所受的约束，因此 τ = 0 ，所以有

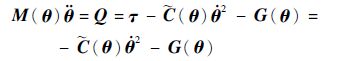(23)

由于右侧基座将右侧机械手固定于地面，因此该约束可表示为

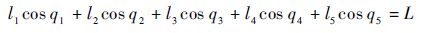(24)

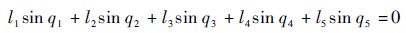(25)

分别对式(24)和式(25)两次求导，并结合式(2)有

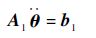(26)

式中：

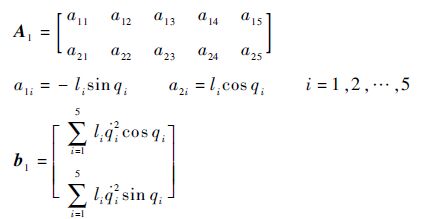假设木棒的质心坐标为(x₃，y₃)，质心运动轨迹为

(27)

根据图 2所示，又有如下几何关系：

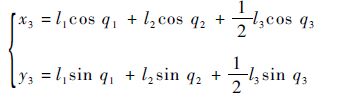(28)

分别对式(27)~式(28)两次求导，并结合式(2)有

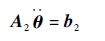(29)

式中：

联合式(26) 和式(29)表示为式(2)的形式：

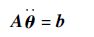(30)

式中： A = [A ₁ ? A ₂]^T； b = [b ₁ ? b ₂]^T。
由式(4)、式(23)可得各杆所需附加力矩为

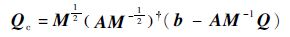(31)

进而可获得双臂协调搬运机械手的动力学方程为

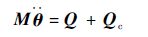(32)

3.2 数值仿真 假设各杆质量m₁=m₂=m₃=m₄=m₅=1 kg，各杆长度l₁=l₂=l₃=l₄=l₅=1 m，转动惯量I₁=I₂=I₃=I₄=I₅=1 kg·m²。初始条件q₁=q₄=45°，q₂=q₅=-45°，q₃=0°。初始角速度 ₁= ₂= ₃= ₄= ₅=0 (°)/s。双臂协调机械手初始位姿示意图如图 4所示，τ =[τ₁ ?τ₂ ?τ₃? τ₄ ?τ₅ ?τ₆]^T。仿真软件采用MATLAB 2011a。

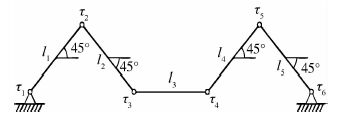图 4 双臂协调搬运机械手初始位姿示意图 Fig. 4 Sketch map of initial configuration of dual-armcooperating manipulators carrying a bar

图选项

此外，由于该系统有5个杆件组成，为此产生6个关节。也就是说每个杆件所需的附加力矩 Q _c均由该杆件相邻的两个驱动电机提供。即

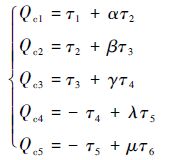(33)

将式(33)表示为矩阵形式：

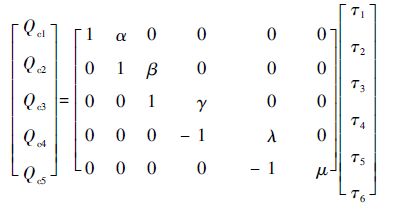(34)

式中： α、β、γ、λ和μ为电机常数，根据实际情况赋予合适的常数。在这里取α=β=-1，γ=λ=μ=1。
进一步可得

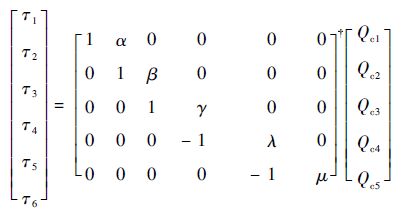(35)

仿真结果如图 5~图 8所示。图 5表明q₃≡0，表示木棒在水平方向上没有位移，木棒始终保持水平。1、5杆从初始位置向上运动到大约65°，然后回到初始位置，两杆运动方向相反。同时2、4杆从初始位置向上运动到近似水平位置后，然后回到初始位置。两杆运动方向相反。与此同时，可以观察到1、2、4、5杆的运动是周期性的，也就是说，木棒在水平方向与垂直方向的极限位置之间做上下往复运动。图 6为木棒y轴方向运动位移示意图，符合式(27)的预定轨迹。图 7和图 8分别为各杆所需附加力矩和关节力矩示意图。

图 5 关节角度示意图 Fig. 5 Sketch map of joint angles

图选项

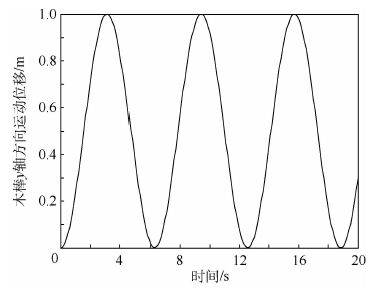图 6 木棒y轴方向运动位移示意图 Fig. 6 Sketch map of motion displacement of bar in y axis direction

图选项

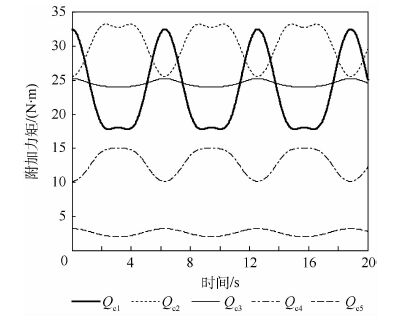图 7 附加力矩示意图 Fig. 7 Sketch map of additional torque

图选项

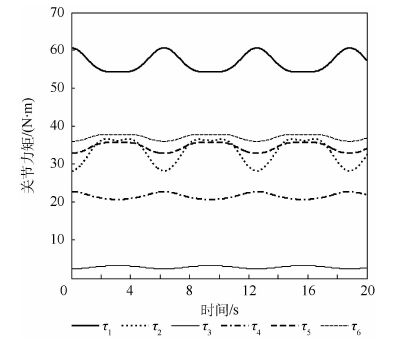图 8 关节力矩示意图 Fig. 8 Sketch map of joint torque

图选项

4 结 论 本文针对平面双臂协调搬运机械手的动力学建模问题，提出了一种基于Udwadia-Kalaba方程的动力学建模方法，研究过程揭示的主要结论如下：
1) 给出并证明了平面多杆机械手动力学方程的一般表达式，为建立未受约束时双臂协调搬运机械手的动力学方程奠定了基础。
2) 将系统本身固有的几何关系与木棒运动轨迹视为系统的外在约束，利用Udwadia-Kalaba方程的建模思想巧妙地将约束关系对系统的影响融入到动力学方程中。该方法思路清晰，运算简洁，有效地克服了传统拉格朗日方程需借助拉格朗日乘子获得动力学方程的缺点。
3) 数值仿真结果证明该方法建立的动力学方程符合实际情况。但数值仿真是在初始条件满足约束方程的前提下进行的，也就是说，将两个机械手的末端机械手与木棒视为一个杆件实际上是为初始条件满足系统约束方程创造了条件。因此，初始条件不满足约束条件的动力学建模问题将是进一步研究的问题。
此外，由于三维的双臂协调机械手动力学建模的复杂性，如何将Udwadia-Kalaba方程的建模思想推广应用到三维的双臂协调机械手动力学建模中也将是未来进一步研究的问题。

参考文献

[1]	熊有伦. 机器人技术基础[M].15版武汉: 华中科技大学出版社, 1996: 89-91.XIONG Y L. Fundamentals of robot techniques[M].15th edWuhan: Huazhong University of Science and Technology Press, 1996: 89-91.(in Chinese)
[2]	SANCHEZ-SANCHEZ P, ARTEAGA-PEREZ M A. Simplied methodology for obtaining the dynamic model of robot manipulators[J].International Journal of Advanced Robotic Systems, 2012, 9(6): 700–709.
[3]	TARN T J,BEJCZY A K,XUN X.Design of dynamic control of two cooperating robot arms:Closed chain formulation[C]//IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE Press,1987,4:7-13.
[4]	NAKAMURA J, GHOUDOUSSI M. Dynamics computation of closed-link robot mechanisms with non-redundant and redundant actuators[J].IEEE Transactions on Robotics and Automation, 1989, 5(3): 294–302.DOI:10.1109/70.34765
[5]	LUH J Y S, ZHENG Y F. Computation of input generalized forces for robots with closed kinematic chain mechanisms[J].IEEE Journal on Robotics and Automation, 1985, 1(2): 95–103.DOI:10.1109/JRA.1985.1087008
[6]	SMITH D A. Reaction force analysis in generalized machine systems[J].Journal of Manufacturing Science and Engineering, 1973, 95(2): 617–623.
[7]	WANG L C T, MING J K. Dynamic load-carrying capacity and inverse dynamics of multiple cooperating robotic manipulators[J].IEEE Transactions on Robotics and Automation, 1994, 10(1): 71–77.DOI:10.1109/70.285588
[8]	UDWADIA F E, KALABA R E. A new perspective on constrained motion[J].Mathematical and Physical Sciences, 1992, 439(1906): 407–410.DOI:10.1098/rspa.1992.0158
[9]	UDWADIA F E, SCHUTTE A D. Equations of motion for general constrained systems in Lagrangian mechanics[J].Acta Mechanica, 2010, 213(1-2): 111–129.DOI:10.1007/s00707-009-0272-2
[10]	UDWADIA F E, KALABA R E. Explicit equations of motion for mechanical systems with nonideal constraints[J].Journal of Applied Mechanics, 2001, 68(3): 462–467.DOI:10.1115/1.1364492
[11]	UDWADIA F E, KALABA R E. On constrained motion[J].Applied Mathematics and Computation, 2005, 164(2): 313–320.DOI:10.1016/j.amc.2004.06.039
[12]	UDWADIA F E, WANICHANON T. Control of uncertain nonlinear multi-body mechanical systems[J].Journal of Applied Mechanics, 2013, 81(4): 1–11.
[13]	UDWADIA F E, WANICHANON T, HANCHEOL C. Methodology for satellite formation-keeping in the presence of system uncertainties[J].Journal of Guidance Control and Dynamics, 2014, 37: 1611–1624.DOI:10.2514/1.G000317
[14]	SCHUTTE A D, UDWADIA F E. New approach to the modeling of complex multi-body dynamical systems[J].Journal of Applied Mechanics, 2010, 78(2): 856–875.
[15]	HUANG J, CHEN Y H, ZHONG Z H. Udwadia-Kalaba approach for parallel manipulator dynamics[J].Journal of Dynamic Systems,Measurement,and Control, 2013, 135(6): 1012–1030.
[16]	ZHAO H, ZHEN S C, CHEN Y H. Dynamic modeling and simulation of multi-body systems using the Udwadia-Kalaba theory[J].Chinese Journal of Mechanical Engineering, 2013, 26(5): 839–850.DOI:10.3901/CJME.2013.05.839