在文献[6]的基础上,Bosgiraud[7]于2008年提出并利用小型化的AMBs研制了一种二自由度MSSG,验证了MSSG角速率敏感的可行性以及控制的精确性。但这种方法要求电磁装置具备电机功能,从而产生了复杂的动力学平衡问题,同时测量结果中表现出的低通特性也限制了测量精度的提高。Maruyama等[8]在2008年提出了一种AMBs自身作为敏感装置的MSSG传感器概念,并对MSSG的姿态敏感原理进行了分析和实验,提出了用以扩展其测量带宽的可行方法,但由于缺乏必要的误差补偿措施,实验中角速率测量误差高达10%[9-10]。北京航空航天大学的房建成等[11-12]于2011年提出了一种新型磁悬浮陀螺飞轮,实现了三自由度控制力矩输出和二自由度姿态角速率敏感。但基于磁悬浮支承技术的磁悬浮陀螺飞轮的本质是姿态控制执行装置,因而其三自由度姿态控制力矩输出性能更强,角速率敏感受转子转动与平动的耦合而精度有限。郑世强等[13-14]基于磁悬浮控制力矩陀螺提出分时复用的控制、敏感双模式概念,通过使用交叉解耦反馈控制器,使X、Y方向的角速度耦合得以减小,但由于双框架支承MSSG中框架固有摩擦力矩的存在,这种方法测量精度和实时性还有待提高。
由于MSSG的概念提出较新,其结构与测量原理与已有静电悬浮陀螺、超导磁悬浮陀螺等有较大区别,对这种新型陀螺的角速率敏感机理尚未开展系统理论研究,也没有从理论上对此类陀螺敏感精度的影响因素进行系统分析。为了减少陀螺转子平动、转动耦合,提高MSSG的角速率敏感精度,本文提出了一种双球形包络面转子结构的MSSG。陀螺的定子、转子磁极包络面均设计为球形,实现了转子转动对平动的解耦,同时,转子的转动采用洛伦兹力磁轴承单独控制,解决了2种运动控制互相耦合的问题,为MSSG的高精度角速率敏感提供了结构基础。本文在描述MSSG结构和测量原理的基础上,建立了MSSG动力学模型,分析了转子所受电磁力、电磁力矩与其平动、转动之间的变化规律,以及影响角速率敏感精度的主要因素,并通过有限元仿真对理论分析结果进行了验证。
1 MSSG结构与工作原理 1.1 MSSG结构 双球形包络面转子MSSG结构如图 1所示。陀螺房中,定子的轴向和径向磁轴承磁极面分别位于2个不同半径的球形包络面上,共同形成一个中心腔体,其中轴向磁轴承磁极的包络面直径较小,径向磁轴承磁极的包络面直径较大,径向、轴向磁极均为电磁结构。转子位于定子形成的中心腔体中,径向、轴向磁轴承磁极面也为球形包络面结构,转子由整块磁性材料加工而成。陀螺转子与定子之间的空隙为0.35mm,转子、定子各磁极包络面球心完全重合。轴向磁轴承由2对磁极组成,主要用于转子在Z方向的平动控制;径向磁轴承由4对磁极组成,每2对磁极实现一个方向的平动控制,磁极之间安装隔磁材料,使X、Y通道的磁力线互相独立,从而保证磁轴承对X、Y方向平动的独立控制。陀螺的偏转由洛伦兹力磁轴承独立控制,通过洛伦兹线圈产生的洛伦兹力使转子沿X或Y轴偏转。在陀螺转子磁极包络面为理想球形的情况下,径向、轴向磁轴承产生的磁力将指向转子几何中心,而不对转子产生力矩作用。
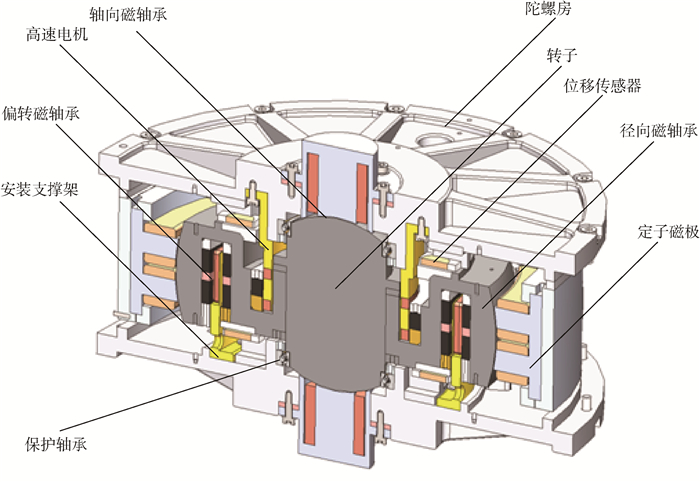 |
| 图 1 MSSG结构示意图 Fig. 1 Schematic diagram of configuration of MSSG |
| 图选项 |
双球形包络面的设计可从几何结构上实现平动与转动的解耦,为高精度的角速率敏感提供结构基础,同时,这种结构也可以输出较大的控制力矩,实现姿态控制功能。
1.2 MSSG角速率敏感原理 根据动量矩定理,高速转子角动量在惯性空间方向的改变只取决于其所受到的外部力矩,而MSSG转子所受到的外力矩只能来自磁轴承,因此,通过对转子所受磁悬浮力矩的测量,就可以间接得到转子相对于惯性空间的角速率ωI。
根据欧拉动力学原理,可得载体姿态角速率矢量测量方程:
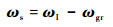 | (1) |
式中:ωs为载体相对于惯性空间的姿态角速率,即输入角速率;ωgr为磁悬浮转子相对于陀螺房的角速率。
因为洛伦兹力磁轴承的控制带宽和位移传感器的测量带宽远高于载体的姿态变化频率,所以MSSG的控制系统在其控制带宽内,总能保证式(1)成立。
在力臂已知的条件下,转子所受的偏转力矩由洛伦兹力磁轴承产生的洛伦兹力唯一确定,因此,ωI即可通过检测洛伦兹力磁轴承线圈中的电流实时获得,而磁悬浮转子相对于陀螺房的角速率ωgr则可通过对转子位移的检测获得。因此,载体角速率ωs就可以通过实时检测洛伦兹力磁轴承电流和转子位移,根据式(1)矢量解算得到。
2 数学模型 定义如下坐标系:转子坐标系C-xyz,原点C为转子几何中心,z为转子转轴方向,转子绕该轴以角速度Ω高速转动;定子坐标系O-XYZ,原点O为定子几何中心,并定义与定子坐标系相对应的球坐标系(R, φ, θ),如图 2所示。
2.1 电磁力模型 转子磁极上某一微元面积dS所受电磁力可以表示为[15]
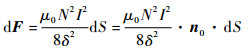 | (2) |
式中:μ0为真空磁导率;N为线圈匝数;I为线圈控制电流;n0为受力面积微元法线的单位向量;δ为定转子磁极间气隙大小。
当转子处于平衡位置时,各方向上气隙值相等,直接用式(2)积分即可得到转子所受电磁力大小。
若转子发生平移,转子几何中心从O点平移到C点,则每个磁极面处的气隙值将发生变化。设P为转子面上一点,连线CP的延长线与定子磁极面相交于点Q,如图 2所示,定子磁极与转子磁极之间的间隙大小可表示为
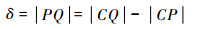 | (3) |
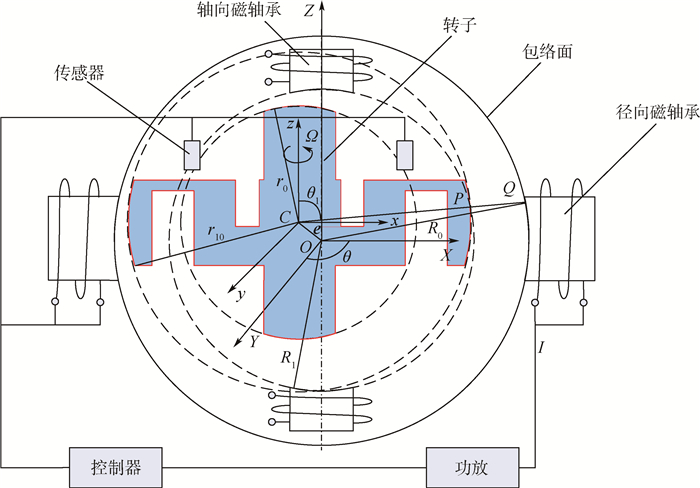 |
| 图 2 MSSG坐标系统 Fig. 2 Coordinate systems of MSSG |
| 图选项 |
由于转子平移远小于转子半径,因此CQ、OQ可视为同方向,根据矢量三角形COQ的几何关系,式(3)可写为
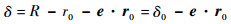 | (4) |
式中:R为定子磁极包络面半径;r0为相应转子磁极包络面半径;r0为r0的单位矢量;δ0为理想气隙值;e为O到C的线性位移矢量,即转子位移量,可表示为
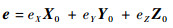 | (5) |
其中:X0、Y0和Z0分别为定子坐标系各轴单位向量。
r0在定子坐标系中可表示为
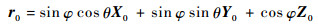 | (6) |
式中:φ为OP与Z轴夹角;θ为OP方位角。
将式(5)、式(6)代入式(4)可得
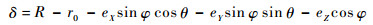 | (7) |
假设转子仅在轴向发生了偏移eZ+,根据式(7),定转子间气隙在磁极面间任一点上均会发生变化,从而每个磁轴承上的磁力也会发生变化,其气隙表达式变为
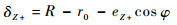 | (8) |
基于转子包络面理想球形的假设,当转子位置变化时,转子包络面上所有点的受力方向仍然指向转子几何中心。此时,偏移前转子上任意一点[r0cosθsinφ r0sinθsinφ r0cosφ]所受磁力的方向向量变为[r0cosθsinφ r0sinθsinφ r0cosφ-eZ+],代入式(2)可得dFZ+,如式(9)所示。
对于轴向磁轴承,产生磁力的磁极面积是转子几何中心与定子磁极棱线连线在转子包络面上所围的面积,为计算方便,将该磁极面积近似为定子磁极面,因此,转子Z方向发生偏移时,转子受Z轴正方向单个轴向磁轴承电磁力为FZ+_Z+,如式(10)所示。
在差动的安装方式下,转子在同一个方向上所受的力是相对的2个磁极产生电磁力之差,因此,轴向磁轴承所产生的电磁力为FZZ,如式(11)所示。
显然,当转子处于平衡位置时,定转子磁极之间的气隙处处相等,径向、轴向磁轴承合力均为0。但当转子在Z正方向产生平移时,由于定子磁极Z正方向处磁极间气隙变窄,磁力线变得更为密集,从而将产生更强的磁力,而在Z负方向处,磁极间气隙变宽,与转子处于平衡位置时所产生的磁力相比,定子对转子产生的作用力将变小。对于差动安装的一对定子磁极而言,上下磁极在Z方向产生的磁力变化方向一致,因此,其总效果近似单个磁极所产生电磁力的2倍。而在X和Y方向上,定转子磁极间气隙的变化分别关于两轴对称,磁力变化对称,因此2个方向的合磁力仍为0。
如果转子在径向发生平移,例如在X正方向偏移eX+,则轴向磁轴承产生的电磁力可表示为FZX,如式(12)所示。
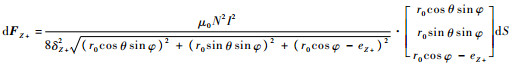 | (9) |
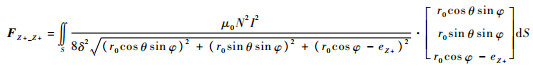 | (10) |
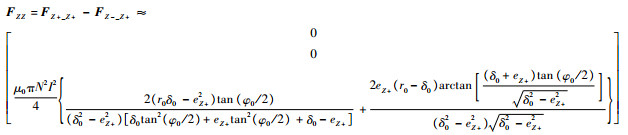 | (11) |
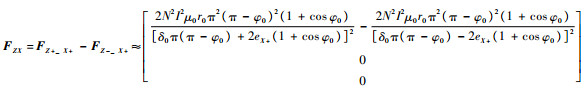 | (12) |
式中:φ0为轴向磁轴承定子磁极面对圆心的张角。
式(12)表明,当转子在X方向发生平移时,由于轴向磁轴承定子磁极X正方向处磁极间气隙变窄,磁力线变得更密集,从而将产生更强的磁力,而在X负方向处,磁极间气隙变宽,与转子处于平衡位置时所产生的磁力相比,定子对转子产生的作用力将变小,轴向磁轴承定子上下磁极在X方向所产生的磁力变化方向一致,其合力是单个定子所产生磁力的2倍。而在Y方向,由于轴向磁轴承定转子磁极间气隙的变化关于OXZ平面对称,磁力变化对称,因此Y方向磁力之和为0。在Z方向上,对于单个定子磁极而言,由于磁极间隙的变化导致气隙内磁场分布不均匀,从而产生Z方向磁力,但对于差动安装的2个轴向磁轴承定子磁极,其磁力变化关于OXY平面对称,因此,Z方向合磁力也为0。
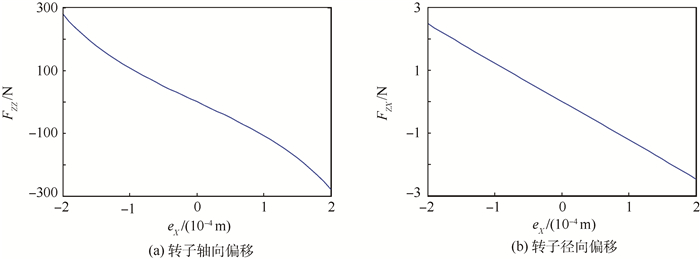
MSSG转子发生轴向和径向偏移时,其受到轴向磁轴承的电磁力随转子偏移量的变化如图 3所示,计算过程中的MSSG各项参数如表 1所示。
 |
| 图 3 轴向磁轴承电磁力与转子偏移量关系 Fig. 3 Relations between electromagnetic forces of axial bearing and rotor translations |
| 图选项 |
表 1 MSSG部分设计参数 Table 1 Partial design parameters of MSSG
| 参数 | 数值 |
| 磁极间气隙δ/mm | 0.35 |
| 轴向磁轴承定子磁极张角φ0/(°) | 32.6 |
| 真空磁导率μ0 | 4π×10-7 |
| 转子径向磁极包络面半径r01/mm | 73.65 |
| 转子轴向磁极包络面半径r0/mm | 41 |
| 定子轴向磁极包络面半径R0/mm | 41.35 |
| 定子径向磁极包络面半径R1/mm | 74 |
| 磁轴承保护间隙d0/mm | 0.2 |
| 洛伦兹力磁轴承线圈半张角φ0/(°) | 37 |
| 洛伦兹力磁轴承线圈匝数n | 200 |
| 轴向磁轴承线圈匝数N | 100 |
| 轴向磁轴承线圈电流I/A | 0.14 |
| 洛伦兹力磁轴承线圈电流ib/A | 1 |
| 洛伦兹力磁轴承磁场磁密B/T | 0.4 |
| 洛伦兹力磁轴承支撑架半径Lr/mm | 57.5 |
表选项
从图 3中可以看出,电磁力的变化与转子偏移量近似成正比,在相同的偏移量下,转子轴向偏移时轴向磁轴承对转子的作用力远远大于转子径向偏移时的电磁力。
在转子微小偏移条件下,2种情况产生的电磁力与偏移量的关系均可近似为线性关系,根据计算结果得到的等效位移刚度分别为-1.39N/μm和-0.012N/μm,前者是后者的近110倍。
为了对上述分析结果进行确认,利用电磁场有限元仿真软件,对提出的MSSG模型进行了有限元仿真与分析。图 4(a)为根据表 1参数建立的有限元模型。图 4(b)为MSSG转子发生轴向偏移时,转子受轴向磁轴承电磁力与偏移量关系的计算结果比较。可见,有限元仿真计算结果具有更明显的线性特性,变化规律与理论计算结果相同,有限元计算得到的等效位移刚度约-1.28N/μm,理论与仿真结果的误差约8.59%。误差原因主要在于理论计算中对磁场漏磁的忽略以及计算过程中的各种简化处理。
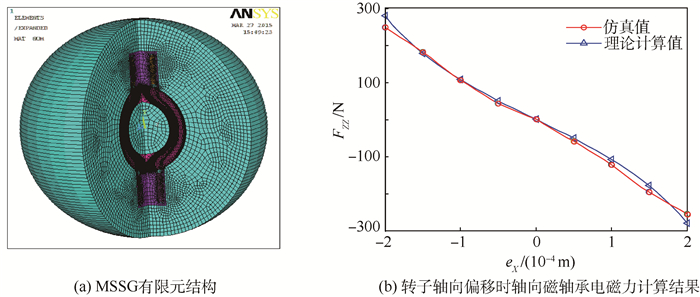 |
| 图 4 MSSG仿真结构与计算结果比较 Fig. 4 Comparison between MSSG simulation structure and computed results |
| 图选项 |
对于转子的任意平移运动,任意定子磁极所产生电磁力可表示为
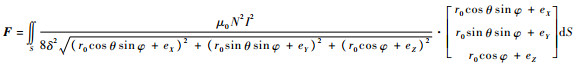 | (13) |
在转子磁极包络面为理想球面的条件下,无论转子向任何方向平移,转子所受电磁力的合力均通过转子几何中心,因此,转子平移并不产生使转子发生转动的力矩,但会造成转子振动,影响转子运行稳定性,需要采取措施进行振动控制。
对于轴向磁轴承和径向磁轴承而言,转子在X、Y、Z 3个方向平移时,磁轴承所产生的合力分别由3个部分组成,即磁轴承在自身方向偏移时产生的电磁力,以及另外2个磁轴承沿其自身方向偏移时所产生的耦合电磁力,可表示为
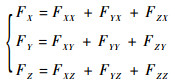 | (14) |
式中:Fi为i方向上的磁轴承在转子平移时所产生的电磁合力;Fij为转子在i方向平移时,该磁轴承在j方向上所产生的电磁力,i, j=X, Y, Z。
2.2 电磁力矩模型 当位于磁密为B的永磁体磁场、长度为L的线圈中通入与磁场方向垂直的电流ib时,线圈将会受到洛伦兹力的作用,其方向由左手定则确定。洛伦兹力可以表示为
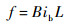 | (15) |
基于上述原理的MSSG偏转磁轴承由永磁体、线圈、阻磁材料和铁芯(用于永磁体磁路的闭合)等部分组成,结构原理如图 5所示。永磁体安装于陀螺转子径向边缘的凹槽内,用于产生磁场,线圈安装于钟形支撑架上,支撑架与陀螺定子固定,其中心与转子中心对齐于Z轴上。4组线圈分别在X、Y方向上对称安装。4个线圈在定子坐标系中的圆周角分别表示为
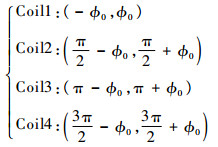 | (16) |
 |
| 图 5 洛伦兹力磁轴承结构原理 Fig. 5 Structure principle of Lorentz force bearing |
| 图选项 |
转子平衡时,若线圈中通入激励电流i,则线圈微元Lrdφ上产生的洛伦兹力微元为
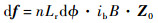 | (17) |
式中:φ为线圈微元方位角。
当转子绕X轴偏转α时,由于磁场方向变化,洛伦兹线圈上任一点所产生的洛伦兹力方向,由原来与线圈平面夹角90°变化为90-α′,如图 6所示,其中,
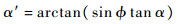 | (18) |
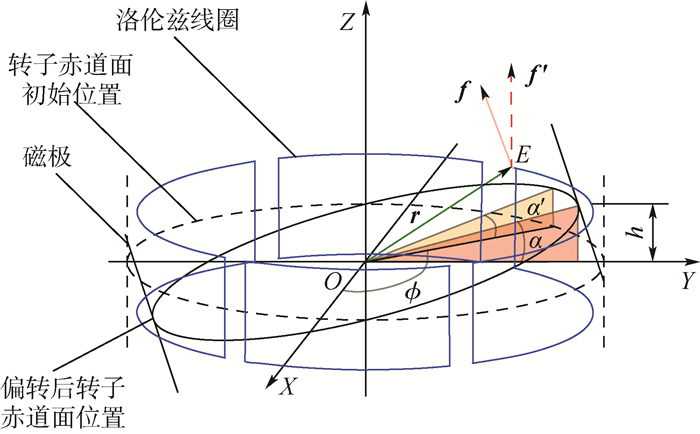 |
| 图 6 转子偏转时洛伦兹力方向变化示意图 Fig. 6 Schematic diagram of direction change of Lorentz force when spinning axis tilts |
| 图选项 |
线圈产生洛伦兹力的部分分为上下两部分,分别位于转子赤道平面的上下h距离平面处。转子偏转时,洛伦兹力仅方向发生变化,产生偏转力矩的力臂r不变,线圈上半部分产生的电磁力dfup和电磁力矩微元dTup为
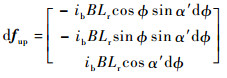 | (19) |
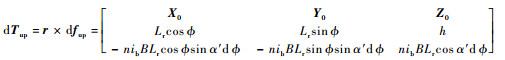 | (20) |
对式(19)、式(20)按照线圈的圆周角积分,可得到线圈上半部分产生的电磁合力与电磁合力矩。将其上下两部分产生的电磁力与电磁力矩相加,即可得到单个线圈在激励电流ib作用下产生的电磁力与电磁力矩。
如果在转子绕X轴偏转α的条件下,在Y方向上的线圈2、4中接入大小相等、方向相反的激励电流iX,在X方向上的线圈1、3中接入大小相等、方向相反的电流iY,根据式(19)、式(20),2个方向上线圈产生的电磁力和偏转电磁力矩可表示为
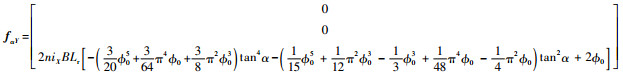 | (21) |
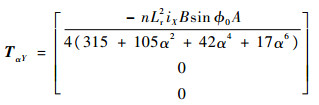 | (22) |
式中:A=-5040+840α2sinφ02-1680α2-378α4sinφ04+840α4sinφ02-672α4-630α6sinφ04+3640α6sinφ02+224α6+225α6sinφ06。
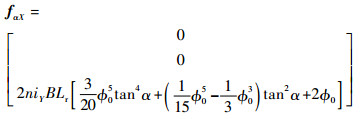 | (23) |
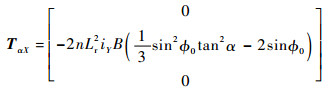 | (24) |
由式(21)~式(24)可见,当转子绕X轴偏转α时,Y方向的线圈仅产生使转子绕X轴旋转的电磁力矩,在其他2个方向上不产生力矩,而X方向的线圈也仅产生使转子绕Y轴旋转的电磁力矩。但是2个方向上线圈产生的电磁力合力均在Z方向上。图 7(a)为转子偏转角、激励电流与X、Y方向线圈产生的洛伦兹力关系。可以看出,在相同激励电流的作用下,X、Y 2个方向上洛伦兹线圈产生的电磁力随α的变化近似二次曲线,其中Y方向上线圈产生的电磁力随α的变化更快,但电磁力的变化范围小于1N。图 7(b)为转子偏转角、激励电流与X、Y方向电磁力矩关系。可知,虽然2个电磁力矩的表达式不同,但当线圈中接入的激励电流值大小相同时,不同方向线圈产生的电磁力矩大小和随转子偏转角和激励电流变化的趋势几乎完全相同,且电磁力矩随α变化的范围小于0.01N·m。MSSG中洛伦兹力磁轴承产生的电磁力与电磁力矩均与激励电流成线性关系,根据计算结果,电磁力fαY的电流刚度约为28.20N/A,f
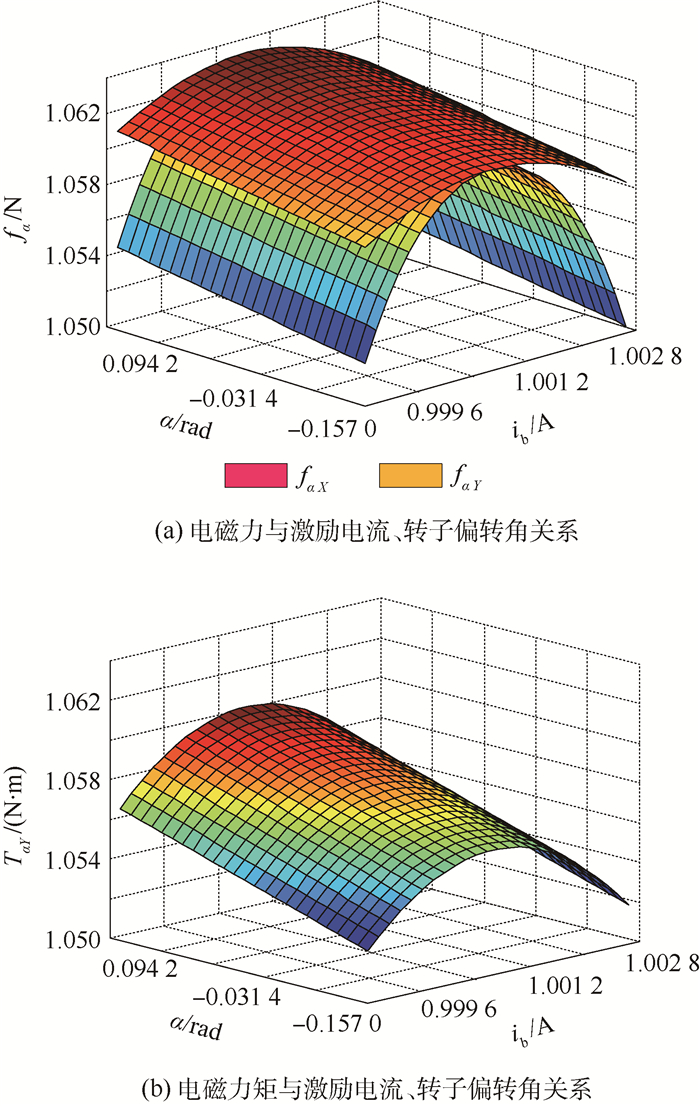 |
| 图 7 洛伦兹力磁轴承电磁力、力矩与激励电流及转子偏转角的关系 Fig. 7 Relations among electromagnetic force and moment of Lorentz force bearing, exciting current and rotor deflection angles |
| 图选项 |
当转子绕Y轴旋转β时,洛伦兹线圈产生的电磁力和电磁力矩也可按上述方法计算。最终,洛伦兹线圈产生的电磁力fl和电磁力矩Tl可以表示为
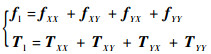 | (25) |
式中:fij(i,j=X,Y,Z)为i方向洛伦兹线圈绕j轴偏转时所产生的电磁力;Tij(i,j=X,Y,Z)为i方向洛伦兹线圈绕j轴偏转时所产生的电磁力矩。
根据牛顿第二定律和陀螺技术方程,结合式(14)、式(25),可得双球形包络面转子MSSG动力学模型为
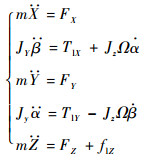 | (26) |
式中:Jz为转子转动惯量。
3 敏感精度影响因素分析 根据MSSG角速率敏感原理可知,影响MSSG敏感精度的主要影响因素为转子所受干扰力矩,在干扰力矩作用下,转子转轴将逐渐偏离原位置,从而在ωI的测量结果中引入漂移角速率误差,使MSSG敏感精度降低。
根据角动量定律,干扰力矩Td作用下,陀螺转子产生的漂移角速率可表示为
 | (27) |
式中:α0、β0和γ0为转子转轴在定子坐标系的方向余弦角。
由式(27)可知,MSSG所受干扰力矩主要来自2个方面:一是由于转子结构非球形,导致转子所受电磁力合力不再通过转子几何中心从而产生干扰力矩;二是转子的洛伦兹力磁轴承在生成偏转力矩时引入误差而形成干扰力矩。
3.1 转子非球形误差 如果MSSG转子、定子磁极包络面为理想球面,且所对应球面几何中心重合,各通道的测量、控制设备性能参数完全相同,则转子绕极轴稳定转动时,转子表面各处磁力均通过球心,系统无干扰力矩影响,无漂移角速率产生。但是由于材料自身结构和机械加工、装配精度、离心变形等原因[16],实际的定子、转子磁极包络面将偏离理想球面,这种偏离将使转子所受电磁力不再通过转子几何中心而形成对转子几何中心的矩,进而产生漂移角速率[17-18]。
为简化分析,假设转子磁极包络面为近似球面的旋转曲面,其外形可由勒让德多项式级数描述如下:
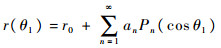 | (28) |
式中:r(θ1)为转子坐标系中,转子包络面上一点的矢径的大小;θ1为r与z轴之间的夹角;an为描述包络面形状的谐波系数;Pn (cosθ1)为勒让德多项式级数,可表示为
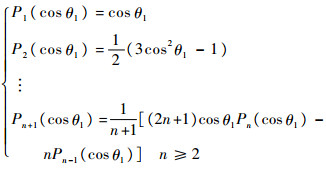 | (29) |
因此,式(7)中定子磁极与转子磁极之间的间隙可以表示为
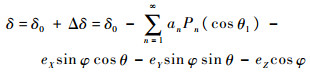 | (30) |
式中:δ0=R-r0。
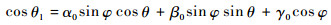 | (31) |
而当转子包络面形状偏离理想球面,成为一个准球形封闭面时,磁场力相对于转子几何中心产生干扰力矩,其微分形式为
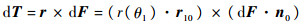 | (32) |
积分后的干扰力矩方程可表示为[19]
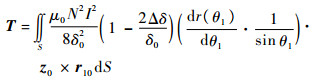 | (33) |
式中:z0=α0X0+β0Y0+γ0Z0为转子转轴在定子坐标系中的矢量表达式。
将式(6)、式(29)、式(31)代入式(33),并将dS转换到球坐标系,同时分别计算6个定子磁极产生的干扰力矩,可得该MSSG由于转子非球形产生的干扰力矩为
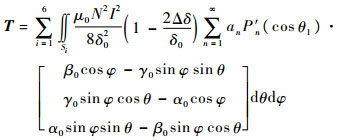 | (34) |
由于式(28)中的偶次谐波表示转子的对称变形,因此,在转子处于平衡位置时,偶次谐波不产生干扰力矩,但当转子偏离平衡位置时,则偶次、奇次谐波均产生干扰力矩。图 8为表 1所示参数转子在eX=eY=eZ=10μm时,径向干扰力矩随非球形系数的变化情况。可知,随着a1和a2的增长,径向干扰力矩近似线性增长,干扰力矩随a1的增长速度更快,当非球形系数为0时,干扰力矩消失,即转子包络面为理想球形时,磁轴承的支承力对转子不产生力矩。
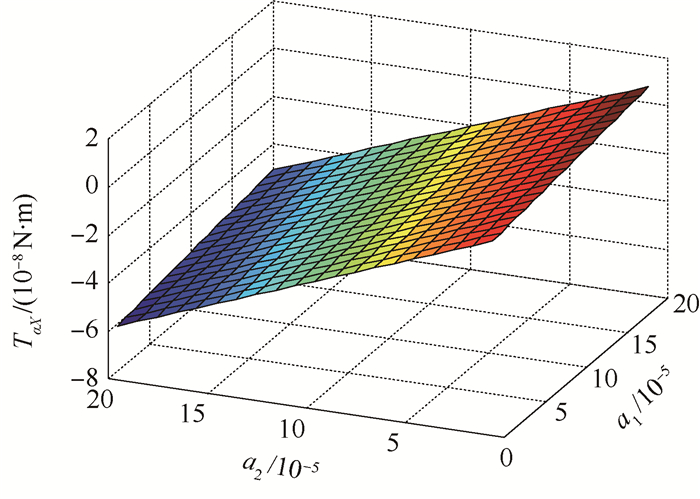 |
| 图 8 干扰力矩与转子非球形系数关系 Fig. 8 Relations of disturbance torque and rotor aspheric coefficients |
| 图选项 |
3.2 洛伦兹力磁轴承误差 由式(23)、式(25)可知,当洛伦兹线圈所处的环形磁场径向分布不均时,转子的径向平动将会引起洛伦兹线圈所处磁场变化,从而导致干扰力矩产生;当环形磁场轴向分布不均时,转子的轴向运动将会导致洛伦兹线圈所处磁场发生变化,产生干扰力矩。而转子的偏转,会使洛伦兹线圈相对环形磁场发生更加复杂的相对运动,也会使洛伦兹线圈所处磁场发生变化,导致干扰力矩产生。上述3种干扰力矩产生的情况,都是由于洛伦兹磁轴承转子磁极磁场分布不均导致的。ANSYS软件仿真洛伦兹力磁轴承的磁场及磁力线分布剖面如图 9所示。可见,环形磁场的上下两部分磁密分布基本相同,磁密在轴向上呈现中心强、两边弱的分布,在径向上呈现中心弱、两边强的分布,整体上分布不均匀,因此,洛伦兹力磁轴承磁场的实际分布必然会导致干扰力矩的产生。
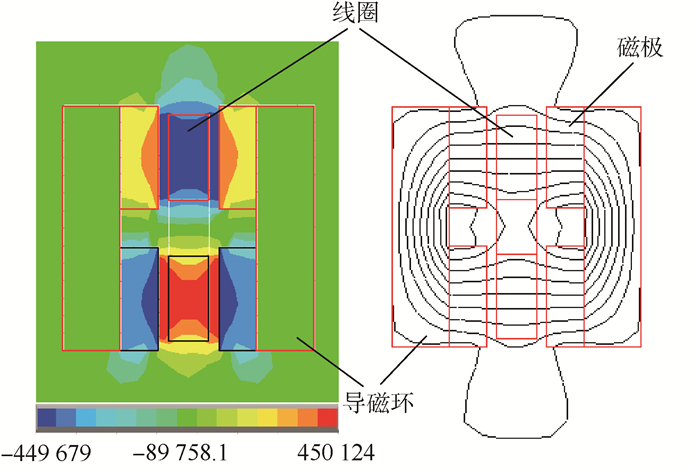 |
| 图 9 洛伦兹力磁轴承磁场与磁力线分布仿真 Fig. 9 Simulation of magnetic field and magnetic lines distribution in Lorentz force bearing |
| 图选项 |
除磁场不均导致洛伦兹力磁轴承产生干扰力矩外,洛伦兹线圈钟形支撑架半径的加工误差也会导致洛伦兹力及力臂的变化,使洛伦兹线圈产生的偏转力矩中附带干扰力矩,且加工误差会与磁密分布误差互相耦合,使干扰力矩的变化更为复杂。例如2种误差共同作用下,转子偏转α时,X方向洛伦兹线圈产生的干扰力矩可表示为
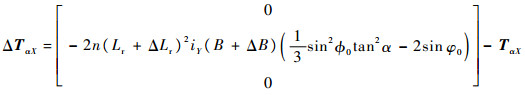 | (35) |
实际上,由于磁场分布的不对称和支撑架半径误差沿周向分布的不对称,洛伦兹线圈可能在X、Z方向也会耦合出相应的干扰力矩。
2种误差耦合导致的干扰力矩变化如图 10所示。可知,干扰力矩随着磁密误差和加工误差的增大而增大,在小范围内近似线性,干扰力矩随磁密误差变化的斜率更大,说明磁场分布的不均匀性对陀螺的检测精度影响更大。
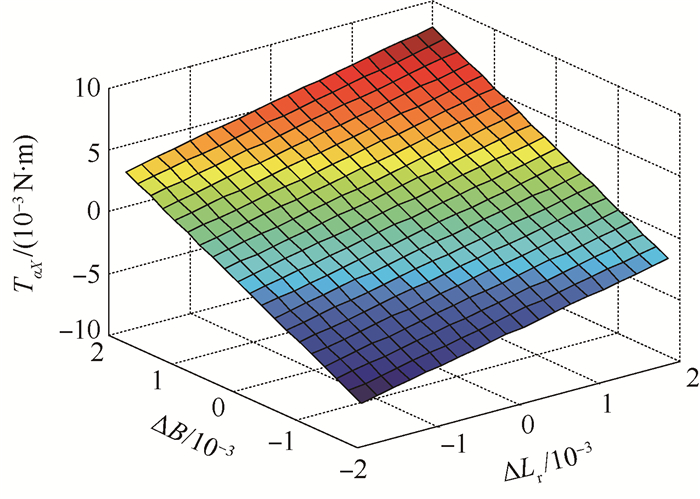 |
| 图 10 磁密分布及支撑架加工误差与干扰力矩关系 Fig. 10 Relations among magnetic density distribution, frame processing errors and disturbing torque |
| 图选项 |
4 结论 基于AMBs的MSSG具有敏感姿态角速率的功能,可以实现同时对二自由度姿态的敏感,具有高精度、高带宽的发展潜力。本文设计了一种具有双球形包络面转子的MSSG,通过定转子磁极面的球面设计,可使转子转动过程中所受电磁力通过转子几何中心,实现平动对转动的解耦。
1)在对该MSSG结构和测量原理分析的基础上,构建了动力学模型,得到了径向、轴向磁轴承电磁力以及偏转磁轴承电磁力矩的解析表达式。
2)仿真计算表明,当转子包络面为理想球形时,转子的平移运动仅会导致定子磁极对转子电磁力的作用,而不会对转子产生力矩作用,平移运动在垂直方向上的耦合电磁力比运动方向上的主电磁力小2个数量级,理论计算与有限元仿真结果基本吻合。
3)洛伦兹力磁轴承单独控制的偏转力矩对转子偏转角度不敏感,但磁轴承对转子的转动控制会在转子轴向上产生耦合电磁力,其值小于1N。
4)基于MSSG的动力学解析模型,得到了转子非球形条件下干扰力矩解析表达式,分析了洛伦兹力偏转磁轴承加工误差对MSSG敏感精度的影响。初步分析表明,转子非球形和洛伦兹力陀螺磁场分布不均是产生干扰力矩的2个关键因素,转子包络面非球形系数中,奇次谐波系数对干扰力矩的生成贡献更大,当转子位于平衡位置时,由于转子形状的对称性,偶次谐波系数不会导致干扰力矩的生成。
本文的研究可为MSSG高转速下的动力学特性分析提供理论基础,并为悬浮类陀螺的误差分析与补偿设计提供有益参考。
参考文献
| [1] | FANG J C, ZHENG S Q, HANG B C. AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J].IEEE/ASME Transactions on Mechatronics, 2013, 18(1): 32–43.DOI:10.1109/TMECH.2011.2161877 |
| [2] | REN Y, FANG J C. Current-sensing resistor design to include current derivative in PWM H-bridge unipolar switching power amplifiers for magnetic bearings[J].IEEE Transactions on Industrial Electronics, 2012, 59(12): 4590–4600.DOI:10.1109/TIE.2011.2179277 |
| [3] | REN Y, FANG J C. High-precision and strong-robustness control for an MSCMG based on modal separation and rotation motion decoupling strategy[J].IEEE Transactions on Industrial Electronics, 2014, 61(3): 1539–1551.DOI:10.1109/TIE.2013.2257147 |
| [4] | REN Y, FANG J C. Modified cross feedback control for a magnetically suspended flywheel rotor with significant gyroscope effects[J].Mathematical Problems in Engineering, 2014, 2014: 1–11. |
| [5] | FANG J C, REN Y, FAN Y H. Nutation and precession stability criterion of magnetically suspended rigid rotors with gyroscopic effects based on positive and negative frequency characteristics[J].IEEE Transactions on Industrial Electronics, 2014, 61(4): 2003–2014.DOI:10.1109/TIE.2013.2266077 |
| [6] | BOLETIS A, BARROT F, MOSER R.Three axis active magnetic levitation for inertial sensing systems:US7252001B2[P].2007-08-07. |
| [7] | BOSGIRAUD T.Two degrees of freedom miniaturized gyroscope based on active magnetic bearings[D].Lausanne:Ecole Polytechnique Federale de Lausanne, 2008:22-35. |
| [8] | MARUYAMA Y, MIZUNO T, TAKASAKI M, et al. An application of active magnetic bearing to gyroscopic and inertial sensors[J].Journal of System Design and Dynamics, 2008, 2(1): 155–164.DOI:10.1299/jsdd.2.155 |
| [9] | MARUYAMA Y, MIZUNO T, TAKASAKI M, et al. Extension of measurement bandwidth in an AMB-based gyroscopic sensor[J].Mechatronics, 2009, 19(8): 1261–1268.DOI:10.1016/j.mechatronics.2009.08.002 |
| [10] | MARUYAMA Y, MIZUNO T, TAKASAKI M, et al.Proposal of a new configuration for magnetically suspended gyro[C]//35th Annual Conference of IEEE Industrial Electronics.Piscataway, NJ:IEEE Press, 2009:1911-1916. |
| [11] | 房建成, 刘彬, 王志强, 等.一种磁悬浮陀螺飞轮:CN 200910241243.3[P].2012-07-25.FANG J C, LIU B, WANG Z Q, et al.A magnetically suspended gyrowheel:CN200910241243.3[P].2012-07-25(in Chinese). |
| [12] | 刘彬, 房建成, 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析[J].航空学报, 2011, 32(8): 1478–1487.LIU B, FANG J C, LIU G. Design of a magnetically suspended gyrowheel and analysis of key technologies[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1478–1487.(in Chinese) |
| [13] | FANG J C, ZHEN S Q, HAN B C. Attitude sensing and dynamic decoupling based on active magnetic bearing of MSDGCMG[J].IEEE Transactions on Instrument and Measurement, 2012, 61(2): 338–348.DOI:10.1109/TIM.2011.2164289 |
| [14] | ZHEN S Q, HAN B C. Investigations of an integrated angular velocity measurement and attitude control system for spacecraft using magnetically suspended double-gimbal CMGs[J].Advances in Space Research, 2013, 51(12): 2216–2228.DOI:10.1016/j.asr.2013.01.015 |
| [15] | 房建成, 孙津济, 樊亚洪. 磁悬浮惯性动量轮技术[M].北京: 国防工业出版社, 2012: 112-115.FANG J C, SUN J J, FAN Y H. Magnetically suspended inertial momentum wheel technology[M].Beijing: National Defense Industry Press, 2012: 112-115.(in Chinese) |
| [16] | HU X N, WANG Q, CUI C Y, et al. Torque compensation system design for a spherical superconducting rotor[J].IEEE Transactions on Instrument and Measurement, 2014, 63(12): 2789–2794.DOI:10.1109/TIM.2014.2318872 |
| [17] | HE C, WANG Q. Force characteristics analysis on a superconducting sphere suspended by spherical coils[J].Cryogenics, 2007, 47(7-8): 413–417.DOI:10.1016/j.cryogenics.2007.04.007 |
| [18] | LIU J H, WANG Q, LI X. Modeling of the superconducting suspension system with shaping blocks[J].IEEE Transactions on Applied Superconductivity, 2010, 20(1): 47–51.DOI:10.1109/TASC.2009.2038361 |
| [19] | 崔春艳, 胡新宁, 程军胜, 等. 超导磁悬浮支承系统干扰力矩及漂移误差分析[J].物理学报, 2015, 64(1): 379–389.CUI C Y, HU X N, CHENG J S, et al. Analysis of magnetic disturbance torque and drift error in a superconducting suspension system[J].Acta Physica Sinica, 2015, 64(1): 379–389.(in Chinese) |
