多子阵交错稀疏优化布阵的关键问题在于如何在保证子阵方向图性能近似一致的情况下减小子阵方向图的旁瓣峰值,目前已有一些****对此类问题提出了探索性的解决方案,并取得了不错的效果。研究主要集中在利用差集与互补差集及其延拓实现多子阵的交错稀疏布阵。文献[3-5]利用循环差集及其“补集”实现了多子阵的稀疏交错布阵,并将其成功地应用于宽带天线、极化捷变天线和雷达收发双置天线的综合设计。文献[6-8]利用几乎差集对两子阵的稀疏交错优化设计进行了深入研究,并将其应用于极化捷变天线的综合和超声成像收发双置天线的设计。但现有的差集还比较少,基于差集的交错稀疏优化方法还只能对一些阵元数量特定的部分阵列进行优化,而且产生的交错子阵方向图旁瓣峰值还有进一步优化的空间。文献[9-10]利用遗传算法设计了两子阵交错布阵的共享孔径线阵天线,并将其成功应用于单脉冲和差波束阵列天线的实现。但对于大孔径多子阵的稀疏交错共享孔径天线,遗传算法存在优化目标函数过多,收敛速度慢,运算效率低,容易陷入局部最优等缺陷。
迭代快速傅里叶变换(FFT)算法利用均匀阵列天线方向图与阵元激励间存在的傅里叶变换的关系,通过对阵元激励的优化选择,实现稀疏、低副瓣的天线设计[11-13]。本文通过对线阵天线方向图的频谱激励能量分布的分析,根据密度加权阵的相关原理[14],通过将天线方向图的频谱能量等额均分,实现了多子阵的稀疏交错布阵。本文的主要工作如下:
1) 基于均匀阵列天线方向图与阵元激励间存在的傅里叶变换的关系,详细分析并提出了基于方向图频谱能量平均分配的均匀线阵多子阵交错方法,从理论和仿真上验证了该方法的有效性和可行性。
2) 提出了改进迭代FFT算法,实现了多子阵交错稀疏布阵。
3) 通过实验仿真证明,利用新提出的均匀线阵交错方法能够有效对多子阵交错的共享孔径天线进行优化设计。并通过分析孔径利用率,子阵间旁瓣峰值的差值及子阵旁瓣峰值等参数对交错方法的性能进行了详细的评估。通过控制不同子阵主瓣波束指向,实现了多波束指向的多功能稀疏交错共享孔径天线的设计。
1 多子阵交错阵列天线优化模型 由于线阵天线方向图满足乘法定理,为了方便研究阵元位置与天线阵列方向图之间的关系,可以将天线单元看成全向性点元。当主瓣指向 θ0方向,来波信号波长为λ,一个阵元数为N、阵元栅格间距为λ/2、入射方位角为θ、阵元激励为In的均匀线阵,其方向图可表示为
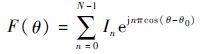 | (1) |
对式(1)进行傅里叶逆变换可得
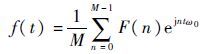 | (2) |
式中:M为周期;t为傅里叶变换的采样点数,1<t<M;ω0=2π/M为采样间隔。
由式(1)和式(2)可知,阵元的激励In与阵因子之间存在傅里叶变换的关系[11]。多子阵的稀疏交错共享孔径阵列天线是指利用孔径空分复用技术,将多个子阵交错布置在同一个孔径上,使各个子阵的方向图性能近似一致,旁瓣电平都能处于一个较低的水平。根据交错阵列天线的设计要求可知,其数学优化模型可以表示为
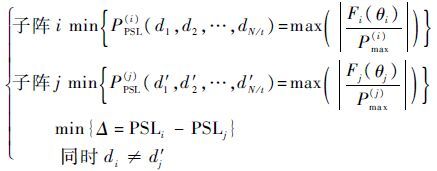 | (3) |
式中PPSL(i)和PPSL(j)分别为第i、j个子阵的旁瓣峰值;Fi(θi)和Fj(θj)分别为第i、j个子阵旁瓣区域的值;Pmax(i)和Pmax(j)分别为第i、j个子阵的主瓣增益值;θi和θj分别为子阵i、j旁瓣区域的方位角。
2 直线阵列多子阵交错方法 由于直线阵列天线阵元激励与方向图函数之间存在傅里叶变换的关系,将阵元激励看成离散的“频谱信息”,则其对应的方向图曲线可以看成是阵列天线的“时域信号”。不失一般性,以400元直线阵列天线为例,对本文提出的方法进行详细的描述。假设子阵数目为4(T=4),阵列天线的稀疏率为75%,生成初始的随机0、1序列I,该序列含100个1值,300个0值。对I做2 048点的FFT逆变换生成时域信号P,将P旁瓣区域中大于约束旁瓣的值置为-25 dB,其余值保持不变,从而生成新的时域信号,如图 1(a)所示。对约束后的方向图做FFT变换生成激励矢量,由文献[13]可知,可以截取其前400个点的激励频谱值作为迭代约束后的阵元满阵激励IN,对其进行由大到小的排序,生成Ir如图 1(b)所示。
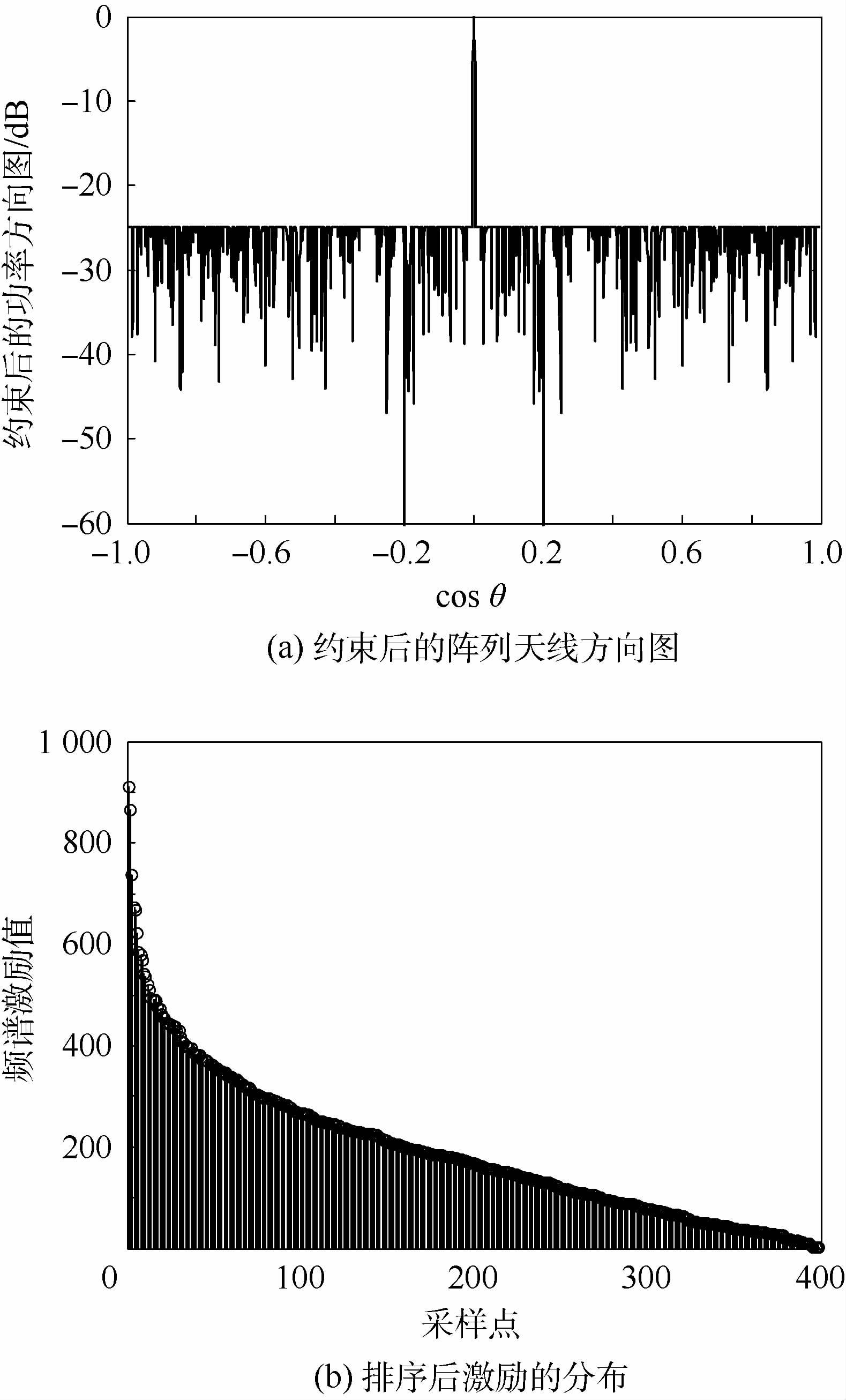 |
| 图 1 约束后的阵列天线方向图及其阵元激励 Fig. 1 Restraint pattern and array element excitations |
| 图选项 |
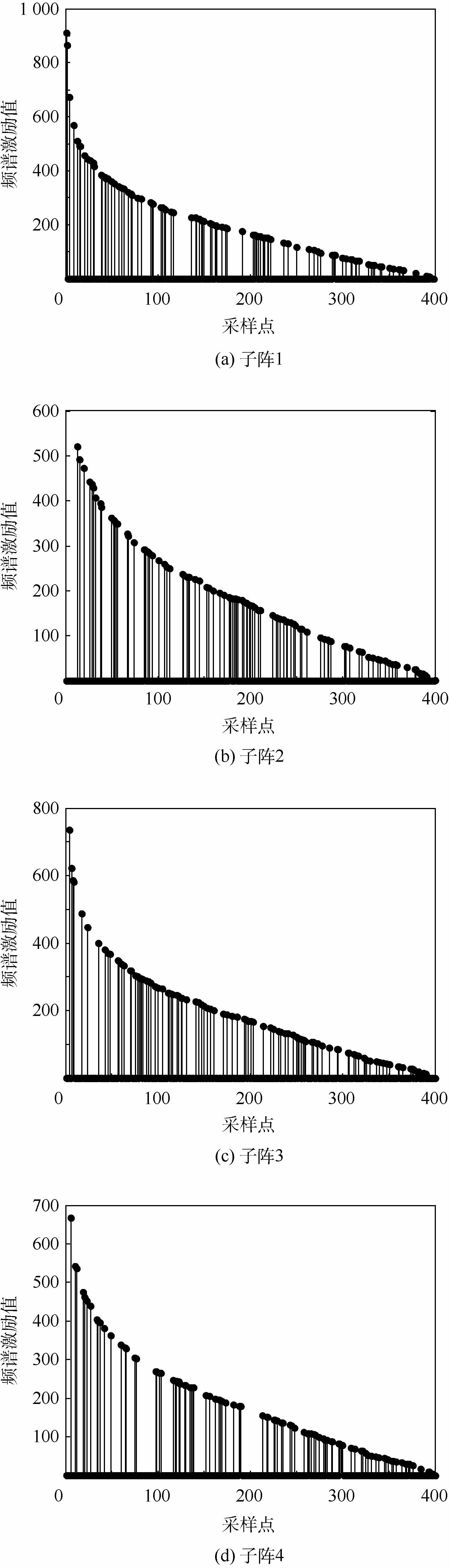
为了均分阵列天线的频谱能量,以交错的方式对I1进行选择,被选择激励相对于原天线孔径所在的位置即为子阵阵元所在的位置,其数学表述如式(4) 所示。4个子阵阵元的位置及其激励值如图 2所示。从图 2中可知,4个子阵的阵元位置是交错稀疏分布在同一个天线孔径上的,子阵的激励分布趋势及相应的值基本相同。
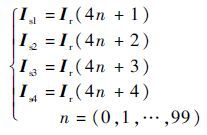 | (4) |
 |
| 图 2 交错子阵单元的激励与位置 Fig. 2 Excitations and positions of interleavedsubarray elements |
| 图选项 |
式中:Isi为第i个子阵的激励。根据密度加权阵的相关原理,线阵栅格点上阵元存在的概率取决于线阵栅格点上的激励权值分布,权值幅度大的栅格点上阵元存在的概率就大。因此可以设置存在阵元位置上的值为“1”,表示阵元存在,无阵元位置的栅格处的值为“0”。经过一次迭代后的子阵天线方向图如图 3所示。从图 3中可知,通过该交错方法形成的4个子阵方向图旁瓣值近似相同,子阵1的旁瓣峰值为-12.01 dB,子阵2的旁瓣峰值为-15.15 dB,子阵3的旁瓣峰值为-13.11 dB,子阵4的旁瓣峰值为-15.14 dB,子阵间的旁瓣峰值最大差值为3.14 dB,最小差值仅为0.01 dB。为了进一步减小子阵的旁瓣峰值,可以循环迭代使用FFT算法,最终实现多子阵交错的共享孔径直线阵列天线的设计。
 |
| 图 3 四子阵交错的天线方向图 Fig. 3 Patterns of four interleaved subarrays |
| 图选项 |
考虑一个阵元数为N,交错子阵数为T,稀疏率为R的等栅格分布的均匀直线阵列天线,首先随机生成N/T 个“1”值的0、1序列作为阵列天线的初始激励值,对其作Q点的FFT变换,得到阵列天线的方向图值,令阵列天线方向图旁瓣区域中大于约束旁瓣值的点上的值等于约束旁瓣,然后对约束后的阵列天线方向图进行Q点的FFT变换,获得Q个点激励幅值I。截取前N个值作为满阵激励值IN,并对其进行由大到小排序,形成新的序列Ir,则可以选取向量(Ir(1),Ir(1+T),…,Ir(1+T×K))对应向量A所在的位置作为稀疏子阵1的单元位置,(Ir(2),Ir(2+T),…,Ir(2+T×K))对应向量IN所在的位置作为子阵2的阵元位置,……,(Ir(T),Ir(2T),…,Ir(T×(K+1))对应向量IN所在的位置作为子阵T的阵元位置(K=N/T-1)。所有子阵均为密度加权阵,激励值置为1。以第一个子阵天线单元激励值作为输入值,进入下一次的迭代。采用这样的迭代方式原因在于,根据文献[11]可知,通过少量的迭代进行FFT变换,天线单元的激励能量值会更集中于采样点的前端,这样能让子阵天线的旁瓣峰值更接近于约束旁瓣值,从而达到降低子阵旁瓣的目的。图 4为改进型迭代FFT算法的流程图,其具体步骤可概括如下。
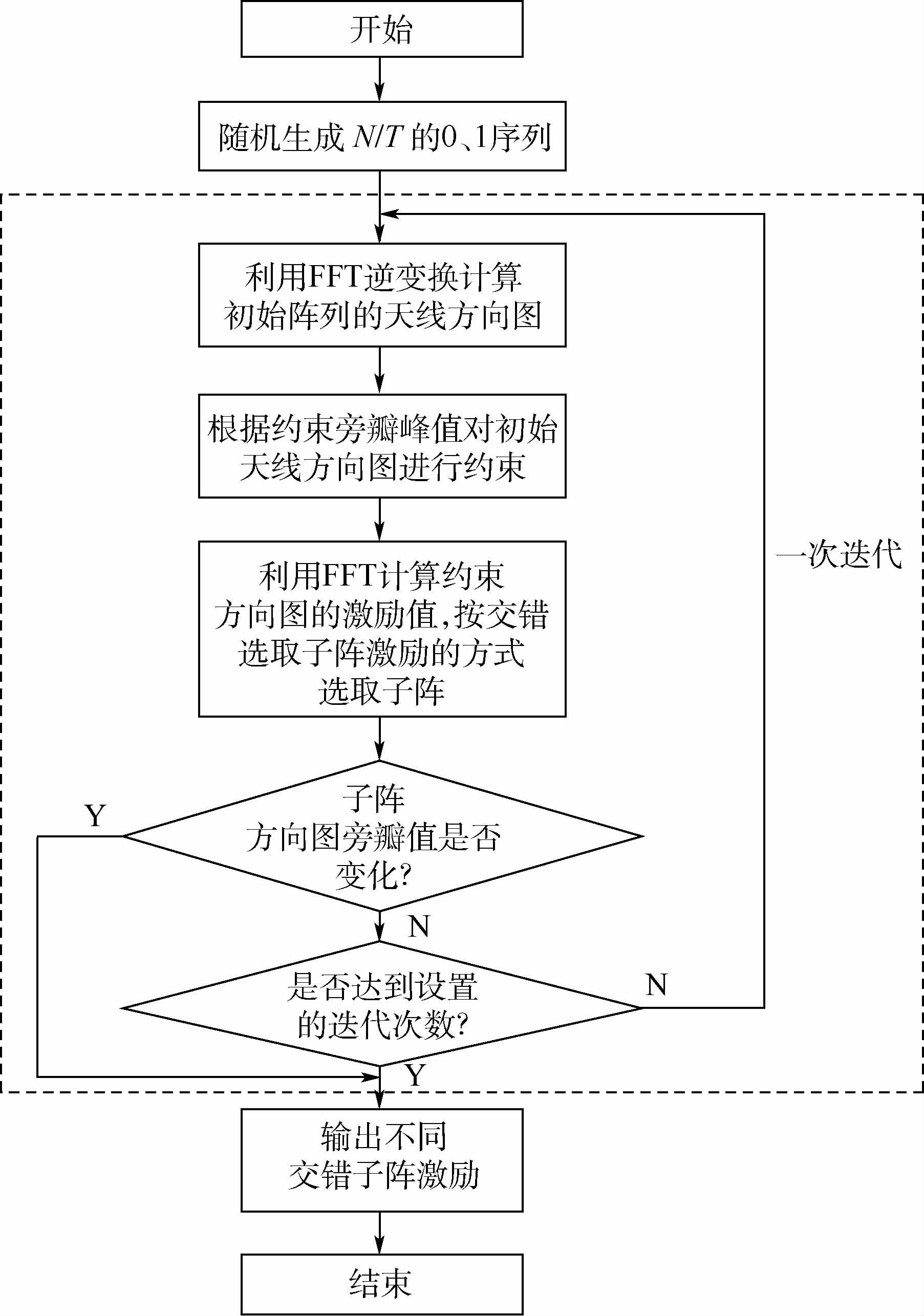 |
| 图 4 改进型迭代FFT算法流程图 Fig. 4 Flowchart of modified iterative FFT algorithm |
| 图选项 |
1) 按稀疏率R=1/T随机稀疏阵元数为N的均匀直线阵列,设置阵列激励值I为1。
2) 对I做Q点的FFT逆变换,得到P。
3) 对P旁瓣区域的值进行判定,令幅值大于约束旁瓣值区域上的点值等于约束旁瓣值,其他点上的值保持不变。
4) 对校正后的P进行Q点的FFT变换,得到新的激励值I。
5) 截取I中的前N个值,生成新的激励矩阵,对其进行由大到小排列,生成新的激励向量IN。
6) 以(Ir(i),Ir(i+T),…,Ir(i+T×K))位置处的激励对应在A上的位置作为第i个子阵单元所在的位置,同时将该位置上的激励值置为1。
7) 对新生成的子阵1的激励向量进行FFT逆变换,判断更新后的天线方向图旁瓣峰值相对于上一次迭代时的旁瓣峰值是否有变化,是则继续下一步的计算,否则输出结果。
8) 将子阵1的单元激励序列作为新的输入值进入下一轮的迭代,重复步骤2)~步骤8),直到新生成的天线方向图旁瓣峰值不再变化,输出优化后的结果。
3 实验仿真与分析 3.1 四子阵交错的共享孔径直线阵列天线 为了验证基于迭代FFT算法的直线阵列多子阵交错的有效性和可行性,首先对100元等间隔分布的均匀直线阵列进行四子阵交错的优化设计(T=4)。阵列的稀疏率为75%,单个子阵阵元数量为25,此时,在利用迭代FFT算法时,应以以下方式选取子阵单元的激励:
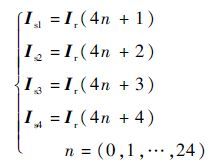 | (5) |
设置旁瓣约束值为-20 dB,对其做2 048点的FFT变换。得到图 5所示的四子阵交错的单元结构。其中,“1”代表该点处有阵元,“0”代表该点处的阵元被稀疏。从图 5中可知,4个子阵交错分布在同一个天线孔径,各个子阵孔径大小与原均匀阵列天线孔径基本一致,且避免了不同子阵天线单元的位置重叠。若以式(6)表示阵列的孔径利用率
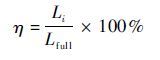 | (6) |
 |
| 图 5 四子阵交错的天线孔径结构 Fig. 5 Aperture architecture of four interleaved subarrays |
| 图选项 |
式中:Li为稀疏子阵i的阵列天线孔径电尺寸大小;Lfull为均匀阵列天线孔径电尺寸大小。可以得出子阵1的孔径利用率为97%,子阵2的孔径利用率为92%,子阵3的孔径利用率为88%,子阵4的孔径利用率为96%。交错布阵的4个子阵使得100元的均匀阵列天线的孔径利用率大幅提高,单个子阵的阵列天线分辨率得到大幅提高。
为了对本文提出的交错方法的性能进行评估,首先对25元均匀布阵的直线阵列和100个阵元以稀疏率为25%随机稀疏的直线阵列天线方向图进行实验仿真,仿真结果如图 6所示。从图 6(a)中可知,当阵列以25单元均匀布阵时,阵列天线方向图旁瓣值为-13.21 dB,但由于该阵列天线的天线孔径为10λ,导致阵列天线的分辨率较低,此时方向图零点主瓣宽度为10°。若采用100个等间隔栅格以随机稀疏的方式布置25个阵元,由于此时阵列天线的孔径为45.5λ,阵列天线的分辨率大幅增加,方向图零点主瓣宽度为2.5°,但由此导致的问题就是方向图旁瓣峰值较大,此时的阵列天线副瓣电平为-6.448 dB。交错稀疏共享孔径阵列天线就是将交错方法与阵列稀疏优化方法有机协同,设计出子阵方向图旁瓣低且孔径利用率高的阵列天线。对图 5结构的阵列天线进行仿真计算,得到的仿真结果如图 7所示。
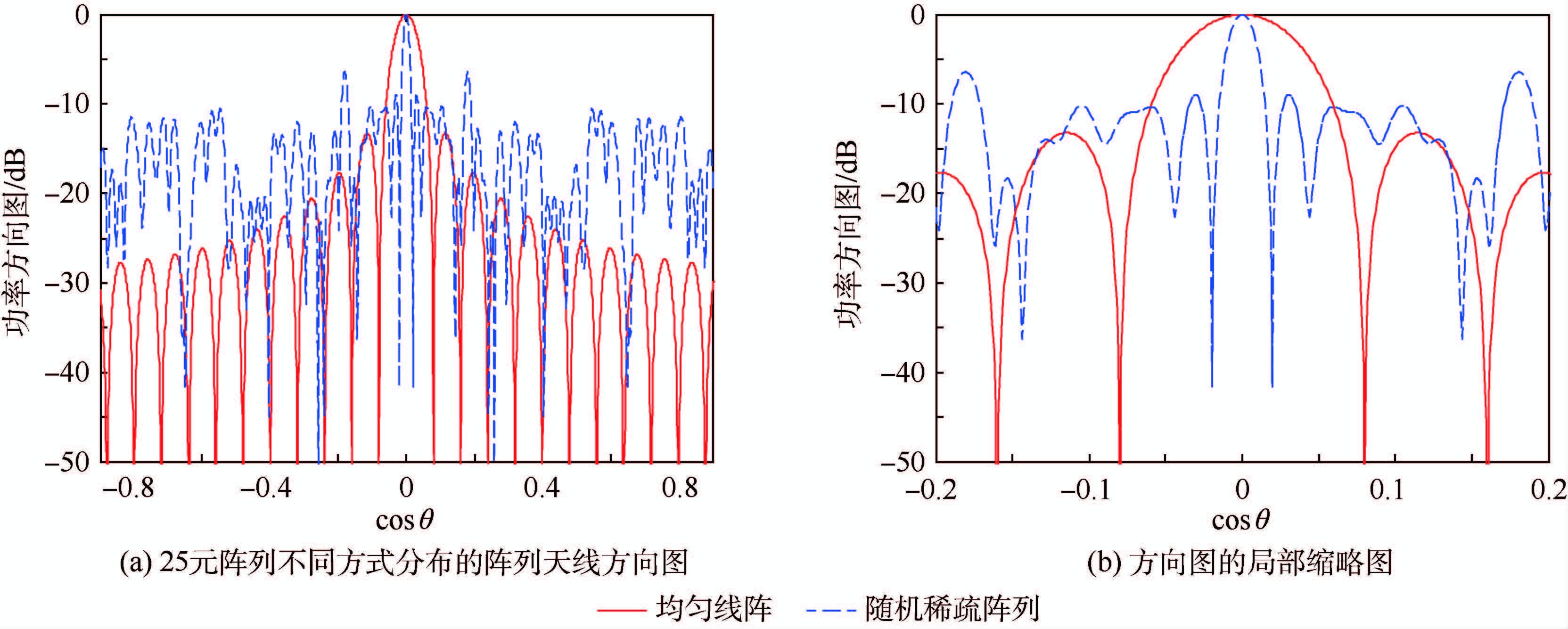 |
| 图 6 不同方式分布的直线阵列天线方向图 Fig. 6 Patterns of linear array antenna with different layouts |
| 图选项 |
从图 7中可知,通过交错稀疏的共享孔径阵列天线的旁瓣峰值相对于随机稀疏的子阵有了相应的减小,且各个子阵充分利用了天线孔径,4个子阵方向图的零点主瓣宽度同为3.6°,且可以得出子阵1的方向图旁瓣峰值为-9.911 dB,子阵2的旁瓣峰值电平为-9.556 dB,子阵3的旁瓣峰值电平为-9.965 dB,子阵4的旁瓣峰值电平为-8.901 dB。子阵间的旁瓣峰值电平最大差值为1.064 dB,最小差值仅为0.054 dB,这就保证了4个子阵方向图性能基本一致,证明基于迭代FFT算法的直线阵列多子阵交错方法是有效的。
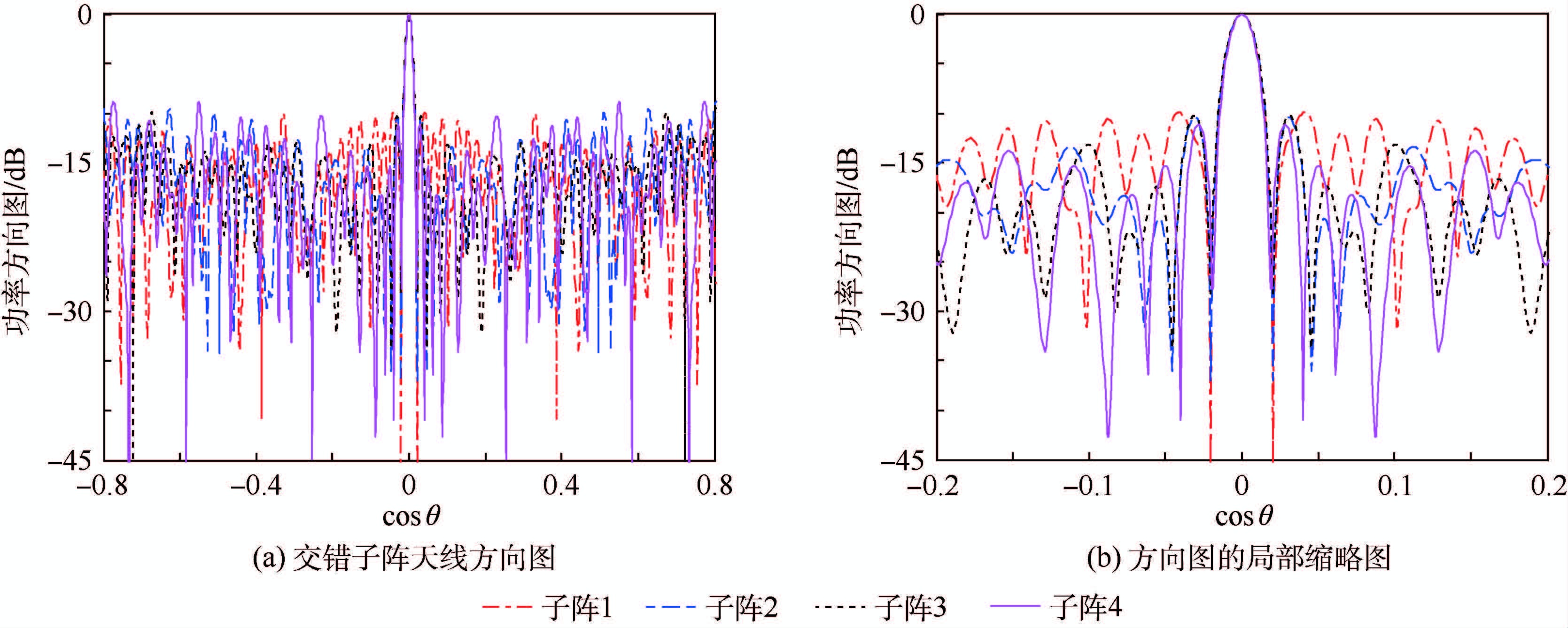 |
| 图 7 四子阵交错的直线阵列天线方向图 Fig. 7 Patterns of linear array antenna for four interleaved subarrays |
| 图选项 |
3.1.1 激励权值对基于迭代FFT交错子阵方向图的影响 本文主要研究的是阵列单元位置对天线方向图的影响,寻求多子阵交错稀疏分布在同一个天线孔径的优化方法,通过优化单元位置来降低子阵天线方向图旁瓣峰值,实现阵列天线稀疏优化布阵。需要特别说明的是,阵列天线设计在工程应用中是一个需要系统解决的优化问题。虽然利用本文方法稀疏交错优化后的阵列天线旁瓣峰值相对于工程应用要求来说较高,但阵列天线单元位置优化是阵列天线其他优化研究工作的基础和前提(包括阵元激励优化、阵元扰动、互耦和通道不一致误差的估计与消除),在优化子阵单元位置后,可以通过优化算法(如遗传算法、萤火虫算法[15-16]等)对交错稀疏子阵单元上的激励进行进一步优化,以进一步降低子阵天线方向图旁瓣峰值,本文不再详述。
3.1.2 改进型迭代FFT算法旁瓣约束值的讨论 旁瓣约束值主要是针对满阵天线,它的选取直接影响了阵列采样点激励在前段的集中程度,其目的主要是为了降低子阵天线旁瓣峰值,当阵列天线为满阵时,天线的旁瓣值能够满足约束要求,但由于稀疏子阵只选取了阵列天线的部分激励点,因此稀疏后的子阵天线方向图(部分激励点做傅里叶变换获得的值)旁瓣峰值是无法满足约束要求的,选取一个合理的旁瓣约束值能够使目标方向图对应的激励点值集中分布在激励的前段部分,使得在只选取激励前段部分点值做傅里叶逆变换得到的方向图旁瓣峰值更好地接近约束旁瓣值,达到降低子阵天线方向图旁瓣值与约束旁瓣值之间差值的目的,因此旁瓣约束值并不是越大越好或者越小越好,前期通过大量的实验仿真结果得出,在选取约束旁瓣峰值时一般选大于优化后稀疏阵列天线旁瓣峰值10~15 dB的值优化效果最好。
3.2 多子阵交错的多波束指向共享孔径阵列天线设计 现代导航定位系统往往要求人们对多个空中和地面目标进行精确定位,这就要求雷达天线能够同时接收不同方向的来波信号。而传统数字多波束天线的设计相对固定,收发使用不灵活。设计多子阵交错的共享孔径阵列天线能有效解决这些问题。为了实现多波束指向阵列天线的设计,本文对阵元数为100、稀疏率为80%的直线阵列进行5子阵交错的优化布阵。为了使子阵方向图频谱能量近似相同,在确定子阵天线结构,选取子阵单元方向图频谱能量时,应以式(7)的方式进行选取,优化后的阵列天线单元位置结构图如图 8所示。从图中可以得出,子阵1的孔径利用率为96%,子阵2的孔径利用率为96%,子阵3的孔径利用率为96%,子阵4的孔径利用率为95%,子阵5的孔径利用率为94%,5个子阵交错共享于同一个天线孔径,孔径利用率得到了大幅提高。
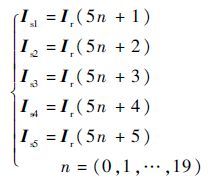 | (7) |
 |
| 图 8 五子阵交错的天线孔径结构 Fig. 8 Aperture architecture of five interleaved subarrays |
| 图选项 |
对图 8结构的阵列天线方向图进行仿真,仿真结果如图 9所示。图 9(a)和图 9(b)分别为5个子阵主瓣都指向90°时天线方向图及其缩略图。从图中可看出,5个子阵方向图形状大致相同,由于单个子阵阵元数量的减少,相对于四子阵交错的共享孔径阵列天线,五子阵交错的阵列天线旁瓣峰值略有增大。其中子阵1的旁瓣峰值电平为-7.49 dB,子阵2的旁瓣峰值为-7.09 dB,子阵3的旁瓣峰值为-6.98 dB,子阵4的旁瓣峰值电平为-7.17 dB,子阵5的旁瓣峰值电平为-8.66 dB,子阵间最大峰值电平差为1.68 dB,最小峰值旁瓣电平差为0.017 dB。证明基于迭代FFT算法的多子阵交错方法是稳健的。使子阵主瓣波束分别指向不同的方向,能形成不同波束指向的共享孔径多功能阵列天线,如图 10所示。
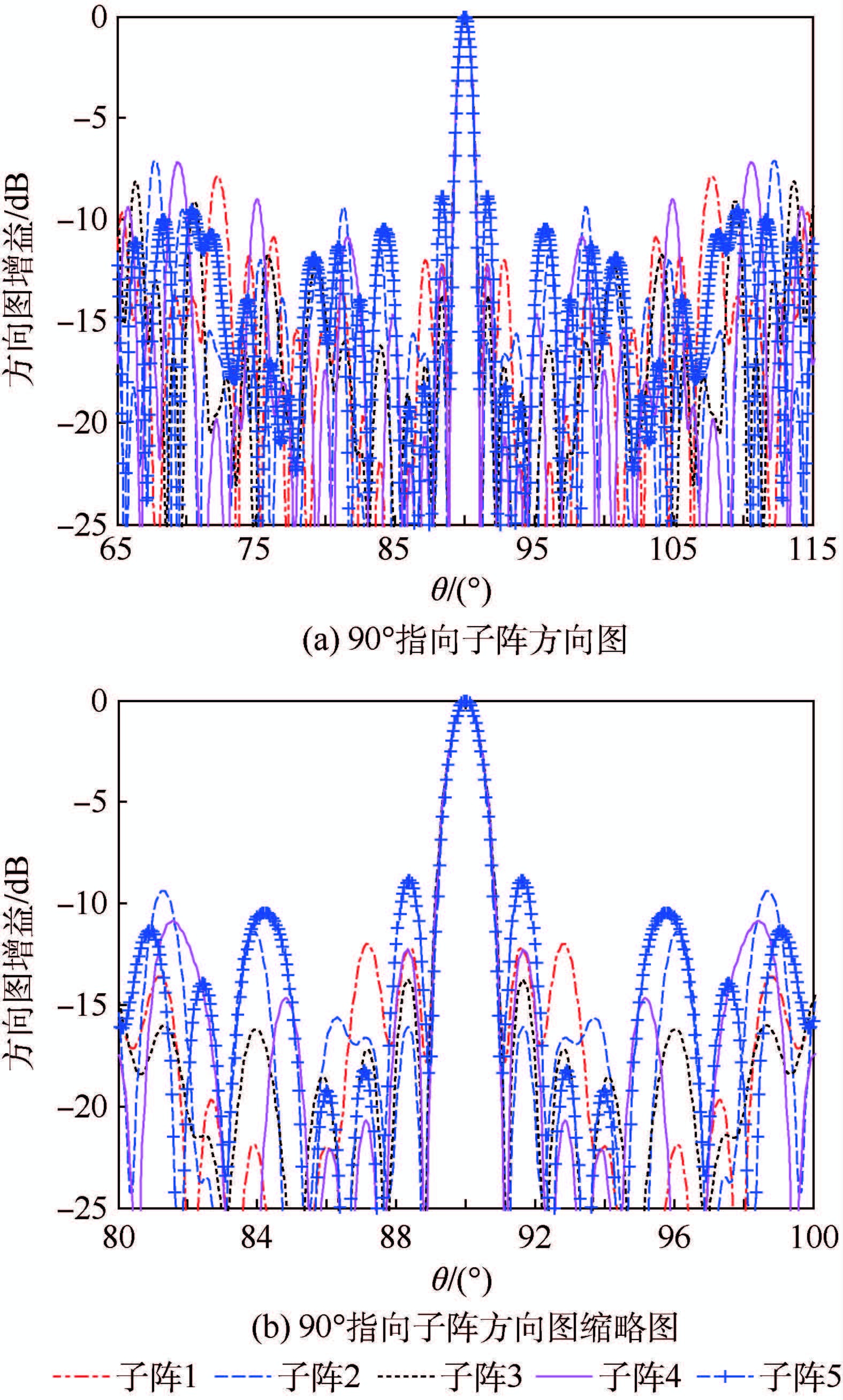 |
| 图 9 同一波束指向的五子阵交错阵列方向图 Fig. 9 Patterns of five interleaved subarrays array inthe same beam direction |
| 图选项 |
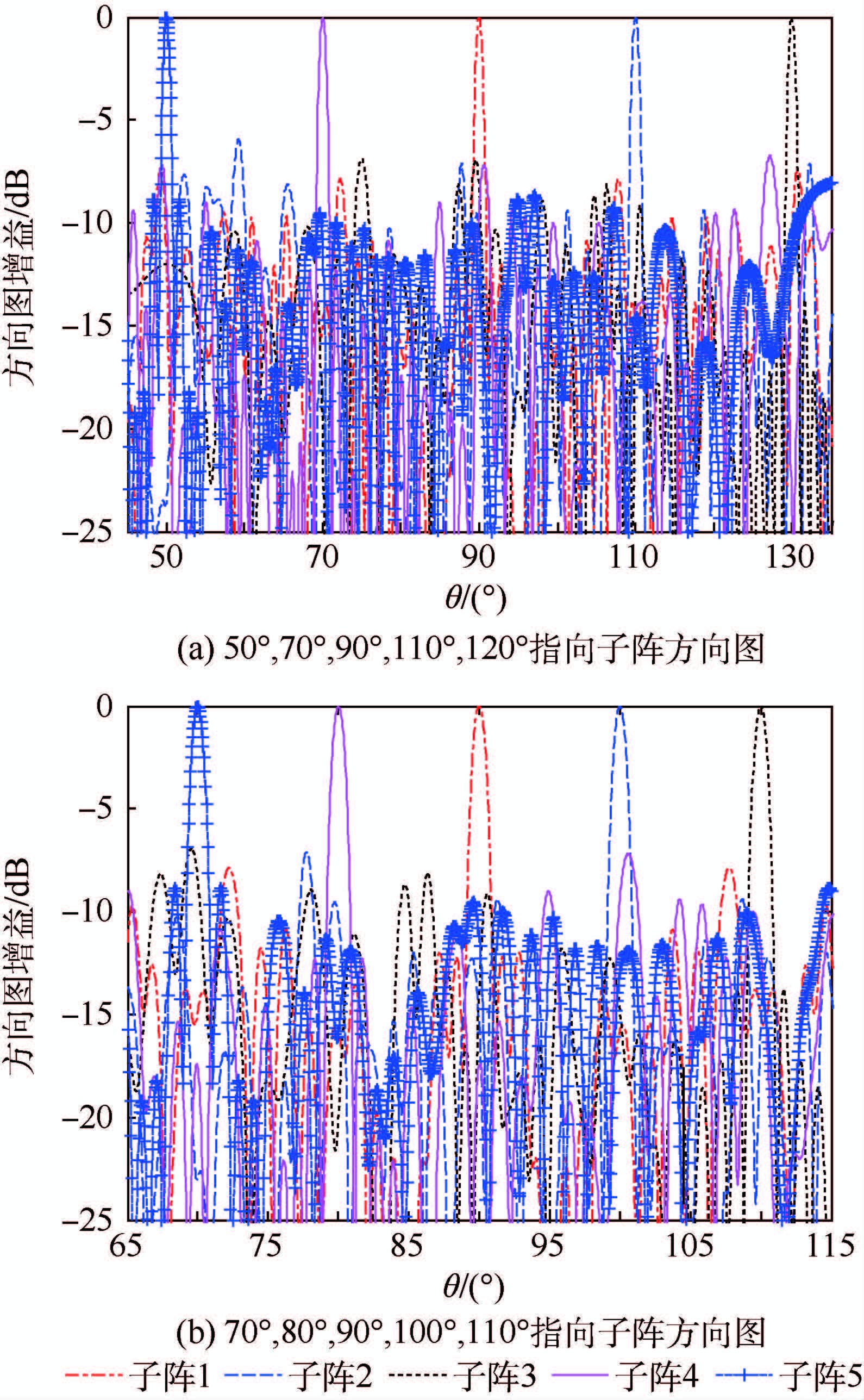 |
| 图 10 不同波束指向的五子阵交错阵列方向图 Fig. 10 Patterns of five interleaved subarrays array indifferent beam directions |
| 图选项 |
从图 10中可知,当子阵分别指向50°、70°、90°、110°、120°和70°、80°、90°、100°、110°时阵列天线拥有近似一致的方向图性能,因此可以通过交错稀疏多个子阵,灵活控制子阵主瓣波束指向,实现多波束指向的多功能阵列天线设计。
4 结 论 利用改进型迭代FFT算法,通过将均匀线阵方向图频谱能量等额分配给不同的交错子阵单元,得出以下结论:
1) 该方法可以实现多子阵的交错稀疏设计,且每个子阵都有较高的孔径利用率和性能近似一致的功率方向图,其方向图旁瓣峰值能够接近同等孔径下的均匀直线阵列天线旁瓣峰值。
2) 通过控制不同子阵方向图主瓣波束指向,可以实现空域多功能阵列天线的设计。
3) 需要说明的是阵列天线优化设计是一个需要系统解决的问题,本文主要研究的是阵元位置对阵列天线方向图的影响,虽然稀疏阵列由于阵元之间的距离较大,使得子阵内和子阵间的耦合效应较小,但互耦仍然是影响阵列天线方向图性能的重要因素,因此下一步工作需要着重解决子阵间和子阵内部单元互耦的联合校正问题。
参考文献
| [1] | JOSEFSSON L P. Conformal array antenna theory and design[M].Toronto: Wiley-IEEE Press, 2006: 230-246. |
| [2] | ASIM A K, ANTHONY K B. Null steering in irregularly spaced sparse antenna arrays using aperture distributed subarrays and hybrid optimizer[J].IET Microwaves,Antennas & Propagation, 2014, 8(2): 86–92. |
| [3] | COMAN C I,LAGER I E,LIGTHART L P.A deterministic solution to the problem of interleaving multiple sparse array antennas[C]//Proceedings of 2nd European Radar Conference-EuRAD.Piscataway,NJ:IEEE Press,2005:243-246.http://cn.bing.com/academic/profile?id=2064614111&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] | QIN Y, GAO S, SAMBELL A, e t, a l. Design of a broadband square-ring-slot coupled patch antenna[J].Microwave Optical Technology Letter, 2005, 47(5): 454–457.DOI:10.1002/(ISSN)1098-2760 |
| [5] | SIMEONI M, LAGER I E, COMAN C I. Implementation of polarization agility in planar phased-array antennas by means of interleaved subarray[J].Radio Science, 2009, 44(44): 538–549. |
| [6] | OLIVERI G, MASSA A. Fully interleaved linear arrays with predictable sidelobes based on almost difference sets[J].IET Radar,Sonar and Navigation, 2010, 4(5): 649–661.DOI:10.1049/iet-rsn.2009.0186 |
| [7] | OLIVERI G,LIZZI L,MASSA A.ADS interleaved arrays with reconfigurable polarization[C]//2010 IEEE International Symposium on Antennas and Propagation and CNC-USNC/URSI Radio Science Meeting-Leading the Wave,AP-S/URSI 2010.Piscataway,NJ:IEEE Press,2010:1-4.http://cn.bing.com/academic/profile?id=2116266650&encoded=0&v=paper_preview&mkt=zh-cn |
| [8] | OLIVERI G, MASSA A. ADS-based array design for 2-D and 3-D ultrasound imaging[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control, 2010, 57(7): 1568–1582.DOI:10.1109/TUFFC.2010.1587 |
| [9] | HAUPT R L. Interleaved thinned linear arrays[J].IEEE Transactions on Antennas and Propagation, 2005, 53(9): 2858–2864.DOI:10.1109/TAP.2005.854522 |
| [10] | HAUPT R L.Interleaving thinned sum and difference linear arrays[C]//Proceedings of 2006 IEEE Antennas and Propagation Society International Symposium,Albuquerque.Piscataway,NJ:IEEE Press,2006:4773-4776.http://cn.bing.com/academic/profile?id=2146431687&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | HOU Q S,GUO Y,WANG B H,et al.A novel method for analyzing sidelobe structure of nonuniform sparse linear array[C]//IET International Radar Conference 2009.Stevenage:IET Press,2009:1-4.http://cn.bing.com/academic/profile?id=1974179934&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | DAVID B D. Low-sidelobe pattern synthesis using iterative fourier techniques coded in MATLAB[J].IEEE Antennas and Propagation Magazine, 2009, 51(2): 137–150. |
| [13] | WARREN P D P. Weighted thinned linear array design with the iterative FFT technique[J].IEEE Transactions on Antennas and Propagation, 2011, 59(9): 3473–3477.DOI:10.1109/TAP.2011.2161450 |
| [14] | WILL P M N K. Synthesis of thinned planar circular and square arrays using density tapering[J].IEEE Transactions on Antennas and Propagation, 2014, 62(4): 1555–1563.DOI:10.1109/TAP.2013.2267194 |
| [15] | 严韬, 陈建文, 鲍拯. 基于改进遗传算法的天波超视距雷达二维阵列稀疏优化设计[J].电子与信息学报, 2014, 36(12): 3014–3020.YAN T, CHEN J W, BAO Z. Optimization design of sparse 2-D arrays for over-the-horizon radar(OTHR) based on improved genetic algorithm[J].Journal of Electronics & Information Technology, 2014, 36(12): 3014–3020.(in Chinese) |
| [16] | WANG G G, GUO L, DUAN H, et al. A new improved firefly algorithm for global numerical optimization[J].Journal of Computational and Theoretical Nanoscience, 2014, 11(2): 477–485.DOI:10.1166/jctn.2014.3383 |
