?车辆行驶过程中传动系统承受的载荷受加速、减速、换挡等工况影响在不断变化，传动系统零部件设计优化、疲劳耐久性分析等研究工作中需要模拟多种工况下车辆传动系统的动态载荷特性。因此，需要建立能够模拟发动机及传动部件实时工作状态、具有较高精度的动力传动系统仿真模型。
与普通车辆相比，多轴车辆具有系统复杂、传动环节多等特点。建立多轴车辆动力传动系统仿真模型涉及3个关键问题：①发动机动态模型的建立。目前发动机动态模型常用的建模方式有3种：基于物理模型的建模方法、基于中值模型的建模方法以及基于发动机稳态特性的建模方法^[1]。发动机物理模型及中值模型建模方法要求提供较为详细的发动机结构信息，限制了此类方法在车辆建模与仿真中的应用^[2-5]；基于稳态特性的建模方法一般根据发动机稳态试验数据，采用动态修正模型、指数曲线拟合模型、一阶惯性环节模型、神经网络模型等不同的方法进行拟合^[6-9]，常用于车辆整车性仿真分析，建模精度与试验数据量、经验等关系较大。②变速器换挡及液力变矩器、换挡离合器不同状态切换过程的仿真。文献[10-11]中对离合器结合/分离与液力变矩器闭锁/解锁状态切换产生的多种相的组合以及离合器建模方法进行了研究。③多级传动的扭矩分配。多轴车辆传动系统建模涉及多桥间/轮间扭矩分配问题，文献[12-13]考虑了分动器和差速器的作用建立了2轴全轮驱动车辆模型，文献^[14]建立了包含轮间差速器、轴间差速器和分动器的3轴全轮驱动车辆模型，讨论了轮间差速器对车辆在对开路面行驶稳定性的影响和轴间差速器对车辆陡坡行驶能力的影响。
本文利用发动机负荷特性台架试验数据，采用多元线性回归理论构建循环供油量-转速-扭矩MAP图，基于模糊PI控制建立了柴油发动机循环供油量控制模型，同时简化了换挡离合器、变速器模型，将换挡过程连续化，保证仿真过程的稳定运行。在MATLAB/Simulink软件平台中集成各总成模型，开发出多轴车辆动力传动系统动力学仿真模型，通过实车试验对比分析，验证了多轴车辆动力传动系统动力学建模和仿真方法的有效性。
1 动力传动系统模型 1.1 柴油发动机模型 柴油发动机是一个复杂系统，所建模型需要进行大量假设和简化。本文根据负荷特性台架试验数据，利用发动机实时循环供油量和发动机实际转速计算发动机输出特性，仿真模拟柴油发动机动态过程。采用PI控制器对柴油发动机进行循环供油量调节，以油门开度为输入量，发动机转速为被控制参数，循环喷油量为控制量，通过执行器对发动机进行控制，系统框图如图 1所示。

图 1 柴油发动机系统框图 Fig. 1 Diesel engine system diagram

图选项

1.1.1 发动机循环供油量-转速-扭矩MAP图 通过发动机负荷特性台架试验可以测量不同转速下扭矩、功率和燃油消耗率，则发动机循环供油量可按式(1)计算。

(1)

式中：q_r为发动机循环供油量，g/r；b_e为燃油消耗率，g/(kW·h)；P_e为发动机有效功率，kW；N_e为发动机转速，r/min。
将P_e=T_eN_e/9 550代入式(1)可得

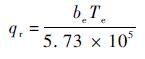(2)

式中：T_e为发动机扭矩，N·m。
建立发动机扭矩T_e与转速N_e、循环供油量q_r的函数，根据多元线性回归理论进行曲面拟合，回归模型为

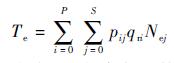(3)

式中：p_ij为待定系数；P和S分别为多项式中q_ri和N_ej的最高次幂。
利用MATLAB/Curve fitting工具箱，通过计算，获得P=2、S=2时的拟合结果，见表 1，调整复相关系数R=0.994 5。
表 1 回归方程系数拟合结果 Table 1 Fitting results of regression equation coefficient

系数	p00	p10	p01	p20	p11	p02
拟合结果	586.8	0.814 6	2 497	-2.976×10-4	-0.117 7	389.8

表选项






将拟合参数代入式(3)，得到的发动机循环供油量-转速-扭矩MAP如图 2所示。

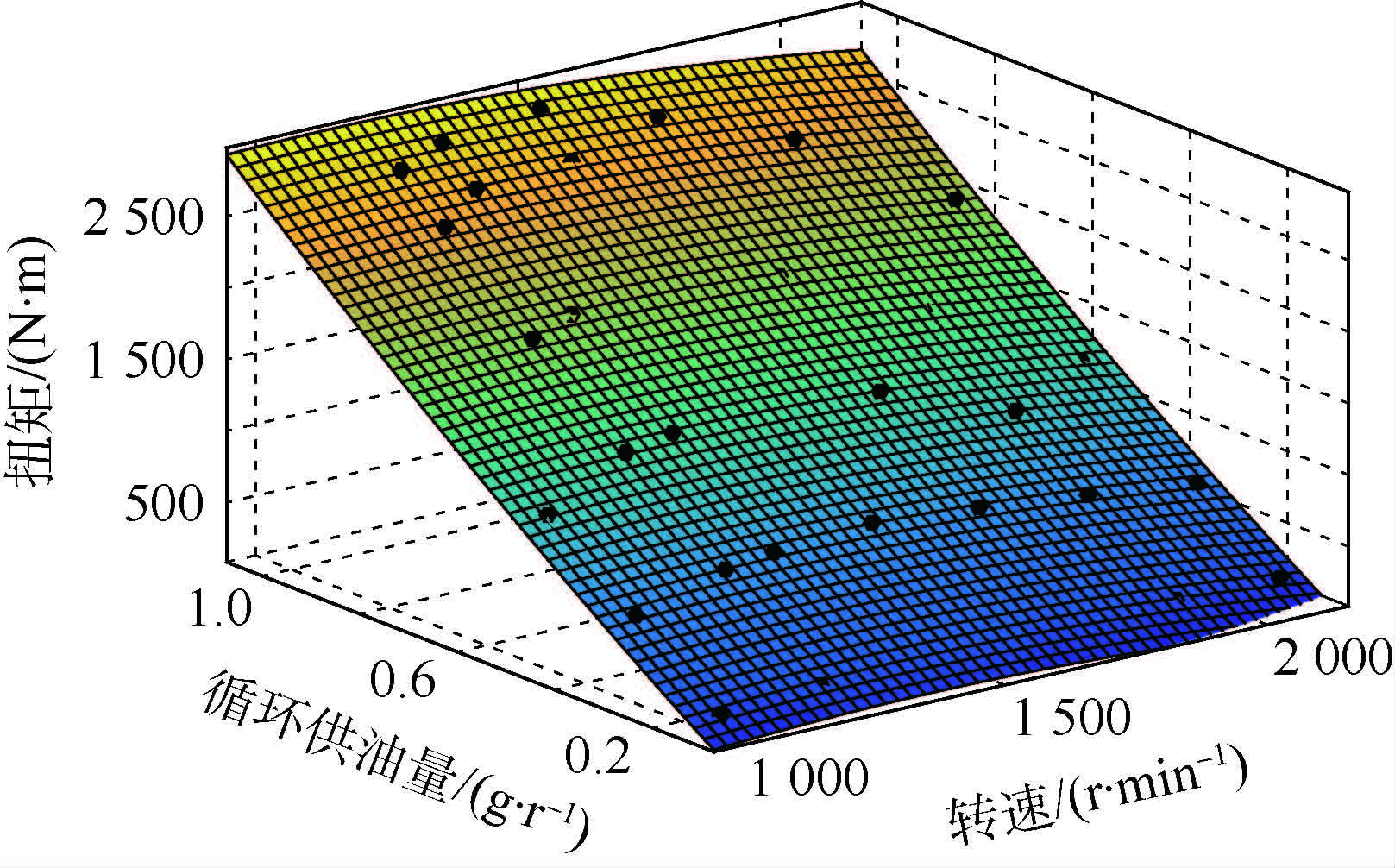图 2 发动机输出特性拟合曲面 Fig. 2 Engine output characteristics fitting surface

图选项

1.1.2 柴油发动机循环供油量控制模型 本文采用PI控制对柴油发动机循环供油量q_r(t)进行控制，根据发动机实际转速与目标转速差e(t)调节循环供油量，控制规律为

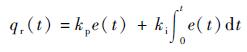(4)

式中：k_p为比例系数；k_i为积分作用系数。
实际转速由整车动力学计算获得。目标转速计算方法为

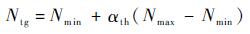(5)

式中：N_tg为发动机目标转速；N_max和N_min分别为发动机最高、最低转速；α_th为油门开度，其变化范围为0~100%。
单一参数设定无法满足控制精度要求，本文采用模糊规则调节实现PI参数整定。模糊规则以转速差e(t)和转速差变化量e_c(t)为输入，控制参数的增量Δk_p、Δk_i作为输出。变量的模糊语言值为{正大，正中，正小，零，负小，负中，负大}，对应的英文为{PB，PM，PS，ZO，NS，NM，NB}，根据试验数据观测和分析总结控制信息，制定模糊规则如表 2所示。
表 2 模糊控制规则 Table 2 Fuzzy control rules

e(t)	ec(t)
	PB/PM/PS	ZO	NS/NM/NB
PB	PS/ZO	PS/ZO	PS/ZO
PM	PM/ZO	PM/ZO	PM/ZO
PS	PB/PS	PB/PS	PB/PS
ZO	NB/PB	PB/PB	PB/PB
NS	NB/NS	NB/ZO	NB/ZO
NM	NM/ZO	NM/ZO	NM/ZO
NB	NS/ZO	NS/ZO	NS/ZO

表选项






首先确定参数的初值k_p0、k_i0，然后根据模糊规则表查出Δk_p/Δk_i修正参数代入式(6)得到PI控制参数：

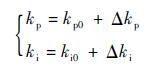(6)

1.1.3 柴油发动机动态扭矩 控制器送来的循环供油量控制信号q_r(t)，经执行器传送给扭矩MAP图进行查表，获得当前时刻发动机输出扭矩M_e。执行器简化为一阶惯性系统^[15]，定义时间常数为T_a，传递函数为

(7)

式中：s为拉氏变换参数。

1.1.4 发动机负载模型 柴油发动机转速的变化由发动机扭矩和负载扭矩的差值决定，由达朗贝尔原理，其动力学方程为

(8)

式中：J_e为等效转动惯量，即发动机飞轮、传动轴及液力变矩器泵轮转动惯量(液力变矩器解锁状态)/发动机飞轮、传动轴、液力变矩器及换挡离合器输入盘转动惯量(液力变矩器闭锁状态)；ω_e为发动机角速度；M_d为负载扭矩，即液力变矩器泵轮输入扭矩(液力变矩器解锁状态)/换挡离合器输入扭矩(液力变矩器闭锁状态)。

1.1.5 发动机动态仿真模型 在Simulink中建立发动机循环供油量-转速-扭矩MAP图、模糊PI控制器和负载模型，得到的柴油发动机动态仿真模型如图 3所示。

图 3 柴油发动机动态仿真模型 Fig. 3 Diesel engine dynamic simulation model

图选项

1.2 液力变矩器模型 液力变矩器模型分为稳态模型和动态模型2种，稳态模型可由试验数据获得，基于流体力学理论的动态模型建模相对复杂。当液力变矩器非稳态工况下的泵轮转速变化不超过±52 rad/s时，可以用稳态特性代替动态特性^[16]。本文采用基于稳态试验数据的方法进行建模。
液力变矩器无因次特性为^[17]

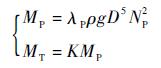(9)

式中：M_P和M_T分别为泵轮和涡轮的扭矩,其中M_P与式(8)中M_M相同；N_P为泵轮转速；λ_P为泵轮转矩系数；ρ为工作油密度；D为液力变矩器有效直径；K为变矩比。
通过台架试验测得变矩比K、基准扭矩M_P1000(泵轮在1 000 r/min基准转速下的扭矩)和效率η随不同转速比i(涡轮转速与泵轮转速之比)的变化曲线，即可获得液力变矩器的原始特性曲线，如图 4所示。

图 4 液力变矩器的原始特性曲线 Fig. 4 Original characteristic curves of torque converter

图选项

一定转速比i之下有一λ_P值，已知1 000 r/min基准转速下的泵轮扭矩，则可按式(10)计算任意转速下的泵轮扭矩。

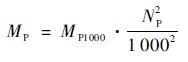(10)

为了提高液力变矩器在高速下的传动效率，设置了闭锁离合器，在满足一定条件时闭锁离合器将变矩器锁止，功率直接传送给传动轴。闭锁条件为： N_P＞N₁，i＞i₁；解锁条件为：N_T＜N₂。其中：N₁和i₁分别为闭锁时泵轮转速门限值、转速比门限值；N_T为涡轮转速；N₂为解锁时涡轮转速门限值。
闭锁离合器结合过程中发动机与液力变矩器联合工作的动力学方程为

(11)

式中：M_f为闭锁离合器摩擦阻力矩。
1.3 换挡离合器模型 换挡离合器为膜片弹簧离合器，可传递的最大静摩擦扭矩为

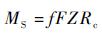(12)

式中：f为摩擦系数；F为压盘施加在摩擦面上的工作压力；Z为摩擦面数；R_c为摩擦片的平均摩擦半径。
离合器踏板位移D_CL与离合器所传递的最大静摩擦扭矩M_S,x关系如图 5所示。图中，M_S,max为最大静摩擦扭矩极大值。D_CL=0时，离合器踏板位于原始位置；D_CL=x₁时，离合器位于空程消失位置；D_CL=x₂时，离合器位于完全分离位置。

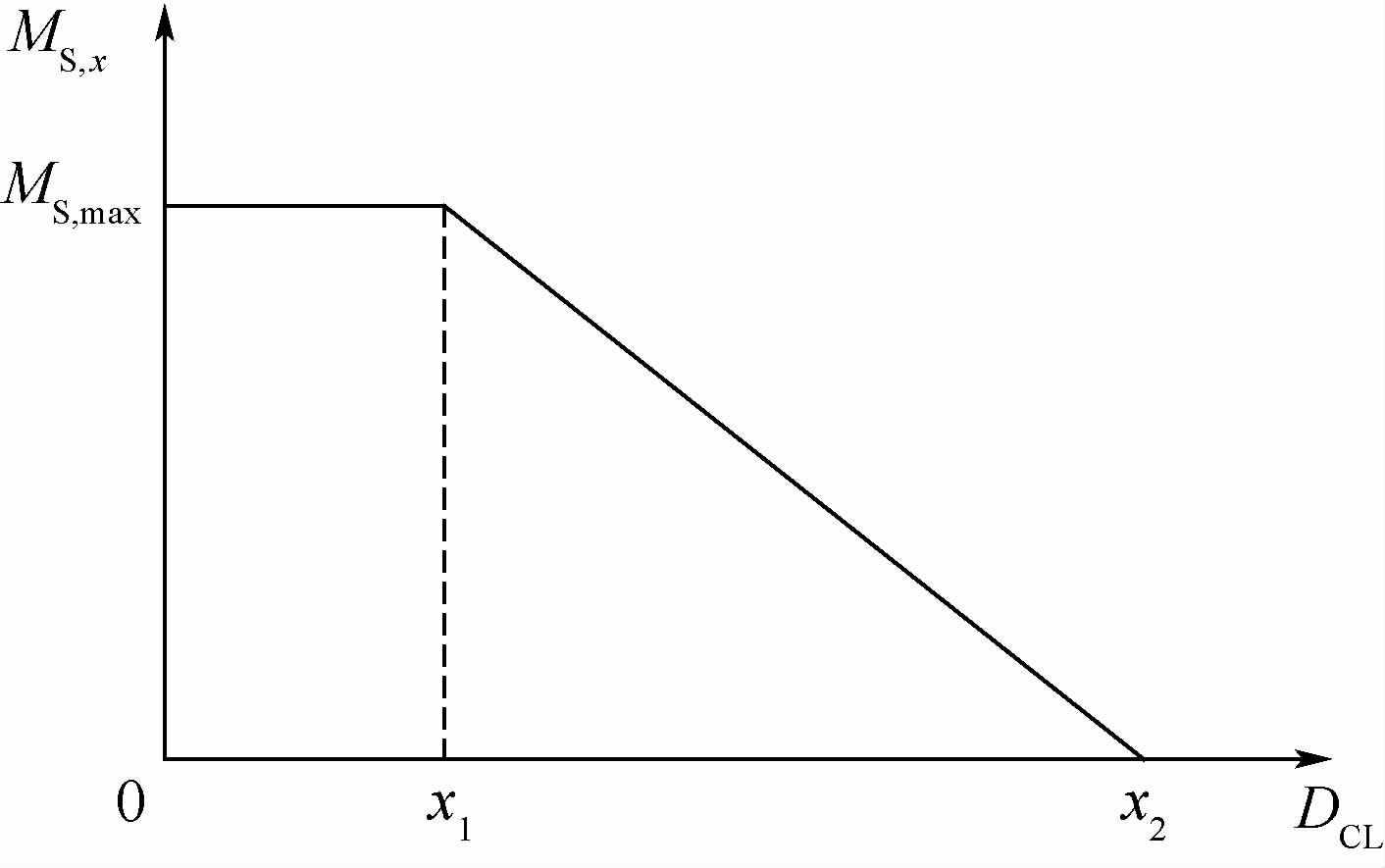图 5 离合器踏板位移与最大静摩擦扭矩的关系 Fig. 5 Clutch pedal displacement versusmaximum static friction torque

图选项

忽略摩擦片的滑磨过程，离合器所传递的扭矩为

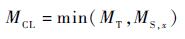(13)

1.4 变速器模型 变速器由主、副箱组成，主变速器由输入轴、中间轴和输出轴组成，副变速器为行星齿轮变速器。变速器换挡过程涉及传动比变化和同步过程，精确进行建模比较复杂。本文将变速器简化为两级传动部件。
如图 6所示，两级传动部件J₁和J₂分别代表变速器换挡齿轮前、后等效集中惯量；ω₁和ω₂分别代表两级传动部件角速度；M_CL为输入力矩；

图 6 两级传动部件动力学模型 Fig. 6 Dynamic model of two-stage transmission component

图选项

M_1,out为J₁输出扭矩；M_2,in为J₂输入扭矩；M_Trs为变速器输出扭矩。其动力学方程为

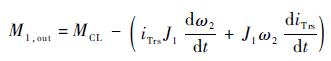(14)

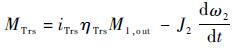(15)

式中：${{i}_{\text{Trs}}}{{J}_{1}}\frac{\text{d}{{\omega }_{2}}}{\text{d}t}$代表加速惯量所需要的扭矩，i_Trs为变速器的传动比；${{J}_{1}}{{\omega }_{2}}\frac{\text{d}{{i}_{\text{Trs}}}}{\text{d}t}$代表由于传动比变化带来的附加扭矩；η_Trs为变速器的传动效率。传动比改变时，两级传动比间考虑为线性变化，由此可以解决传动比改变带来的转速与扭矩突变，简化了系统中同步环作用过程的建模。
1.5 分动箱、过桥齿轮箱模型 分动箱和过桥齿轮箱将扭矩按比例分配到各驱动桥上，以提高车辆的驱动能力。假设分动箱前后车轴所分配的扭矩比为k_Tr-C∶1(过桥齿轮箱可表示为k_IA-D∶1)，速比为i_Tr-C(过桥齿轮箱速比为1)，则其动力学特性可表示为

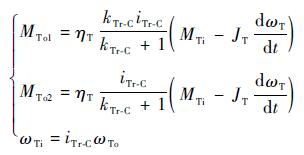(16)

式中：ω_Ti、ω_To分别为分动箱或过桥齿轮箱输入、输出角速度；M_To1和M_To2分别为前、后输出轴扭矩；J_T为等效到输入轴的转动惯量；η_T为传动效率。
1.6 主减速器、轮间差速器、轮边减速器模型 主减速器、轮边减速器均为固定速比传动部件，其动力学模型统一表示为

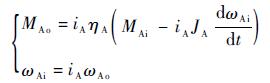(17)

式中：J_A为部件等效到输入端的转动惯量；M_Ai、M_Ao分别为其输入、输出扭矩；ω_Ai、ω_Ao分别为其输入、输出角速度；i_A为其传动速比；η_A为其传动效率。
轮间差速器模型为

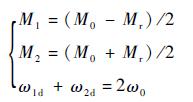(18)

式中：M₀、ω₀分别为差速器壳扭矩、角速度；M₁、ω_1d和M₂、ω_2d分别为左右传动轴扭矩、角速度；M_r为差速器内摩擦转矩。
2 整车仿真模型 将整车考虑为单质量模型，则整车纵向动力学方程为

(19)

式中：M_WL,i、M_WR,i分别为第i驱动桥左右车轮的驱动扭矩；G为整车重量；f_k为滚动阻力系数；α为坡度角；C_D为空气阻力系数；A为迎风面积；u_k为车速，km/h；u表示车速，m/s；r为车轮滚动半径；δ为考虑车轮转动惯量的汽车旋转质量换算系数，$\delta =1+\frac{\sum{{{J}_{\text{W}}}}}{m{{r}^{2}}}$，J_W为单个车轮的转动惯量；m为汽车质量。
以某5轴驱动车辆为研究对象，其动力传动系统结构如图 7所示。动力由发动机(Engine)发出，经过液力变矩器(TC)、换挡离合器(CL)、变速器(Trs)，由分动箱(Tr-C)将动力分配给前后过桥齿轮箱(IA-D)，再由过桥齿轮箱(IA-D)、主减速器(M-D)及轮间差速器(D-F)分配到各桥驱动轴，最终经轮边减速器(W-R)传递到车轮，轴间差速器包含在分动器和过桥齿轮箱中。

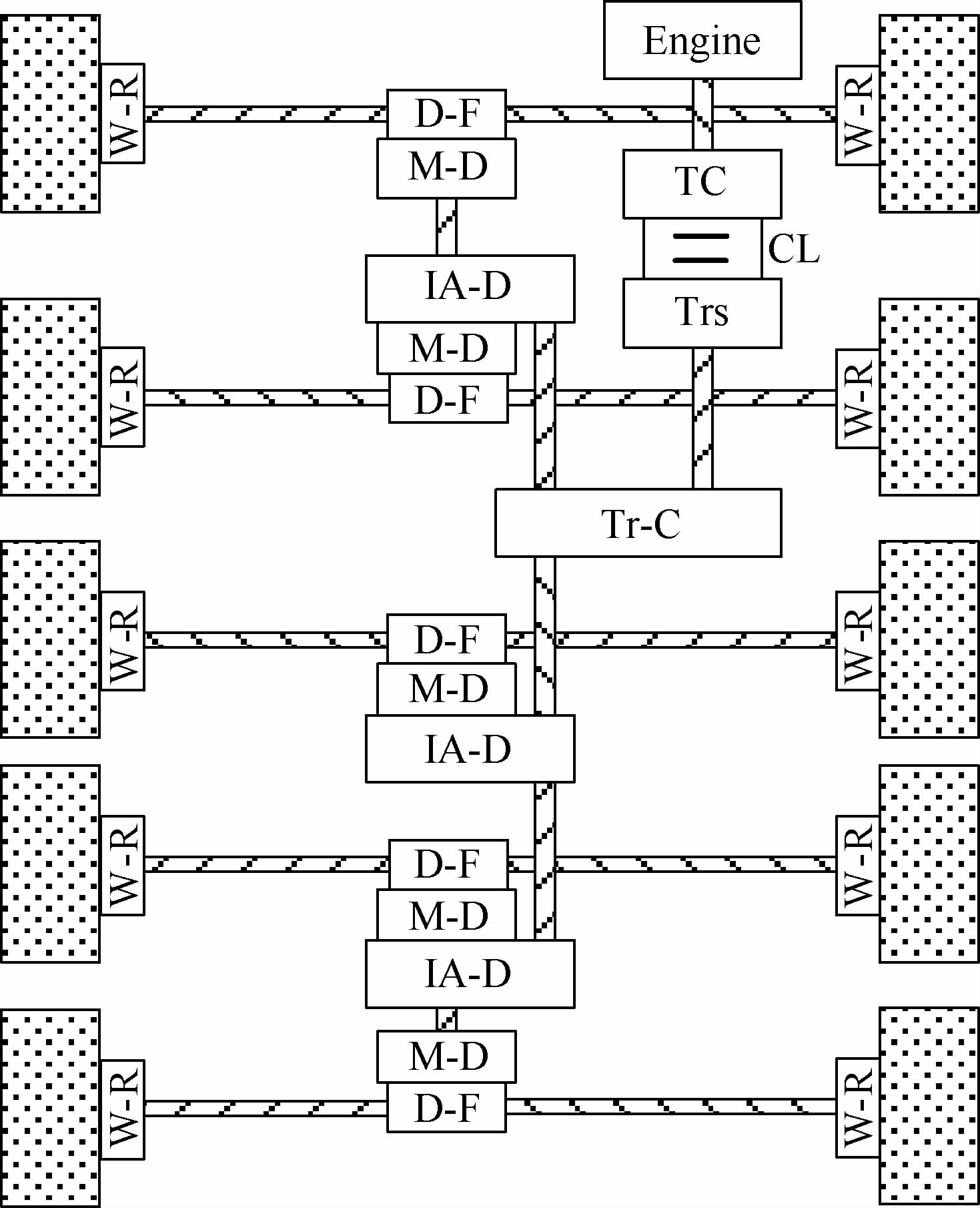图 7 多轴车辆动力传动系统结构框图 Fig. 7 Structure diagram of multi-axlevehicle powertrain system

图选项

建立各总成模型，再将各总成模型有效集成。整车仿真原理如图 8所示，在Simulink中，将上述各总成集成建立多轴车辆动力传动系统前向仿真模型，即根据驾驶员操作(油门踏板位置、离合器踏板位置及挡位设置)，计算得到传动系统运行状态。

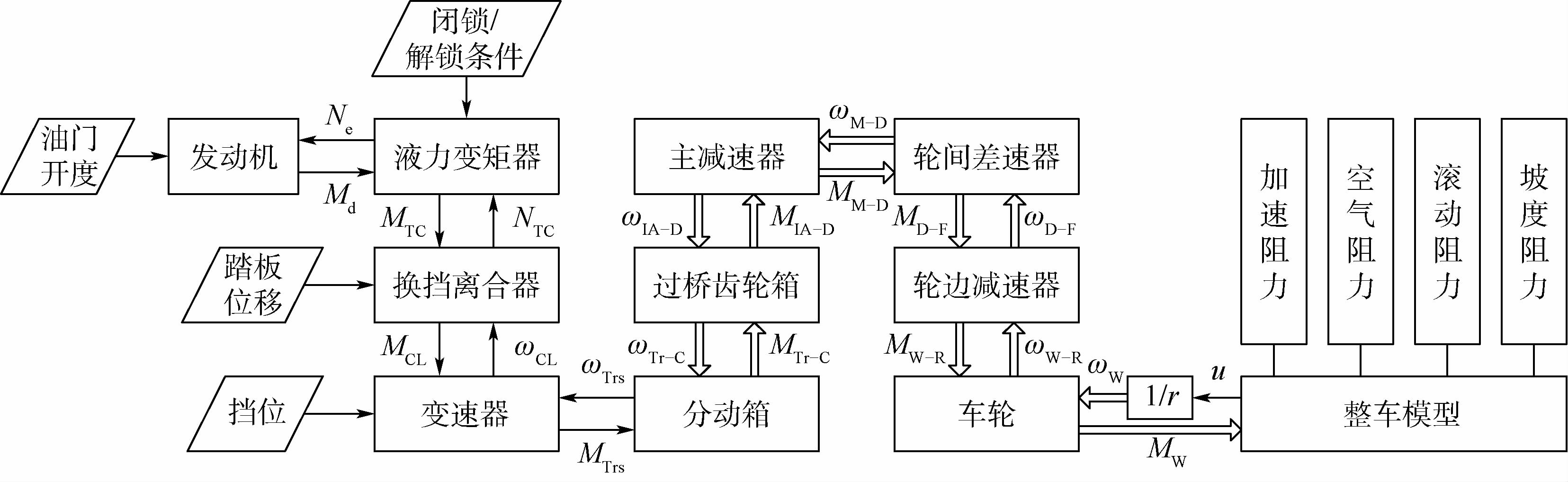图 8 多轴车辆动力传动系统仿真原理图 Fig. 8 Schematic diagram of multi-axle vehicle powertrain system simulation

图选项

3 仿真结果验证及分析 以前述多轴车辆为研究对象建立仿真模型，进行多工况仿真。仿真以实车试验采集的油门开度、离合器踏板行程、挡位信息作为输入参数，以仿真车速、发动机输出扭矩/转速、变速器输出扭矩/转速为输出结果，选取2种工况的仿真结果与实车试验数据进行对比分析。
3.1 行驶加速工况 此工况包含3个匀速段及加速过程。在匀速段，油门维持相对固定，车辆匀速行驶。车辆在一个匀速段加速进入更高车速时，油门踏板踩至最大，达到目标车速后回落到稳态值。
图 9给出了变速器6挡时仿真与试验数据对比曲线图。试验中记录了车辆在3种车速下的试验数据，图 9(a)为油门采集信号作为输入参数。匀速段主要表征了发动机及传动系统的稳态特性，图 9(d)、图 9(e)、图 9(f)表明，仿真结果与试验数据吻合度较高。驾驶过程中，油门抖动造成了发动机及传动系统扭矩波动较大，且随车速升高波动更加剧烈，试验及仿真均反映了这个特点。

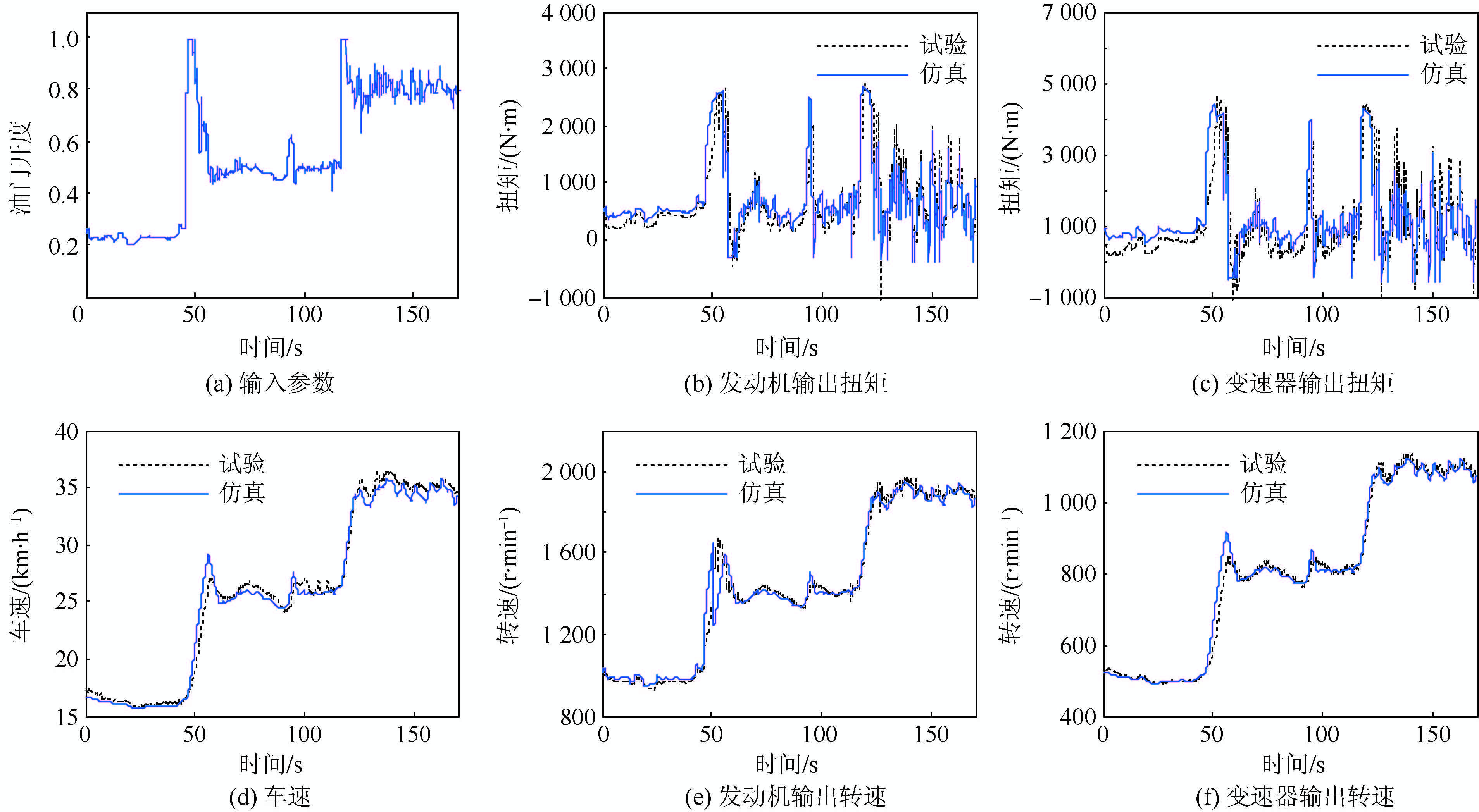图 9 6挡行驶时仿真结果与试验对比 Fig. 9 Comparison between simulation results and test data of 6-gear driving

图选项

图 9中还反映了突踩油门时发动机及传动系统的动态转速响应。当车辆由当前车速提升到更高车速时，驾驶员突加油门，带来发动机输出转速及变速器输出转速的急剧变化，车速达到目标值时转速回落到稳态值附近。
3.2 连续换挡加速工况 在此工况下，油门开度全开，在每个挡位下，发动机转速由当前转速加速到换挡车速后进入换挡过程，油门开度下降到0，离合器踏板位移至最大，换挡后油门开度上升，离合器踏板位移至0。车辆由3挡起步，连续换挡加速到8挡。
图 10为连续换挡加速过程仿真与试验数据对比曲线图，给出了车辆在不同挡位下动力传动系统动态特性曲线。试验车辆由3挡起步，发动机加速至换挡转速后，降低油门同时离合器断开进行换挡，然后重新连接离合器并增加油门开度至100%。图 10(b)~图 10 (f)表明，仿真结果有效模拟了换挡过程发动机及传动系统扭矩和转速的动态变化，表 3给出了连续换挡加速过程中仿真与试验结果对比分析，仿真结果与试验数据吻合度较高。

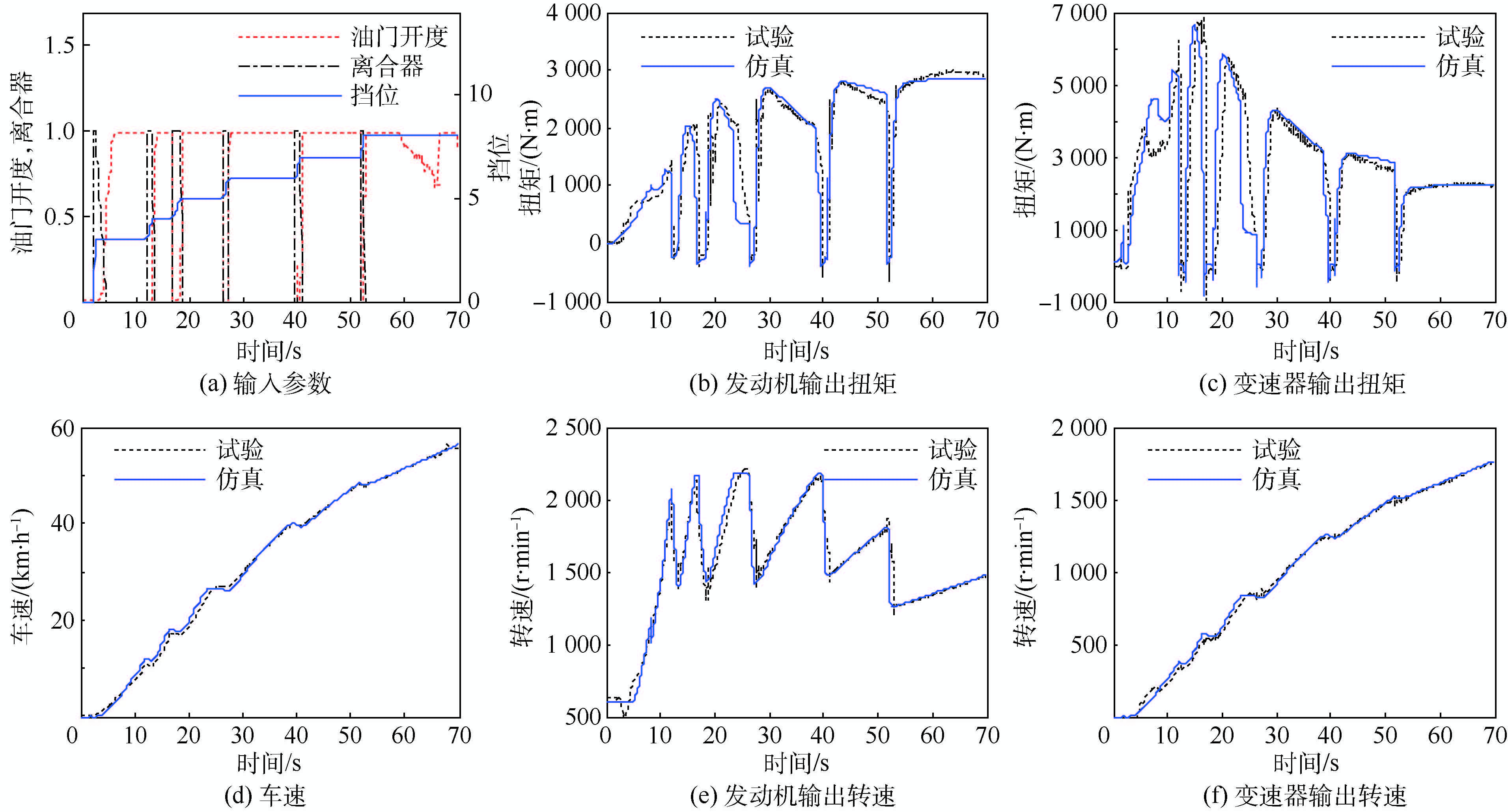图 10 连续换挡加速仿真结果与试验对比 Fig. 10 Comparison between simulation results and test data of acceleration with continuous shift

图选项

表 3 仿真与试验结果对比 Table 3 Simulation results versus test data

挡位	最高车速/ (km·h-1)				发动机最高输出 转速/(r·min-1)				发动机最大输出 扭矩/(N·m)				变速器输出 转速/(r·min-1)				变速器最大输出 扭矩/(N·m)
	试验	仿真	误差/%		试验	仿真	误差/%		试验	仿真	误差/%		试验	仿真	误差/%		试验	仿真	误差/%
3	11.0	12.2	9.8		2 007	2 070	3.1		1 450	1 270	-16.7		355	381	7.3		6 243	5 416	-13.2
4	17.4	18.2	4.6		2 131	2 180	2.3		2 070	2 054	-0.8		566	572	1.1		6 880	6 634	-3.6
5	27.2	26.5	-2.6		2 210	2 181	-1.3		2 490	2 437	-2.1		845	832	1.5		5 785	5 828	0.7
6	40.0	39.9	-0.3		2 168	2 175	0.3		2 694	2 663	-1.2		1 250	1 253	0.2		4 315	4 278	-1.0
7	48.4	48.1	-0.6		1 795	1 810	0.3		2 802	2 798	-0.1		1 525	1 520	-0.3		3 090	3 080	-0.3
8	56.5	56.3	-0.4		1 794	1 794	0		3 008	2 867	-4.7		1 765	1 765	0		2 305	2 222	-3.6

表选项






综上所述，仿真结果符合测试数据，较好地反映了车辆在多工况下的动态载荷特性和速度特性。
4 结 论 本文建立了多轴车辆动力传动系统动力学仿真模型，分析了多工况下的速度特性和动态载荷特性，对比仿真与车辆实测结果可以看出：
1) 利用发动机负荷特性试验数据，建立的基于模糊PI控制和循环供油量-转速-扭矩MAP图的柴油发动机模型，有效地模拟了发动机动态特性。
2) 仿真模型较为精确模拟了车辆行驶过程中动力传动系统的动态特性，并能反映车辆行驶时油门抖动对传动系统动态载荷的影响。

参考文献

[1]	?OSBORNE R P, WEAVER N.Optimum engine models for diesel automotive powertrain development processes[C]//IPDS 2006:Integrated Powertrain and Driveline Systems 2006.New Delhi:Woodhead Publishing Ltd.,2006:67-76.
[2]	周龙保. 内燃机学[M].北京: 机械工业出版社, 2005: 37-41.ZHOU L B. Internal combustion engine theory[M].Beijing: China Machine Press, 2005: 37-41.(in Chinese)
[3]	DENNIS A, WALTER B,NABIL C.Integration and use of diesel engine, driveline and vehicle dynamics models for heavy duty truck simulation:1999-01-0970[R].Warrendale,PA:SAE International,1999.
[4]	BROOMHEAD T,MANZIE C,BREAR M, et al.Model reduction of diesel mean value engine models:2015-01-1248[R].Warrendale,PA:SAE International,2015.
[5]	WU Z H,PEI R.Torque based spark ignition engine and powertrain modeling[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation,WCICA08.Piscataway,NJ:IEEE Press,2008:4767-4772.
[6]	YIN H B, LI H W, LV Q J. Integrated modeling and simulation on torsional loads of tracked vehicle's power train and propulsion system[J].Journal of System Simulation, 2008, 20(19): 5171–5175.
[7]	周云波, 常思勤, 魏巍. 基于MATLAB/SimDriveline的某型军用车辆起步过程仿真研究[J].南京理工大学学报, 2011, 35(4): 507–512.ZHOU Y B, CHANG S Q, WEI W. Military vehicle starting process simulation and analysis based on MATLAB/SimDriveline[J].Journal of Nanjing University of Science and Technology, 2011, 35(4): 507–512.(in Chinese)
[8]	BARAK A,KLIR V,CERVENKA L.Powertrain simulation tool:2011-37-0027[R].Detroit:SAE Technical Paper,2011.
[9]	杨得军, 林柏忠, 郭学立, 等. 汽车传动系实时动力学仿真模型[J].汽车工程, 2006, 28(5): 430–432.YANY D J, LIN B Z, GUO X L, et al. A real-time dynamics simulation model for vehicle powertrain[J].Automotive Engineering, 2006, 28(5): 430–432.(in Chinese)
[10]	戴振坤, 刘艳芳, 徐向阳, 等. 液力自动变速器传动系统建模与换挡特性仿真[J].北京航空航天大学学报, 2012, 38(8): 1027–1031.DAI Z K, LIU Y F, XU X Y, et al. Drive line modeling and shift charateristic simulation of automatic transmission powertrain system[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 1027–1031.(in Chinese)
[11]	逄淑一, 管欣, 杨得军. 基于总成特性的动力传动系统建模研究[J].汽车工程, 2013, 35(10): 873–877.PANG S Y, GUAN X, YANG D J. A research on powertrain modeling based on subsystem characteristics[J].Automotive Engineering, 2013, 35(10): 873–877.(in Chinese)
[12]	SALAANI M K,GUENTHER D A,HEYDINGER G J.Vehicle dynamics modeling for the national advanced driving simulator of a 1997 jeep cherokee:1999-01-0121[R].Warrendale,PA:SAE International,1999.
[13]	SALAANI M K,GUENTHER D A.Powertrain and brake modeling of the 1994 ford taurus for the national advanced driving simulator:981190[R].Warrendale,PA:SAE International,1998.
[14]	管欣, 卢萍萍, 詹军, 等. 多轴全轮驱动车辆动力传动系模型的建立与应用[J].汽车工程, 2011, 33(3): 183–187.GUAN X, LU P P, ZHAN J, et al. Modeling and application of powertrain model for multi-axle all-wheel-drive vehicle[J].Automotive Engineering, 2011, 33(3): 183–187.(in Chinese)
[15]	袁银南, 朱磊, 陈笃红, 等. 基于准线性模型的柴油机电子调速仿真和实验研究[J].内燃机学报, 2006, 24(3): 263–269.YUAN Y N, ZHU L, CHEN D H, et al. Simulation and experiment study of electronic governor of diesel engine based on quasi-linear model[J].Transactions of CSICE, 2006, 24(3): 263–269.(in Chinese)
[16]	项昌乐.车辆传动系轴类零件疲劳设计与变矩器动态特性研究[D].北京:北京理工大学,2001:34.XIANG C L.Fatigue design of shaft parts in vehicle transmission and research of the torque converter dynamic characteristics[D].Beijing:Beijing Institute of Technology,2001:34(in Chinese).
[17]	余志生. 汽车理论[M].北京: 机械工业出版社, 2009: 15.YU Z S. Auto theory[M].Beijing: China Machine Press, 2009: 15.(in Chinese)