然而上述液压驱动设备都是通过阀控伺服系统来实现阻抗控制。电动静液作动器(Electro-Hydrostatic Actuator,EHA)作为一种新型电液作动系统,相比阀控系统具有能量利用率高、结构易于集成等优点。在使用EHA实现阻抗控制的研究中,Kaminaga等[12-14]开展了相关工作。他们设计了一类具有逆向驱动能力的EHA,并辅以阻抗控制将其用于人形机器人、机器手以及膝关节助力器等设备中。但由于这种作动器在受到外力作用时会被其驱动向反方向运动,属于被动柔顺作动器,因而在控制上难以实现精确的力/位置协同控制。本文则基于常规的EHA来开展阻抗控制研究,从而实现其主动柔顺控制。
此外,基于力的阻抗控制以作动系统的力伺服控制为基础。而阻抗控制中负载特性的不确定以及EHA的部分时变结构参数,使得力控制的响应难以预测,极端情况下甚至会导致系统失稳。这些不确定性给控制器的设计造成了困难。定量反馈理论(Quantitative Feedback Theory,QFT)通过将系统的不确定性及性能指标进行量化,并将量化结果以边界的形式表示在Nichols图上来辅助控制器设计,从而降低了设计难度,保证了系统的鲁棒性[15]。文献[16]采用QFT实现了EHA位置控制器的设计,本文则将其用于力伺服控制器的设计,进而在此基础上实现EHA的阻抗控制。
1 EHA系统组成 在本文中,用于实现阻抗控制的EHA系统,其结构组成如图 1所示。其中,永磁同步伺服电机与定量柱塞泵相连,油泵的进、出油口通过管路连接对称液压缸的两腔,从而能够直接驱动控制液压缸活塞杆的运动。系统中的增压油箱与2个单向阀构成了补油回路,用于弥补油液的泄漏,避免油泵吸油不充分的现象发生。通过向增压油箱中通入0.8 MPa的气压来维持恒定的补油压力。
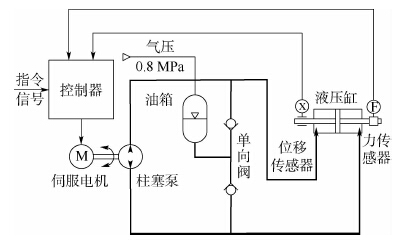 |
| 图 1 EHA控制系统原理图 Fig. 1 Schematic of EHA control system |
| 图选项 |
EHA控制系统主要由力传感器、位移传感器以及控制器组成。其中,力信号为模拟量,位置信号为数字编码量,分辨率为0.031 mm。活塞杆运动速度则可通过对位置量进行线性回归的方法得到[14]。在电机的驱动控制方面,采用了SSt-6000系列的电机伺服驱动器,从而实现了高性能的电机转速伺服控制。控制器部分通过Simulink搭建在Quanser半实物仿真平台上,能够采集传感器的反馈信号,并向电机伺服驱动器下发出±10 V范围内的控制信号,其控制周期为1 ms。
此外,选用多个不同刚度的弹簧为作动器提供弹性负载,并在阻抗控制实验中模拟不同的环境阻抗。
2 EHA数学模型 EHA数学模型的建立是后续力伺服控制器设计的基础。由于采用了高性能的电机伺服驱动器,因而可将电机的转速控制部分视为一个简单的一阶惯性环节,伺服电机转速ωm与控制信号uc的传递函数为
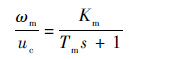 | (1) |
式中:s为拉普拉斯变换中的复数;Km为电机转速增益;Tm为时间常数。在考虑定量柱塞泵泄漏的情况下,其流量方程为
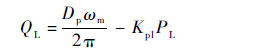 | (2) |
式中:QL为负载流量;Dp为定量柱塞泵的排量;Kpl为定量柱塞泵泄漏系数;PL为负载压力。在作动器的动力学方程中,为了能够得到各物理量间的线性关系,因而仅引入了黏性摩擦对系统动力学的影响,其微分方程为
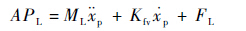 | (3) |
式中:A为液压缸活塞有效面积;ML为活塞杆及外负载的总质量;Kfv为黏性摩擦系数;FL为负载力;xp为液压缸活塞杆位移;${\dot x}$p与${\dot x}$p分别为活塞杆运动的速度与加速度。由于本文研究弹性负载下作动器的力控制与阻抗控制问题,因此负载力与液压缸活塞杆位移满足:
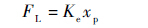 | (4) |
式中:Ke为弹性负载刚度,即环境刚度。由液压泵输出至液压缸的负载流量,除推动活塞杆运动的部分外,还包括油液压缩与泄漏两部分。其流量方程为
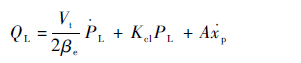 | (5) |
式中:Vt为液压缸两腔及连接管路的总容积;βe为油液的弹性模量;Kcl为液压缸泄漏系数。为了得到便于后续研究的较为简化的EHA系统数学模型,在建模过程中,忽略系统各部分的泄漏,联立式(1)~式(5)并进行拉普拉斯变换,则可得到EHA输出的负载力对于控制信号的开环传递函数,其表达式为
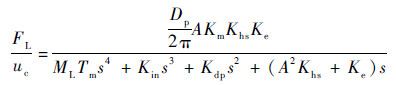 | (6) |
式中:为了简化传递函数的表达式,引入了Kin、Khs与Kdp 3个系数,其定义分别为
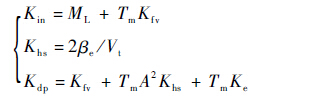 | (7) |
基于本节推导得到的EHA数学模型,即可对相应的力伺服控制器进行设计。
3 力伺服控制器设计 在第2节EHA数学模型的各个参数中,一部分参数的值是唯一确定的且其值易于通过测量、实验或查阅手册得到。这些参数及其参数值如表 1所示。
表 1 EHA模型定常参数 Table 1 Time-invariant parameters of EHA model
| 参数 | 数值 |
| ML/kg | 12.3 |
| Tm/s | 0.05 |
| Km/(rad·s-1·V-1) | 25 |
| Vt/cm3 | 234 |
| A/mm2 | 633 |
| Dp/(cm3·r-1) | 4.9 |
表选项
除上述参数外,油液弹性模量βe的取值会随着油液压力的变化而变化,且其函数关系呈现出非线性;黏性摩擦系数Kfv的值能够通过实验测得,但其在活塞杆运动的2个相反方向上取值并不一致,且在一些外部条件发生变化时,其值也会随之变化[17];而为了使EHA控制系统能够在不同的外部负载条件下正常工作且保证一定的动态特性,在控制器设计过程中,弹性负载刚度Ke的取值也要在较大范围内进行考虑。
由于以上3个时变参数的取值难以确定,因而采用了基于QFT的设计方法,使得力伺服控制器对被控对象结构参数在一定范围内的变化具有一定的鲁棒性。
3.1 对象模板与频率阵列的选取 在设计过程中,首先根据相关参数的经验值以及系统的工作环境,确定时变参数的取值范围,如表 2所示。
在QFT方法中,通过对象模板的形式来描述被控对象在各频率点处的不确定性。为了得到恰当的对象模板,需要根据被控对象的频率特性选取一组频率阵列。
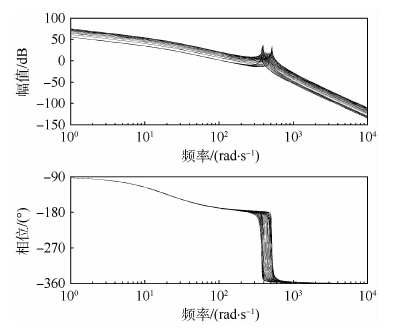
令表 2中的3个参数在各自的范围内分别取若干组值,并相互交叉组合,代入式(6),得到若干个EHA开环传递函数。这些传递函数的开环频率特性变化范围如图 2所示。
表 2 EHA模型时变参数 Table 2 Time-variant parameters of EHA model
| 参数 | 下限值 | 上限值 |
| βe /(108N·m-2) | 5 | 9 |
| Kfv/(N·s·m-1) | 50 | 350 |
| Ke/(kN·m-1) | 20 | 200 |
表选项
 |
| 图 2 EHA开环频率响应的不确定性 Fig. 2 Uncertainty of EHA open-loop frequency response |
| 图选项 |
在组建频率阵列时,应当选择被控对象频率特性差异较大处的频率点,从而使该点处生成的对象模板能够尽可能反映被控对象的不确定性。由图 2可见,EHA在各频率点处幅频特性的差异基本相同,而在400~500 rad/s的频率范围内,相频特性的差异较大。因此,最终将频率阵列选定为:ω={0.1,1,5,10,20,100,450,1 000} rad/s。其中,频率点450 rad/s即是为了体现被控对象相频特性差异而选定的。在以上频率阵列的每个频率点上,将被控对象幅值与相位的变化范围映射到Nichols图上便形成了对象模板。这些模板将被用于边界的生成。
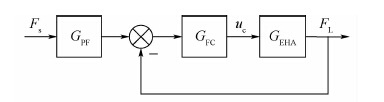
3.2 稳定性边界与跟踪边界的确定 包含前置滤波器以及控制器的EHA力控制系统方框图如图 3所示。
 |
| 图 3 EHA力控制系统方框图 Fig. 3 EHA force control system block diagram |
| 图选项 |
在力伺服控制器以及前置滤波器的设计中,主要考虑系统的鲁棒稳定性和跟踪性能。鲁棒稳定性是指被控对象中不确定的结构参数在一定范围内变化时,控制系统能够始终保持稳定的性质。为了保证系统的鲁棒稳定性,需要在Nichols图上生成相应的稳定性边界,从而对控制器的设计加以限制。稳定性边界可通过对象模板结合以下限制条件得到,对于任意的GEHA均满足:
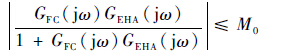 | (8) |
式中:ω为角频率;M0为系统闭环频率特性向量模值的上限,其意义为Nichols图中与开环频率特性曲线相切的等M线的M值。上限值M0与系统的幅值稳定裕度h以及相角稳定裕度γ存在对应关系,因此可以通过设定该值来调整系统的稳定裕度,从而实现鲁棒稳定。其对应关系为
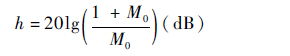 | (9) |
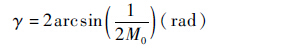 | (10) |
根据系统期望的稳定裕度,将M0设为1.2,则相应的幅值稳定裕度为5.3 dB,相角稳定裕度为0.86 rad。
跟踪性能主要反映系统动态响应的各项指标,决定了响应的平稳性与快速性。在设计中,控制系统的跟踪性能可以通过设定频率响应的上、下限来进行限定,使得系统的动态响应始终处于上、下限所包络的范围内。同样可以通过对象模板结合相应的限制条件在Nichols图上得到跟踪边界。其限制条件为对任意的GEHA均满足:
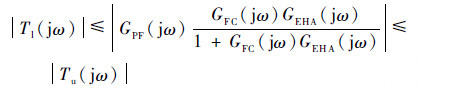 | (11) |
式中:Tl与Tu分别为跟踪性能的下限与上限。根据系统时变结构参数的取值范围以及对平稳性与快速性的要求,将上、下限分别设为
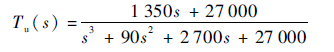 | (12) |
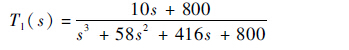 | (13) |
同时满足上述的稳定性边界与跟踪边界,即可确保控制系统性能达到设计要求。
3.3 控制器与前置滤波器的设计 在对象模板中任意选取一个对象作为标称对象,并将该对象的开环频率特性曲线置于Nichols图上。再基于此标称对象得到稳定性边界与跟踪边界,并将2组边界进行合并,在Nichols图上标出各频率点所对应的边界曲线。通过对标称对象开环频率特性曲线进行整形,使其在每个频率点处都满足相应边界的要求,从而完成控制器的设计。含有各频率下的边界曲线以及整形后的开环频率特性曲线的Nichols图如图 4所示。图中开环频率特性曲线上各圆点处所标示的数字为该点所对应的频率,其单位与角频率ω相同,均为rad/s。对于各频率处的边界,实线与虚线分别表示下边界与上边界。
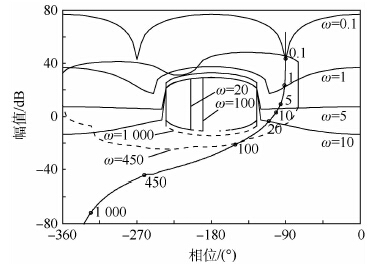 |
| 图 4 综合边界与系统开环频率响应 Fig. 4 Integrated bounds and open-loop frequencyresponse of system |
| 图选项 |
整形过程中,通过配置控制器的零极点来调整开环频率特性曲线的位置及形状,使线上的8个频率点均满足相应边界的限制,最终得到的力伺服控制器为
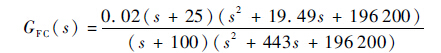 | (14) |
由于Nichlos图中的跟踪边界仅限定了模板动态响应的差异小于跟踪性能上、下限间的差值,还需要通过配置前置滤波器确保系统的动态响应落入上、下限之间。调整后得到的前置滤波器为
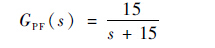 | (15) |
引入前置滤波器前后,力控制系统的闭环频率响应曲线如图 5所示。图中不确定被控对象结合控制器与前置滤波器的闭环频响曲线均位于上、下限之间,从而保证了系统的跟踪性能。
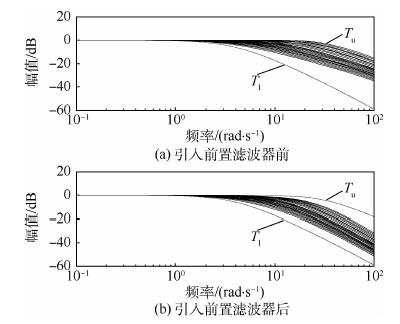 |
| 图 5 引入前置滤波器前后系统闭环频率响应 Fig. 5 Closed-loop frequency responses of systemwith and without pre-filter |
| 图选项 |
3.4 力伺服控制实验 完成基于QFT的设计过程后,通过力伺服控制实验对系统进行了验证。实验中采用3种不同刚度的弹簧作为负载,令系统跟踪1 800 N的力阶跃信号,检验其稳定性与动态性能。3组实验结果如图 6所示。图中,虚线表示响应跟踪性能的上、下限,实线为力伺服控制的实际响应,按照响应速度由快至慢依次对应的弹性负载刚度Ke为125、85以及45 kN/m。
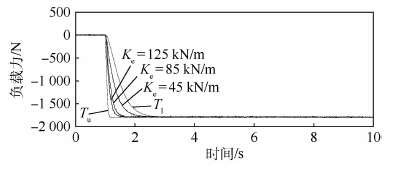 |
| 图 6 不同弹性负载刚度下EHA力控制系统阶跃响应 Fig. 6 Step responses of EHA force control system withvarious elastic load stiffness |
| 图选项 |
在实验过程中,弹性负载刚度、油液弹性模量以及黏性摩擦系数都存在不同程度的变化,而控制系统始终能够保持稳定,且3组动态响应均在限定的范围内。实验结果证明了QFT设计方法的有效性。
4 基于力的阻抗控制 在第3节力伺服控制系统的基础上,引入可设置的目标阻抗环节即可实现EHA的阻抗控制,使作动系统具有所期望的柔顺性。基于力的阻抗控制原理如图 7所示。图中,xs为给定位移,环境阻抗环节由外负载特性决定,在弹性负载下其主要表现为负载刚度。
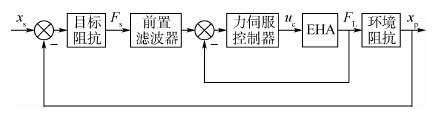 |
| 图 7 基于力的阻抗控制原理图 Fig. 7 Schematic of force based impedance control |
| 图选项 |
目标阻抗环节用于调节位置误差与给定力之间的关系,其传递函数GTI为
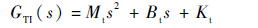 | (16) |
式中:Mt、Bt与Kt分别为目标质量、阻尼以及刚度。由此可以得到
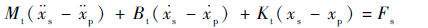 | (17) |
式中:${\dot x}$s与${\ddot x}$s分别为给定速度与加速度。由式(17)可见,可以通过配置3个目标阻抗参数来调整负载力与活塞杆位移的关系,从而使作动系统与外负载(环境)发生接触时表现出期望的阻抗特性。
分别采用静态与动态阻抗控制实验对EHA系统的阻抗关系与柔顺性进行验证。实验中将目标质量与阻尼设为零,暂未考虑其影响,仅研究目标刚度。
4.1 静态阻抗控制实验 使活塞杆与充当弹性负载的弹簧相接触,以弹簧原长作为初始零位置。实验中,将给定位移xs设为-20 mm,使作动器压缩弹性负载,观察在不同目标刚度Kt下活塞杆的实际位移xp,从而判断系统表现出的阻抗特性是否准确。给定位移与活塞杆位移应当满足:
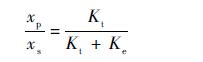 | (18) |
实验中采用刚度为30 kN/m的弹簧作为弹性负载,实验结果如图 8所示。可知,在以上4组实验结果中,系统稳定后的活塞杆位移与给定位移均符合式(18)中的比例关系。
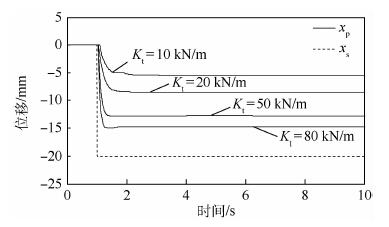 |
| 图 8 静态阻抗控制实验结果 Fig. 8 Static impedance control experiment results |
| 图选项 |
4.2 动态阻抗控制实验 活塞杆处于与静态阻抗控制实验中相同的初始零位置,输入的给定位移xs变为幅值20 mm,频率0.1 Hz的正弦信号。活塞杆不与弹簧固连,在跟踪给定位移信号的过程中,前半周期脱离弹簧,在空载状态下自由运动,后半周期接触并压缩弹簧,在受约束的状态下运动。通过该实验可以同时检验作动系统自由运动状态下的位置跟踪性能以及受约束运动状态下的柔顺性。以刚度为170 kN/m的弹簧作为弹性负载,采用不同目标刚度的动态阻抗控制实验结果如图 9所示。
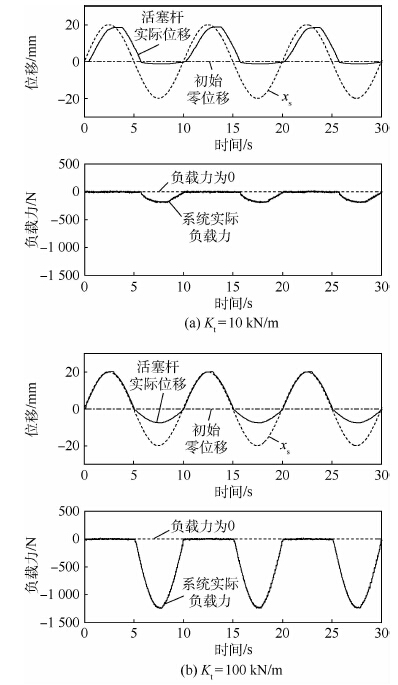 |
| 图 9 动态阻抗控制实验结果 Fig. 9 Dynamic impedance control experiment results |
| 图选项 |
由实验中的约束运动部分可见,目标刚度越小,则负载作用力越小,作动系统柔顺性越好。但在目标刚度为10 kN/m时,系统位置跟踪性能较差,存在0.7 s的滞后。而在目标刚度为100 kN/m时,系统位置跟踪滞后很小。若将阻抗控制系统视为位置伺服系统,则目标刚度相当于开环增益,因而目标刚度越大,系统位置跟踪性能越好。由于位置跟踪性能与柔顺性的矛盾,需要综合考虑系统工作环境与性能指标要求,从而确定阻抗参数的取值。
5 结 论 1) 通过QFT方法能够有效地设计出具有一定鲁棒性的力伺服控制器,使EHA系统在外部负载特性不确定,油液弹性模量与黏性摩擦系数时变的条件下始终保持稳定并达到预期的性能指标要求。
2) 在这一力伺服控制器的基础上,EHA系统成功实现了基于力的阻抗控制。系统力和位移的关系与设定的目标阻抗相一致。
3) 阻抗控制的位置跟踪性能与柔顺性得到了实验验证。动态阻抗控制实验结果表明,随着目标阻抗中目标刚度的减小,系统跟踪性能变差,而柔顺性得到改善。
为了协调阻抗控制跟踪性能与柔顺性的关系,可以根据具体应用的实际需求对目标阻抗参数的配置开展进一步研究。
参考文献
| [1] | HOGAN N. Impedance control:An approach to manipulation, Parts Ⅰ, Ⅱ, Ⅲ[J].Journal of Dynamic Systems, Measurement, and Control, 1985, 107(1): 1–24.DOI:10.1115/1.3140702 |
| [2] | KAZEROONI H. Automated robotic deburring using impedance control[J].Control Systems Magazine, 1988, 8(1): 21–25.DOI:10.1109/37.464 |
| [3] | ERHAN A G, MEHMET A A. The design and control of a therapeutic exercise robot for lower limb rehabilitation:Physiotherabot[J].Mechatronics, 2011, 21(3): 509–522.DOI:10.1016/j.mechatronics.2011.01.005 |
| [4] | RICHARDSON R, BROWN M, BHAKTA B, et al. Design and control of a three degree of freedom pneumatic physiotherapy robot[J].Robotica, 2003, 21(6): 589–604.DOI:10.1017/S0263574703005320 |
| [5] | OTT C, ALBU-SCHAFFER A, KUGI A, et al. On the passivity-based impedance control of flexible joint robots[J].IEEE Transactions on Robotics, 2008, 24(2): 416–429.DOI:10.1109/TRO.2008.915438 |
| [6] | IRAWAN A, NONAMI K. Optimal impedance control based on body inertia for a hydraulically driven hexapod robot walking on uneven and extremely soft terrain[J].Journal of Field Robotics, 2011, 28(5): 690–713.DOI:10.1002/rob.20404 |
| [7] | HA Q P, NGUYEN Q H, RYE D C, et al. Impedance control of a hydraulically actuated robotic excavator[J].Automation in Construction, 2000, 9(5): 421–435. |
| [8] | TAFAZOLI S, SALCUDEAN S E, HASHTRUDI-ZAAD K, et al. Impedance control of a teleoperated excavator[J].IEEE Transactions on Control Systems Technology, 2002, 10(3): 355–367.DOI:10.1109/87.998021 |
| [9] | FATEH M M, ALAVI S S. Impedance control of an active suspension system[J].Mechatronics, 2009, 19(1): 134–140.DOI:10.1016/j.mechatronics.2008.05.005 |
| [10] | FATEH M M. Robust impedance control of a hydraulic suspension system[J].International Journal of Robust and Nonlinear Control, 2010, 20(8): 858–872. |
| [11] | FATEH M M, ZIRKOHI M M. Adaptive impedance control of a hydraulic suspension system using particle swarm optimization[J].Vehicle System Dynamics, 2011, 49(12): 1951–1965.DOI:10.1080/00423114.2011.564289 |
| [12] | KAMINAGA H,ONO J,NAKASHIMA Y,et al.Development of backdrivable hydraulic joint mechanism for knee joint of humanoid robots[C]//Robotics and Automation.Piscataway,NJ:IEEE Press,2009:1577-1582. |
| [13] | KAMINAGA H, AMARI T,KATAYAMA Y,et al.Backdrivability analysis of electro-hydrostatic actuator and series dissipative actuation model[C]//Robotics and Automation.Piscataway,NJ:IEEE Press,2010:4204-4211. |
| [14] | KAMINAGA H,AMARI T,NIWA Y,et al.Development of knee power assist using backdrivable electro-hydrostatic actuator[C]//Intelligent Robots and Systems.Piscataway,NJ:IEEE Press,2010:5517-5524. |
| [15] | YANIV O. Quantitative feedback design of linear and nonlinear control systems[M].Massachusetts: Kluwer Academic Publishers, 1999: 17-18. |
| [16] | 马纪明, 付永领, 高波. 基于定量反馈理论的EHA控制器设计[J].北京航空航天大学学报, 2006, 32(5): 553–557.MA J M, FU Y L, GAO B. EHA controller design based quantitative feedback theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(5): 553–557.(in Chinese) |
| [17] | 郭彦青, 付永领, 张朋, 等. 电液负载模拟器摩擦参数辨识及补偿[J].北京航空航天大学学报, 2014, 40(9): 1256–1262.GUO Y Q, FU Y L, ZHANG P, et al. Friction parameter identification and compensation for electro-hydraulic load simulator[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1256–1262.(in Chinese) |
