以往对含铰链间隙机构的精度分析研究主要集中于开环机构[7-9]及简单的四杆机构[5, 10]或曲柄滑块机构[11]。对于复杂多闭环机械系统,****们往往借助于多体动力学工程软件从动力学的角度通过建立铰接子系统模型考察整个系统的振动冲击特性[12-15],而对其复杂的运动学不确定性分析较少。对于大型空间可展开机构的精度分析,****们也做了很多研究,并取得了一定的成果,但其分析结果是在已知或者假定所研究关键设计参数的随机分布特性的前提下[16],并经过大量近似处理后得到的[4],其结果精确度有待进一步验证。
本文采用智能优化算法求解因铰链间隙引起的指向精度,不需要确定铰链间隙模型的随机分布特性;采用矩阵法构造计算模型,避免了常用几何法因模型简化及向量法因不同数量级数值运算而造成的精度损失。对锁定机构的锁定误差单独建模分析,将误差值作为输入变量输入到单环路模型中进行后续运算,减少了模型的复杂度;从几何误差角度求得卫星天线展开后的极限指向误差,为进一步进行含铰链间隙的动力学误差分析[17]及机构的误差补偿设计奠定了基础。
1 板式卫星天线展开机构构型 采用在航天领域应用广泛的有源驱动折叠式展开机构作为研究对象,其构型关于展开方向与天线板垂线方向所构成的平面对称,在分析其展开指向精度时可按平面连杆机构处理。机构的收拢状态与展开状态构型如图 1所示。图中:铰链O与铰链A与星体固联。
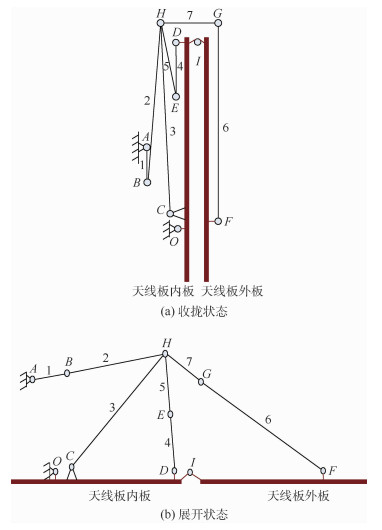 |
| 图 1 展开机构构型 Fig. 1 Deployable mechanism configuration |
| 图选项 |
依平面机构自由度计算公式得此展开机构自由度为
 | (1) |
式中:n为构件数目;PL为平面低副数目;PH为平面高副数目。
在铰链O处布置电机驱动作为主要驱动源,并在铰链B和铰链G处布置扭簧作为被动驱动源辅助机构展开,使得展开机构具有确定的运动。为了确保机构展开死点位置可靠性,在铰链B、铰链E和铰链G处设置锁定机构,其达到180°时自动锁死。
2 含铰链间隙多杆系统建模 2.1 含铰链间隙建模 使用无质量虚拟连杆(massless virtual link)来模拟铰链间隙是分析含铰链间隙机构运动学特性的主要手段[4, 6, 10]。假设通过铰链联结的2个构件在运动过程中始终处于接触状态,原含铰链间隙机构系统转化为无铰链间隙的多杆多自由度系统,虚拟连杆长度r计算如下:
 | (2) |
式中:ri+1为轴套半径;ri为轴销半径。
铰链间隙模型示意图如图 2所示。
 |
| 图 2 铰链间隙模型 Fig. 2 Joint clearance model |
| 图选项 |
2.2 锁定机构精度分析 板式卫星天线可展开机构关键位置铰链需要锁定机构来保证在展开位置的姿态。锁定机构的锁定角度误差对指向精度影响很大[16],需要单独建模分析。一种铰链锁定机构的构型示意图如图 3所示。
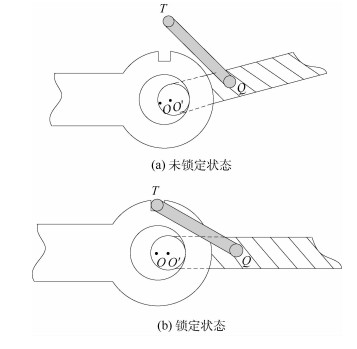 |
| 图 3 锁定机构 Fig. 3 Locking mechanism |
| 图选项 |
铰链自由转动状态时,连杆QT与铰链不构成约束关系,当铰链联结的两连杆呈180°时,连杆QT的T端落入凹槽,将铰链锁死[4]。
铰链间隙、连杆的弹性变形及凹槽与T端的配合间隙等均能造成锁定角度误差,而铰链间隙是误差主要来源。在不考虑铰链间隙时,锁定机构锁定后构成三角形结构(见图 4(a));考虑铰链间隙时,则可等效为四杆机构构型(见图 4(b)),其锁定角度误差可表示为虚拟连杆位置的函数。图 4(b)中:角度γ即为锁定角度误差。
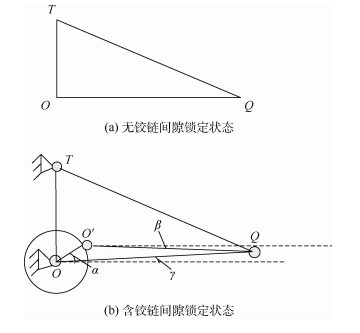 |
| 图 4 含铰链间隙的锁定机构模型 Fig. 4 Locking mechanism model with joint clearance |
| 图选项 |
角度α为一随机量,代表铰链间隙的位置。由几何关系可得
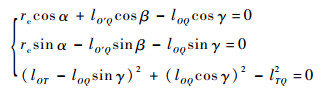 | (3) |
式中:rc=lOO′为铰链间隙大小;lOT、lTQ、lO′Q和lOQ分别为边OT、边TQ、边O′Q和边OQ的长度。
由于三角函数的非线性特性,式(3)的求解十分复杂,在满足精度的前提下,可对式(3)近似处理。由于铰链间隙的大小远小于构件杆长,角度β与γ很小,且一般不会超过2°[16]。取cosβ=cosγ=1,此估计值的绝对误差计算如下:
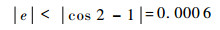 | (4) |
易知,估计的误差限为
 | (5) |
式中:ε1和ε2分别为cosβ和cosγ估计的误差限。
简化后得
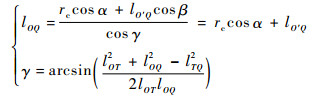 | (6) |
设u=f(cosβ, cosγ)为边OQ长度的函数; v=g(u)为估计误差的函数,则估计的误差限计算如下:
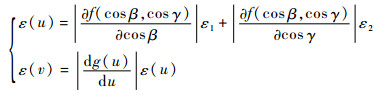 | (7) |
式(3)、式(6)和式(7)中各变量的取值如表 1所示。
表 1 变量取值 Table 1 Parameter values
| 变量 | rc | lOT | lO′Q | lTQ |
| 数值/mm | 0.5 | 30 | 40 | 50 |
表选项
当α取[0°, 360°]时,锁定精度估计及估计误差限变化曲线如图 5所示。
 |
| 图 5 锁定精度估计及估计误差限 Fig. 5 Locking angle error estimation and estimation error limit |
| 图选项 |
由图 5可得,锁定机构的锁定角度误差区间为[-0.94908°-0.00057°, 0.94908°+0.00057°],取估计值精确有效数字,则锁定机构锁定角度误差处于区间[-0.95°, 0.95°]内。
2.3 含铰链间隙的展开机构模型 本文所分析的展开机构含有9根连杆与10个铰链,其构型含有3个封闭环路(见图 1),这给其展开指向误差的分析的带来很大困难。从结构上来看,连杆HE与连杆ED主要功能在于支撑天线板内板,其对整体的展开指向精度影响小,在分析过程中,将其忽略,此时展开机构自由度依然为3:
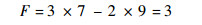 | (8) |
含铰链间隙的展开机构模型示意图如图 6所示。
 |
| 图 6 含铰链间隙的展开机构模型 Fig. 6 Deployable mechanism model with joint clearances |
| 图选项 |
采用矩阵法构建含铰链间隙的天线展开机构数学模型。在笛卡儿坐标系下用齐次变换矩阵描述各构件的平面转动。
设平面一点M绕任一点P逆时针旋转角度θ后到达位置为M′(见图 7),旋转的齐次变换矩阵
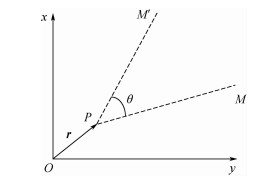 |
| 图 7 平面转动 Fig. 7 Planar rotation |
| 图选项 |
表示为
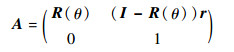 | (9) |
式中:R(θ)为平面转动矩阵;r为向量
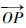
若M点坐标为[xM, yM]T, P点坐标为[xP, yP]T,则旋转后M点坐标表示为
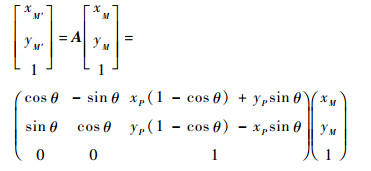 | (10) |
利用齐次变换矩阵对图 6所示的可展开机构闭环Ⅰ进行建模。
建立图 8所示坐标系,则端点A的齐次变换矩阵A1可表示为
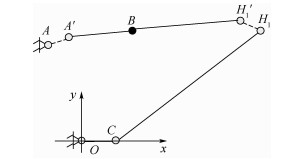 |
| 图 8 环路Ⅰ Fig. 8 LoopⅠ |
| 图选项 |
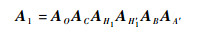 | (11) |
式中:Ax为绕点x旋转运动的齐次变换矩阵,x=O, C, H1, H′1, B, A′。
式(10)目的在于求解连杆AC位置,其为环路Ⅱ的输入。环路I的自由度为4,当连杆OC输入转角及铰链B锁定角度确定后,环路未约束自由度个数与铰链间隙数目一致。
如图 9所示,端点I的齐次变换矩阵A2可表示为
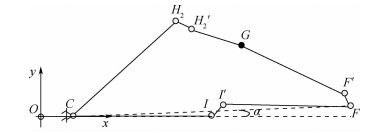 |
| 图 9 环路Ⅱ Fig. 9 LoopⅡ |
| 图选项 |
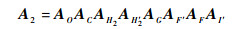 | (12) |
式中:Ax为绕点x旋转运动的齐次变换矩阵,x=O, C, H2, H′2, G, F′, F, I′。环路Ⅱ的自由度为6,当连杆CH2、连杆CI及铰链G确定时,环路未约束自由度数目与铰链间隙数目相同。
综上,该展开机构的不确定自由度数目为7,包含5个铰链间隙自由度与2个由锁定误差造成的不确定度。
3 计算求解 3.1 等式约束与构型初值 由于A1与A2所描述运动形成封闭环路,当机构展开后,点A与点I的坐标已知,由式(10)得约束方程为
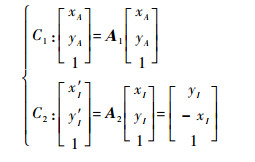 | (13) |
式中:(xA,yA)和(xI,yI)分别为铰链A和铰链I收拢状态坐标;(x′I,y′I)为铰链I展开后坐标。
可展开机构收拢状态下构型参数如表 2所示。
表 2 收拢状态构型参数 Table 2 Configuration parameters in stowed condition
| 变量 | 物理意义 | 数值 |
| r/mm | 铰链间隙 | 0.5 |
| (xO,yO)/mm | 铰链O中心坐标 | (0, 0) |
| (xC,yC)/mm | 铰链C中心坐标 | (0, 120) |
| (xA,yA)/mm | 铰链A中心坐标 | (-40, 1400) |
| (xB,yB)/mm | 铰链B中心坐标 | (-30, 900) |
| (xH,yH)/mm | 铰链H中心坐标 | (-20, 2900) |
| (xG,yG)/mm | 铰链G中心坐标 | (500, 2900) |
| (xF,yF)/mm | 铰链F中心坐标 | (500, 100) |
| (xI,yI)/mm | 铰链I中心坐标 | (250, 2850) |
| θ1/(°) | 天线板内板转角 | -90 |
| θ4′/(°) | 铰链B初始角度 | 1.42 |
| θ6′/(°) | 铰链G初始角度 | 90 |
表选项
铰链间隙模型中虚拟连杆的初始指向对精度分析结果没有影响,此处均取沿x轴负方向。定义转角在逆时针旋转时为正值。
定义θi(i=1, 2, 3, 4, 5, 6, 7)分别代表铰链O, C, H′1, B, H′2, G和F的转角;zi(i=1, 2, 3, 4, 5)分别代表铰链H1, A′, H2, F′和I′处虚拟连杆的转角。
3.2 粒子群优化算法 粒子群优化算法属于进化算法的一种,其具有易实现、精度高和收敛快等优点,广泛应用于解决实际工程问题中。
本文旨在研究含铰链间隙的卫星天线展开后的指向精度,即天线展开后连线OF与x轴正方向的夹角α。由式(10)可得点F展开后的坐标:
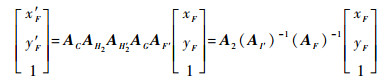 | (14) |
优化的目标可表示为(见图 9)
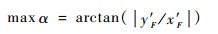 | (15) |
此优化目标含绝对值且非线性很强,对优化的收敛有很大影响,故构造适应度函数为
 | (16) |
式中:μ为放大系数,为弥补两坐标值间数量级的差别,增加收敛速度,避免局部最优解,此处取μ=100。
进行优化计算前,利用等式约束Ci(i=1, 2)进行数值求解以减少设计变量数目,使得该优化变为无约束优化问题(见图 10)。设计变量为铰链间隙变量zi(i=1, 2, 3, 4, 5)与锁定铰链锁定角θi(i=4, 6)。
 |
| 图 10 数值计算流程 Fig. 10 Data computation flow |
| 图选项 |
3.3 数值求解 设计变量取值设定如表 3所示。表中:θ4和θ6取值根据第3.2节结论与表 2初始值得出。
表 3 设计变量取值 Table 3 Design variable values
| 设计变量 | zi(i=1, 2, 3, 4, 5) | θ4 | θ6 |
| 数值/(°) | 0~360 | 177.63~179.53 | 89.05~90.95 |
表选项
设定群个体数目为20,粒子群进化代数与最优粒子个体对应的目标函数值关系如图 11所示。可见,经过43代进化后粒子群收敛,得到最优个体,如表 4所示。
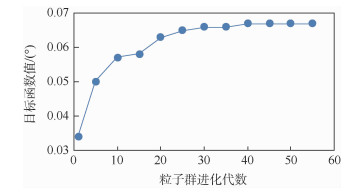 |
| 图 11 优化过程 Fig. 11 Optimization procedure |
| 图选项 |
表 4 最优解 Table 4 Optimum solution
| 变量 | z1 | z2 | z3 | z4 | z5 | θ4 | θ6 |
| 数值/(°) | 89.83 | 61.55 | 205.23 | 259.53 | 279.15 | 178.04 | 89.76 |
表选项
此时,目标函数α值为0.067°,表明此构型下的卫星天线展开机构在极恶劣的铰链间隙工况下展开后的指向误差为0.067°。由于卫星工作轨道很高,此误差的影响也会导致几十千米的偏移,需要考虑天线的指向精度补偿设计。
4 结论 1)?本文建立了刚体运动矩阵表达形式的板式卫星天线指向精度分析模型,从运动学的角度依次分析了铰链间隙影响下的锁定机构锁定误差与整体展开后的指向误差。
2)?提出了分级建模的分析方法,经数值运算,求得该尺寸构型下锁定铰链B和铰链G的锁定误差为±0.95°;提出了基于粒子群优化算法的整体指向精度分析方法,得到整机在极恶劣铰链间隙工况下的展开指向误差为0.067°。
3)?通过建模分析结果可知,在板式卫星天线闭环机械系统中,由于铰链间隙的影响,机构运动存在误差,需要对板式卫星天线进行指向精度补偿设计。
参考文献
| [1] | 马兴瑞, 于登云, 孙京, 等. 空间飞行器展开与驱动机构研究进展[J].宇航学报, 2006, 27(6): 1123–1131.MA X R, YU D Y, SUN J, et al. The researching evolvement of spacecraft deployment and driving mechanism[J].Journal of Astronautics, 2006, 27(6): 1123–1131.(in Chinese) |
| [2] | 王巍, 于登云, 马兴瑞. 航天器铰接结构非线性动力学特性研究进展[J].力学进展, 2006, 36(2): 233–238.WANG W, YU D Y, MA X R. Advances and trends of non-linear dynamics of space joint-dominated structure[J].Advanced in Mechanics, 2006, 36(2): 233–238.(in Chinese) |
| [3] | 阎绍泽. 航天器中含间隙机构非线性动力学问题及其研究进展[J].动力学与控制学报, 2004, 2(2): 48–52.YAN S Z. Development and problems of nonlinear dynamics of the mechanisms with clearances for spacecraft[J].Journal of Dynamics and Control, 2004, 2(2): 48–52.(in Chinese) |
| [4] | LI X, DING X L, CHIRIKJIAN G S. Analysis of angular-error uncertainly in planar multiple-loop structures with joint clearances[J].Mechanism and Machine Theory, 2015, 91: 69–85.DOI:10.1016/j.mechmachtheory.2015.04.005 |
| [5] | ZHANG J F, DU X P. Time-dependent reliability analysis for function generation mechanisms with random joint clearances[J].Mechanism and Machine Theory, 2015, 92: 184–199.DOI:10.1016/j.mechmachtheory.2015.04.020 |
| [6] | TAI M J, LAI T H. Accuracy analysis of a multi-loop linkage with joint clearances[J].Mechanism and Machine Theory, 2008, 43(9): 1141–1157.DOI:10.1016/j.mechmachtheory.2007.09.001 |
| [7] | 丁希仑, 周乐来, 周军. 机器人的空间位姿误差分析方法[J].北京航空航天大学学报, 2009, 35(2): 241–245.DING X L, ZHOU L L, ZHOU J. Pose error analysis of robot in three dimension[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 241–245.(in Chinese) |
| [8] | 庞欢, 喻天翔, 宋笔锋. 平面连杆机构运动精度可靠性及灵敏度分析[J].中国机械工程, 2014, 25(18): 2415–2420.PANG H, YU T X, SONG B F. Analysis of kinematics accuracy reliablility and sensitivity for a planar mechanism[J].China Mechanism Engineering, 2014, 25(18): 2415–2420.(in Chinese) |
| [9] | 潘博, 张东华, 史文华, 等. 星载天线指向精度建模与分析[J].航天器工程, 2011, 20(5): 49–54.PAN B, ZHANG D H, SHI W H, et al. Modeling and analysis on pointing accuracy of antenna in satellite[J].Spacecraft Engineering, 2011, 20(5): 49–54.(in Chinese) |
| [10] | SARDASHTI A, DANIALI H M, VAREDI S M. Optimal free-defect synthesis of four-bar linkage with joint clearance using PSO algorithm[J].Meccanica, 2013, 48(7): 1681–1693.DOI:10.1007/s11012-013-9699-6 |
| [11] | FLORES P, KOSHY C S, LANKARANI H M, et al. Numerical and experimental investigation on multi-body systems with revolute clearance joints[J].Nonlinear Dynamics, 2011, 65(4): 383–398.DOI:10.1007/s11071-010-9899-8 |
| [12] | 曹登庆, 初世明, 李郑发, 等. 空间可展机构非光滑力学模型和动力性研究[J].力学学报, 2013, 45(1): 3–15.CAO D Q, CHU S M, LI Z F, et al. Study on the non-smooth mechanical models and dynamics for space deployable mechanisms[J].Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 3–15.(in Chinese) |
| [13] | 白争锋, 赵阳, 田浩. 含较间间隙太阳帆板展开动力学仿真[J].哈尔滨工业大学学报, 2009, 41(3): 11–14.BAI Z F, ZHAO Y, TIAN H. Dynamics simulation of deployment for solar panels with hinge clearance[J].Journal of Harbin Institute of Technology, 2009, 41(3): 11–14.(in Chinese) |
| [14] | 张慧博, 陈军, 潘冬, 等. 含间隙卫星天线双轴驱动机构动力学特性分析[J].宇航学报, 2012, 33(1): 33–38.ZHANG H B, CHEN J, PAN D, et al. Mechanism for satellite antenna with joint clearance[J].Journal of Astronautics, 2012, 33(1): 33–38.(in Chinese) |
| [15] | 谷勇霞, 杨天夫, 郭峰. 考虑多间隙的帆板式展开机构动力学分析[J].振动、测试与诊断, 2015, 35(1): 36–41.GU Y X, YANG T F, GUO F. Dynamic performance of a solar array deployable mechanism with multiple clearances[J].Journal of Vibration, Measurement and Diagnosis, 2015, 35(1): 36–41.(in Chinese) |
| [16] | 吴建云, 王春洁, 汪瀚. 基于蒙特卡洛法的卫星天线板展开精度分析[J].航天返回与遥感, 2013, 34(6): 89–94.WU J Y, WANG C J, WANG H. Accuracy analysis of satellite antenna plate deployment based on Monte Carlo method[J].Spacecraft Recovery and Remote Sensing, 2013, 34(6): 89–94.(in Chinese) |
| [17] | LI J L, YAN S Z, GUO F, et al. Effects of damping, friction, gravity, and flexibility on the dynamic performance of a deployable mechanism with clearance[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2013, 227(8): 1791–1803.DOI:10.1177/0954406212469563 |
