双向旋转端面气膜密封的研究已经被成功应用。John Carne公司从20世纪80年代后期开始研制双向旋转端面气膜密封,其研制的28BD已成功应用于俄罗斯等国的高速压缩机[5]。德国Burgman公司研发的V型槽结构可在多种密封结构下使用[6]。天津克兰密封有限公司研制的八字型槽气体端面密封在高速透平机上得到了应用[7]。
柱面气膜密封研究开展相对较晚,近年来逐渐引起重视。2001年,Salehi和Heshmat[8]在成功应用的径向柔顺箔轴承的基础上提出并进行了柱面形式的柔顺箔密封研究,其平滑顶箔与高速轴颈之间可形成流体动压密封气膜,并在小型气涡轮发动机模拟器上进行了柔顺箔密封系统的性能实验研究,但其密封界面为光滑圆柱,单向运转。2002年,英国帝国理工大学的Sayma等[9]提出了在大直径航空燃气轮机的转子叶尖处应用气控密封即柱面气膜密封的问题,提出了此密封应有结构柔性和基于Navier-Stokes方程的气弹性分析模型,但未提出具体结构型式。2004年,Shapiro等[10-11]对光滑密封界面、螺旋槽密封界面形式下柱面气膜密封的分析方法、试验结果进行了深入的研究,但其设计及分析试验均是在单向旋转的条件下进行。国内,笔者研究团队针对柱面气膜从数值分析方法、界面结构、稳态特性及动态特性等方面开展了一系列的研究[1, 12],针对的都是单向旋转条件。
柱面气膜密封易具有浮动自适应性,可使密封系统具有较大的柔性,适应系统中振动位移和变形等工况,在高速转子系统密封中具有独特的优势[13-14]。双向旋转柱面气膜密封界面结构能适应双向旋转的工况,避免了只能单向旋转的柱面气膜界面结构的局限,提高了适应范围。本文提出双向旋转的柱面气膜密封界面结构,以倒斜T字型和双层斜槽型柱面气膜为研究对象,采用有限元方法在VC平台上进行自主程序的开发,开发了气膜压力及稳态特性数值计算程序,并计算分析了动态特性。采用基于遗传思想的粒子群多维优化(GAPSO)算法对槽型结构进行多维参数优化,实现气膜密封系统优良密封特性。
1 理论分析 1.1 密封气膜数理模型 柱面气膜密封简化的密封模型如图 1所示。图中:θ为柱坐标θ向坐标维;z为柱坐标z向坐标维;ω为角速度;r为旋转坐标系径向;t为时间;φ为偏位角;Ob为密封环几何中心;Oj为动环几何中心;e为偏心距。密封系统主要包括密封动环(转子)、密封气膜、密封环(浮环)和支撑部分。密封环通过柔性支撑连接在固定结构(箱体或机匣)上,其内表面设计特殊的槽型结构,工作过程中通过转子高速旋转使得转子轴颈和密封环之间产生动压密封气膜,避免了密封副表面之间的直接接触,实现了良好的密封效果。本文提出2种适应双向旋转的柱面密封结构,图 2为倒斜T字型和双层斜槽型界面结构的展开图。
 |
| 图 1 坐标系中的简化密封模型及几何关系 Fig. 1 Simplified seal model and geometric relations in coordinate system |
| 图选项 |
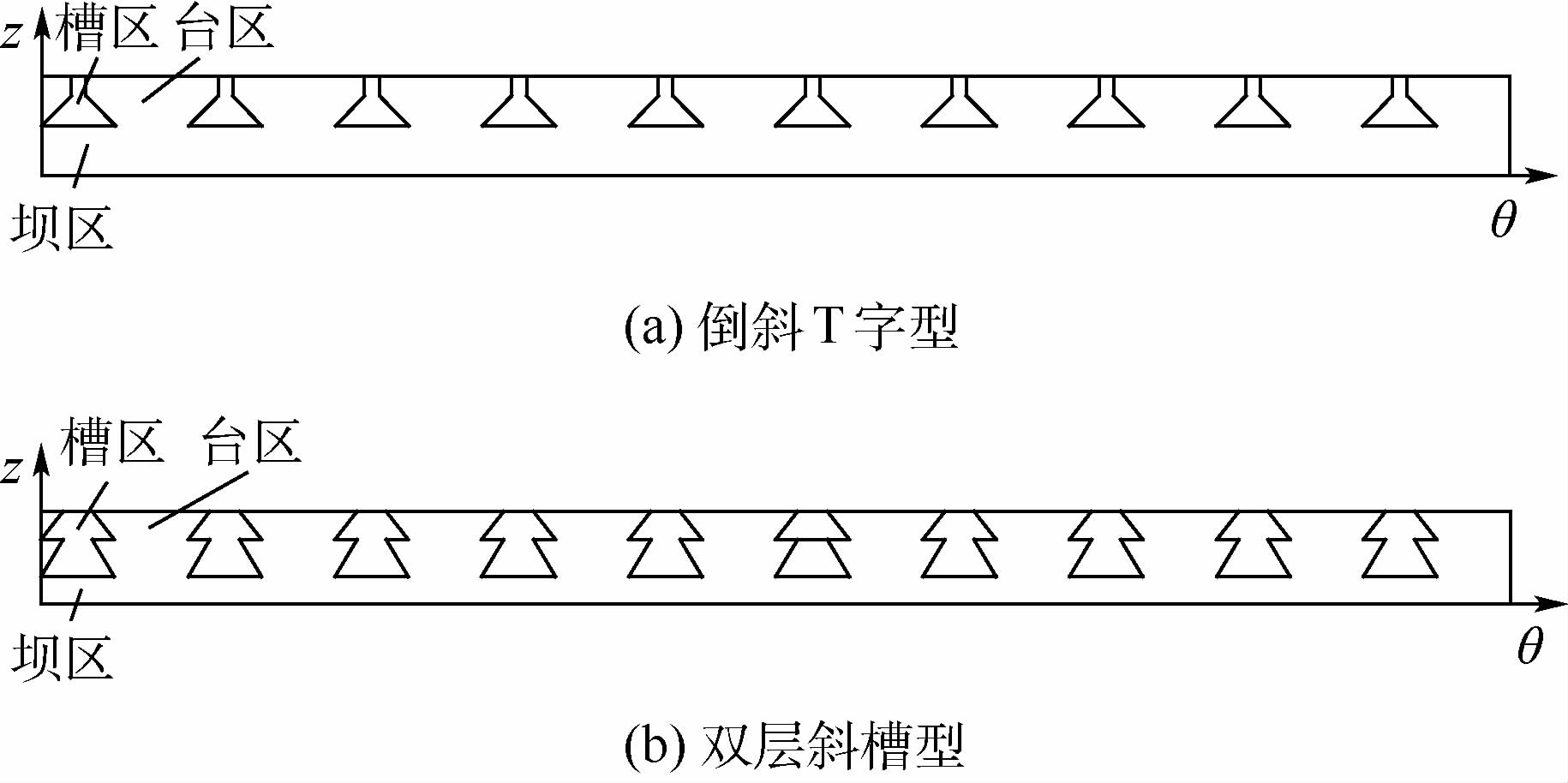 |
| 图 2 倒斜T字型和双层斜槽型界面展开图 Fig. 2 Interface expansion plan of inverted T type and double-groove type |
| 图选项 |
描述柱面密封气膜压力,双柱面旋转较广义的雷诺方程为[12]
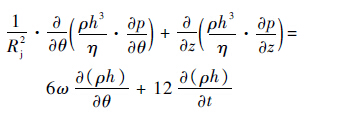 | (1) |
式中:h为膜厚;p为气膜压力;Rj为转子半径;η为气膜黏度;ρ为气膜密度。
1.2 柱面气膜稳态压力微分方程 在旋转坐标系中,不带节流孔的二维柱面坐标稳态压力场方程可由式(1)得到[12]:
 | (2) |
采用无量纲化后的雷诺方程为
 | (3) |
式中:Λ为可压缩数,

稳态膜厚h为
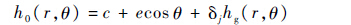 | (4) |
式中:δj为Kronecker数,在有凹凸垫或槽处为1,无凹凸垫或槽处为0;hg(r,θ)为界面凹凸垫或槽引起的稳态膜厚变化(当界面上有槽处,表示增大了稳态膜厚,相应增加量为hg(r,θ))。
求解气膜控制方程采用对复杂结构适应性较强的有限元方法。相关有限元分析模型的建立、数值计算过程和数值算法在文献[12]中已介绍,篇幅所限,且思路相同,本文只进行简要叙述。
2 有限元方法数值计算 2.1 伽辽金法建立变分方程 采用有限元方法进行压力场的数值计算分析。基于微分方程等效积分提法的加权余量思想,使用伽辽金法对柱面气膜压力微分方程改造得到其等效积分形式,将式(3)用伽辽金法建立变分方程:
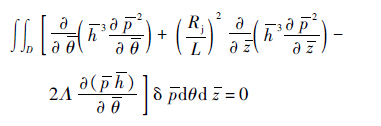 | (5) |
2.2 变分方程的离散求解 1) 解域离散
在解域上进行有限元分割时注意:① 利用周期性将展开的平面代替圆柱解域;② 槽台界限落在单元网格边界上;③ 节点编号顺序,轴向(宽度)优先;④ 分区域划分网格,不同区域设置不同的网格参数,以利于提高计算效率。图 3为以倒斜T字型界面结构为例的网格划分结果。
 |
| 图 3 倒斜T字型网格划分与节点编号 Fig. 3 Mesh generation and node number of inverted T type |
| 图选项 |
2) 方程离散求解
使用伽辽金法对柱面气膜压力微分方程改造得到其等效积分形式,进而得到更利于使用的弱形式而建立起单元刚度矩阵,组集为整体压力场方程组,引入对应的边界条件,确定压力场分布的数值解(具体求解过程见文献[12])。
2.3 气膜的密封特性 1) 气膜的稳态密封特性[12]
气膜反力:
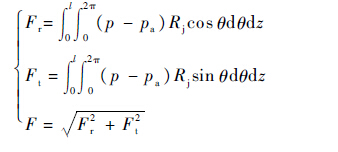 | (6) |
式中:l为柱面密封长度。
无量纲形式:
 | (7) |
密封泄漏量:
 | (8) |
无量纲形式:
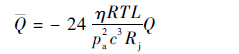 | (9) |
式中:T为绝对温度;R为气体常数。
摩擦转矩:
 | (10) |
无量纲形式:
 | (11) |
气膜刚度系数:
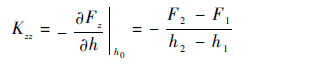 | (12) |
式中:F2为气膜反力2;F1为气膜反力1;h2为偏心距2;h1为偏心距1。
无量纲形式:
 | (13) |
2) 气膜的动态密封特性
在稳态特性计算的基础上,进行动态特性分析。动态刚度系数与动态阻尼系数为[12]
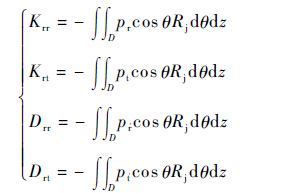 | (14) |
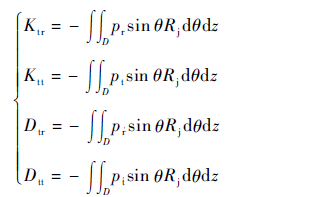 | (15) |
式中:pr、pt为密封气膜对应单位扰动位移的微扰压力。
以有限元分析为基础,在VC平台上自主开发数值计算分析程序,进行气膜稳态特性和动态特性系数的计算。
3 仿真计算及算例验证 3.1 仿真分析方法 选择倒斜T字型结构进行仿真计算。
图 4为在Gambit软件中建立的倒斜T字型柱面密封气膜的数值模型。
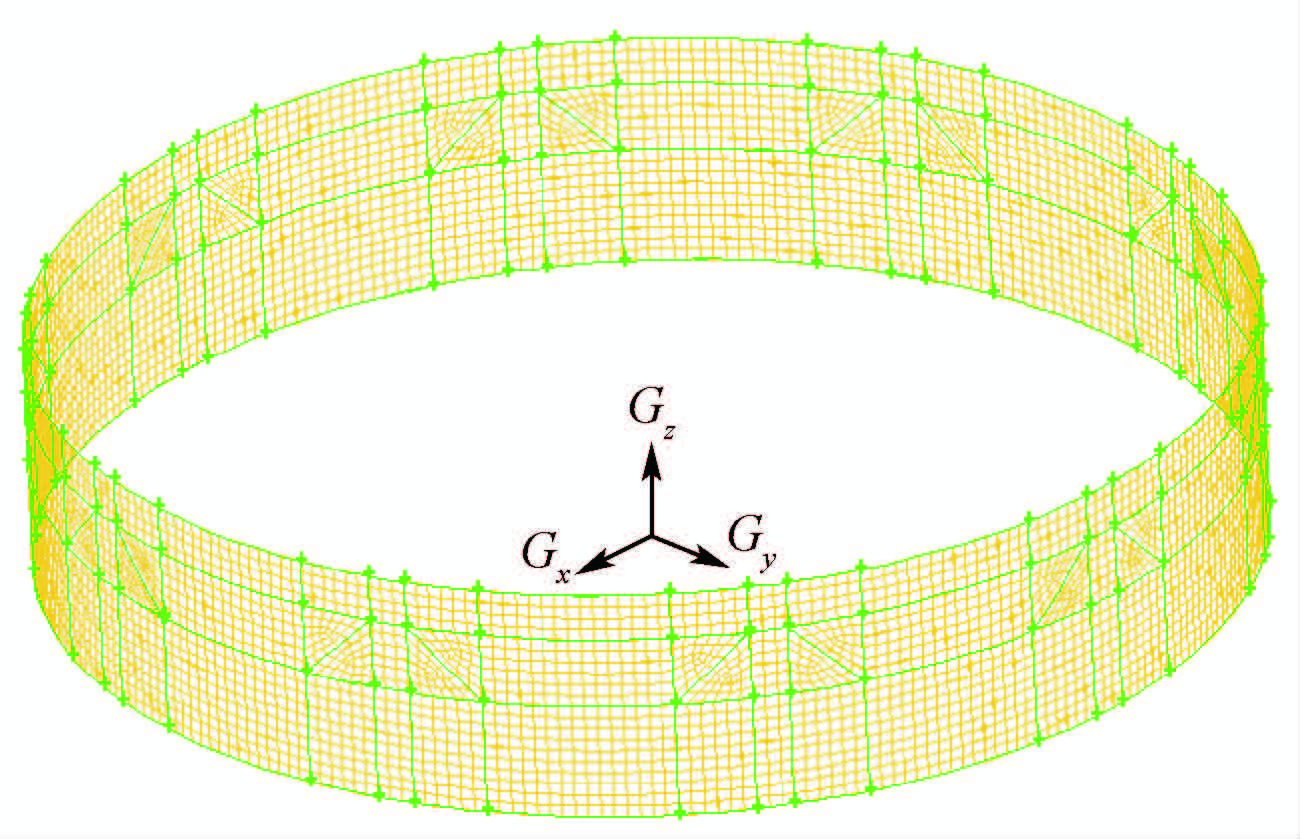 |
| 图 4 Gambit建立模型 Fig. 4 Model in Gambit |
| 图选项 |
将数值分析模型导入FLUENT,进行气膜压力场的仿真求解计算[15]。
3.2 仿真结果 计算参数如表 1时,仿真结果如图 5所示。
表 1 计算参数 Table 1 Calculated parameters
| 参数 | 数值 |
| 转子半径Rj/mm | 50 |
| 密封环轴向宽度L/mm | 20 |
| 平均膜厚c/μm | 10 |
| 槽数 | 10 |
| 偏心率 | 0.5 |
| 1槽宽比pb1 | 0.1 |
| 1槽长比pl1 | 0.2 |
| 2槽长比pl2 | 0.3 |
| 1槽深比pd1 | 2.0 |
| 2槽深比pd2 | 2.0 |
| 2槽宽比pb2 | 0.5 |
| 上游压力Ph/ MPa | 0.3 |
| 下游压力Pl/MPa | 0.1 |
| 角速度ω/(r·min-1) | 20000 |
| 绝对温度T / ℃ | 20 |
| 密封气体 | 空气 |
表选项
 |
| 图 5 总压云图 Fig. 5 Total pressure contours |
| 图选项 |
3.3 对比验证 进行不同膜厚及转速下VC平台上自主开发程序结果与仿真结果的对比验证。图 6为倒斜T字型平均膜厚为10μm和6μm时,气膜反力随转速的变化情况。程序结果与仿真结果相当接近,变化趋势也一致,表明了本文程序倒斜T字型槽柱面气膜密封系统稳态特性的计算分析可信。
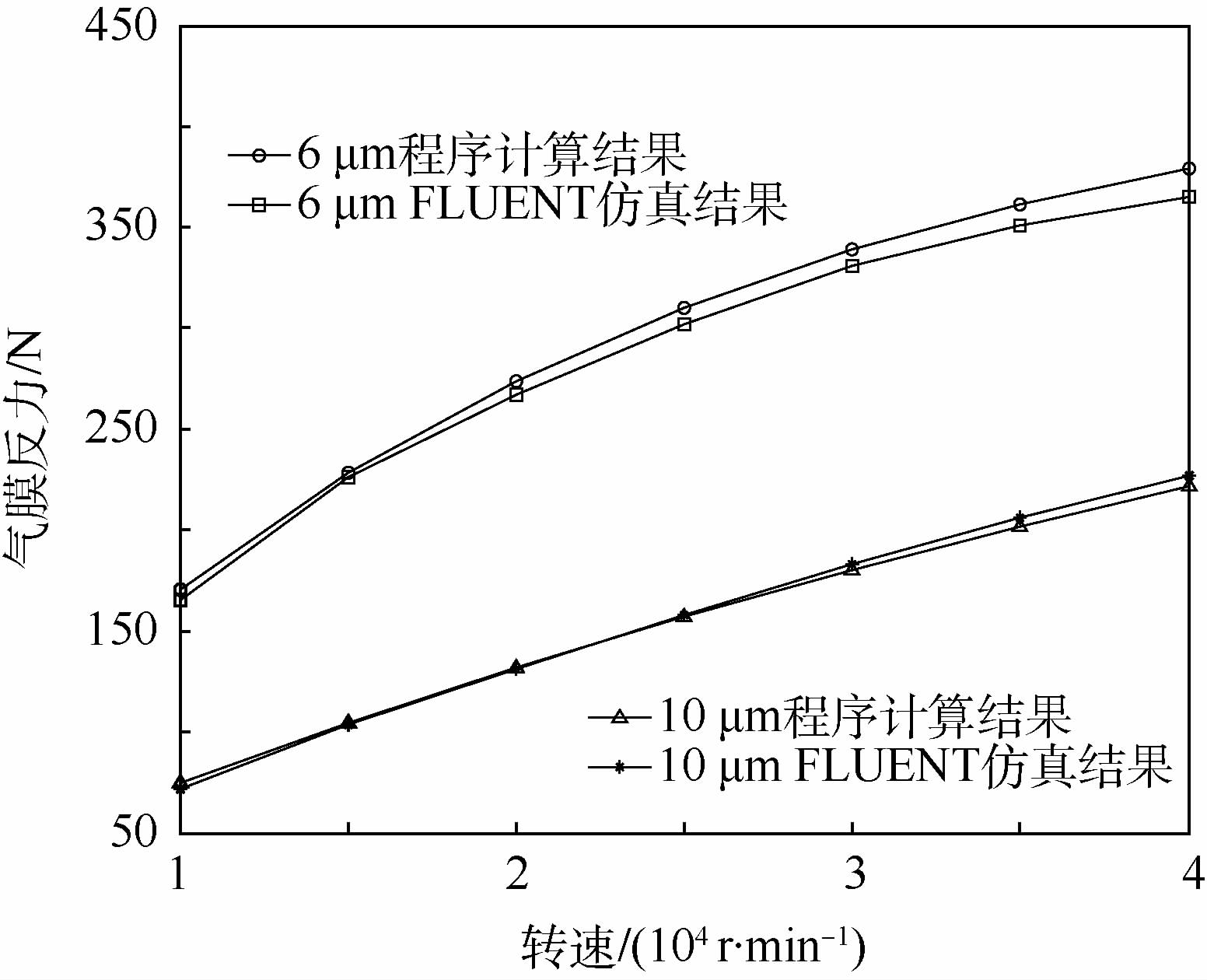 |
| 图 6 气膜反力程序结果与仿真结果对比 Fig. 6 Program results of gas film counter-force compared with simulation results |
| 图选项 |
将膜厚最小处槽、台、坝交界点标记为点1,与其处于同一轴线并且与高压端边界相邻的点标记为点2。进行VC平台上自主开发程序结果与仿真结果对比与误差计算,误差在可接受范围以内,说明了程序的可行性,对比结果如表 2所示。
表 2 代表性节点压力值比较及误差计算 Table 2 Pressure comparison and error calculation of representative nodes
| 转速/(r·min-1) | 膜厚/μm | 点 | 节点压力/MPa | 误差/% | |
| 程序 | 仿真 | ||||
| 15000 | 10 | 1 | 0.41 | 0.43 | 4.88 |
| 15000 | 10 | 2 | 0.33 | 0.34 | 3.03 |
| 15000 | 6 | 1 | 0.60 | 0.63 | 5.00 |
| 15000 | 6 | 2 | 0.36 | 0.35 | 2.78 |
| 25000 | 10 | 1 | 0.49 | 0.51 | 4.08 |
| 25000 | 10 | 2 | 0.35 | 0.36 | 2.87 |
| 25000 | 6 | 1 | 0.73 | 0.76 | 4.11 |
| 25000 | 6 | 2 | 0.42 | 0.43 | 2.38 |
表选项
4 2种界面结构气膜密封性能比较 进行倒斜T字型与双层斜槽型柱面气膜密封系统的稳态特性比较时,计算参数如表 3所示。
表 3 稳态特性比较的计算参数 Table 3 Calculated parameters of comparison of steady state characteristics
| 参数 | 数值 |
| 转子半径Rj/mm | 50 |
| 密封环轴向宽度L/mm | 20 |
| 平均厚膜c/μm | 10 |
| 槽数 | 10 |
| 偏心率 | 0.4 |
| 1槽宽比pb1 | 0.2 |
| 1槽长比pl1 | 0.3 |
| 2槽长比pl2 | 0.4 |
| 1槽深比pd1 | 2.0 |
| 2槽深比pd2 | 2.0 |
| 2槽宽比pb2 | 0.5 |
| 上游压力Ph/ MPa | 0.601325 |
| 下游压力Pl/ MPa | 0.101325 |
| 角速度ω/(r·min-1) | 20000 |
| 绝对温度T / ℃ | 20 |
表选项
4.1 稳态特性的比较 1) 气膜稳态特性随转速的变化
图 7为倒斜T字型与双层斜槽型界面结构的气膜反力、泄漏量、摩擦转矩和静态刚度系数随转速变化的曲线。
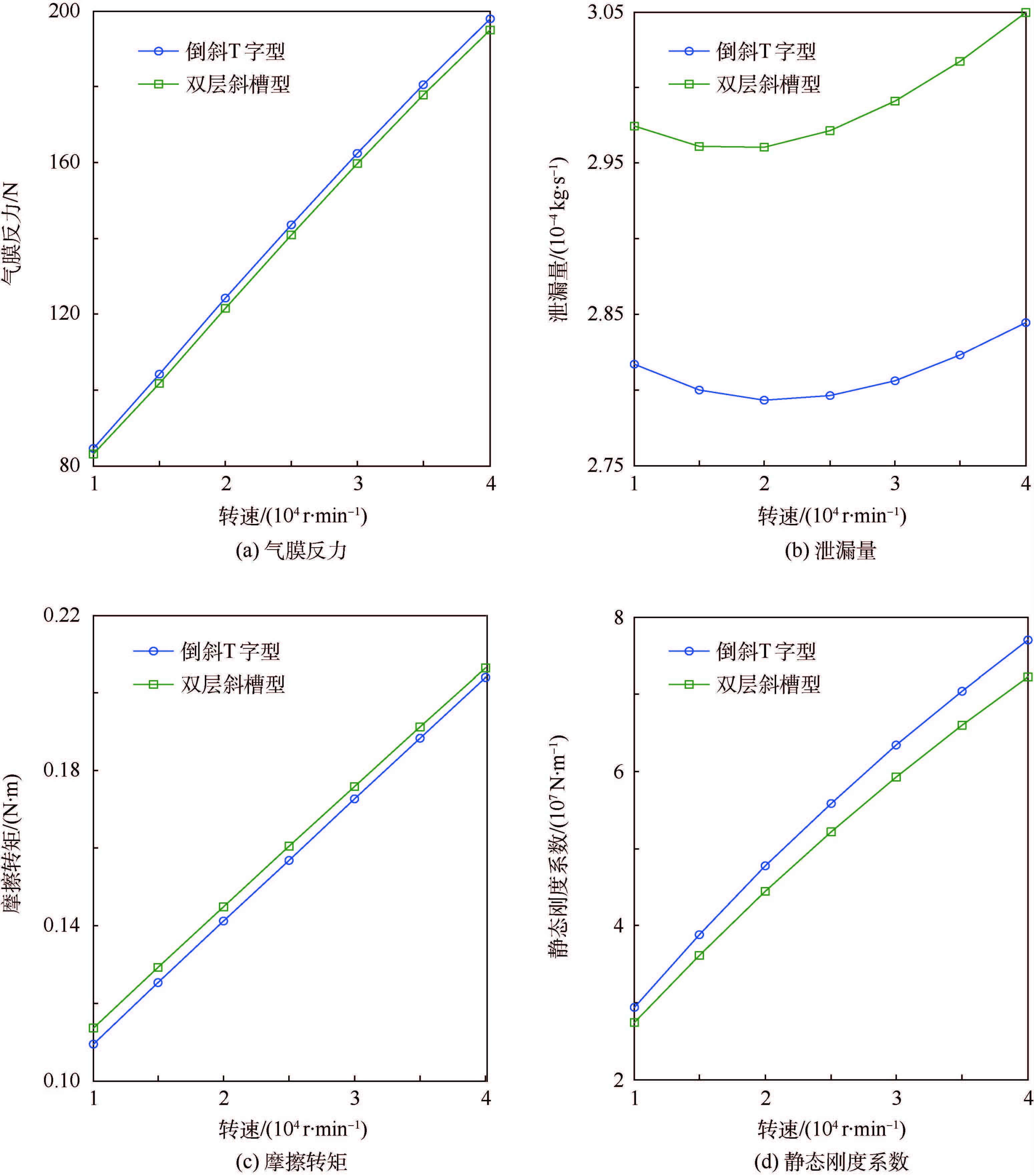 |
| 图 7 不同转速下稳态特性的比较 Fig. 7 Comparison of steady state characteristics under different rotational speeds |
| 图选项 |
由图 7的计算结果可以看出,随着转速的增大,2种界面结构的气膜反力逐渐增大,泄漏量先减小后增大,摩擦转矩逐渐增大,静态刚度系数逐渐增大;相同条件下,气膜反力和静态刚度系数为倒斜T字型大于双层斜槽型,泄漏量和摩擦转矩为倒斜T字型小于双层斜槽型。
2) 气膜稳态特性随平均膜厚的变化
平均膜厚是一个重要的设计参数。图 8为倒斜T字型与双层斜槽型界面结构的气膜反力、泄漏量、摩擦转矩和静态刚度系数随平均膜厚变化的曲线。
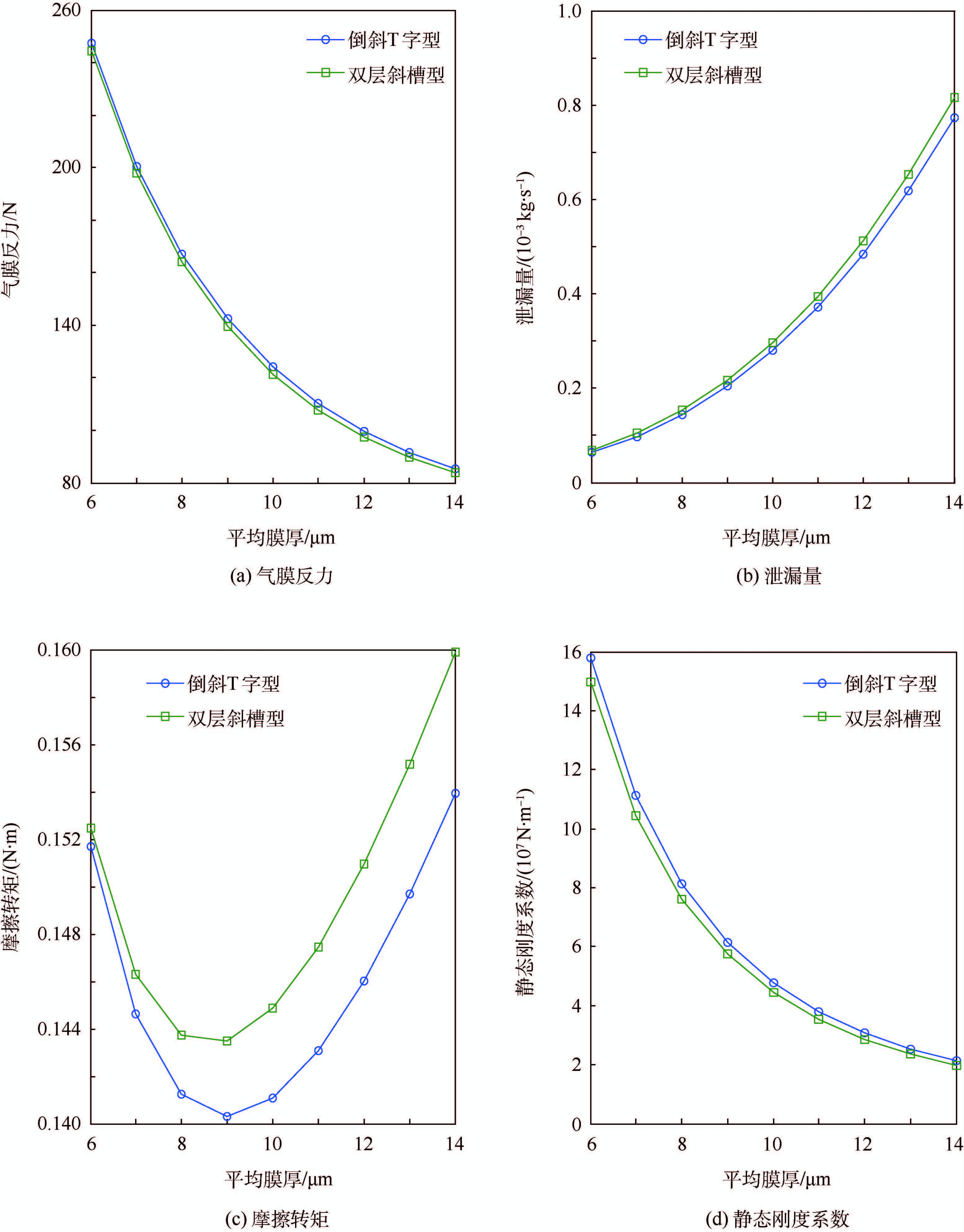 |
| 图 8 不同平均膜厚下稳态特性的比较 Fig. 8 Comparison of steady state characteristics under different average film thickness |
| 图选项 |
由图 8可以看出,随着平均膜厚增大,2种界面结构的气膜反力逐渐减小,泄漏量逐渐增大,摩擦转矩先减小后增大,静态刚度系数逐渐增小;相同条件下,气膜反力和静态刚度系数为倒斜T字型大于双层斜槽型,泄漏量和摩擦转矩为倒斜T字型小于双层斜槽型。
4.2 动态特性的比较 1) 气膜动态刚度系数随转速的变化
图 9为2种界面结构动态刚度系数随转速变化的曲线。随着转速的增大,正向刚度系数Krr、Ktt与交叉刚度系数Krt逐渐增大,交叉刚度系数Ktr逐渐减小。相同参数下,Krr、Krt为倒斜T字型大于双层斜槽型,Ktr、Ktt为倒斜T字型小于双层斜槽型。
 |
| 图 9 不同转速下气膜动态刚度系数比较 Fig. 9 Comparison of dynamic stiffness coefficients of gas film under different rotational speeds |
| 图选项 |
2) 气膜动态阻尼系数随转速的变化
图 10为2种界面结构的动态阻尼系数随转速变化的曲线。随着转速的增大,正向阻尼系数Drr、Dtt与交叉阻尼系数Drt逐渐减小,交叉阻尼系数Dtr先增大后减小。相同参数下,Drr、Dtt、Dtr为倒斜T字型大于双层斜槽型,Drt为倒斜T字型小于双层斜槽型。
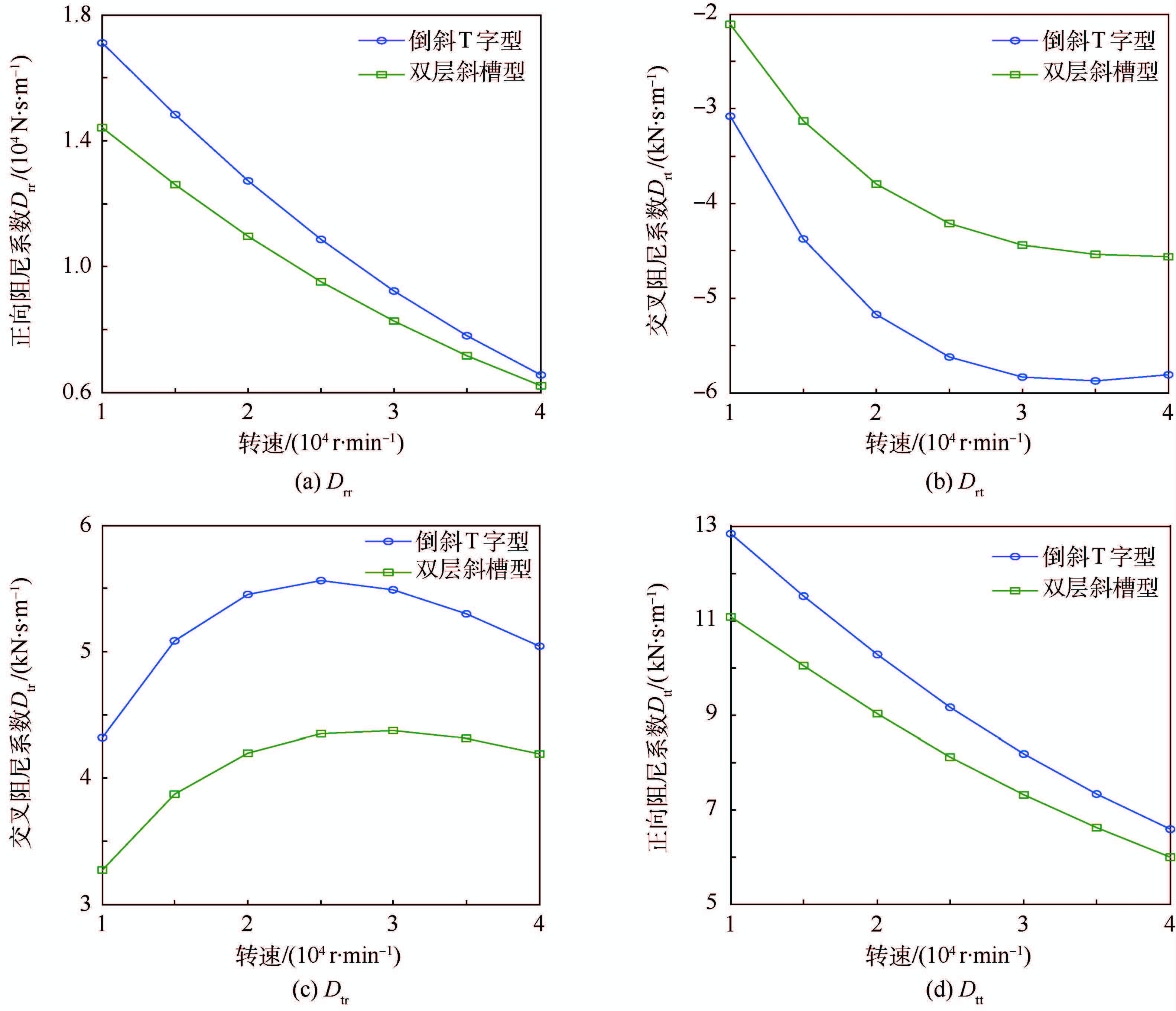 |
| 图 10 不同转速下气膜动态阻尼系数比较 Fig. 10 Comparison of dynamic damping coefficients of gas film under different rotational speeds |
| 图选项 |
5 GAPSO算法多维参数优化 5.1 粒子群优化算法与遗传算法结合 气膜密封系统优良密封特性的实现,首先取决于密封界面的结构,发挥特定界面结构型式优势,需要综合考虑密封界面几何参数。描述槽型几何特征的参数众多,而且具有相关性,气膜密封设计的参数优化是一个非线性、多参数和多目标优化的问题。
利用粒子群优化算法与遗传算法结合,实现柱面气膜密封界面槽形参数的多维优化。本文将各槽型参数pb1、pl1、pl2、pd1、pb2作为设计变量,对密封界面结构参数进行多维优化。
建立GAPSO的优化模型:
Xi=[pb1,pl1,pl2,pd1,pb2]iT
max F(X)
s.t. Xmin<X<Xmax
2种目标函数F(X):① 气膜反力;② 气膜反力与泄漏量的比值。
GAPSO算法流程图如图 11所示(详细过程见文献[16-17])。
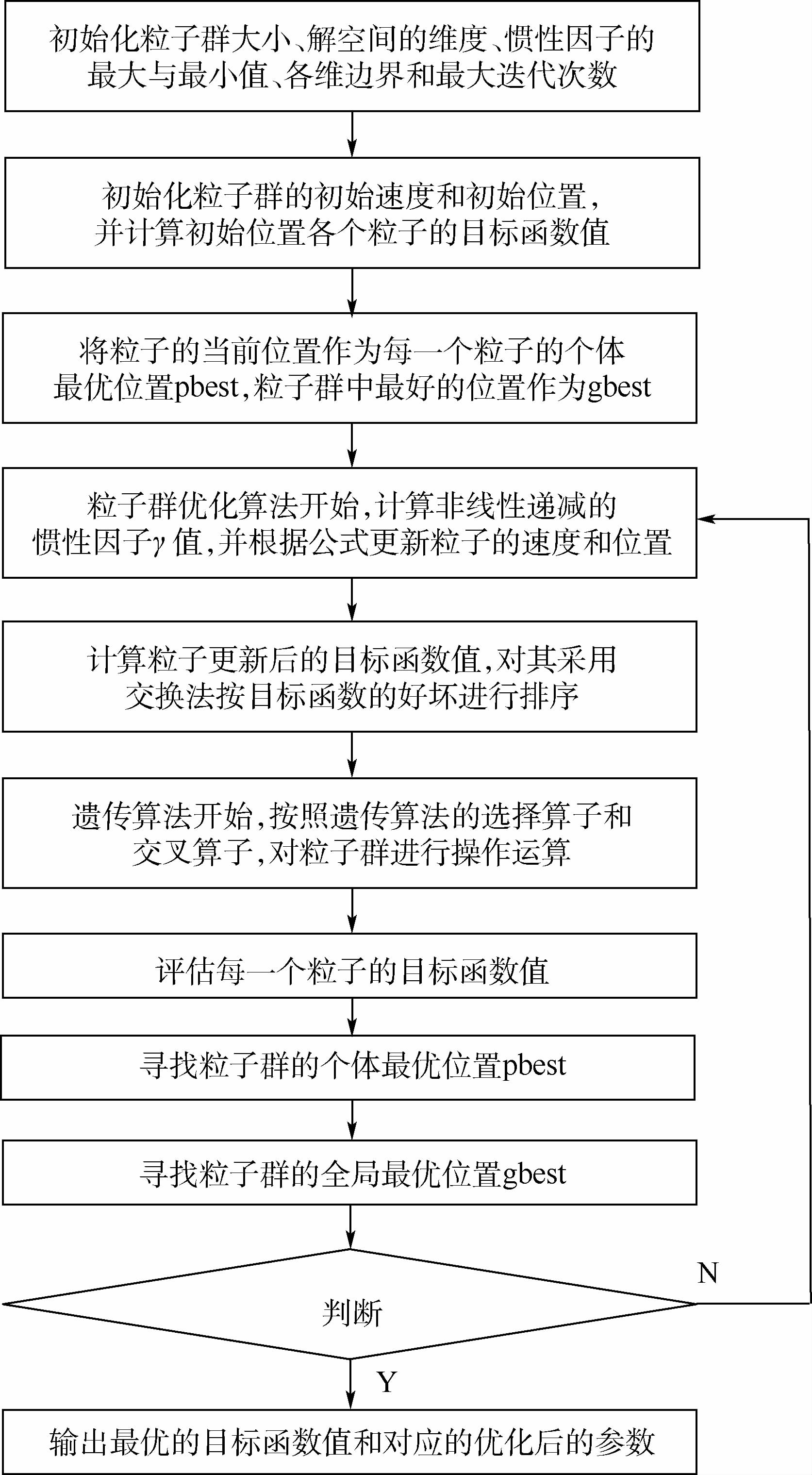 |
| 图 11 GAPSO算法流程图 Fig. 11 Flowchart of GAPSO algorithm |
| 图选项 |
5.2 界面结构参数有无优化的对比 转速不同时利用GAPSO算法对倒斜T字型进行多维优化,优化目标选为气膜反力,结果见图 12。在不同转速下,界面结构参数优化结果不同,表 4为转速为2×104r/min时的优化结果。
 |
| 图 12 气膜反力优化对比 Fig. 12 Comparison of gas film counter-force optimization |
| 图选项 |
表 4 转速为2×104r/min时的优化结果 Table 4 Rotating speed at 2×104r/min optimization results
| 参数 | 初始值 | 优化结果 |
| 1槽宽比pb1 | 0.2 | 0.176706 |
| 1槽长比pl1 | 0.3 | 0.449489 |
| 2槽长比pl2 | 0.4 | 0.448237 |
| 1槽深比pd1 | 2.0 | 3.066440 |
| 2槽宽比pb2 | 0.5 | 0.930887 |
| 目标函数/N | 124.121 | 150.857 |
表选项
平均膜厚不同时,利用GAPSO算法对双层斜槽型进行多维优化,优化目标选为气膜反力与泄漏量的比值,结果见图 13。在不同平均膜厚下,界面结构参数优化结果不同,表 5为平均膜厚为9μm时的优化结果。
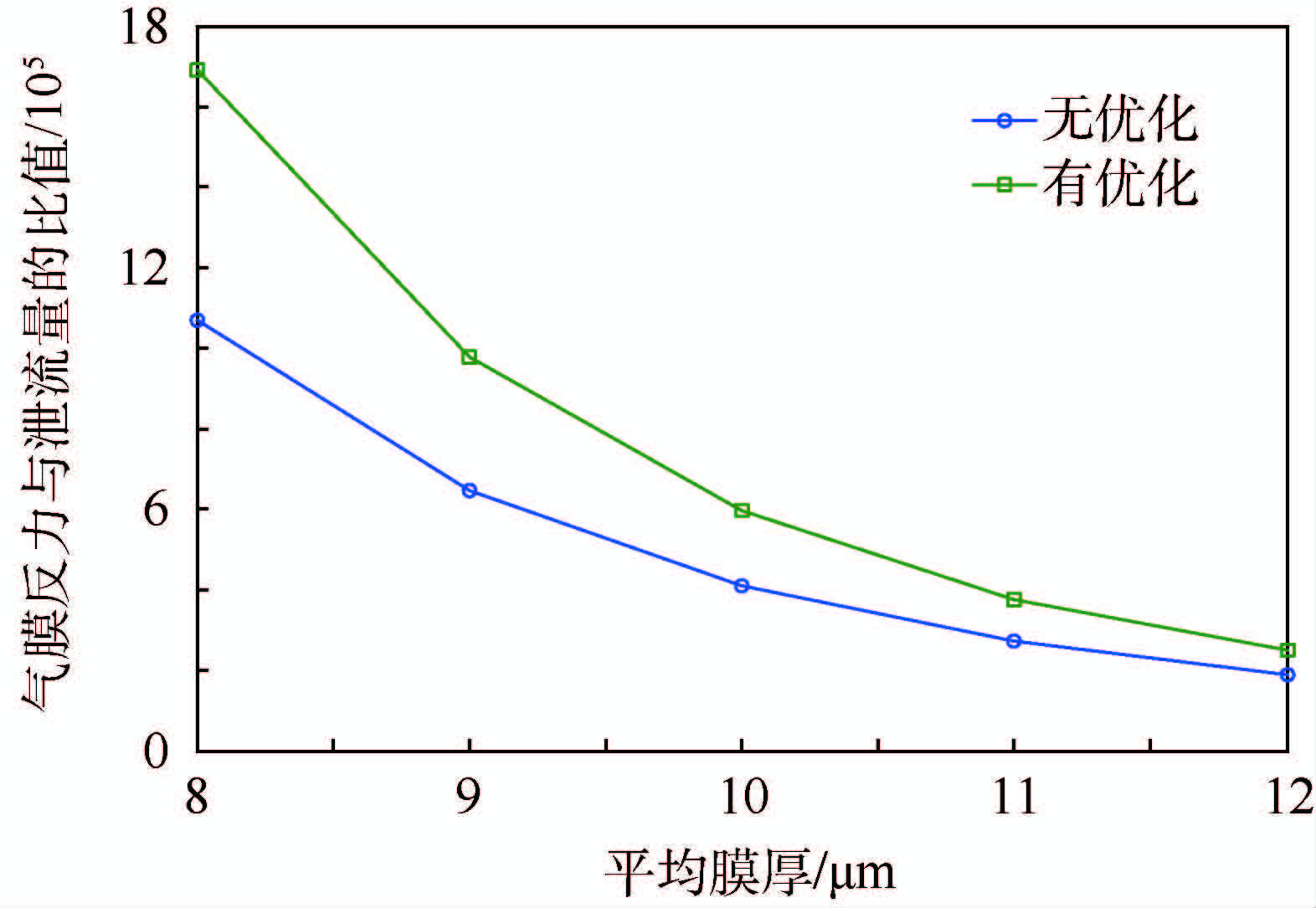 |
| 图 13 气膜反力与泄漏量的比值优化对比 Fig. 13 Comparison of ratio optimization of gas film counter-force and leakage |
| 图选项 |
表 5 平均膜厚为9μm时的优化结果 Table 5 Average film thickness at 9μm optimization results
| 参数 | 初始值 | 优化结果 |
| 1槽宽比pb1 | 0.2 | 0.151854 |
| 1槽长比pl1 | 0.3 | 0.419608 |
| 2槽长比pl2 | 0.4 | 0.263190 |
| 1槽深比pd1 | 2.0 | 1.150060 |
| 2槽宽比pb2 | 0.5 | 0.500367 |
| 目标函数 | 645031.54 | 979997.00 |
表选项
6 结 论 1) 建立了双向旋转倒斜T字型与双层斜槽型柱面气膜密封系统密封气膜的数理模型和基于有限元方法的密封气膜数值分析模型。
2) 在VC平台上开发了基于有限元计算的密封气膜压力分布、密封系统稳态特性与动态特性的计算分析程序。动态特性数值计算的实现突破了目前商业软件在进行动态特性分析的局限。
3) 在Gambit中建立了不同平均膜厚下倒斜T字型柱面气膜的物理模型和有限元分析模型,通过FLUENT进行了密封气膜特性数值仿真,商用软件仿真结果与自主开发程序数值计算结果对比一致性好,验证了开发程序的正确性。
4) 计算分析了转速与平均膜厚对密封特性的影响,对比了相同参数下2种界面结构的密封特性。从稳态特性和动态特性看,倒斜T字型的性能均优于双层斜槽型。
5) 计算对比了2种界面结构有无多维优化的密封特性。通过GAPSO算法进行多维优化可以有效提高密封特性。
参考文献
| [1] | 马纲, 栗秀花, 沈心敏, 等. 柱面气膜密封界面结构与性能分析[J].航空动力学报, 2011, 26(11): 10–16.MA G, LI X H, SHEN X M, et al. Analysis of performance and interface structure of cylinder gas film seal[J].Journal of Aerospace Power, 2011, 26(11): 10–16.(in Chinese) |
| [2] | KOWALSKI C A, BASU P. Reverse rotation capability of spiral-groove gas face seals[J].Tribology Transactions, 1995, 38(3): 549–556.DOI:10.1080/10402009508983441 |
| [3] | YANG P, ZHU K Q, WANG X L. On the non-linear stability of self-acting gas journal bearings[J].Tribology International, 2009, 42(1): 71–76.DOI:10.1016/j.triboint.2008.05.007 |
| [4] | NOSOWICZ J, ZEUS D. A bi-directional gas face seal experience under test conditions and in practical use[J].Lubrication Engineering, 1993, 49(3): 217–221. |
| [5] | GOLD SWAIN I M.Mechanical face seals:EP,US 5375855 A[P].1994-12-27. |
| [6] | 赵亚萍. 双向干气密封的研制情况及技术分析[J].流体机械, 1996, 24(4): 46–47.ZHAO Y P. Development situation of two way dry gas seal and technical analysis[J].Journal of Fluid Mechanics, 1996, 24(4): 46–47.(in Chinese) |
| [7] | 郝木明. 机械密封技术及应用[M].北京: 中国石化出版社, 2010: 80.HAO M M. Mechanical seal technology and its application[M].Beijing: China Petrochemical Press, 2010: 80.(in Chinese) |
| [8] | SALEHI M, HESHMAT H. Performance of a complaint foil seals in a small gas turbine engine simulator employing a hybrid foil/ball bearing support system[J].Tribology Transactions, 2001, 44(3): 458–464.DOI:10.1080/10402000108982481 |
| [9] | SAYMA A I, BREARD C, VAHDATI M, et al. Aerolasticity analysis of air-riding seals for aero-engine applications[J].Journal of Tribology-Transactions of the ASME, 2002, 124(3): 607–616.DOI:10.1115/1.1467086 |
| [10] | SHAPIRO W.Numerical,analytical,experimental study of fluid dynamic forces in seals:NASA/CR 2004-213199/VOL2[R].Latham,NY:Mechanical Technology,Inc.,2004.http://cn.bing.com/academic/profile?id=1637191042&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | WALOWIT J,SHAPIRO W.Numerical,analytical,experimental study of fluid dynamic forces in seals:NASA/CR2004-213199/VOL3[R].Latham,NY:Mechanical Technology,Inc.,2004.http://cn.bing.com/academic/profile?id=844769531&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | 马纲, 席平, 沈心敏, 等. 柔性支承浮环柱面气膜密封准动态特性分析[J].航空动力学报, 2010, 25(5): 1190–1196.MA G, XI P, SHEN X M, et al. Analysis of quasi-dynamic characteristics of compliant floating ring gas cylinder seal[J].Journal of Aerospace Power, 2010, 25(5): 1190–1196.(in Chinese) |
| [13] | LIU Y C, SHEN X M, XU W F. Numerical analysis of dynamic coefficients for gas film face seals[J].Journal of Tribology-Transaction of the ASME, 2002, 124(4): 743–754.DOI:10.1115/1.1472459 |
| [14] | GREEN I, BARNSBY R M. A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting gas face seals[J].Journal of Tribology-Transactions of the ASME, 2001, 123(2): 388–394.DOI:10.1115/1.1308020 |
| [15] | 马纲, 孙晓军, 罗先海, 等. 端柱面组合密封气膜稳态特性仿真数值分析[J].北京航空航天大学学报, 2014, 40(4): 439–443.MA G, SUN X J, LUO X H, et al. Simulation numerical analysis of steady-state properties of gas face and cylinder film seal[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(4): 439–443.(in Chinese) |
| [16] | 陈贵敏, 贾建援, 韩琪. 粒子群优化算法的惯性权值递减策略研究研究[M].西安: 西安交通大学出版社, 2002: 70.CHEN G M, JIA J Y, HAN Q. Research on the strategy of decreasing inertia weight in particle swarm optimization algorithm[M].Xi'an: Xi'an Jiaotong University Press, 2002: 70.(in Chinese) |
| [17] | 曹春红, 张永坚, 李文辉. 杂交粒子群算法在工程几何约束求解中的应用[J].仪器仪表学报, 2004, 25(4): 397–400.CAO C H, ZHANG Y J, LI W H. Applications of hybrid particle swarm optimization in engineering geometric constraint solving[J].Chinese Journal of Scientific Instrument, 2004, 25(4): 397–400.(in Chinese) |
