管道应力研究方面,吴晓南等[3]对压力测试环境下的输气管道进行了应力分析,研究了管道应力的分布及其敏感截面位置。Xia等[4]分析了因地质灾害而出现悬浮的管道在不同长度时的应力分布。Xiao等[5]建立了热油管道应力分析模型,分析了压力的变化对管道应力的影响。但上述研究都只是静态应力分析,忽略了基础振动的影响,而对工作在振动环境下的管道,管道在各时间点的振动形态都不一样,仅求出管道静态应力的分布和最大应力点,不能全面反映管道整个运行过程中的应力幅值及易发生破坏的位置。
管道设计研究方面,耿艳辉和詹晨菲[6]对大长液压管道的特殊设计进行了探讨,提出了内径和厚度的设计方法,并对管道耐压进行了校核计算。朱博[7]在管道通径的选择计算、布管原则及装配等方面进行了分析。Svedeman和Arnold[8]改进了冲蚀与腐蚀运行环境下多相流管道设计准则。美国动力管道标准[9]规定了不同温度范围下不同材料和类型的管道的许用应力值。但现有文献都只给出了管道失效的判据条件,没有进一步给出不同工况和载荷下管道结构参数设计的具体方法和步骤,也没有考虑基础振动对管道的影响。
针对传统液压管道设计是根据流量和压力选择内径和厚度,仅靠经验选择管道固支间距的局限性,本文基于应力分析提出以流量-压力-强振动为依据的TBM抗振结构设计方法,保证基础振动下的管道工作正常可靠,能为在强振动环境下工作的TBM管道抗振结构设计提供一定的指导。
1 横向振动下输液管道数学模型 截取掘进机上一段两端固定支撑的输液管道,不考虑相邻的固支管道对它产生的影响,输液管道模型简化为图 1所示。
 |
| 图 1 管道理论模型 Fig. 1 Theoretical model of pipe |
| 图选项 |
两端固定在TBM支座上的黏弹性液压管道[10],其支座在简谐激励W=N1sin (ωt) 的作用下上下振动,N1为基础振动的幅值,ω为基础振动的频率。
输液管道的横向变形会引起管道在轴向方向的拉伸,导致管道产生附加轴向力[11],根据牛顿定理和达朗伯原理,可得两端固支的输液管道在横向(y方向) 基础振动下的运动微分方程为
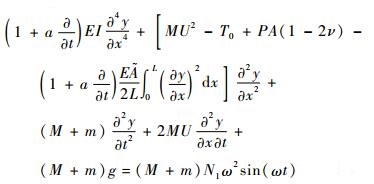 | (1) |
式中:a为管道黏弹性系数;t为时间;y为管道横向振动时的变形,且,y<<L为管道固支长度;x为管道截面的位置坐标;EI为管道抗弯刚度,E为管道弹性模量,I为管道截面惯性矩;M为单位长度流体质量;U为流体流速;T0为初始位置轴向力; P为流体压强;A为管道过流截面积;ν为管道泊松比;
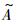
1.1 方程的无量纲化 为简化方程,使得方程求解方便,引入以下无量纲化的参数:


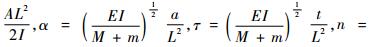
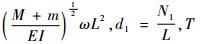
将方程(1) 化为无量纲形式:
 | (2) |
1.2 方程的离散化 运用Galerkin方法将方程(2) 离散化处理[12],令
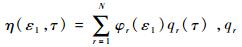
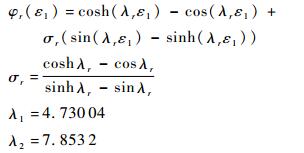 |
因为前两阶振型即可满足精度要求[13],故取前两阶分析:
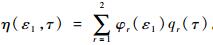
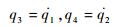
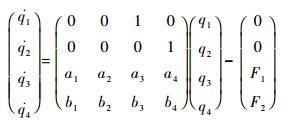 | (3) |
式中:
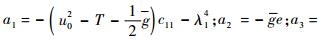
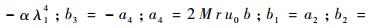
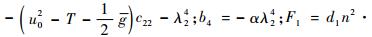

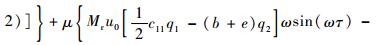
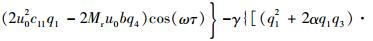
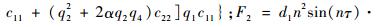
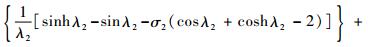

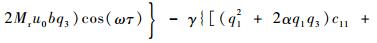
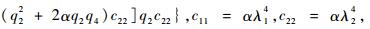
1.3 管道最大应力求解 对于TBM液压管道,在工作过程中受到的轴向应力最大,其由3种应力组成:第1类是因为加载在管道的内压产生的,第2类是由于管道弯曲变形产生的,即弯曲应力,第3类是因轴线变形而产生的附加轴向应力[11]。因此管道最大应力计算公式为
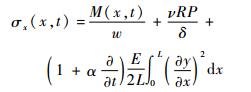 | (4) |
式中:M(x, t) 为作用在x截面上的弯矩; w为管道抗弯截面系数; R为管道外半径; δ为管道厚度。
采用等效弯矩法计算管道任意截面上的弯矩。由挠度计算公式:
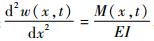
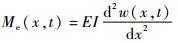
因此,x处截面轴向最大弯曲应力为
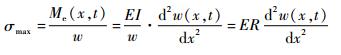 | (5) |
2 管道应力响应仿真及实验验证 2.1 应力响应仿真 根据TBM所处的工作环境,将支座做简谐运动的频率设定为40 Hz、幅值设定为1 mm[14],仿真其应力响应情况,表 1中列出了管道及流体的一些主要参数。
表 1 系统参数设置 Table 1 System parameter setting
| 参数 | 数值 |
| 壁厚/m | 0.004 |
| 管道内径/m | 0.05 |
| 管道弹性模量/GPa | 201 |
| 管道固支间距/m | 2 |
| 管材密度/(kg·m-3) | 7 985 |
| 管材泊松比 | 0.3 |
| 流体平均流速/(m·s-1) | 3 |
| 流体密度/(kg·m-3) | 890 |
表选项
图 2给出了2个典型时刻管道各截面位移、弯矩和最大应力分布。
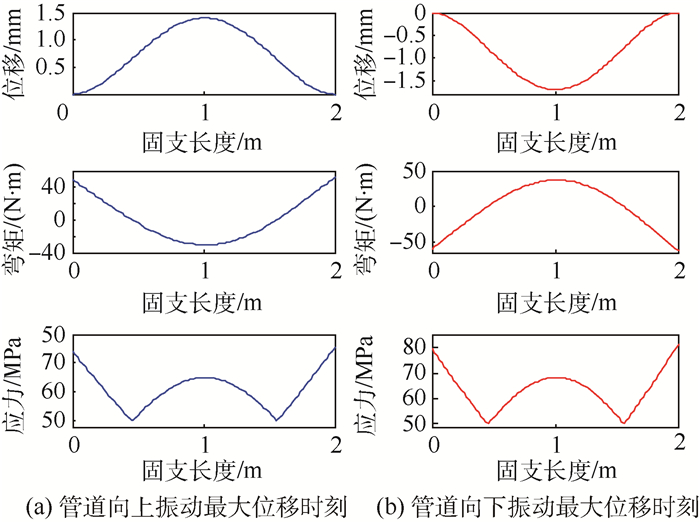 |
| 图 2 2个典型时刻管道位移、弯矩和最大应力的分布 Fig. 2 Displacement, bend moment and maximum stress distribution of pipe at two typical moments |
| 图选项 |
由图 2可知,管道在振动时,在与固定支撑连接处的弯矩绝对值和弯曲应力最大,将此处截面定义为应力敏感截面,即为易破坏位置,工程中液压管道因疲劳破坏而导致的爆管往往就发生在此处。而在应力敏感截面上,受弯曲应力和重力的影响,管道上边缘点为截面上的最大应力点。
上边缘点在不同基础振幅下的最大应力时域响应如图 3所示。
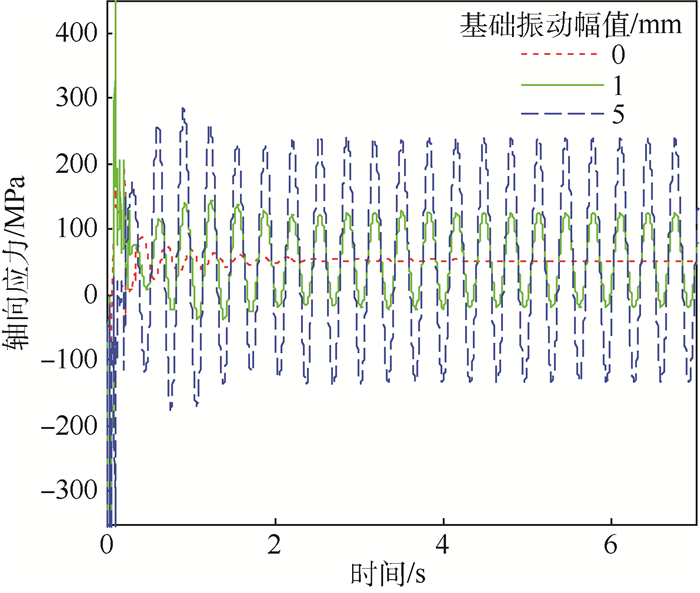 |
| 图 3 应力敏感截面上最大应力响应 Fig. 3 Maximum stress response of stress sensitive section |
| 图选项 |
图 3表明无基础振动存在时,管道仅受重力作用而轴向拉伸,管道最大应力恒定,有基础振动时,受弯曲应力周期变化的影响,最大应力点在稳定后应力响应呈现出等幅波动的情况,且基础振幅越大,管道振动越剧烈,其最大应力波动幅值越大。
2.2 实验验证 为证实本文所建立的横向基础振动下输液管道的数学模型以及管道应力的计算方法的正确性,设计搭建了横向基础振动下输液管道应变的测量平台,实验装置系统原理图如图 4所示。其主要由3部分组成:液压系统、MPA102型振动台激励系统和数据采集和分析系统(USB2821数据采集卡、YD-28A型动态电阻应变仪)。输液管道所需的工作压力及流量由液压泵源提供,管道的振动频率及幅值由实验系统中的激励调节装置来调节,管道应力敏感截面处上边缘应变大小可以通过DH5925动态信号测量仪器得到。
 |
| 1-油源开关;2-变量泵;3,13,17-单向阀;4-调速阀;5,12-电磁溢流阀;6-换向阀;7,15-电磁换向阀;8-液控单向阀;9-动力液压缸;10-惯性负载;11-加载液压缸;14-电磁减压阀;16-溢流阀;18-定量泵;19-过滤器。 图 4 实验系统液压原理图 Fig. 4 Hydraulic schematic diagram of experimental system |
| 图选项 |
实验时,设定振动台振动频率为250 Hz、幅值为0.5 mm,数据采集卡采样间隔为4.4 ms,得到应力敏感截面的上边缘点应变实验值如图 5所示。
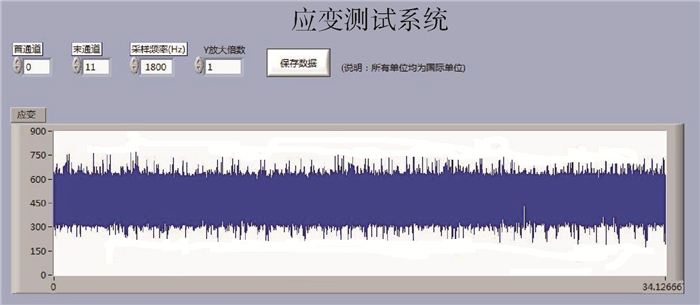 |
| 图 5 应变测试结果 Fig. 5 Strain test results |
| 图选项 |
考虑采集时的放大倍数、微电压和应变的关系以及应力与应变关系σ=Eε, 将测得的应变换算成应力,跟同条件下应力仿真值进行对比,结果如图 6所示。
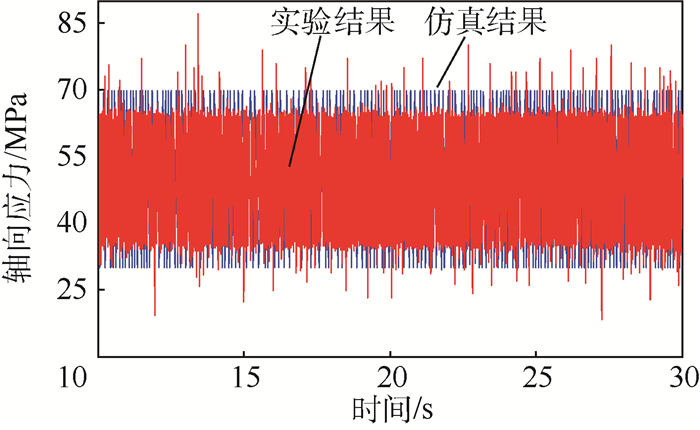 |
| 图 6 应力仿真曲线及与实验结果局部对比图 Fig. 6 Local contrast chart of stress simulation curves and experimental results |
| 图选项 |
图 6表明实验管道固定支撑端的实验应力结果和仿真结果曲线形态大致相同,仿真图中显示应力最大值为69.73 MPa,最小值为31.61 MPa,应力波动幅值为19.56 MPa,实验结果中波峰平均值为63.95 MPa,波谷平均值为29.83 MPa,波动幅值平均值为18.25 MPa,三者相对应的误差分别为8.29%、5.63%和6.70%,都在实验所容允的误差范围以内,验证了建立的输液管道在横向基础振动下的数学模型以及运用等效弯矩法求解管道应力的正确性,误差来源之一是仿真过程中没有考虑到外部阻尼以及轴向剪切力等对管道应力的影响,而且用等效弯矩法和Galerkin方法离散化近似处理方程本身存在误差,二是在于实验数据采集和处理过程中的干扰和误差。
3 管道抗振结构设计方法及实例应用 基于应力的管道设计准则为σmax < [σ],其中σmax为管道最大应力,为管道许用应力,根据标准ASME B31.1b-2009[9],20号钢材料标准号为A672的无缝钢管在不超过20~100℃时的最大许用应力σc=120.67 MPa,当管道最大应力超过材料的最大许用应力,管道极易发生疲劳破坏,因此可认为此时的管道处于工作失效状态。
3.1 管道抗振结构设计方法 为分析振动参数对输液管道的应力的影响,仿真其在振动幅值分别为0.5、1.0和2.0 mm下振动频率在10~100 Hz[15-16]内管壁最大应力的变化规律,分析结果如图 7所示。
 |
| 图 7 最大应力随基础振动频率变化规律 Fig. 7 Change rules of maximum stress with foundation vibration frequency |
| 图选项 |
图 7表明,随着基础振动频率的增大,管道应力先增大后减小,在约60 Hz时,最大应力因管道共振而达到峰值。同一频率下,基础振幅越大,管道应力越大。
以最大应力不超过许用应力为判据条件,研究不同长度的液压管道在频率0~720 Hz、幅值0~5 mm范围内的正常-失效状态,结果如图 8所示,图中深色部分表示最大应力超过许用应力的失效区域。由图可知,不同长度管道在相同基础振动参数范围内的失效区域有显著差异,对于特定振动环境下的管道,合理选取管道固支长度能够有效避免管道应力过大而失效。当振幅较小时,管道失效区域随着管长减小而往高频移动,即在高频低幅环境下管道固支间距不宜过短。
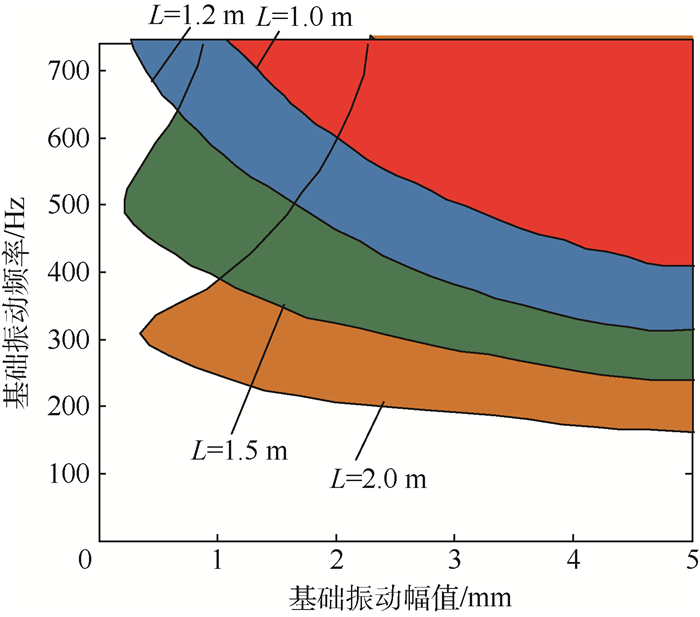 |
| 图 8 不同固支间距下管道失效区域图 Fig. 8 Area chart of pipe failure under different support spans |
| 图选项 |
因此,在管道设计时,应先考察管道所处的工作环境,确定其基础振动频率和幅值范围,再通过选取合理的管道结构参数,使管道处于正常工作区域,其设计流程如图 9所示。
 |
| 图 9 强振动环境下抗振结构设计流程图 Fig. 9 Design flow chart of anti-vibration structure in strong vibration environment |
| 图选项 |
处于强振动环境下的管道,为保证管道应力处于许用应力范围内,制定其结构设计方法如下:根据载荷条件确定管道所需流量和内压,根据国标初步选定合适的管道厚度和内径,并依据现场采集的振动参数确定基础振动幅值和频率范围,以最大基础振幅和中间频率为定值,仿真不同支撑间距下管道最大应力值,根据最大应力的判据条件,得到管道失效的临界支撑间距,进而根据基础振动频率的大小在非失效范围内选取合适的支撑间距,然后仿真不同频率和幅值下管道应力,判断现场采集的基础振动范围内管道应力是否均处于正常工作区域,如果出现小范围处于失效区域,则适当调整管道内径和厚度,再进行上述流程,如果出现大范围处于失效区域,则重选管道支撑间距,再进行上述流程的计算,如果所有范围都处于非失效区域,则确定此种管道结构参数,结构设计完成,确定最优的结构参数。
不同于传统管道结构设计方法,新结构设计方法在原有选择内径和厚度的基础上,考虑了基础振动的影响,能保证在强振动环境中不因管道应力过大而失效。
3.2 实例应用 某TBM推进液压系统中液压长管道总长20 m,要求最高压力20 MPa,最大流量160 L/min,并处于频率ω=300~400 Hz、幅值0.5~2.2 mm的振动环境中,钢管密度为7 895 kg/m3,液压油密度890 kg/m3,弹性模量E=201 GPa,要求设计其结构参数。
结构设计过程:根据最高压力要求初步选定管道厚度为3 mm,而由最大流量的规定,根据流量计算公式Q=VA=Vπd2/4,V为流速,初选流速为5 m/s,得到其内径为d=0.026 m。
针对管道所处的振动环境,先分析其中间频率为350 Hz和极端幅值为2.2 mm下的临界管道固支间距。仿真在此振动环境下不同固支间距时的管道最大应力值,结果如图 10所示。图中虚线为应力警戒线,其大小为许用应力值,超过此线则认为失效。
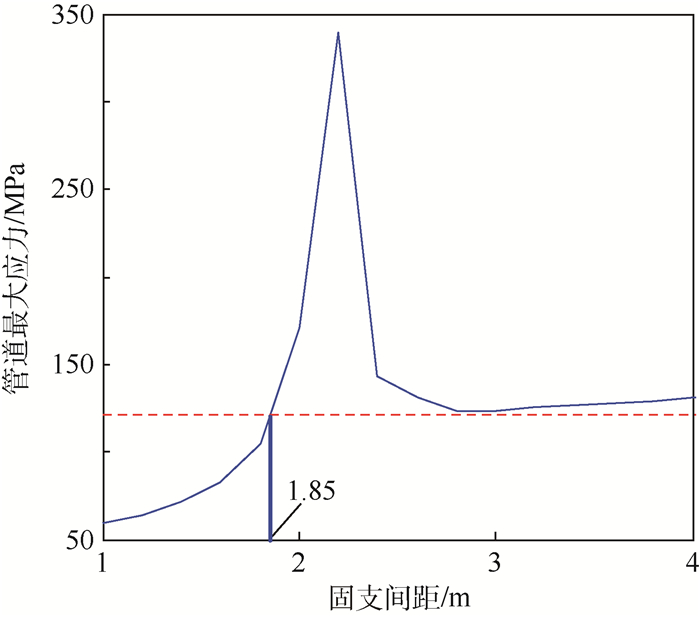 |
| 图 10 不同固支间距下管道最大应力 Fig. 10 Maximum pipe stress underdifferent support spans |
| 图选项 |
得到管道许用应力范围内固支间距范围为[0,1.85] m,由于管道过长,振动位移会加大,并且管道稳定性也随管道长度增大而变差,因此得到管道正常工作的固支间距最大值为1.85 m。
选取固支间距为1.8 m,仿真管道在不同基础振动频率和幅值下的失效区域,考察实例中实际频率和幅值范围内管道的失效/正常情况,结果如图 11所示。
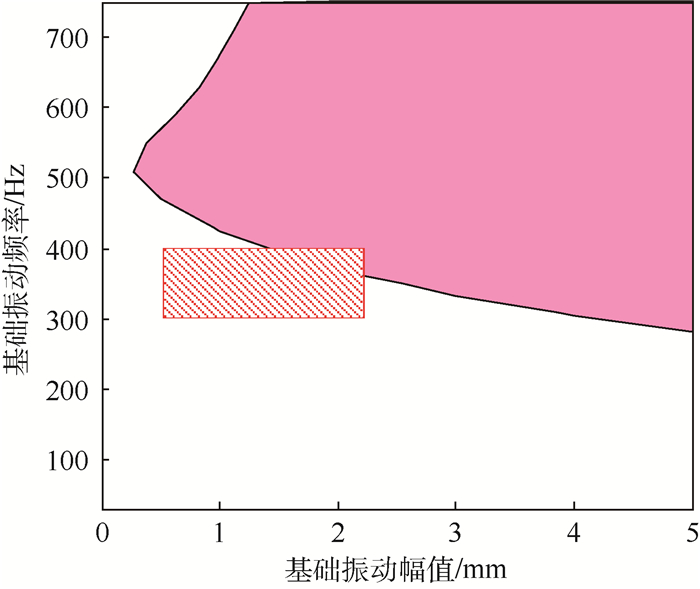 |
| 图 11 不同基础振动参数下的失效区域 Fig. 11 Failure area of different foundationvibration parameters |
| 图选项 |
结果显示,频率在300~400 Hz、幅值在0.5~2.2 mm范围(阴影部分) 内,有小部分区域仍然属于失效区,根据第3.1节抗振结构设计方法,将通过管径和厚度的调整来实现整个振动范围的正常工作。将内径增大到30 mm,厚度变为4 mm,再次仿真其不同频率和幅值下的应力结果和失效区域,结果如图 12所示。
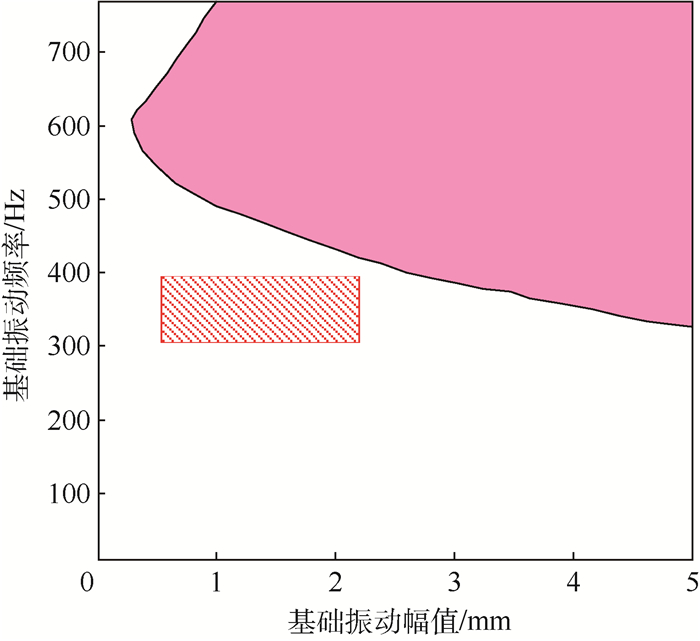 |
| 图 12 调整内径后的失效区域图 Fig. 12 Failure area chart after innerdiameter's optimization |
| 图选项 |
由图 12可以看到,在管道所处的频率在310~400 Hz、幅值在0.5~2.2 mm范围的振动环境下,管道应力值均小于许用应力,管道工作正常,达到了设计要求。因此确定管道的内径为0.03 m,厚度为0.004 m,并每1.8 m分布一个支撑。
3.3 实例验证 实验设定振动台频率为400 Hz,振动幅值为2.2 mm,实验管道内径0.03 m,厚度为0.004 m,管长1.8 m,得到管道应力敏感截面上的最大应力响应如图 13所示。
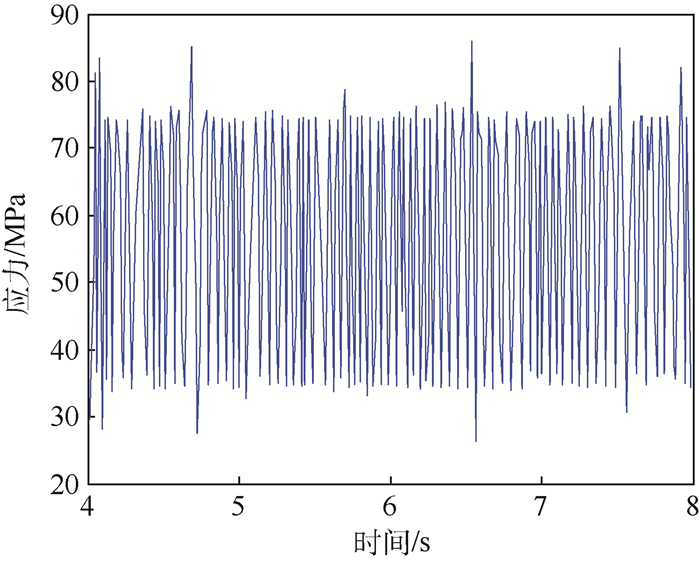 |
| 图 13 优化后应力敏感截面上最大应力响应 Fig. 13 Maximum stress response of stresssensitive section ofter optimizing |
| 图选项 |
由图 13可知,应力的波峰平均值为74.68 MPa,管道应力值均小于许用应力,验证了实例应用的正确性。
4 结论 1) 确定了管道在不同基础振动参数下工作的正常-失效区域,能有效判断强振动环境下的管道是否满足工作要求。
2) 振幅较小时,管道失效区域随着管长减小而往高频移动,即在高频低幅环境下管道固支间距不宜过短。
3) 制定了不同基础振动下以流量-压力-强振动为依据的抗振结构设计方法,能有效改善强振动环境下管道的工作性能。
参考文献
| [1] | KOYAMA Y. Present status and technology of shield tunneling method in Japan[J].Tunnelling and Underground Space Technology, 2003, 18(2): 145–159. |
| [2] | LI X H, YU H B, YUAN M Z, et al.Study on the linear dynamic model of shield TBM cutterhead driving system[C]//IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society.Piscataway, NJ:IEEE Press, 2011:3864-3871. |
| [3] | 吴晓南, 舒浩纹, 昝林峰, 等. 试压工况下盾构隧道内输气管道应力分析[J].天然气工业, 2013, 33(3): 73–77.WU X N, SHU H W, ZAN L F, et al. Stress analysis of gas pipeline in tunnels on pressure testing condition[J].Natural Gas Industry, 2013, 33(3): 73–77.(in Chinese) |
| [4] | XIA L, HUANG K, HONG F L, et al. Stress analysis of suspended gas pipeline[J].Applied Mechanics and Materials, 2013, 448(1): 1359–1362. |
| [5] | XIAO N W, SHI J W, HONG F L, et al. Analysis of hot oil pipe-line stress influencing factors[J].Advanced Materials Research, 2014, 887(1): 899–902. |
| [6] | 耿艳辉, 詹晨菲. 生产线液压系统长大管道设计[J].流体传动与控制, 2012, 52(3): 21–24.GENG Y H, ZHAN C F. Design of long and large pipeline of hydraulic system used in product line[J].Fluid Power Transmission and Control, 2012, 52(3): 21–24.(in Chinese) |
| [7] | 朱博. 工程机械液压系统管路设计及装配原则[J].建筑机械, 2011(2): 94–97.ZHU B. Principle of pipeline design and assembly for hydraulic system of construction machinery[J].Construction Machinery, 2011(2): 94–97.(in Chinese) |
| [8] | SVEDEMAN S J, ARNOLD K E. Criteria for sizing multiphase flowlines for erosive/corrosive service[J].SPE Production & Facilities, 1996, 9(1): 74–80. |
| [9] | NAYYAR M L.ASME code for pressure piping, B31:ASME B31.1b-2009[S].New York:ASME, 2009:6-10. |
| [10] | JIN J D, ZOU G S. Bifurcations and chaotic motions in the autonomous system of a restrained pipe conveying fluid[J].Journal of Sound and Vibration, 2003, 260(5): 783–805.DOI:10.1016/S0022-460X(02)00982-3 |
| [11] | SEMLER C, LI G X, PAIDOUSSIS M P. The nonlinear equations of motion of pipes conveying fluid[J].Journal of Sound and Vibration, 1994, 169(5): 577–599.DOI:10.1006/jsvi.1994.1035 |
| [12] | 邹光胜, 金基铎, 闻邦椿. Melnikov方法在输流管混沌运动研究中的应用[J].力学与实践, 2004, 26(2): 29–32.ZOU G S, JIN J D, WEN B C. Application of Melnikov method in the study of chaotic motions of pipe conveying fluid[J].Mechanics in Engineering, 2004, 26(2): 29–32.(in Chinese) |
| [13] | PAIDOUSSIS M P, LI G X, RAND R H. Chaotic motions of a constrained pipe conveying fluid:Comparison between simulation analysis and experiment[J].ASME Journal of Applied Mechanics, 1991, 58(2): 559–565.DOI:10.1115/1.2897220 |
| [14] | STOSIAK M. Vibration insulation of hydraulic system control components[J].Archives of Civil and Mechanical Engineering, 2011, 11(1): 237–248.DOI:10.1016/S1644-9665(12)60186-1 |
| [15] | 陈炳瑞, 冯夏庭, 曾雄辉, 等. 深埋隧洞TBM掘进微震实时监测与特征分析[J].岩石力学与工程学报, 2011, 30(2): 275–283.CHEN B R, FENG X T, ZENG X H, et al. Real-time microseismic monitoring and its characteristic analysis during TBM tunneling in deep-buried tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 275–283.(in Chinese) |
| [16] | 苏华友.双护盾TBM开挖深埋隧洞围岩稳定性研究[D].成都:西南交通大学, 2009:36-40.SU H Y.Surrounding rock stability study of double-shield TBM during tunneling in deep-buried tunnel[D].Chengdu:Southwest Jiaotong University, 2009:36-40(in Chinese). |
