基于电导检测的流体参数测量是流体参数测量领域的经典方法之一，然而现有的电导测量技术多采用接触式的测量方法，电极表面与管道内被测流体直接接触，易发生电极极化、电化学腐蚀等问题^[1-8]，从而对测量造成了不利的影响，限制了其在工业测量中的应用。
电容耦合式非接触电导检测(Capacitively Coupled Contactless Conductivity Detection，C⁴D) 技术自提出以来，由于其测量电极与待测流体不直接接触，可有效克服传统接触式电导检测中存在的电极极化、电化学腐蚀等问题，受到了广泛的关注^{[5-6, 9]}。然而作为一种新兴的测量技术，C⁴D传感器目前多用于实验室中毛细管电泳及微流控驱动等方面的检测^{[1-3, 10-11]}，在毫米级管径的流体参数检测中的应用较少，仍处于发展阶段^[12-15]。
C⁴D传感器中存在径向和轴向2种典型结构。有研究表明，在测量性能方面轴向结构的传感器要优于径向结构，然而为保证其测量精度，须保持电极宽度及电极间距离与管道直径的比例足够大，即传感器部分的总尺寸通常为管道直径的5倍以上，有时甚至要达到10倍^{[1-4, 7-8]}，这使得将轴向结构C⁴D传感器应用于常规管径管道内的流体参数检测受到制约。与之相比，径向C⁴D传感器的结构更为简单，体积亦相对较小，但目前针对径向结构C⁴D传感器的研究较少^{[4, 7-8]}。
本文设计研发了一种新型径向C⁴D传感器，引入电感模块，利用串联谐振的原理消除耦合电容对测量的不利影响。传感器采用径向两电极结构，安装方便且占用空间少，有利于实现装置的小型化。同时，由于所设计的传感器要获取待测流体的电导信号，则传感器必须能够较敏感地反映管道内流体的等效电导的变化；由于传感器的几何参数对测量值有较大的影响^[16]，为达到最佳测量精度，用仿真软件与具体实验测试相结合的方式对其进行优化设计，以获得传感器的最佳设计方案。
1 C⁴D测量原理 图 1给出了C⁴D传感器的2种典型结构^[1-2]，图中：u_i为输入的交流激励电压；u_o为输出的直流电压；i_o为输出的交流电流。2种结构的测量系统均由4个部分构成：交流激励源、绝缘管道、激励/检测电极和信号处理电路。在轴向结构的传感器中，激励电极和检测电极均为环形金属电极，并以一定的间距贴于绝缘管道外壁；径向结构传感器的激励电极和检测电极为径向金属电极片，相对分布于绝缘管道外壁两侧。2种结构的C⁴D传感器等效电路模型一致，如图 2所示。图中：C₁和C₂为两电极、绝缘管道与导电流体形成的2个耦合电容；R_x为两电极间流体的等效电阻。施加交流激励信号u_i于激励电极上使之形成交流通路，则可由检测电极获得反应流体电导信息的电流信号i_o。电容耦合式非接触电导检测技术为流体电导信号的非接触测量提供了良好的方案。

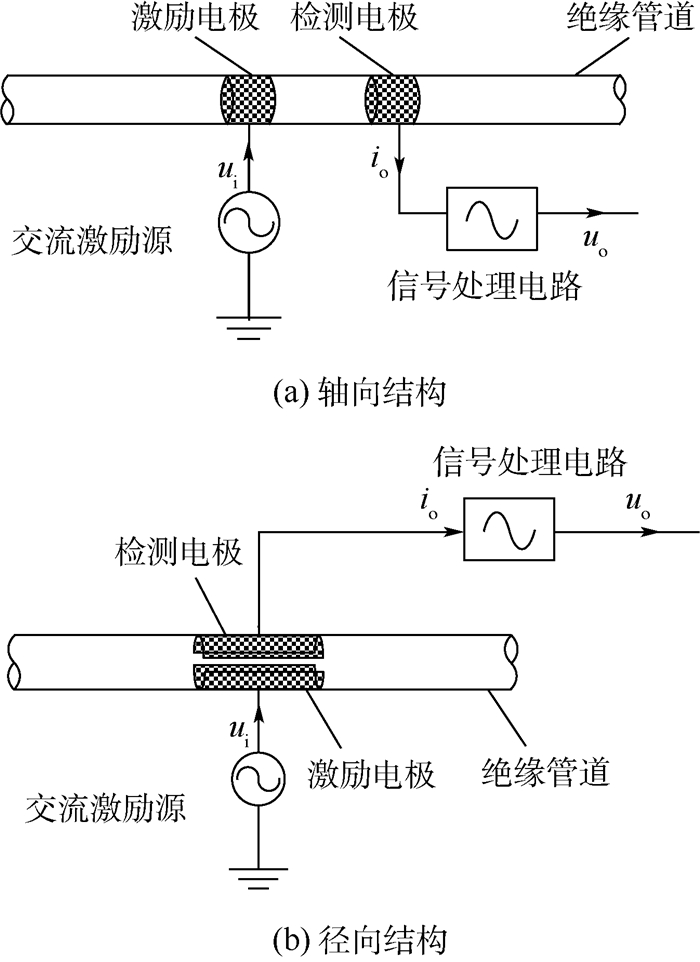图 1 C4D传感器典型结构 Fig. 1 Typical structure of C4D sensor

图选项

图 2 C4D传感器等效电路 Fig. 2 Equivalent circuit of C4D sensor

图选项

在设计C⁴D传感器时，要根据具体情况选择相应的结构，研究表明，在测量性能方面轴向结构的传感器要优于径向结构，然而径向结构更为简单，体积亦相对较小^[1-4]，更适宜应用于较大管径的流体参数测量。
2 新型径向两电极C⁴D传感器 本文所设计的新型C⁴D传感器如图 3所示，其组成部分包括交流激励源、激励电极、检测电极、绝缘管道、串联电感和信号处理模块等。

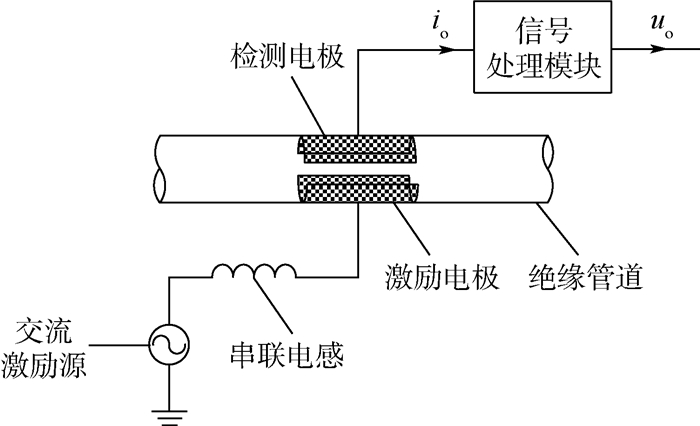图 3 径向两电极传感器结构 Fig. 3 Structure of radial two-electrode sensor

图选项

当激励源对激励电极施加交流激励信号时，检测回路的等效电路如图 4(a)所示，其中，耦合电容C₁和C₂值受传感器几何参数及绝缘管道相对介电常数的影响，R_x值受传感器的几何参数以及待测流体的电导率的影响，L为串联电感。耦合电容C₁和C₂作为测量交流通路的重要组成部分，使流体电导测量得以实现的同时产生了无效的背景信号，此背景信号的存在给传感器的测量灵敏度、测量范围以及分辨率带来了不利的影响^[12]。检测回路的总阻抗Z可表示为

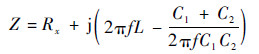(1)

式中：f为激励频率。

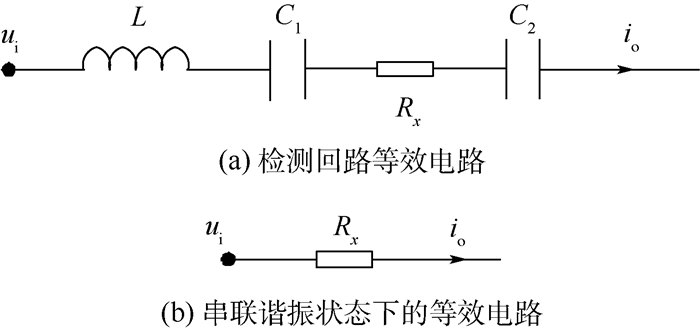图 4 径向两电极传感器等效电路 Fig. 4 Equivalent circuit of radial two-electrode sensor

图选项

由式(1) 可知当电路等效阻抗虚部为零，即电路达到串联谐振状态时的频率f₀可表示为

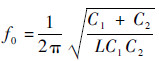(2)

则当激励频率为f₀时，电路中电感产生的感抗与耦合电容产生的容抗相互抵消，电路呈纯阻性，此时检测回路的总阻抗Z可表示为

(3)

串联谐振时的等效电路如图 4(b)所示，则背景信号C₁和C₂的影响被消除，信号处理模块从检测电极上得到的电流信号i_o仅包含流体的电导信息，进一步处理i_o，即可得到待测流体的等效电导值。
3 传感器优化 由于电极片的张角对耦合电容以及待测流体等效电导值都有较大的影响，为获得最佳的设计方案，分别采用COMSOL有限元建模仿真以及对比实验2种方法对其进行对比分析。
由于传感器敏感场域满足准静态电磁场的条件，则建模时选用准静态电场条件进行仿真模拟，所设计的传感器内部场域方程及边界条件可描述为

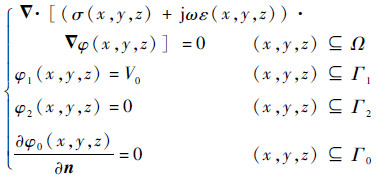(4)

式中:σ(x, y, z)、ε(x, y, z) 和φ(x, y, z) 分别为模拟环境与管壁及其内部场域的电导率、相对介电常数以及电势；ω为角频率; Г₁为激励电极的空间位置; Г₂表示检测电极的空间位置; Г₀为模拟外部环境的边界; Ω表示传感器场域; n为相对于边界面的单位法向量; V_o为设定的电势常数。
由此可得，各电极边界条件分别为：激励电极所处的空间位置设为交流激励电位能，检测电极所处的空间位置设为接地，管内壁以及外壁无电极片区域设为连续，模拟外部环境介质为空气，外部环境边界设为悬浮电位。传感器基础模型截面结构如图 5所示，图中：l为电极片宽度；θ为电极片张角；D为绝缘管道外径；d为绝缘管道内径。

图 5 传感器基础模型截面结构 Fig. 5 Basic model cross-section structure of sensor

图选项

基础模型的各参数分别为：传感器管道内径d=9 mm，外径D=13 mm，管道长度50 mm，管壁相对介电常数ε_pipe=4，空气的相对介电常数为ε₀=1。显然，电极片的长度对传感器灵敏度有较大影响，长度越长则电极片有效面积越大，灵敏度也会相应增加，但电极片长度过长亦会造成平均效应，综合考虑各因素，通过实验确定电极片宽l为外径D的1.5倍。模拟外部环境应越大越好，然而外部空间越大则剖分网格越多，计算时间越长，则用500 mm边长的正方体模型模拟外部环境。保持电极片宽度不变，分别改变电极片张角θ=60°，90°，120°，150°，以此来观察传感器响应的变化。管道内介质电导率的变化范围为0.01~100 mS/cm，仿真结果如图 6所示。

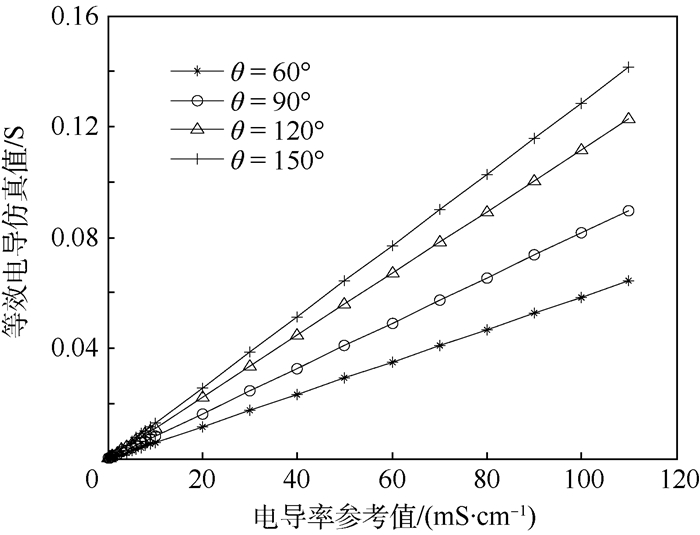图 6 电极片张角改变时两电极间等效电导仿真值 Fig. 6 Simulation equivalent conductivity value betwee two electrodes when angle of electrode changes

图选项

由仿真结果可以看出，随着电极片张角的增加，传感器灵敏度提高，然而当张角大于120°后，灵敏度增加的趋势减弱。
由于仿真实验数值是在理想环境中得到的结果，为进一步探究传感器在实际情况下的应用特性，在d=9.1 mm、D=12.8 mm的水平有机玻璃管道上对上述4个传感器进行对比实验，实验以不同浓度的KCl溶液为待测介质，参考电导率值由商业型接触式电导率仪(梅特勒-托利多FE30，电导率测量范围0~199.9 mS/cm，测量精度±5% F.S.) 测定，电导率的变化范围同上。电极片张角改变时传感器的输出特性变化如图 7所示，电极片张角小于120°时，传感器灵敏度随张角的增加而增大，但张角为150°时，灵敏度反而下降了，在所测试的4种不同张角的传感器中，电极片张角为120°时的测量效果最好。

图 7 不同电极张角时传感器的输出特性 Fig. 7 Output characteristics of sensors with different electrode angles

图选项

通过比对仿真与实验的结果可以发现，当电极片张角由120°增加至150°时，仿真结果灵敏度仍然在增加，只是其增加的趋势减小，但实际实验中张角为150°时传感器的灵敏度比张角为120°时的灵敏度低，初步分析其原因，是由于电解质溶液的导电机制与金属导体及固态电解质不同，对其进行仿真和模拟更为复杂，所应用的仿真软件模块未能考虑这些因素，使得仿真结果与实测结果出现差异^[17]。
由上述结果可知，加大电极片张角即可增加检测的有效面积，理论上可有效提高传感器输出灵敏度，则在选择电极张角时，应选择较大的电极张角。然而当电极片张角过大，两电极间距离缩小，则两电极通过空气形成的杂散电容对测量的影响增加，导致传感器的信噪比降低，综合考虑，选择电极片的张角为120°较好。
4 电导测量实验结果 分别在5个不同管径的水平有机玻璃管道上对所设计的电导测量传感器进行了测试实验，实验介质的选取与参考值的获取途径如前所述。电极张角设为120°，激励电压为12 V。传感器特征尺寸和相应的交流激励频率如表 1所示。
表 1 传感器参数及激励频率 Table 1 Sensor parameters and excitation frequencies

传感器编号	d/mm	D/mm	l/mm	f/kHz
1	5.0	8.0	12.0	288
2	7.5	10.0	15.0	281
3	9.1	12.8	19.2	277
4	10.2	14.0	21.0	267
5	12.0	16.0	24.0	263

表选项






此外，根据优化设计实验的结果，可以看出当管道内流体的电导率范围达到20 mS/cm以上时，传感器的灵敏度显著降低，测量效果较差，传统的径向C⁴D传感器的可测量范围为0.01~10 mS/cm，本文在保证灵敏度的前提下，验证实验管道内KCl溶液的浓度变化范围调整为1.0×10^-4~0.2 mol/L，即电导率范围变化为0.01~24 mS/cm，比较传统径向传感器测量范围提高了1倍以上。实验结果如图 8所示, 可以看出，利用本文所设计的电导测量装置在5个不同管径下进行电导测量实验，所得到的测量值与参考值的相对误差均小于5%。结果表明，本文所设计的电导测量装置在实际电导测量中是可行、有效的。

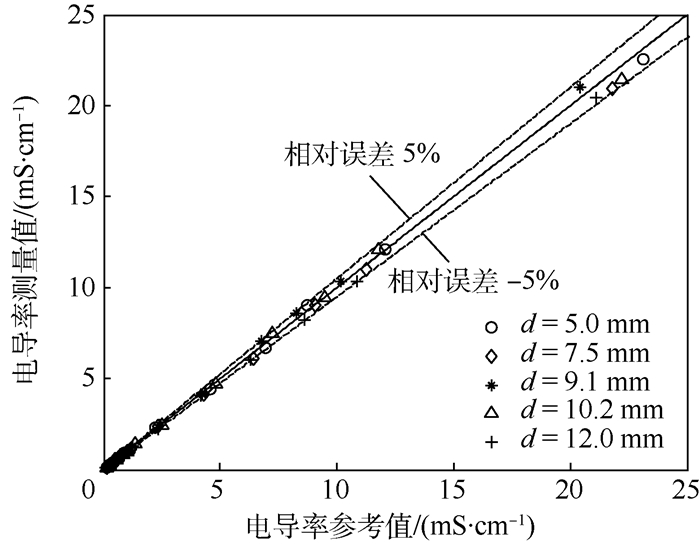图 8 电导率测量实验结果 Fig. 8 Experimental results of conductivity measurement

图选项

5 结论 1) 本文基于串联谐振原理，设计了一种径向结构的新型C⁴D传感器，扩大了现有径向C⁴D传感器的应用范围，提高了测量灵敏度。
2) 仿真和实验结果表明，电极张角对测量效果有重要影响，张角增加时，测量灵敏度会相应增大，但如果张角过大，会引入一些对测量不利的影响因素，导致灵敏度下降。综合考虑，建议电极张角为120°时最佳。
3) 在内径为5.0、7.5、9.1、10.2和12.0 mm的5个管道中进行的电导测量实验表明所研发的电导测量系统是有效的，电导测量相对误差均小于5%，为流体的参数检测提供了一种可行的方案。

参考文献

[1]	KUBAN P, HAUSER P C. A review of the recent achievements in capacitively coupled contactless conductivity detection[J].Analytica Chimica Acta, 2008, 607(1): 15–29.DOI:10.1016/j.aca.2007.11.045
[2]	KUBAN P, HAUSER P C. Review contactless conductivity detection for analytical techniques:Developments from 2010 to 2012[J].Electrophoresis, 2013, 34(1): 55–69.DOI:10.1002/elps.v34.1
[3]	KUBAN P, HAUSER P C. Contactless conductivity detection for analytical techniques:Developments from 2012 to 2014[J].Electrophoresis, 2015, 36(1): 195–211.DOI:10.1002/elps.v36.1
[4]	OPEKAR F, TUMA P, STULIK K. Contactless impedance sensors and their application to flow measurements[J].Sensors, 2013, 13(3): 2786–2801.DOI:10.3390/s130302786
[5]	ZEMANN A J, SCHNELL E, VOLGGER D, et al. Contactless conductivity detection for capillary electrophoresis[J].Analytical Chemistry, 1998, 70(3): 563–567.DOI:10.1021/ac9707592
[6]	SILVA J A F D, LAGO C L D. An oscillometric detector for capillary electrophoresis[J].Analytical Chemistry, 1998, 70(20): 4339–4343.DOI:10.1021/ac980185g
[7]	NOVOTNY M, OPEKAR F, STULIK K. The effects of the electrode system geometry on the properties of contactless conductivity detectors for capillary electrophoresis[J].Electroanalysis, 2005, 17(13): 1181–1186.DOI:10.1002/(ISSN)1521-4109
[8]	KUBAN P, HAUSER P C. Ten years of axial capacitively coupled contactless conductivity detection for CZE-A review[J].Electrophoresis, 2009, 30(1): 176–188.DOI:10.1002/elps.v30:1
[9]	BARD A J, FAULKNER L R.电化学方法:原理和应用[M].2版.邵元华, 朱果逸, 董献堆, 等, 译.北京:化学出版社, 2008:373-398.BARD A J, FAULKNER L R.Electrochemical methods:Fundamentals and applications[M].2nd ed.SHAO Y H, ZHU G Y, DONG X D, et al, translated.Beijing:Chemical Industry Press, 2008:373-398(in Chinese).
[10]	CAHILL B P, LAND R, NACKE T, et al. Contactless sensing of the conductivity of aqueous droplets in segmented flow[J].Sensors and Actuators B:Chemical, 2011, 159(1): 286–293.DOI:10.1016/j.snb.2011.07.006
[11]	PUMERA M. Contactless conductivity detection for microfluidics:Designs and applications[J].Talanta, 2007, 74(3): 358–364.DOI:10.1016/j.talanta.2007.05.058
[12]	HUANG Z Y, JIANG W W, ZHOU X M, et al. A new method of capacitively coupled contactless conductivity detection based on series resonance[J].Sensors and Actuators A:Physical, 2009, 143(1): 239–245.DOI:10.1016/j.snb.2009.08.032
[13]	HUANG Z Y, LONG J, XU W B, et al. Design of capacitively coupled contactless conductivity detection sensor[J].Flow Measurement and Instrumentation, 2012, 27(10): 67–70.
[14]	JI H F, LYU Y C, WANG B L, et al. An improved capacitively coupled contactless conductivity detection sensor for industrial applications[J].Sensors and Actuators A:Physical, 2015, 235: 273–280.DOI:10.1016/j.sna.2015.09.038
[15]	JI H F, LI Z Z, WANG B L, et al. Design and implementation of an industrial (CD)-D-4 sensor for conductivity detection[J].Sensors and Actuators A:Physical, 2014, 213: 1–8.DOI:10.1016/j.sna.2014.03.024
[16]	DEVIA F, FOSSA M. Design and optimization of impedance probes for void fraction measurements[J].Flow Measurement and Instrumentation, 2003, 14(4-5): 139–149.DOI:10.1016/S0955-5986(03)00019-0
[17]	KUBAN P, HAUSER P C. Fundamental aspects of contactless conductivity detection for capillary electrophoresis.Part I:Frequency behavior and cell geometry[J].Electrophoresis, 2004, 25(10): 3387–3397.