近年来,电荷耦合器件(Charge Coupled Device,CCD) 图像传感器技术飞速发展,因其像素尺寸小,空间分辨率高,光电灵敏度高,易与计算机相结合,数字扫描能力强,体积小重量轻,安装方便等优点使得使用CCD代替传统的光电探测器采集散射信号具有较大的应用前景。但随着散射角越来越小,获取纯净的散射信号也会变得越来越困难,主要原因是中心光过强和小角度下杂散光的严重干扰,造成信噪比不高[3-4],这在基于CCD的前向小角散射颗粒测量技术最为明显。而大多数采用的解决方法主要是在保证光路绝对对准的情况下,用针尖等装置去除中心光强;或进行空白测试获取背景光强,采用直接做差的方法去除背景杂散光。前者方法会使测量装置复杂化,而且存在针尖衍射,会影响实际的散射信号;后者方法中因中心光、散射光和背景杂散光这三者之间并不是简单的数值相加,直接做差容易使散射信号丢失,从而导致反演精度较低。
近场散射(Near Filed Scattering, NFS) 技术克服了基于CCD的前向小角散射系统中的一些缺陷[5]:在无需添加去除中心光的复杂装置的情况下,使系统设备简单紧凑,可以实现被测颗粒粒径及分布的测量;不需要任何角分辨检测,扩展了散射角范围,并且克服了光学系统中杂散光对散射光强的影响,提高测量精度;在图像处理算法中可去除近场散斑中杂散光成分,因此对使用环境的要求低。
本文研究了近场散射原理,搭建了近场散射粒径测量系统,通过对散斑图像的傅里叶频谱分析得到颗粒的散射光强分布,再利用Chahine循环算法对颗粒粒径进行了反演。最后,利用标准聚苯乙烯乳胶球溶液对该测量系统进行了试验研究。
1 近场散射颗粒粒径测量原理 图 1为近场散射测量原理图。经过空间滤波准直的激光光束照射待测颗粒群样品而发生散射,在距离样品很近的z处因散射光和透射光的干涉叠加而形成的散斑图像经显微物镜被CCD相机所接收,该图像包含了颗粒的粒径信息。CCD相机上的每一个像素可以接收到系统所能散射的最大角度内的散射光,然后通过傅里叶频谱分析就可得到角散射光强度,从而反演出颗粒粒径信息[6-8]。
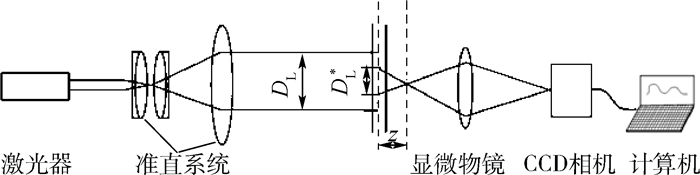 |
| 图 1 近场散射原理图 Fig. 1 Schematic diagram of NFS |
| 图选项 |
根据范西特-泽尼克(Van Cittert-Zernike) 定理[9],远场散斑大小为dsp=λz/DL,其中:DL为入射光光斑直径;λ为入射光的波长;z为观测面距被测样品的距离。此时的散斑大小与z有关,而不包含样品的物理信息。但当观测面靠近样品,即z很小时,观测面所采集到的光线仅来自于直径为DL*=zλ/D的区域,其中:D为颗粒粒径。此时,近场散斑大小为dsp=λz/DL*=D。从中可以看出散斑大小只与颗粒有关,而与入射光波长λ和距离样品z无关。这是近场散射与远场散射显著不同的地方。从上可知近场的条件是DL*≤DL,也即z < DL/Θ*,其中:Θ*为光进出显微物镜的最大锥角,近似等于显微物镜数值孔径的2倍。
CCD相机拍摄到的散斑是较强的透射光与很弱的散射光干涉的结果,并且散射光强要比透射光强弱得多,所以根据干涉理论[10]得到散斑强度分布为
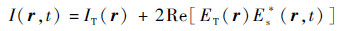 | (1) |
式中:IT=|ET|2为透射光强度;ET和Es分别为透射光场和散射光场;Re为取实部运算;“*”为共轭运算;r=(x, y) 为空间时域下的坐标点;t为时间。
透射光强值IT是与空间位置r有关,而与时间t无关的静态参考量。在小角度下,透射光中包含着杂散光。因为散射信号的随机性,Es(r, t) 和Es*(r, t) 的时间平均值为零。所以对于式(1) 进行时间平均得到
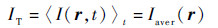 | (2) |
式中:Iaver为多张散斑图像的算术平均光强值。
为了去除杂散光和光路误差所带来的影响,通常采用差分归一化处理方法[11-12]。所得差分信号为
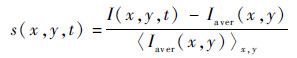 | (3) |
采用快速傅里叶变换(FFT) 求得散斑强度的功率谱函数为
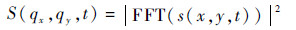 | (4) |
式中:(qx, qy) 为与空间频率(fx, fy) 有关的傅里叶向量,qx=2πfx,qy=2πfy。
对于各向同性的静态样品,对式(4) 按照q=
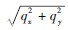
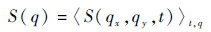 | (5) |
二维近场散斑强度的功率能量谱包含着散射光强的信息,最后要做的是建立平均能量谱S(q) 和散射光强Is(Q) 之间的关系[13-14]。图 2为近场散射矢量图。图中:k0为入射光波矢,ks为散射光波矢,Q=ks-k0为传递波矢;q为傅里叶矢量;θ为散射角,弹性散射下入射光波矢与散射光波矢的模相等,即|ks|=|k0|=k=2π/λ。
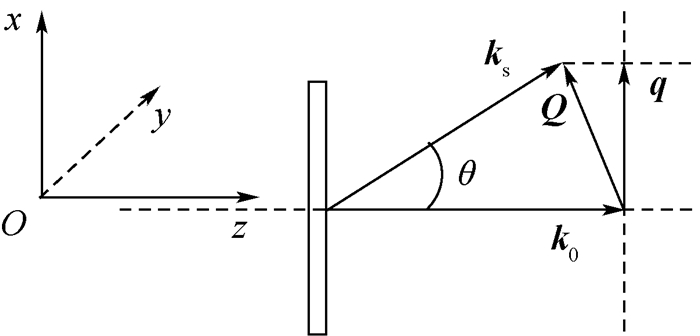 |
| 图 2 近场散射矢量图 Fig. 2 Schematic diagram of vectors in NFS |
| 图选项 |
从图 2可以得到传递波矢量和傅里叶矢量的模长分别为
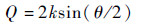 | (6) |
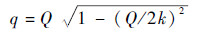 | (7) |
式中:k为光波矢的模长。
从式(6) 和式(7) 可以看出当θ→0时q~Q。则散射光强度可以表示为
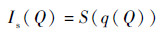 | (8) |
这与采用小角散射获取的散射光强度具有一致性。
实验测量的散射光强度包含着颗粒的粒径信息,对颗粒群而言,在不考虑粒子间的相关多散射情况,散射光强如式(9) 所示,对其采用反演算法就可得到待测对象的粒径分布。
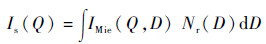 | (9) |
式中:IMie(Q, D) 为直径为D的颗粒在散射波矢为Q时Mie散射光强度; Nr(D) 为需要反演出的颗粒粒径的频率分布。
2 颗粒粒径反演算法 颗粒粒径反演问题的求解归结为第一类Fredholm积分方程的求解[15]。本文采用Chahine循环算法[16-17]对颗粒粒径分布进行反演。该循环算法的优点之一是可以自动满足非负条件,只要初始粒径分布为正,所得求解结果必然是非负值。
Chahine循环算法最初是在测量大气温度分布时提出的,后经过多年的发展开始应用于光散射测量颗粒粒径分布。具体的迭代格式如下:
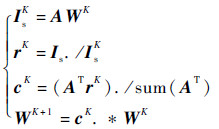 | (10) |
式中:K为迭代次数;W为颗粒粒径分布;A为Mie散射归一化光强分布系数矩阵;Is为归一化实验测量值;“./”表示向量中各对应元素相除;“.*”表示向量中各对应元素相乘;sum (A) 表示矩阵A的列向量中的元素之和。
3 近场散射颗粒粒径测量系统 图 3为近场散射颗粒粒径测量系统实验装置。本实验中He-Ne激光器(波长λ=632.8 nm,光束直径d=0.7 mm,功率P=10 mW),经过空间滤波准直系统得到准直光束,其直径DL为10 mm (在激光能量的1/e2处直径)。空间滤波准直系统由标准显微物镜(10x)、凸透镜(焦距f=45 mm) 和一针孔滤波器(针孔孔径Dh=50 μm) 组成,可以滤除大部分由激光器产生的杂散光,并且对光束进行准直和10倍扩束。滤波准直的光束照射装有待测对象的石英比色皿(光程为10 mm) 中。收集透镜是由放大倍数为40倍的标准显微物镜实现(数值孔径NA=0.65,盖玻片标准厚度0.17 mm,有效工作距离0.48 mm,镜筒长度160 mm),系统所能接收到的最大散射角是由显微物镜的数值孔径决定的,它描述光进出透镜时的锥角大小,为θmax=arcsin (NA)=40.5°。一般地,前向小角散射测量系统的最大散射角在10°以内,而角度越小,中心光越强,要想获取纯净的散射光强比较困难。所以散射角度的提升,减弱了中心光强的影响。根据式(6) 得最大散射波矢大小为Qmax=4π/λ·arcsin (NA/2)=6.88 μm-1。系统对应的近场条件所允许的距离z≤7.7 mm。收集透镜距离比色皿外表面1 mm,则观测面到比色皿中心的距离z=5.5 mm,满足近场条件。
 |
| 图 3 近场散射粒径测量系统实验装置图 Fig. 3 Experimental setup of NFS particle sizing measurement system |
| 图选项 |
图像采集由8位的CCD相机(分辨率为1 280×1 024,像素尺寸为14 μm) 和PC机完成。相机放置在收集透镜后160 mm处,并且稍微高于光轴,以便降低杂散光的干扰,这是因为散射角越小,杂散光干扰越严重,尤其是光轴处。稍微偏离光轴,从系统上减少杂散光的影响。后期在图像处理中可以更大程度地去除杂散光的影响。40倍放大倍数的显微物镜保证了散斑尺寸与颗粒尺寸在同一个数量级,并且大于CCD相机的像素尺寸。显微物镜的放大倍数决定了图像的有效计算边长L=14 μm×(1 024/40)=358.4 μm,则对应的该系统所能测量到的最小散射波矢大小为Qmin=2π/L=0.017 5 μm-1。
为了验证该系统对颗粒粒径的可行性和准确性,实验选用国家标准颗粒进行测试。标准颗粒具有良好的单分散性,其直径偏差很小。表 1为2种粒径的标准颗粒溶液。
表 1 2种标准聚苯乙烯乳胶球 Table 1 Two certified polystyrene latex spheres
| 编号 | 直径/μm |
| GBW (E)120028 | 39.2±0.6 |
| GBW (E)120047 | 67.3±3.8 |
表选项
4 实验结果与讨论 4.1 单峰分布颗粒系溶液 采用标准颗粒GBW (E)120028(39.2 μm),以水为分散剂,配制体积分数为1%的待测样本,对其进行多次取样多次测量。实验中设定CCD的帧率为50帧/s,采集图像N=500帧。总的测量时间则为T=10 s。
图 4(a)为39.2 μm聚苯乙烯乳胶球的500张近场散斑图像之一,它是由透射光与散射光叠加而形成的。为了计算近场散斑的二维功率谱,首先根据式(3) 计算近场散斑的差分信号,图 4(b)为39.2 μm聚苯乙烯乳胶球的差分信号图像。再采用FFT即可计算出其二维功率谱,如图 4(c)所示呈明暗相间的环状光环。按照式(5) 对图 4(c)进行处理,可得到39.2 μm乳胶球的散射光强分布,如图 5所示。已知散射光强值,采用Chahine算法反演可得39.2 μm乳胶球的粒径概率分布,如图 6所示。从图 6可以直观地看出,粒径主要落在[37.6, 43.3] μm内,占了86%。描述该粒径概率分布特征的长度平均粒径:
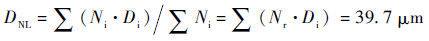 |
式中:Ni为以Di中值的粒径区间内的颗粒数。
 |
| 图 4 近场散射测量图像 Fig. 4 Measurement images in NFS |
| 图选项 |
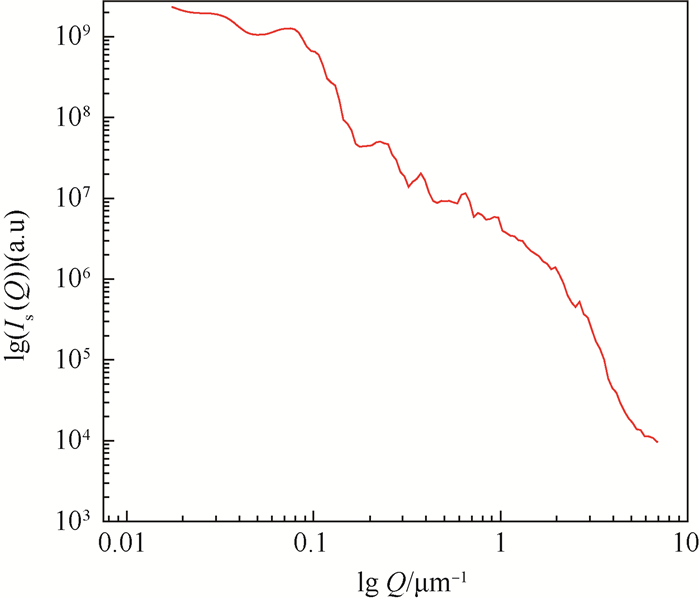 |
| 图 5 39.2μm乳胶球的散射光强分布 Fig. 5 Scattered intensity distribution of 39.2 μm latex spheres |
| 图选项 |
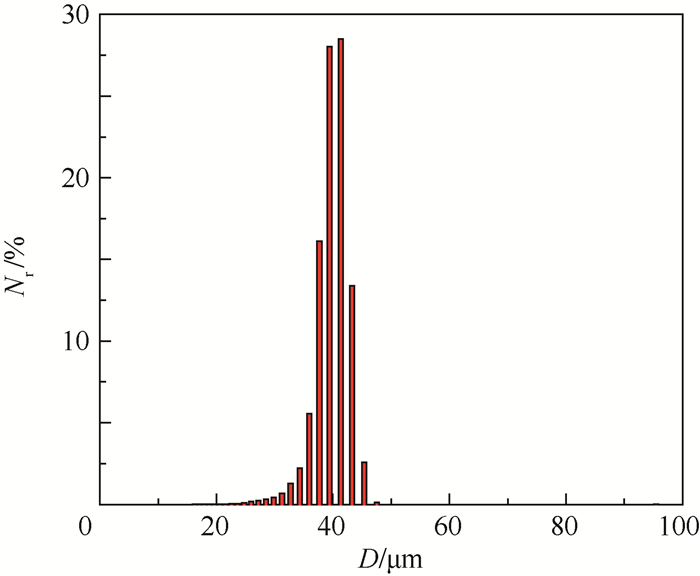 |
| 图 6 39.2μm乳胶球的粒径概率分布 Fig. 6 Particle size probability distribution of 39.2 μm latex spheres |
| 图选项 |
按照上述步骤,对39.2 μm和67.3 μm乳胶球溶液进行多次测量,得到的典型数据如图 7所示。从多次测量结果上看,对39.2 μm乳胶球溶液,所测得的粒子群平均尺寸Dm=40.3±1.9 μm;对67.3 μm乳胶球溶液,所测得的粒子群平均尺寸Dm=68.7±2.4 μm。从整体上,近场散射测量系统的粒径测量具有较好的稳定性:对同一对象的多次测量,39.2 μm乳胶球溶液的测量标准偏差为1.9 μm,67.3 μm乳胶球溶液的测量标准偏差为2.4 μm。该系统可以实现粒径的稳定测量,但结果与标准颗粒物的检定结果之间也存在一定的误差,如表 2所示,测量误差在5%以内。纵观实验,产生误差的原因主要有:
1) 溶液配制的不均匀性,悬浮颗粒分布不均匀,以及存在气泡等可能会导致测量结果偏大,而且在连续测量过程中,溶液会发生沉淀,导致悬浮颗粒数变少而使测量结果偏小。
2) 粒子群浓度的不均匀,可能会产生局部的多次散射而增加测量误差;此外粒子群浓度的稀疏会造成拍摄图像的信噪比低,使得计算出的散射光强值不准确。
3) 光学仪器如透镜和比色皿的部分地方不清洁,也会影响最终的测量结果。
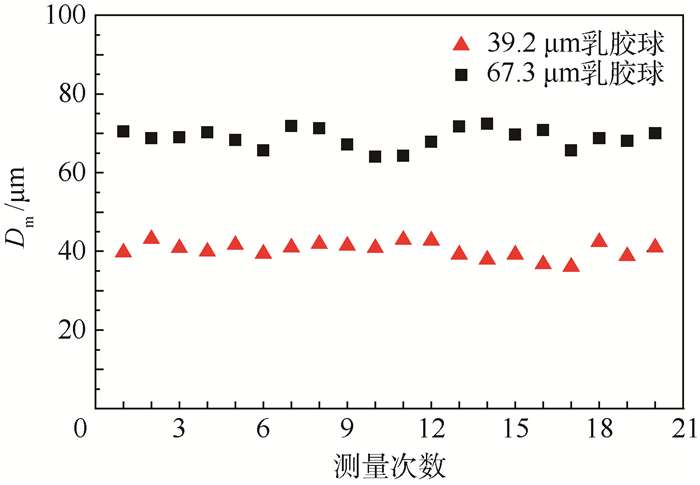 |
| 图 7 39.2 μm和67.3 μm乳胶球测量结果 Fig. 7 Measurement results of 39.2 μm and 67.3 μm latex spheres |
| 图选项 |
表 2 标准聚苯乙烯乳胶球测量值对比 Table 2 Comparison between the measurements of certified polystyrene latex spheres
| 标定直径/μm | 测量直径/μm | 误差/% |
| 39.2±0.6 | 40.3±1.9 | 3.8 |
| 67.3±3.8 | 68.7±2.4 | 4.0 |
表选项
4.2 双峰分布颗粒系溶液 实验中将39.2 μm和67.3 μm按照质量比1:2进行混合。图 8为混合溶液的散射光强值分布曲线。根据重建的散射光强值反演得到的混合溶液粒径双峰分布如图 9所示。图中显示分别在43.3 μm和74.1 μm处出现明显峰值,相对于标准值,误差分别为10.5%和10.1%。很显然,在测量双峰分布溶液的误差比单峰溶液的要大,主要是因为2种粒径混合时,振荡不够均匀,颗粒间聚团现象比较严重,且2种颗粒的沉降速度不同,因此无法保证光路所经过的颗粒系绝对的分散。
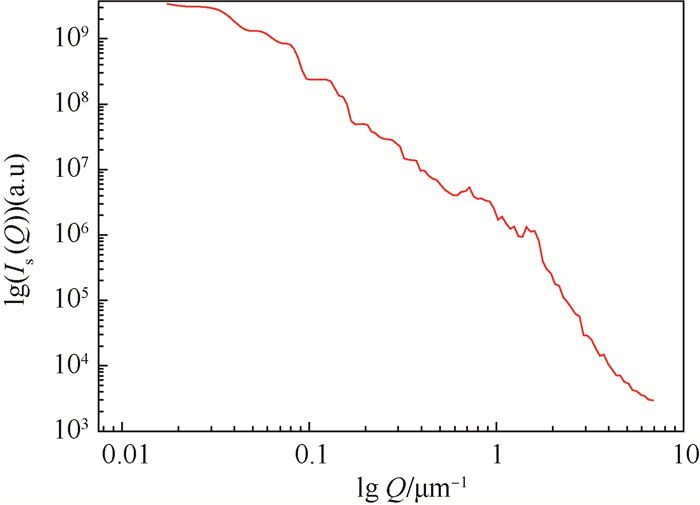 |
| 图 8 混合乳胶球的散射光强分布 Fig. 8 Scattered intensity distribution of mixture latex spheres |
| 图选项 |
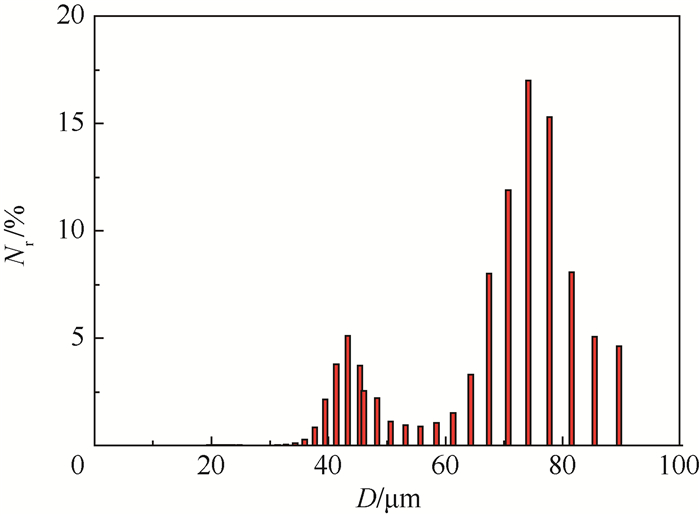 |
| 图 9 混合乳胶球的粒径概率分布 Fig. 9 Particle size probability distribution of mixture latex spheres |
| 图选项 |
5 结论 本文通过研究近场散射原理,搭建了粒径测量系统,结合Chahine循环算法对颗粒粒径进行了反演,并使用标准颗粒物进行实验验证。得到如下结论:
1) 与传统的前向小角散射相比,近场散射测量系统装置紧凑、简单,采用图像差分方法可有效去除中心光和杂散光成分,无需冗杂的空白测量;扩大了散射角范围,削弱了小角度下散射光强的振荡对反演结果的影响;采用快速傅里叶频谱分析近场散斑图像可间接获取散射光强分布。
2) 分别测量了39.2 μm和67.3 μm这2种单峰分布颗粒系溶液的粒径分布,有较高的准确性和稳定性,误差在5%之内。
3) 测量了39.2 μm和67.3 μm混合溶液,得到在43.3 μm和74.1 μm处出现峰值,峰值误差分别为10.5%和10.1%。
参考文献
| [1] | 邵鸿飞, 柴娟, 黄辉. 粒度分析及粒度标准物质研究进展[J].化学分析计量, 2012, 21(2): 99–101.SHAO H F, CHAI J, HUANG H. Research progress of particle size analysis and particle size standard reference material[J].Chemical Analysis and Meterage, 2012, 21(2): 99–101.(in Chinese) |
| [2] | 王乃宁. 颗粒粒径的光学测量技术及应用[M].北京: 原子能出版社, 2002: 168-175.WANG N N. Optic Measurement technology of particle size and its application[M].Beijing: Atomic Energy Press, 2002: 168-175.(in Chinese) |
| [3] | FERRI F. Use of a charge coupled device camera for low-angle elastic light scattering[J].Review of Scientific Instruments, 1997, 68(6): 2265–2274.DOI:10.1063/1.1148135 |
| [4] | 王式民, 陆勇, 叶茂. 前向小角散射法测量颗粒平均尺寸[J].武汉大学学报(自然科学版), 1997, 43(5): 691–696.WANG S M, LU Y, YE M. Measurement of the particle mean size by the ratio of the scattering light intensitied at small angles near-forward[J].Journal of Wuhan University (Natural Science Edition), 1997, 43(5): 691–696.(in Chinese) |
| [5] | BROGIOLI D, VAILATI A, GIGLIO M. Heterodyne near-field scattering[J].Applied Physics Lertters, 2002, 81(22): 4109–4111.DOI:10.1063/1.1524702 |
| [6] | SCHEFFOLD F, CERBINO R. New trends in light scattering[J].Current Opinion in Colloid & Interface Science, 2007, 12(1): 50–57. |
| [7] | MAGATTI D, ALAIMO M D, POTENZA M A C, et al. Dynamic heterodyne near field scattering[J].Applied Physics Lertters, 2008, 92(24): 241101–1.DOI:10.1063/1.2937841 |
| [8] | CERBINO R, VAILATI A. Near-field scattering techniques:Novel instrumentation and results from time and spatially resolved investigations of soft matter systems[J].Current Opinion in Colloid & Interface Science, 2009, 14(6): 416–425. |
| [9] | DAINTY J C. Laser speckle and related phenomena[M].Berlin: Springer-Verlag, 1984: 132-135. |
| [10] | BORN M, WOLF E, HECHT E. Principles of optics:Electromagnetic theory of propagation, interference and diffraction of light[J].Brain Research Molecular Brain Research, 2005, 141(1): 30–38.DOI:10.1016/j.molbrainres.2005.07.012 |
| [11] | GIGLIO M, BROGIOL D, POTENZA M A C, et al. Near field scattering[J].Physical Chemistry Chemical Physics, 2004, 6(7): 1547–1550.DOI:10.1039/B314600F |
| [12] | DORIANO B.Near filed speckles[D].Milano:Universita di Milano and INFM, 2009:73. |
| [13] | POTENZA M A C, PESCINI D, MAGATTI D, et al. A new particle sizing technique based on near field scattering[J].Nuclear Physics B-Proceedings Supplements, 2006, 150(1): 334–338. |
| [14] | FERRI F, MAGATTI D, PESCINI D, et al. Heterodyne near-field scattering:A technique for complex fluids[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 70(4 Pt 1): 174–195. |
| [15] | KOUZELIS D, CANDEL S M, ESPOSITO E, et al. Particle sizing by laser light diffraction:Improvements in optics and algorithms[J].Particle & Particle Systems Characterization, 1987, 4(1-4): 151–156. |
| [16] | 曹丽霞.基于静态光散射的颗粒粒度检测技术的研究[D].杭州:中国计量学院, 2015:27-30.CAO L X.Research on measurement technology of particle size based on static light scattering[D].Hanzhou:China Jiliang University, 2015:27-30(in Chinese). |
| [17] | 曹丽霞, 赵军, 孔明, 等. 基于改进的Chahine迭代算法的粒径分布反演[J].红外与激光工程, 2015, 44(9): 2837–2843.CAO L X, ZHAO J, KONG M, et al. Inversion of particle size distribution based on improved Chahine algorithm[J].Infrared and Laser Engineering, 2015, 44(9): 2837–2843.(in Chinese) |
