过程层析成像(Process Tomography，PT) 通过安装在被测容器周围的传感器阵列，在容器内形成覆盖被测空间的敏感场，通过场内介质对敏感场调制作用，利用传感器阵列获取被测对象信息，再通过图像重建算法再现被测容器内部的介质分布。PT技术在化工、石油、冶金与物料运输等工业生产过程中有广泛的应用前景，但目前普遍存在工作范围较窄、分辨率低等问题^[1]。
电阻层析成像(Electrical Resistance Tomography，ERT) 是利用物场内介质电导率变化获取物场信息，进而重建介质分布的检测技术^[2]，通常采用电流激励-电压测量的相邻采集工作方式^[3]，通过向管道内注入电流，形成电场，当管道内介质发生变化时，电场分布随之变化，进而获得描述管道内介质分布的边界电压。ERT为保证较高测试精度需在导电介质为连续相条件下工作^[4]，故测量范围有限^[5]。超声层析成像(Ultrasound Tomography，UT) 技术通过超声波与被测物体之间的相互作用获取被测对象内部信息^[6]。超声与不同材料的被测物体之间的作用分为3类：透射作用、反射作用和衍射作用^[7]。超声透射层析成像(Ultrasound Transmission Tomography，UTT) 利用超声波在传播过程中发生的衰减，因此接收探头上的超声波声压变化包含了场域内介质的变化信息^[8]。UTT系统通常采用单发单收或一发多收的工作方式^[9]，由于介质中超声波传播速度有限，UTT系统的实时性受限^[10]，测量对象的强非均质性影响成像质量^[11]。
利用不同敏感原理的传感器可获取被测对象不同特性的信息，通过综合多种敏感信息可克服单一模态中测量范围与获得信息有限的缺点^[12]。2001年，Hoyle等^[13]提出将ERT/ECT (Electrical Conductance Tomography)/UT不同原理的传感器分别安装在管道不同截面，实现多种敏感数据的测量，扩充敏感范围。该方法虽具有结构简单且敏感场互不影响的优势，但测量结果不能反映同一时间、同一流体过程信息，因此在多相流检测中存在信息难以对准的问题^[14]。在同一测试截面上安装多模态传感器，可获得管道内同一被测对象同一时间的多敏感信息，具有信息量互补、图像重建效果好的优势^[15]。2014年，Yunus等^[16]以电场分布为目标优化同截面ERT/UTT双模态系统电极宽度，提高了管道中心电场灵敏度。2015年，Teniou和Meribout^[17]报道了一种ERT/URT (Ultrasound Reflection Tomography) 双模态系统，将电学与超声传感器安装在同一截面上，证明ERT/URT双模态系统在图像重建效果上优于单模态ERT或URT系统。
层析成像的敏感原理要求，被测区域内的敏感场均匀性与灵敏性越高测试信息代表性越好，且边界测量值的数量越多所获被测对象的信息越丰富。当电极与超声探头安装于同一被测截面时，需在降低电极与超声探头间干扰的前提下获得更多的投影数据。当同一截面内的电极与超声探头距离较近时，超声波会在电极与管道界面处、电极与介质界面处发生反射与衍射现象，降低超声场敏感性。而电极尺寸过小则会影响电学敏感场的分布，为此需综合优化电极与超声探头安装结构与尺寸。利用COMSOL仿真优化同截面的16电极、16超声探头均匀间隔放置时的传感器尺寸，根据超声传播路径宽度与电极对声场的影响情况，得到最优安装结构，描述电学与超声敏感场分布互补情况，分析电极宽度与超声探头直径对声场的影响，以提高声场平均灵敏度与均匀性为目标，优化电极宽度与超声探头尺寸。
1 双模态传感器结构优化 超声波在不同介质的界面上存在反射、衍射与透射现象，反射率、透射率与界面两侧介质的声阻抗(Z=ρc，其中：Z为传播介质声阻抗；ρ为介质密度；c为该介质中超声波声速) 有关。由于ERT电极采用金属材料制成，管道材料为有机玻璃，管道内介质通常为水，金属材料、有机玻璃和水的声阻抗相差很大，故电极与管道、电极与介质的界面上反射现象明显，影响超声波传播。
1.1 超声波传播路径宽度 为降低电极对超声传播的影响，应优化电极安装位置，研究超声传播路径宽度分布。当超声探头直径越大，超声传播路径越宽，对电极之间的间隔要求更大。
COMSOL仿真中，管道材料为有机玻璃，管道内介质为水，管道内径100 mm，考虑超声波近场区的距离，在管道上距离管道内壁10 mm的位置，正对管道中心，安装一个直径为6 mm的超声探头，安装方式如图 1所示。采用压力声学频域模型，将超声频率设置为1 MHz，在超声探头正下方11 mm位置对声压强度进行检测，检测位置如图 1所示，声压强度分布如图 2所示。

图 1 超声探头安装位置与声压强度检测位置 Fig. 1 Ultrasonic sensor installation position and sound pressure intensity detection position

图选项

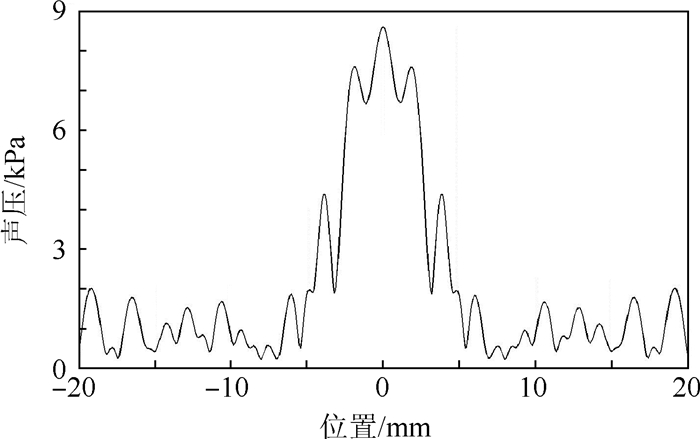图 2 声压强度分布 Fig. 2 Sound pressure intensity distribution

图选项

图 2中，以探头中心正下方11 mm为原点，超声波集中分布在(-5, 5) mm之间，即超声传播路径宽度在10 mm以内。为避免电极对超声传播的影响，需保证电极之间存在10 mm间隔。
1.2 电极对声场的影响 考察电极与管道和电极与管道内介质界面上超声波的反射现象对超声层析成像系统影响。当没有电极存在时，超声波仅在管道和介质之间的界面上发生反射，声场分布如图 3所示。当存在电极时，超声在电极与管道之间和电极与管道内介质之间的界面上发生反射，不同数量的电极对超声传播的影响不同，同样电极宽度下，16电极和30电极下声场分布如图 4、图 5所示。

图 3 无电极时超声场分布 Fig. 3 Ultrasonic field distribution with no electrode

图选项

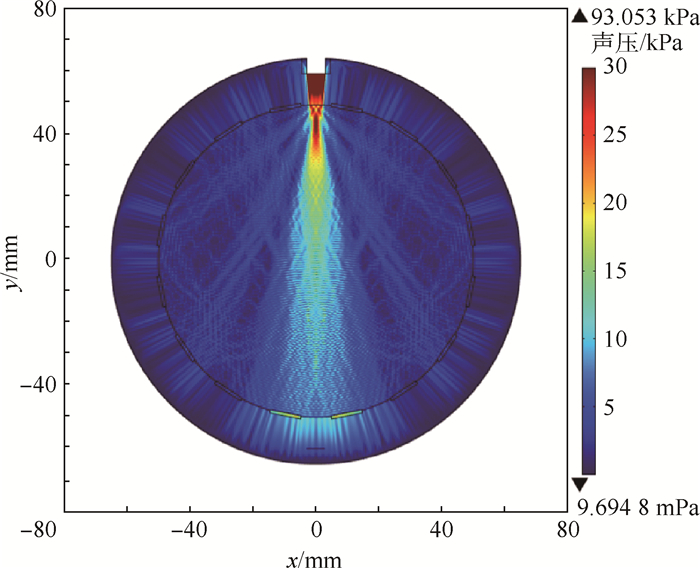图 4 16电极时超声场分布 Fig. 4 Ultrasonic field distribution with 16 electrodes

图选项

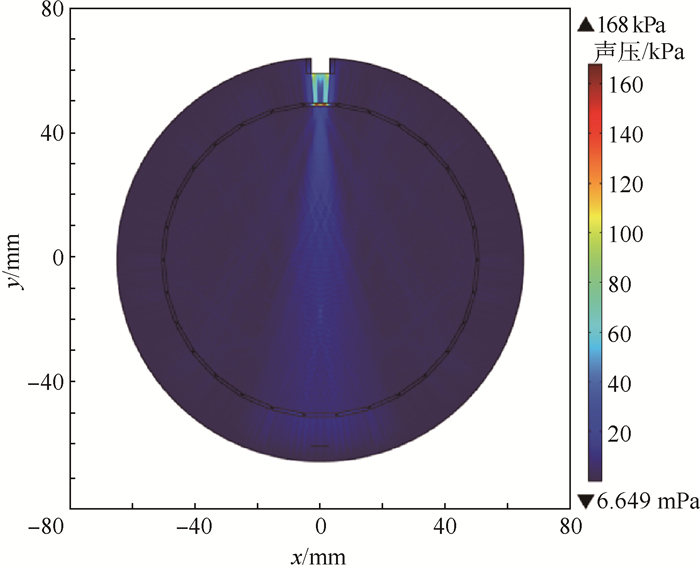图 5 30电极时超声场分布 Fig. 5 Ultrasonic field distribution with 30 electrodes

图选项

表 1为不同电极数量时接收到的声压。由表 1可知，30电极等间距放置时，电极位于超声波传播路径上，导致超声波在管道与电极之间的界面、电极和介质之间的界面上发生反射，降低接收到的声压，进而影响UTT系统的信噪比。基于超声波传播路径宽度，与电极对超声系统接收到声压强度，可知16电极与16超声探头间隔放置结构中，电极可避免位于超声波传播路径上，且使接收到的声压强度不受电极影响。在ERT/UTT双模态系统中，16电极与16超声探头间隔放置为最优空间结构，如图 6所示。
表 1 不同电极数量时接收到的声压 Table 1 Received sound pressure with different electrode quantities

电极个数	接收到的声压值/Pa
0	3 180
16	2 130
30	79

表选项

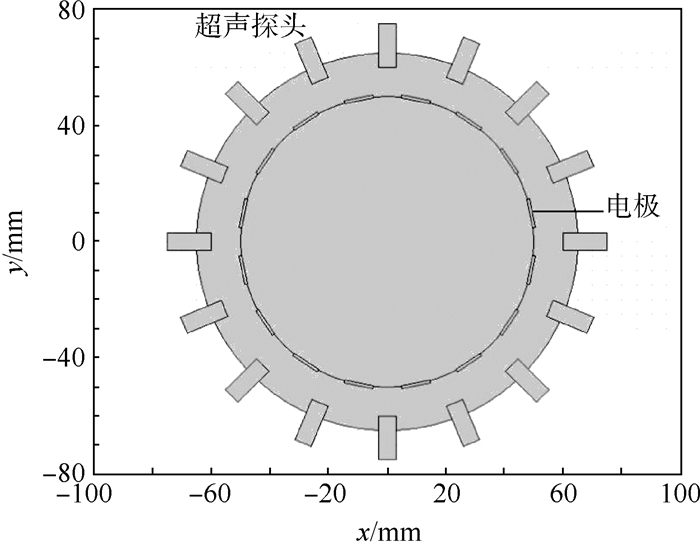图 6 16电极、16超声探头结构 Fig. 6 Configuration of 16 electrodes and 16 ultrasonic transducers

图选项

2 ERT/UTT敏感场分布 2.1 超声与电学敏感场仿真模型网格无关性 为验证超声与电学模型中仿真结果精度与有限元仿真中网格尺寸之间的关系，分别考察超声与电学模型中不同网格尺寸条件下的仿真结果。压力声学频域模型中，频率1 MHz，将网格单元尺寸分别设置为空气中超声波波长λ的1/3，1/4，1/5，1/6，1/10，1/15，获得中心位于(0, 0) 位置上的正方形设置为空气时收到的声压和，如表 2所示。电学模型中，将网格单元尺寸分别设置为COMSOL中尺寸预定义的“标准”、“粗化”、“细化”3种单元尺寸参数，获得中心位于(0, 0) 位置上的正方形设置为空气时的边界电压值，如表 3所示。
表 2 不同网格尺寸时接收到的声压 Table 2 Received sound pressure with different mesh sizes

网格尺寸/mm	声压/Pa
λ/3	10 561.062 93
λ/4	10 557.267 59
λ/5	10 555.664 34
λ/6	10 554.588 87
λ/10	10 554.581 65
λ/15	10 554.690 08

表选项






表 3 不同网格尺寸时边界电压 Table 3 Boundary voltage with different mesh sizes

编号	边界电压/V
	粗化	标准	细化
1	1.004 99	1.004 99	1.004 99
2	0.509 37	0.509 37	0.509 37
3	0.323 59	0.323 59	0.323 59
4	0.237 78	0.237 78	0.237 78
5	0.194 76	0.194 76	0.194 76
6	0.174 63	0.174 63	0.174 63
7	0.169 52	0.169 52	0.169 52
8	0.177 88	0.177 88	0.177 88
9	0.202 52	0.202 52	0.202 52
10	0.253 13	0.253 13	0.253 13
11	0.354 68	0.354 68	0.354 68
12	0.580 70	0.580 70	0.580 70
13	1.214 00	1.214 00	1.214 00

表选项






由表 2可知，超声模型中仿真结果随着网格尺寸的变化，仿真模型中网格尺寸的选择影响仿真结果的精度。声压模型中网格尺寸大于λ/6时，仿真结果的精度有很大影响，当网格尺寸小于等于λ/6后，仿真结果基本不变。减小网格尺寸会造成计算量增加。故声压模型中网格尺寸设定为λ/6。
由表 3可知，电学模型中网格尺寸对于仿真结果无任何影响。减小网格尺寸会造成计算量增加。故电学模型中网格尺寸可采用尺寸预定义中的“粗化”。故声压模型中网格尺寸设定为λ/6。电学模型中网格尺寸可采用尺寸预定义中的“粗化”。
2.2 电学敏感场分布 ERT系统中，激励电流在被测区域中产生一个电场，电场分布取决于被测区域中介质电导率，除激励电极与接地电极外，其余电极作为测量电极，获得敏感场边界的电势。实际应用中，ERT敏感场为似稳场。对于电场内任何一点，

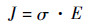(1)

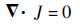(2)

式中：J为电流密度；σ为电导率；E为电势强度。又由于

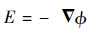(3)

式中：φ为场内电势分布，φ满足

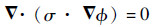(4)

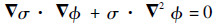(5)

在均匀、线性、各向同性的媒质中，σ为常数，故式(5) 可简化为

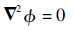(6)

为描述管道内电场区域上每个位置的电学灵敏度，将被测截面剖分成780个边长为3 mm的正方形区域，将每一正方形区域设置为气和水时边界电压的相对变化定义该点电学灵敏度。仿真中，电极宽度E_l=11 mm，管道内径D=100 mm，相对宽度E_l^*=E_l/D=0.11，如图 7所示。

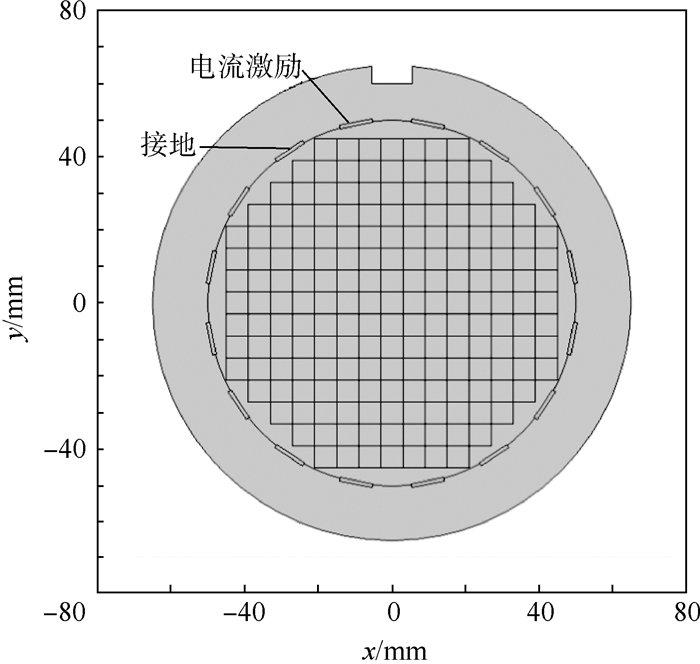图 7 780个正方形区域、激励电极和接地电极位置 Fig. 7 Position of 780 square mesh, exciting electrodes and grounding electrodes

图选项

ERT/UTT双模态系统中ERT系统采取电流激励-电压测量的相邻采集工作方式，每次激励可测得13个有效的边界电压值。与管道内全部为水的情况比较，仅将某一正方形区域填充为空气时，可获得13个电学灵敏度，即

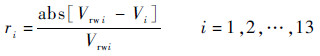(7)

式中：abs为绝对值函数；V_rwi为管道内全部为水时第i个独立边界电压值；V_i为该正方形区域为空气、管道内其余区域为水时第i个独立边界电压值。综合每次激励下每个区域上的13个独立灵敏度值，取其均值作为该位置上的电学灵敏度。

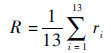(8)

式中：R为该正方形区域的电学灵敏度，用于衡量电场对该位置的灵敏程度，电学灵敏度值越大，电场对于该位置越灵敏。
ERT完成一周循环激励后，对于管道内每个位置，取16次激励下灵敏度最大值为该位置的电学综合灵敏度，电学灵敏度分布如图 8所示。

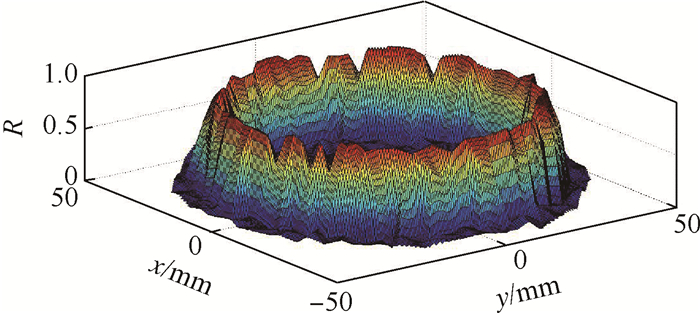图 8 管道内电学灵敏度分布 Fig. 8 Electrical sensitivity distribution inside pipeline

图选项

图 8中管道内电学灵敏度分布表明，靠近电极的区域电学灵敏度均较高，即靠近管道内壁的区域电学灵敏度较高，而管道中心区域的电学灵敏度均较低。
2.3 超声敏感场分布 为描述管道内超声场每个位置的超声灵敏度，同样采用图 7所示剖分网格，通过对每一正方形区域分别设置为气和水时接收声压差的相对变化定义该点的超声灵敏度。ERT/UTT双模态系统中UTT系统采取一发三收的工作方式，一次超声激励下每个正方形区域的灵敏度定义为

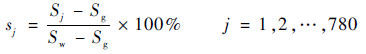(9)

式中：s_j为某个正方形区域的超声灵敏度；S_w为管道内全部为水时，3个接收探头收到的声压强度之和；S_g为管道内全部为空气时，3个接收探头收到的声压强度之和；S_j为某正方形区域为空气，管道内其余区域为水时，3个接收探头收到的声压强度之和。
超声一周循环激励后，对于管道内每个位置，取16次激励下灵敏度最大值作为该位置的超声综合灵敏度，分布如图 9所示，靠近管道中心区域超声灵敏度较高，而靠近管道内壁的区域不能被完全覆盖在超声传播路径内，故灵敏度较低。

图 9 管道内超声灵敏度分布 Fig. 9 Ultrasonic sensitivity distribution inside pipeline

图选项

对比图 8与图 9所示的电学灵敏度与超声灵敏度分布，若进一步优化同一截面内的双模态传感器布置方式，可实现灵敏度场的互补。
3 电极与超声传感器尺寸优化 为降低传感器配置对超声敏感场的影响，提高超声灵敏场的灵敏度与均匀性，对电极宽度与超声探头直径进行研究与优化。
3.1 超声敏感场平均灵敏度与均匀度 选取超声灵敏场域内全部正方形剖分区域灵敏度均值作为平均灵敏度，即

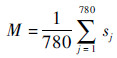(10)

标准差越小，敏感场均匀性越好。每完成一周循环激励后，管道内全部剖分区域的标准差为

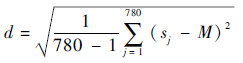(11)

由以上定义可知，敏感场平均灵敏度越高，对气/水两相流越灵敏；敏感场标准差越小，均匀性越好，逆问题线性度更好，成像质量较好。
3.2 电极宽度优化 为降低电极对超声敏感场的影响，以提高超声敏感场平均灵敏度M、降低标准差d为优化目标，优化电极宽度。仿真中管道材料为有机玻璃，管道内介质为气和水，电极材料为不锈钢。超声探头直径为12 mm，安装距离管道内壁为10 mm，频率为1 MHz，采用压力声学频域模型，考察电极相对宽度E_l^*在0.08~0.17之间时，电极对超声敏感场平均灵敏度与标准差的影响。
图 10为电极相对宽度对超声场平均灵敏度与标准差的影响。图 10中，当E_l^*在0.13以内时，超声敏感场的平均灵敏度随着电极宽度的增大而增大，而标准差随电极的增大而减小；当E_l^*超过0.13后，超声敏感场的平均灵敏度迅速降低，而标准差随电极的增大缓慢上升。E_l^*在0.11~0.13之间时，超声敏感场的平均灵敏度均可保持较高值。

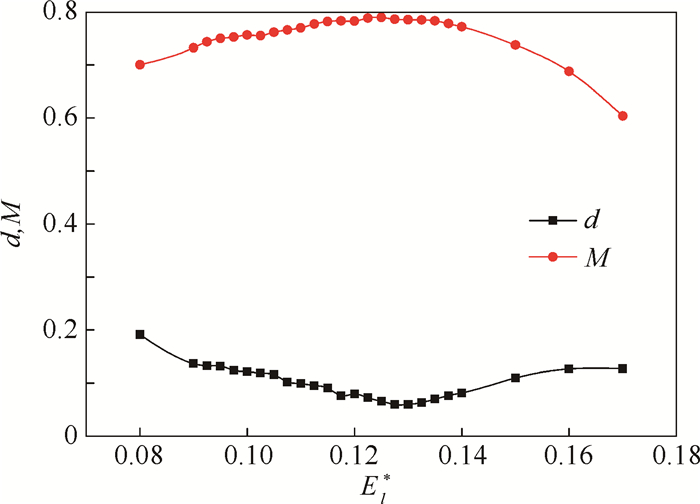图 10 电极相对宽度对超声场平均灵敏度与标准差的影响 Fig. 10 Influence of relative electrode width on average sensitivity and standard deviation of ultrasonic field

图选项

3.3 超声探头直径优化 为考察超声探头直径对于超声敏感场平均灵敏度和标准差的影响，定义为超声探头相对直径U^*=U/D，其中U为超声探头直径。超声探头频率设置为1 MHz，采用压力声学频域模型，将电极设置为9 mm。超声探头安装距离管道内壁10 mm。考察U^*在0.06~0.13之间时，超声探头对于超声敏感场平均灵敏度与标准差的影响。
图 11为超声探头直径对超声敏感场平均灵敏度的影响。图 11中随着超声探头相对直径U^*增大，超声敏感场平均灵敏度M上升；U^*>0.12后，超声敏感场平均灵敏度M均可保持较高值，且基本保持不变，故U^*>0.12对于超声敏感场平均灵敏度为最优超声探头直径。

图 11 超声探头相对直径对超声敏感场平均灵敏度的影响 Fig. 11 Influence of ultrasonic sensor relative diameter on average sensitivity of ultrasonic field

图选项

当U^* < 0.10时，标准差d基本不变；U^*>0.11后，随着超声探头直径增大，d迅速降低，并保持较低值，即U^*>0.11对于超声敏感场标准差为最优超声探头直径。
为综合考察敏感场平均灵敏度M与标准差d，提出M/d作为考察敏感场的参数：M值越大，敏感场标准差值d越小时，M/d值越大，即敏感场越灵敏，标准差越好。图 12为超声探头直径与电极宽度对超声敏感场平均灵敏度与标准差比值的影响。图 12中，电极相对宽度E_l^*=0.13时，超声敏感场灵敏度与标准差比值M/d最大，为最优电极宽度。随着超声探头相对直径U^*增大，超声场灵敏度与标准差比值M/d上升，当U^*超过0.12后，M/d降低，即U^*=0.12为最优超声探头直径。在以上参数条件下，电极相对宽度为0.13，即电极覆盖率为0.66时，超声探头相对直径为0.12，即超声探头覆盖率为0.51时，16电极与16超声探头ERT/UTT系统敏感场分布最优。

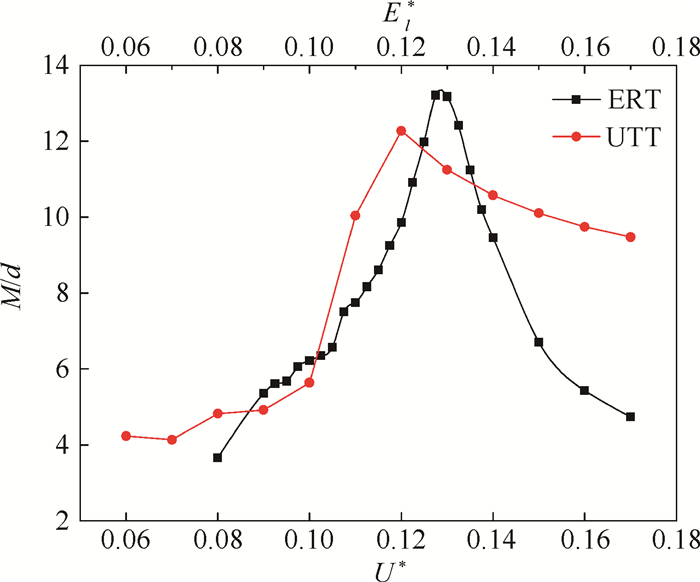图 12 超声探头相对直径与电极相对宽度对超声敏感场M/d的影响 Fig. 12 Influence of ultrasonic sensor relative diameter and relative electrode width on M/d of ultrasonic field

图选项

4 结论 为获得对同一被测对象的多模态测试，克服单一模态层析成像技术的缺点，提出同截面ERT/UTT双模态传感器结构。由于电极对超声敏感场存在影响，当电极与探头间隔放置时，需优化其尺寸参数，以获得更敏感和均匀的测试场。
数值仿真结果指出，同截面ERT/UTT双模态传感器的敏感场区域分布上互补。提出灵敏度与标准差比值M/d作为敏感场综合表征指标，结果表明电极相对宽度E_l^*最优值为0.13，超声探头相对直径U^*最优值为0.12。此时电极覆盖率为0.66，超声探头覆盖率为0.51。
通过对电极与超声探头安装结构及尺寸的研究，降低了对超声敏感场的影响，提高了超声敏感场的灵敏度并降低标准差。

参考文献

[1]	谭超, 董峰. 过程层析成像与多相流测量应用[J].仪器仪表用户, 2010(1): 3–6.TAN C, DONG F. An overview on process tomography and its applications[J].Electronic Instrumentation Customer, 2010(1): 3–6.(in Chinese)
[2]	KARHUNEN K, SEPPANEN A, LEHIKOINEN A, et al. Electrical resistance tomography imaging of concrete[J].Cement and Concrete Research, 2010, 40(1): 137–145.DOI:10.1016/j.cemconres.2009.08.023
[3]	DONG F, TAN C, LIU J W, et al. Development of single drive electrode electrical resistance tomography system[J].IEEE Transactions on Instrumentation and Measurement, 2006, 55(4): 1208–1214.DOI:10.1109/TIM.2006.877751
[4]	LI Y, YANG W Q.Measurement of multi-phase distribution using an integrated dual-modality sensor[C]//2009 IEEE International Workshop on Imaging Systems and Techniques.Piscataway, NJ:IEEE Press, 2009:335-339.
[5]	WANG Q, WANG H X, CUI Z Q, et al. Fast reconstruction of electrical resistance tomography (ERT) images based on the projected CG method[J].Flow Measurement and Instrumentation, 2012, 27: 37–46.DOI:10.1016/j.flowmeasinst.2012.03.009
[6]	RADOVAN J, IGOR P, NICOLE R, et al. Sound-speed image reconstruction in sparse-aperture 3-d ultrasound transmission tomography[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2012, 59(2): 254–264.DOI:10.1109/TUFFC.2012.2185
[7]	SCHLABERG H I, YANG M, HOYLE B S. Ultrasound reflection tomography for industrial processes[J].Ultrasonics, 1998, 36(1-5): 297–303.DOI:10.1016/S0041-624X(97)00053-X
[8]	SUPARDAN M D, MASUDA Y, MAEZAWA A, et al. The investigation of gas holdup distribution in a two-phase bubble column using ultrasonic computed tomography[J].Chemical Engineering Journal, 2007, 130(2-3): 125–133.DOI:10.1016/j.cej.2006.08.035
[9]	YUNUS F R M, AZLAN N A N, AYOB N M N, et al. Simulation study of bubble detection using dual-mode electrical resistance and ultrasonic transmission tomography for two-phase liquid and gas[J].Sensors and Transducers, 2013, 150(3): 97–105.
[10]	RAHIMAN M H F, RAHIM R A, RAHIM H A, et al. An investigation on chemical bubble column using ultrasonic tomography for imaging of gas profiles[J].Sensors and Actuators B:Chemical, 2014, 202(10): 46–52.
[11]	AYOB N M N, RAHIMAN M H F, ZAKARIA Z, et al.Detection of small gas bubble using ultrasonic transmission-mode tomography system[C]//Industrial Electronics and Applications.Piscataway, NJ:IEEE Press, 2010:165-170.
[12]	QIU C, HOYLE B S, PODD F J W. Engineering and application of a dual-modality process tomography system[J].Flow Measurement and Instrumentation, 2007, 18(5-6): 247–254.DOI:10.1016/j.flowmeasinst.2007.07.008
[13]	HOYLE B S, JIA X, PODD F J W, et al. Design and application of a multi-modal process tomography system[J].Measurement Science and Technology, 2001, 12(8): 1157–1165.DOI:10.1088/0957-0233/12/8/324
[14]	RAHIM R A, RAHIMAN M H F, ZAIN R M, et al. Image fusion of dual-modal tomography (electrical capacitance and optical) for solid/gas flow[J].International Journal of Innovative Computing Information and Control, 2011, 7(9): 5119–5132.
[15]	SUN J T, YANG W Q. A dual-modality electrical tomography sensor for measurement of gas-oil-water stratified flows[J].Measurement, 2015, 66: 150–160.DOI:10.1016/j.measurement.2015.01.032
[16]	YUNUS F R M, RAHIM R A, AW S R, et al. Simulation study of electrode size in air-bubble detection for dual-mode integrated electrical resistance and ultrasonic transmission tomography[J].Powder Technology, 2014, 256(2): 224–232.
[17]	TENIOU S, MERIBOUT M. A multimodal image reconstruction method using ultrasonic waves and electrical resistance tomography[J].IEEE Transactions on Image Processing, 2015, 24(11): 3512–3521.DOI:10.1109/TIP.2015.2445575