全球卫星导航系统(Global Navigation Satellite System, GNSS)具有全天候、全球性和连续的导航定位能力。全球定位系统(Global Positioning System, GPS)是最为成熟的卫星导航系统。我国的北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)目前已进入全球组网建设阶段，在轨运行卫星23颗，预计2020年全面建设完成。卫星导航系统的完好性是衡量其性能的重要指标之一，特别是对可靠性要求苛刻的航空以及交通领域等特殊应用来说，完好性监测是接收机必备的功能之一^[1-3]。完好性监测方式主要有3种^[4]：①卫星自主完好性监测；②利用接收机内部冗余信息的接收机自主完好性监测(Receiver Autonomous Integrity Monitoring，RAIM)；③增强系统。其中，RAIM包括利用伪距观测量的快照(Snapshot)算法和卡尔曼滤波算法。上述算法对于测量噪声为非高斯时性能下降^[5-7]。由于导航信号传输过程的各种干扰，使其残差分布不是严格的高斯分布^[8]，此时，卡尔曼滤波算法性能将下降。国内外很多研究人员将粒子滤波(Particle Filter, PF)用于非高斯噪声处理问题^[9-10]，但PF存在粒子退化和多样性丧失等问题^[11-12]。
本文采用粒子群优化粒子滤波(Particle Swarm Optimization Particle Filter, PSO-PF)，使粒子样本更加精确地表示状态概率密度函数的真实分布，并将其与似然比方法结合构建PSO-PF RAIM算法。
1 PSO-PF算法 设非线性系统的状态方程和观测方程为

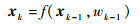(1)

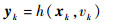(2)

式中：x_k为过程向量；y_k为测量向量；f为转移函数；h为传递函数；w_k-1为过程噪声；v_k为量测噪声。
在PF算法中，由于存在粒子退化，引入重采样能够减少粒子中的无效粒子，但重采样会带来新的问题，即多次重采样会增加计算负担，同时也会产生样本枯竭、粒子多样性丧失等问题。针对PF算法的缺点，将智能优化算法与PF算法相结合^[13]。PSO是一种群智能优化算法，将其引入到PF算法中，可有效改善采样过程。
在PSO算法中，每个粒子依据个体极值和全局极值对各自的速度大小和位置进行更新^[14]。在n维空间中，个体极值P_i=(p_i1, p_i2, …, p_in)为该粒子经过数次迭代计算，从初始时刻到当前时刻产生的个体最优解；全局极值G=(g₁, g₂, …, g_n)为整个种群从初始时刻到当前时刻搜索产生的群体最优解。更新公式如下：

(3)

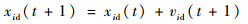(4)

式中：r_1d和r_2d为介于(0，1)区间的随机数；w为惯性系数；c₁和c₂为学习因子。
令粒子适应度函数为

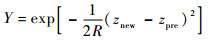(5)

式中：R为观测噪声；z_new为最新观测值；z_pre为预测值。
利用粒子的适用度函数值不断驱动所有种群粒子向最优解的粒子移动。PSO-PF算法步骤如下：
1)初始化粒子集。在k=0时刻，从重要性函数抽样N个粒子，{xⁱ₀, i=1, 2, …, N}。
2)计算粒子适应度值。令k=k+1，利用式(5)计算每一个粒子的适应度值。
3)粒子的权值计算。权值计算公式为

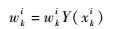(6)

利用式(3)和式(4)更新粒子的速度和位置，更新后粒子位置为{x_k^j, j=1, 2, …, N}。利用式(7)进行权值归一化处理：

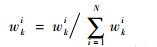(7)

4)粒子重采样。利用式(8)计算有效粒子数N_eff来衡量粒子数匮乏程度。

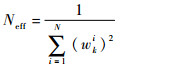(8)

将N_eff与门限值N_thr比较，若N_eff < N_thr，则进行粒子重采样，重采样后得到等权值的粒子集为：{x_k^m, 1/N}_m=1^N。
5) PSO-PF输出。
系统状态估计：

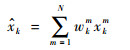6)判断算法是否结束。若未结束，则返回步骤2)；若结束，则退出算法执行步骤。
2 PSO-PF RAIM算法 将PSO-PF算法与RAIM结合检测GNSS的故障卫星。根据接收机获取的量测值，利用PSO-PF算法对系统状态进行估计，计算在不同组合量测值下各时刻的对数似然比(log-Likelihood Ratio, LLR)，在时间窗内进行累加，得到累加LLR^[15]，建立LLR检验统计量，通过一致性检验对故障进行检测。
2.1 GNSS的状态方程和量测方程 GNSS系统的状态方程：

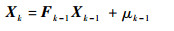(9)

GNSS系统的量测方程：

(10)

式中:X_k=[r_x, r_y, r_z, Δδ]^T为接收机的三维位置坐标和接收机钟差值；F为转移矩阵，当接收机静止时，F为单位矩阵；μ为GNSS系统状态过程噪声；ρⁱ为第i颗卫星(S_xⁱ, S_yⁱ, S_zⁱ)到接收机的伪距值；为第i颗卫星到接收机的距离；c为光速；Δδⁱ为第i颗卫星与接收机的时间偏差；Tⁱ为对流层延迟；Iⁱ为电离层延迟；Eⁱ为星历误差；vⁱ为量测噪声^[16-17]。
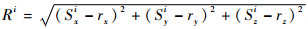
设接收机定位解算的可见卫星数目m=9，且存在一个故障，令y₁、y₂、y₃、y₄、y₅、y₆、y₇、y₈和y₉为测量值。PSO-PF RAIM算法的原理框图如图 1所示。图中：y_M为全部观测伪距集合；y_A，y_B，…，y_J为去掉一个测量值后的部分观测伪距集合；Main PSO_PF为主滤波器；Sub PSO_PF Q(Q=A, B, …, J)为辅滤波器；(i=M, A, …, J)为状态估计；pⁱ(y)(i=M, A, …, J)为概率密度函数；S (i)(i=A, B, …, J)为累加LLR。

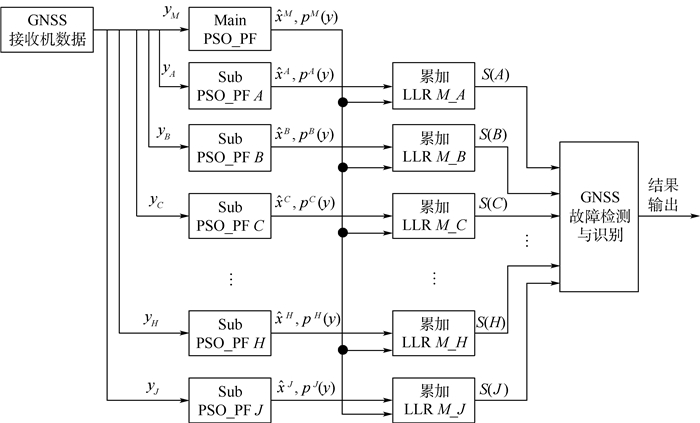图 1 PSO-PF RAIM原理框图 Fig. 1 Principle block diagram of RAIM based on PSO-PF

图选项

在图 1中，当只有一颗卫星发生故障时，9个辅滤波器中有一个不含故障卫星的测量组合，若一致性检验超出告警阈值，则检测出故障。
2.2 LLR检验统计量 累加LLR检验统计量为

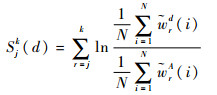(11)

一致性检验的判决函数为

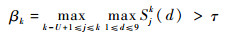(12)

式中：U为时间窗；τ为检测门限。
当β_k>τ时，检测出故障，发出告警，并将告警时刻记为t_a，依据式(13)可得到故障卫星：

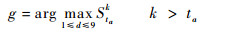(13)

在系统正常工作的情况下，S_j^k函数曲线平稳；当系统在某时刻数据发生变化时，S_j^k函数曲线会在数据变化之后产生一个明显的正向曲线漂移，即会有较大的曲线变化率，以此来判断是否发生故障^[18-20]。
PSO-PF RAIM算法的步骤如下：
1)粒子初始化。设接收机的初始坐标为(r_x, r_y, r_z)，根据接收机的初始坐标产生Main PSO_PF初始粒子集{x^M₀(i), i=1, 2, …, N}和Sub PSO_PF Q(Q=A, B, …, J)初始粒子集{x^q₀(i), i=1, 2, …, N}。
2)在第k时刻重复步骤(1)~步骤(9)：
(1)粒子状态预测。将初始化粒子集分别代入GNSS状态方程式(9)，得到粒子的状态预测值x^M_k|k-1(i)和x^q_k|k-1(i)。
(2)粒子适应度计算。根据接收机的量测值，将第q颗卫星的坐标值(s_x^q, s_y^q, s_z^q)、钟差Δδ、星历误差E^q、对流层延迟T^q、电离层延迟I^q和x^M_k|k-1(i)、x^q_k|k-1(i)代入测量方程式(10)中，计算每个粒子对第q颗卫星的伪距预测值x^q_k|k-1(i)。将接收机测量的伪距值ρ^q和预测伪距值x^q_k|k-1(i)代入适应度公式(5)，计算粒子的适应度，得到粒子的权值。
(3)粒子速度和位置的更新。对粒子的速度和位置进行更新，得到优化后的粒子x^M_k|k-1(i)和x^q_k|k-1(i)。
(4)粒子的权值归一化。将粒子的权值进行归一化处理，得到和。
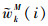
(5)累加LLR。计算累加LLR。
(6)判决函数。计算故障判决函数β_k。
(7)故障检测。若β_k < τ，则当前时刻未检测到故障发生，跳至步骤(9)；若β_k>τ，则检测到有故障，记故障告警时刻为t_a=k，跳至步骤(8)。
(8)故障识别。在t_a=k条件下，计算出Q个子PSO-PF中最大的累加LLR值，进行故障识别。
(9)重采样和状态更新。计算x^M_k|k-1(i)和x^q_k|k-1(i)的有效粒子数N_eff，与门限值N_thr比较。若进行重采样，则经过重采样的粒子为x^M_k|k-1(i)和x^q_k|k-1(i)，权值为1/N。状态更新为

3 算法验证与结果分析 采用2014年5月29日所采集的数据验证本文算法，数据采集的时间长度为86 400 s。从数据中提取卫星坐标、伪距值、电离层误差和对流层误差等数据。在算法验证中，选择其中1 000 s的数据，此时解算的卫星共有9颗，卫星编号分别为1、12、14、15、17、22、24、26和28。
为验证本文算法的性能，t=500 s时，在1号卫星的无故障的观测伪距值中，人为地加入不同偏差，进而验证算法对不同偏差的检测结果，并选择基于基本PF RAIM算法进行比较。粒子数N=50，检测门限值τ=20，窗函数长度U=30，粒子群优化迭代次数k=10。
t=500 s时，在1号卫星的观测伪距中分别加入15 m、20 m和30 m阶跃偏差，在不同偏差下得到的累加LLR值和不同算法的判决函数如图 2~图 4所示。

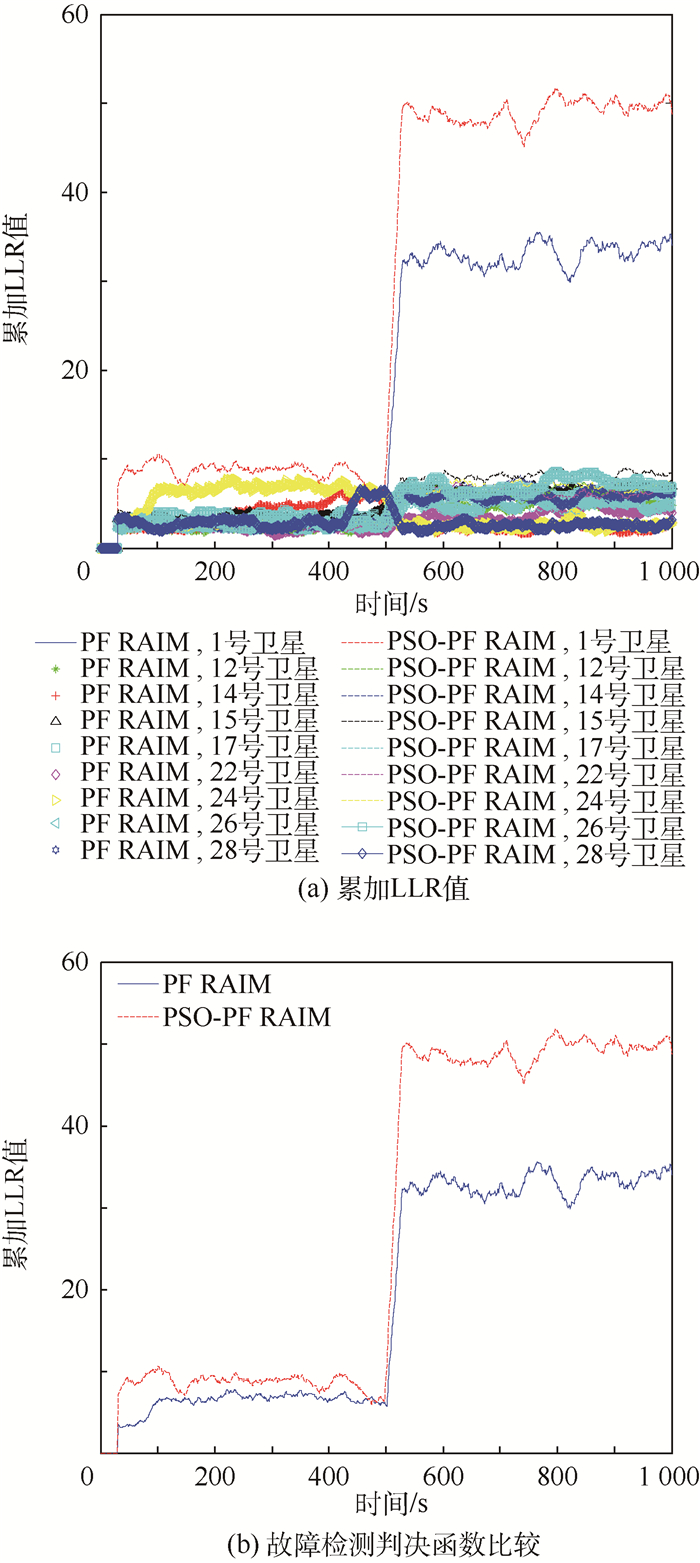图 2 偏差为15 m时累加LLR值和故障检测判决函数比较 Fig. 2 Cumulative LLR and comparison of decision function for fault detection under 15 m step failure

图选项

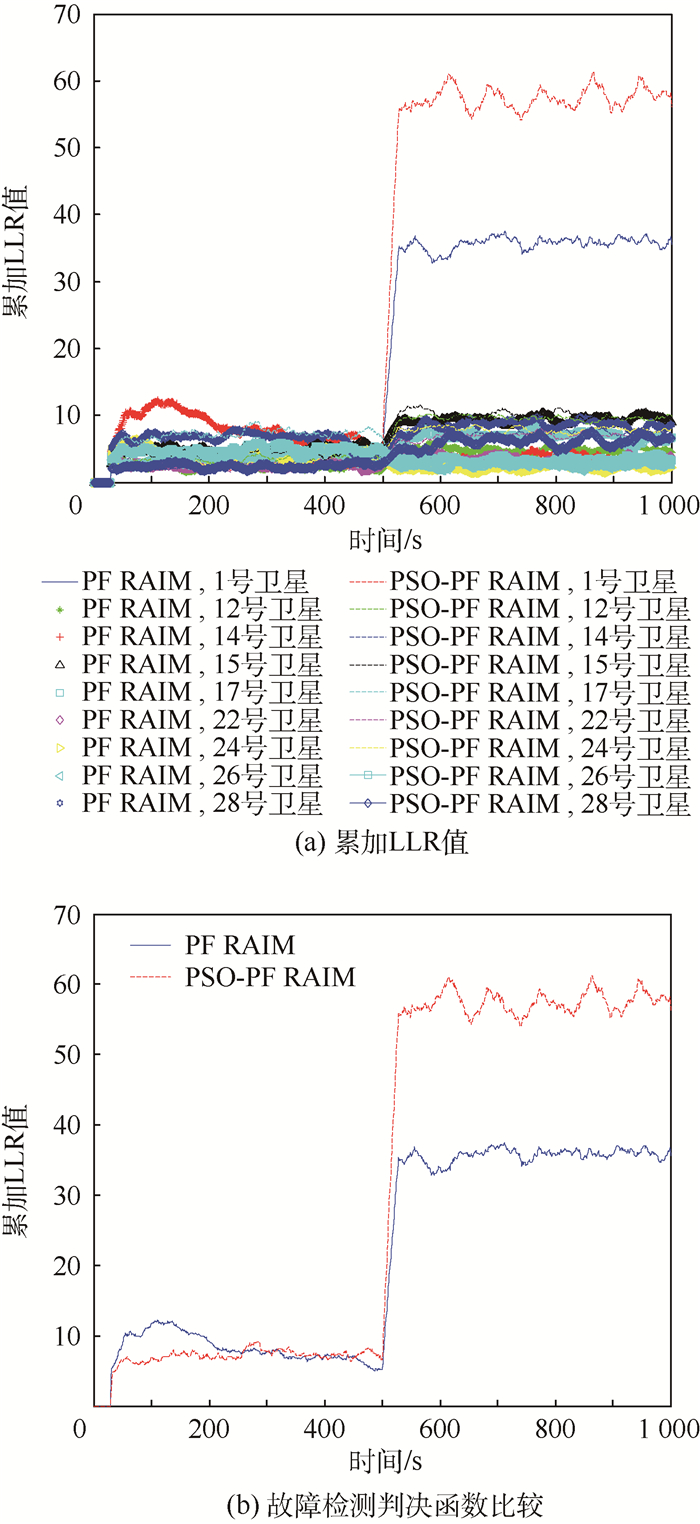图 3 偏差为20 m时累加LLR值和故障检测判决函数比较 Fig. 3 Cumulative LLR and comparison of decision function for fault detection under 20 m step failure

图选项

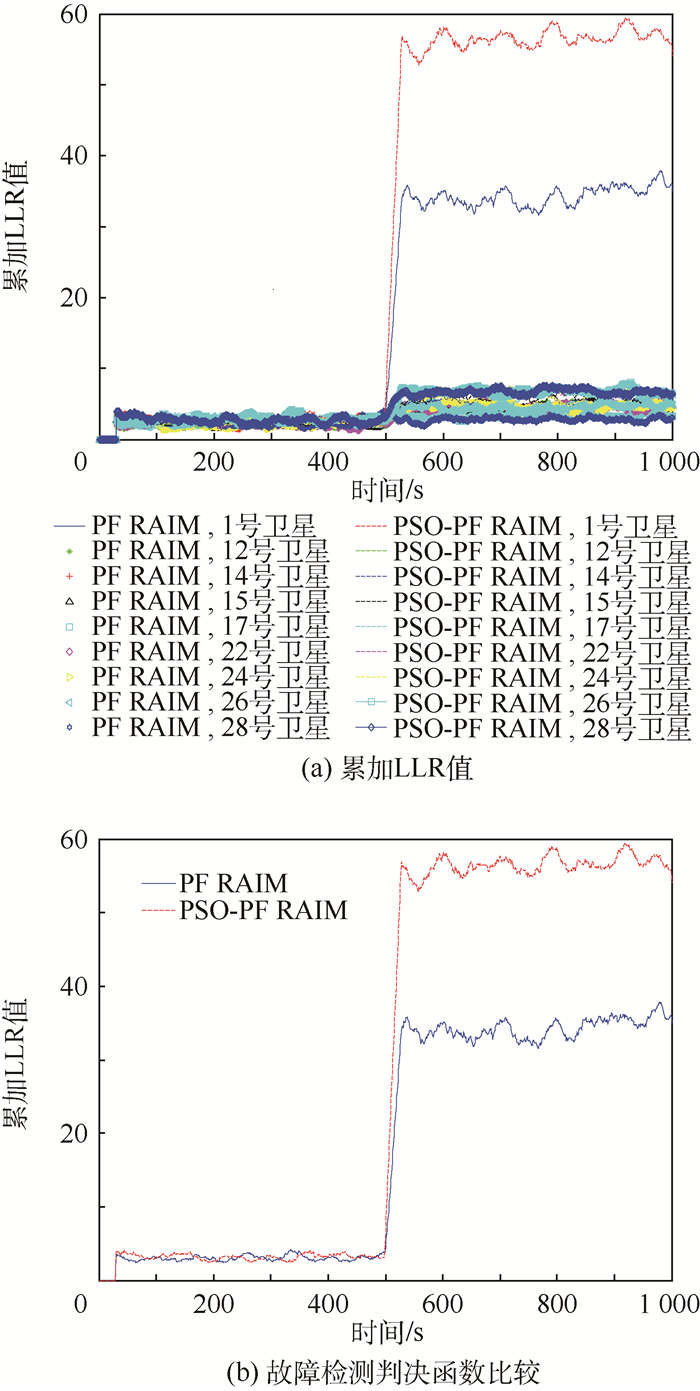图 4 偏差为30 m时累加LLR值和故障检测判决函数比较 Fig. 4 Cumulative LLR and comparison of decision function for fault detection under 30 m step failure

图选项

从图 2~图 4的结果可以看出，t=500 s时，在不同的偏差下，PSO-PF RAIM算法和PF RAIM算法得到的累加LLR值都出现了较大跳变。在15 m、20 m和30 m偏差情况下，偏差越大，故障检测统计量的累加LLR值越大，超过检测门限τ，可以检测并识别出故障卫星。从图 2~图 4中结果也可以看出，在相同偏差下，PSO-PF RAIM算法比PF RAIM算法具有更好的检测性能。
PSO-PF RAIM算法和PF RAIM算法检测到故障时的告警时刻对比如表 1所示。
表 1 PSO-PF RAIM算法和PF RAIM算法的故障检测告警时刻比较 Table 1 Comparison of alarm time for fault detection for PSO-PF RAIM algorithm and PF RAIM algorithm

伪距偏差/m	告警时刻/s
	PSO-PF RAIM算法	PF RAIM算法
15	510	518
20	505	514
30	505	509

表选项






在不同偏差下，PSO-PF RAIM算法和PF RAIM算法得到的平均有效粒子数如表 2所示。
表 2 不同偏差下PSO-PF RAIM算法和PF RAIM算法的平均有效粒子数(N=50) Table 2 Average effective number of particles under different bias for PSO-PF RAIM algorithm and PF RAIM algorithm (N=50)

伪距偏差/m	平均有效粒子数
	PSO-PF RAIM算法	PF RAIM算法
15	43.8	42.1
20	44.7	42.0
30	44.6	42.8

表选项






从表 1和表 2可以看出，PSO-PF RAIM算法故障检测告警的时间比PF RAIM算法的告警时间要短，PSO-PF RAIM算法比PF RAIM算法有更高的故障检测灵敏度。在加入相同的伪距偏差情况下，PSO-PF RAIM算法的平均有效粒子数比PF RAIM算法的平均有效粒子数多。对不同伪距偏差下，PSO-PF RAIM算法和PF RAIM算法的平均有效粒子数进行平均得到：PSO-PF RAIM算法的平均有效粒子数为44.4，PF RAIM算法平均有效粒子数为42.3。通过比较可知，采用PSO-PF RAIM算法能够增加有效粒子数，可提高RAIM算法的检测性能。
4 结论 本文将PSO-PF算法引入RAIM算法中进行故障检测与隔离。建立了故障检测与故障识别算法模型，利用累加LLR比建立检验统计量进行RAIM。通过采集观测数据，加入不同的伪距偏差，验证了PSO-PF RAIM算法的故障检测性能。结果表明：
1)在加入不同伪距偏差的情况下，PSO-PF RAIM算法能够有效检测出卫星故障。
2) PSO-PF RAIM算法提高了有效粒子数目，其整体性能优于PF RAIM算法的性能。
3) PSO-PF RAIM算法在卫星故障检测中是可用且有效的，该研究对BDS接收机自主完好性监测具有一定的参考。

参考文献

[1]	JOERGER M, CHAN F C, LANGEL S, et al.RAIM detector and estimator design to minimize the integrity risk[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington, D.C.:ION, 2012:2785-2807.
[2]	BINJAMMAZ T, AL-BAYATTI A, AL-HARGAN A.GPS integrity monitoring for an intelligent transport system[C]//Proceedings of the 10th Workshop on Positioning Navigation and Communication.Piscataway, NJ:IEEE Press, 2013:1-6.
[3]	BROCARD P, JULIEN O, MABILLEAU M.Autonomous integrity monitoring proposal for critical rail applications[C]//Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington, D.C.:ION, 2015:706-734.
[4]	徐肖豪, 杨传森, 刘瑞华. GNSS用户端自主完好性监测研究综述[J].航空学报, 2013, 34(3): 451–463.XU X H, YANG C S, LIU R H. Review and prospect of GNSS receiver autonomous integrity monitoring[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 451–463.(in Chinese)
[5]	孙国良, 孙明菡, 陈金平. 时-集综合的接收机自主完好性监测方法研究[J].航空学报, 2006, 27(6): 1171–1175.SUN G L, SUN M H, CHEN J P. A study on time and set combined method for receiver integrity autonomous monitoring[J].Acta Aeronautica et Astronautica Sinica, 2006, 27(6): 1171–1175.(in Chinese)
[6]	卢德兼, 陈秀万. GNSS系统接收机自主完好性监测算法[J].计算机工程, 2009, 35(11): 10–12.LU D J, CHEN X W. Algorithm for global navigation satellite system receiver autonomous integrity monitoring[J].Computer Engineering, 2009, 35(11): 10–12.(in Chinese)
[7]	JOERGER M, PERVAN B.Integrity risk of Kalman filter-based RAIM[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington, D.C.:ION, 2011:3856-3867.
[8]	SAYIM B, PERVAN S, PULLEN P, et al.Experimental and theoretical results on the LAAS Sigma overbound[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington, D.C.:ION, 2002:29-38.
[9]	YUN Y, KIM D.Integrity monitoring algorithms using filtering approaches for higher navigation performance:Consideration of the non-Gaussian GNSS measurements[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington, D.C.:ION, 2007:3070-3081.
[10]	GUSTAFSSON F, GUNNARSSON F, BERGMAN N, et al. Particle filters for positioning, navigation, and tracking[J].IEEE Transactions on Signal Processing, 2002, 50(2): 425–437.DOI:10.1109/78.978396
[11]	DOUCET A, GODSILL S, ANDRIEU C. On sequential Monte Carlo sampling method for Bayesian filtering[J].Statistics and Computing, 2000, 10(3): 197–208.DOI:10.1023/A:1008935410038
[12]	ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].IEEE Transactions on Signal Processing, 2002, 50(2): 174–188.DOI:10.1109/78.978374
[13]	王尔申, 庞涛, 曲萍萍, 等. 基于混沌的改进粒子群优化粒子滤波算法[J].北京航空航天大学学报, 2016, 42(5): 885–890.WANG E S, PANG T, QU P P, et al. Improved particle filter algorithm based on chaos particle swarm optimization[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(5): 885–890.(in Chinese)
[14]	方正, 佟国峰, 徐心和. 基于粒子群优化的粒子滤波定位方法[J].控制理论与应用, 2008, 25(3): 533–537.FANG Z, TONG G F, XU X H. A localization method for particle-filter based on the optimization of particle swarm[J].Control Theory and Application, 2008, 25(3): 533–537.(in Chinese)
[15]	ROSIHAN, INDRIYATMOKO A, CHUN S, et al.Particle filtering approach to fault detection and isolation for GPS integrity monitoring[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation.Washington D.C.:ION, 2006:873-881.
[16]	KAPLAN E, HEGARTY C. Understanding GPS:Principles and application[M].2nd edLondon: Artech House, 2006: 39-45.
[17]	王尔申, 张淑芳, 蔡明, 等. 遗传粒子滤波的GPS接收机自主完好性监测[J].西安电子科技大学学报(自然科学版), 2015, 42(1): 136–141.WANG E S, ZHANG S F, CAI M, et al. GPS receiver autonomous integrity monitoring algorithm using the genetic particle filter[J].Journal of Xidian University (Natural Science), 2015, 42(1): 136–141.(in Chinese)
[18]	KADIRKANATHAN V, LI P, JAWARD M H, et al. Particle filtering based fault detection in non-linear stochastic systems[J].International Journal of Systems Science, 2002, 33(4): 259–265.DOI:10.1080/00207720110102566
[19]	WEI T, HUANG Y, CHEN C L P. Adaptive sensor fault detection and identification using particle filter algorithms[J].IEEE Transactions on Systems, Man, and Cybernetics.Part C-Applications and Reviews, 2009, 39(2): 201–213.DOI:10.1109/TSMCC.2008.2006759
[20]	LI P, KADIRKAMANATHAN V. Particle filtering based likelihood ratio approach to fault diagnosis in nonlinear stochastic systems[J].IEEE Transactions on Systems, Man, and Cybernetics.Part C-Applications and Reviews, 2001, 31(3): 337–343.DOI:10.1109/5326.971661