为满足结构重量设计要求,整体结构件中存在大量的槽腔结构,转角是槽腔结构的重要子特征[3]。转角数量大,并且包含碎面、自由曲面等复杂结构。因此,转角数控编程需要在零件数模中大量地重复拾取几何元素、创建几何辅助元素、设置加工参数等操作,造成了编程难度大、重复工作量大、效率低、质量不稳定等问题,使得编程时间占据整个零件编程时间的30 %以上。因此,如何提高转角数控编程效率和质量是飞机生产中亟待解决的难点问题。
特征识别技术被应用于零件特征信息的提取,成为自动编程技术的关键[4]。当前特征识别方法的种类很多,从整体上可以分为3类:①基于边界匹配的特征识别方法,常见的有规则法、图匹配法和痕迹法[5-9],此类方法存在识别特征简单或效率低下,易丢失小特征面等缺陷,无法满足包含碎面转角的识别要求;②基于体分解特征识别方法,常见的有凸包分解法和单元体分解法[10-12],此类方法实现难度大且需要大量的布尔运算,效率低,不适合复杂转角的识别;③分层求交特征识别方法[13-14],对于包含碎面的转角,将导致中间分层数量增加、计算量变大,影响识别效率,另外,对于复杂曲面识别效率较低,因此不适合转角识别。
本文根据转角的几何特征和加工工艺特点,给出了转角特征的明确定义,并提出了基于转角面的自动扩展技术,实现转角特征的计算;结合工艺知识,通过切元计算、干涉域构建等技术建立转角加工模型,在此基础上开发了转角数控加工自动编程系统,该技术满足多种复杂类型转角的自动数控编程需求,而且编程质量稳定、效率高。通过实例测试和生产应用验证该技术的有效性、可行性和实用性。
1 转角及其加工模型定义 从飞机结构件设计数模中,提取必要的几何信息来构建转角加工模型,是实现转角数控加工自动编程技术的基础和前提。下面给出转角的几何定义和表示。
1.1 转角 如图 1所示,以转角所在槽腔的底面体外法向为z轴方向建立局部坐标系Oxyz,转角r可用一个序偶定义和表示为
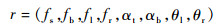 |
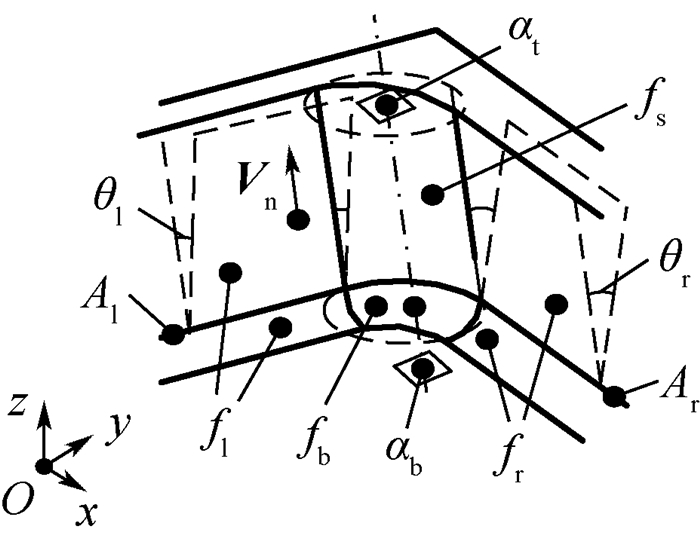 |
| 图 1 转角 Fig. 1 Corner |
| 图选项 |
式中:fs为侧转面;fb为底曲面,即侧转面与槽腔底面之间过渡性的凹特征;fl和fr分别为左侧面和右侧面;αt和αb分别为顶面和底面,并要求αt//αb//xOy;θl和θr分别为左侧面倾角和右侧面倾角。
设Vn为转角的正轴向,即转角轴向与z轴夹角较小的方向。根据右手螺旋定则判定左侧面和右侧面,即掌心面向转角轴线握拳,大拇指指向与Vn一致,四指指向即“fr→fs或fb→fl”方向。
与侧转面相连的左侧面绕曲线Al旋转至与槽腔底面垂直所转过的最小角度为θl;同样的方式可确定θr。
设Vs为侧面体外法向,α=arccos[Vs·z/(|Vs||z|)],若π/2 < α < π,则侧面为闭角面,侧面倾角θ < 0;若0 < α < π/2,则侧面为开角面,侧面倾角θ>0;若α=π/2,则侧面为竖直面,侧面倾角θ=0。
实际数模中,侧转面与底曲面可能是由若干曲面片构成的,如图 2所示,将这些曲面片统称为转角面(rounded corner face),用fc表示。此外,转角加工主要是针对侧转面,因此下文提及的转角面,若无专门说明,皆指构成侧转面的转角面。根据转角面的几何特点,可将其分为柱面和近似柱面等2类。
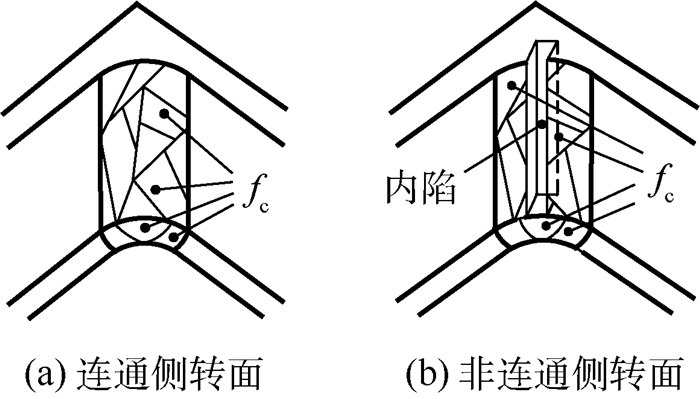 |
| 图 2 转角面 Fig. 2 Rounded corner face |
| 图选项 |
设s={fci|i=1, 2, …, m}为侧转面fs的转角面集,且m>1,若s组成的区域为连通域,则称fs为连通侧转面,如图 2(a)所示,否则,称fs为非连通侧转面,如图 2(b)所示。
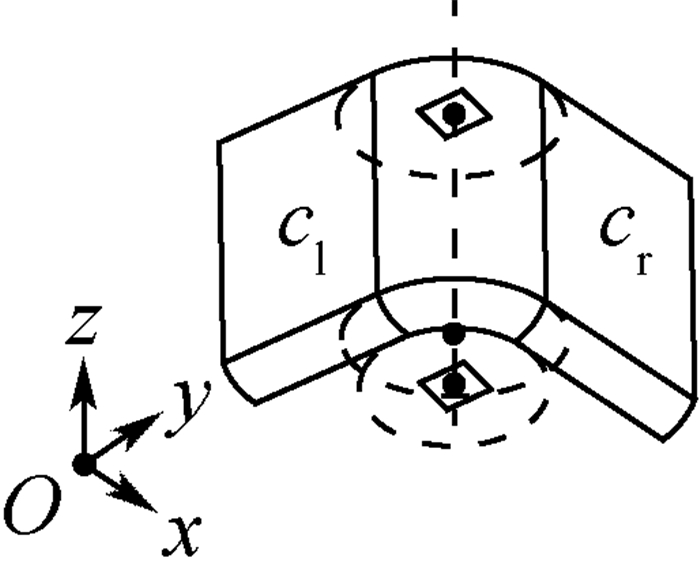
1.2 加工模型 如图 3所示,根据转角及其加工信息建立模型,称为转角加工模型,用Mc表示,并用序偶定义和表示为
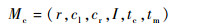 |
 |
| 图 3 转角加工模型 Fig. 3 Processing model of corner |
| 图选项 |
式中:cl和cr分别为左切元和右切元;I为转角加工干涉域;tc为模型类型;tm为转角加工类型(0表示定轴加工; 1表示变轴加工)。
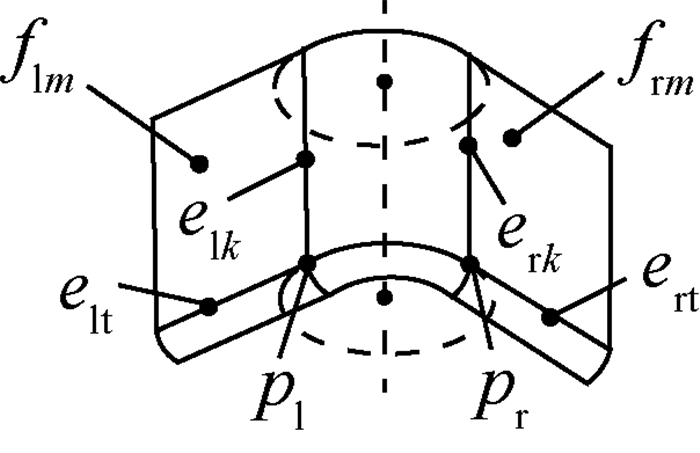
切元(分为左切元cl和右切元cr)是侧转面边界的拓延部分,如图 4所示,切元定义和表示为
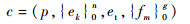 |
 |
| 图 4 切元 Fig. 4 Cutting element |
| 图选项 |
式中:p为界点,逆时针进刀时,最先与刀具接触和最后与刀具分离且在底曲面边界上的侧转面顶点,分别称为右界点pr(右切元的界点)和左界点pl(左切元的界点);ek为界边,p共点关联边中与侧转面轴线平行的转角面边界或与该边界共线的转角面边界,其中,0 < k≤n,n为界边的个数(左切元的界边,称为左界边elk;右切元的界边,称为右界边erk);et为切边,p共点关联边中不属于转角面和底曲面边界的边(左切元的切边,称为左切边elt;右切元的切边,称为右切边ert);fm为切面,侧面被加工区域的面片,其中,0 < m≤g,g为切面的个数(左切元的切面,称为左切面flm;右切元的切面,称为右切面frm)。
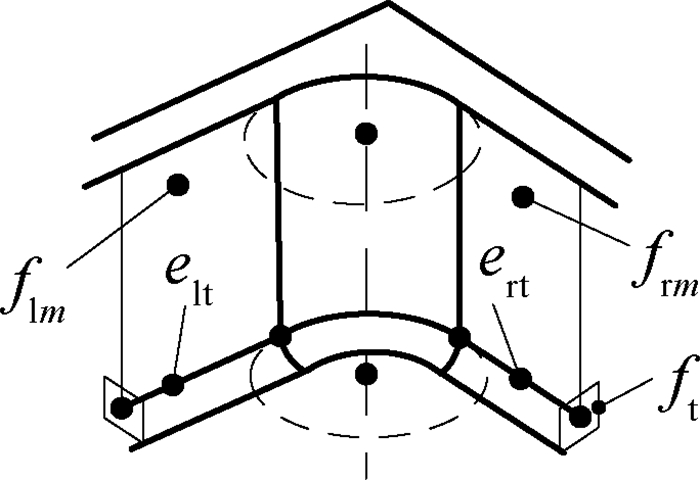
如图 5所示,切元高于转角顶面且对转角加工产生干涉的区域,称为转角加工干涉域,简称干涉域(interference region),表示为
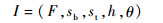 |
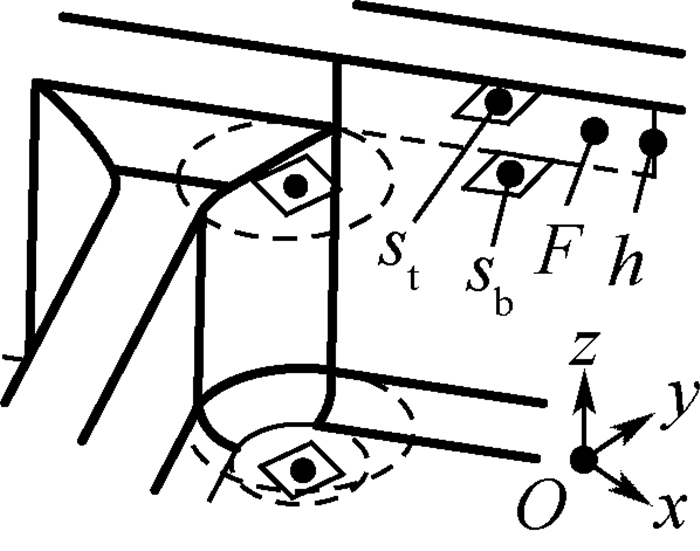 |
| 图 5 干涉域 Fig. 5 Interference region |
| 图选项 |
式中:F为干涉面集;sb和st分别为干涉域的底面和顶面,并要求sb//st//xOy;h为干涉域高度。
干涉域是切元的附属结构,切元是其计算和加工的基础,根据切元的类型,可将干涉域分为左干涉域Il和右干涉域Ir 2类,如图 6和图 7所示。
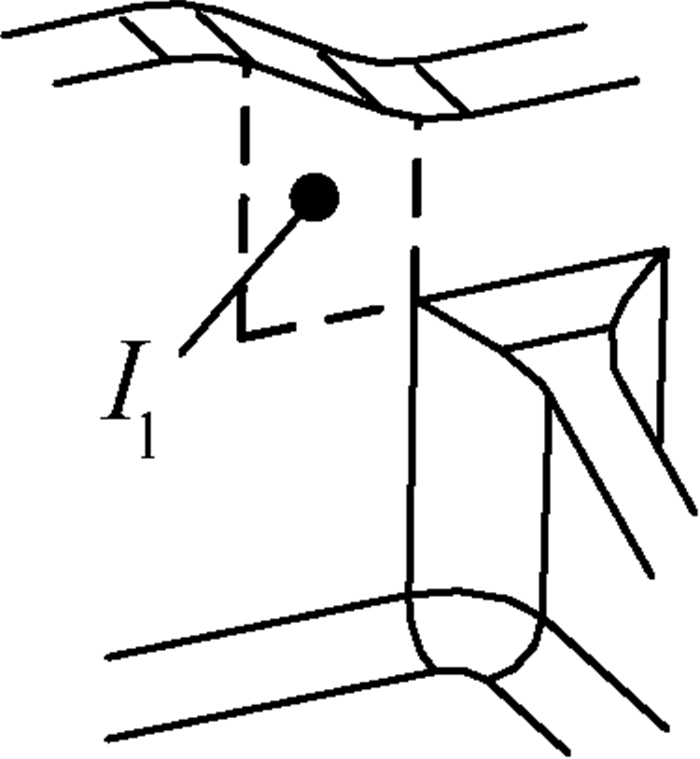 |
| 图 6 左干涉域 Fig. 6 Left interference region |
| 图选项 |
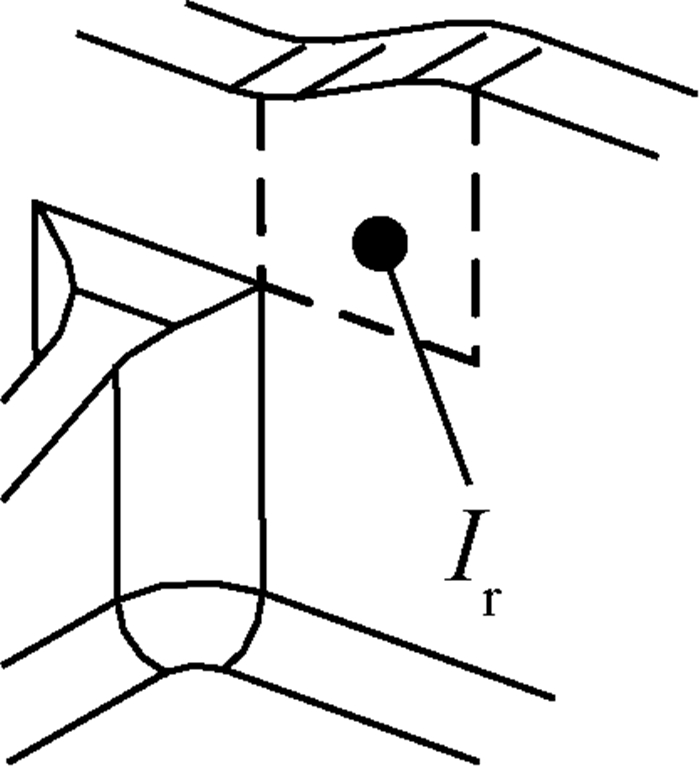 |
| 图 7 右干涉域 Fig. 7 Right interference region |
| 图选项 |
根据I的存在情况,将Mc分为如下4类:
1)若I={Il},则称Mc为左干涉模型。
2)若I={Ir},则称Mc为右干涉模型。
3)若I={Il, Ir},则称Mc为全干涉模型。
4)若I=?,则称Mc为无干涉模型。
对应以上4种类型,tc分别为1,-1,2,0。
加工方式tm为:若θl≠0或θr≠0,则tm=1,否则,tm=0。
2 加工模型构建算法 2.1 算法流程 转角加工模型的构建流程如图 8所示,其中,加工模型的有效性判定,可根据如下准则进行判断:
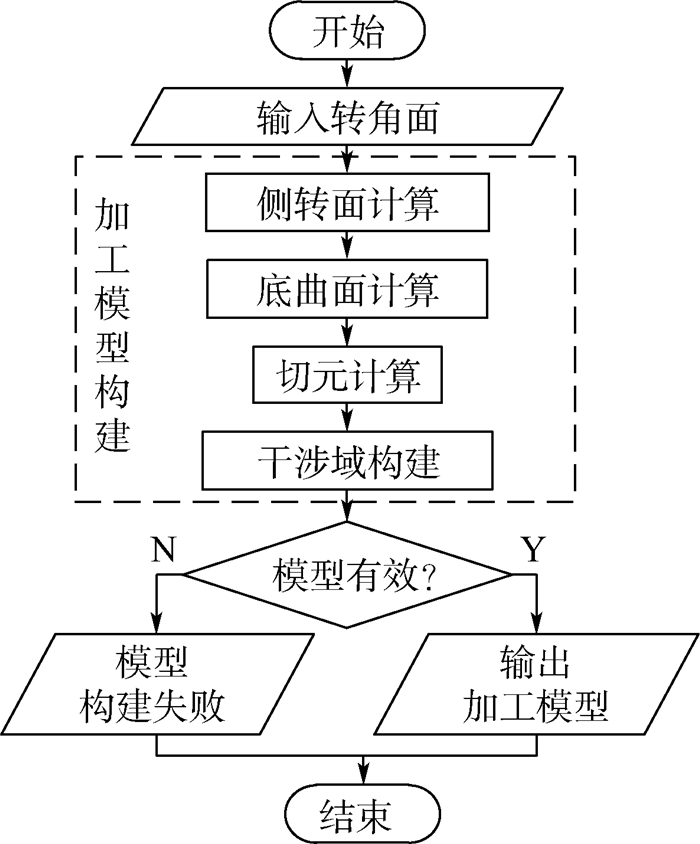 |
| 图 8 加工模型构建流程 Fig. 8 Flowchart of processing model building |
| 图选项 |
有效性判定准则 ??设转角所允许的最大和最小夹角为αmax和αmin,最大和最小半径为rmax和rmin,若加工模型Mc同时满足如下条件:
1)夹角θ满足αmin≤θ≤αmax。
2)侧转面半径R满足rmin≤R≤rmax。
3)包含完整的切入元或切出元。
则Mc为有效加工模型。
2.2 关键技术及算法 加工模型构建的关键技术主要包括侧转面计算、切元计算和干涉域构建等技术,具体如下。
2.2.1 侧转面计算 侧转面计算原理:任选侧转面中一转角面,通过自动扩展技术计算出侧转面的所有转角面,并对侧转面进一步直纹处理,得到一张满足加工要求的侧转面。其计算的关键方法如下。
1)转角面自动扩展技术
转角面的自动拓展是侧转面计算过程中的关键,其计算原理为:利用有效边和有效面的判断方法,以初级转角面为基准,计算出二级转角面,以k级转角面为基准,计算出k+1级转角面,依次逐步计算出所有转角面;计算流程如图 9所示,其中有效边和有效面的判断方法如下:
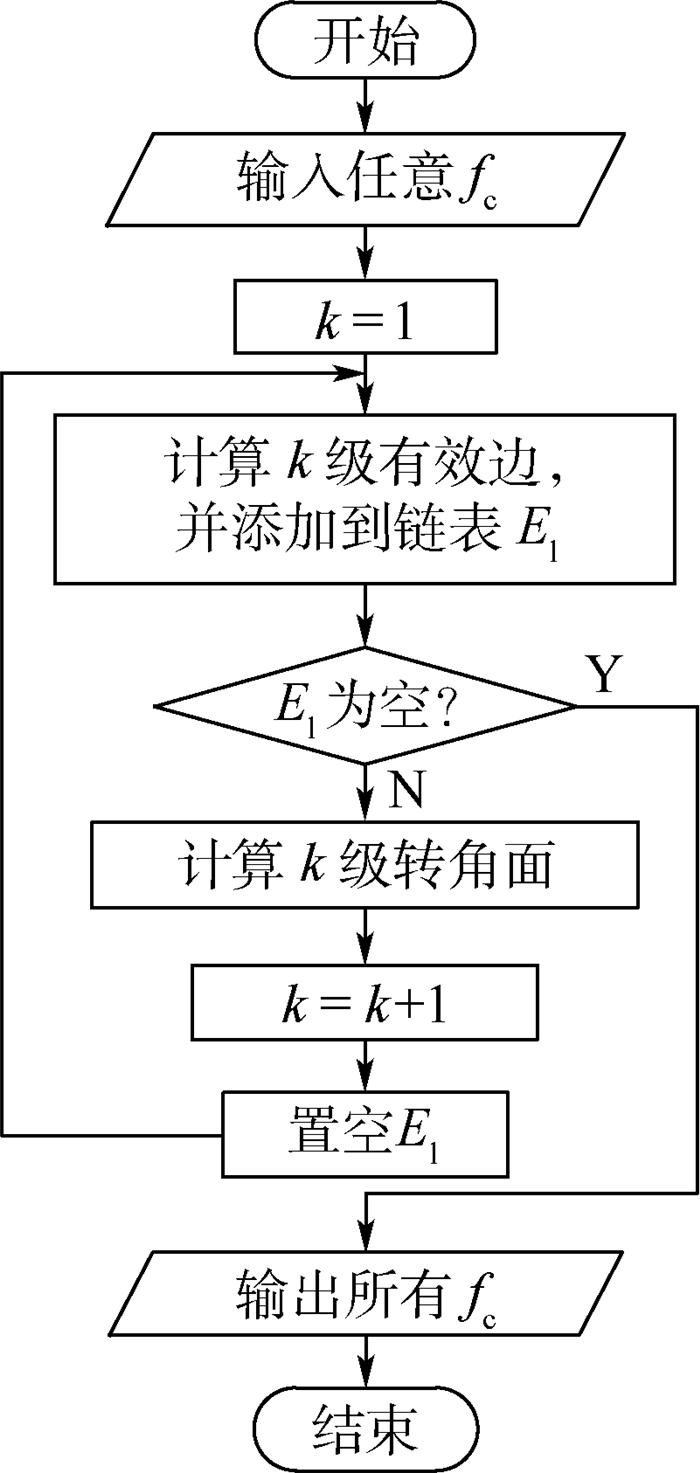 |
| 图 9 转角面自动扩展技术算法流程 Fig. 9 Algorithm flowchart of auto-extended technology for rounded corner face |
| 图选项 |
设lc={li|i=1, 2, …, n}为转角面fc的边集合,且n≥3,li∈lc,li的共边面集合s={fi|i=1, 2},不妨设f1=fc, f2≠fc,若f1和f2满足G2以上连续性,则称li为fc的有效边,f2为fc的有效面。
输入的转角面称为初级转角面,以初级转角面为基准计算所得的所有有效面,称为二级转角面,以n-1级转角面为基准计算所得的所有有效面,称为n级转角面。
n级和n-1级转角面集合分别为fcn和fcn-1,fcn所有转角面的边lc={li|i=1, 2, …, m; m≥3},li∈lc,li的共边面集合s={fi|i=1, 2},不妨设f1∈fcn,若f1和f2满足G2连续,且f2?fcn,f2?fcn-1,则称li为n级有效边,f2为n级有效面。
对于连通侧转面,如图 10(a)所示,可通过输入任意转角面fc,直接利用上述方法计算其所有转角面;对于非连通侧转面,如图 10(b)所示,利用分而治之的思想,分别计算侧转面各部分曲面上的转角面,进而计算出所有转角面。
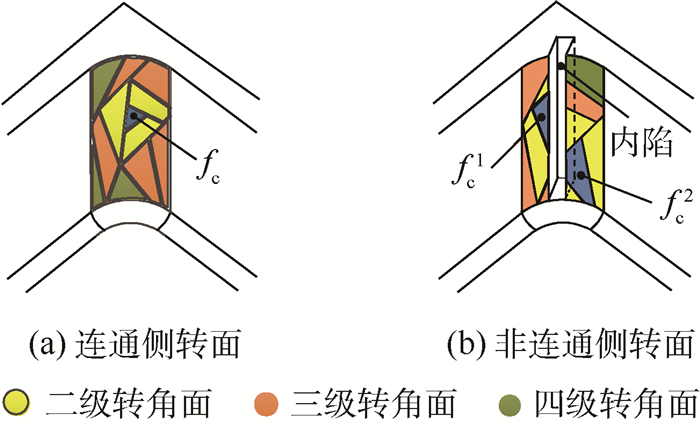 |
| 图 10 转角面计算 Fig. 10 Rounded corner face calculation |
| 图选项 |
2)直纹处理
Zhou等[15]提出基于特征的碎面自动拟合方法,该方法不适合非连通侧转面等复杂类型侧转面的处理;通常直纹面造型需要给定2条相对的初始边界,2条边界称为基线,然后将基线上相应的等参数点用直线相连接来构造直纹面[16]。本文采用此直纹面造型方法,并结合侧转面的几何特点,给出其直纹面拟合的主要步骤如下。
①截面线生成
为了获取侧转面的大致外形,以一组平面与其求交,得到交线称为截面线[17]。截面线是拟合直母线的基础,为了得到有效的截面线,需要合理地布置各截平面。在此,截平面是以侧转面与底曲面的交线为参考等距生成的,如图 11所示,将此参数线的切矢作为平面的法向量可得到截平面,各截平面之间的距离可视碎面大小而定。
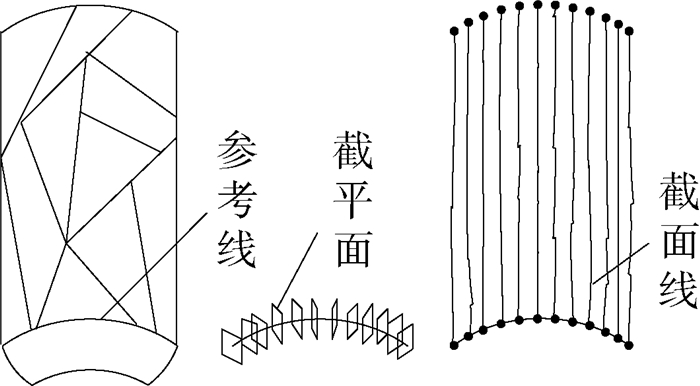 |
| 图 11 截面线生成 Fig. 11 Section curves creation |
| 图选项 |
②母线拟合
得到截面线后,以等参数采样的方法从截面线中获取一组离散的点,采用最小二乘法将这组离散点拟合成一条直线作为母线,重复进行便可得到所有母线。
③基线拟合
在上一步所拟合母线的基础上,以三次B样条曲线插值于所有母线的端点,可得到直纹面的2条基线。再利用Deboor算法,分别在2条基线上计算出更多的数据点。当数据点密集到一定程度后,连接2条基线上对应的数据点即可得到所需拟合的直纹面,并将此直纹面作为侧转面的近似面。
2.2.2切元计算
由切元定义可知,其主要包括界点、界边、切边、切面等参数,下面详细阐述切元的计算过程。
1)界点计算
任意转角,如图 12所示,其正轴向为Vn,转角面集合为s,左界点和右界点计算算法如下:
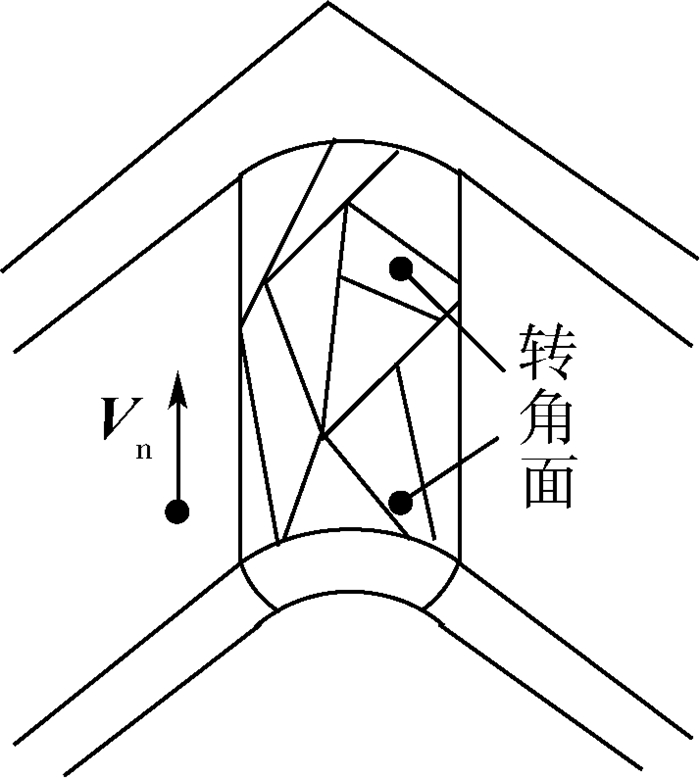 |
| 图 12 转角示例 Fig. 12 Corner sample |
| 图选项 |
步骤1 ??提取s中所有元素的顶点p1, p2, …, pm, m>1, Oc为侧转面的原点。
步骤2 ??计算Oc与p1, p2, …, pm之间的向量,并计算其在Vn垂直方向上的分量,形成向量序列为
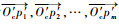
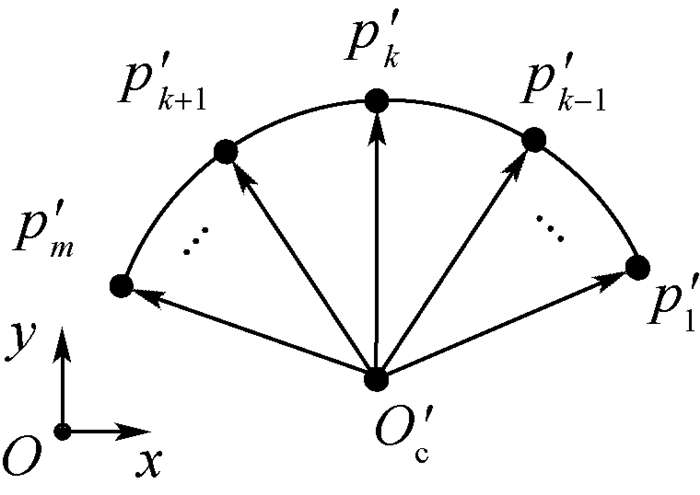 |
| 图 13 投影向量 Fig. 13 Projected vector |
| 图选项 |
步骤3??任取向量
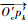
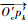
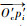
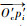
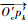
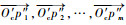
 |
| 图 14 更新顶点 Fig. 14 Update vertices |
| 图选项 |
步骤4 ??计算与
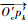
步骤5 ??分别计算顶点序列p′′1, p′′2, …, p′′l和p′′m-1, …, p′′m-j中z坐标最小的点pr和pl,pl和pr即为转角左界点和右界点。
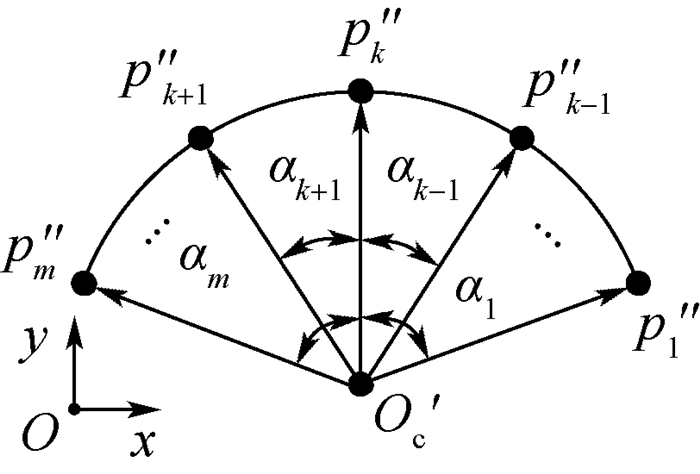
如图 15所示,分别过p′′1和p′′m作向量
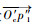
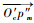
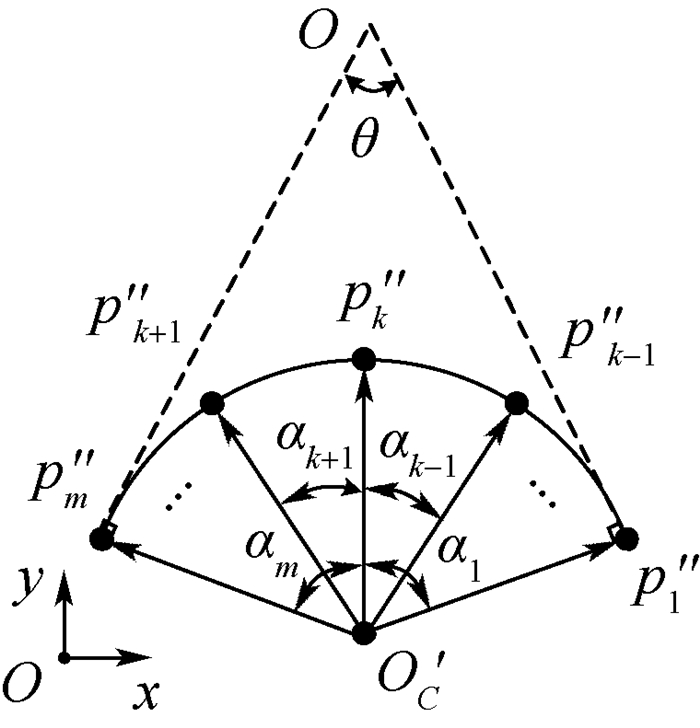 |
| 图 15 转角夹角 Fig. 15 Corner angle |
| 图选项 |
2)界边
界边是侧转面的边界,其判定准则如下:
界边判定准则 ??设s所有元素的边集合为ec,以界点p为端点的边集合为es,若边e同时满足如下条件:①e∈ec, e∈es;②e//Vn。
那么,与e共线且属于ec的所有边集合eb={ei|i=1, 2, …, n; n≥1}即为界边集合。
根据pl和pr,可分别计算左右界边集合{elk}0n和{erk}0n。
3)切面及切边计算
与界边共边的侧面为平面的转角,其精加工区域的轴向外轮廓G,是计算切面及切边的基础,如图 16所示,G可分为3段:①右切段:以prs为起点,pre为终点的直线段,表示为Gr,逆时针进刀时,刀具沿该段逐步切入侧转面且切宽逐渐增大,长度为lr;②圆弧段:以pre为起点,pls为终点的圆弧段,表示为Ga,转角加工过渡段;③左切段:以pls为起点,ple为终点的直线段,表示为Gl,刀具沿该段逐步切出侧转面且切宽逐渐减少,长度为ll。
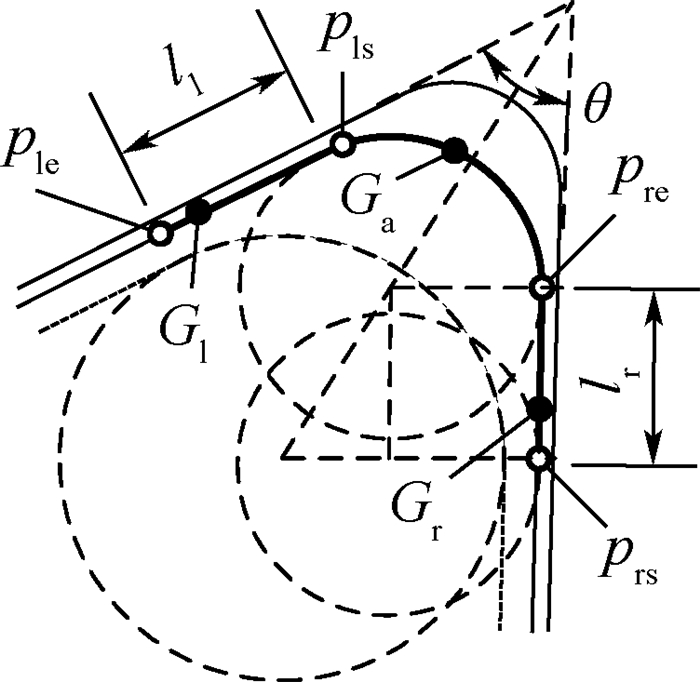 |
| 图 16 加工区域轴向外轮廓 Fig. 16 Axial-profile of machining region |
| 图选项 |
如图 16所示,左切段和右切段长度为
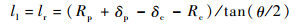 |
式中:Rp为上把刀具半径;δp为上把刀具切削余量;Rc为当前刀具半径;δc为当前刀具切削余量。
圆弧段半径Ra为:①若Rc≤R-δc,则Ra=R-δc;②若Rc>R-δc,则Ra=Rc。由此,完成外轮廓G计算。
右切边计算流程如下:
步骤1 ??获取pr共点边集合erc,并计算erc中满足et∈erc, et?ec, et⊥Vn的元素et,若et不存在,则ert是以pr为端点,
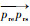
步骤2以
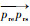
 |
| 图 17 切边 Fig. 17 Cutting edge |
| 图选项 |
同样的方法可计算elt。
右切面计算流程如下:
步骤1 ??获取{erk}0n的所有共边面集合fr,并计算fr=fr-s,若集合fr为空,则fr为侧转面在右界边处沿
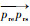
步骤2 ??若ft与fr存在交线,其交线集合为ei,则{frm}0h为fr存在{erk}0n和ei之间的部分;若ft与fr不存在交线,则{frm}0h=fr。
同样的方法可计算{flm}0h。
2.2.3 干涉域构建 干涉域构建流程如图 18所示,根据左切面和右切面可分别判断左干涉域和右干涉域存在与否,并对其进行计算。其中,右干涉域计算结果如图 19所示。
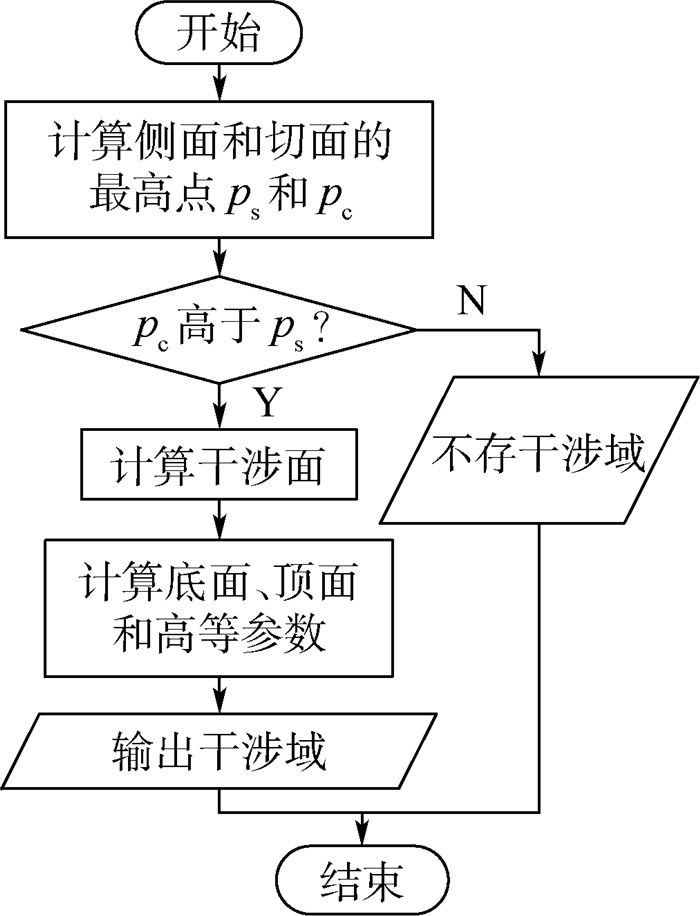 |
| 图 18 干涉域构建流程 Fig. 18 Flowchart of interference region building |
| 图选项 |
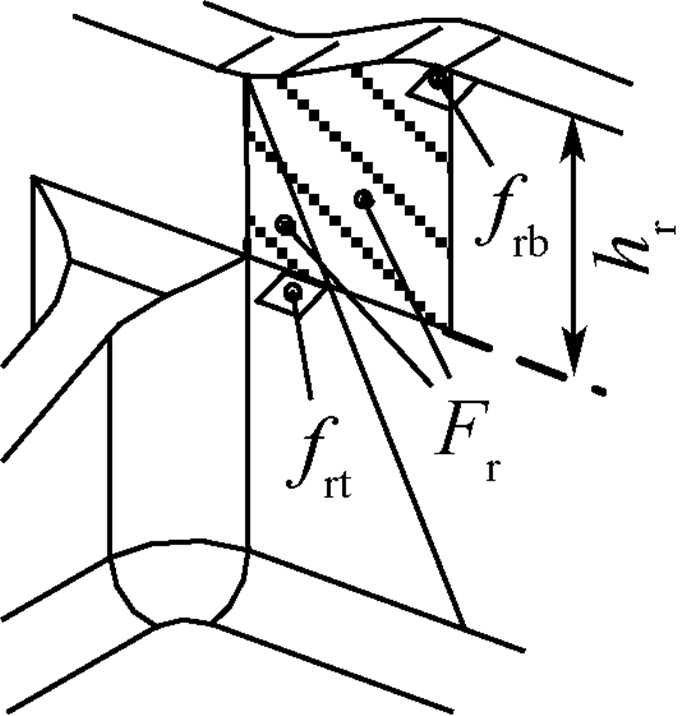 |
| 图 19 右干涉域计算结果 Fig. 19 Calculation results of right interference region |
| 图选项 |
3 算法实现及测试 基于CATIA V5软件平台,利用专业的开发工具CAA (Component Application Architecture),在Visual Studio 2008环境中以VC++为编程语言对本文所研究的内容进行开发,并在此基础上开发了“转角数控加工自动编程系统”。本文以不同类型的转角特征为测试对象,其中,转角加工模型实例如图 20所示,基于转角加工模型计算的转角加工刀轨的仿真如图 21所示。生产应用表明,该技术构建不同类型的转角加工模型,并能够计算出正确加工刀轨的比率如表 1所示。从表中数据可知,对于连通侧转面和非连通侧转面类型的转角特征计算正确率分别达到97.5%和95.1%以上,验证本文所研究内容的正确性和有效性。
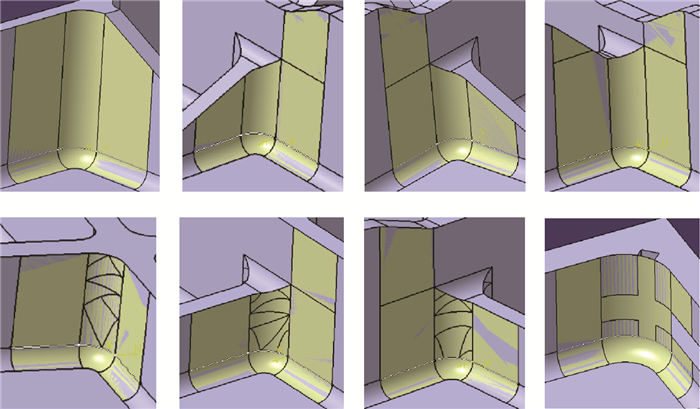 |
| 图 20 转角加工模型实例 Fig. 20 Case of processing model of corner |
| 图选项 |
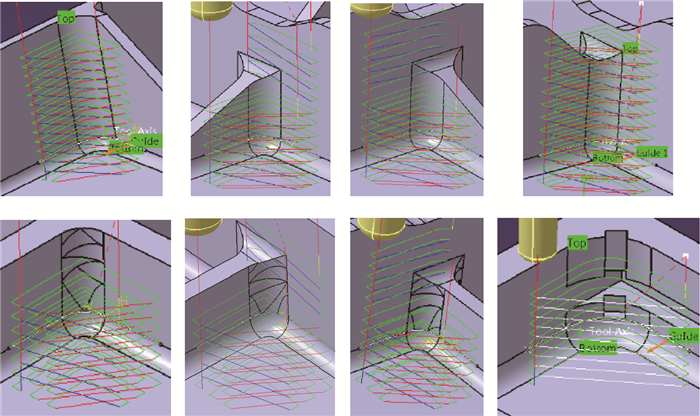 |
| 图 21 转角加工刀轨仿真 Fig. 21 Tool path simulation of corner machining |
| 图选项 |
表 1 转角特征计算正确率 Table 1 Calculation accuracy of corner feature
| 类型 | tc | 正确率/% |
| 连通侧转面 | 0 | 98.5 |
| 1 | 98.2 | |
| -1 | 98.2 | |
| 2 | 97.5 | |
| 非连通侧转面 | 0 | 97.2 |
| 1 | 96.5 | |
| -1 | 96.5 | |
| 2 | 95.1 |
表选项
以数控程序编制交互次数表示编程工作量,各类转角加工数控程序编制工作量及耗时对比如表 2所示,其中ηt和ηw分别表示时间效率和工作效率。从表中数据可知,自动编程与手工编程相比,对于连通侧转面类型的转角,提高时间效率和工作效率在99.2%和97.5%以上;对于非连通侧转面类型的转角,提高时间效率和工作效率在98.3%和92.5%以上。由此说明,本文所研究的内容可以显著提高转角加工效率,降低工作量。
表 2 转角加工数控编程工作量及耗时对比 Table 2 Workload and time-consumption of corner machining numerical control programing
| 类型 | tc | 平均交互次数 | 平均耗时/s | 效率/% | |||
| 手工 | 自动 | 手工 | 自动 | ηt | ηw | ||
| 连通侧转面 | 0 | 40 | 1 | 120 | 1 | 99.2 | 97.5 |
| 1 | 60 | 1 | 180 | 1 | 99.4 | 98.3 | |
| -1 | 60 | 1 | 180 | 1 | 99.4 | 98.3 | |
| 2 | 70 | 1 | 240 | 1 | 99.6 | 98.6 | |
| 非连通侧转面 | 0 | 40 | 3 | 120 | 2 | 98.3 | 92.5 |
| 1 | 60 | 3 | 180 | 2 | 98.9 | 95.0 | |
| -1 | 60 | 3 | 180 | 2 | 98.9 | 95.0 | |
| 2 | 70 | 3 | 240 | 2 | 99.2 | 95.7 | |
表选项
4 结论 本文研究的转角特征计算和加工模型构建方法是在总结转角数控加工工艺特点、数控编程方法以及转角结构特点的基础上提出的,取得的具体成果如下:
1)该技术无需进行繁琐的交互操作和复杂的几何计算,只需交互选取任意一转角面,即可自动完成转角特征计算,并建立其加工模型,特征计算准确、高效,实用性强。
2)基于加工模型研究开发的转角数控加工自动编程系统已成功应用于某型号飞机的生产,转角数控加工程序编制效率提高95%以上,而且加工质量更高、更稳定。
生产应用表明,本文所研究的内容具备很高的实用价值。
参考文献
| [1] | CHEN S L, ZHENG G L, ZHOU M, et al. Process-scheme-driven automatic construction of NC machining cell for aircraft structural parts[J].Chinese Journal of Aeronautics, 2013, 26(5): 1324–1335.DOI:10.1016/j.cja.2013.07.035 |
| [2] | 施建飞, 李迎光, 刘旭, 等. 基于属性边点图的飞机结构件筋特征识别方法[J].计算机集成制造系统, 2014, 20(3): 521–529.SHI J F, LI Y G, LIU X, et al. Rib feature recognition method for aircraft structural parts based on vertex attributed adjacency graph[J].Computer Integrated Manufacturing Systems, 2014, 20(3): 521–529.(in Chinese) |
| [3] | 高鑫, 李迎光, 张臣, 等. 飞机结构件内型转角一体加工刀轨生成方法[J].航空学报, 2014, 35(9): 2660–2671.GAO X, LI Y G, ZHANG C, et al. An integrated machining tool path generation method for corner and profile of aircraft structural parts[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2660–2671.(in Chinese) |
| [4] | TOLOUEI-RAD G M, PAYEGANEH G. A hybrid approach to automatic generation of NC programs[J].Journal of Achievements in Materials and Manufacturing Engineering, 2005, 14(1-2): 83–89. |
| [5] | HAN J H, PRATT M, REGLI W C. Manufacturing feature recognition from solid models:A status report[J].IEEE Transactions on Robotics, 2000, 16(6): 782–796.DOI:10.1109/70.897789 |
| [6] | HENDERSON M R, ANDERSON D C. Computer recognition and extraction of form features:ACAD/CAM link[J].Computers in Industry, 1984, 5(4): 329–339.DOI:10.1016/0166-3615(84)90056-3 |
| [7] | JOSHI S, CHANG T C. Graph-based heuristics for recognition of machined features from a 3D solid model[J].Computer-Aided Design, 1988, 20(2): 58–66.DOI:10.1016/0010-4485(88)90050-4 |
| [8] | 刘雪梅, 张树生, 崔卫卫, 等. 逆向工程中基于属性邻接图的加工特征识别[J].计算机集成制造系统, 2008, 14(6): 1162–1167.LIU X M, ZHANG S S, CUI W W, et al. Machined features recognition based on attributed adjacency graph in reverse engineering[J].Computer Integrated Manufacturing Systems, 2008, 14(6): 1162–1167.(in Chinese) |
| [9] | VANDENBRANDE J H, REQUICHA A A G. Spatial reasoning for the automatic recognition of machinable features in solid models[J].IEEE Transactions on Transacitions on Pattern Analysis & Machine Intelligence, 1993, 15(12): 1269–1285. |
| [10] | TSENG Y J, JOSHI S B. Recognition of interacting rotational and prismatic machining features from 3D mill-turn parts[J].International Journal of Production Research, 1998, 36(11): 3147–3165.DOI:10.1080/002075498192346 |
| [11] | WOO T C.Feature extraction by volume decomposition[C]//Proceedings CAD/CAM Technology in Mechanical Engineering.Cambridge:MIT, 1982:76-94. |
| [12] | SAKURAI H, DAVE P. Volume decomposition and feature recognition, Part Ⅱ:Curved objects[J].Computer-Aided Design, 1996, 28(6-7): 519–537.DOI:10.1016/0010-4485(95)00067-4 |
| [13] | SHEEN B T, YOU C F. Machining feature recognition and tool-path generation for 3-axis CNC milling[J].Computer-Aided Design, 2006, 38(6): 553–562.DOI:10.1016/j.cad.2005.05.003 |
| [14] | YU F F, DU B, REN W, et al. Slicing recognition of aircraft integral panel generalized pocket[J].Chinese Journal of Aeronautics, 2008, 21(6): 585–592.DOI:10.1016/S1000-9361(08)60178-8 |
| [15] | ZHOU G, LI Y, LIU C, et al. A feature-based automatic broken surfaces fitting method for complex aircraft skin parts[J].International Journal of Advanced Manufacturing Technology, 2015, 84(5-8): 1001–1011. |
| [16] | WANG C C L, ELBER G. Multi-dimensional dynamic programming in ruled surface fitting[J].Computer-Aided Design, 2014, 51(6): 39–49. |
| [17] | 任朴林, 周来水, 安鲁陵, 等. 基于散乱数据截面线的曲面重构算法研究[J].机械设计与制造工程, 2003, 32(3): 82–85.REN P L, ZHOU L S, AN L L, et al. A surface reconstruction algorithm based on planar contours of discrete data[J].Machine Design and Manufacturing Engineering, 2003, 32(3): 82–85.(in Chinese) |
