主动磁悬浮轴承 (Active Magnetic Bearings,AMBs) 具有非接触、高转速、长寿命、低功耗及无需润滑等优点[2-3]。基于AMBs的磁悬浮飞轮是常用的姿态控制执行机构,具有输出力矩精度高、振动干扰小等突出优势[4]。普通磁悬浮飞轮仅通过改变飞轮角动量大小输出单自由度姿控力矩,无法明显改善其输出力矩的带宽和响应速度。而具有转轴偏转能力的磁悬浮飞轮还能够改变飞轮角动量的方向,使得单台飞轮就具有3自由度的力矩输出能力,可以对瞬时大干扰力矩进行快速抑制,满足高精度和高稳定度的姿控需求,是实现高分侦查任务的理想执行机构[5-6]。
为提高微框架磁悬浮飞轮的偏转精度,相关磁悬浮技术研究单位和人员利用洛伦兹力型主动磁轴承进行飞轮转子的悬浮支承和扭转输出力矩控制,提高了最大可偏转角和最大偏转力矩,实现了高精度偏转控制[7-11]。采用洛伦兹力磁轴承 (Lorentz Force-type Magnetic Bearing,LFMB) 进行2个自由度的扭转控制具有悬浮功耗低的优点,又可以提高偏转控制的精度。LFMB的电磁力依据安培力定律,位于平行放置的永磁体磁场的通电线圈受到安培力的作用,因此气隙磁密的分布直接决定电磁力的精确度,实际情况下气隙磁密呈非均匀分布,呈现非线性特点。针对LFMB进行高精度偏转控制,研究人员考虑到了气隙磁密的非线性对偏转控制的影响,分别从电磁力矩的非线性建模与补偿[12-14]和改进控制方法[1, 15-16]2个角度进行研究以提高偏转控制的精度和响应速度,却没有从根本上解决LFMB气隙磁密的非线性、非均匀性问题。
为实现甚稳超静,近年来,研究人员提出了基于ABMs的磁悬浮控制敏感陀螺 (Magnetically Suspended Control & Sensing Gyroscope, MSCSG) 新概念,集成惯性执行机构的姿态控制功能和角速率敏感器的姿态测量功能。其中,LFMB实现转子的万向偏转提高控制力矩的精度和带宽。本文介绍了5自由度的球面悬浮的MSCSG结构及其万向偏转特性;基于LFMB基本构型建立了电磁力和电磁力矩模型,分析其精度的主要影响因素为气隙磁密均匀度;针对传统LFMB的气隙磁密非均匀分布问题,通过增加1J50导磁薄片提升磁密均匀度,通过改变永磁体形状增强磁密分布降低功耗和增强其在转子高速旋转下的稳定性,仿真结果表明所设计的LFMB能够有效提高偏转控制精度和角速率测量精度。
1 MSCSG结构及特性 1.1 MSCSG结构及悬浮方案 新提出的MSCSG集惯性测量与惯性执行机构于一体,尚处于概念阶段,须进一步深入研究。MSCSG主要由飞轮转子、径向磁轴承、轴向磁轴承、偏转LFMB、传感器和高速电机等部分组成,其结构如图 1所示。其中高速飞轮转子设计为扁平结构,以获取较大的转动惯量-质量比,减小飞轮质量,从而减小径/轴向磁轴承的体积和承重功耗。
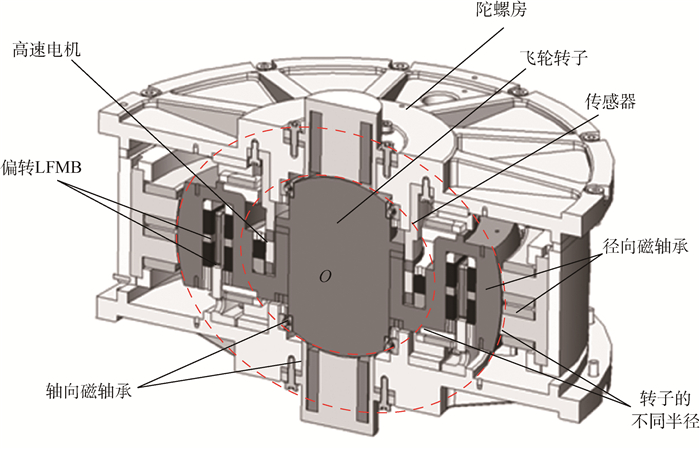 |
| 图 1 MSCSG结构示意图 Fig. 1 Structural schematic diagram of MSCSG |
| 图选项 |
MSCSG的3个自由度的平动主要通过径向球面磁轴承和轴向球面磁轴承悬浮实现,二者转子为分体式同心不同半径双球面结构,同时被2个磁轴承的定子极面组成的同心不同半径的双球面所包络。所用轴承均为纯电磁磁轴承,具有刚度可调、精度可控及耦合最低的优点。径向球面磁轴承采用2对极差动驱动,分别实现x、y方向的平动控制,同时当径向磁轴承转子球面磁极与陀螺转子质心重合时,可实现径向2个平动自由度对径向2个扭动自由度解耦。轴向球面磁轴承采用1对极差动驱动,实现z方向的平动控制。径向2个扭动自由度通过偏转LFMB实现。因此,MSCSG的3个自由度的平动控制和2个自由度的扭动控制可以单独考虑和设计。
1.2 MSCSG转子的万向偏转特性 由于MSCSG采用有间隙的弹性支承,其高速旋转的磁悬浮转子可在有限间隙里作万向扭动,提高控制力矩的带宽,具有万向偏转特性,见图 2。
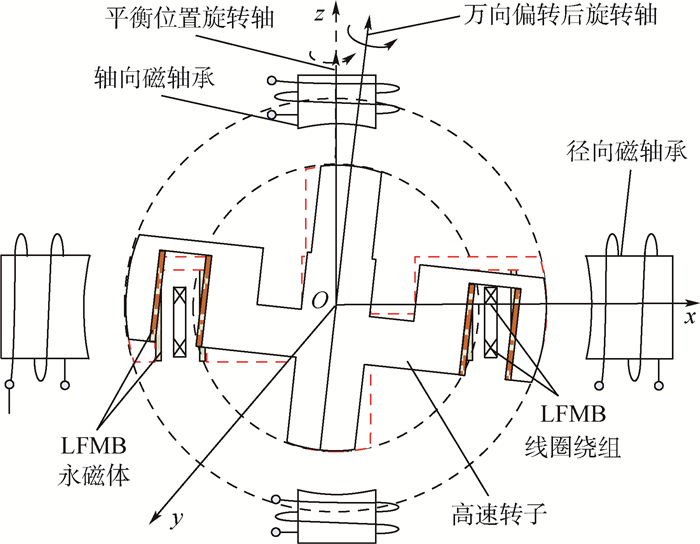 |
| 图 2 MSCSG转子的万向偏转特性 Fig. 2 Universal deflection characteristic of MSCSG rotor |
| 图选项 |
MSCSG不仅可以像惯性执行机构一样,通过框架的转动或转速的变化,输出低带宽的姿态控制力矩;而且它利用磁悬浮有间隙、无摩擦的优势,通过电磁力直接驱动转子任意方向高频往复偏转,驱动电流小,所以带宽高、精度高,正好可以用于抑制天基平台的周期性振动,为解决甚稳超静平台的高频角振动问题提供了新的途径。相比控制力矩陀螺,其偏转力矩通过直驱方式进行,且无摩擦、幅值小,从而实现高精度高带宽力矩输出。
与框架力矩相比,偏转力矩高精度、高带宽的原因主要体现在以下3个方面:①从驱动力方式来看,框架力矩是间接旋转驱动,存在摩擦和传动延时,而偏转力矩是直接线性驱动,不存在摩擦和传动延时;②从驱动力方向来看,框架力矩采用的是磁力切向分力 (与转角位置成非线性,控制精度低),而偏转力矩采用的是法向力 (与位移成线性,控制精度高);③从运动检测精度来看,框架力矩采用的是测角 (最小量程),精度低,而偏转力矩则测位移 (最大量程),精度高。
2 LFMB电磁力矩建模与分析 LFMB用来驱动磁悬浮转子进行高频万向偏转,输出高精度、高带宽的偏转控制力矩,根据LFMB基本模型,构建其电磁力矩数学模型,用于精确分析影响力矩精度的关键因素,对LFMB的优化设计提供指导。
2.1 LFMB的基本模型 LFMB主要由内外永磁体、定子骨架、线圈绕组和传感器等组成,基本结构如图 3 (a) 所示。
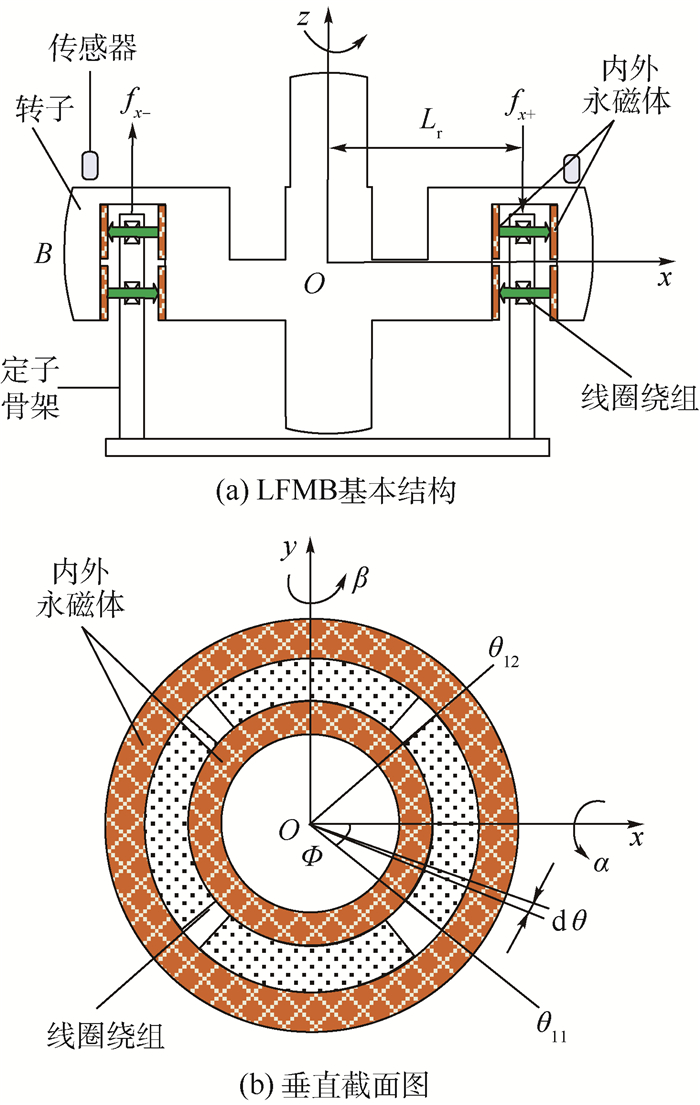 |
| Lr—定子半径;fx+—x+向转子所受电磁力;fx-—x-向转子所受电磁力;B—线圈位置气隙磁密;β—绕y轴的偏转角;α—绕x轴的偏转角;θ11—第1组线圈的起端角度;θ12—第1组线圈的末端角度;dθ—线圈微元;2Φ—线圈周向张角。 图 3 LFMB结构示意图 Fig. 3 Structural schematic diagram of LFMB |
| 图选项 |
图 3中,内外永磁体沿周向安装在转子凹槽内,为了使磁路闭合,内外永磁体磁性相反,在二者之间产生稳定的磁场。4个同匝数线圈绕组位于定子骨架上,成对串联使用,线圈处于内外永磁体之间的间隙内。传感器用来检测转子偏转时的轴向位移,测量数据用于计算转子的偏转角。
2.2 LFMB电磁力矩建模 如图 3所示,坐标系Oxyz的原点位于LFMB定子的几何中心,x轴和y轴分别定义为与2对线圈的中心线重合,z轴符合右手定则。
LFMB产生的电磁力依据安培力定律,即位于永磁体磁场的通电线圈受到安培力的作用,方向由左手定则确定。由LFMB结构可知,在平衡位置时,其线圈沿Oxy平面对称分为上下两半部分。在第i组线圈上半部分,沿周向选择微元dθ,则其所受安培力可表示为
 | (1) |
式中:n为线圈匝数;I为激励电流。此处假设气隙磁密分布均匀,B为常数。
由dfi产生的电磁力矩dT位于Oxy平面, 可表示为
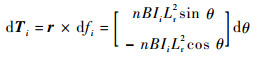 | (2) |
式中:r为电磁力dfi的作用力臂。
则第i组线圈上下部分产生的有效电磁合力矩为
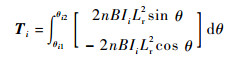 | (3) |
其中:θi1和θi2指第i组线圈沿周向两端的角度坐标,定义为
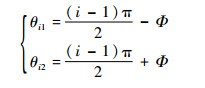 | (4) |
则4个线圈产生的有效电磁合力矩为
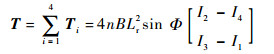 | (5) |
该力矩即为LFMB为MSCSG提供2个自由度扭转运动的偏转控制力矩。4组线圈绕组成对串联使用时,电流I2与I4、I3与I1大小相等,方向相反,此时有效电磁合力矩为
 | (6) |
传统LFMB的气隙磁密分布具有以下特点:轴向上气隙磁场在线圈中心位置磁密最大,沿着中心位置两端逐渐减小;径向上也呈现出中心线磁密大,沿中心位置两端逐渐减小的趋势,故其磁密大小B具有非线性。同时,在实际的偏转控制中,采用线圈中心位置气隙磁密取值,即气隙磁密幅值对转子进行偏转控制,若转子发生偏转或平动,线圈必然偏离中心位置,气隙磁密的非均匀分布必然导致对偏转控制产生干扰力矩:
 | (7) |
另外,载体相对于惯性空间的姿态角速率,亦为MSCSG的输入角速率,该角速率正比于LFMB线圈电流差[17]
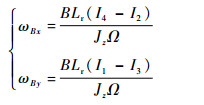 | (8) |
式中:Ω为飞轮转速;Jz为转子的极转动惯量;ωBx和ωBy分别为姿态角速率沿x、y轴的分量。显然,电流I和气隙磁密B的精度直接影响姿态角速率ωB的精度。
3 LFMB结构设计与磁密分析 3.1 LFMB基本结构与磁密分析 对于LFMB,其产生电磁力依据安培力定律,稳定的磁场和置于磁场中的通电线圈是产生电磁力的两大要素。LFMB主要由内外磁钢、内外导磁环、定子骨架、线圈绕组组成。为了使磁路闭合,内外磁钢均具有2个充磁方向相反的磁钢,在内外磁钢间产生稳定的磁场,同时内外磁钢中同处一层的磁钢充磁方向亦相反。4个线圈绕组位于定子骨架上,成对串联使用,线圈处于内外磁钢之间的间隙内。当4个线圈绕组匝数相同时,产生的安培力大小相等,方向相反形成力偶,不会对3个平动方向产生干扰。根据MSCSG指标要求,按文献[1]描述的LFMB基本构型进行设计和仿真,如图 4所示 (Ⅰ型LFMB)。
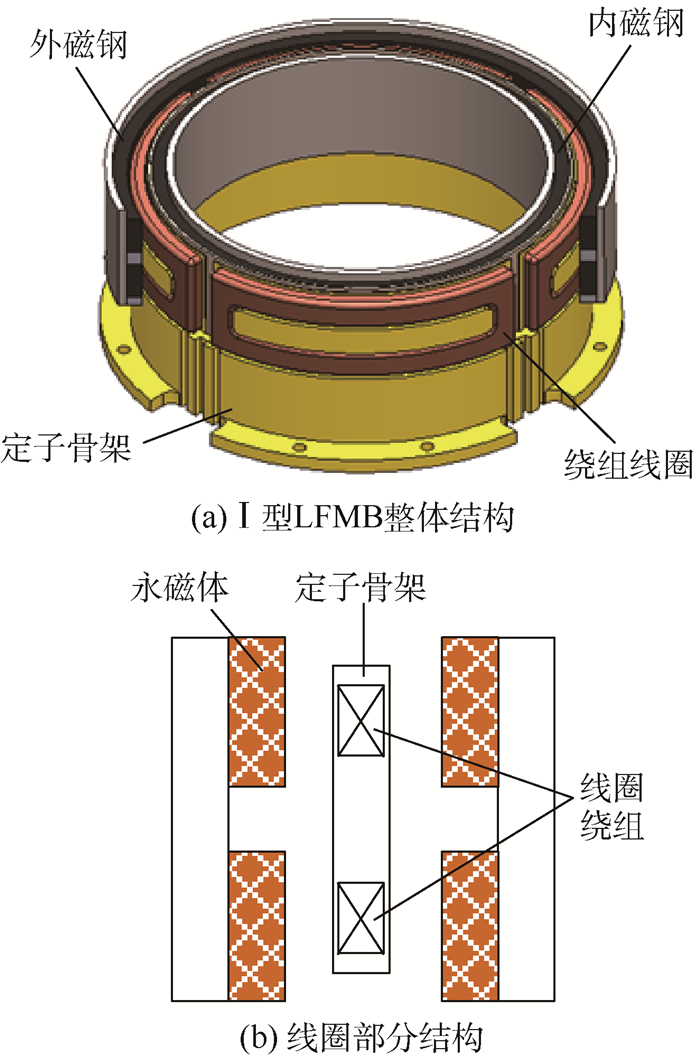 |
| 图 4 Ⅰ型LFMB机械结构 Fig. 4 Mechanical structure of LFMBⅠ |
| 图选项 |
Ⅰ型LFMB主要设计参数和计算结果如表 1所示。Ⅰ型LFMB磁密分布云和磁力线分布如图 5所示,气隙磁密的分布呈现以下特点:①径向上,以气隙中间位置为中心,气隙磁密分布中间弱两边强;②轴向上,以线圈中心位置为中心,气隙磁密分布中间强两边弱。气隙中间位置的轴向磁密分布如图 6所示,可明显看出在气隙中间线圈中心位置气隙磁密取得最大值,沿两边迅速减小,上下线圈的气隙磁密分布呈近似正弦曲线。由此可见,该种LFMB的气隙磁密分布均匀性较差。同时,在转子发生偏转或者平动后,仍使用线圈中心位置的气隙磁密值进行偏转控制,必然会产生干扰力矩,影响偏转控制和角速度测量的精度。因此,需要通过结构优化不断提高气隙磁密分布的均匀性,将其定义为气隙磁密均匀度。
表 1 Ⅰ型LFMB主要参数 Table 1 Main parameters of LFMBⅠ
| 参数 | 数值 |
| 内永磁体内径/mm | 103.4 |
| 内永磁体外径/mm | 111.4 |
| 外永磁体内径/mm | 124 |
| 外永磁体外径/mm | 132 |
| 永磁体轴向长度/mm | 11 |
| 上下永磁体间轴向距离/mm | 4 |
| 线圈轴向长度/mm | 8.5 |
| 单个线圈沿周向张角/(°) | 84 |
| 单个线圈匝数 | 200 |
| 槽满率/% | 49 |
| 单个线圈电阻/Ω | 14.3 |
| 内转子铁心磁密/T | 1.2 |
| 外转子铁心磁密/T | 1.2 |
| 气隙磁密幅值/T | 0.516 |
| 扭转输出1 N·m力矩时电流/A | 0.6 |
| 线圈铜耗/W | 10.3 |
表选项
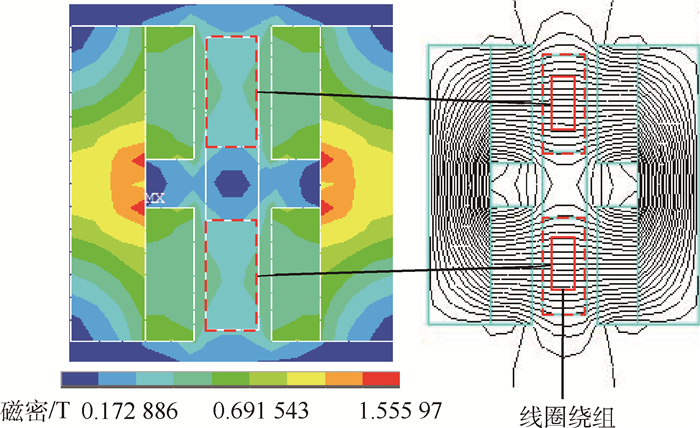 |
| 图 5 Ⅰ型LFMB磁密分布云与磁力线图 Fig. 5 Graph of magnetic density cloud distribution and magnetic field line for LFMBⅠ |
| 图选项 |
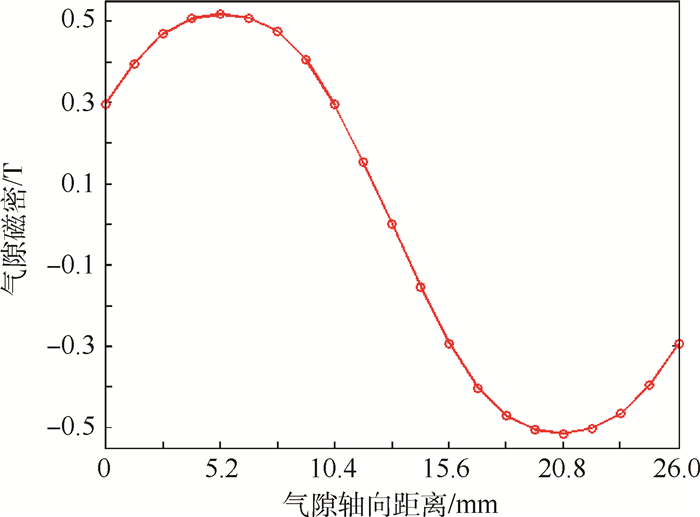 |
| 图 6 Ⅰ型LFMB气隙中间位置的轴向磁密分布 Fig. 6 Axial magnetic density distribution at middle of air gap for LFMBⅠ |
| 图选项 |
气隙磁密均匀度uB用来表征气隙磁密分布的均匀程度,其有效区域是由转子偏转或发生平动时线圈运动工作气隙范围。具体定义为
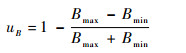 | (9) |
式中:Bmax和Bmin分别为线圈工作气隙磁密的最大值和最小值。同时,由于气隙磁密以上下磁钢中间位置为界方向相反,仅选取上半部分进行气隙磁密均匀度计算。
3.2 LFMB结构优化与磁密分析 经仿真分析与实验研究发现,在永磁体表面增加1J50导磁薄片和改变永磁体形状能够对气隙磁密的分布和气隙磁密幅值带来影响。
为提高气隙磁密均匀度,通过在内外矩形永磁体表面增加1J50导磁薄片 (Ⅱ型LFMB),其气隙磁密分布云和磁力线分布如图 7所示。与Ⅰ型LFMB相比:①径向上,与Ⅰ型LFMB总体相似,以气隙中间位置为中心,气隙磁密分布中间弱两边强,但Ⅱ型LFMB线圈位置趋向平行的区域更大;②轴向上,与Ⅰ型LFMB相比,其线圈位置气隙磁密分布相对均匀,且区域更大。仿真结果表明气隙磁密均匀度 (0.8683) 得到显著提高,提升幅度为16.1%。但同时引起功耗的升高,经分析功耗的升高是由于气隙磁密幅值 (0.438 T) 的下降,下降幅度为15.1%。
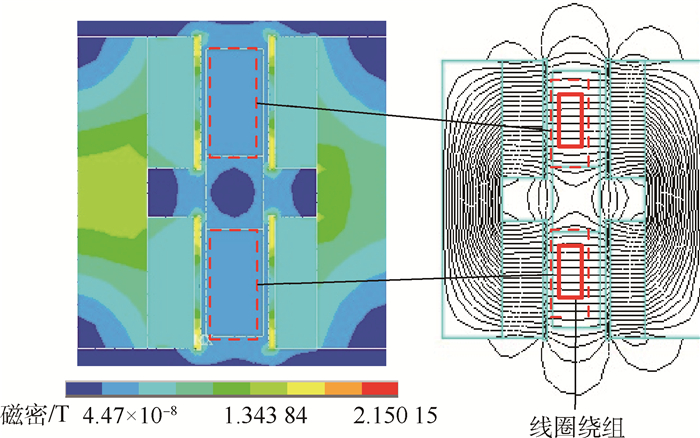 |
| 图 7 Ⅱ型LFMB磁密分布云与磁力线图 Fig. 7 Graph of magnetic density cloud distribution and magnetic field line for LFMB Ⅱ |
| 图选项 |
低功耗是采用LFMB进行偏转控制的主要优点之一,因此气隙磁密的幅值需得到保证,在Ⅱ型LFMB的基础上,将矩形永磁体优化为等腰梯形永磁体 (Ⅲ型LFMB)。即在原永磁体的基础上,对其靠近线圈面的永磁体进行形状优化,使其剖面呈等腰梯形,长边与原永磁体相等,长短边差为2 mm,其线圈部分结构如图 8所示。梯形永磁体相比矩形永磁体具有2个显著特点:①梯形永磁体能够提供更大的供磁面积;②梯形永磁体便于进行限位,提高其在转子高速旋转下的稳定性。
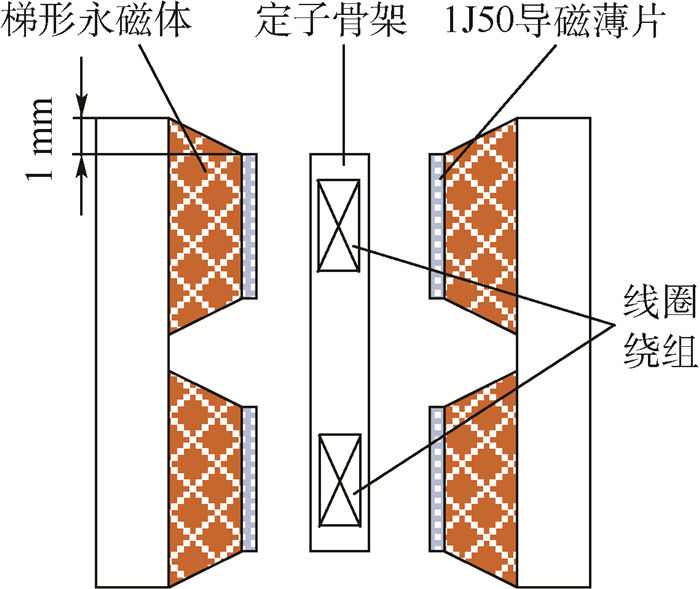 |
| 图 8 Ⅲ型LFMB线圈部分结构 Fig. 8 Structure of part near coil for LFMB Ⅲ |
| 图选项 |
Ⅲ型LFMB气隙磁密分布云和磁力线分布如图 9所示,其气隙磁密的分布与Ⅱ型LFMB基本一致。经计算其气隙磁密均匀度为0.8684,与Ⅱ型LFMB基本一致,气隙磁密幅值为0.462 T,提升了5.5%。结果表明,永磁体形状的改变对气隙磁密分布的均匀性影响不大,但对气隙磁密的幅值影响较大。
 |
| 图 9 Ⅲ型LFMB磁密分布云与磁力线图 Fig. 9 Graph of magnetic density cloud distribution and magnetic field line for LFMB Ⅲ |
| 图选项 |
为进一步说明Ⅲ型LFMB的优点,在其基础上去掉1J50导磁薄片 (Ⅳ型LFMB) 后进行仿真实验。结果表明:①Ⅳ型LFMB气隙磁密的均匀度为0.785 1,相比Ⅲ型LFMB显著下降,下降了9.6%;②其气隙磁密得到了显著增强,气隙磁密幅值 (0.528 T) 比Ⅲ型LFMB提高了14.3%。
将4种LFMB气隙中间位置的轴向磁密分布进行对比,如图 10所示,可以发现:①增加了1J50导磁薄片的Ⅱ、Ⅲ型LFMB在气隙磁密均匀度上有了显著提高,但同时会增加永磁体之间的漏磁,引起气隙磁密幅值的降低,带来功耗的增加;②在永磁体轴向长度不变时,梯形磁铁相比矩形磁铁能提供更大的供磁面积,相同位置的气隙磁密会增加,但由于气隙磁密均匀部分集中在线圈所在位置的中心处,外围磁场的增加对该部分的影响不大,因此永磁体形状的改变对于磁密均匀度基本没有影响。
 |
| 图 10 不同LFMB气隙中间位置的轴向磁密分布比较 Fig. 10 Comparison of axial magnetic density distribution at middle of air gap for different LFMBs |
| 图选项 |
表 2将以上4种LFMB的结构及其他性能进行比较。结果表明:①增加导磁薄片可提高气隙磁密均匀度,但会引起气隙磁密幅值的减小;②梯形截面永磁体可提高气隙磁密幅值,但不会对气隙磁密均匀度产生影响;③梯形截面的永磁体能够便于限位,在转子高速旋转过程中保持稳定性。综合以上比较,在进行LFMB优化设计时采用在永磁体内外表面增加1J50导磁薄片和梯形永磁体的组合方案,即Ⅲ型LFMB结构。
表 2 不同LFMB结构及其他性能比较 Table 2 Comparison of structure and other properties for different LFMBs
| LFMB结构 | 永磁体形状 | 是否添加导磁薄片 | 气隙磁密幅值/T | 气隙磁密均匀度 | 安装稳定性 |
| Ⅰ型 | 矩形 | 否 | 0.516 | 0.7476 | 差 |
| Ⅱ型 | 矩形 | 是 | 0.438 | 0.8683 | 差 |
| Ⅲ型 | 梯形 | 是 | 0.462 | 0.8684 | 好 |
| Ⅳ型 | 梯形 | 否 | 0.528 | 0.7851 | 好 |
表选项
采用Ⅲ型LFMB结构,气隙范围内线圈部分磁密分布均匀,其值约等于气隙中间位置磁密幅值 (本文为0.462 T)。对于偏转控制力矩数学模型,n、Lr及Φ是已知常数,均匀磁场磁密为B (0.462 T),根据MSCSG偏转控制需求通入相应精确的控制电流I,输出偏转控制力矩精确,能够对转子进行高精度的偏转控制。同时,所设计的LFMB通过保证气隙磁密B的精度,也保证了电流I的精度,显然角速率测量的精度也得到了保证。同时,电流微小变化也将快速反应到角速率的测量,提升角速率测量的敏感度。
4 结论 新型MSCSG集成惯性执行机构的姿态控制功能和角速率敏感器的姿态测量功能,通过转子的万向偏转输出高精度的偏转控制力矩,能够为抑制甚稳超静平台的高频角振动提供一种解决途径。
1) 基于MSCSG用LFMB的基本结构,构建了电磁力和电磁力矩的数学模型,分析了影响偏转控制力矩精度的主要因素是气隙磁密均匀度,同时还会影响角速度测量精度。
2) 仿真结果表明:对于LFMB,在永磁体轴向长度保持一定时,改变永磁体形状,引起供磁面积的变化,可影响气隙磁密分布强弱,但对气隙磁密均匀度基本没有影响,梯形截面永磁体能够提供更大的供磁面积,增强气隙磁密分布。
3) 通过在内外永磁体表面增加1J50导磁薄片可显著提高LFMB气隙磁密均匀度,但同时会增加永磁体之间的漏磁,引起气隙磁密分布变弱,增加功耗。
4) 采用在内外永磁体表面增加1J50导磁薄片和梯形截面永磁体的组合方案,既能够提高气隙磁密的均匀度又能一定程度上增强气隙磁密分布以降低功耗,同时梯形永磁体还能在转子高速旋转时保持稳定性。
本文可为具有偏转特性的磁悬浮类转子陀螺进行高精度偏转控制提供理论和实践基础,也为磁悬浮飞轮的角速率测量提供有益参考。
参考文献
| [1] | 余远金. 全主动磁悬浮飞轮转轴偏转控制方法及实验研究[D]. 北京: 北京航空航天大学, 2015.YU Y J.Study on the control method and experiment of the shaft tilting for the fully active magnetically suspended flywheel[D].Beijing:Beihang University, 2015(in Chinese). |
| [2] | FANG J C, ZHENG S Q, HANG B C. AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J].IEEE Transactions on Mechatronics, 2013, 18(1): 32–43.DOI:10.1109/TMECH.2011.2161877 |
| [3] | REN Y, FANG J C. Current-sensing resistor design to include current derivative in PWM H-bridge unipolar switching power amplifiers for magnetic bearings[J].IEEE Transactions on Industrial Electronics, 2012, 59(12): 4590–4600.DOI:10.1109/TIE.2011.2179277 |
| [4] | 解永春. 磁悬浮动量轮的主动振动控制[J].航天控制, 2001(2): 1–6.XIE Y C. Active vibration suppression for magnetically suspended momentum wheels[J].Aerospace Control, 2001(2): 1–6.(in Chinese) |
| [5] | 刘侃. 动量矩可偏置磁悬浮动量轮结构设计[D]. 长沙: 国防科学技术大学, 2005.LIU K.The structure design of magnetic suspension momentum wheel with deflection angular momentum[D].Changsha:National University of Defense Technology, 2005(in Chinese). |
| [6] | 房建成, 孙津济, 樊亚洪. 磁悬浮惯性动量轮技术[M].北京: 国防工业出版社, 2012: 9-10.FANG J C, SUN J J, FAN Y H. Magnetically suspended inertial momentum wheel technology[M].Beijing: National Defense Industry Press, 2012: 9-10.(in Chinese) |
| [7] | BICHLER U, ECKARDT T.A gimbaled low noise momentum wheel[C]//27th Aerospace Mechanisms Symposium.1993, 1:181-196. |
| [8] | SAWADA H, HASHIMOTO T, NINOMIYA K. High-stability attitude control of satellites by magnetic bearing wheels[J].Transaction of the Japan Society for Aeronautical and Space Science, 2001, 44(145): 133–141.DOI:10.2322/tjsass.44.133 |
| [9] | ROSSINI L, CHETELAT O, ONILLON E, et al. Force and torque analytical models of a reaction sphere actuator based on spherical harmonic rotation and decomposition[J].IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1006–1018.DOI:10.1109/TMECH.2012.2195501 |
| [10] | SEDDON J, PECHEV A. 3-D wheel:A single actuator providing three-axis control of satellites[J].Journal of Spacecraft and Rockets, 2012, 49(3): 553–556.DOI:10.2514/1.A32039 |
| [11] | 王春娥. 惯性执行机构用高承载比低功耗磁轴承设计方法与实验研究[D]. 北京: 北京航空航天大学, 2014.WANG C E.Design method and experimental research on high specific load capacity and low loss magnetic bearing in inertia actuator[D].Beijing:Beihang University, 2014(in Chinese). |
| [12] | JASTRZE BSKI R P, P?LL?NEN R. Compensation of nonlinearities in active magnetic bearings with variable force bias for zero-and reduced-bias operation[J].Mechatronics, 2009, 19(5): 629–638.DOI:10.1016/j.mechatronics.2009.01.013 |
| [13] | HAN F T, GAO Z Y, LI D M, et al. Nonlinear compensation of active electrostatic bearings supporting a spherical rotor[J].Sensors and Actuators A:Physical, 2005, 119(1): 177–186.DOI:10.1016/j.sna.2004.08.030 |
| [14] | CHEN M, KNOSPE C. Feedback linearization of active magnetic bearings:Current-mode implementation[J].IEEE/ASME Transactions on Mechatronics, 2005, 10(6): 632–639.DOI:10.1109/TMECH.2005.859824 |
| [15] | CHEN S, LIN F. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system[J].IEEE Transactions on Control Systems Technology, 2011, 19(3): 636–643.DOI:10.1109/TCST.2010.2050484 |
| [16] | GROCHMAL T, LYNCH A. Precision tracking of a rotating shaft with magnetic bearings by nonlinear decoupled disturbance observers[J].IEEE Transactions on Control Systems Technology, 2007, 15(6): 1112–1121.DOI:10.1109/TCST.2006.890300 |
| [17] | 刘彬, 房建成, 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析[J].航空学报, 2011, 32(8): 1478–1487.LIU B, FANG J C, LIU G. Design of a magnetically suspended gyrowheel and analysis of key technologies[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1478–1487.(in Chinese) |
