对于优秀的人类球手,在精确瞄准的同时还需要选择适当的力度与旋转使母球在与目标球碰撞后停到一个合理的位置以便于连续得分。对于机器人而言,控制母球走位是一个复杂问题。母球在球杆初始冲量的作用下,其运动过程伴随着质心的平动与绕质心的转动、与目标球的碰撞以及若干次与边库的碰撞;在这个过程中,球体的运动状态由滑动变为纯滚动直到最终静止。因此,走位问题是一个非线性非光滑的复杂问题。目前对该问题的解决方法主要是理论分析与数值模拟。Doménech[7]分析并建立了母球与目标球碰撞的非光滑模型。在其工作的基础上,Mathavan等[8]对考虑摩擦力的球体碰撞模型进行了数值仿真,并进一步研究了母球与边库碰撞的非光滑模型。文献[9]以碰撞力学为基础,给出了球体间以及球体与边库间碰撞的详细力学分析,其优点是模型完整且有详细的理论依据;但另一方面,其模型的准确性依赖于物理参数的选取,如球体运动中侧旋衰减的角加速度、球体与球体碰撞时的动摩擦因数、边库被球体冲撞时的凹陷形变量以及反弹径向力的方向等。一方面,这些参数的选取影响着模型的准确性却难以有效的获取。另一方面,由于模型的仿真需要多次迭代,无法获得解析解,因此运行效率较低。
在理论分析方法开展的同时,相关问题还吸引着神经感知方面的****对其进行研究。他们希望借助人类球手的经验和学习过程去提升机器人的能力。Yang等[3]设计了一种模糊神经补偿器用于研究撞球运动中的投掷效应,并提升了机器人击球的准确性。
神经网络 (NN) 在模式识别、智能控制及预测等方面已经展现了其优越性[10-12]。由一个输入层、一个隐藏层以及一个输出层所组成的3层网络在理论上可以以任意精度逼近任何非线性连续函数。在处理复杂问题时,使用神经网络方法具有如下几个优点:实现了非线性非光滑关系的隐式表达、容错性好、预测精度高,具有较强的联想、记忆与泛化能力。
本文使用神经网络的方法对矩形球桌区域中母球的走位问题展开研究。首先对坐标系进行阐述并给出了击球模型;然后在理想光滑的假设下通过理论分析提出了母球的理想运动模型与边库反弹的理想镜像模型;进而使用神经网络方法对理想模型进行修正,并对不同的轨迹模式进行分析与分类:①对只包含球体碰撞不包含边库反弹的轨迹模式进行分析;②对球体碰撞后只包含1次边库反弹的走位问题进行研究。在此基础上,通过模式分类对包含2次边库反弹的走位问题进行讨论,提出了轨迹模式的分类方法,并将问题延伸至包含多次边库反弹的情况,同时通过分析轨迹的几何特征对包含多次反弹的神经网络模型进行降维处理。经过学习和训练,为每一种走位模式建立相应的神经网络模型,并给出了测试结果,验证方法的可行性。
1 理想模型与神经网络模型 1.1 坐标系的定义
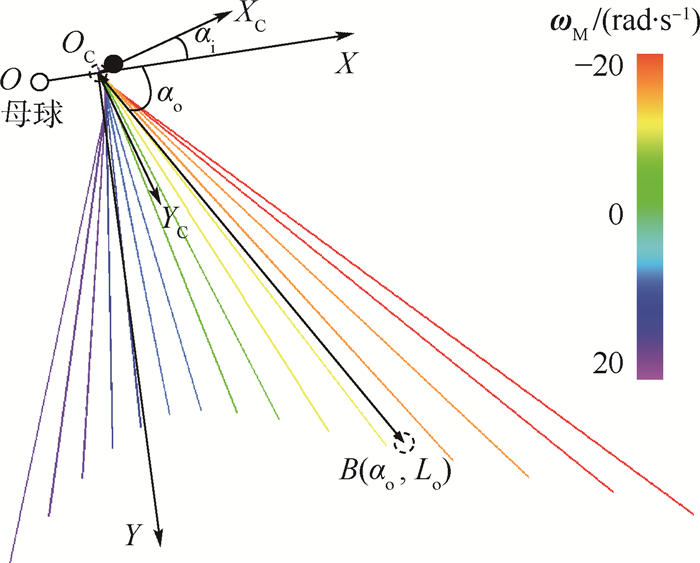
1.1.1 全局坐标系OT-XTYTZT 全局坐标系用于描述球体的绝对位置,在球桌的2维平面俯视图中,全局坐标系的原点OT位于左上角,轴OTXT的方向向右,轴OTYT的方向向下,如图 1所示。轴OTZT的方向由OTXT与OTYT根据右手定则确定。击打坐标系为O-XYZ,碰撞坐标系为OC-XCYCZC,αi为球体碰撞入射角。图 1中球桌的4条边库编号分别为1、2、3和4。
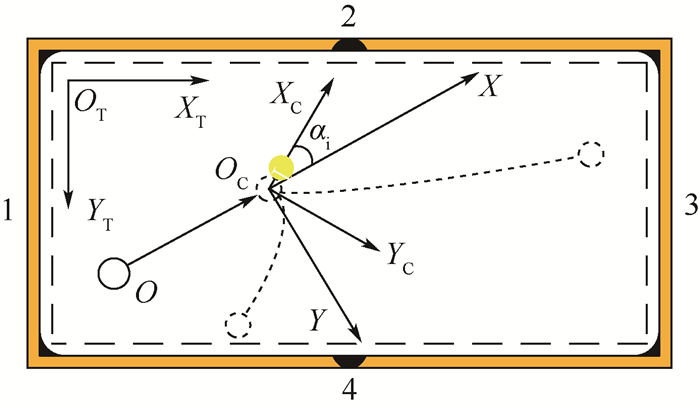 |
| 图 1 全局坐标系、击打坐标系与碰撞坐标系 Fig. 1 Global coordinate system, stroking coordinate system and collision coordinate system |
| 图选项 |
1.1.2 击打坐标系O-XYZ 击打坐标系用于描述击球过程,原点O位于母球质心在桌面上的初始点,轴OX指向击球方向,轴OY与轴OX垂直,且与母球与目标球的连线成钝角。OZ与OTZT方向相同。
击球通过球杆对球的冲撞完成。在约200 μs[13]时间内,球杆将冲量传递给母球。假设在水平冲量PI=FItI作用下,质量为M的母球获得速度V0 (方向与PI相同) 以及角速度ω0 (FI和tI分别为击球水平冲力和球杆和球撞击的作用时间)。其中角速度被分解为横向角速度ω0H以及纵向角速度ω0V,如图 2所示。设冲力FI作用点为PA (Sx, Sy, 0),Sx和Sy分别为击球正视图中击球点距离球心的水平与竖直距离,则由动量定理和动量矩定理可得
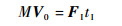 | (1) |
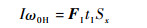 | (2) |
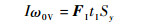 | (3) |
 |
| 图 2 击球的正视图与侧视图 Fig. 2 Front view and side view of stroking |
| 图选项 |
式中:I为球体的转动惯量。
因此,在控制量FI、Sx、Sy作用下,得到了球体初始速度与角速度在击打坐标系中的投影:
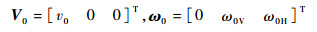 |
1.1.3 碰撞坐标系OC-XCYCZC 碰撞坐标系用于描述母球与目标球的碰撞过程,原点OC位于母球与目标球的碰撞点,轴OCXC指向母球与目标球的连线。轴OCYC垂直于OCXC且与击打系的OX轴成锐角。OCZC与OTZT方向相同。
1.2 球体的运动学模型 在击打坐标系下,母球以速度vM,角速度ωM,角度αi与目标球发生斜碰, 如图 3 (a)所示。球与桌面的动摩擦因数为μs。假设碰撞过程光滑、无能量损失,且不考虑球体与球体之间的摩擦作用,不考虑边库反弹。在与目标球碰撞后的瞬时,母球在击打坐标系下的速度为
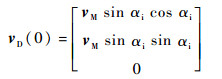 | (4) |
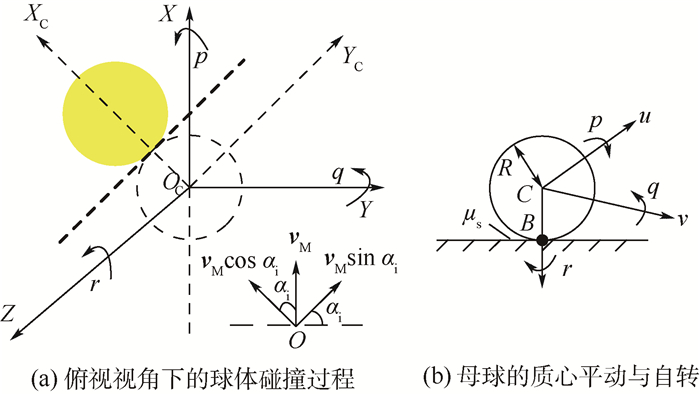 |
| 图 3 击打坐标系下母球与目标球的碰撞示意图 Fig. 3 Schematic diagram of collision of cue ball and object ball in stroking coordinate system |
| 图选项 |
两球碰撞后,对母球的运动过程进行理论分析,见图 3 (b)。设B为母球与桌面的接触点,B点对桌面的相对速度表示为
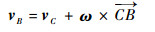 | (5) |
式中:vC为运动中母球质心速度;ω为绕质心转动的角速度;
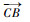
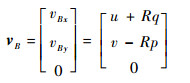 | (6) |
式中:R为球体的半径。
球体在运动中受到滑动摩擦力fs的作用:
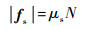 | (7) |
式中:N为桌面对球体的支持力,其方向总是指向球桌正上方。滑动摩擦力的方向与vB的方向相反,因此:
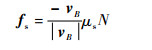 | (8) |
式中:
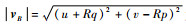
 | (9) |
除滑动摩擦力外,球体在运动中还受到重力G=[0 0 Mg]T (g为重力加速度常数) 与桌面的支持力N=[0 0 -N]T,由刚体质心的动量定理及动量矩定理有
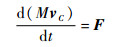 | (10) |
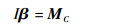 | (11) |
式中:F为球体所受的合外力;β为球体自转的角加速度;t为时间变量;MC为质心受到的合力矩,可表示为
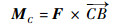 | (12) |
在击打坐标系下, 将式 (10) 展开得到
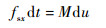 | (13) |
 | (14) |
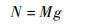 | (15) |
在击打坐标系下β=[βx βy βz]。结合式 (10)~式 (12) 得到
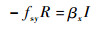 | (16) |
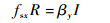 | (17) |
将式 (13)~式 (17) 在时间[0, ti]上积分得到
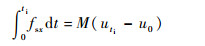 | (18) |
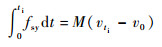 | (19) |
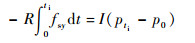 | (20) |
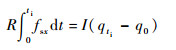 | (21) |
由式 (18)~式 (21) 得到
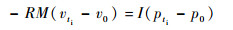 | (22) |
 | (23) |
另一方面,式 (6) 对时间进行微分可得
 |
即
 | (24) |
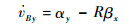 | (25) |
式中:u0、v0与p0、q0分别表示球体在0时刻的速度与角速度分量;uti、vti与pti、qti分别表示球体在时刻ti的速度与角速度分量;αx、αy为球体质心加速度分量。
将式 (13)~式 (17) 代入式 (24) 和式 (25),可得
 |
式中:I=2/5 (MR2),即
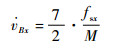 | (26) |
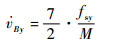 | (27) |
将式 (9) 和式 (6) 代入式 (26) 和式 (27),得到
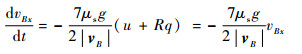 | (28) |
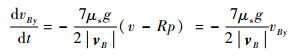 | (29) |
令
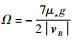
 |
因此:
 | (30) |
求解微分方程式 (30),得到
 | (31) |
故:
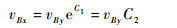 |
式中:C1、C2为常数。式 (31) 表明:在母球的滑动过程中,底部接触点B对桌面的相对速度方向始终保持不变。因此,滑动摩擦力的方向和大小也始终保持不变,母球在进入纯滚动状态前的运动轨迹为二次曲线。
在与目标球发生完全弹性碰撞后的瞬时,母球将以式 (4) 中给出的速度继续运动,角速度的大小与方向与碰撞前保持一致。由于碰撞后球体底部的速度方向保持不变,设:
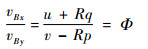 |
则球体受到的滑动摩擦力在击打坐标系2轴上的投影为
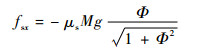 | (32) |
 | (33) |
因此:
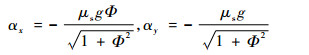 |
在球体滑动的过程中,质心速度为
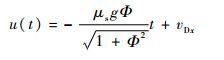 | (34) |
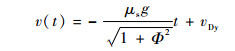 | (35) |
式中:vDx、vDy分别为母球与目标球碰撞结束瞬时母球速度在击打坐标系中的投影。
当运动至纯滚动状态时,满足
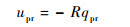 | (36) |
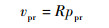 | (37) |
式中:upr、vpr和ppr、qpr分别为球体在纯滚动状态下击打坐标系下的速度分量与角速度分量。
将式 (36) 和式 (37) 代入式 (22) 和式 (23),得到纯滚动发生瞬时球体的速度分量为
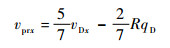 | (38) |
 | (39) |
式中:vprx和vpry分别为球体进入纯滚动状态瞬时的速度分量;pD和qD分别为母球与目标球碰撞结束瞬时母球自转角速度在击打系中的投影。
则击打系下的滑动轨迹为
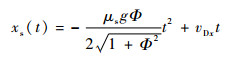 | (40) |
 | (41) |
当母球进入滚动状态后,底部B点与桌面间的相对速度为0,滑动摩擦力为0,母球将在滚动摩擦阻力、空气阻力的作用下运动至静止。由于纯滚动阶段球体的运动加速度较低,因此将该过程中的阻力加速度α′设为定值 (设α′ > 0),α′在击打系下的投影为
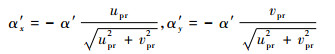 |
则纯滚动阶段球体的运动轨迹表述为
 |
经过上述推导,结合滑动与纯滚动2个阶段的运动过程可以预测出在理想条件下母球最终静止的位置 (击打坐标系)。设定球体直径为26.25 mm, 质量为0.1406 kg,球体与桌面的动摩擦因数取0.5,在斜碰角度为25.0°、速度为1.0 m/s的条件下,对母球以不同角速度ωM与目标球进行碰撞后的分离轨迹进行仿真,如图 4所示,碰撞时母球的前旋角速度越大,分离轨迹沿X轴正向且离Y轴越远;碰撞时母球的后旋角速度越大,分离轨迹沿X轴负向且离Y轴越远。
 |
| 图 4 以不同角速度碰撞后的母球运动轨迹仿真 Fig. 4 Cue ball trajectory simulation under different angular velocity after balls collision |
| 图选项 |
为了便于后续分析,使用碰撞坐标系中的极坐标对母球的初始位置O与最终位置B进行描述,角∠BOCYC=αo为输出角,并规定当∠BOCO为钝角时αo为正;B与OC的距离
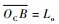
此外,推导过程表明,在无边库反弹的情况下,球体的运动轨迹与球体自身的侧旋角速度r无关,这与相关文献中论述的结果一致[10]。
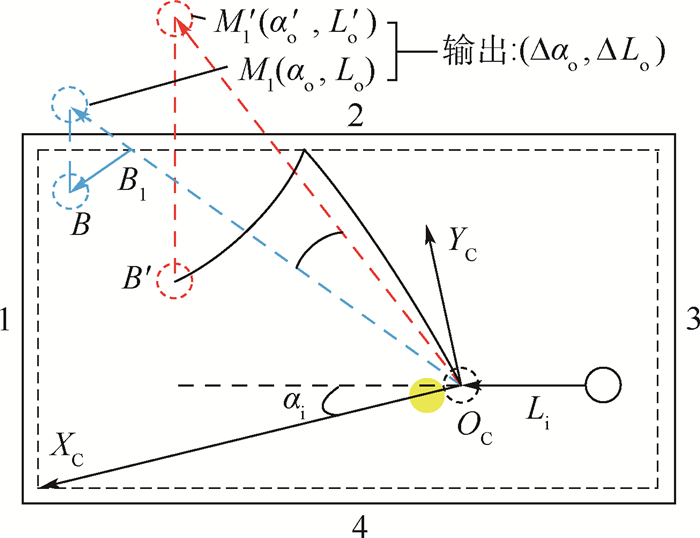
1.3 边库反弹的理想镜像模型 在完全光滑、无摩擦、无变形和无能量损失的假设下,边库反弹的理想路径可通过光的反射定律得到。假设球桌的4条边库编号分别为1~4,如图 1所示。首先在第1.2节所述的理想条件下计算出母球在碰撞坐标系中的最终位置M1 (αo, Lo),再通过光的反射定律将M1点顺次映射到桌面上,得到母球在与目标球碰撞后的理想镜像轨迹:设该轨迹按顺序分别与边库c1, c2, …, cnum (ci={1, 2, 3, 4}) 在B1, B2, Bnum点发生碰撞,最终停在终点B处。如图 5所示,Mnum,Mnum-1, …, M1为B点与相应边库直线的镜像点。则该理想镜像轨迹可以由碰撞坐标系中的输出点M1 (αo, Lo) 与各轨迹段的长度进行描述,共num+3维数据。
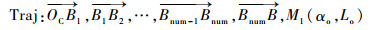 |
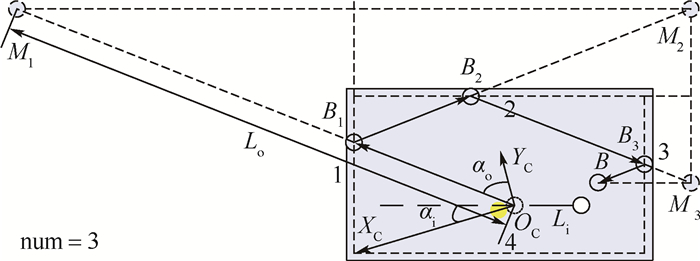 |
| 图 5 母球的理想镜像轨迹 Fig. 5 Ideal mirror trajectory of cue ball |
| 图选项 |
根据光的反射定律有
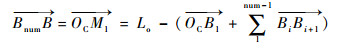 |
因此轨迹的维度降至num+2维,即
 |
1.4 神经网络模型 综上所述,球体的理想轨迹模型由2个部分组成,即:球体的运动学模型与边库反弹的理想镜像模型。理想模型能够定性地反映出球体运动的规律,但是无法准确地预测出母球最终停留的位置,因此并不能有效地解决本文提出的走位问题,这主要是因为:不论球体间的碰撞还是球体与边库的碰撞都存在着能量损失以及材料的变形,走位问题是一个非光滑非线性的复杂问题。球体间碰撞的能量损失与碰撞的角度、速度以及角速度都存在着复杂的关系,其中涉及到的重要物理参数如恢复系数、球体间的滑动摩擦系数很难通过实验给出准确值。球体在与边库碰撞时,边库会在冲量作用下产生凹陷的变形,且会对球体与边库的径向速度、切向速度与角速度产生复杂的影响。由于传统的理论分析方法难以有效地解决走位问题,本文尝试使用神经网络方法展开研究。
在控制量、输入角与输入距离已知,母球与边库的碰撞顺序给定的前提下,抛开球体运动过程中受到的复杂因素影响,母球的最终位置B都可以作为确定的结果被机器人获取。在母球与目标球碰撞后由OC运动至终点B的过程中,若干种不同的撞库模式都可能满足走位的要求,其中的一些轨迹路线如图 6所示。
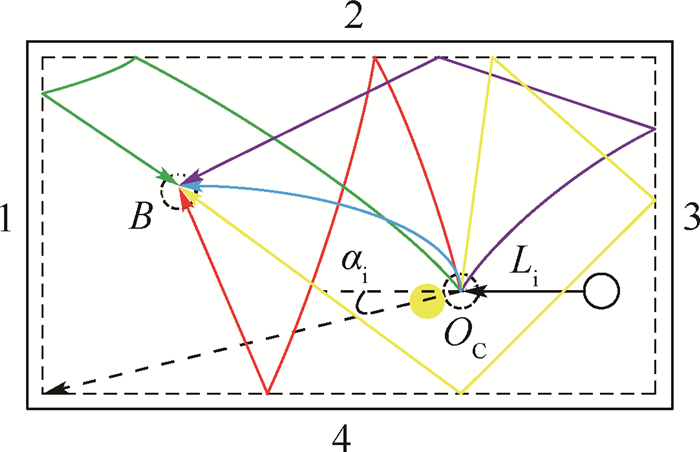 |
| 图 6 一些可能的轨迹模式 Fig. 6 A number of potential trajectory patterns |
| 图选项 |
本文使用神经网络的方法,使机器人通过不断的训练掌握各种不同轨迹模式的母球走位。每一种轨迹模式都对应着一个BP神经网络模型,如图 7所示。网络模型采用经典的3层结构,即,输入层、隐藏层与输出层。模型的输入层由控制量、几何特征量以及一个旋转分类参数3部分组成。控制量包含击球的力量FI、作用点Sx和Sy。几何特征量由输入角αi、输入距离Li以及理想镜像轨迹所包含的num条轨迹段
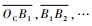
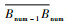
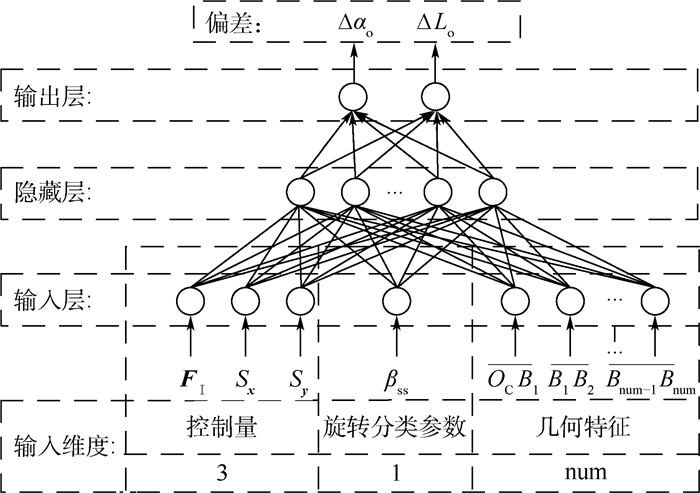 |
| 图 7 包含任意num次边库反弹的母球走位的BPNN模型 Fig. 7 BPNN model with arbitrary num cushion rebounds for cue ball controlling |
| 图选项 |
2 轨迹模式的分析与分类 2.1 无边库反弹的轨迹模式 不包含边库反弹的轨迹属于最简单的模式,母球在与目标球碰撞后将直接走向目标点,如图 8所示,这种轨迹模式称之为模式0。在模式0对应的神经网络模型中,输入量对应的几何特征只有2维:输入角αi与输入距离Li。输出量为理论模型到实际模型的偏差Δαo与ΔLo。在给定控制量与几何特征输入的条件下,机器人会通过理论模型计算出模式0对应的终点B,再通过模式0的神经网络模型得到输出偏差并对B进行修正,预测出母球的最终位置B′。另外,1.2节的理论推导过程表明,不包含边库反弹的轨迹与侧旋角速度无关,因此,在模式0对应的神经网络模型的输入量中不用考虑βss的影响,模型的输入量与输出量如表 1所示。
 |
| 图 8 模式0对应的理想轨迹与实际轨迹 Fig. 8 Ideal trajectory and actual trajectory of Pattern 0 |
| 图选项 |
表 1 模式0神经网络模型 Table 1 Neural network model for Pattern 0
| 输入 (5维) | 输出 (2维) |
| 控制量FI, Sx, Sy | 位置偏差Δαo, ΔLo |
| 几何特征量αi, Li |
表选项
2.2 只包含1次边库反弹的轨迹模式 在包含边库反弹的走位问题中,首先考虑的是只包含1次边库反弹的情况,这种轨迹模式称为EASY,如图 9所示。在输入量一定的情况下,母球最终的实际位置与理论计算得到的位置分别为B′与B,对应的镜像点M′1与M1在碰撞坐标系中极坐标位置的偏差Δαo, ΔLo为网络的输出 (图 9中的

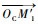
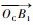
 |
| 图 9 包含1次边库反弹的母球走位路线 Fig. 9 Trajectory with one-time cushion rebound for cue ball controlling |
| 图选项 |
此外,当输入量中Sx≠0时,球体在运动中将会出现侧向旋转,即ωz≠0,当球体与边库的碰撞伴随着侧旋时,需要引入旋转分类参数βss对侧旋与边库运动的相对方向进行分类,定义如下:
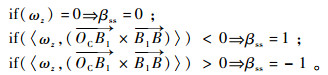 |
βss的含义为:当初始角速度ωz与理想镜像轨迹中的向量
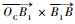
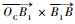
表 2 模式EASY神经网络模型 Table 2 Neural network model for Pattern EASY
| 输入 (7维) | 输出 (2维) |
| 控制量FI,Sx,Sy | 位置偏差Δαo,ΔLo |
几何特征αi,Li,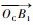 | |
| 旋转分类参数β |
表选项
2.3 包含2次边库反弹的走位问题
2.3.1 轨迹段的起点编号与终点编号 为了便于后文讨论,此处对轨迹段的起点编号与终点编号进行定义,参考图 10:对于任意有向轨迹段
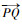
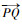
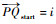
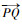

 |
| 图 10 轨迹段的起点编号与终点编号定义 Fig. 10 Definition of start point and end point of trajectory segment |
| 图选项 |
2.3.2 包含2次边库反弹轨迹模式的UN分类器 由轨迹段起点编号与终点编号的定义,将包含2次边库反弹的母球轨迹分类为2种情况,如图 11 (a)与图 11 (b)所示,根据这2种轨迹的形态将其称为N型轨迹与U型轨迹。
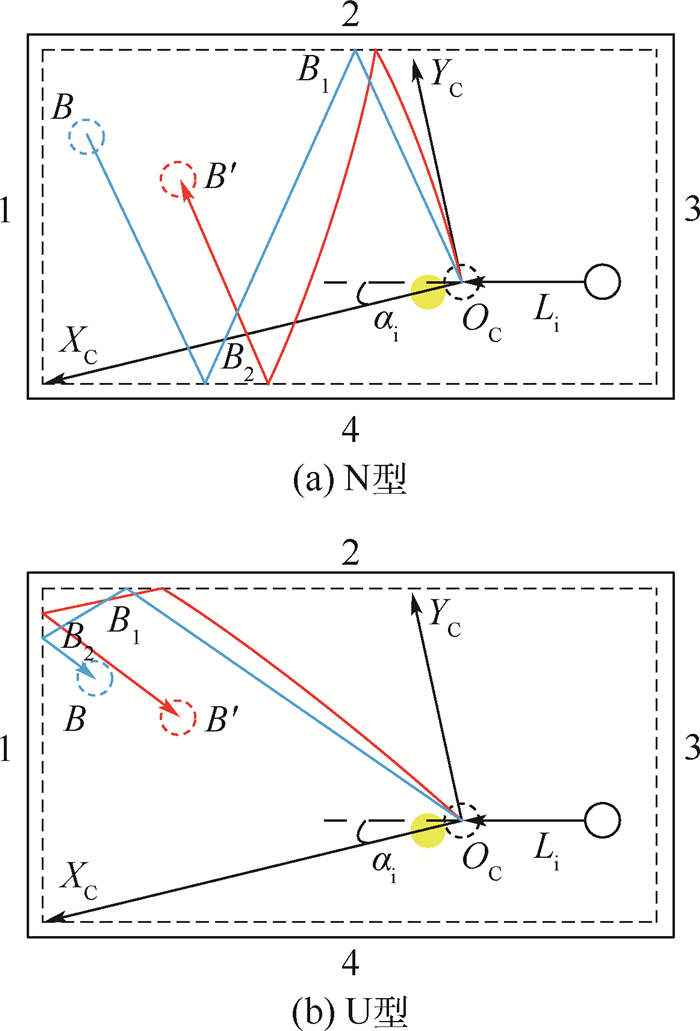 |
| 图 11 包含2次边库反弹轨迹的分类讨论 Fig. 11 Classified discussion for trajectory with two-time cushion rebounds |
| 图选项 |
N型轨迹与U型轨迹的差异与理想镜像轨迹的第2个轨迹段B1B2的起点与终点编号有关,判断逻辑如下:
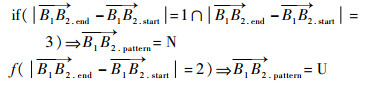 |
其中:
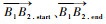
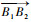
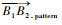
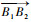
对于包含2次边库反弹的母球轨迹定义如下:如果
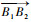
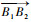
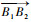

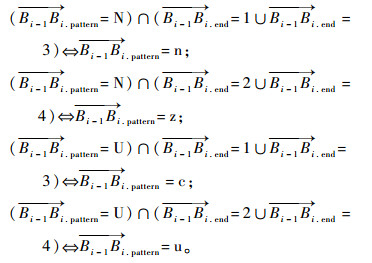 |
2.4 母球走位轨迹模式的UN金字塔分类器 基于上述对轨迹段的定义,显然对包含num (num≥2) 次边库反弹的走位轨迹模式,都可以看做是有限个c、u、n、z轨迹段的组合。假设在包含num次边库反弹的理想镜像轨迹中,母球与目标球碰撞后的第2至第num轨迹段分别为
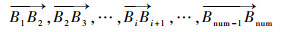 |
那么,整个轨迹的模式则可由各个轨迹段的模式组合给出。这样的组合可以用金字塔的下塔过程进行类比,如图 12所示。
 |
| 图 12 轨迹模式的UN金字塔分类器 Fig. 12 UN pyramid classification of trajectory patterns |
| 图选项 |
在从金字塔顶层开始的下塔过程中,每一层代表着一个轨迹段,该轨迹段的模式对应着这一层中的c、u、n、z节点。那么,当下到金字塔底部时,下塔过程中途经的所有节点的顺次排列就构成了整条轨迹的模式。显然,对于任意包含多次碰撞的母球轨迹,都可以使用UN金字塔分类方法将其有效归类。
2.5 包含多次边库反弹走位轨迹的神经网络模型以及降维处理 根据1.4节的论述,对于包含num次边库反弹的走位问题,其神经网络模型的输入量由3部分组成:控制量、旋转分类参数以及几何特征量。其中几何特征量包括输入角αi、输入距离Li以及撞库轨迹包含的num条轨迹段长度:
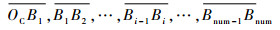 |
当母球与边库反弹的次数较多时,过高的维度 (num值) 将导致收集数据的时间与训练难度大大增加。因此必须降低几何特征的输入维度以避免“数据爆炸”。下面分2种不同的情况对轨迹段的几何特征进行讨论。
1) N型轨迹段
分别考虑如图 13 (a)所示的N型理想镜像轨迹段
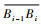
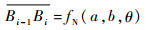 |
 |
| 图 13 U型轨迹与N型轨迹的几何特征 Fig. 13 Geometric feature for Pattern U and Pattern N |
| 图选项 |
因此,如果任意包含num次边库反弹的走位轨迹模式仅由若干个N型轨迹段组成,则其神经网络的几何特征输入量将仅由3维数据构成:输入角αi、输入距离Li以及第1个轨迹段
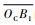
表 3 N型轨迹模式的神经网络模型 Table 3 Neural network model for pattern N
| 输入 (7维) | 输出 (2维) |
| 控制量FI,Sx,Sy | 位置偏差Δαo,ΔLo |
几何特征αi,Li,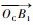 | |
| 旋转分类参数β |
表选项
2) U型轨迹段
考虑一组模式为UN…N…NU的轨迹段序列,序列中的第1个轨迹段
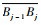
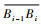
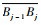
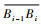
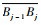
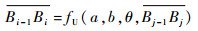 |
因此,对于任意包含num次边库反弹的走位轨迹,如果其模式包含若干个U型轨迹段,则其神经网络的几何特征输入量仅由4维数据组成:αi、Li、
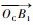
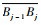
表 4 U型轨迹模式的神经网络模型 Table 4 Neural network model for pattern U
| 输入 (8维) | 输出 (2维) |
| 控制量FI,Sx,Sy | 位置偏差Δαo,ΔLo |
几何特征αi,Li,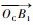 , ,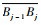 | |
| 旋转分类参数β |
表选项
综上所述,对包含多次边库反弹的走位轨迹模式,其对应的神经网络模型中几何特征的输入维度都不会超过4维。为了便于叙述,将所有轨迹段都为N模式的轨迹统称为N型,将至少存在一个U模式轨迹段的轨迹称为U型。对机器人而言,在碰库次数相同的情况下,更高的输入维度导致了U型走位轨迹将比N型走位轨迹更难于学习。
3 验证与测试 3.1 撞球机器人程序的学习过程 使用本文论述的方法,撞球机器人程序被开发并用于对母球的走位进行学习。经过训练的机器人可以掌握所学到的各种轨迹模式的走位规律。学习过程分为数据收集与训练2个阶段,其流程如图 14所示。蒙特卡罗方法用于训练数据的收集。机器人每进行一次击球练习,其使用的控制量、理论模型中的几何特征量、旋转分类参数以及理论与实际模型的输出位置偏差会自动写入到相应轨迹模式的数据库中。数据收集完成后,每一种轨迹模式中的数据都会导入到对应的BP神经网络模型中进行离线训练。对于轨迹模式0,训练样本约为10000组,测试样本约为1000组。训练样本与测试样本间是互无交集的。网络隐藏层神经元的数量根据经验在15~30个之间选取。
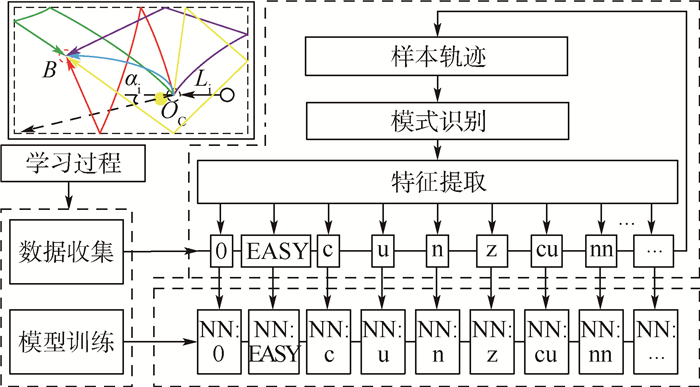 |
| 图 14 撞球机器人的学习过程 Fig. 14 Learning process for billiard robot |
| 图选项 |
3.2 模型测试结果 在验证测试中,机器人将会在给定的轨迹模式下,控制母球在与目标球碰撞后走向参考的目标点。在几何特征输入给定的条件下,机器人会穷举出所有可能的控制量组合,对于每一组控制量 (FI, Sx, Sy),机器人的计算过程分为2步:①计算出每一种组合对应的理想轨迹的终点;②使用相应的神经网络模型修正得到预测点。
经过穷举过程,机器人将选出一组最优控制量用于击球并计算对应的预测点B′。如果母球的实际最终位置B″与B′的偏差距离小于球体直径D,则判为成功;否则判为失败,如图 15所示。
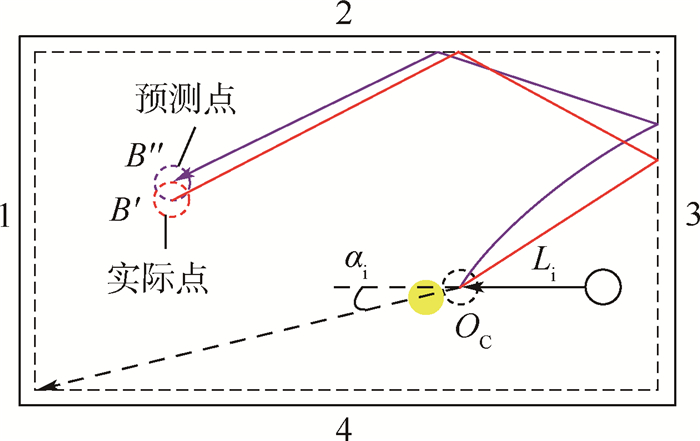 |
| 图 15 给定模式c下的走位测试 Fig. 15 Test for cue ball controlling with Pattern c |
| 图选项 |
部分轨迹模式的平均走位成功率统计结果见表 5。由于较低的输入维度,模式0的走位成功率能够达到96%;通过更新数据库,包含多次边库碰撞的走位成功率也提升至80%以上;另外,U型轨迹的走位成功率要稍稍低于N型轨迹,这与第2.5节中分析的结果一致。
表 5 部分轨迹模式的平均走位成功率统计结果 Table 5 Statistical results of average controlling rate for some trajectory patterns
| 模式 | 数据量 | 成功率/% |
| 0 | 5611 | 90 |
| EASY | 4786 | 80 |
| c | 2566 | 74 |
| u | 2609 | 73 |
| n | 2048 | 78 |
| z | 2367 | 76 |
| 0 | 10423 | 96 |
| EASY | 9387 | 90 |
| c | 5872 | 83 |
| u | 5163 | 82 |
| n | 4759 | 85 |
| z | 4821 | 86 |
表选项
图 16中统计了在0、EASY、U、N模式下不同输入角与输入距离对应的平均走位成功率。统计结果表明更小的输入角度与更短的输入距离对应着更高的走位成功率,更利于机器人对母球的最终位置进行准确的预测。这与人类球手打球的规律相符。在比赛中,人类会尽量避免远距离大角度的射球,其中的一个重要原因就是这样的击球难以预测出母球最终的位置,不利于连续得分。
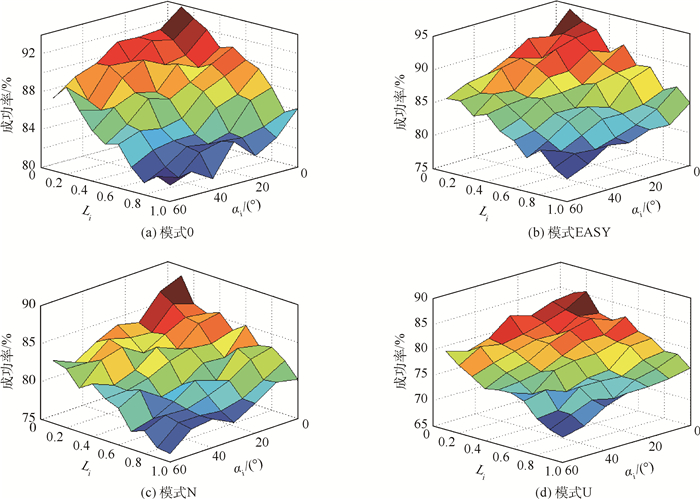 |
| 图 16 不同轨迹模式下输入 (αi,Li) 对走位成功率的统计结果 Fig. 16 Statistical results of inputs (αi, Li) versus controlling rate under different trajectory patterns |
| 图选项 |
另外,由于神经网络本身可以以任意精度逼近任何非光滑连续函数,因此在不使用理论模型的情况下直接用神经网络预测也是一个可行方案。这里将本文提出的理论模型结合神经网络的方法与直接使用神经网络方法的效果进行了对比,对于模式EASY的误差收敛曲线与训练完成时的回归曲线如图 17所示。对比结果表明,使用神经网络对理论模型进行修正的方法可以获得更好的训练效果以及更高的精度。网络的泛化效果也更好,理论模型的建立为神经网络的预测提供了重要依据,避免了单一使用神经网络导致的过拟合,易出现野值等不良现象。
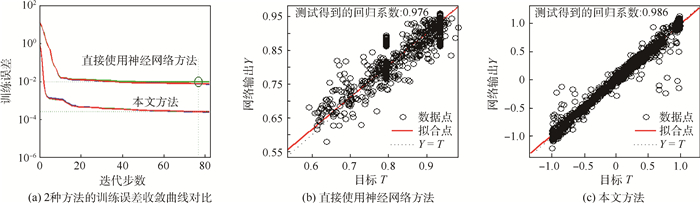 |
| 图 17 2种方法的训练与测试效果比较 Fig. 17 Comparison of training and test effect between two methods |
| 图选项 |
4 结论 本文对撞球机器人的母球控制问题展开研究。设计了一种基于神经网络的控制器使机器人能够在给定轨迹模式下完成母球的走位,主要结论如下:
1) 基于理论分析的方法,得到了理想光滑假设下球体的运动学模型,并给出了仿真结果。当母球的运动状态为滑动时,其底部与桌面接触点的绝对速度方向不发生变化,球体所受的摩擦力方向亦不发生变化。
2) 通过采用神经网络对理想模型进行修正的方法,使机器人能够有效地预测出母球的最终位置,避开了复杂的非光滑非线性建模过程。相比于单一的使用神经网络方法,理论模型的建立可以有效的提升网络的品质,降低了训练误差。
3) 针对母球轨迹的模式分类问题,提出了UN金字塔分类方法,即任何一条复杂轨迹的模式都可以看做是有限个U与N的组合。通过进一步分析,得到:任何一种包含多次边库反弹的轨迹模式对应的神经网络模型的几何特征输入维度不会超过4维。
4) 经过训练的机器人能够掌握所学到的任何轨迹模式的走位规律,与人类相似,机器人更善于在输入距离与输入角较小的条件下对母球进行控制。通过更新数据库,可以有效提升机器人对相应轨迹模式学习的效果。
参考文献
| [1] | HO K H L, MARTIN T, BALDWIN J.Snooker robot player-20 years on[C]//IEEE Symposium on Computational Intelligence and Games, 2007.(CIG 2007).Piscataway, NJ:IEEE Press, 2007:1-8. |
| [2] | YANG J S, CHEN Y M.The design of jump shot decision-making system for a billiard robot[C]//2010 IEEE Conference on Robotics Automation and Mechatronics (RAM).Piscataway, NJ:IEEE Press, 2010:409-413. |
| [3] | CHENG B R, LI J T, YANG J S.Design of the neural-fuzzy compensator for a billiard robot[C]//2004 IEEE International Conference on Networking, Sensing and Control.Piscataway, NJ:IEEE Press, 2004:909-913. |
| [4] | LEGG P A, PARRY M L, CHUNG D H S, et al.Intelligent filtering by semantic importance for single-view 3D reconstruction from Snooker video[C]//IEEE International Conference on Image Processing.Piscataway, NJ:IEEE Press, 2011:2385-2388. |
| [5] | LECKIE W, GREENSPAN M A. Pool physics simulation by event prediction 1:Motion transitions[J].ICGA Journal, 2005, 28(4): 214–222. |
| [6] | LANDRY J F, DUSSAULT J P, MAHEY P. A heuristic-based planner and improved controller for a two-layered approach for the game of billiards[J].IEEE Transactions on Computational Intelligence & AI in Games, 2013, 5(4): 325–336. |
| [7] | DOMéNECH A. Non-smooth modelling of billiard-and superbilliard-ball collisions[J].International Journal of Mechanical Sciences, 2008, 50(4): 752–763.DOI:10.1016/j.ijmecsci.2007.11.006 |
| [8] | MATHAVAN S, JACKSON M R, PARKIN R M. Numerical simulations of the frictional collisions of solid balls on a rough surface[J].Sports Engineering, 2014, 17(4): 227–237.DOI:10.1007/s12283-014-0158-y |
| [9] | MATHAVAN S, PARKIN R M, JACKSON M R. A theoretical analysis of billiard ball dynamics under cushion impacts[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2010, 224(9): 1863–1873.DOI:10.1243/09544062JMES1964 |
| [10] | GAO J, HE Q, ZHAN Z, et al.Dynamic modeling based on fuzzy neural network for a billiard robot[C]//IEEE International Conference on Networking, Sensing and Control.Piscataway, NJ:IEEE Press, 2016:1-4. |
| [11] | ZUO Z, WANG C. Adaptive trajectory tracking control of output constrained multi-rotors systems[J].IET Control Theory & Applications, 2014, 8(13): 1163–1174. |
| [12] | LOU W, GUO X.Adaptive trajectory tracking control using reinforcement learning for quadrotor[J/OL].International Journal of Advanced Robotic Systems, 2016, 13(38).[2016-03-09].http://cdn.intechopen.com/pdfs-wm/49981.pdf.DOI:105772/62128. |
| [13] | LECKIE W, GREENSPAN M A. Pool physics simulation by event prediction 2:Collisions[J].ICGA Journal, 2006, 29(1): 24–31. |
