飞行器编队飞行，即多架飞行器为适应任务要求按照一定的结构形式进行三维空间队形排列，使其在飞行过程中保持稳定的队形，以体现整个机群的协同一致性^[1-2]。相对于单个飞行器，多飞行器的协同编队通常有着更好的容错性和鲁棒性，能够以较低的成本更有效地完成任务^[3-5]，在环境监测、资源勘探、军事侦察、目标打击等民用和军用领域都有着突出的优势，具有广阔的应用前景。飞行器编队控制正逐步成为协同控制领域研究的热点。
同单飞行器相比，多飞行器系统的模型和控制方法更为复杂^[6-8]。文献[9]采用了改进的领航者-跟随者模型研究了多枚导弹的编队控制问题，提出了一种候补领航弹的模式来减少多导弹系统对领航弹的依赖。崔艳和贾英民^[10]使用了树型结构描述多个个体之间的拓扑关系，研究了存在扰动情况下多智能体系统编队问题。在文献[11]中，仿照鸽群层级建立了领航者-跟随者的“人”字形编队飞行的控制方法。文献[12]将多飞行器系统转换为一个二阶模型，并基于多智能体一致性理论研究了编队飞行控制问题，给出了编队系统稳定性的充分条件。然而，通常情况下的协同控制律要求个体根据相邻飞行器的实时信息调节自身的状态，以达到协同编队的目的。这就需要飞行器之间保持持续的通信连接。然而，对于飞行器来说其通信资源是有限的，持续的通信会造成较大的能量消耗；在实际复杂环境中，持续的通信实现起来也较为困难，而且容易受到干扰，对协同控制的效果造成不良影响。
事件驱动控制能够较好地解决上述问题^[13-14]。在事件驱动控制系统中，控制器的输出计算并不根据时间来进行，而是通过“事件”，即系统运行状态满足给定条件时，认为触发了一个事件，此时控制器才进行更新。事件驱动控制在近年来取得了许多研究成果^[15-17]。王航飞等^[18]采用事件驱动机制研究了多智能体系统的环形编队控制问题，在降低个体控制更新频率的情况下系统能形成给定的编队；文献[19-20]分别研究了一阶和高阶多智能体一致性的事件触发方法，允许个体有不同的触发方式；Meng和Chen^[21]在多智能体网络中设置了同步时钟，并以此采样数据进行了事件驱动控制；文献[22-23]利用测量误差构造了事件触发函数，解决了一般线性多智能体的趋同问题。但是，相比于通常的时间驱动方法，事件驱动方式飞行器编队的研究仍有需要关注的地方。例如文献[18]的方法只限于队形为环形，而且对通信拓扑的要求也是固定的；文献[19-21]要求通信拓扑为无向图等；设计合适的触发函数也是影响事件驱动控制效果的关键。
受到以上方法的启发，本文将多智能体事件驱动机制引入到多飞行器协同控制中，针对有向通信拓扑情况下飞行器在三维空间中的编队控制问题，设计了一种更为一般形式的触发函数和控制律，使得飞行器系统能形成空间任意给定的队形。设计的触发函数和控制律只要求飞行器之间在触发时刻进行通信，因此飞行器之间不需要始终保持通信连接，也不需要在同一时刻所有飞行器进行触发或设置同步时钟。相比需要持续通信和控制的方法，这不仅降低了对通信的要求，也降低了传输能量的消耗，更适于实际应用。
1 问题描述 1.1 飞行器系统建模 本文中使用的坐标系定义为^[24]：地面坐标系O_gx_gy_gz_g固定在地球表面，原点O_g位于地面任意选定的某固定点，O_gx_g轴指向地平面某任意选定方向，O_gz_g轴铅垂向下，Oy_g轴垂直于O_gx_gz_g平面，指向右；航迹坐标系Ox_ky_kz_k的原点O位于飞行器质心，Ox_k指向飞行器的速度方向，Oz_k轴位于包含Ox_k轴的铅垂平面内，并垂直于Ox_k轴指向下, Oy_k轴垂直于Ox_kz_k平面，指向右。
航迹倾角γ定义为航迹轴Ox_k与水平面Ox_gy_g的夹角，规定航迹向上倾斜时，γ为正；航迹偏角χ为航迹轴Ox_k在水平面Ox_gy_g上的投影与Ox_g轴之间的夹角，规定航迹向右偏转时，χ为正。
在航迹坐标系中的飞行器质心动力学方程组可以表示为

(1)

式中：V为飞行速度; m为飞行器质量; g为重力加速度; T_xk、T_yk和T_zk分别为推力在航迹坐标系上的投影; A_yk和A_zk分别为气动力在航迹坐标系y轴和z轴上的投影; D为气动阻力。令a_x为切向加速度，a_y和a_z为法向加速度的垂直与水平分量，则有

(2)

假设飞行器做无侧滑飞行，并且不考虑地球曲率的影响，在航迹坐标系中的位置坐标为x_g、y_g和h_g。综上所述，可以得到飞行器三自由度质点运动学模型^[25]：

(3)

定义系统的状态向量：

(4)

则由式 (3) 可得

(5)

令a=[a_x a_y a_z]^T，g=[0 0 g]^T，定义矩阵

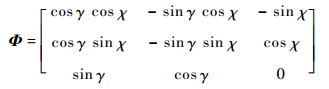(6)

注意到Φ是可逆的，则可以取待设计的控制律u满足如下关系：

(7)

进一步，根据式 (5) 可知第i个飞行器系统的状态空间方程为

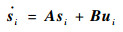(8)

式中：

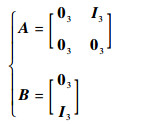(9)

0₃和I₃分别表示3阶零矩阵和单位矩阵。
1.2 通信拓扑与队形描述 本文采用图论的相关知识对多飞行器间的通信拓扑进行描述。设表示一个包含N个顶点的加权有向图，其中为图的顶点集，ε为图的边集，称为图的邻接矩阵。在多飞行器编队问题中，将每一个飞行器抽象成图的一个顶点，那么飞行器之间的通信关系就可以用相应的边来表示。若a_ij > 0，则表示边 (j, i)∈ε，也即第i个飞行器能够从第j个飞行器获得其状态信息，否则a_ij=0。a_ij也代表了对应连接的权重，在控制器设计中作为控制参数。由此定义顶点i的邻居集为

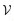
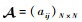
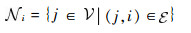(10)

并记的势为。
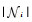
定义图的度矩阵?=diag{d₁, d₂, …, d_N}，其中。图的Laplacian矩阵定义为。如果包含生成树，那么有且只有一个0特征值，而其他的特征值均具有正实部。
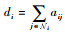
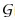
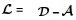
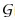
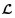
在三维空间中，编队队形可以通过飞行器之间的相对坐标来表示。在位置坐标系中，设编队中心为点O_r，r_i和r_j分别表示飞行器i和j到O_r的距离向量。r_ij=r_i－r_j表示这2个飞行器的相对位置, 如图 1所示。

图 1 飞行器空间相对位置描述 Fig. 1 Illustration of relative spatial positions between flight vehicles

图选项

那么，指定的飞行队形即可以用飞行器之间的相对位置关系来描述，即通过r_ij表示。本文旨在设计基于事件驱动的编队控制协议，使得多飞行器能够按照给定的队形实现稳定的飞行。若N个飞行器能形成指定的队形，则有

(11)

式中：为关于δ₁的函数，δ₁≥0为待设计的参数且有δ₁→0, Δ(δ₁)→0。
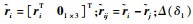
2 基于事件驱动的多飞行器协同控制设计 本节提出了一种基于事件驱动的协同控制方法。在每个飞行器的控制器中分别设置独立的触发条件，即整个系统是异步触发的，不同飞行器的触发时刻允许不同。飞行器只在满足自身的触发条件时，才和周围的邻居进行通信，并相应地更新控制器参数。在其他时间里，飞行器之间无需保持通信链接，只按照自身的控制进行飞行。设计事件驱动协同控制律为

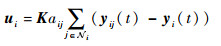(12)

式中：

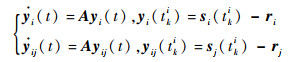(13)

K为控制增益矩阵；t_kⁱ表示第i个飞行器的第k次触发时刻；y_ij (t) 为在第i个飞行器中对飞行器的构造值。
在编队协同控制方法中，每个飞行器i利用自身状态信息以及其邻居飞行器的信息s_j (t) 来构造控制律。在采用事件驱动机制的情形下，飞行器i只能获得离散的触发时刻的邻居信息s_j (t_kⁱ)。在其他时间 (即非触发时间，t≠t_kⁱ) 里，飞行器i不能获得其他飞行器的实时状态，是独立运行的。在这种情况下，本文设计在飞行控制器i中构造状态y_i (t) 和y_ij (t) 以代替s_i (t) 和s_j (t) 生成控制律，如式 (11) 所示。如果进行了新的一次触发t=t_k+1ⁱ，则利用状态s_i (t_k+1ⁱ)、s_j (t_k+1ⁱ) 对y_i (t)、y_ij (t) 进行更新。
注1??通常的事件驱动律使用的是触发时刻的静态值s_i (t_kⁱ)、s_j (t_kⁱ)，对应的控制律是零阶保持器的形式。相比之下，式 (12) 和式 (13) 使用触发时刻的系统状态，在非触发时间内对控制律进行了动态地构造，从而能够更有效地利用这些信息。
2.1 多飞行器协同控制分析 令ε (t)=[ε₂^T (t) ε₃^T (t) … ε_N^T (t)]，其中。再令误差，那么

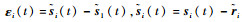
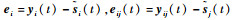
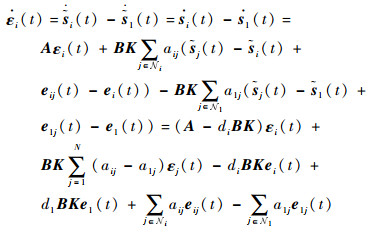(14)

记

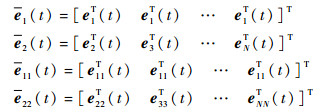其中:e_ii (t)=(e_ij (t))，为阶列向量。
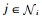
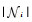
于是

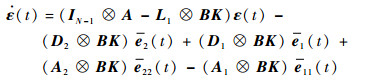(15)

式中：

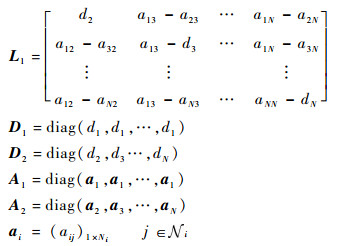下面讨论控制参数K的设计。如果飞行器的拓扑图包含生成树，那么L₁的特征值λ_i (L₁) 均具有正实部。记，P为如下Riccati方程的解:

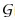
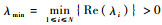
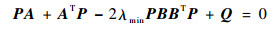(16)

式中：Q为给定的一个正定矩阵。令K=kB^TP，k≥1。则容易验证，所有的A－λ_i (L₁) BK的特征根均在左半平面。由此可知，(I_N－1?A－L₁?BK) 也是稳定的。于是，对于初始时刻t₀及t≥t₀，存在适当的正数M和α使得

(17)

由式 (15) 可知，

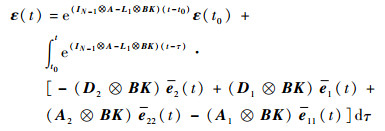(18)

那么，再考虑到式 (17) 有

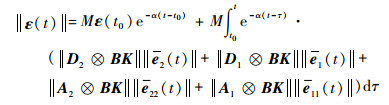(19)

根据矩阵直积的性质，有‖A?B‖=‖A‖‖B‖。记，那么

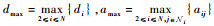
(20)

式中：

同理可得

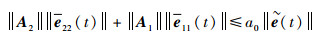式中:

于是

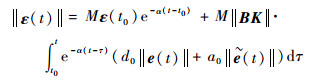(21)

2.2 触发函数设计 触发函数根据适当的条件产生事件，即出现触发时刻。基于以上的分析，设计第i个飞行器的触发函数为

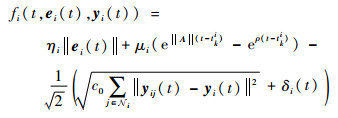(22)

式中:，c₀为给定常数，且满足，l_max为和L有关的常数；，b₀≥c₀ > 0；μ_k^ij=；δ_i (t)=δ₀ⁱe^－σ_it+δ₁ⁱ；A₀、ρ、δ₀ⁱ、δ₁ⁱ和σ_i为给定常数。
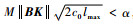
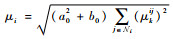
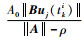
相应地，触发时刻定义为

(23)

在t=t_k+1ⁱ时刻系统进行触发时，第i个飞行器更新自身的控制律，更新后对应的触发函数再次小于0。
2.3 编队协同稳定性分析 在给出主要定理之前，有如下引理成立：
引理1??记，其中。再记

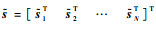
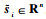
(24)

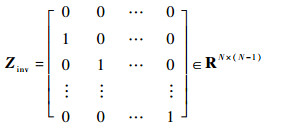(25)

L=(l_ij)，其中：。
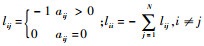
则有如下等式成立：

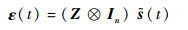(26)

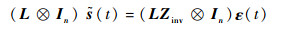(27)

证明??容易验证，下面主要证明式 (27)。由于

(28)

而

(29)

且L1_N=0，1_N为元素全为1的N维列向量。所以L (I_N－Z_invZ)=0。结合式 (28)，结论得证。
定理1??考虑由N个飞行器组成的系统，每个飞行器的模型由式 (3) 描述。假定N个飞行器的通信拓扑包含有向生成树。那么，根据设计的触发函数式 (22) 和触发时刻式 (23)，在事件驱动控制律式 (12) 的作用下，多飞行器系统能够按照给定的队形实现稳定飞行。即有

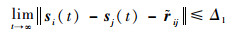(30)

式中:

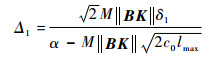证明??首先证明式 (31)。

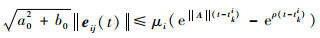(31)

记‖e_ij (t)‖的Dini导数为D⁺‖e_ij (t)‖，则有

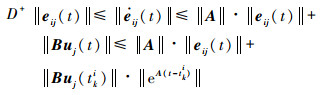(32)

由于存在A₀≥1, ρ≤‖A‖使得‖e^{A (t-t_ki)}‖≤A₀e^{ρ (t-t_ki)}，再令z=e^{-ρ (t-t_ki)}‖e_ij (t)‖，那么

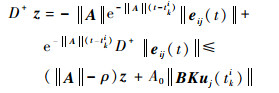(33)

求解式 (33) 可以得到式 (31) 的结论。
再根据触发函数式 (22) 可知：

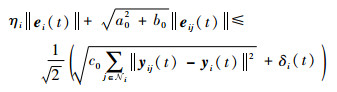(34)

即

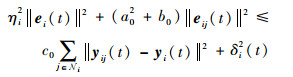(35)

式中：

(36)

则有

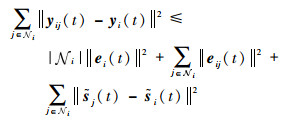(37)

由引理1可以得到

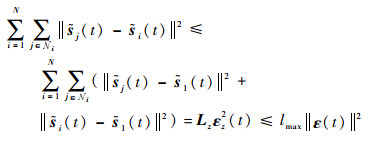(38)

式中:L_z=∣LZ_inv∣，|·|表示矩阵每个元素取绝对值后所获得的矩阵；l_max为L_z各列元素和的最大值；ε_z² (t)=[‖ε₂ (t)‖² ‖ε₃ (t)‖² … ‖ε_N (t)‖²]^T。
记δ (t)=δ₀e^－σt+δ₁，其中，。根据柯西不等式可知:

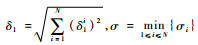
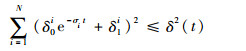(39)

由此得到

(40)

结合式 (40)，对式 (35) 两边同时求和，并经过化简可以得到

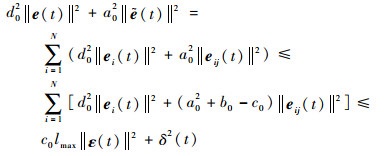(41)

即

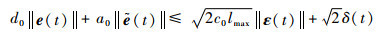(42)

将式 (42) 代入到式 (21) 中，可以获得‖ε (t)‖的上界估计：

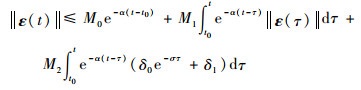(43)

式中：M₀=M‖ε₀ (t)‖；；。
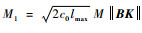
由于α < M₁，存在β∈(0, α) 使得。
下面要证明式 (44)。

(44)

式中：
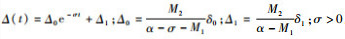
用反证法，若式 (44) 不成立，假设在t=t^*时刻有‖ε (t^*)‖ > b (t^*)，而t < t^*时‖ε (t)‖≤b (t)。那么

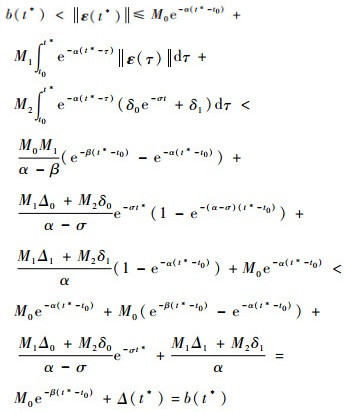(45)

矛盾。由此可以得到

(46)

注2??在触发函数中，由于

所以在ρ→‖A‖时μ_i (e^{‖A‖(t-t_ki)}-e^ρ(t-t_ki)) 趋近于。而如果在控制律中使用触发时刻状态的静态值，即在式 (12) 中取?_i (t)=0，?_ij (t)=0，那么ρ=0，(e^{‖A‖ (t-t_ki)}-e^ρ(t-t_ki)) 即成为 (e^{‖A‖ (t-t_ki)}-1)，这和文献[23]中的形式是相同的。文献[23]使用状态静态值做触发控制可以看作是式 (12) 的一种特殊情况。
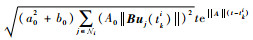
注3??在触发函数式 (22) 中，δ_i (t)=δ₀ⁱe^-σ_it+δ₁ⁱ和起到了动态阈值的作用。δ (t) 也与收敛到给定队形时的精度有关。∣δ_i (t)∣越小表示精度越高，但这同时也会使事件触发更加频繁。相比静态的阈值，δ_i (t) 可以在飞行编队初始形成时容许有较大的容差以减少触发的频率，而在系统运行一段时间后减小容差以获得较好的精度。
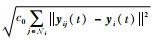
3 多飞行器编队算例 本节将通过算例来验证所设计的基于事件驱动协同控制律在多飞行器编队飞行中的有效性。考虑含有5个飞行器的系统，各飞行器的初始参数见表 1, 飞行器间的拓扑见图 2。
表 1 飞行器初始状态 Table 1 Initial conditions of flight vehicles

飞行器	位置/m	速度/(m·s-1)	航迹偏角/(°)	航迹倾角/(°)
1	(0, 0, 39)	63.2	5.1	18.4
2	(43, -55, 0)	59.8	21.8	25.7
3	(117, 19, -40)	72.1	56.3	0
4	(80, 0, -20)	58.4	69.6	-9.8
5	(100, -78, 0)	72.2	88.3	14.4

表选项

图 2 飞行器之间的拓扑 Fig. 2 Topology among flight vehicles

图选项

对应拓扑间的权重为a₁₄=0.58，a₂₃=0.33，a₃₅=0.25，a₄₁=0.21，a₄₃=0.40，a₅₁=0.37。期望形成的队形如图 3所示。

图 3 飞行器期望队形 Fig. 3 Desired formation of flight vehicles

图选项

即r₁₄=(0, -150, 0)^T，r₂₃=(0, -150, 0)^T，r₃₅=(75, 75, -120)^T，r₄₁=(0, 150, 0)^T，r₄₃=(-150, 0, 0)^T，r₅₁=(75, 75, 120)^T。
选取Q=10^-3diag (0.8，0.8，7.2，5，5，5)，求解方程式 (16) 可得

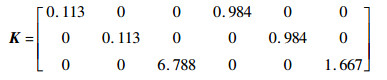(47)

由此可以设置M、α、λ_i、μ_i、c₀以及δ_i (t)，从而获得每个飞行器的触发函数。
图 4给出了多飞行器在空间中的飞行轨迹以及相应的参数变化。从图 4 (a) 和图 4 (b) 中可以看出，5个飞行器在触发函数及协同控制协议的作用下能够实现按照给定队形进行飞行，验证了方法的有效性。图 4 (c) 和图 4 (d) 反映了各飞行器航迹偏角和轨迹倾角的变化曲线。从图中可以看出，多飞行器在水平和垂直方向上的一致性良好，能够连续平滑地完成队形的协同。

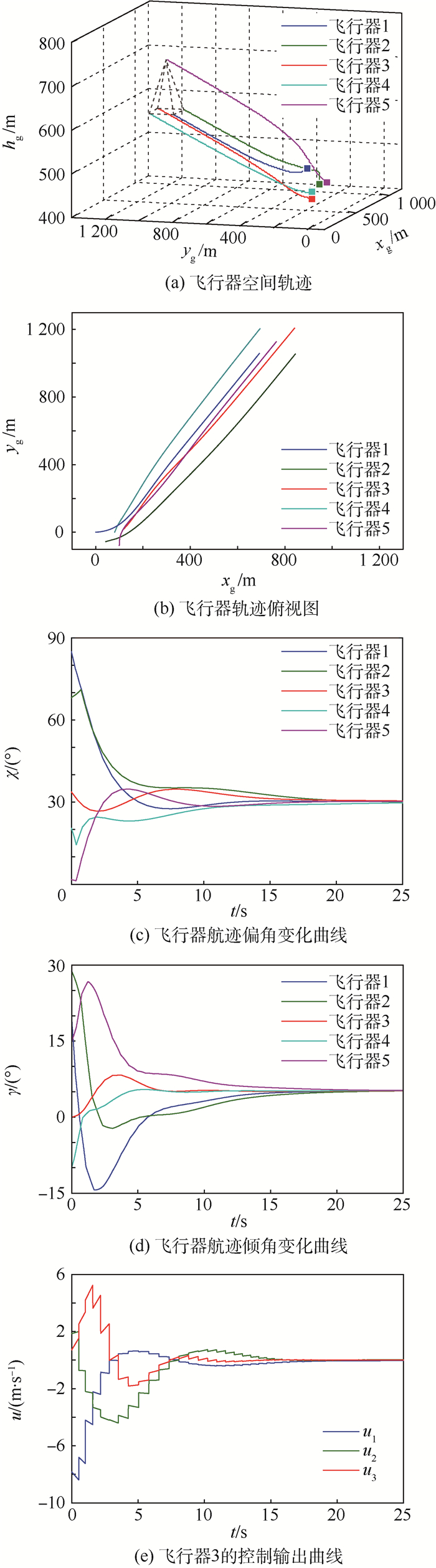图 4 多飞行器编队飞行仿真结果 Fig. 4 Simulation results of multiple flight vehicles formation

图选项

为了描述控制量变化的情况，本例中选取了其中一个飞行器的控制器输出作为说明，其他飞行器的控制器情形与之相似。图 4 (e) 为第3个飞行器的控制曲线，其中u₁、u₂和u₃为控制输出u的3个分量。从图中可以看出，文中所提的方法能够以较少的触发频率较快地实现给定的队形。在触发时刻 (折线上的转折点) 控制器会对当前的控制值作出调整。在非触发时刻，控制器的输出不依赖于其他飞行器的实时状态，并根据上一次触发信息构建控制律，直至满足触发条件时才进行更新。这也是事件触发机制的一个特点。
为了描述队形形成的准确程度，引入加权误差函数Y来表示多飞行器编队与期望队形之间的差异，可以通过Y值的变化来反映控制方法的性能。由于状态ε_i包含飞行器位置、角度、速度，因此采用权值矩阵W使得误差处于同一数量级尺度下。定义Y为

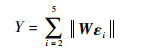(48)

式中:W=diag (w₁, w₂, w₃, w₄, w₅, w₆) 为对应权重。在本例中，选取Y=0.1来对比不同参数情形下的收敛时间。
如表 2和图 5所示，不同的触发函数参数会对飞行器的触发情况和控制性能产生影响。在∣δ_i (t)∣较小时，会有更快的收敛速度，但同时也会增加控制器的触发次数，反之亦然。此外，从图 5可以看出，相比传统连续通信的编队控制^[12]，
表 2 不同触发参数结果对比 Table 2 Results comparison of different trigger parameters

情形	触发函数参数 (δ0i, δ1i, σi)	飞行器1~5的触发次数	收敛时间/s
1	(-3, -0.7, 0.05)	43, 41, 41, 42, 42	23.76
2	(-5, -0.7, 0.05)	26, 29, 30, 30, 31	24.47
3	(-5, -0.7, 0.03)	22, 24, 25, 26, 26	24.70
4	(-3, -0.1, 0.05)	59, 55, 55, 56, 57	23.49
文献[12]			22.95

表选项

图 5 不同参数下Y值变化曲线 Fig. 5 Variation curves of Y with different parameters

图选项

本文提出的基于事件驱动的方法仍能够保持较好地控制精度；而从通信要求的角度来看，不需要连续通信会使其在实际应用中更有优势。
4 结论 本文研究了有向拓扑通信情况下多飞行器系统空间编队协同控制问题。
1) 相比传统方法，引入事件驱动方式设计多飞行器协同控制方法是有效的，通过事件触发函数和控制器的设计使得多飞行器能够形成任意给定队形的空间编队。
2) 利用触发时刻的状态可以构造协同控制律，同时，本文提出的方法避免了每个控制器对全局信息的使用，使得飞行器只需要和其邻居在触发事件时进行信息交互，更具有实际应用意义。
3) 触发函数的参数选择会对触发频率和控制精度产生影响。若在较短时间获得较高的精度，通常需要较多的触发次数。
4) 仿真算例结果表明，多飞行器系统能够实现稳定的编队飞行，验证了方法的有效性。

参考文献

[1]	李文皓, 张珩. 无人机编队飞行技术的研究现状与展望[J].飞行力学, 2007, 25(1): 9–11.LI W H, ZHANG H. Reviews on unmanned aerial vehicle formation-flight[J].Flight Dynamics, 2007, 25(1): 9–11.(in Chinese)
[2]	OH K K, PARK M C, AHN H S. A survey of multi-agent formation control[J].Automatica, 2015, 53: 424–440.DOI:10.1016/j.automatica.2014.10.022
[3]	樊琼剑, 杨忠, 方挺, 等. 多无人机协同编队飞行控制的研究现状[J].航空学报, 2009, 30(4): 683–691.FAN Q J, YANG Z, FANG T, et al. Research status of coordinated formation flight control for multi-UAVs[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 683–691.(in Chinese)
[4]	罗德林, 张海洋, 谢荣增, 等. 基于多agent系统的大规模无人机集群对抗[J].控制理论与应用, 2015, 32(11): 1498–1504.LUO D L, ZHANG H Y, XIE R Z, et al. Unmanned aerial vehicles swarm conflict based on multi-agent system[J].Control Theory & Applications, 2015, 32(11): 1498–1504.(in Chinese)
[5]	徐肖豪, 孟令航, 赵嶷飞. 基于几何方法的洲际航空编队飞行路径规划[J].北京航空航天大学学报, 2015, 41(7): 1155–1164.XU X H, MENG L H, ZHAO Y F. Geometric approach for intercontinental formation flight path planning[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7): 1155–1164.(in Chinese)
[6]	王祥科, 李迅, 郑志强. 多智能体系统编队控制相关问题研究综述[J].控制与决策, 2013, 28(11): 1601–1613.WANG X K, LI X, ZHENG Z Q. Survey of developments on multi-agent formation control related problems[J].Control and Decision, 2013, 28(11): 1601–1613.(in Chinese)
[7]	RUDY C G, NEJAT O. Stability of formation control using a consensus protocol under directed communications with two time delays and delay scheduling[J].International Journal of Systems Science, 2016, 47(2): 433–449.DOI:10.1080/00207721.2014.886745
[8]	邵龙飞, 师鹏, 赵育善. 电磁航天器编队动力学建模与运动规划方法[J].北京航空航天大学学报, 2015, 41(4): 738–743.SHAO L F, SHI P, ZHAO Y S. Dynamics modeling and motion programming for electromagnetic formation flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 738–743.(in Chinese)
[9]	马培蓓, 纪军. 多导弹三维编队控制[J].航空学报, 2010, 31(8): 1660–1666.MA P B, JI J. Three-dimensional multi-missile formation control[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1660–1666.(in Chinese)
[10]	崔艳, 贾英民. 树型变换下高阶多智能体系统鲁棒一致性方法[J].北京航空航天大学学报, 2013, 39(3): 386–390.CUI Y, JIA Y M. Robust consensus approach to high-order multi-agent systems based-on tree-type transformation[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 386–390.(in Chinese)
[11]	邱华鑫, 段海滨, 范彦铭. 基于鸽群行为机制的多无人机自主编队[J].控制理论与应用, 2015, 32(10): 1298–1304.QIU H X, DUAN H B, FAN Y M. Multiple unmanned aerial vehicle autonomous formation based on the behavior mechanism in pigeon flocks[J].Control Theory & Applications, 2015, 32(10): 1298–1304.(in Chinese)
[12]	薛瑞彬, 宋建梅, 张民强. 具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究[J].兵工学报, 2015, 36(3): 492–502.XUE R B, SONG J M, ZHANG M Q. Research on distributed multi-vehicle coordinated formation flight control with coupling time-delay and jointly-connected topologies[J].Acta Armamentarii, 2015, 36(3): 492–502.(in Chinese)
[13]	HEEMELS W P M H, SANDEE J H, BOSCH P P J V D. Analysis of event-driven controllers for linear systems[J].International Journal of Control, 2008, 81(4): 571–590.DOI:10.1080/00207170701506919
[14]	AL-AREQI S, G?RGES D, LIU S. Event-based networked control and scheduling codesign with guaranteed performance[J].Automatica, 2015, 57: 128–134.DOI:10.1016/j.automatica.2015.04.003
[15]	邵浩宇, 胡爱花. 基于事件驱动控制的非线性多智能体的一致性[J].信息与控制, 2015, 44(1): 38–42.SHAO H Y, HU A H. Consensus of nonlinear multi-agent systems with event-triggered control[J].Information and Control, 2015, 44(1): 38–42.(in Chinese)
[16]	FAN Y, FENG G, WANG Y, et al. Distributed event-triggered control of multi-agent systems with combinational measurements[J].Automatica, 2013, 49(2): 671–675.DOI:10.1016/j.automatica.2012.11.010
[17]	LIU T, JIANG Z P. Event-based control of nonlinear systems with partial state and output feedback[J].Automatica, 2015, 53: 10–22.DOI:10.1016/j.automatica.2014.12.027
[18]	王航飞, 禹梅, 谢广明, 等. 基于事件驱动的环形编队多智能体系统[J].系统科学与数学, 2014, 34(7): 815–827.WANG H F, YU M, XIE G M, et al. Event-driven circle formation control for multi-agent systems[J].Journal of Systems Science and Complexity, 2014, 34(7): 815–827.(in Chinese)
[19]	DIMAROGONAS D V, FRAZZOLI E, JOHANSSON K H. Distributed event-triggered control for multi-agent systems[J].IEEE Transactions on Automatic Control, 2012, 57(5): 1291–1297.DOI:10.1109/TAC.2011.2174666
[20]	KIA S S, CORTéS J, MARTíNEZ S. Distributed event-triggered communication for dynamic average consensus in networked systems[J].Automatica, 2015, 59.
[21]	MENG X, CHEN T. Event based agreement protocols for multi-agent networks[J].Automatica, 2013, 49(7): 2125–2132.DOI:10.1016/j.automatica.2013.03.002
[22]	GARCIA E, CAO Y, CASBEER D W. Decentralized event-triggered consensus with general linear dynamics[J].Automatica, 2014, 50(10): 2633–2640.DOI:10.1016/j.automatica.2014.08.024
[23]	ZHU W, JIANG Z P, FENG G. Event-based consensus of multi-agent systems with general linear models[J].Automatica, 2014, 50(2): 552–558.DOI:10.1016/j.automatica.2013.11.023
[24]	方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005: 16-20.FANG Z P, CHEN W C, ZHANG S G. Atmospheric flight dynamics[M].Beijing: Beihang University Press, 2005: 16-20.(in Chinese)
[25]	张磊, 方洋旺, 刁兴华, 等. 多导弹协同攻击编队非线性最优控制器设计[J].北京航空航天大学学报, 2014, 40(3): 401–406.ZHANG L, FANG Y W, DIAO X H, et al. Design of nonlinear optimal controller for multi-missile formation[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 401–406.(in Chinese)