为了降低单位度电成本,风力机的大型化已成为发展趋势,这对风力发电技术提出了新的挑战。当风速高于额定风速时,为了保证风力机各部件的安全性和稳定性,应使风力机的输出功率稳定在额定值附近。目前, 风力机控制风能吸收的方式主要有2种: ①被动地利用桨叶失速性能来限制高风速下的风能吸收;②主动变桨距来控制风能的吸收[2]。被动失速控制通过设计叶片的气动特性,使叶片在大风速下被动失速。但是在风速较大时,叶片的载荷较大,因此在设计叶片时除了考虑叶片的气动特性还需充分考虑叶片的强度,因而会增加叶片的质量,导致成本升高。主动变桨控制需要叶片实现大幅而又快速的变桨操作,因而存在控制带宽小、滞后严重、附加质量大以及维护成本高等问题。
近年来,具有可变尾缘襟翼的智能风力机成为大型风力机研究的热点[3-5]。文献[4]在风洞中开展了具有襟翼的风力机系统的控制试验,基于辨识出来的系统设计了H∞鲁棒控制器,风洞试验结果表明,变襟翼技术有效降低了风力机叶片受到的风载波动。文献[5]基于FAST/Aerodyn商用软件集成了尾缘襟翼的模拟仿真接口,设计了基于Simulink的PID控制器,仿真结果显示,变襟翼技术可以有效改变风力机系统所受到的载荷。与变桨控制相比,襟翼控制具有响应快、质量轻、可靠性高等优点,不需要增大风力机及其附属设备的质量,克服了桨距控制磨损轴承和执行机构的缺点。通过控制襟翼、改变叶片的升力系数等气动参数,可达到控制风力机受到的气动载荷、稳定输出的目的[6]。
目前,风力机气动力学分析、计算常用的方法有叶素动量方法 (Blade Element Momentum Method, BEM)[7]、广义动态尾流 (Generalized Dynamic Wake, GDW) 理论[8]、计算流体力学 (Computational Fluid Dynamics, CFD)[9]等。BEM是目前风力机设计和校核计算中应用最为广泛的方法,其计算方法较为简单,计算资源消耗较少,适合工程应用,对风力机气动计算模型进行了较大的简化,无法对流场细节进行模拟和分析。GDW方法早期为研究直升机而诞生,优点在于包含了动态尾流效应、叶尖损失和偏斜流等,不足之处在于低风速、大气弹偏移或大叶轮锥角等条件下,可能出现较大气动偏差甚至不稳定现象。CFD方法基于求解Navier-Stokes方程,可以较为细致地研究风力机运行过程中的流场细节,但需要花费大量的时间。
在恒功率控制方面,目前研究成果主要集中于变桨控制领域。针对变桨距风力机非线性模型,目前所采用的方法主要可以分为2类:①PID控制和模糊PID控制等方法[10-11];②在反馈线性化的基础上结合鲁棒控制、最优控制[12-13]。文献[10]基于模糊推理分析了桨距角前馈值,并且与模糊PID相结合,较好地实现了额定风速以上的恒功率控制。文献[11]借助流体计算软件分析了桨叶-功率的关系,获得了桨距角敏感性数据,由此设计出了非线性PID控制器,并借助专业软件GHBladedr进行了仿真验证。文献[12]针对额定风速以上的恒功率控制问题,将局部反馈线性化理论和H∞鲁棒理论相结合,仿真结果验证所设计的桨距角H∞控制器能够实现发电机输出功率的恒定。
需要指出的是,针对变襟翼风力机系统,目前的研究工作多集中在变襟翼风力机系统的气动力学的机理研究,主要采用CFD等大型计算软件进行分析。面向控制器设计的变襟翼风力机气动力学建模以及相应的控制器设计的研究工作国内外开展的很少。因此,本文基于修正的BEM建立变襟翼风力机气动模型,将襟翼偏转角对翼型气动参数的影响引入动力学模型中。在所建立的变襟翼风力机非线性动力学模型的基础上,将动态逆方法和H∞状态反馈方法相结合,设计了非线性变襟翼恒功率控制器。仿真结果表明,变襟翼控制系统能有效稳定系统的输出功率。
1 风电系统建模 1.1 具有尾缘襟翼的风力机气动模型 为了设计合适的变襟翼控制器,需要建立襟翼偏转角与风力机输出功率之间的关系。由于变襟翼风力机的功率系数Cp的表达式很难从理论上获得,因此本文首先基于BEM计算不同襟翼偏转角β和叶尖速比λ时风力机的输出功率系数Cp,再通过数值拟合获得功率系数Cp关于叶片襟翼偏转角β和叶尖速比λ的表达式。
1.1.1 基于BEM计算风力机功率输出 BEM将动量理论与实际叶片上发生的局部情况结合起来。将流管离散成N个高度为dr的环形单位,如图 1所示。这些单位的外侧边界由流线形成,即单位之间没有流动。
 |
| 图 1 BEM中使用的形状像环形单元的控制体积 Fig. 1 Control volume shaped as an annular element used in BEM model |
| 图选项 |
在BEM中,对环形单元作如下假设[14]:
1) 离散的各个叶素之间是相互独立的,即其中任意某一个叶素对其他叶素不会有影响。
2) 每个环形单元中,叶片作用在流动上的力是定常的 (该假设对应于叶片数为无穷的情况,建模时通过引入普朗特叶尖损失因子修正这一严格的假设)。
由于已经假定不同控制体积之间是相互独立的,每一个窄长条即单元都可以单独处理,即对每一控制体积可以运用下述算法:
步骤1?对轴向和切向诱导因子a和a′初始化,取a=a′=0。
步骤2?根据如下方程计算入流角?:
 | (1) |
式中:v0为风速;ωr为风力机的转速;r为控制体积距离旋转轴的径向距离。
步骤3?根据如下方程计算迎角α:
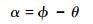 | (2) |
式中:θ为叶片的局部桨距角,即桨距角与叶片扭角之和。
步骤4?从相关图表中读取不同迎角α和襟翼偏转角β时翼型的升力系数Cl和阻力系数Cd,其中升力系数和阻力系数与α和β的关系可由风洞试验或者CFD数值计算获得。文献[15-16]对具有尾缘襟翼的Ris?-B1-18翼型进行了二维流体计算,计算中假设完全湍流,湍流模型使用SST k-ω模型,采用二维不可压缩雷诺平均Navier-Stokes方程求解器EllipSys2D求解,并在风洞试验中验证了计算结果的可靠性[17]。因此,本文采取如图 2所示的襟翼相对弦长为20%的Ris?-B1-18翼型随迎角变化的升力系数和升阻比数据作为计算依据[15-16]。
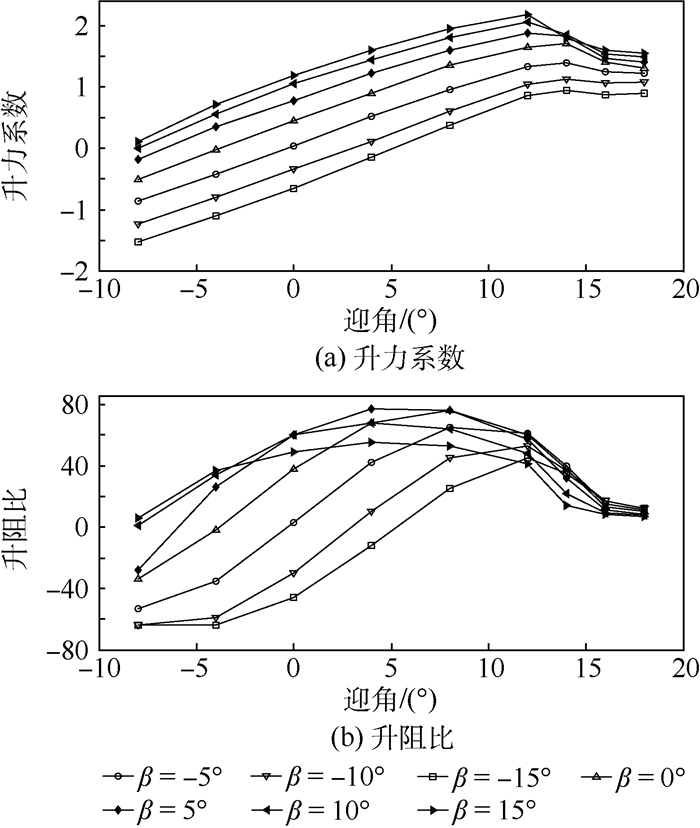 |
| 图 2 升力系数和升阻比随迎角的变化 Fig. 2 Variation of lift coefficient and lift-drag ratio with angle of attack |
| 图选项 |
步骤5?根据如下方程计算法向力系数Cn和切向力系数Ct:
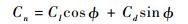 | (3) |
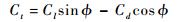 | (4) |
步骤6?为了修正假设2),即叶片数无穷假设,在此处引入普朗特叶尖损失因子F。
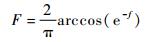 | (5) |
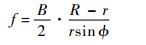 | (6) |
式中:B为风轮叶片数;R为整个风轮半径。
步骤7?根据如下方程更新轴向和切向诱导因子a和a′:
 | (7) |
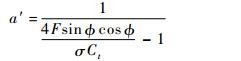 | (8) |
式中:实度σ定义为控制体积中环形面积被诸叶片覆盖的比值,其表达式为
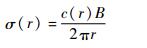 | (9) |
式中:c(r) 为局部弦长。
步骤8?轴向诱导因子a较大时,进行Glauert修正。当轴向诱导因子a>0.2时,需要对轴向诱导因子a的值进行修正。推力系数CT和轴向诱导因子a之间存在不同经验关系式,其中一种表示为[14]
 | (10) |
式中:ac=0.2。
对于环形体积而言,CT的定义式为
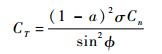 | (11) |
当a≤0.2时,轴向诱导因子a的表达式不变, 直接跳到步骤10。当a>0.2时,利用式 (10) 和式 (11) 相等,可以得到Glauert修正后轴向诱导因子a的表达式为
 | (12) |
式中:
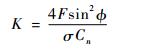 | (13) |
步骤9?比较步骤8所更新和步骤8更新之前的a和a′的值,若大于容许偏差,则返回步骤2重新计算。否则,进入步骤10。
步骤10?根据前面计算出的轴向诱导因子a和切向诱导因子a′计算叶片上的载荷,在该叶素上对dT、dM积分可以求得作用在该叶素上的推力和扭矩。
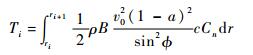 | (14) |
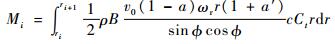 | (15) |
式中:ρ为空气密度。
步骤11?计算风力机组受到的总推力及捕获的功率分别为
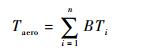 | (16) |
 | (17) |
推力系数和功率系数分别为
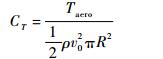 | (18) |
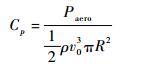 | (19) |
1.1.2 气动转矩模型 采用第1.1.1节所述的计算方法可以获得不同叶尖速比λ和襟翼偏转角β下的风力机功率系数Cp,如图 3所示。叶尖速比λ表达为
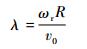 | (20) |
 |
| 图 3 功率系数随叶尖速比和襟翼偏转角的变化 Fig. 3 Variation of power coefficient with tip speed ratio and flap deflection angle |
| 图选项 |
需要指出的是,为获得最大的控制效果,将叶片襟翼安装在叶素的径向距离相比于叶片半径65%~90%之间的位置上。
为了保证模型的准确度,将得到的功率系数对襟翼偏转角的数据进行插值运算,将襟翼偏转角β的间隔由5°插值变为1°,拟合时襟翼偏转角β一共选取了31个点,范围为-15°~15°。叶尖速比λ一共选取了14个点,其范围为2.424 0~5.288 8。在保证模型精确度的前提下,功率系数Cp关于叶尖速比λ和襟翼偏转角β的表达式应尽可能简单。图 3为根据BEM计算的功率系数Cp的拟合结果,拟合相关系数为0.999 7。功率系数Cp的表达式为
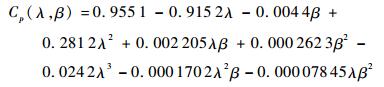 | (21) |
风力机的气动转矩Maero可以表达为
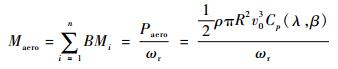 | (22) |
1.2 发电机模型 发电机模型如下所示[12-13]:
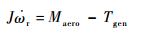 | (23) |
式中:J为风力机及发电机总的转动惯量;Tgen为发电机的电磁转矩。
1.3 襟翼执行机构 考虑到系统的时滞特性,驱动襟翼的执行机构可以假定为一阶惯性环节,即
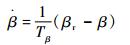 | (24) |
式中:Tβ为时间常数;βr为襟翼偏转角控制量。
1.4 风电系统的整体模型 电磁转矩Tgen是由发电机的特性所决定的,为简化分析,在风力机额定运转下,电磁转矩Tgen可以假定为定值。式 (21)~式 (24) 构成了可变尾缘襟翼风电系统的非线性模型。考虑一定外部扰动w的情况下,风电系统的模型可以表示为
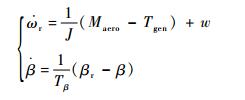 | (25) |
2 基于动态逆方法的变襟翼控制器设计 2.1 控制问题描述 根据风电机组的运行特性,当风速高于额定风速时,控制目标就是保证风电机组的恒定功率输出。恒功率运行情况下,风力机电磁转矩可以设为常值,因此,风电机组功率控制就转换成了风力机转速的控制[12-13]。本文将风电机组的额定转速与实际转速的差作为反馈,襟翼偏转角作为控制输入,通过调节叶片襟翼偏转角来改变功率系数。通过控制使风力机转速在高风速的工况下保持在额定值,从而实现风力机发电机组的恒功率控制,控制框图如图 4所示。
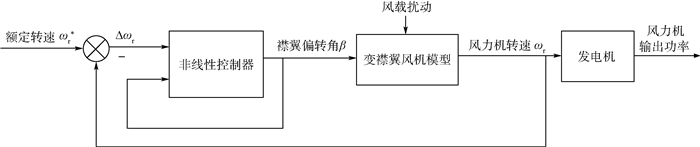 |
| 图 4 风电系统的变襟翼控制框图 Fig. 4 Control block diagram of variable flap of wind power system |
| 图选项 |
2.2 基于动态逆方法的智能风电系统的线性化 由式 (21)~式 (24) 描述的风电系统是一个非线性系统。对于这样一个非线性系统,本文采用动态逆控制策略设计控制器。动态逆方法的基本思想是:对于给定的非线性系统,利用对象的模型生成一种用反馈方法实现的原系统的积分逆系统,将对象补偿成为具有线性传递关系的一种规范化系统——伪线性系统,再应用线性系统理论完成系统控制器的设计[18]。
对于风电系统模型式 (25),选取转速ωr和襟翼偏转角β作为状态变量,可得
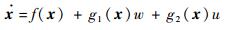 | (26) |
式中:
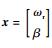
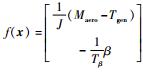
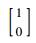
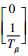
首先,检验该系统是否可以使用动态逆方法线性化。本文中的控制目标是使Δωr=0,即ωr*-ωr=0,因此选取输出函数为
 | (27) |
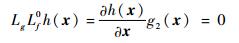 | (28) |
 | (29) |
系统关系度m=2。系统的阶数n=2,即m=n,满足动态逆的要求[18]。
其次,选取合适的坐标变换。令
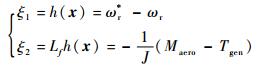 | (30) |
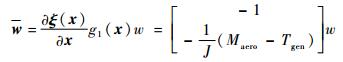 | (31) |
原非线性系统就转换为
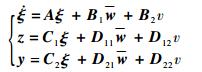 | (32) |
式中:
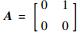
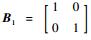
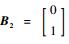
2.3 基于LMI算法的H∞控制器设计 针对式 (32) 描述的系统,采用状态反馈H∞控制方法设计控制器。将系统的观测输出定义为系统的状态变量,即
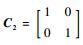
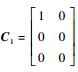
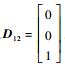
对于形如式 (32) 所描述的系统,如果存在标量γ>0和控制律v=Kξ,使得其相应的闭环传递函数
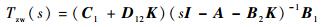 | (33) |
满足:
 | (34) |
可以求解系统式 (32) 的γ-最优控制器,设X为正定矩阵,W为合适维数的矩阵,标量p>0,使得如下线性矩阵不等式 (Linear Matrix Inequality, LMI)[19]有解:
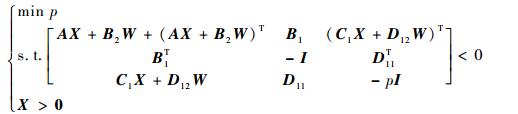 | (35) |
可以得到系统式 (32) 的最优H∞控制器为
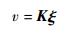 | (36) |
式中:K=WX-1。相应的最小扰动抑制度为p。线性化后的系统是可控可观测的,因此可以采用LMI算法设计控制器。
3 仿真结果及分析 仿真中,变襟翼风力机模型的参数如下:风力机额定功率P*=500 kW,额定风速v0*=11.75 m/s,风力机额定转速ωr*=2.838 rad/s,风轮半径R=20.5 m,风力机的总转动惯量J=2.36×105 kg·m2,空气密度ρ=1.225 kg/m3。
采用第2.2节和第2.3节的控制器设计方法,利用MATLAB的LMI工具箱对式 (35) 求解,经过4次迭代优化,得控制器设计结果为
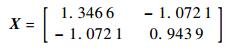 |
 |
可得线性控制律为
 | (37) |
相应的扰动抑制度γ=1.344 1,得原非线性系统的控制律为
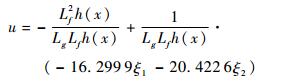 | (38) |
式中:
 |
本文对比了在变桨距风力机恒功率控制中使用较多的PID控制和基于动态逆方法的最优控制。
取e=ωr*-ωr,得PID控制器
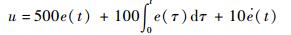 | (39) |
对于式 (32) 所描述的线性系统,取代价函数为
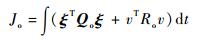 | (40) |
式中:
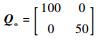
利用MATLAB工具箱可解得线性控制律为
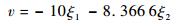 | (41) |
代入式 (38) 中可得非线性控制律。
当风况为12~16 m/s阶跃变化时,仿真结果如图 5所示。可知,当风速由12 m/s骤变到16 m/s时,尾缘襟翼向负方向增加,所采取的控制策略可使风力机的转速迅速恢复到2.838 rad/s,并将波动控制在一个较小的范围内,从而实现了风力机的恒功率控制。图 5(a)为阶跃风模型。基于动态逆方法的H∞鲁棒控制下风力机的角速度能更快、更平滑地收敛到额定转速,且具有更少的超调量,因而控制效果优于PID控制和基于动态逆方法的最优控制。
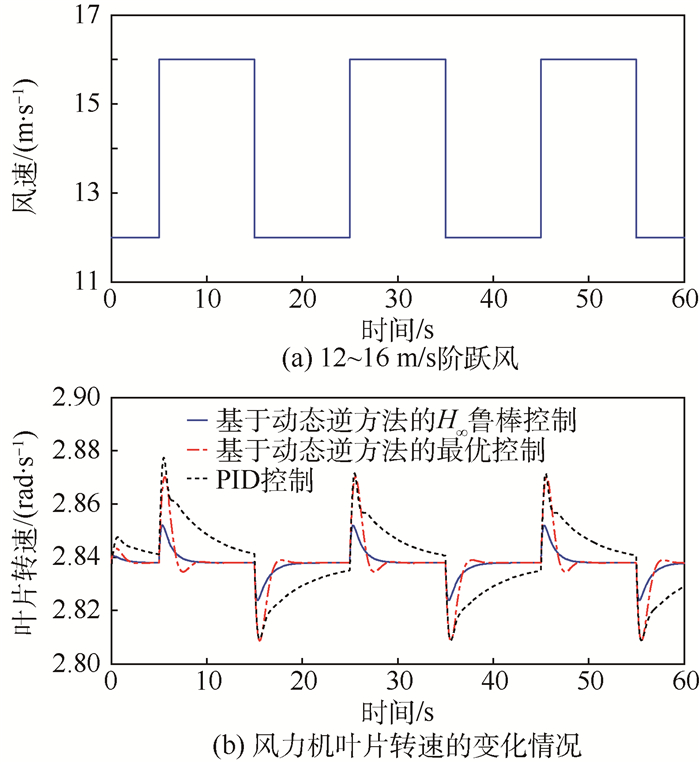 |
| 图 5 12~16 m/s阶跃风下风力发电系统响应 Fig. 5 Response of wind power system with 12-16 m/s step wind |
| 图选项 |
模拟实际风速的模型,目前国内外使用较多的是风速四分量模型,即基本风V、阵风VWG、渐变风VWR和随机风VWN,实际风速建模如图 6(a)所示。控制过程中的襟翼偏转角如图 6(b)所示。图 6(c)和图 6(d)分别给出了风载变化时风力机转速和功率输出的变化曲线。从仿真结果中可以看出,基于动态逆方法的H∞鲁棒控制的效果明显优于另外2种控制方法。基于动态逆方法的H∞鲁棒控制器能够将外界干扰对控制系统输出的影响抑制在一个较小的范围内,使风力机的转速ωr稳定在额定值2.838 rad/s附近,因而将控制系统的输出功率P也稳定在额定值500 kW附近,控制器具有较强的鲁棒性。
 |
| 图 6 实际风下风力发电系统响应 Fig. 6 Response of wind power system with actual wind |
| 图选项 |
4 结论 1) 基于修正的BEM建立尾缘襟翼偏转角对风力机吸收风能的影响的模型。不同于目前使用较多的系统辨识方法,本文借助文献[15-16]的数据作为计算依据,利用修正的BEM建立了一个在叶素的径向距离比于叶片半径为65%~90%之间的位置上装有襟翼执行机构,额定功率为500 kW的变襟翼风力机模型。为以后分析其他型号的襟翼风力机拓宽了思路。
2) 在所建立的变襟翼风力机非线性动力学模型的基础上,本文将动态逆方法和H∞状态反馈方法相结合,设计了非线性变襟翼恒功率控制器。为了验证非线性襟翼控制器的有效性,本文基于Simulink模拟了额定风速以上阶跃风况和基于四分量模型所建立的实际风况下襟翼风力机的发电情况。仿真结果表明,非线性襟翼控制器能够将风力机的转速和输出功率控制在额定值附近,表明所提控制策略有效且具有良好的鲁棒性。
参考文献
| [1] | 贺德馨. 中国风能发展战略研究[J].中国工程科学, 2011, 13(6): 95–100.HE D X. Research on China's wind energy development strategy[J].Engineering Sciences, 2011, 13(6): 95–100.(in Chinese) |
| [2] | 高峰, 徐大平, 吕跃刚. 大型风力机组的前馈模糊-PI变桨距控制[J].动力工程, 2008, 28(4): 537–542.GAO F, XU D P, LU Y G. Feed forward fuzzy-PI pitch-control for large-scale wind turbines[J].Journal of Power Engineering, 2008, 28(4): 537–542.(in Chinese) |
| [3] | MALCOLM D J, HANSEN A C.WindPACT turbine rotor design study[R].Golden:National Renewable Energy Laboratory, 2002. |
| [4] | VAN WINGERDEN J, HULSKAMP A, BARLAS T, et al. Two-degree-freedom active vibration control of a propotyped "smart" rotor[J].IEEE Transactions on Control Systems Technology, 2011, 19(2): 284–296.DOI:10.1109/TCST.2010.2051810 |
| [5] | 余畏. 基于柔性尾缘襟翼的大型风力机叶片载荷智能控制研究[D]. 北京: 中国科学院大学, 2013.YU W.Investigation on smart load control for a large-scale wind turbines using deformable trailing edge flap[D].Beijing:University of Chinese Academy of Sciences, 2013(in Chinese). |
| [6] | BARLAS T K, VAN KUIK G A M. Review of state of the art in smart rotor control research for wind turbines[J].Progress in Aerospace Sciences, 2010, 46(1): 1–27.DOI:10.1016/j.paerosci.2009.08.002 |
| [7] | 邱静, 王国志, 刘恒龙, 等. 基于BEM理论的小型风机叶片设计与分析[J].液压气动与密封, 2011, 31(6): 71–74.QIU J, WANG G Z, LIU H L, et al. The research on small scale wind turbine blade based on BEM theory[J].Hydraulics Pneumatics & Seals, 2011, 31(6): 71–74.(in Chinese) |
| [8] | 刘雄, 张宪民, 陈严, 等. 基于动态入流理论的水平轴风力机动态气动载荷计算模型[J].太阳能学报, 2009, 30(4): 412–419.LIU X, ZHANG X M, CHEN Y, et al. Trasient aerodynamic load prediction model for horizontal axis wind turbines based on dynamic inflow theory[J].Acta Energiae Solaris Sinica, 2009, 30(4): 412–419.(in Chinese) |
| [9] | 张师帅, 罗亮, 李伟华. 基于CFD分析的空调用贯流风机的性能预测[J].流体机械, 2008, 36(5): 18–20.ZHANG S S, LUO L, LI W H. Research on perform ance prediction of the cross-flow fans for air conditioning[J].Fluid Machinery, 2008, 36(5): 18–20.(in Chinese) |
| [10] | 郭鹏. 模糊前馈与模糊PID结合的风力发电机组变桨距控制[J].中国电机工程学报, 2010, 30(8): 123–128.GUO P. Variable pitch control of wind turbine generator combined with fuzzy feed forward and fuzzy PID controller[J].Proceedings of the CSEE, 2010, 30(8): 123–128.(in Chinese) |
| [11] | 郑黎明, 林宇, 陈严, 等. 大型风力机恒功率桨距非线性PID控制方法研究[J].太阳能学报, 2012, 33(5): 727–731.ZHENG L M, LIN Y, CHEN Y, et al. Research on blade pitch nonlinear PID control for a large-scale wind turbine under constant power[J].Acta Energiae Solaris Sinica, 2012, 33(5): 727–731.(in Chinese) |
| [12] | 张先勇, 吴捷, 杨金明, 等. 额定风速以上风力发电机组的恒功率H∞鲁棒控制[J].控制理论与应用, 2008, 25(2): 321–324.ZHANG X Y, WU J, YANG J M, et al. H-infinity robust control of constant power output for the wind energy conversion system above rated wind[J].Control Theory & Applications, 2008, 25(2): 321–324.(in Chinese) |
| [13] | 秦生升, 胡国文, 顾春雷, 等. 风力发电系统的恒功率非线性H∞鲁棒控制[J].控制理论与应用, 2012, 29(5): 617–622.QIN S S, HU G W, GU C L, et al. Nonlinear H-infinity robust control of constant power for wind power system[J].Control Theory & Applications, 2012, 29(5): 617–622.(in Chinese) |
| [14] | HANSEN M O L. Aerodynamics of wind turbines[M].London: Earthscan, 2008. |
| [15] | TROLDBORG N. Computational study of the RisφB1-18 airfoil with a hinged flap providing variable trailing edge geometry[J].Wind Engineering, 2005, 29(2): 89–113.DOI:10.1260/0309524054797159 |
| [16] | TROLDBORG N.Computational study of the RisφB1-18 airfoil equipped with actively controlled trailing edge flaps[D].Copenhagen:Technical University of Denmark, 2004. |
| [17] | BAK C, GAUNAA M, ANDERSEN P B, et al. Wind tunnel test on wind turbine airfoil with adaptive trailing edge geometry:AIAA-2007-1016[R].Reston:AIAA, 2007. |
| [18] | 段富海, 韩崇昭. 动态逆方法和微分几何反馈线性化方法的对[J].自动化与仪器仪表, 2002(3): 4–5.DUAN F H, HAN C Z. Comparison between the dynamic inversion and the differential geometric feedback linearization[J].Automation and Instrumentation, 2002(3): 4–5.(in Chinese) |
| [19] | 俞立. 线性矩阵不等式处理方法[M].北京: 清华大学出版社, 2002: 41-67.YU L. Robust control based on linear matrix inequalities approach[M].Beijing: Tsinghua University Press, 2002: 41-67.(in Chinese) |
