与隔离型和单管非隔离型升降压电路相比,双管级联式的Buck-Boost和Boost-Buck电路更符合高效、大功率场合的使用要求,但是如何控制2只开关管协同工作成为了一个新的难题。串联结构使得前后两级存在耦合关系,即前一级电路的输出是后一级电路的输入,如果工作模式标准选择不当,很容易在升降压转换过程中产生严重的振荡,振荡会随着功率的增加而恶化。此外,由于开关延时导致的真实占空比的不连续性和Boost模式下输出电压到占空比的非线性直流增益将使得瞬态响应变得更糟[11]。
双管级联电路主要有同步、交错和组合3种控制方式。同步控制[12]电路简单,没有工作模式的切换,但需要较大的储能电感,开关管的电流应力较大,每只管子在每个开关周期内均需开通关断一次,因而开关损耗大;交错控制[8]保留了同步控制的优点,电感的体积也相对减小;组合控制开关管的电流应力较小,由于在每个开关周期内只有一只管子开通关断一次,因而开关损耗较低,但2种工作模式的平滑过渡比较困难,需要复杂的控制电路来实现。为了解决该问题,文献[13]在升降压模式切换时插入Buck-Boost模式,在该模式下电流应力和开关损耗较高;文献[4]引入一种滤波模式使得输入、输出电压接近时具有较高的效率,该方法属于开环控制,过渡过程不平滑;文献[14]提出一种Buck和Boost相结合的闭环控制方法,提升了变换效率;文献[11]针对模式切换时的占空比不连续性和Boost电路的非线性给出了补偿措施并实现了平滑过渡,但补偿方法较为复杂;文献[15]提出一种输入电压的前馈补偿方法,减少了输入扰动对输出的影响;文献[16]给出了一种新颖的IPOSBHB (Input-Parallel Output-Series Buck-Half-Bridge) 变换器,从电路结构上避免了双管级联电路前后两级的耦合关系和Boost的非线性直流增益,实现了稳态时的高效控制和动态的升降压切换,但升降压模式切换时输出电压的过渡过程不平滑;文献[17]对升降压变换器拓扑及控制方法做了总结。
针对上述问题,本文阐述了IPOSBHB的电路结构和基本关系,建立了IPOSBHB电路的降压模式和升压模式的开环小信号模型,设计了载波平移的组合控制方法,分析了升降压模式切换时传递函数的不一致性、占空比的不连续性和输入电压的扰动对变换器输出特性的影响,并设计了补偿方法,通过一台15 kW样机加以验证。
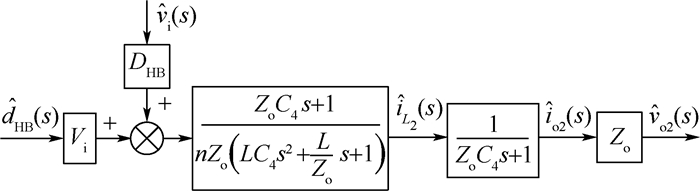
1 IPOSBHB变换器 1.1 电路结构 IPOSBHB电路结构如图 1所示。Buck电路由电容C3、开关管T3、快恢复二极管D5和电感L1组成,Half-bridge电路由电容C1、C2、开关管T1、T2、快恢复二极管D1~D4、电感L2和变压器B组成,变压器B的原边绕组匝数为NP,副边绕组匝数为NS。Buck和Half-bridge模块输入端采用并联方式,共同从输入端电源Vi取电,输出端采用串联方式,共用电感L,变换器总输出电压Vo等于2个模块输出电压之和。
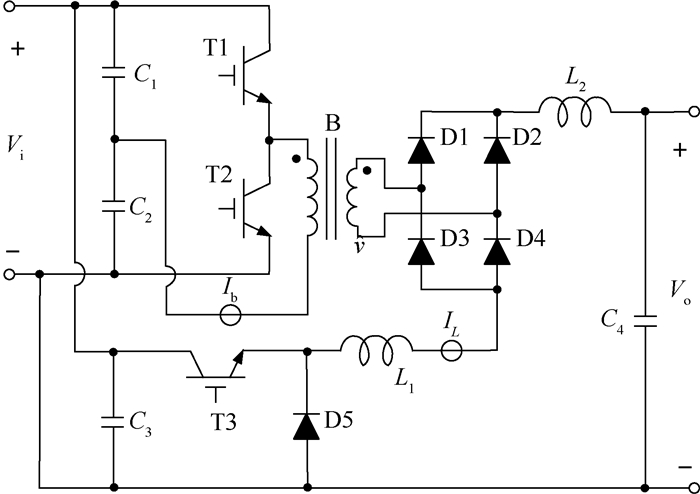 |
| 图 1 IPOSBHB变换器 Fig. 1 IPOSBHB converter |
| 图选项 |
1.2 基本关系 IPOSBHB变换器高效工作时,降压模式和升压模式下的等效电路如图 2所示,基本关系如式 (1) 和式 (2) 所示[14]。
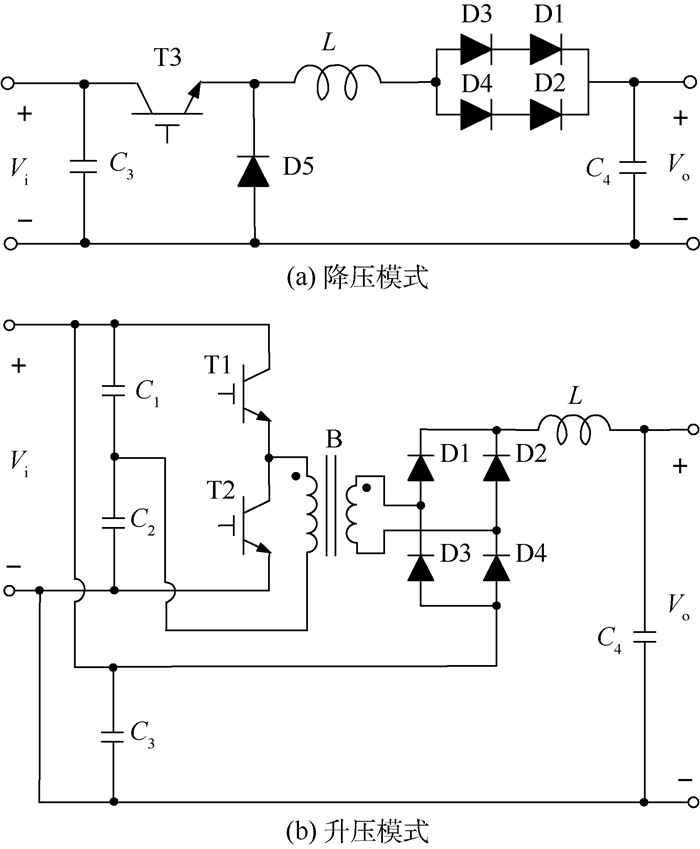 |
| 图 2 IPOSBHB等效电路 Fig. 2 Equivalent circuit of IPOSBHB |
| 图选项 |
降压模式的稳态电压变比为
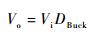 | (1) |
升压模式的稳态电压变比为
 | (2) |
式中:DBuck为开关管T3占空比的周期平均量; DHB为开关管T1占空比的周期平均量。
2 数学模型建立 2.1 降压模式开环小信号模型 为了方便分析,首先假定功率开关器件、二极管和变压器均为理想器件,开关频率远大于变换器中低通滤波器的转折频率。选取电感电流iL和电容C4电压vC4为状态变量,并根据降压模式下不同的开关模态构造状态空间方程,其中Zo为输出负载的等效阻抗。
如图 3 (a)所示,当T3导通时有
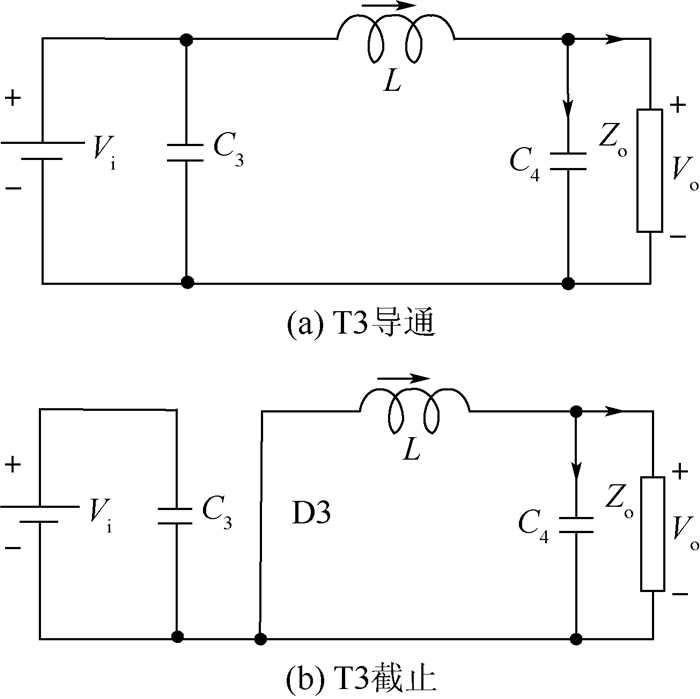 |
| 图 3 降压模式等效电路 Fig. 3 Equivalent circuit in Buck mode |
| 图选项 |
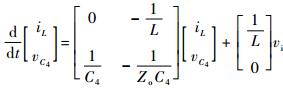 | (3) |
如图 3 (b)所示,当T3截止时有
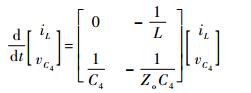 | (4) |
设T3导通占空比为dBuck,则关断时占空比为1-dBuck。根据式 (3) 和式 (4) 在一个开关周期内应用状态空间平均法,可得到状态空间平均方程为
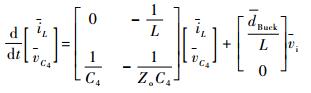 | (5) |
式中:
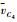
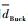
根据变换器稳态工作时,电感电流和电容电压在一个开关周期内变化量为零,可以得到变换器静态工作点方程为
 | (6) |
对平均模型中的状态变量加入小信号扰动,即将含有扰动量的状态变量Io+
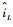
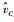
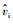
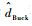
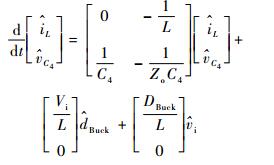 | (7) |
再对式 (7) 进行拉氏变换并化简,可得降压模式小信号状态方程为
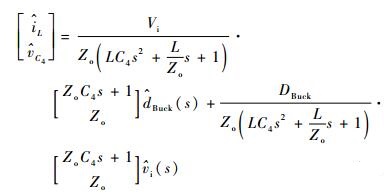 | (8) |
由式 (8) 可以得到
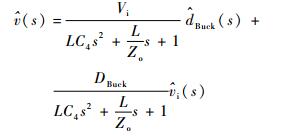 | (9) |
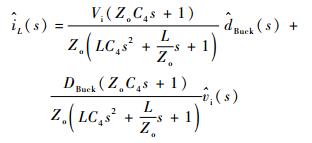 | (10) |
由式 (9) 和式 (10) 可以得到
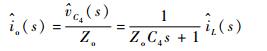 | (11) |
IPOSBHB电路降压模式的开环小信号模型如图 4所示。
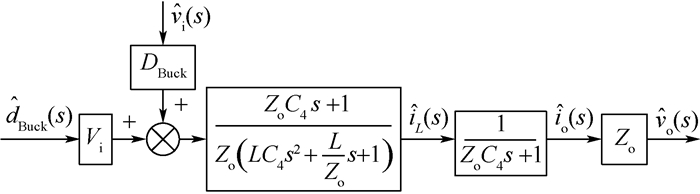 |
| 图 4 降压模式开环小信号模型 Fig. 4 Open-loop small-signal model in Buck mode |
| 图选项 |
式 (9) 和式 (10) 为降压模式IPOSBHB电路的开环小信号模型的解析式。
2.2 升压模式开环小信号模型 由图 2(b)可知,升压模式时Buck电路直通,Half-bridge电路工作,变换器输出端由输入电源和Half-bridge模块串联组成。而在利用状态空间平均法推导变换器小信号模型时,是按线性系统处理的,因此可以应用叠加原理,图 2(b)可以拆分为如图 5所示的2个电路:直通部分和升压部分,分别加以分析后再求和。
 |
| 图 5 升压模式等效电路 Fig. 5 Equivalent circuit in Boost mode |
| 图选项 |
升压部分的Half-bridge电路也是Buck型变换器,小信号模型推导方法与Buck相同。假设Half-bridge电路每个周期内开关管T1和T2的占空比相等且均为dHB,参照图 5可以得到Half-bridge开关小信号模型,如图 6所示。图中:
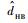
 |
| 图 6 Half-bridge开环小信号模型 Fig. 6 Open-loop small-signal model of half-bridge |
| 图选项 |
 |
| 图 7 Buck (T3直通) 开环小信号模型 Fig. 7 Open-loop small-signal model in Buck mode (T3 is on) |
| 图选项 |
 |
| 图 8 升压模式开环小信号模型 Fig. 8 Open-loop small-signal model in Boost mode |
| 图选项 |
解析式为
 | (13) |
3 控制系统设计 3.1 总体结构 IPOSBHB全数字化控制系统的结构总图如图 9所示。采用DSP2407为核心处理器,霍尔传感器将测得的电容C4两端电压vo和流过电感L的电流iL作为变换器输出电压和电流的反馈信号送至DSP2407,经A/D转换后与当前目标电压vg或目标电流ig比较,得到电压或电流的误差信号eu和ei,经过补偿算法得到控制占空比的调制波误差信号vctrl,该信号与定时器生成的载波信号比较即可得到对应的占空比,经驱动电路放大后作为最终的开关管驱动信号。
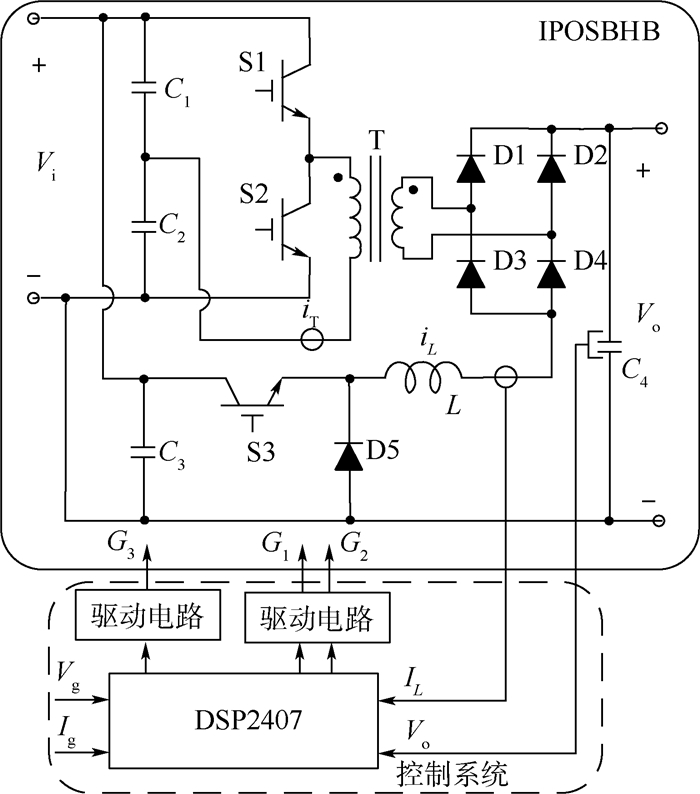 |
| 图 9 控制系统结构总图 Fig. 9 General view of control system structure |
| 图选项 |
载波平移的PWM调制方法如图 10所示。图中:vtri1和vtri2分别为Buck和Half-bridge的载波信号,设定幅值均为1,且频率相同。vtri1采用非对称三角波,vtri2采用对称三角波。驱动信号G1~G3为1时代表开通,0代表关断。G3由调制波误差信号vctrl与vtri1比较生成,当vctrl高于vtri1时,G3输出为1。G1直接由vctrl与vtri2比较生成,当vctrl高于vtri2时,输出为1;G2由vtri2幅值与vctrl做差后得到辅助信号v′ctrl,再将v′ctrl与vtri2比较,当vctrl低于vtri2时,输出为1。这种调制方式无需额外的分相电路即可实现相位相差180°的桥式驱动信号。
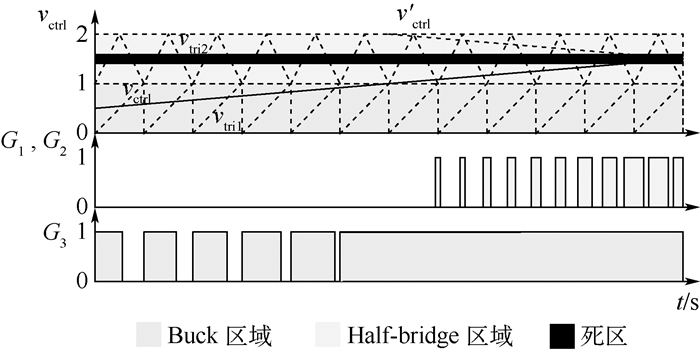 |
| 图 10 PWM调制方法 Fig. 10 PWM modulation approach |
| 图选项 |
为了实现IPOSBHB的高效控制,将vtri2由[0, 1]平移到[1, 2],当Vo≤Vi时,有vctrl∈[0, 1],只与vtri1相交且始终低于vtri2,此时G1、G2关闭,G3有PWM信号输出;当Vo>Vi时,有vctrl∈[1, 2],只与vtri2相交且始终高于vtri1,此时G3始终输出为1,G1、G2有PWM信号输出。需要特别指出的是,在Half-bridge区域中,需要对vctrl进行限幅以便将G1、G2占空比限制在50%以内,防止T1、T2直通,造成管子烧毁。
3.2 传递函数的不一致性补偿 由式 (1)、式 (2)、式 (9)、式 (12) 可以看出,IPOSBHB电路升压模式占空比比降压模式多乘了系数NS/NP,当此系数不为1时,势必会导致降压和升压模式下的直流增益曲线出现拐点,此拐点一方面会使过渡过程的瞬态响应变坏,另一方面使得变换器的传递函数在升压和降压模式下不一致,这样对于同一补偿算法Gc,很难在降压和升压2种模态下均取得理想的控制效果,只能折中设计Gc。如果能将2种模态下的传递函数补偿一致,则完全可以忽略升降压模态的不同对控制器Gc的影响,以补偿后的传递函数为依据设计和优化控制器Gc,来获得2种模态下都较为理想的控制效果。
基于上述思想,本文设计的传递函数一致性补偿原理框图如图 11所示。图中:H为采样系数;Gcmp1和Gcmp2为补偿环节;dBuck_act和dHB_act为考虑器件开关时间后的真实占空比。以Buck模式的传递函数为标准,取Gcmp1=1,Gcmp2=NP/NS,可得到补偿后的新的控制对象G′p。由于设定的载波幅值为1,故省略了调制波误差信号到占空比的传递函数。此外,图 11中将升压模式下调制波误差信号vctrl向下平移代替图 10中将载波vtri2向上平移的方法以方便编程实现,2种方法本质的思想是相同的,不影响控制效果。关于由器件开关时间造成的延时补偿方法将在第3.3节的内容中介绍。
 |
| 图 11 传递函数不一致性补偿原理框图 Fig. 11 Functional block diagram of inconformity compensation of transfer functions |
| 图选项 |
3.3 占空比的不连续性补偿 由于开关器件在导通和关断时存在延时,使得开关管的真实占空比在理论值接近0时变为0,理论值趋向1时提前变为1,即
 | (14) |
式中:DZ1和DZ2分别为开通和关断延时对应的占空比;dctrl和dact分别为占空比的理论值和真实值。
对于IPOSBHB电路,当输入、输出电压接近时,恰恰DHB趋向于1而DHB向于0,因此模式切换时也必然存在一段不连续区,如图 12所示。由于vtri1和vtri2幅值均为1,则当vctrl处于[1-DZ2, 1+DZ1]之间时,IPOSBHB变换器将进入不连续区。不连续区的存在将使模态切换时变换器的瞬态响应变坏,这主要体现在2个方面:①不连续区内Buck处于直通状态,而Half-bridge处于关闭状态,此时输出电压将跟随输入电压,输入电压的扰动对输出电压的影响难以控制;②不连续区内vctrl的增长并没有带来dact的提升,这势必会导致变换器在模式切换时的动态响应出现一段平台期,降低了响应速度。因而当DZ1和DZ2不能忽略时,有必要对不连续区加以补偿。
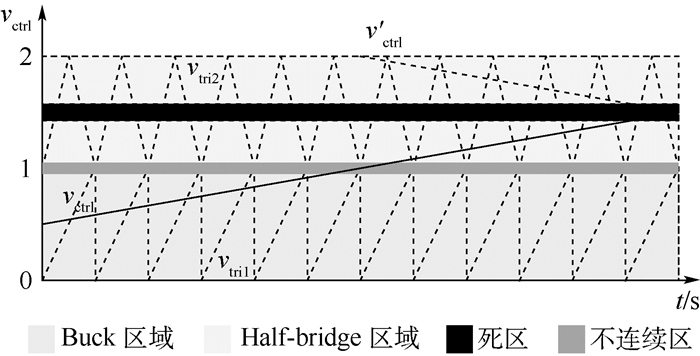 |
| 图 12 开关器件延时导致的不连续区 Fig. 12 Discontinuous region caused by switching time delay |
| 图选项 |
从图 12中可以看出,如果将Half-bridge的载波向下平移,不连续区将减小,当平移距离dshift=DZ1+DZ2时,不连续区将刚好消除,如果平移距离进一步增大,开关管T1~T3将出现同时动作的现象,造成额外的开关损耗,应避免这种情况的发生。引入模式切换的不连续补偿方法后,系统的原理框图如图 13所示。
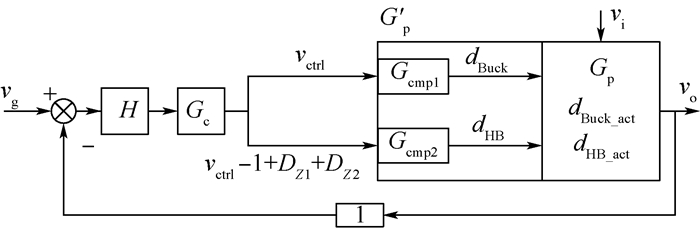 |
| 图 13 模式切换时占空比的不连续性补偿原理框图 Fig. 13 Functional block diagram of duty cycle discontinuity compensation at mode change |
| 图选项 |
3.4 输入电压扰动的前馈补偿 如第2节所述,无论降压模式还是升压模式,IPOSBHB传递函数中均含有扰动量输入电压
IPOSBHB由Buck和Half-bridge组合而成,2个模块本身都属于Buck型变换器,可以方便地引入KF/vi作为前馈因子实现前馈控制,KF为前馈增益系数。前馈通道的占空比分量与输入电压呈反比关系。当输入电压突然增大时,该分量迅速减小,总占空比随之减小,抑制输出电压的增高;当输入电压突然减小时,该分量迅速增大,总占空比随之增大,抑制输出电压的降低,从而提高了系统对
 |
| 图 14 输入电压扰动的前馈补偿原理框图 Fig. 14 Functional block diagram of feedforward compensation for input voltage disturbance |
| 图选项 |
4 实验 本文研制了IPOSBHB变换器原理样机一台,变换器的规格为:额定功率15 kW,输入电压范围为220~450 V,输出电压范围为270~350 V可控,各器件参数如表 1所示 (其中部分二极管为绝缘栅双极型晶体管 (IGBT) 的体二极管)。搭建以DSP2407为核心处理器的全数字化控制系统,实物图如图 15所示。
表 1 样机参数 Table 1 Prototype parameters
| 参数 | 数值 |
| 输入电压/V | 220~450 |
| 输出电压/V | 270~350 |
| 功率/kW | 15 |
| T1~T3,D5 | FF200R12KS4 |
| D1~D4 | DSEP2-101-04 A |
| 电感/μH | 600 |
| 变压器原边与副边线圈匝数比 | Np:Ns=0.67 |
| C1~C3的容量/耐压 | 2×40 μF/1 250 V |
| C4的容量/耐压 | 4×40 μF/1 250 V |
表选项
 |
| 图 15 15 kW样机控制系统实物图 Fig. 15 Control system picture of 15 kW prototype |
| 图选项 |
图 16为降压模式下测得的IGBT开通和关断时的延时,vCE3为开关管T3集电极和射极间的电压,开关频率为20 kHz,开通延时约为0.4 μs,关断延时约为1.3 μs,对应的DZ1=0.008,DZ2=0.026。
 |
| 图 16 开关延时波形 Fig. 16 Waveforms of switching time delay |
| 图选项 |
图 17为输出目标电压vg=270 V,负载R=40 Ω时输入电压vi由400 V下降到240 V的瞬态响应图。变换器在vi=vo时发生降压模式到升压模式的自动切换,图 17中以变压器原边的采样电流iB来表征Half-bridge的工作状态 (该采样电流为示波器产生包络现象后的电流波形)。图 17中一致性补偿系数Gcmp2分别设定为0.4、0.7和1.5,其中,Gcmp2=0.7时与理论值Gcmp2=NP/NS=0.67最接近,从图 17 (b) 中可以看出,由于vi的下降,变换器降压和升压模式下vo的动态值均略低于vg,但两模态下的电压调整率接近;由图 17(a)及图 17(c)可以看出,当Gcmp2=0.4时,变换器升压模式的电压调整率略低于降压模式,当Gcmp2=1.5时,升压模式的电压调整率略高于降压模式。模式切换时,vo存在一段明显的下降区,此下降区的宽度和幅度随着补偿系数Gcmp2的增大而减小。
 |
| 图 17 引入不一致性补偿后输出电压的瞬态响应 Fig. 17 Transient response of output voltage after introducing inconformity compensation |
| 图选项 |
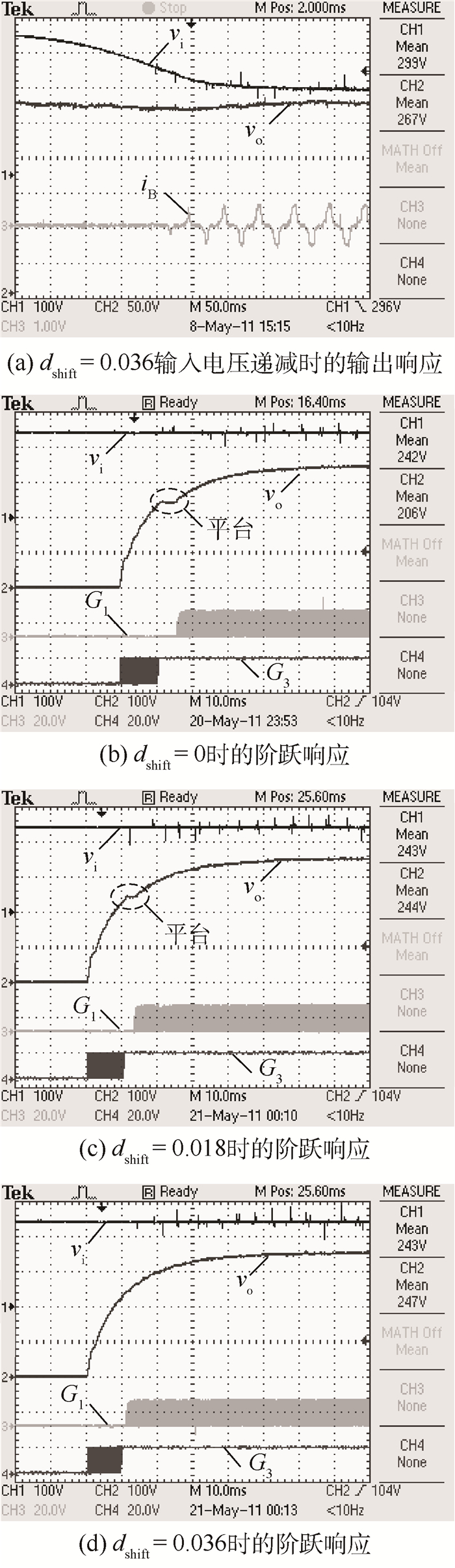
图 18(a)为Gcmp2=0.7时采用第3.3节的方法对不连续区进行补偿的波形图,当平移系数dshift=0.036,补偿后下降区基本消除。图 18(b)~图 18(d)以驱动信号G1和G3来表征Half-bridge的工作状态,分别对不同dshift下vo的阶跃响应进行了对比,仍取Gcmp2=0.7,当vi=245 V,R=40 Ω时,vo由0到280 V阶跃变化,模式切换的平台随dshift的增加而减小,当dshift=0.036时,基本消除,响应时间有明显的缩短。
 |
| 图 18 引入不连续性补偿后输出电压的瞬态响应图 Fig. 18 Transient response of output voltage after introducing discontinuity compensation |
| 图选项 |
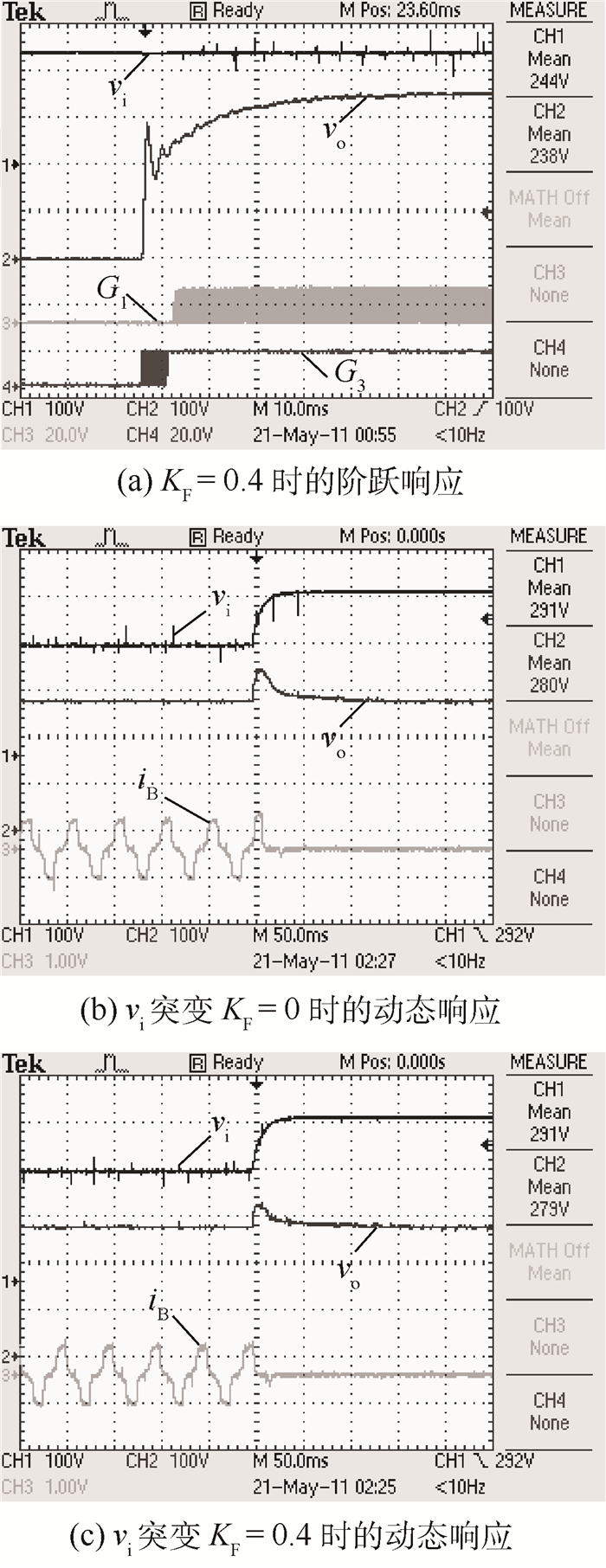
图 19(a)为引入前馈后变换器的阶跃响应。与图 18(d)相比,引入前馈后vo启动阶段的上升速度得到明显提高;图 19(b)及图 19(c)为vi由240 V向350 V突变时引入前馈前后的动态响应对比图。可以看出,当vi突然增大时,引入前馈后vo的瞬时电压波动峰值降低了约20 V,证明前馈对vi波动的抑制作用明显。
 |
| 图 19 引入前馈补偿后输出电压的瞬态响应 Fig. 19 Transient response of output voltage after introducing feedforward compensation |
| 图选项 |
5 结论 1) 建立了IPOSBHB电路降压模式和升压模式下的开环小信号模型。
2) 设计了载波平移的全数字控制方法,实现了IPOSBHB电路的降压模式和升压模式的高效控制。
3) 针对IPOSBHB电路升降压模式切换时传递函数的不一致性、占空比的不连续性设计了补偿措施,实现了升降压模式切换时的平滑过渡。
4) 针对输入电压的扰动引入前馈补偿,改善了变换器的动态响应。
参考文献
| [1] | SAHU B, RINCON-MORA G A. A low voltage, dynamic, noninverting, synchronous buck-boost converter for portable applications[J].IEEE Transactions on Power Electronics, 2004, 19(2): 443–452.DOI:10.1109/TPEL.2003.823196 |
| [2] | CHAKRABORTY A, KHALIGH A, EMADI A.Combination of buck and boost modes to minimize transients in the output of a positive buck-boost converter[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics.Piscataway, NJ:IEEE Press, 2006:4075-4080. |
| [3] | 任小永, 阮新波, 李明秋, 等. 双沿调制的四开关Buck-Boost变换器[J].中国电机工程学报, 2009, 29(12): 16–23.REN X Y, RUAN X B, LI M Q, et al. Dual edge modulated four-switch Buck-Boost converter[J].Proceedings of the CSEE, 2009, 29(12): 16–23.(in Chinese) |
| [4] | 任小永, 唐钊, 阮新波, 等. 一种新颖的四开关Buck-Boost变换器[J].中国电机工程学报, 2008, 28(21): 15–19.REN X Y, TANG Z, RUAN X B, et al. A novel four switch Buck-Boost converter[J].Proceedings of the CSEE, 2008, 28(21): 15–19.(in Chinese) |
| [5] | 罗明玲. 微小卫星电源系统MPPT模块的设计与实现[D]. 杭州: 浙江大学, 2014.LUO M L.Design and implement on MPPT module of micro-satellite power system[D].Hangzhou:Zhejiang University, 2014(in Chinese). |
| [6] | FERNANDEZ RANDYLL R M JR.A novel photovoltaic power converter for military and space applications[D].Monterey:Naval Postgraduate School, 2015. |
| [7] | QIAO H B, ZHANG Y C, YAO Y T, et al.Analysis of Buck-Boost converters for fuel cell electric vehicles[C]//ICVES 2006.Piscataway, NJ:IEEE Press, 2006:109-113. |
| [8] | 肖华锋, 谢少军. 用于光伏并网的交错型双管Buck-Boost变换器[J].中国电机工程学报, 2010, 30(21): 7–12.XIAO H F, XIE S J. An interleaving double-switch Buck-Boost converter for PV grid-connected inverter[J].Proceedings of the CSEE, 2010, 30(21): 7–12.(in Chinese) |
| [9] | NAKANISHI F, IKEGAMI T, EBIHARA K, et al.Modeling and operation of a 10 kW photovoltaic power generator using equivalent electric circuit method[C]//Photovoltaic Specialists Conference.Piscataway, NJ:IEEE Press, 2000:1703-1706. |
| [10] | ZUE A O, CHANDRA A.Simulation and stability analysis of a 100 kW grid connected LCL photovoltaic inverter for industry[C]//Power Engineering Society General Meeting.Piscataway, NJ:IEEE Press, 2006:1-6. |
| [11] | LEE Y J, KHALIGH A, EMADI A.A compensation technique for smooth transitions in non-inverting Buck-Boost converter[C]//IEEE Applied Power Electronics Conference & Exposition.Piscataway, NJ:IEEE Press, 2009:608-614. |
| [12] | CHOMSUWAN K, PRISUWANNA P, MONYAKUL V.Photovoltaic grid-connected inverter using two-switch Buck-Boost converter[C]//Photovoltaic Specialists Conference.Piscataway, NJ:IEEE Press, 2002:1527-1530. |
| [13] | GABORIAULT M, NOTMAN A.A high efficiency, non-inverting, Buck-Boost DC-DC converter[C]//Proceedings of 19th Annual IEEE Applied Power Electronics Conference and Exposition.Piscataway, NJ:IEEE Press, 2004:1411-1415. |
| [14] | LEE Y J, KHALIGH A, CHAKRABORTY A, et al. Digital combination of Buck and Boost converters to control a positive Buck-Boost converter and improve the output transients[J].IEEE Transactions on Power Electronics, 2009, 24(5-6): 1267–1279. |
| [15] | YAO C, RUAN X B, CAO W, et al. A two-mode control scheme with input voltage feed-forward for the two-switch Buck-Boost DC-DC converter[J].IEEE Transactions on Power Electronics, 2014, 29(4): 2037–2048.DOI:10.1109/TPEL.2013.2270014 |
| [16] | 杜青, 齐铂金, 张涛, 等. 一种新型大功率输入并联输出串联Buck半桥变换器[J].中国电机工程学报, 2012, 32(6): 47–55.DU Q, QI B J, ZHANG T, et al. A novel high-power input-parallel output-series Buck-halfbridge converter[J].Proceedings of the CSEE, 2012, 32(6): 47–55.(in Chinese) |
| [17] | FENG W, QI B J, WANG Y P, et al.High power DC-DC converter for renewable energy power system[C]//2014 IEEE Conference and Exposition on Transportation Electrification Asia-Pacific (ITEC Asia-Pacific).Piscataway, NJ:IEEE Press, 2014:1-4. |
