研究者们在接收机邻道干扰方面做了大量的研究工作。文献[6]给出了接收机邻道阻塞干扰模型,对电台邻道干扰进行了测试,并采用折线拟合法对测试数据进行拟合;文献[7]给出了邻道干扰信噪比模型并进行了测试,但模型计算结果和实测数据未进行对比分析;文献[8]给出了邻道干扰减敏经验公式,但未进行实际测试;文献[9]讨论了基于测试数据的邻道干扰减敏分析,但未考虑非线性的影响;文献[10]对邻道干扰在接收机前端的非线性响应特性进行了分析,并提出了一种邻道干扰抵消方法。
分析以上的研究工作发现,由于难于获取接收机内部的详细参数,单纯利用理论计算模型或经验公式[11]对邻道干扰减敏特性进行的建模往往误差较大,难以与测试数据进行很好的比对,只能在一定程度上进行趋势预测;而另一方面,对邻道干扰减敏特性的测试在没有理论支撑的情况下,测试频点多、工作量大,测试模型也难以应用于实际机载电台间的邻道干扰评估。
为了解决上述难题,考虑到邻道干扰信号与本振相位噪声混频而产生的噪声,本文提出了噪声修正因子,结合接收机前端的非线性响应模型和信噪比模型,推导出超短波电台接收机邻道干扰减敏模型,并结合减敏模型给出机载超短波电台邻道干扰的评估方法。
1 基于噪声修正的邻道干扰建模 邻道干扰是指接收机工作在某通信频道时,受到了相邻或相近频道信号的干扰,而无法正常工作的现象。
根据超短波电台的结构 (见图 1),当超短波电台受到邻道干扰时,一般干扰信号强度较大,经过低噪声放大器的非线性作用后,产生各种频率分量[12]。甚至当干扰信号功率足够大时,会使有用信号产生增益下降,造成增益压缩现象[13]。图 1中:ωI为干扰信号的频率; ωS为有用信号频率; ωo为混频后的中心频率。
 |
| 图 1 超短波电台接收机前端邻道干扰示意图 Fig. 1 Schematic diagram of adjacent channel interference at front end of VHF radio receiver |
| 图选项 |
虽然射频预选滤波器会对带外信号有一定的抑制作用,但是其通带较宽,无法抑制与有用信号频率相近的干扰信号。同时,由于接收机本振信号频率不纯,邻近频率的干扰信号与本振相位噪声进行混频[6],会提高接收机本底噪声,造成输出信噪比下降,无法正常解调出有用信号,使得接收机灵敏度减小,造成减敏现象。
因此,对邻道干扰的建模重点在于邻道干扰的非线性建模与输出信噪比的建模。
1.1 邻道干扰接收机前端非线性建模 假设接收机的输入时域信号表示为
 | (1) |
式中:xI(t) 为输入的时域干扰信号;vI为干扰信号幅度;xS(t) 为输入的有用信号;vS为有用信号幅度。
使用泰勒级数来描述接收机前端的非线性响应特性,输入信号的非线性响应可用n阶泰勒级数表示[14]:
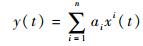 | (2) |
式中:ai(i=1, 2, …, n) 为非线性特征系数,而对于通信系统中有|a1|>|a2|>…>|an|,且由于增益压缩特点,一般a3 < 0;y(t) 为时域输出信号;输出信号的第i阶响应为aixi(t)。
将输入时域信号式 (1) 代入式 (2) 中,得到非线性的输出响应为
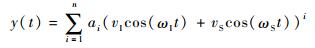 | (3) |
将式 (3) 展开后,得到的第i阶响应频率是由i个输入频率任意组合的结果,幅度由输入信号幅度和非线性系数决定。表 1给出了前3阶非线性响应的幅度和频率信息。
表 1 双信号输入下的前3阶非线性响应 Table 1 First three order nonlinear response of dual-channel input signal
| 编号 | 响应幅度 | 响应频率 | 响应类型 |
| 1 | a1vI | ωI | 1阶线性 |
| 2 | a1vS | ωS | 1阶线性 |
| 3 | 0.5a2vI2 | 2ωI | 2阶谐波 |
| 4 | 0.5a2vS2 | 2ωS | 2阶谐波 |
| 5 | a2vIvS | ωI±ωS | 2阶交调 |
| 6 | 0.25a3vI3 | 3ωI | 3阶谐波 |
| 7 | 0.25a3vS3 | 3ωS | 3阶谐波 |
| 8 | 0.75a3vI2vS | 2ωI±ωS | 3阶交调 |
| 9 | 0.75a3vS2vI | 2ωS±ωI | 3阶交调 |
| 10 | 0.75a3vI3 | 2ωI-ωI | 3阶压缩 |
| 11 | 0.75a3vS3 | 2ωS-ωS | 3阶压缩 |
| 12 | 1.5a3vIvS2 | ωI+ωS-ωS | 3阶交调 |
| 13 | 1.5a3vSvI2 | ωS+ωI-ωI | 3阶交调 |
表选项
总的非线性响应是各阶次响应的总和。而对于输出的有用信号和干扰信号,由于非线性作用产生了各阶次的谐波、交调和压缩分量,输出信号的构成比较复杂,为了推导方便,必须对输出信号的成分进行化简,忽略微小项:
1) 从幅度上来看,由于干扰信号幅度远大于有用信号,即vI



2) 从频率上来看,由于是邻道干扰,干扰信号频率与有用信号频率差值较小。因此,ωI±ωS项、2ωI±ωS项和各阶谐波项均比ωI项远离有用信号频率,考虑到射频和中频滤波器的频率选择特性,这些项可忽略,如图 2所示。
 |
| 图 2 非线性输出项幅度和频率筛选 Fig. 2 Output of nonlinear response screening by amplitude and frequency |
| 图选项 |
基于以上2点考虑,得到经非线性作用后输出的干扰信号和有用信号表达式为
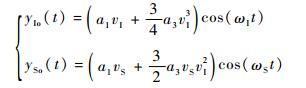 | (4) |
式中:yIo(t) 为输出的时域干扰信号;ySo(t) 为输出的时域有用信号。
根据有效功率计算式P=V2/2R(通信系统中一般R=50 Ω),经非线性作用后输出的有用信号和干扰信号的功率为
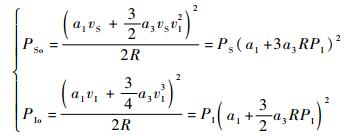 | (5) |
式中:PSo和PIo分别为输出的有用信号和干扰信号功率;PS和PI分别为输入的有用信号和干扰信号功率。
1.2 邻道干扰接收机输出端信噪比模型 在无干扰情况下,信噪比 (Signal to Noise Ratio, SNR) 定义为有用信号功率与噪声功率的比值,如下[15]:
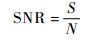 | (6) |
式中:S为有用信号功率;N为接收机的噪声功率。
如果实际接收机并没有给出噪声功率,可用式 (7) 进行计算:
 | (7) |
式中:k≈1.38×10-23 J/K为玻尔兹曼常数;B为接收机的噪声带宽;T为噪声温度。
在无干扰信号的情况下,由于输入的有用信号较弱,接收机工作在线性工作范围内,此时输出的信噪比为
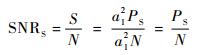 | (8) |
在邻道干扰情况下,由于干扰信号功率较大,输出的总噪声功率不仅包括接收机本身的宽带噪声 (假设有干扰前后接收机本身的宽带噪声近似不变),还包括干扰信号通过放大器非线性作用后产生的各类干扰分量。而邻近频率的干扰信号与本振相位噪声进行混频,会提高接收机本底噪声功率。故在有邻道干扰情况下,接收机输出的信噪比变为
 | (9) |
式中:S′为有干扰情况下的有用信号输出功率;N′为邻道干扰时的噪声功率;CΔf=L+a10-0.34Δf/B0为噪声修正因子,L为混频噪声控制因子,a为频率控制因子,Δf为干扰信号与有用信号的频率偏差,B0为接收机的中频带宽。
根据式 (5)、式 (8) 和式 (9),可以得到在邻道干扰情况下的减敏公式为
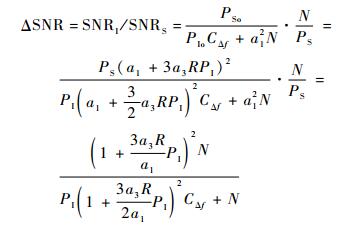 | (10) |
1.3 邻道干扰减敏模型验证 为了验证邻道干扰减敏模型的有效性,对某型超短波电台进行了邻道干扰测试。选用的超短波电台工作频率为30~87.975 MHz,SNR=12 dB时接收机灵敏度为-110 dBmW,3 dB中频带宽B=10.35 kHz。试验配置如图 3所示。
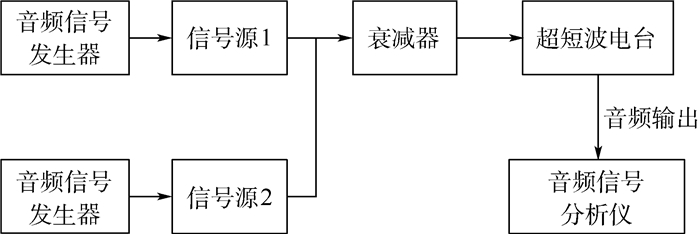 |
| 图 3 邻道干扰试验配置 Fig. 3 Test configuration of adjacent channel interference |
| 图选项 |
信号源1模拟有用信号 (幅度调制),信号源2模拟干扰信号 (频率调制),干扰信号和有用信号经过衰减器连接超短波电台射频输入端口,超短波电台音频输出端接入音频信号分析仪来观测信噪比。
在电台话音测试时,一般认为当输出信噪比SNR≥12 dB时,电台接收的语音信号能够非常清晰且易懂,故邻道干扰试验方法如下:
1) 调节有用信号功率,使接收机音频端口检测到的信噪比SNR=12 dB。
2) 提高有用信号功率,使接收机音频端口检测到的信噪比提升到SNR=12 dB+ΔSNR。
3) 开始注入干扰信号,并逐渐增加干扰信号功率,直到接收机音频端口检测到的信噪比下降到SNR=12 dB。
4) 此时在有邻道干扰的情况下,输出信噪比下降幅度为ΔSNR,并记录此时干扰信号功率。
试验过程中发现,对于不同的有用信号频率,相同的频率偏差具有较好的一致性,而不同的频率偏差测试得到的信噪比下降曲线差异很大,故试验测试的干扰信号和有用信号频率偏差为25、50、100、300、500、700和1 000 kHz共计7种情况。图 4给出了信噪比下降3 dB和6 dB情况下干扰信号功率与频率偏差的关系。
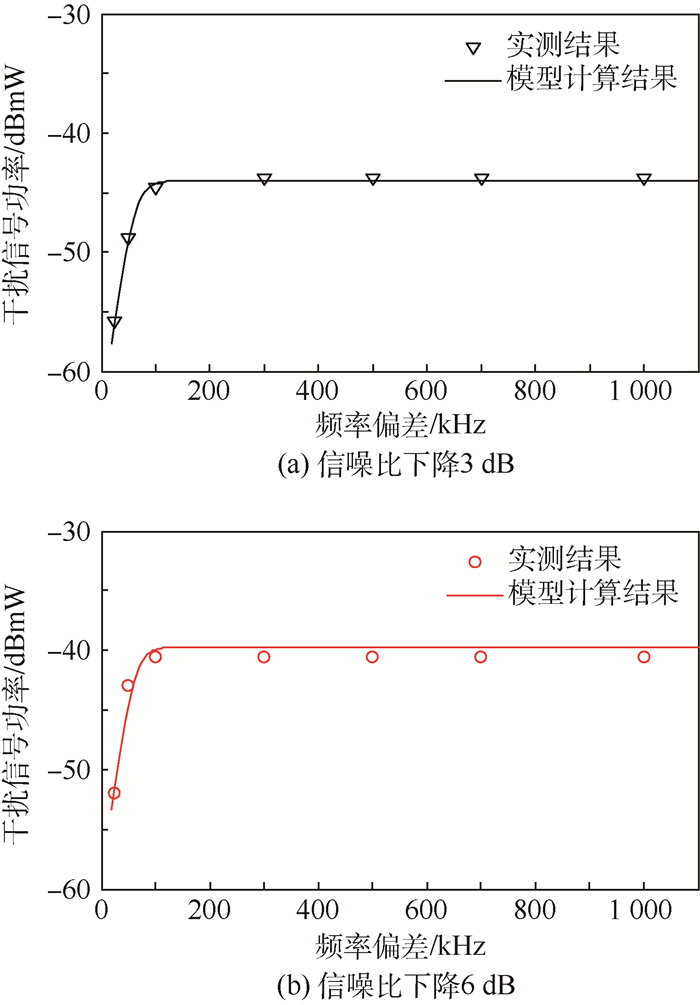 |
| 图 4 信噪比下降3 dB和6 dB时干扰信号功率与频率偏差关系 Fig. 4 Relation between interference signal power and frequency deviation when SNR decreases by 3 dB and 6 dB |
| 图选项 |
从图 4中可以看出,当干扰信号频率越接近有用信号频率时,使信噪比下降3 dB或6 dB所需的干扰信号功率越小。当频率偏差大于300 kHz时,几乎相同的干扰信号功率就能够使信噪比下降相同的量级。图 5给出了25、50和100 kHz3种频率偏差下干扰信号功率与信噪比下降幅度的关系。
 |
| 图 5 3种频率偏差下干扰信号功率与信噪比下降幅度关系 Fig. 5 Relation between interference signal power and reduction of SNR under three kinds of frequency deviation |
| 图选项 |
从图 5中可以看出,信噪比下降幅度在1~6 dB之间时,信噪比曲线下降比较缓慢。随着干扰信号功率的增加,当信噪比下降超过6 dB以后,曲线下降迅速。模型中的噪声修正因子CΔf=4×10-5+4×10-0.34Δf/B0-3,实测结果与模型计算结果趋势一致,吻合较好,除频率偏差100 kHz时,信噪比下降20 dB的单一点误差较大外,其余误差均在3 dB以内。图 6给出了25、50和100 kHz3种频率偏差下计算与实测的信噪比下降结果误差对比。
 |
| 图 6 3种频率偏差下计算与实测的信噪比下降误差对比 Fig. 6 Error comparison between calculated and measured reduction of SNR under three kinds of frequency deviation |
| 图选项 |
2 机载超短波电台邻道干扰评估方法 由于机载平台空间有限,通信设备越来越密集,通信频道重叠越严重。为了保证机载超短波电台之间能够兼容工作,需要对邻道干扰情况进行评估,做出干扰判断或频率规划,具体评估流程如图 7所示。
 |
| 图 7 机载超短波电台邻道干扰评估流程 Fig. 7 Assessment procedure of adjacent channel interference of airborne VHF radio |
| 图选项 |
对于干扰信号方面,发射机产生的干扰信号经过天线辐射和空间衰减后被接收天线拾取并进入射频端口,其中涉及的因素较多,耦合到接收机射频端口处的干扰信号功率可用式 (11) 进行计算:
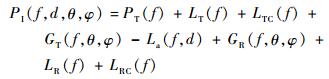 | (11) |
式中:f为频率,MHz;d为天线间的距离,km;θ和φ分别为收发天线间的俯仰角和方位角,rad;PT(f) 为发射机的发射功率,dBmW;LT(f) 和LR(f) 分别为发射机和接收机的馈线损耗,dB;GT(f, θ, φ) 和GR(f, θ, φ) 分别为发射天线和接收天线在相对角度的增益,dB;LTC(f) 和LRC(f) 为双工器的正向损耗,dB;La(f, d) 为电磁波在天线之间耦合通道的衰减,dB。
如果按照电磁波在自由空间衰减公式,La(f, d) 可以通过式 (12) 计算:
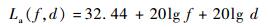 | (12) |
如果收发天线间的空间衰减不适用于自由空间衰减公式,可借助于其他算法或者一些商用的数值仿真软件求解。
对于接收机方面,一般灵敏度是在一定的信噪比情况下所定义的。在超短波电台正常工作时,接收机所接收到的有用信号功率通常大于等于灵敏度,所以接收机在受到干扰时的信噪比裕量为
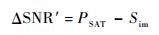 | (13) |
式中:ΔSNR′为信噪比裕量,dB;PSAT为基准信号功率,dBmW;Sim为接收机灵敏度,dBmW。
如果已知2部电台间工作的频率偏差,则可利用邻道干扰减敏模型计算出此频率偏差Δf对应的信噪比下降曲线,若信噪比裕量ΔSNR′和干扰信号功率PI的交汇点在曲线的左侧,则无邻道干扰;若在曲线右侧,则产生邻道干扰。如果未知2部电台的频率偏差,则信噪比裕量ΔSNR′和干扰信号功率PI交汇点对应曲线所代表的频率偏差,就是此时不产生邻道干扰的最小频率偏差。
3 机载超短波电台邻道干扰评估案例 考虑如图 8所示的情况。2架直升机编队飞行,相距150 m。超短波电台A工作在接收状态并与地面塔台进行通信,其灵敏度在SNR=12 dB时为-110 dBmW,与地面塔台正常通信时的基准信号功率为-96 dBmW。超短波电台B执行其他通信任务,工作在发射状态,发射频率为75 MHz,发射功率为30 dBmW。为了保证2部电台各自独立工作,需要对2部电台的邻道干扰进行评估。
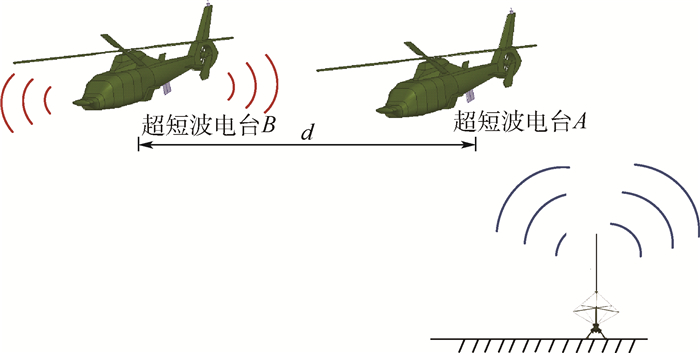 |
| 图 8 直升机编队飞行邻道干扰场景 Fig. 8 Scene of helicopter formation flight interfered by adjacent channel |
| 图选项 |
干扰源方面,2部超短波电台相距150 m,利用式 (12),可计算出电磁场在自由空间衰减La=53.5 dB。综合考虑馈线损耗、双工器损耗和天线增益等因素,到达超短波电台A接收机端口的干扰信号功率为PI=-33.5 dBmW,如图 9所示。
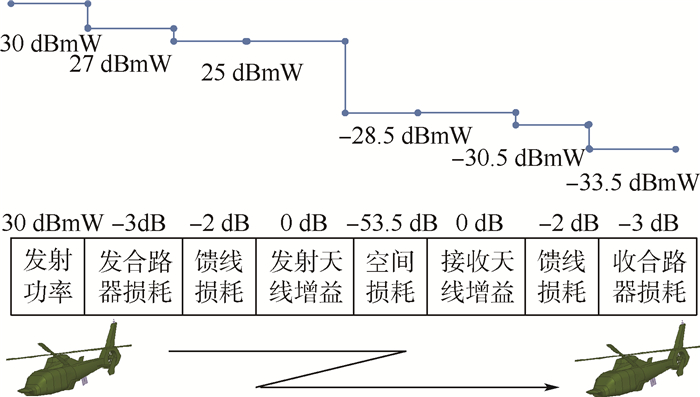 |
| 图 9 干扰信号功率计算示意图 Fig. 9 Schematic diagram of interference signal power calculation |
| 图选项 |
由式 (13) 可计算得到超短波电台A的信噪比裕量ΔSNR′=PSAT-Sim=14 dB。利用邻道干扰减敏模型,可以对此时的邻道干扰情况进行评估。
假设已知2部电台工作时的频率间隔为200 kHz,如图 10所示。信噪比裕量与干扰信号功率的交汇点在200 kHz频率偏差信噪比下降曲线的左侧,则可判定此时不会产生邻道干扰。此时图 10中红色阴影区域为干扰信号功率安全裕量,蓝色阴影区域为信噪比安全裕量。
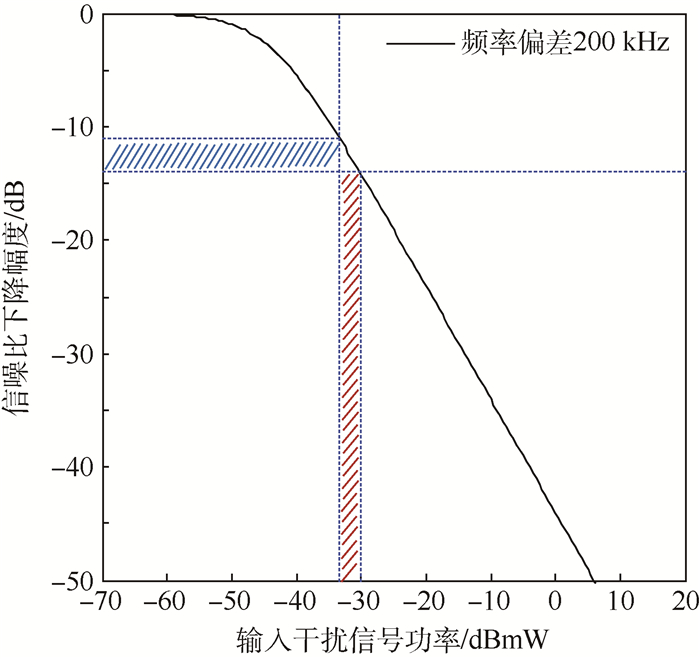 |
| 图 10 已知工作频率偏差的邻道干扰评估 Fig. 10 Adjacent channel interference assessment of known operating frequency deviation |
| 图选项 |
当2部电台工作频率偏差未知时 (见图 11),信噪比裕量与干扰信号功率交汇点对应为频率偏差60 kHz时的曲线,考虑到超短波电台25 kHz为一个频道,故为了避免电台间的邻道干扰致使超短波电台A无法正常工作,2部电台应至少错频75 kHz工作,即超短波电台A不能工作在74.925~75.075 MHz频段内。
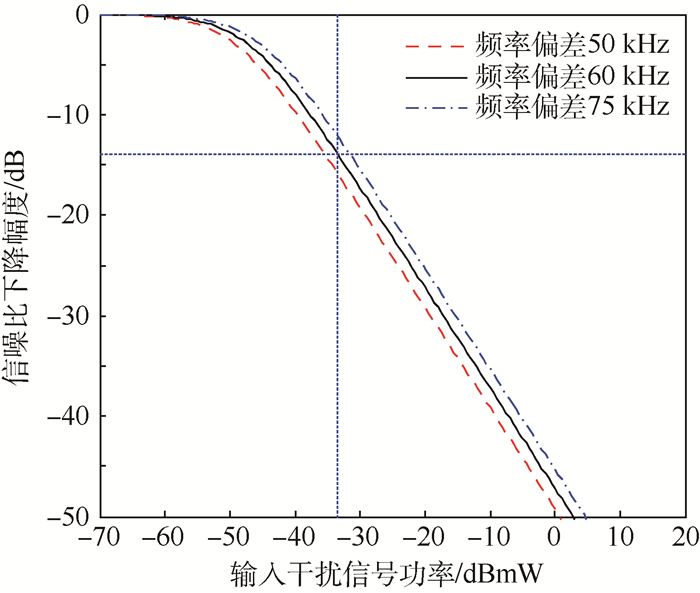 |
| 图 11 不产生邻道干扰时的频率偏差评估 Fig. 11 Assessment of frequency deviation without adjacent channel interference |
| 图选项 |
4 结论 现有的邻道干扰模型因忽略接收机内部的详细参数,单纯利用理论计算模型或经验公式,造成计算结果与实测结果偏差较大。因此,本文结合接收机前端非线性响应模型和信噪比模型,针对性地提出了一种噪声修正因子,给出了超短波电台接收机邻道干扰的减敏模型。
1) 模型以超短波电台物理模型和噪声修正因子为基础,避免了过度理想化,与实测数据相比误差约为3 dB。
2) 模型可直接应用于机载超短波电台间的邻道干扰评估,可获得信噪比下降或工作频率间隔等量化指标,具有一定的工程应用价值。
本文方法可向其他机载射频收发设备间的干扰预测和减敏特性分析方面拓展,这也是本文下一步的研究工作。
参考文献
| [1] | 苏东林, 王冰切, 金德琨, 等. 电子战特种飞机电磁兼容预设计技术[J].北京航空航天大学学报, 2006, 32(10): 1241–1245.SU D L, WANG B Q, JIN D K, et al. EMC pre-design technologies on EW special aircraft[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(10): 1241–1245.(in Chinese) |
| [2] | 王冰切, 苏东林, 全力民, 等. 电子战特种飞机的天线隔离度测试[J].宇航计量技术, 2007, 27(3): 1–5.WANG B Q, SU D L, QUAN L M, et al. Measurement between antennas on EW special aircraft[J].Journal of Astronautic Metrology and Measurement, 2007, 27(3): 1–5.(in Chinese) |
| [3] | 魏嘉利, 贾云峰, 谢树果, 等. 航空电子系统电磁环境复杂度量化评估方法[J].航空学报, 2014, 35(2): 487–496.WEI J L, JIA Y F, XIE S G, et al. Complexity assessment method on electromagnetic environment for avionic systems[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 487–496.(in Chinese) |
| [4] | 杨志敏, 李式巨, 王彦波, 等. 阻塞干扰下跳频通信系统差错控制[J].浙江大学学报 (工学版), 2008, 42(3): 481–484.YANG Z M, LI S J, WANG Y B, et al. Error control for frequency hopping communication systems under man-made noise[J].Journal of Zhejiang University (Engineering Science), 2008, 42(3): 481–484.(in Chinese) |
| [5] | 周文兵, 陈志君. 直升机超短波通信链路分析[J].直升机技术, 2012(3): 34–37.ZHOU W B, CHEN Z J. Analysis of UHF communication link in helicopter[J].Helicopter Technique, 2012(3): 34–37.(in Chinese) |
| [6] | 何洪涛, 聂纯, 刘继东, 等. 无线电接收机阻塞干扰响应的建模方法研究[J].微波学报, 2014, 30(s2): 61–64.HE H T, NIE C, LIU J D, et al. The study on the modeling method of blocking interference response of wireless receiver[J].Journal of Microwaves, 2014, 30(s2): 61–64.(in Chinese) |
| [7] | 成伟兰, 刘坚强, 谌丽. 干扰条件下接收机减敏机理分析[J].舰船科学技术, 2012, 34(3): 122–129.CHENG W L, LIU J Q, ZHAN L. Analysis of receiver desensitization mechanism in the presence of interference[J].Ship Science and Technology, 2012, 34(3): 122–129.(in Chinese) |
| [8] | 赵波, 全厚德, 崔佩璋. 同址干扰对车载通信系统的影响分析[J].系统仿真学报, 2012, 24(5): 957–961.ZHAO B, QUAN H D, CUI P Z. Analysis of co-site interference effect on vehicular communication system[J].Journal of System Simulation, 2012, 24(5): 957–961.(in Chinese) |
| [9] | 魏崇毓, 顾有军. CDMA/GSM双模双待机移动终端射频干扰的研究[J].微波学报, 2008, 24(s1): 202–207.WEI C Y, GU Y J. Study on RF interference of CDMA/GSM dual-mode mobile[J].Journal of Microwaves, 2008, 24(s1): 202–207.(in Chinese) |
| [10] | GOMES H C, CARVALHO N B.Interference cancellation:New configuration technique forcancellation of strong interferences from adjacent frequency bands[C]//Integrated Nonlinear Microwave and Millimetre-Wave Circuits.Piscataway, NJ:IEEE Press, 2008:65-68. |
| [11] | 中国人民解放军总参谋部无线电管理技术站. 同站址干扰的评估方法: GJB 3624-1999[S]. 北京: 中国人民解放军总装备部, 1999: 9-10.The General Staff Radio Management Technology Station of Chinese People's Liberation Army.Methods for the evaluation of go-sit interference:GJB 3624-1999[S].Beijing:General Armament Department of Chinese People's Liberation Army, 1999:9-10(in Chinese). |
| [12] | 张肇仪, 周乐柱, 吴德明. 微波工程[M].3版北京: 电子工业出版社, 2006: 430-437.ZHANG Z Y, ZHOU L Z, WU D M. Microwave engineering[M].3rd edBeijing: Publishing House of Electronics Industry, 2006: 430-437.(in Chinese) |
| [13] | GRAY B, PONTON M, SUARES A, et al.Analytical modeling of transducer gain and gain compression in degenerate parametric amplifiers[C]//Radio and Wireless Symposium.Piscataway, NJ:IEEE Press, 2012:351-354. |
| [14] | BASSEL F B. A study of nonlinearity including feedback memory with application to RF amplifiers[J].IEEE Transactions on Communications, 2016, 26(3): 198–200. |
| [15] | 王琼, 苏东林, 谢树果, 等. 射频接收机系统级建模中的噪声谱分析[J].北京航空航天大学学报, 2006, 32(4): 395–398.WANG Q, SU D L, XIE S G, et al. Noise density research in the system-modeling of RF receivers[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(4): 395–398.(in Chinese) |
