发射机互调(IM) 是由于发射机末级功率放大器包含非线性元器件,当同时存在多个信号时,这些信号间由于相互调制而产生的增生信号[1-2]。通常,发射机互调发生于距离较近的多部发射机同时工作时,若一个运载平台上配置有多部无线电设备,此类干扰最为突出。发射机互调抑制能力用发射机互调抑制比来表征,文献[1]将其定义为:当干扰信号功率电平低于发射机调谐信号功率电平30 dB时,发射机互调产物电平相较于发射机调谐信号功率电平的衰减量。文献[2]将其定义为:发射机互调产物电平相较于干扰信号功率电平的衰减量。二者的定义实质上是一致的。
在发射机互调研究中,人们更多地关注发射机互调危害的分析预测[3-5],以及对此类干扰的抑制或削弱的技术方法[6-9],而对发射机互调测试方法的研究相对较少。发射机互调测试的关键在于待测发射机与信号源间有足够的单向隔离度,以保证信号源不会被发射机的大功率信号烧毁,且到达测试接收机处的信号源互调发射电平应远低于待测发射机的互调发射电平,同时保证信号源到达待测发射机的信号具有足够的强度。目前,常用的发射机互调测试方法有2类:①以环形器和隔离器为关键测试器件的测试方法;②利用衰减器和定向耦合器为关键测试器件的测试方法。发射机互调研究的相关文献均采用这2类方法中的一种[3-10]。文献[1]采用的是第1类测试方法,文献[2]对2类测试方法都进行了规定,但这2类测试方法均直接采用测试数据作为最终评定结果,为保证测试结果的准确性,对测试器件的带宽、隔离度等性能的要求较高,从而带来测试成本高、测试带宽窄及发射机发射功率受限等问题。
本文针对上述问题进行研究,提出了新的发射机互调测试方法,经实测验证,该方法对器件的要求较低,适用范围宽,更具灵活性。
1 发射机互调发射模型理论分析 非线性元器件时域模型主要包括多项式模型、Saleh模型、Volterra级数模型及神经网络模型等[11-14]。其中对于VHF/UHF通信发射机来说,多项式模型具有简单直观、计算方便的特点,易于发现非线性器件的非线性特性规律。
发射机射频(RF) 功率放大器的V-I特性用多项式模型表示为[15]
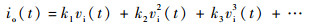 | (1) |
式中:kp为p次方项系数,p=1,2,3,…。
当同时存在频率分别为fi和fj、最大幅度分别为Ai和Aj的2个信号时,忽略相位项,vi(t) 可表示为
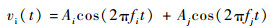 | (2) |
代入式(1),可得频率为fm=|mfi+nfj|的N阶互调电流分量的幅度为
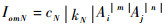 | (3) |
式中:m和n定义为fi和fj的频率变换系数,为非零整数;N为互调分量的阶数,N=|m|+|n|;cN为对应N阶互调产物的常数项;kN为式(1) 中N次方项系数。
将式(3) 以V-I表示的互调响应关系转换为以功率电平表示。设功率放大器在频率fm、fi和fj处的阻抗分别为RijN、Ri和Rj,根据欧姆定律有
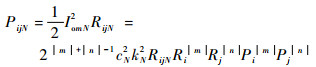 | (4) |
式中:PijN为fm=|mfi+nfj|的互调发射功率;Pi为频率fi的信号功率,Pi=Ai2/(2Ri);Pj为频率为fj的信号功率,Pj=Aj2/(2Rj)。
对于电台发射机电路,大多数情况下可以做出以下假设:
1) 外加干扰信号功率一般小于发射机功率,发射机工作状态不变。
2) 产生发射机互调的非线性效应由发射机末级功率放大电路产生。
电台发射机发射电路可表示为图 1所示的简化模型。
 |
| 图 1 电台发射机发射电路简化模型 Fig. 1 Simplified model of radio station's transmitter radiating circuit |
| 图选项 |
设fi为发射机的调谐信号频率,fj为干扰信号频率,IL-(fj) 为射频滤波器在fj的反向插入损耗系数,IL+(fm) 为射频滤波器在fm的正向插入损耗系数。考虑到射频滤波器的滤波作用,依据式(4),到达天线端口的互调发射功率为
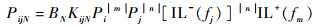 | (5) |
式中:BN为常数项,BN=2|m|+|n|-1cN2;KijN为物理参数项,KijN=kN2RijNRi|m|Rj|n|。
由于KijN为射频功率放大器的固有物理属性,在一定的频率范围和功率范围内可近似视为常数,因此,电台射频滤波器的射频滤波特性是决定互调发射功率随频率变化规律的主要因素。由式(5) 可以看出,射频滤波器从2个方面对互调发射功率产生影响:①通过衰减系数IL+(fm) 对互调发射信号进行衰减,如图 2所示;②通过衰减系数IL-(fj) 对入射干扰信号进行衰减,并使互调发射电平以IL-(fj) 的|n|次幂衰减。
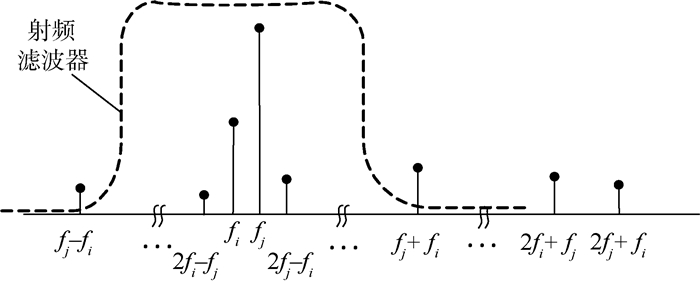 |
| 图 2 射频滤波器的频率筛选特性 Fig. 2 Frequency selection characteristics of RF filter |
| 图选项 |
对于特定的干扰频率fj,BN、KijN、IL+和IL-均为常数,式(5) 可表示为
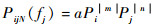 | (6) |
式中:a=BNKijN[IL-(fj)]|n|IL+fm。
将式(6) 以dB值表示:
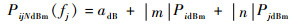 | (7) |
式中:adB=10lg a。
再对式(7) 等式两边的参数项进行调整,得
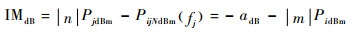 | (8) |
由式(8) 可见,IMdB只与发射机本身的物理特性相关,根据IMdB可以很容易计算出不同入射干扰功率所产生的N(m,n) 阶互调发射电平。对比文献[1-2]的互调抑制比定义,IMdB只适用于fm=2fi-fj的情况,若仍按文献[1-2]定义其他互调发射频率的互调抑制比,则该参数同时包含了测试时的入射干扰功率,不能直接反映发射机本身的物理特性,也不便于应用。
根据以上分析,可以得出如下结论:
1) 根据互调发射频率的不同而分别定义互调抑制比更为合理,本文将其定义为:外界干扰信号的频率变换系数n的绝对值与干扰信号功率电平的乘积,该乘积与N阶互调产物功率电平之差,为N(m,n) 阶互调抑制比,即式(8)。其中,干扰信号功率电平和互调产物功率电平均以dBm为单位。
2) 发射机射频滤波器的滤波特性决定了互调抑制比的频率响应特性。根据式(5) 可知,fm与fi的偏差,以及fj的频率变换系数|n|越小,互调发射功率越大。因此,fm=2fi-fj时三阶互调发射最为严重,此时n=-1,且与fi的偏差最小;当fj距离fi较近时,fm=2fj-fi的三阶互调发射也是比较严重干扰源,但相较于fm=2fi-fj的三阶互调发射小得多。测试经验表明,发射机的二阶和三阶互调发射显著存在,更高阶次的互调发射可以忽略。
3) 对fm=2fi-fj时的式(5) 进行变换,令Δfj=fj-fi,代入式(5),可得
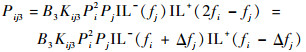 | (9) |
若在相同的频率情况下ILdB-和ILdB+相等,则对应fm=2fi-fj的三阶互调抑制比关于fi对称。其中,ILdB-=10 lg IL-,ILdB+=10 lg IL+。
4) 根据式(8),二阶互调抑制比和频率为fm=2fi-fj的三阶互调抑制比与入射干扰电平PjdBm成斜率为1的线性关系,fm=2fj-fi的互调抑制比与PjdBm成斜率为2的线性关系。
2 发射机互调的测试方法 2.1 传统测试方法的局限性 1) 测试方法1
以环形器和隔离器为关键测试器件的测试链路配置[2]如图 3所示。
 |
| 图 3 测试方法1测试链路配置 Fig. 3 Test link configuration of the 1st test method |
| 图选项 |
该测试方法存在以下局限性:
①要求环形器具有足够的带宽,以保证互调发射功率“无损”地通过环形器,同时应具有足够的反向隔离度,以保证信号源的安全。然而,环形器的带宽和反向隔离度是相互矛盾的指标,特别是在低频段更难以兼顾。文献[2]对环形器的隔离度、带宽和测试频率范围进行了明确规定,且只适用于fm=2fi -fj的互调发射测试。但实际测试结果表明,超出规定带宽和测试频率范围,互调发射仍然显著存在。因此,该方法受环形器性能的限制较大。
②一般UHF/VHF频段的环形器利用铁氧体材料在磁场中的各向异性来实现环形器的功能。此类环形器端接不同负载时,其插入损耗和阻抗与端接50 Ω负载时的标定结果有较大的差异,然而待测发射机天线端口的输入阻抗一般不是50 Ω,故信号源输出功率不能直接记录为激发发射机互调的干扰信号功率,需另外引入测量端口。
③由于待测发射机输出信号功率较大,若为保证测试带宽而采用反向隔离度较小的环形器,干扰信号源也将产生互调发射产物,该产物在发射机端口产生较大反射,该反射物与发射机互调发射产物叠加,无法区分。
2) 测试方法2
以定向耦合器和衰减器为关键测试器件的测试链路配置[1-2]如图 4所示。
 |
| 图 4 测试方法2测试链路配置 Fig. 4 Test link configuration of the 2nd test method |
| 图选项 |
文献[1-2]均采用如图 4所示的测试链路配置,不同的是2个衰减器的衰减量不同。由于定向耦合器具有带宽宽、阻抗稳定的特性,从而避免了测试方法1的局限性,但又产生了新的问题:
①一般情况下,互调发射信号电平比发射机调谐信号电平低约20 dB以上,二者经衰减器1同时进入频谱分析仪,要保证频谱分析仪的安全,衰减器1的衰减量不应太小,而为准确测量低电平的互调发射信号,使被测信号处于频谱分析仪的动态范围内,衰减器1的衰减量不应太大,这是一对矛盾。
②基于保护信号源的考虑,要求衰减器的衰减量不应太小,而另一方面,为使到达发射机天线端口的干扰信号功率激发待测发射机产生互调发射,要求衰减器的衰减量不应太大,这同样也是一对矛盾。
基于以上2点,测试方法2需要对发射机的发射功率进行限制。
2.2 改进的发射机互调发射电平测试方法
2.2.1 测试链路配置 综合第2.1节的分析可以发现,测试方法1测试带宽窄,但测试功率范围宽;测试方法2测试功率范围窄,但测试带宽宽。为解决传统测试方法中存在的局限性,本文综合了二者的优点,提出了改进的测试方法,主要包括以下3个方面的内容:
1) 利用定向耦合器测量待测发射机互调发射,以实现宽带测量。
2) 利用环形器限制待测发射机入射到信号源的功率,又不损失信号源入射到待测发射机的功率,以适应较大的发射机功率范围。
3) 增加数据处理的环节,抵消因环形器阻抗失配和信号源互调发射等因素对测试数据的影响,以确保测试结果的准确性。
在上述3个方面中,第3) 条是本文测试方法的关键。本文测试方法的测试链路配置图如图 5所示。
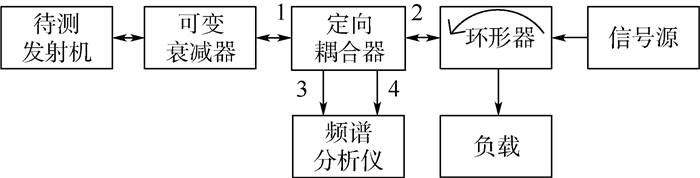 |
| 图 5 改进后的测试链路配置 Fig. 5 Improved test link configuration |
| 图选项 |
设待测量的N阶互调发射频率为fm=|mfi±nfj| (N=|m|+|n|),为实现后续的数据处理,在测量过程中需获得以下测量数据:
1) 可变衰减器衰减系数分别为1,D1,…,DM(M≥3) 时,在定向耦合器端口3的频率为fm的互调发射信号功率测量值分别为PN0-,PN1-,…,PNM-,单位为mW。
2) 可变衰减器衰减系数分别为1, D1,…,DM(M≥3) 时,在定向耦合器端口4的频率为fm的互调发射信号功率测量值分别为PN0+,PN1+,…,PNM+,单位为mW。
3) PjdBm:信号源输出的干扰信号电平,单位为dBm。
2.2.2 |n|≠|m|+1情况下的发射机互调发射电平计算 依据图 5,定向耦合器端口1的互调发射产物由3部分构成:待测发射机互调发射电平、信号源互调发射产物在待测发射机端口形成的反射电平,以及环形器和待测发射机间形成的发射机互调发射二次反射电平。
设可调衰减器衰减系数为Dx(x=0,1,…,M) 时,到达定向耦合器端口1的待测发射机的互调发射功率为PxtN,信号源的互调发射功率为PxsN,环形器与待测发射机间的发射机互调发射二次反射功率为PxcN,根据式(6),以及互调发射信号经过可变衰减器的次数,可以得到
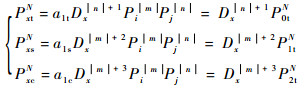 | (10) |
式中:a1t和a1s分别为与待测发射机和信号源的互调发射电平相关的系数,与式(6) 中的a相比,还包含器件插损、阻抗失配损耗等因素;a1c为待测发射机互调信号在环形器和待测发射机之间的二次反射损耗系数,当频率和功率固定时,a1t、a1s和a1c为常数;P0tN=a1tPi|m|Pj|n|,P1tN=a1sPi|m|Pj|n|,P2tN=a1cPi|m|Pj|n|,其中P0tN为Dx=1时的待测发射机的N阶互调发射电平,为待求量。
设定向耦合器端口1与端口3间的耦合系数为Dc1,定向耦合器端口3的测量值PNx-为式(10) 中3个功率分量的总和与Dc的积,即
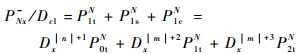 | (11) |
当Dx分别取不同值时的定向耦合器端口3的测量值代入式(11),可得
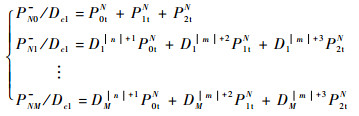 | (12) |
将式(12) 以矩阵形式表示为
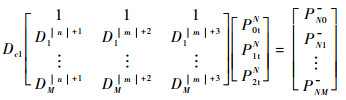 | (13) |
由于|n|≠|m|+1,因此式(13) 为列满秩矩阵,可采用最小二乘法求得P0tN的唯一解。以dB值表示为
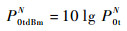 | (14) |
2.2.3 |n|=|m|+1情况下的发射机互调发射电平计算 当|n|=|m|+1时,式(13) 变换为
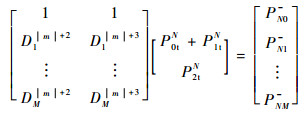 | (15) |
由于无法从P0tN+P1tN的解中分离出P0tN,因此第2.2.2节讨论的方法无法得出|n|=|m|+1情况下的互调发射功率P1tN,为此利用定向耦合器端口4的测量数据获得该频率的发射机互调发射在环形器端口的反射功率,再根据反射系数的测量值,推算该频率的P1tN。
依据图 5,端口4测量的互调发射产物由2部分构成:待测发射机互调发射产物在环形器端口形成的反射电平Pt′N和信号源互调发射电平PsN。
设当可调衰减器衰减系数为Dx(x=0,1,…,M) 时,到达定向耦合器端口2的待测发射机和信号源的互调发射功率分别为Pxt′N和PxsN,根据各信号传播路径的不同,可得到
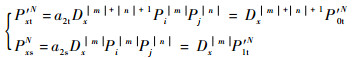 | (16) |
式中:a2t和a2s分别为与待测发射机和信号源的互调发射电平相关的系数,当频率和功率固定时,a2t和a2s为常数;P0t′N=a2tPi|m|Pj|n|,P1t′N=a2sPi|m|·Pj|n|,其中P0t′N为待测发射机产生的互调发射经环形器端口反射后,到达定向耦合器端口2的功率,为待求量。
设定向耦合器端口2与端口4间的耦合系数为Dc2,采用与第2.2.2节相同的方法,可建立矩阵方程为
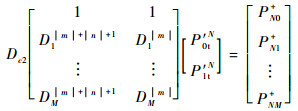 | (17) |
式(17) 为列满秩矩阵,可采用最小二乘法求得P0t′N的唯一解。以dB值表示为
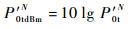 | (18) |
为计算待测发射机的互调发射,还需获得待测发射机至环形器链路的反射系数。反射系数的测试链路配置如图 6所示。不改变图 5的待测发射机至环形器的链路配置,将图 5的待测发射机替换为信号源,图 5中的信号源用50 Ω匹配负载替代,其他测试器件的状态保持不变。
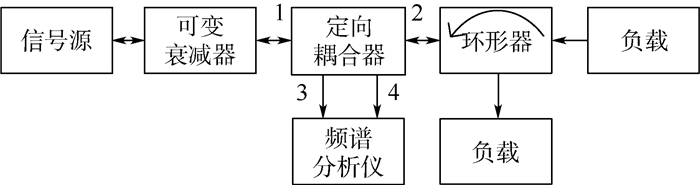 |
| 图 6 反射系数测试链路配置 Fig. 6 Test link configuration of reflection coefficient |
| 图选项 |
信号源输出信号频率为fm,频谱分析仪测量定向耦合器3端口的前向功率PpdBm和4端口的后向功率PndBm,计算出反射系数ρdB为
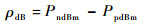 | (19) |
根据ρdB,可计算出待测发射机的互调发射电平P0tdBmN为
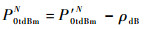 | (20) |
2.2.4 发射机互调抑制比 一般情况下,实际设备发射机的发射功率是一个或少数几个固定值,而干扰信号功率则是随着设备间配置的改变而不同,因此需将发射机互调测试值进行相对于干扰电平的归一化处理,即获取发射机的互调抑制比。根据式(8),可得到互调发射频率为fm的互调抑制比为
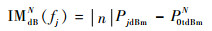 | (21) |
式中:PjdBm为从定向耦合器端口4获得的干扰信号电平,dBm。
3 测试实例及验证 本文以某型超短波电台为例,该电台射频滤波器组由30~42.975 MHz、43~61.975 MHz和62~87.975 MHz 3个频段无源低通滤波器构成。
对比测试方法1和本文测试方法,若将本文测试链路中可变衰减器衰减量设置为0 dB,则本文测试链路与测试方法1的测试链路基本相同,利用定向耦合器端口3监测待测发射机互调发射信号的前向传输数据,利用端口4监测来自环形器和信号源的互调信号的后向传输数据。若互调发射信号处于环形器带宽范围内,则测试方法1获取的测试数据应与前向传输数据一致。
测试方法2主要受限于被测发射机的发射功率,当发射功率较小,衰减器衰减量选择合理的条件下,可获取较为准确的测试数据。因此,本文主要对测试方法1和本文测试方法进行对比。
3.1 二阶互调发射测试结果对比分析 图 7为fm=|fi-fj|和fm=fi+fj时的二阶互调测试结果。fi=45 MHz,环形器工作频段为45~55 MHz,带宽为10 MHz (在低频段环形器难以实现更高的带宽),反向隔离度为15 dB。图 7中:横轴干扰信号频率fj与发射机调谐频率fi之比表示fj偏离fi的程度。由于干扰信号功率电平为0 dB,因此图中互调发射电平也是相应的该互调发射的抑制比。
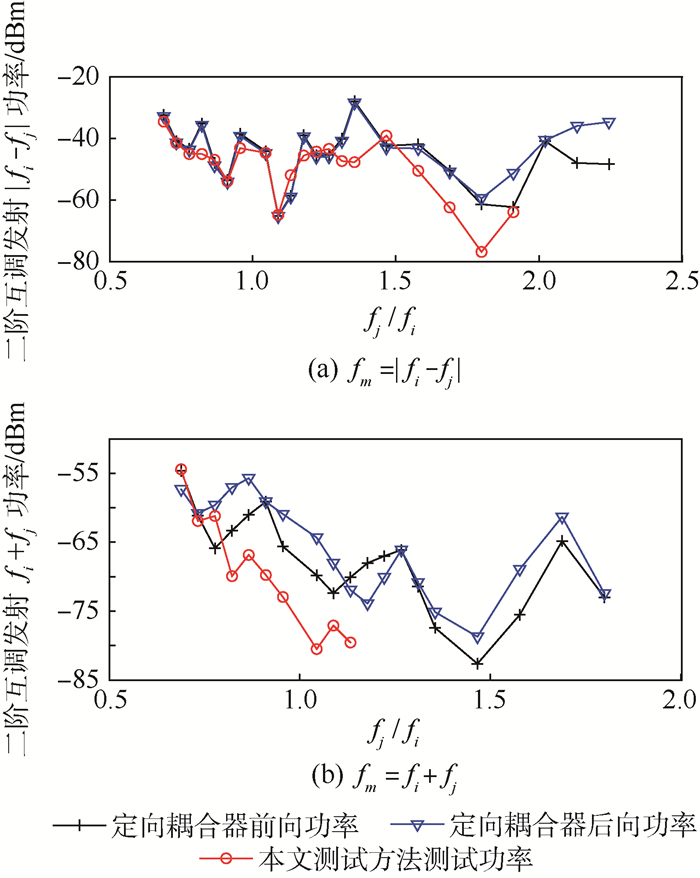 |
| 图 7 fm=fi-fj和fm=fi+fj时的互调发射测试电平 Fig. 7 Test intermodulation level of fm=fi-fj and fm=fi+fj |
| 图选项 |
由图 7可见,定向耦合器前向功率与后向功率基本相同,而且在部分频段后向功率大于前向功率,说明由于fm远离环形器的有效工作频段,因阻抗严重失配引起非常大的反射。部分频段后向功率大于前向功率,说明后向功率不仅包括环形器反射分量,还包括信号源产生互调发射分量。由于发射机互调的大部分能量被反射回去,从环形器测试端口难以获得准确的测试结果。
由于信号源产生的互调分量和发射机互调二次反射分量经待测发射机天线端口反射后又传输到定向耦合器端口3,从定向耦合器端口3获取的功率电平是发射机互调发射电平、信号源互调发射反射电平和发射机互调二次反射电平的合成,因此定向耦合器的前向功率应大于发射机互调发射电平,在本文的测试方法中考虑了对信号源互调发射反射电平和发射机互调二次反射电平的抵消,因此测试结果应小于定向耦合器端口的测试结果。观察图 7中按本文测试方法获得的测试曲线,完全符合上述分析结论。
该型电台采用低通射频滤波器。观察图 7,当fj>1.2fi时,已无法测得频率为fm=fi+fj的互调发射,并且频率为fm=|fi-fj|的互调发射大于频率为fm=fi+fj的互调发射,符合该型电台低通射频滤波器的物理特性。
3.2 三阶互调发射测试结果对比分析 采用第3.1节相同的fi和测试器件。为充分利用环形器的带宽,应使fm落入环形器的频带内,即
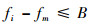 | (22) |
式中:fi=45 MHz;B=10 MHz。
图 8为频率为fm=2fi-fj的互调测试结果。由式(22) 可计算出满足环形器阻抗匹配要求的fj/fi范围为
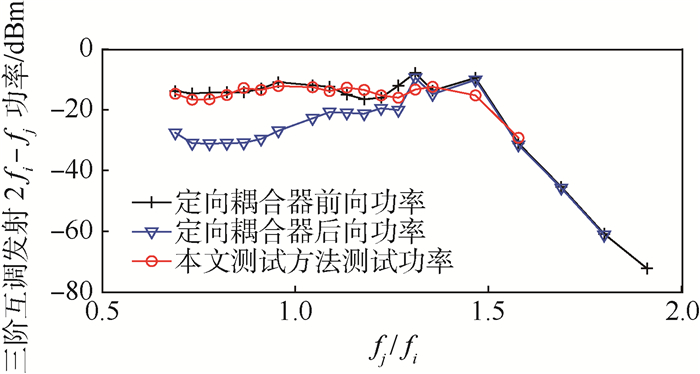 |
| 图 8 fm=2 fi-fj时的互调发射测试电平 Fig. 8 Test intermodulation level of fm=2fi-fj |
| 图选项 |
0.78≤fj/fi<1
此时,定向耦合器前向功率可近似无损地通过环形器,虽然前向功率中还包含了频率为fm=2fi-fj的信号源互调发射在发射机天线端口的反射功率,根据第1节的结论2),该功率分量较小,可以忽略,此时测试方法1的测试结果应与本文测试方法所得到测试结果一致。
观察图 8的前向功率和后向功率测试曲线,在该频率比范围内前向功率大于后向功率约30 dB,说明环形器的失配损耗可以忽略不计,符合上述分析的结论。随着偏离该频率比范围程度的增加,环形器失配愈来愈严重,从而无法从环形器测试端口获得准确的测试结果。
图 9为频率为fm=2fj-fi的互调测试结果。由式(22) 可计算出环形器阻抗匹配的fj/fi范围为
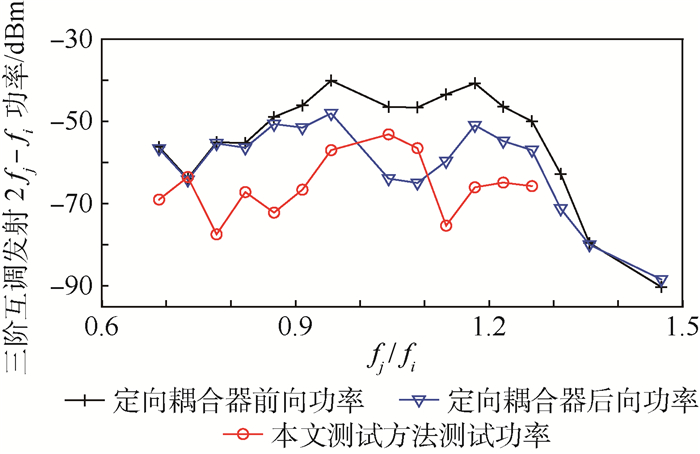 |
| 图 9 fm=2fj-fi时的互调发射测试电平 Fig. 9 Test intermodulation level of fm=2fj-fi |
| 图选项 |
1<fj/fi≤1.1
此时,定向耦合器前向功率虽然可近似无损地通过环形器,但前向功率中还包含了fm=2fj-fi的信号源互调发射在发射机天线端口的反射功率,根据第1节的结论2),对于信号源而言,该类型的互调发射最为严重,虽然经发射机天线端口反射的衰减,其量值仍不可忽视。本文测试方法中消除了这一因素,因此相应的测试结果小于前向功率测试结果。从图 9的测试数据曲线趋势来看,符合上述分析的结论。
3.3 三阶互调发射测试数据与理论分析验证 根据第1节的结论2),三阶互调发射最为严重,因此着重对三阶互调发射测试数据进行分析。
图 10为fi工作于不同工作频段、fm=2fi-fj的发射机互调抑制比IMdB3-测试结果。图中:横轴为Δf=fj-fi。由于无源滤波器的正向插损IL+与反向插损IL-近似相等,根据第1节的结论3),IMdB3-应关于电台调谐频率fi对称。从图 10可见,IMdB3-测试结果与第1节结论3) 相一致。
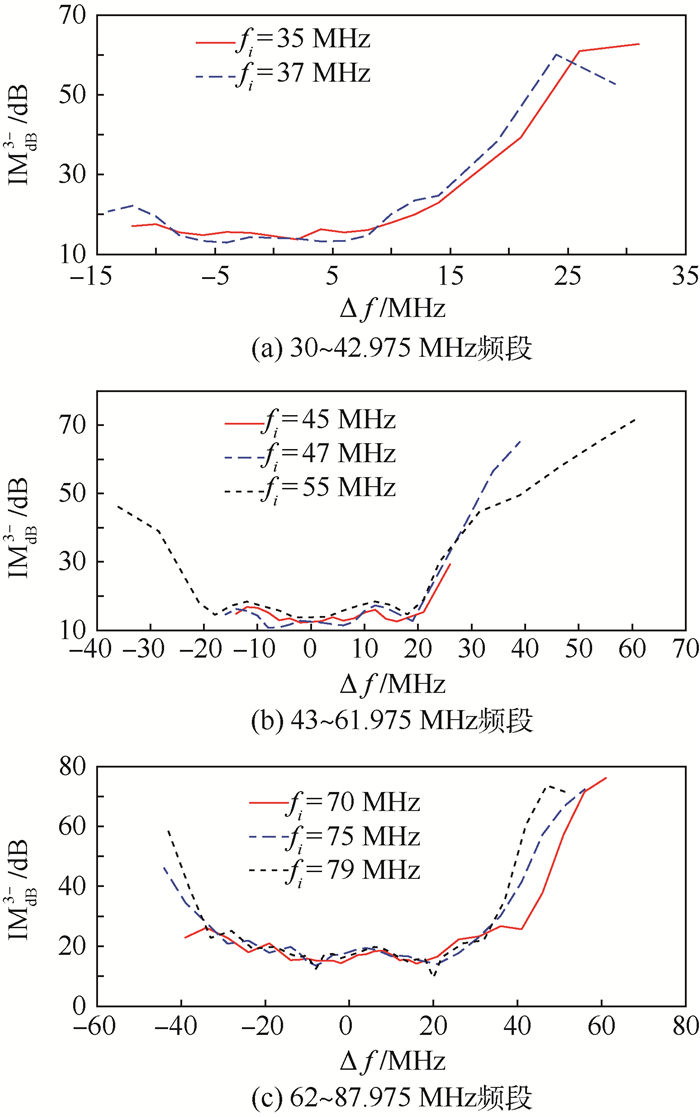 |
| 图 10 fm=2fi-fj时不同工作频段的互调抑制比IMdB3- Fig. 10 Intermodulation attenuation ratio IMdB3- of fm=2fi-fj on different bands |
| 图选项 |
fm=2fj-fi的互调抑制比IMdB3+随干扰频率变化规律见图 11。可见,IMdB3+波动较大,这是由于信号源和待测发射机的射频端口阻抗不一致造成的,用信号源代替待测发射机标定反射系数,测试状态发生了变化,反射系数的测量存在一定的误差。
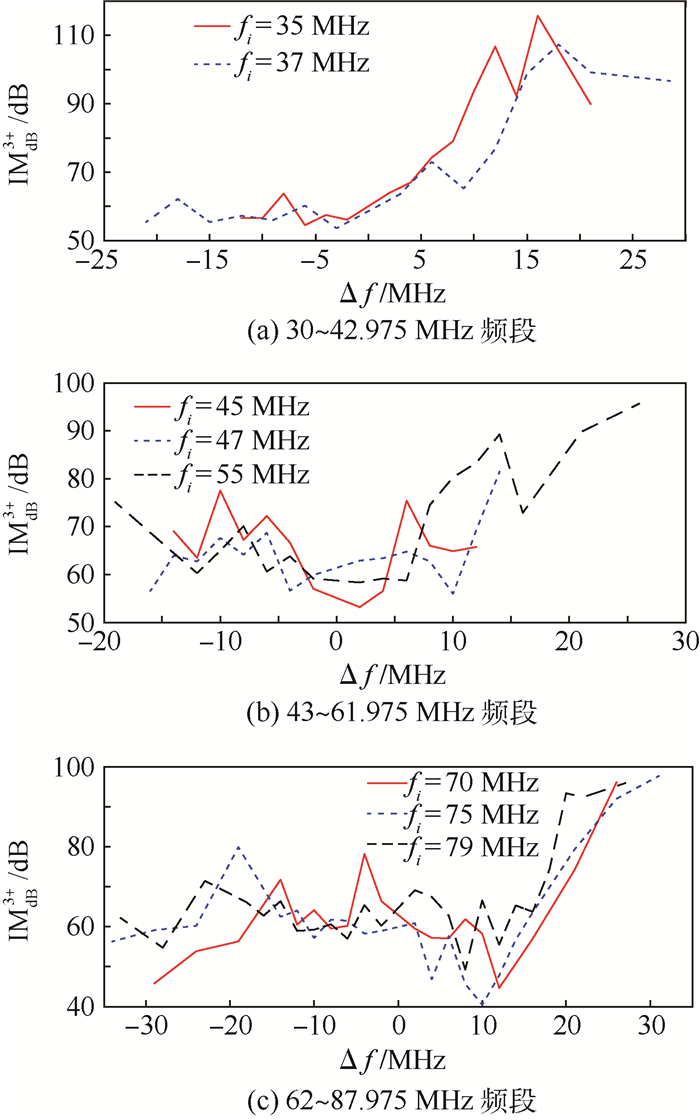 |
| 图 11 fm=2fj-fi时不同工作频段的互调抑制比IMdB3+ Fig. 11 Intermodulation attenuation ratio IMdB3+ of fm=2fj-fi on different bands |
| 图选项 |
对比图 10(a)和图 11(a)、图 10(b)和图 11(b)、图 10(c)和图 11(c),IMdB3+大于IMdB3-约30 dB以上,从测试数据的总体趋势来看,IMdB3+大于IMdB3-约30 dB左右,符合第2节的结论2)。
对于电台不同的发射频率和信号源不同的干扰频率,在-70~25 dBm范围内调整信号源的输出功率(信号源最大输出功率为25 dBm),相应得出的IMdB3-和IMdB3+严格符合第1节的结论4),从而说明了本文测试方法的合理性和测试结果的准确性,同时说明第1节结论1) 中对互调发射抑制比定义的修正是合理的。
4 结论 1) 建立了发射机的简化模型,并以该模型和表征射频功率放大器非线性的多项式模型为基础,建立了发射机互调抑制比的理论模型和基本结论。
2) 对发射机互调抑制比的定义进行了修正,根据修正后的互调抑制比定义,互调抑制比能够更好地反映发射机本身的物理特性,便于应用于无线电设备间的互调发射干扰预测。
3) 吸收了传统测试方法的优点,提出了以可调衰减器、环形器和定向耦合器为核心的新的测试方法,新的测试方法扩展了测试频率范围和功率范围,降低了对测试设备的要求,消除了信号源互调发射和环形器阻抗失配的影响。
通过与传统测试方法对比分析,在符合传统测试规定条件下,测试结果基本一致,证明了该测试方法的准确性。对于|n|=|m|+1情况下的发射机互调电平的测试,由于部分改变了测试链路的工作状态,从而引起测量值的波动,这是本文测试方法的一个缺陷,还需要进一步研究加以改进。
参考文献
| [1] | Recommendation ITU-R SM.1446(04/2000).Definition and measurement of intermodulation products in transmitter using frequency, phase, or complex modulation techniques[S].ITU International Telecommunication Union, 2000:5-12. |
| [2] | 中国人民解放军总装备部.VHF/UHF频段发射机互调抑制比要求和测试方法:GJB 4471-2002[S].北京:总装备部军用标准出版发行部, 2003:1-6.The General Armament Departmant of PLA.The intermodulation attenuation ratio requirements and measuring methods for VHF/UHF band transmitters:GJB 4471-2002[S].Beijing:The General Armaments Department Army Published Standard Delivery, 2003:1-6(in Chinese). |
| [3] | 张亦明. 移动通信中发射机互调干扰的数学模型[J].通信学报, 1990, 11(3): 72–76.ZHANG Y M. The mathematical models of transmitter intermodulation interferences in mobile communication[J].Journal of China Institute Communications, 1990, 11(3): 72–76.(in Chinese) |
| [4] | 李胤, 郑重, 刘久文, 等. 基于行为级建模的通信电台同址干扰预测分析[J].电子测量技术, 2011, 34(11): 122–126.LI Y, ZHENG Z, LIU J W, et al. Prediction and analysis of co-site interference between radio communications based on behavioral modeling[J].Electronic Measurement Technology, 2011, 34(11): 122–126.(in Chinese) |
| [5] | 杨会杰, 王烟青, 杨昭, 等. 甚高频无线通信系统发射机互调干扰研究[J].通信技术, 2014, 47(8): 865–868.YANG H J, WANG Y Q, YANG Z, et al. Study on transmitter intermodulation interference for VHF radio communication system[J].Communications Technology, 2014, 47(8): 865–868.(in Chinese) |
| [6] | HAYASHI H, MURAGUCHI M. A low distortion technique for reducing transmitter intermodulation[J].IEICE Transactions on Electronics, 1997, 80(6): 768–774. |
| [7] | EAKIN J. Application notes on control of base station transmitter reradiated intermodulation in the land mobile services[J].IEEE Transactions on Vehicular Communications, 1966, 15(1): 6–12.DOI:10.1109/TVC.1966.33018 |
| [8] | SHAIRI N A, IBRAHIM I M, RAHMAN T A.Third order intermodulation distortion effect on the constellation error in RF transmitter of IEEE 802.11a WLAN system[C]//IEEE Sym-posium on Industrial Electronics & Application.Piscataway, NJ:IEEE Press, 2011, 4(1):223-226. |
| [9] | 易炎高.基站电调天线无源互调研究[D].广州:华南理工大学, 2012:5-15.YI Y G.Research on passive intermodulation in the base station antennas[D].Guangzhou:South China University of Technology, 2012:5-15(in Chinese). |
| [10] | ZHU A, BRAZIL T J. Behavioral modeling of RF power amplifiers based on pruned Volterra series[J].IEEE Microwave and Wireless Components Letters, 2004, 14(12): 563–565.DOI:10.1109/LMWC.2004.837380 |
| [11] | PEDRO J C, MAAS S A. A comparative overview of microwave and wireless power-amplifier behavioral modeling approaches[J].IEEE Transactions on Microwave Theory and Techniques, 2005, 53(4): 1150–1163.DOI:10.1109/TMTT.2005.845723 |
| [12] | MASS S A. Nonlinear microwave circuits[M].Norwod: Artech House, 1988: 17-19. |
| [13] | HUNTER I W, KORENBERG M J. The identification of nonlinear biological systems:Wiener and Hammerstein caseade models[J].Biological Cybernetics, 1986, 55(2): 135–144. |
| [14] | 刘辉.射频功率放大器线性化技术研究[D].西安:西安电子科技大学, 2005:8-20.LIU H.Research on linearization technologies for radio frequency power amplifier[D].Xi'an:Xidian University, 2005:8-20(in Chinese). |
| [15] | 华晓杰.射频功率放大器大信号表征及频域非线性特征建模[D].哈尔滨:哈尔滨工业大学, 2008:2-19.HUA X J.Research on large signal frequency domain behavioral modeling for RF power amplifier[D]. Harbin:Harbin Institute of Technology, 2008:2-19(in Chinese). |
