电磁辐射发射是电子设备进行电磁兼容性试验的核心考核内容之一，为了尽可能提高试验精度，该类测试需要在符合标准规定的开阔场或暗室中进行。随着科技的发展，各类无线电磁信号越来越复杂，已经很难找到满足标准要求的开阔场试验环境，因此，电磁兼容半电波暗室已成为电子设备进行电磁辐射发射测试的主要场所。
在暗室中进行电磁辐射发射试验时，由于电磁信号在传播过程中经过地面、涂覆吸波材料的墙壁时发生反射、折射、绕射，并受到多径效应影响，不同试验点位的测试结果存在误差。为了减小试验点位对辐射发射测试结果的影响，电磁兼容试验标准中提出了静区的概念^[1]。静区是暗室内受反射干扰最弱的区域，也是暗室中最适合做电磁辐射发射测试的点位^[2]。国内外许多****围绕暗室静区的计算和测量进行了深入研究^[3-8],但是在实际试验过程中，由于受到测试设备、被试品、陪试品等客观因素的限制，电磁辐射发射试验往往不能在暗室的标准静区点位进行^[9-10]。许多****对暗室和测试设备对试验结果影响进行了卓有成效的研究,并提出了新的试验理论和方法^[11-13]。但是尚未有相关文献对被试品在暗室不同试验点位进行辐射发射试验的测试结果进行系统的计算分析。因此，本文针对该问题进行了一系列建模计算，并通过试验验证了模型的有效性。
1 数学建模与计算 电磁兼容半电波暗室的电尺寸非常大，一般的全波计算方法很难对暗室环境下的电磁辐射发射试验进行数学建模计算。本文采用基于一致性绕射理论和几何光学的方法对暗室中电磁辐射发射的传播过程进行建模和仿真计算。
为了使数学建模计算能够与试验实测结果相比对，如图 1所示，给出已知尺寸的3 m法电磁兼容性测试半电波暗室。根据该暗室的设计，其静区位于转台点位。按照国家军用标准GJB 151B—2013^[1]中规定的电磁辐射发射测试方法，当进行试验时，被试品和接收天线相距1 m，并应在静区范围内进行试验。

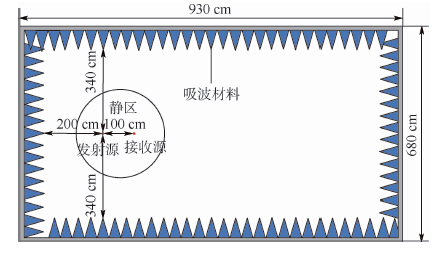图 1 半电波暗室静区标准点位试验示意图 Fig. 1 Schematic diagram of standard location testing inquiet zone of semi-anechoic chamber

图选项

进行电磁辐射发射试验时，作为发射源的被试品一般是向空间发射全向信号，除了正对接收源的信号被直接接收外，其他方向的信号都需通过一定的传播路径到达接收源。电磁波在传播过程中，可以认为半电波暗室的金属地全反射电磁波，涂覆吸波材料的墙壁则可根据吸波材料的电性能参数，计算出信号经过吸波材料反射、折射、绕射后的结果。电磁波在经过吸波材料时的传播路径如图 2所示。
如图 2所示，发射源E发出的信号通过绕射、反射、折射的传播方式到达接收源R，已知发射源E和接收源R在半电波暗室中的点位，两块锥形吸波材料的高度和角度也是确定的，当电磁波从E到达R时，根据电磁波传播的路径信息，通过几何光学算法可以算出电磁波到达R时的场强。
锥形波材料高度为H₂，顶角为α，发射源E和接收源R相距为L₁，发射源到吸波材料高度为H₁。发射源E发出的电磁波入射到吸波材料M2的C处发生一次反射，反射角为θ，然后，电磁波在另一个吸波材料M1的D处发生二次反射，反射角为β，最后，反射电磁波到达接收源R。
通过几何光学的路径计算^[14]，可以算出经反射后到达R的二次反射场强E_r2，计算公式为

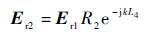(1)

式中：$k = \sqrt {{\mu _0}{\varepsilon _0}} $为自由空间传播常数，μ₀为真空磁导率，ε₀为真空介电常数，ω=2πf 为电磁波的角频率，f为电磁波的频率；E_r1=E₀R₁e^-jkL₂·e^-jkL₃，E₀为从发射源E发出的电磁波的场强。

图 2 电磁波经过吸波材料传播路径图 Fig. 2 Propagation path of electromagnetic wavethrough absorber material

图选项

根据斯涅耳定律，可得

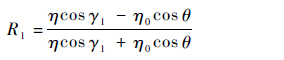(2)

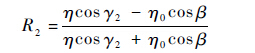(3)

式中：R₁为电磁波入射到吸波材料M1时的反射系数；R₂为电磁波入射到吸波材料M2时的反射系数；γ₁为电磁波在M1上发生反射后折射入吸波材料的折射角；γ₂为电磁波在M2上发生反射后折射入吸波材料的折射角；系数η和η₀的定义分别为$\eta = \sqrt {{\varepsilon \over \mu }} $，${\eta _0} = \sqrt {{{{\varepsilon _0}} \over {{\mu _0}}}} $,ε和μ分别为半电波暗室中涂覆吸波材料的相对介电常数和磁导率，在计算模型中，根据实际情况，吸波材料设为聚氨酯材料。
如图 3所示，信号源发出的电磁波在暗室中经过多次反射后到达接收源。图 3中，P1为直射路径，P2、P3为多次反射路径。当电磁波在传播路径中经过多次反射时，已知传输路径距离和反射角，根据式(1)，利用叠加原理，在任意反射传输路径中，第n次反射场强为

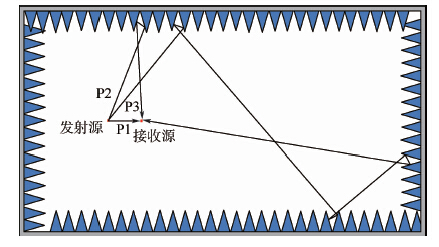图 3 电磁信号多路径反射传输示意图 Fig. 3 Schematic diagram of multipath reflection transmission of electromagnetic signal

图选项

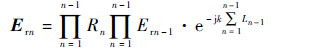(4)

式中：R_n为电磁波第n次反射的反射系数；E_rn-1为电磁波第n-1次反射场强；L_n-1为第n-1次反射路径的距离。
为使计算与试验验证具有可比性，计算中，在发射源360°信号传输路径中，每隔5°，按照传输路径进行一次反射场强计算。
根据一致性绕射理论，当电磁波遇到物体的边缘、尖端和其他不连续点时，会发生绕射，因此绕射的类型主要包括边缘绕射，尖端绕射和曲面绕射。在图 2所示的绕射路径中，根据绕射定律，电磁波发生绕射后的场强E_R的计算公式为

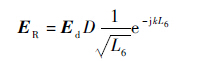(5)

式中：E_d为电磁波入射到绕射边缘或尖端后的场强，E_d=E₀e^-jkL₅； D为阻抗劈绕射系数，按照式(6)计算^[15]：

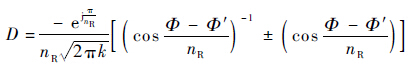(6)

式中：n_n为绕射次数。正负号取负号时表示入射电矢量与边缘平行的情况，此时D为电极化边缘绕射系数；取正号时表示入射波磁矢量与边缘平行的情况，此时D为磁极化边缘绕射系数。
电磁信号在传播路径中除了会受到反射、折射和绕射等影响，考虑到不同频率的信号在传播过程中，还会受到由信号波长和传播路径共同作用而产生的多径效应影响，下面给出考虑信号波长，接收源收到的场强值计算公式^[16]：

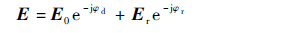(7)

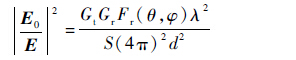(8)

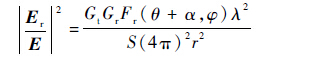(9)

式中：E为接收端收到的和场强；E_r为一次反射场强；φ为电磁信号的相位，信号初始相位通过传播常数和天线点位计算；φ_d和φ_r分别为直达信号和多径信号的相位；G_G和G_G分别为发射天线和接收天线的增益；F_r(θ，φ)为单极子天线的归一化功率方向图；S为测试系统的系统损耗；λ为信号的波长；d为两天线间的直射距离；r为电磁信号反射路径的距离。
根据上述分析和计算，结合一致性绕射理论、几何光学算法并考虑不同波长的电磁信号引起的多径效应，建立电磁信号从发射源发出到接收源收到整个电磁辐射发射过程的数学计算模型。
通过数学公式表示整个计算过程，接收源接收到的最终场强为E，E通过矢量叠加直射场强E_d，反射场强E_r和绕射场强E_R计算得到，其计算公式为

(10)

式(10)中，直射场强可以通过初始场强E₀进行计算：

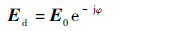(11)

初始场强E₀是由发射源和接收源整个试验系统决定的，其计算公式为

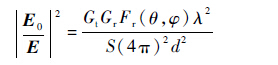(12)

反射场强E_r由前次反射场强和反射系数计算，计算公式为

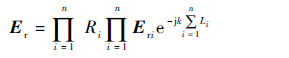(13)

初始反射场强可用发射源和接收源整个试验系统进行计算，计算公式为

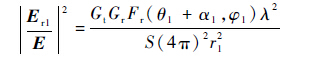(14)

绕射场强E_R通过绕射系统和反射场强进行计算，计算公式为

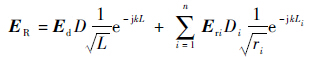(15)

式中：r_i为第i次反射的路径距离。
根据式(15)，建立起半电波暗室内电磁辐射发射电磁信号传播路径的数学模型，通过迭代运算，可以计算半电波暗室中不同点位的发射源到接收源的电磁传播过程。其中，由于计算模型的局限性，将半电波暗室地面对发出的电磁波处理为无耗全反射，吸波材料的吸收损耗按照聚氨酯材料的参数计算。
电磁兼容半电波暗室可以认为是规则的矩形屏蔽体，因此半电波暗室符合矩形导体的谐振定律。根据矩形导体的谐振定律，半电波暗室的固有谐振频率为^[17]

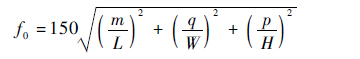(16)

式中：f₀为固有谐振频率，MHz；L、W和H分别为半电波暗室的长、宽和高，m；m、q和p为半电波暗室激励模式的阶数，可取0~9的正整数倍，但不能同时取2个或3个参数为零。根据式(16)，可以计算出已知尺寸的暗室在不同模式下的固有谐振频率^[18]，本节所述尺寸暗室在主模式下的谐振频率如表 1所示。
表 1 半电波暗室主要模式的谐振频率 Table 1 Resonant frequency of dominant semi-anechoicchamber mode

m	q	p	f0/MHz
0	1	1	21.7
0	2	1	31.0
0	3	1	42.0
0	4	1	53.8
0	5	1	66.0
0	6	1	78.3
0	7	1	90.7
0	8	1	103.2
0	9	1	115.8

表选项






利用MATLAB软件对建立的数学模型进行计算。考虑到计算结果的普适性和试验验证比对，选取试验验证使用天线的起始频率、终止频率和中间频率及半电波暗室的典型固有谐振频点为模型的计算频率，其他参数按照试验验证使用的设备参数选取，将参数代入暗室中电磁辐射发射传播模型进行计算。
考虑计算模型的典型性和有效性，选取静区中心点位和半电波暗室中实际测试的点位进行计算，计算点位和距离如图 4所示。图 4中，A、B点位为静区试验位置，A′、B′点位为非静区对比试验位置。数学计算模型中，辐射发射信号的场强根据国家军用标准GJB 151B—2013^[1]中关于电磁辐射发射测量极限值的要求，设为100 dB·μV/m。为使计算与试验结果比对更具代表性，电磁信号在发射源360°范围内，每隔5°计算一次接收源接收到的矢量场强，并减去发射源和接收源之间的直射场强，然后对多角度反射、折射、绕射和多径效应综合计算结果利用矢量叠加并归一化求解，最终得到拟合矢量场强值，计算结果如图 5所示。

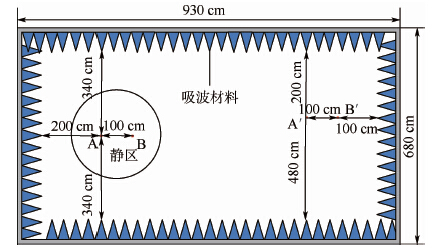图 4 半电波暗室中典型试验点位选取示意图 Fig. 4 Schematic diagram of selection of typical testinglocation in semi-anechoic chamber

图选项

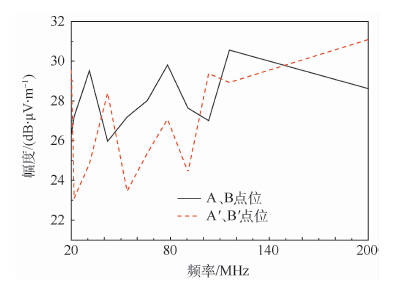图 5 半电波暗室内不同试验点位典型谐振频率剔除直射场强数学模型计算结果 Fig. 5 Calculation results of typical resonant frequencysignal mathematical model in different testing locations ofsemi-anechoic chamber with direct field strength eliminated

图选项

图 5给出了剔除直射场强后，电磁信号经过反射、折射、绕射和多径综合效应影响后得到的计算结果。第2节将通过实测试验来验证数学计算模型的有效性。
2 试验验证 在暗室典型谐振频率范围内，试验采用频率范围20~200 MHz的电磁兼容用双锥天线，分别作为发射天线和接收天线。为使试验验证结果与仿真计算结果更有效地比对，分别在暗室和开阔场进行试验，通过计算得到消除直射场强影响的试验结果。试验结果计算中使用的参数均采用实际试验用系统和设备参数。两者的试验场景如图 6所示。

图 6 半电波暗室及开阔场试验场景图 Fig. 6 Semi-anechoic chamber open area testing scene

图选项

在暗室和开阔场分别进行试验。因为开阔场电磁环境满足电磁兼容性试验要求，并且，除地面外，无其他遮挡，电磁信号不会受到反射、折射、绕射和多径效应影响。因此，通过将暗室中试验结果减去开阔场试验结果，可以剔除直射场强对试验验证的影响^[19]。
为满足计算和实测结果的比对要求，需计算实际试验在发射天线端口和接收天线端口的场强。计算发射天线端口场强公式为

(17)

式中：|E₀|为发射天线端口场强值；P_P为发射机所需发射的功率；A_Fr为发射天线系数；L_L为系统损耗(线缆衰减和设备插损等)；107为发射功率和电平之间的对数换算系数，该系数仅适用于特征阻抗均为50 Ω的系统。根据式(17)可以计算出当发射天线端口场强为100 dB·μV/m时，实际信号源的输出值。
接收天线端口场强根据接收机实际测到的结果，在50 Ω匹配的测试系统时，接收天线端接收到场强值E_R的计算公式为

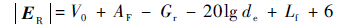(18)

式中：V₀为接收机测到的端口电压；A_A为天线系数;d_d为接收天线的有效长度;6 dB为系统终端换算为开放口的校正值。根据式(18)可以通过接收机测到的结果计算出到接收天线端口的场强值。
根据上述计算方法，在暗室和开阔场分别进行试验。暗室中在对应计算模型的A、B点位和A′、B′点位进行试验，开阔场中，选择四周最空旷的一处点位进行试验，暗室和开阔场试验的场强计算结果分别如图 7所示。

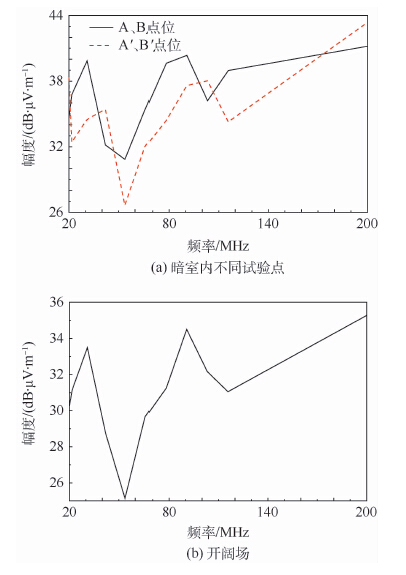图 7 半电波暗室内不同试验点和开阔场典型谐振频率辐射发射实测模型计算结果 Fig. 7 Calculation results of typical resonant frequencyradiated emission actual testing model in different testinglocation of semi-anechoic chamber and in open area

图选项

将暗室实测模型计算结果(图 7(a))减去开阔场实测模型计算结果(图 7(b))，并与剔除直射场强的数学模型计算结果进行比对，结果如图 8所示。

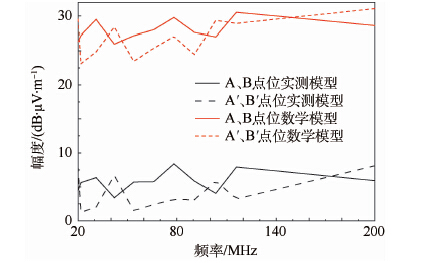图 8 不同试验点位典型谐振频率数学模型和实测模型剔除直射场强计算结果对比图 Fig. 8 Calculation results comparison diagram of typicalresonant frequency mathematical model and actual testingmodel in different testing locations with direct fieldstrength eliminated

图选项

从图 8中可以看出，实测结果与计算结果在趋势上具有良好的一致性。计算结果比实测结果在幅度上大22~25 dB，是由于计算中未考虑天线、线缆和连接器等对试验结果的影响。通过分析，可认为天线线缆和连接器对试验结果的影响为22~25 dB，此结果通过多点均值计算，可作为经验值引入数学计算模型。
在不同试验点位，不同频率的电磁信号，由于传输路径不同，信号在传播过程中会出现叠加或抵消，因此，接收源接收到的信号幅度大小不同。对于不同频率的信号，在不同试验点位试验时，其修正幅度需要进行具体的求解计算。
为了更直观地比对计算和实测结果，图 9给出了不同试验点位，实测模型计算结果和数学传播模型计算结果在暗室典型谐振频率的差值。

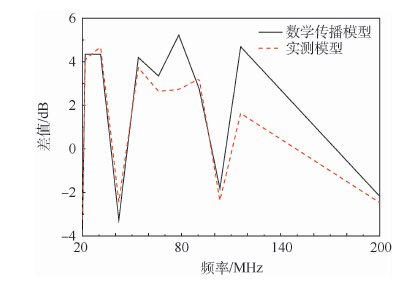图 9 不同试验点位典型谐振频率实测模型和数学传播模型差值计算结果 Fig. 9 Difference value calculation results of typical resonantfrequency actual testing and math propagation model indifferent testing locations

图选项

从图 9中可以看出，通过分别对数学模型和实测模型中的不同试验点位计算结果做差值，消除了实测时测试设备和测试方法的影响。实测模型与数学传播模型的计算结果具有较好的一致性，验证了数学计算模型的有效性，证明该模型具备一定的理论参考价值。
3 结 论 1) 通过对半电波暗室中进行的辐射发射试验进行计算，给出了半电波暗室中不同试验点位的电磁辐射发射传播的数学计算模型，并对模型进行了试验验证。
2) 建立数学模型和试验实测模型后，剔除了直射场影响，并通过分析数学模型和实测模型的计算结果，比对不同试验点位，实测模型和数学传播模型在暗室典型谐振频率的差值，验证了数学计算模型的有效性。
3) 为数学修正暗室中不同试验点位的电磁辐射发射测试结果提供了理论依据，具有一定的理论参考价值，有助于提高暗室中电磁辐射发射试验的测试精度。
致谢    
感谢中国人民解放军驻吉某部张春喜同志提供开阔场测试条件及协助测试。
参考文献

[1]	Electronic Information Department of General Armament Department of the Chinese People's Liberation Army. Requirements and measurement of electromagnetic emission and susceptibility for military equipment and subsystems:GJB 151B-2013[J].Beijing:Commission of Science Technology and Industry for National Defense of the PRC, 2013: 59–65.
[2]	HENRY W O. Electromagnetic compatibility engineering[M].NewYork: Wiley, 2009: 116-148.
[3]	马永光, 陈海波, 何国瑜. 射频仿真暗室的静区分析[J].北京航空航天大学学报, 2006, 32(12): 1431–1434.MA Y G, CHEN H B, HE G Y. Quiet zone analysis of a RF simulation anechoic chamber[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(12): 1431–1434.(in Chinese)
[4]	SHINOZAKI A, SASAKI R, HARIYA E. Performance comparison of 10 m semi-anechoic chamber for EMI measurement using CISPR16-1:Anechoic chamber performance verification experiment report using CALT theoretical value[J].IEICE Technical Report Electromagnetic Compatibility, 2004, 104: 19–26.
[5]	洪丽娜, 樊友谊, 郝晓军, 等. 吸波材料电参数改变对暗室静区性能的影响分析[J].电子测量技术, 2010, 33(8): 121–124.HONG L N, FAN Y Y, HAO X J, et al. Analysis on the quiet zone performance due to degraded absorbers[J].Electronic Measurement Technology, 2010, 33(8): 121–124.(in Chinese)
[6]	HAO X,LIU R,CHEN Y,et al.Calculation and optimization of quiet-zone in RF anechoic chamber[C]//7th IEEE International Symposium on Antennas,Propagation & EM Theory,2006(ISAPE'06).Piscataway,NJ:IEEE Press,2006:1-3.
[7]	SONG D A,FANG C,ZHANG Q,et al.The technologies for reducing quiet zone level of anechoic chamber[C]//IEEE International Symposium on Signals Systems and Electronics(ISSSE),2010.
[8]	CHANG D C, LIAO C H, WU C C. Compact antenna test range without reflector edge treatment and RF anechoic chamber[J].IEEE Antennas & Propagation Magazine, 2004, 46(4): 27–37.
[9]	SPANO I L,SULIS S,SERPI A,et al.EMC Characterization of implantable cardiac medical devices in an anechoic chamber[C]//2014 IEEE International Symposium on Electromagnetic Compatibility(EMC Europe).Piscataway,NJ:IEEE Press,2014:872-877.
[10]	KURIHARA H, SAITO T, SUZUKI Y, et al. Investigation on 10 m semi anechoic chamber by using grid-ferrite and open-top hollow pyramidal EM wave absorber[J].IEICE Transactions on Electronics, 2006, 89(1): 16–23.
[11]	何洋, 苏东林, 李艳, 等. 一种电磁兼容测量天线系数温度误差修正方法[J].北京航空航天大学学报, 2015, 41(10): 1821–1829.HE Y, SU D L, LI Y, et al. Method for EMC antenna factor temperature error correction[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1821–1829.(in Chinese)
[12]	苏东林, 戴飞, 谢树果, 等. 天线系数的测试误差与NSA测试的改进[J].北京航空航天大学学报, 2007, 33(11): 1291–1294.SU D L, DAI F, XIE S G, et al. Errors of antenna factor and improved method for NSA test[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(11): 1291–1294.(in Chinese)
[13]	LIN M S,JI J M,HSU C I G,et al.Simulation and analysis of emc chambers by ray tracing method[C]//IEEE International Symposium on Electromagnetic Compatibility,2007(EMC 2007).Piscataway,NJ:IEEE Press,2007:1-4.
[14]	MIGLIORE M D. Filtering environmental reflections in far-field antenna measurement in semi-anechoic chambers by an adaptive pattern strategy[J].IEEE Transactions on Antennas & Propagation, 2004, 52(4): 1112–1115.
[15]	吴良超, 汪茂光. 阻抗劈一致性绕射系数的一种简洁表达式[J].电波科学学报, 1994(4): 76–80.WU L C, WANG M G. A concise expression of uniform diffracted coefficient of an impedance wedge[J].Chinese Journal of Radio Science, 1994(4): 76–80.(in Chinese)
[16]	唐东, 张麟兮, 呼斌, 等. 基于距离差分法消除天线测试多径干扰[J].现代电子技术, 2014(11): 101–103.TANG D, ZHANG L X, HU B, et al. Elimination of multipath interference in antenna test based on distance difference method[J].Modern Electronics Technique, 2014(11): 101–103.(in Chinese)
[17]	CHUNG B K, CHUAH H T. Design and construction of a multipurpose wideband anechoic chamber[J].IEEE Antennas & Propagation Magazine, 2003, 45(6): 41–47.
[18]	HERRERA J F, MORENO P. Calculation of reflection losses in a small anechoic chamber[J].IEEE Latin America Transactions, 2015, 13(5): 1258–1264.DOI:10.1109/TLA.2015.7111977
[19]	MUNTEANU I, KAKEROW R. Simulation methodology for the assessment of field uniformity in a large anechoic chamber[J].IEEE Transactions on Magnetics, 2014, 50(2): 213–216.DOI:10.1109/TMAG.2013.2283154