目前已有研究人员对考虑多因素的样本分配方法展开了研究,这些研究在考虑多因素时均运用了加权的思想,有效改善了样本结构,提高了指标估计的准确性。比如何洋等[10]考虑了故障模式数、故障率、故障扩散强度总和与危害度,提出了基于多因子的分配方案;张西山等[11]在提出的综合加权分配方法中统筹了故障率、故障影响、平均故障修复时间 (MTTR) 和测试费用的影响。邓露等[12]定义了故障属性的概念,在故障属性中考虑了故障率、危害度、严酷度、扩散度和检测难度5个因素;余思奇等[13]根据故障率、危害度、检测隔离时间、维修性和测试研发代价5个因素构建了可更换单元贡献度层次模型,提出了基于贡献度的样本分配方案。但由于受试对象的差别和试验阶段的局限,这些方案在考虑的因素方面存在明显差异,没有形成更具普适性的分配方法,使得考虑多因素的样本分配方法难以实现工程上的应用。
故障模式影响及危害性分析 (Failure Mode Effect and Critically Analysis,FMECA) 也是测试性验证试验的关键技术之一,旨在鉴别出产品一切有可能发生的故障模式,并将这些故障模式作为试验的备选样本[1-2, 14]。FMECA中的信息包含样本分配需要考虑的因素,且不同形式的FMECA能够体现受试对象和试验阶段的区别[15-17]。这方面常春贺等[18]提出了利用研制信息的测试性验证试验方案,但还没给出样本分配方案。本文将充分分析影响样本分配的FMECA信息,在此基础上提出基于FMECA信息的样本分配方法,并通过实例验证,与基于故障率的分层抽样以及现有的考虑多因素的分配方法进行对比分析,检验该方法的效果。
1 基于FMECA信息的样本分配基本原理 1.1 影响样本分配的FMECA信息分析 FMECA是分析系统中每个产品所有可能发生的故障模式及其所有可能造成的影响,并按照每个故障模式的严重程度、检测难易和发生度分类的归纳分析法。根据FMECA可以寻找分析对象的薄弱环节,鉴别典型的故障模式、故障原因,分析每个可能的故障模式产生的影响及其检测方法和补偿措施,对系统中每一产品按照故障发生概率和严重程度进行评估[14]。FMECA详细的分析内容及结构层次如表 1所示;面向不同类型的产品及寿命周期中不同阶段的FMECA方式略有不同,如表 2所示。
表 1 FMECA详细分析内容和层次 Table 1 Detailed analysis content and level of FMECA
| 分析项目 | 分析层次 | 样本分配影响因素 |
| 故障模式分析 | 故障模式 | 故障模式数 |
| 故障原因分析 | 故障模式 | |
| 故障影响分析 | 故障模式 | 故障扩散度,严酷度,故障影响 |
| 危害性分析 | 故障模式,产品或功能标志 | 故障率,危害度,风险优先数 |
| 检测方法分析 | 故障模式 | 检测难度,检测隔离时间,维修性,测试费用 |
| 补偿措施分析 | 故障模式 | 测试研发代价 |
表选项
表 2 面向不同阶段不同产品的FMECA方式 Table 2 FMECA approach for different products and different stages
| 方式 | 功能FMECA | 硬件FMECA | 软件FMECA | 损坏模式及影响分析DMEA | 过程FMECA | 样本分配影响因素 |
| 产品 | 方案中的产品 | 图纸及实装 | 嵌入式软件 | 发生战损的武器装备 | 过程中的设备 | 根据产品性质和试验所处的阶段确定 |
| 方案阶段 | √ | 故障模式数,故障率,故障影响,风险优先数 | ||||
| 研制阶段 | √ | √ | √ | √ | √ | 故障模式数,故障率,故障影响,危害度,检测难度,维修性 |
| 生产阶段 | √ | 故障模式数,故障率,故障影响,危害度,检测难度 | ||||
| 使用阶段 | √ | √ | √ | √ | 故障率,故障影响,危害度,检测难度,维修性,费用 |
表选项
由表 1和表 2可知,目前基于多因子的样本分配方法研究中所考虑的影响因素几乎都可以通过FMECA的信息得到,但面对不同的试验对象,处在不同的寿命周期阶段进行的测试性验证试验所考虑的影响因素的选取受试验对象性质、所处寿命周期阶段验证目的的约束。因此,FMECA可以为样本分配工作提供相当充分的信息,考虑多因子的样本分配的关键在于如何科学的选取影响因素以及融合各个因素对样本集和评估结果有作用的信息。需要指出的是,工程上进行FMECA时,分析内容应避免不必要的重复,比如:采用检测/隔离时间表征的检测难度与采用MTTR表征的维修性存在重复,且检测隔离时间在研制阶段难以通过仿真得到,因此往往只对维修性即MTTR进行分析。
1.2 基于FMECA信息的样本分配方法 根据统计试验理论,对总体指标估计值总体影响更大的单元应当分配到更多样本。对每个单元而言,有多个影响其本身和总体测试性指标的因素。对于不同的试验对象以及试验所处的不同寿命阶段,第1.1节的影响因素也略有不同。
定义1??单元影响系数Li(i=1, 2, …, N) 表示单元i对总体测试性指标的影响大小。按照分层抽样的理论[2],各单元分配的样本数量如式 (1) 所示:
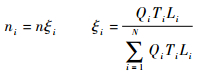 | (1) |
式中:n为总体样本量; ni为单元i应分配到的样本量; ξi为单元i分配样本的相对权重;Qi和Ti分别为第i个单元的数量和工作时间系数。单元影响系数Li的值受多个影响因素影响,每个影响因子对Li的影响程度不同,因此需要对影响因素及其权值进行进一步定义。
定义2??单元影响因子向量li=(li, 1, li, 2, …, li, m)(i=1, 2, …, N) 表示单元i中第1~m个影响因素构成的线性空间中的一个向量。
定义3??权值向量W,表示向量li中各元素的影响因素权值。由此可以得到单元影响系数的计算表达式:
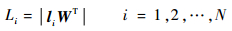 | (2) |
上述定义中的各影响因素可从FMECA信息中得到,并依据FMECA的内容进行无量纲化量化,以便进行样本分配计算。基于FMECA的样本分配方法如图 1所示。
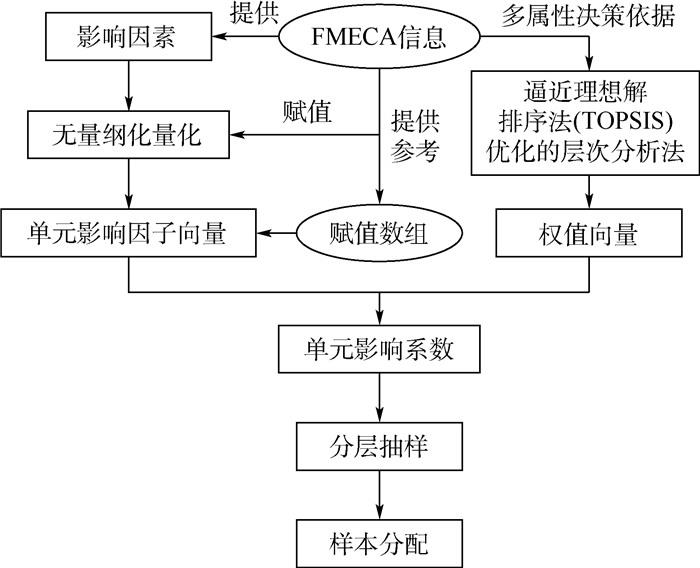 |
| 图 1 基于FMECA的样本分配方法 Fig. 1 Sample allocation method based on FMECA |
| 图选项 |
图 1中,基于FMECA信息的样本分配方法的具体实现步骤如下。
步骤1依照FMECA信息得到影响因素,并根据不同的受试对象以及试验所处的不同寿命阶段对单元影响因子向量进行赋值。
步骤2??依据FMECA提供的影响因素,运用多属性决策问题的方法计算权值向量。
步骤3??按照式 (2) 计算单元影响系数。
步骤4??按照分层抽样理论,根据式 (1) 实现样本分配。
实现该方法的重点在于确定单元影响因子向量和权值向量。
2 单元影响因子向量的确定 2.1 单元影响因子向量中各元素的确定 单元影响因子向量中各元素表征影响样本分配结果的各个影响因素,它们的信息由FMECA提供。首先,应当对各个影响因素之间统一量纲,即进行无量纲化处理。下面以一些典型的影响因素为例进行说明。
1) 故障率。故障率与分配的样本数量成正比,其值一般可通过查阅相关资料获得。用于表征故障率的元素确定如式 (3) 所示:
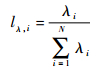 | (3) |
式中:λi为单元i的故障率。在产品研制早期缺乏相关资料难以获得λi时,可通过先验信息以及对故障率规律的认识进行准确推断[17]。对于寿命服从指数分布的产品,可取Gamma分布作为其验前分布,故障率的推断可参考文献[11]中的方法。
2) 故障影响。故障影响越大的单元应当分配到更多的样本,但作为一个定性指标,需要通过严酷度或者故障扩散强度等指标定量化表达。用于表征故障影响的元素确定如式 (4) 所示:
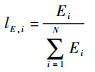 | (4) |
式中:Ei为第i个单元所有故障模式的故障影响指标之和。采用严酷度表征故障影响时,为避免严酷度分析的主观性和不确定性,可采用模糊语言辅助判定。在影响严酷度等级划分的基础上,参照风险分析中影响严重度等级 (Effect Severity Ranking, ESR) 评分准则,对每个等级定义其梯形模糊数,如表 3所示。对于每个故障模式的严酷度均有其对应的梯形隶属度函数f(f1, f2, f3, f4),如图 2所示。
表 3 严酷度等级及其梯形模糊数 Table 3 Severity level and its trapezoidal fuzzy numbers
| 严酷度等级 | 故障影响 | ESR评分 | 梯形模糊数 |
| Ⅳ级 (轻度的) | 不会造成人员伤害,轻度经济损失或产品损坏,致非计划性维修 | 1, 2, 3 | (0, 0.15, 0.25, 0.40) |
| Ⅲ级 (中度的) | 造成人员中度伤害,中度经济损失,产品中度损坏 | 4, 5, 6 | (0.30, 0.45, 0.55, 0.70) |
| Ⅱ级 (致命的) | 造成人员严重伤害,严重经济损失,产品严重损坏 | 7, 8 | (0.60, 0.70, 0.80, 0.90) |
| Ⅰ级 (灾难的) | 造成人员伤亡,产品毁坏,重大经济损失 | 9, 10 | (0.85, 0.90, 1, 1) |
表选项
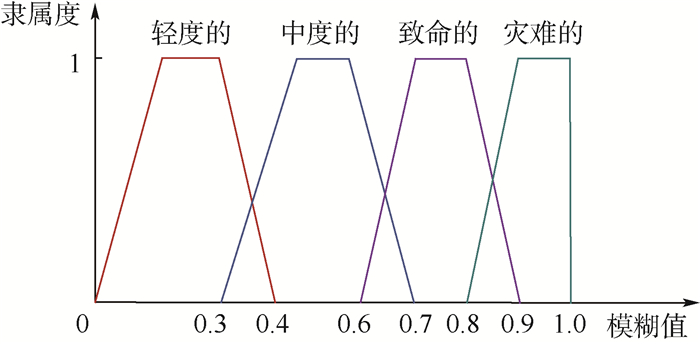 |
| 图 2 严酷度隶属度函数 Fig. 2 Membership function of severe degree |
| 图选项 |
赋值之后,隶属度函数f(f1, f2, f3, f4) 的去模糊值如式 (5) 所示:
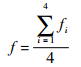 | (5) |
采用故障扩散度表征故障影响时,其值IF可按照文献[8]中计算,并按式 (4) 无量纲化处理[7]。
3) 费用因素。依据表 1,费用因素主要包括测试、维修方面的测试资源费用、人工费用,以及测试研发代价等,它们的关系是相加的。费用因素一般与应分配的样本量成反比,用于表征费用因素的元素确定如式 (6) 所示:
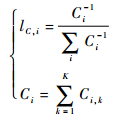 | (6) |
式中:Ci为单元i的各类费用因素之和。
4) 时间因素。包括检测、隔离以及维修所用的时间,反映了测试性、维修性的设计要求,与应分配的样本量之间也是反比的关系。表征时间因素的元素确定如式 (7) 所示:
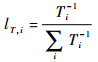 | (7) |
式中:Ti为单元i的时间因素。
5) 危害度与风险优先数。危害度与风险优先数都是用于表征危害性的指标,它们应用的对象略有不同[14, 16]。风险优先数的计算如式 (8) 所示[1]:
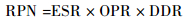 | (8) |
式中:RPN表示风险优先数;ESR表示故障模式严酷度等级;OPR表示故障模式发生概率等级;DDR表示故障模式被检测难度等级。故障模式危害度的计算如式 (9) 所示[1]:
 | (9) |
式中:α为故障模式频数比,表示该故障模式发生次数与产品所有可能故障模式数的比率;β为故障模式影响概率,表示故障模式导致“初始约定层次”出现某严酷度等级的条件概率[1];λ为故障率;t为工作时间。这2个指标均考虑了多种因素,且与分配的样本量成正比。表征危害性的元素确定如式 (10) 所示:
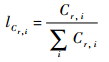 | (10) |
式中:Cr, i为单元i的危害性指标之和。
6) 其他因素。与样本量成正比关系的可参照式 (3)、式 (4) 和式 (10), 成反比的可参照式 (6) 和式 (7) 计算。
2.2 基于试验信息的元素初始赋值 2.1节单元影响因子向量中的一些元素之间考虑的因素存在冗余和重复等问题。基于不同试验对象和所处的时机,这些元素无须全部考虑。基于此,提出一套基于试验信息的单元影响因子向量元素赋值方法。
首先,根据受试对象和时机,参考表 2,选出需考虑的元素按第2.1节中的方法处理。假设有m个元素。定义Lm为影响因子空间,该空间是m维线性空间,向量组e1, e2, …, em是该空间的自然基,每个基向量对应相应的影响因素。进而,对这些无量纲化的各元素顺序排列, 可以得到数组li, 1, li, 2, …, li, m, 即自然基下的坐标。定义x1, x2, …, xm为赋值数组,数组中的元素对应着相应的影响因素,服从以下规则。
规则1??存在重复和冗余的每2个指标对应的元素之间有一个须赋值为0。
规则2??已考虑了多个因素的指标对应的数组中的元素优先赋值为0。
规则3??所有未赋值为0的数组中的元素赋值为1。
按照式 (11) 可计算出单元影响因子向量li:
 | (11) |
得到后还需要求解权值向量才能实现分配方法。
3 权值向量的确定 3.1 基于TOPSIS优化的层次分析法 权值向量的确定属于多目标决策问题。目前处理该问题的方法主要是结合了Delphi法的质量功能展开 (Quality Function Deployment, QFD)、层次分析法 (Analytic Hierarchy Process, AHP) 以及TOPSIS等。但QFD在各种指标排序上存在很大主观性,AHP在利用专家系统构建判断矩阵时也存在一定主观性,且一致性尚有争议。而TOPSIS主要针对排序问题而不是计算权值[17, 19-20]。
基于上述原因,首先对各个因素的重要性进行专家打分;进而采用TOPSIS对这些因素进行量化排序,以弱化专家打分的主观性;最后可基于AHP建立评判矩阵,根据排序信息进行重要性等级赋值,最终得到权值向量。
3.2 基于TOPSIS的影响因素量化排序 TOPSIS以构造的理想解F(x)*和负理想解F(x)-为基准,以目标与理想解的距离S*以及与负理想解的距离S-之间的距离作为排序的判断依据C*。C*的计算如式 (12) 所示:
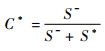 | (12) |
假设有k名专家对各影响因素进行了打分,影响因素有m个,打分形式如表 4所示。
表 4 影响因素及其打分量化 Table 4 Influence factor and its quantitative scoring
| 影响因素 | 专家顺序 | 总分 | |||
| 1 | 2 | … | k | ||
| 1 | a11 | a12 | … | a1k | A1 |
| 2 | a21 | a22 | … | a2k | A2 |
| ? | ? | ? | … | ? | ? |
| m | am1 | am2 | … | amk | Am |
表选项
假设采用xM分制,认为重要性最高为xM分,最低为x0分。按照Minkowski距离法[21],S*与S-的计算如式 (13) 和式 (14) 所示。
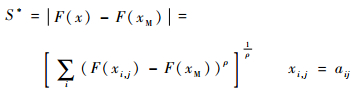 | (13) |
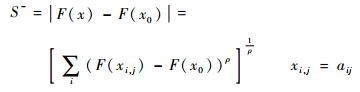 | (14) |
式中:ρ为一个变参数。
排序依据C*值从大到小依次排列。
3.3 基于层次分析法的权重向量计算 建立如式 (15) 所示的判断矩阵:
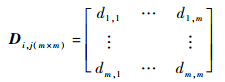 | (15) |
式中:dij表示元素i比j的重要程度,显然有dij>0,dii=1,dij=1/dji。
利用专家系统并根据3.2节中的排序结果对式 (15) 中的元素进行重要性等级赋值,赋值规则如表 5所示。
表 5 元素两两比较的重要性及其赋值 Table 5 Importance of elements pairwise comparison and their assignment
| 序号 | 重要性等级 | 赋值 |
| 1 | i比j极端不重要 | 1/9 |
| 2 | i比j强烈不重要 | 1/7 |
| 3 | i比j明显不重要 | 1/5 |
| 4 | i比j稍微不重要 | 1/3 |
| 5 | i与j同等重要 | 1 |
| 6 | i比j稍微重要 | 3 |
| 7 | i比j明显重要 | 5 |
| 8 | i比j强烈重要 | 7 |
| 9 | i比j极端重要 | 9 |
表选项
得到评判矩阵后首先对其正规化,如式 (16) 所示,权值向量中的每个元素按式 (17) 计算:
 | (16) |
 | (17) |
最终得到权值向量W=(ω1, ω2, …, ωm)。
3.4 一致性检验 为检验判断矩阵的构造合理性,可引入一致性比率CR进行一致性检验,如式 (18) 所示:
 | (18) |
式中:λmax为判断矩阵最大特征根;CI为一致性指数;RI为随机一致性指标均值,其值与判断矩阵阶数有关,如表 6所示。当CR < 0.1时,认为判断矩阵具有一致性,否则还需返回调整直到满足该条件[22]。
表 6 RI取值 Table 6 Value of RI
| 阶数 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
表选项
4 实例验证 4.1 受试对象基本情况 模块A是一个处在研制阶段的外场可更换模块。模块A作为一个控制执行系统的核心,用以实现与上级计算机的数据传递、与下级计算机之间的信息交换,完成整个控制执行过程的逻辑关系处理、状态控制和检测,如图 3所示。其中电源支持单元将输入的大电压直流电源转换为各功能单元工作所需的+5、+12和-12 V电源;处理单元有一处理器,可实现数据、逻辑关系处理和状态控制;A/D转换功能单元、异步通讯单元和同步通讯单元为模块支持单元,对处理器和机内测试 (BIT) 电路的工作提供支持与实现作用。
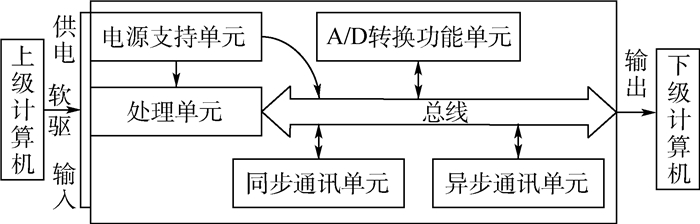 |
| 图 3 模块A的功能框图 Fig. 3 Function block diagram of module A |
| 图选项 |
4.2 基于FMECA信息的样本分配 在面向模块A的测试性验证试验中,采用文中提出的基于FMECA信息的样本分配方法。首先,进行该寿命阶段的FMECA,以模块A的A/D转换功能单元为例,该单元的研制阶段的硬件FMECA内容如表 7所示。
表 7 模块A的A/D转换功能单元FMECA主要内容 Table 7 Main content of FMECA for A/D conversion function unit of module A
| 产品或功能标志 | 功能 | 故障模式 | 故障原因 | 故障影响 | 严酷度等级 | 故障率 | 故障模式频数比 | MTTR | RPN |
| A/D转换功能单元 | 实现对执行系统中设备控制线的电源检测 | 译码控制芯片EPM7128STI损坏 | 过流或过压 | 不能正确实现译码控制功能 | Ⅳ | 0.12 | 12 | 15 | 18 |
| A/D转换芯片AD674损坏 | 过流或过压 | 不能进行模拟电压到数字电压的转换 | Ⅳ | 0.12 | 30 | 15 | 15 | ||
| D/A转换芯片AD667损坏 | 过流或过压 | 不能进行数字电压到模拟电压的转换 | Ⅳ | 0.12 | 30 | 15 | 15 | ||
| 隔离放大器芯片AD203SN损坏 | 过流或过压 | 不能将输入电压隔离放大 | Ⅳ | 0.12 | 13 | 15 | 21 | ||
| 模拟开关芯片MAX4588损坏 | 过流或过压 | 不能完成对输入通道进行多路切换输入 | Ⅳ | 0.12 | 20 | 15 | 6 |
表选项
进而可知模块A中各个单元故障情况以及可能影响样本分配的影响因素,如表 8所示。
表 8 模块A各功能单元及影响因素 Table 8 Function units and influence factors of module A
| 功能单元 | 故障模式数 | 严酷度评分之和 | 故障率 | MTTR | RPN之和 |
| 电源支持单元 | 9 | 5 | 0.19 | 25 | 189 |
| 处理单元 | 5 | 4 | 0.12 | 20 | 144 |
| A/D转换单元 | 5 | 2 | 0.12 | 15 | 85 |
| 异步通讯单元 | 9 | 5 | 0.18 | 15 | 178 |
| 同步通讯单元 | 5 | 3 | 0.15 | 15 | 121 |
表选项
再以A/D转换单元为例,按照第3节方法得到的单元影响因子向量如及对应的影响因素,如表 9所示。
表 9 A/D转换功能单元影响因子向量 Table 9 Influence factor vector of A/D conversion function unit
| 影响因素 | 故障率 | 严酷度 | MTTR | 危害性 |
| 对应元素 | l3, 1=0.105 | l3, 2=0.158 | l3, 3=0.230 | l3, 4=0.119 |
| 赋值数组 | 1 | 1 | 1 | 0 |
| 单元影响因子向量 | l3=(0.105, 0.158, 0.230, 0) | |||
表选项
接下来,依据第3.2节和第3.3节方法得到的权值向量及对应影响因素,如表 10所示。
表 10 权值向量 Table 10 Weight vector
| 影响因素 | 故障率 | 严酷度 | MTTR | 危害性 |
| 权重元素 | ω1=0.32 | ω2=0.18 | ω3=0.12 | ω4=0.38 |
| 权值向量 | W=(0.32, 0.18, 0.12, 0.38) | |||
表选项
得到各单元影响因子向量和权值向量之后,可按式 (2) 计算各单元影响系数;得到各单元影响系数后,按式 (1) 进行样本分配;为保证充分性,样本不足整数的取大于分配值的最小整数[2-4]。最后,可以实现基于FMECA信息的故障样本分配。
4.3 与基于故障率的样本分配方法对比 将本文提出的样本分配方法与现有分配方法进行对比。利用文献[2]中基于故障率的样本分配方法对模块A进行样本分配,如式 (19) 所示[2]:
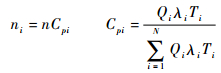 | (19) |
基于上述2种方法的样本分配及测试性评估结果对比如表 11所示。
表 11 样本分配及测试性评估结果对比 Table 11 Results comparison of samples allocation and testability evaluation
| 功能单元 | 故障率 | 单元影响系数 | 基于故障率的分配结果 | 基于FMECA信息的分配结果 |
| 电源支持单元 | 0.19 | 0.145 | 11(0, 4) | 10(0, 4) |
| 处理单元 | 0.12 | 0.116 | 7(6, 6) | 8(7, 7) |
| A/D转换单元 | 0.12 | 0.090 | 7(0, 2) | 6(0, 2) |
| 异步通讯单元 | 0.18 | 0.154 | 10(2, 2) | 11(3, 3) |
| 同步通讯单元 | 0.15 | 0.114 | 9(0, 2) | 8(0, 2) |
| 合计 | 0.76 | 0.619 | 44(8, 16) | 43(10, 18) |
| 故障检测率点估计/% | 内场测试设备 | 81.8 | 79.1 | |
| 机内测试 | 63.6 | 58.1 | ||
| 注:括号 (, ) 内数据分别表示内场测试设备和机内测试测试失败的样本数量。 | ||||
表选项
4.4 与现有考虑多因素的样本分配方法对比 现有考虑多因素的样本分配方法均是考虑了多种影响样本分配因素的加权分配方法[10-13]。这些方法中所考虑的影响因素往往局限于特定的研究对象和试验阶段,本文则利用构建的单元影响因子向量和提出的赋值规则,充分利用了FMECA中的原始信息,扩大了适用的对象和寿命周期。限于篇幅,以文献[11]中的综合加权分配方法为例进行对比分析。文献[11]考虑的影响因素为:故障率、故障影响、MTTR、测试费用,与文献[2]中测试性设计时综合加权分配测试性指标时考虑的因素相同[2, 11]。但是,对于生产研制中的装备,测试费用难以准确量化,这些阶段进行FMECA时分析的因素一般不包括费用因素[1]。若试验处于使用阶段,FMECA采用硬件方式,则本文中的方法所考虑的因素将与文献[11]完全一样,分配过程将非常近似。若试验对象处于第4.2节案例中的寿命周期中,文献[11]在影响因素计算上将存在困难。
4.5 讨论 1) 与基于故障率的样本分配结果对比。由表 11上半部分可知:按照基于故障率的样本分配方法,故障率相对较高的电源支持单元和异步/同步通讯单元得到更多样本,而故障率小的处理单元样本较少。本文中提出的分配方法充分考虑了故障模式的影响以及时间因素,在基于FMECA信息的分配结果中故障影响较大的处理单元和异步通讯单元所分配得到的样本数量得到了增长;故障影响不大,故障模式数不多的同步通讯单元、电源支持单元以及A/D转换单元分配得到的样本量有所减少。由此可见基于FMECA信息的样本分配方法能够有效且全面地考虑到各影响因素。
2) 测试性指标评估结果对比。由表 11下半部分可知:无论内场测试还是机内测试,基于FMECA信息的样本分配方法得到的测试性评估指标都略低于基于故障率的样本分配方法。这是由于单元影响系数较大的处理单元和异步通讯单元分配到了更多样本,使这些单元中存在的不能成功测试的故障模式被体现出来。由此可见基于FMECA信息的样本分配方法得到的样本集更加合理,测试性指标评估结果也更为灵敏。
3) 与现有考虑多因素的分配方法对比。本文中提出的样本方法在全面考虑各影响因素的情况下,面对不同寿命周期的不同对象时,可以依据表 1、表 2和第3节的赋值数组灵活处理,对不同对象和寿命周期的适应性较好。面向特定的阶段和受试对象时,本文中的方法会与相应的现有考虑多因素的样本分配方法有相似的过程和结果。
5 结论 本文针对测试性验证试验中的故障样本分配技术存在的问题提出了基于FMECA信息的样本分配方法。该方法有以下3个优点:
1) 该方法充分利用了FMECA的信息,考虑了多种可能影响样本分配的因素,相比于现有的基于故障率的分配方法考虑更加全面,可实现样本集的优化。
2) 在确定权值时首先运用TOPSIS对专家评分的因素进行排序,一定程度上弱化了层次分析法中判断矩阵元素确定的主观性,相比于现有的样本分配方法中的权值确定方法,权值取值更加准确。
3) 利用所定义的单元影响因子向量、赋值数组以及赋值规则,实现了面对不同阶段不同对象时的灵活应用;相比于现有的考虑多因素的样本分配方法,在工程上更具有普适性。
参考文献
| [1] | Department of Defense.Maintenance verification demonstration evaluation:MI-STD-471A[S].Washington, D.C.:U.S.Government Printing Office, 1973:2-8. |
| [2] | 石君友. 测试性设计分析与验证[M].北京: 国防工业出版社, 2011: 282-286.SHI J Y. Testability design analysis and verification[M].Beijing: National Defense Industry Press, 2011: 282-286.(in Chinese) |
| [3] | 石君友, 康锐. 基于通用充分性准则的测试性试验方案研究[J].航空学报, 2005, 26(6): 691–695.SHI J Y, KANG R. Study on the plan of testability demonstration based on the general adequacy criterion[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(6): 691–695.(in Chinese) |
| [4] | 石君友, 康锐, 田仲. 基于信息模型的测试性试验样本集充分性研究[J].北京航空航天大学学报, 2005, 31(8): 874–878.SHI J Y, KANG R, TIAN Z. Study on sufficiency of sample set in testability demonstration based on information model[J].Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(8): 874–878.(in Chinese) |
| [5] | 徐萍, 康锐. 考虑FDR的测试性测定试验及其相关方法[J].北京航空航天大学学报, 2007, 33(3): 357–360.XU P, KANG R. Concept of testability determine test and relative method for FDR[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3): 357–360.(in Chinese) |
| [6] | WANG C, QIU J, LIU G, et al. Testability evaluation using prior information of multiple sources[J].Chinese Journal of Aeronautics, 2014, 27(4): 867–874.DOI:10.1016/j.cja.2014.03.029 |
| [7] | 李天梅, 邱静, 刘冠军, 等. 基于故障扩散强度的故障样本选取方法[J].兵工学报, 2008, 29(7): 829–833.LI T M, QIU J, LIU G J, et al. A method of failure sample selection based on failure pervasion intensity[J].Acta Armamentarii, 2008, 29(7): 829–833.(in Chinese) |
| [8] | 李天梅, 邱静, 刘冠军. 基于故障率的测试性验证试验故障样本分配方案[J].航空学报, 2009, 30(9): 1661–1665.LI T M, QIU J, LIU G J. Allocation plan of failure samples based on failure rate in testability[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(9): 1661–1665.(in Chinese) |
| [9] | 赵建扬, 李小珉, 雷琴. 基于危害度相对比值的故障样本分配方案[J].探测与控制学报, 2011, 33(2): 55–59.ZHAO J Y, LI X M, LEI Q. Relative criticality ratio based on failure samples allocation[J].Journal of Detection & Control, 2011, 33(2): 55–59.(in Chinese) |
| [10] | 何洋, 李洪涛, 王志新. 基于多因子的机电设备测试性验证样本分配方案[J].电光与控制, 2015, 22(1): 97–100.HE Y, LI H T, WANG Z X. A multi-factor based sample allocation scheme for testability verification of electromechanical equipment[J].Electronics Optics & Control, 2015, 22(1): 97–100.(in Chinese) |
| [11] | 张西山, 黄考利, 敖贤野, 等. 测试性验证试验中的故障样本综合加权分配方法[J].计算机测量与控制, 2015, 23(1): 139–142.ZHANG X S, HUANG K L, AO X Y, et al. Synthetic weighted method of failure samples allocation in testability[J].Computer Measurement & Control, 2015, 23(1): 139–142.(in Chinese) |
| [12] | 邓露, 许爱强, 赵秀丽. 基于故障属性的测试性验证试验样本分配方案[J].测试技术学报, 2014(2): 103–107.DENG L, XU A Q, ZHAO X L. Allocation plan of samples based on failure attribute in testability demonstration test[J].Journal of Test & Measurement Technology, 2014(2): 103–107.(in Chinese) |
| [13] | 余思奇, 景博, 黄以锋. 基于贡献度的测试性验证试验样本分配方案研究[J].中国测试, 2015, 41(2): 91–95.YU S Q, JING B, HUANG Y F. Study on allocation scheme of failure sample in testability validation tests based on contribution[J].China Measurement & Test, 2015, 41(2): 91–95.(in Chinese) |
| [14] | Department of Defense.Procedures for performing a failure mode, effects, and criticality analysis:MIL-STD-1629A[S].Washington, D.C.:U.S.Government Printing Office, 1980:4-8. |
| [15] | ARABIAN-HOSEYNABADI H, ORAEE H, TAVNER P J. Failure modes and effects analysis (FMEA) for wind turbines[J].International Journal of Electrical Power & Energy Systems, 2010, 32(7): 817–824. |
| [16] | COLLI A. Failure mode and effect analysis for photovoltaic systems[J].Renewable & Sustainable Energy Reviews, 2015, 50: 804–809. |
| [17] | TAPIA C, DIES J, PESUDO V, et al. IFMIF accelerator:Database, FMEA, fault tree and RAM[J].Fusion Engineering & Design, 2011, 86(9-11): 2722–2725. |
| [18] | 常春贺, 杨江平, 曹鹏举. 基于研制信息的测试性验证试验方案研究[J].航空学报, 2012, 33(11): 2057–2064.CHANG C H, YANG J P, CAO P J. Study on the scheme of testability demonstration test based on development information[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2057–2064.(in Chinese) |
| [19] | 张朋程, 李伟娟. 油企与地方关系和谐度评价[J].可持续发展, 2011, 1(1): 1–5.ZHANG P C, LI W J. Appraise harmony about relationship between oil companies and local[J].Sustainable Development, 2011, 1(1): 1–5.DOI:10.12677/sd.2011.11001(in Chinese) |
| [20] | KILPEL?INEN A, PELTOLA H, RYYPP? A, et al. A hybrid method of FEM, modified NSGAⅡ and TOPSIS for structural optimization of sandwich panels with corrugated core[J].Journal of Sandwich Structures & Materials, 2014, 16(4): 398–417. |
| [21] | VEGA A, AGUARóN J, GARCíA-ALCARAZ J, et al. Notes on dependent attributes in TOPSIS[J].Procedia Computer Science, 2014, 31: 308–317.DOI:10.1016/j.procs.2014.05.273 |
| [22] | SAATY T L. Basic theory of the analytic hierarchy process:How to make a decision[J].Revista De La Real Academia De Ciencias Exactas Físicas Y Naturales, 1999, 93(4): 395–423. |
