为减小捕获时间,采用快速傅里叶变换 (FFT) 运算是行之有效的方法[1-5],文献[1]运用改进的FFT并行快速捕获,考虑到直接FFT运算点数较大,在进行FFT之前先进行平均采样来降低FFT的点数;文献[2]采用相干-非相干捕获算法,合理选择相干和非相干时间长度可实现高动态下弱信号的捕获;文献[3]将FFT与循环卷积相结合计算粗略伪码相位,然后增加采样率通过循环卷积来计算精确伪码相位。文献[4]对匹配滤波捕获算法进行改进,将延时叠加和同相累加方法进行结合,可以在加快搜索速度的同时,保证抗干扰能力。文献[6]引入延迟累加器辅助频谱分析实现多个卫星多普勒频移成分的分离、估计[6],提高了捕获速度。
文献[1]采用FFT运算的点数也不小,捕获时间较长;而文献[2-3]时间长度选择困难,需要权衡捕获速度和捕获性能。文献[4]仅采用匹配滤波,输出信号相关峰值会有很大衰减,导致漏检。文献[6]中引入延迟累加器较复杂,增加了硬件资源。
另一方面,在工程实践中,要考虑到捕获实现的硬件资源问题,因此粗捕时采用部分匹配滤波 (PMF) 和FFT运算相结合的快速捕获算法,PMF可有效减小后续FFT的点数,而FFT运算可补偿PMF带来的随着多普勒频移增加相关峰值急剧衰减的问题,因此在实现上PMF+FFT不仅大大降低了硬件资源消耗,而且也加快了捕获速度。又因为考虑到随后高动态跟踪时采用扩展卡尔曼估计方法,该方法对捕获后的参数精度要求较高,而PMF+FFT的捕获精度不能满足跟踪要求,因此需要在粗捕后缩小频率范围,进行线性调频Z变换 (CZT),提高最终捕获参数精度。粗捕和精捕的结合实现使得高动态下的GPS信号能被快速和精确地捕获。
1 高动态GPS数字中频信号产生 1.1 GPS卫星信号组成 GPS在载波L1上正交调制有被数据码调制后的C/A码和P (Y) 码,载波L2上只调制有被数据码调制后的P (Y) 码,卫星发射的信号[7-8]可表示为
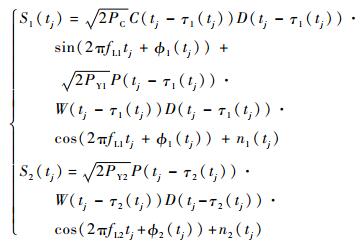 | (1) |
式中:tj为第j时刻采样时间:S1和S2为L1、L2频段输出的信号;C为C/A码;D为导航数据电文;P为P码;W为W加密码;PC为C/A码信号的平均功率;PY1和PY2分别为载波L1和L2上P (Y) 码信号的平均功率;?1和?2为L1和L2的载波相位;fL1和fL2为L1和L2的中频加上多普勒频移的频率和;τ1和τ2为L1和L2频段的码相位;n1和n2分别为L1和L2频段的高斯白噪声。
1.2 多普勒频移模拟 产生中频信号中核心的问题是模拟高动态下载波多普勒频移和伪码多普勒频移[9],由于高动态下产生的多普勒频移范围较大,因此高动态对于伪码多普勒的影响不容忽视。卫星信号的多普勒频移是由用户接收机与卫星在两者之间的连线方向上的相对运动所引起的。
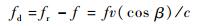 | (2) |
式中:fd为多普勒频率;fr为信号接收频率;f为卫星发射信号频率;v为用户接收机的运动速度;β为从接收机的运动方向到信号入射方向的夹角;c为光速。
高动态下,多普勒效应对载波和伪码有显著的动态变化影响,为实现高动态捕获,需要模拟出高动态下每一接收时刻的卫星信号。假设该接收机具有加速度a和加加速度a′,则该动态模型可表示为
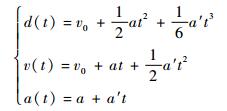 | (3) |
式中:d (t)、v (t) 和a (t) 分别为径向运动的实时位移、实时速度和加速度;v0为初始时刻速度。
对应于多普勒变化,则有
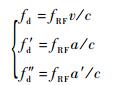 | (4) |
式中:fRF为对应频段的射频频率;fd′为多普勒频率变化率;fd″为多普勒频率的二阶变化率。L1频段的发射信号表达为
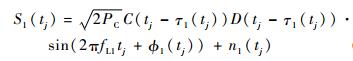 | (5) |
fd(t) 和fL1(t) 计算公式为
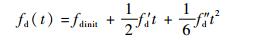 | (6) |
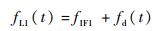 | (7) |
式中:fdinit为多普勒频率的初始值;fIF1为L1频段的中频频率。
卫星信号经过传输到达地面时会产生传输时延τ,该延时的构成表示如下:
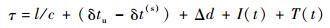 | (8) |
式中:l/c为几何距离传播时间,l为卫星距用户接收机的距离;δtu为接收机时钟钟差;δt(s)为卫星时钟钟差;Δd为多普勒频移引起的时延;I (t) 为电离层时延[10];T (t) 为对流层时延。本文对于各种误差时延只考虑多普勒引起的延时,则多普勒频移引起的时延可表示如下:
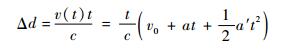 | (9) |
伪码的多普勒频移公式如下:
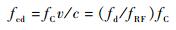 | (10) |
式中:fC为伪码的标称码率;fcd为伪码的码率偏移,若对于L1频段的C/A码,那么C/A码的码率偏移为载波多普勒频移的1/1 540,即fcd=fd/1 540,明显可得高动态下时的伪码码率偏移不可忽略。
对连续信号进行离散化采样处理,设采样频率为fs,则在t=n/fs(n为第n个采样时刻) 时刻的中频数字信号输出为
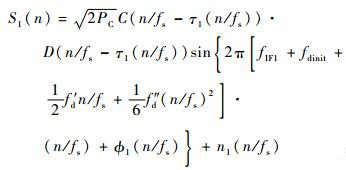 | (11) |
1.3 动态伪码NCO实现 为模拟高动态下伪码产生,采用码NCO产生动态的伪码码率[11],码NCO实际上是由加法器和寄存器组成的相位累加器,工作过程为:累加以及溢出归零后再累加,Mc是控制输入的相位控制字,NCO在每个时钟周期其寄存器计数值就增加Mc,当寄存器计数值达到最大2N-1(N为计数器的位数) 后,就溢出归零,相应地就完成了一个周期,则输出的周期信号频率为
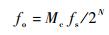 | (12) |
为提高码NCO的频率分辨率,一般取N为32,由式 (10) 可得到伪码的码率偏移,则伪码NCO的频率控制字如下:
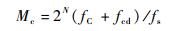 | (13) |
对每个采样点时刻的伪码NCO频率控制字进行累加,当其累加值达到最大值2N-1后,码相位累加器就产生一次溢出,整码片计数器加1,则一个完整的伪码码片周期完成。
2 粗捕实现 捕获的实质是对该卫星信号的载波频率和伪码码相位的二维搜索[12],由于高动态下不仅需要快速捕获,也需要覆盖较大的多普勒频移范围[13],因此采用部分匹配滤波来对去载波后的数据进行相关累加操作,达到降采样的目的,即减少后续进入FFT模块的运算点数,降低硬件资源,大大缩短捕获时间;随后进行FFT运算使得部分匹配滤波器的幅频响应在频率上得以延伸,使得PMF+FFT[14]能在更大的多普勒频移范围内正常工作。综合考虑,PMF+FFT捕获方法无论从捕获速度、捕获范围和硬件要求上都更加适合高动态捕获的要求[15]。
2.1 卫星快速盲搜方法 由于本文的高动态接收机是处于盲搜状态[16],没有任何星历和历书的信息来辅助搜索卫星,传统的卫星搜索方法是串行地搜索32颗卫星,这样浪费了搜星的时间,本文运用了一种组合码相关的卫星快速盲搜方法,提高了卫星搜索效率。首先同时对多个卫星信号进行搜索,若检测到有相关峰值时,再通过对其中单个卫星信号检测最高峰和第二高峰的比值与捕获阈值大小来判定是否捕获成功,直至捕获到4颗卫星信号为止。若同时对4个卫星进行搜索,则对于32颗GPS卫星来说,搜捕卫星时间最少可减少1/4。
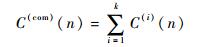 | (14) |
式中:C(i)(n) 为卫星i的伪码;C(com)(n) 为k颗卫星的伪码组合码。让伪码发生器复制出多个卫星的组合码,再与接收信号进行相关运算,即相当于同时对k颗卫星信号进行搜索和检测。若这k颗卫星没有一颗可见,则接收机通道在搜索过程中检测不到任何显著的相关峰值,于是这k颗卫星可以一并全部被认为不存在,然后接收机可以转向另外k颗卫星,如果检测到一个或多个相关峰值,则可以断定这k颗卫星中有一颗或多颗可见,因此进一步在这k颗卫星进行捕获,直到捕获到4颗卫星为止。
对相关峰值的判决采用自适应门限值调整法,当检测到第一高峰时,通过开窗原理[17],继续检测次高峰,将最高峰和次高峰的比值与门限值进行比较,若大于门限值则该颗卫星存在,反之不存在。但由于本地伪码的相位与接收信号伪码的相位相近,因此检测次高峰时需要在最高峰附近设置一个窗口,以最高峰时相位值CPha为中心,如图 1所示,在[1:Range1, Range2 : PerCodeS]范围内继续检测次高峰,其中Range1和Range2距离CPha分别有一个码片,PerCodeS为1 ms信号的总采样点数。
 |
| 图 1 单个伪码检测时开窗示意图 Fig. 1 Windowing schematic of single pseudo code detection |
| 图选项 |
当同时检测多颗卫星时,可能存在多个峰值,同样用自适应门限值调整法,若次高峰与最高峰的偏差比较小时证明有2个峰值,同样设置窗口,如图 2所示,在[CPRange1,CPRange2,CPRange3]范围内继续检测第三高峰,将最高峰和第三高峰的比值与门限值进行比较,若大于门限值则存在2颗卫星。
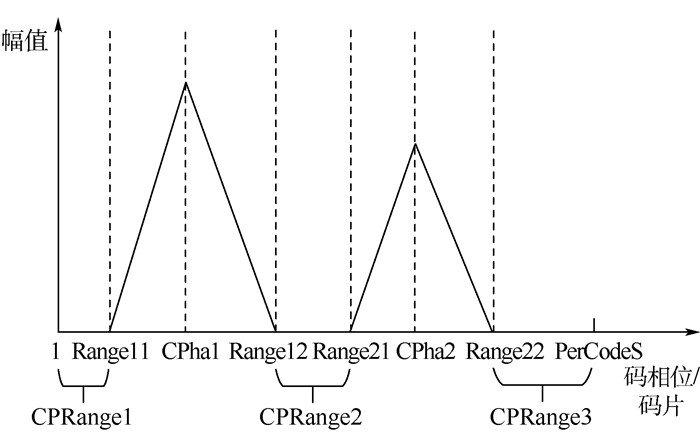 |
| 图 2 多个伪码检测时开窗示意图 Fig. 2 Windowing schematic of multiple pseudo code detection |
| 图选项 |
2.2 PMF+FFT实现原理 如图 3所示为改进的PMF+FFT的结构示意图,中频信号经去载波处理后,I和Q支路合并信号分段与对应分段伪码相关,首先由捕获频率分辨率fresolu=1/T决定积分长度T,频率覆盖范围fall=NFFT/T确定FFT点数NFFT,该系统有K个PMF,M=TfC为在积分时间T内要进行的总的相关运算,则每个匹配滤波器的长度为L=TfC/K。对于某一个相位,第1个PMF将接收序列的前L个码片与本地伪码的前L个码片做相关累加,第2个PMF处理接下来的L个码片,依次类推,直至第K个PMF完成最后的L个码片的处理,总共有L个相位。最后将PMF结果送入NFFT点的FFT,NFFT≥K。之后再通过捕获判决得出多普勒频移和码相位偏移。
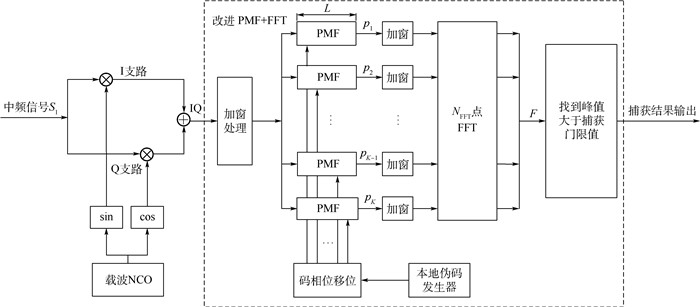 |
| 图 3 改进的PMF+FFT结构示意图 Fig. 3 Schematic of improved PMF+FFT structure |
| 图选项 |
PMF+FFT实现原理分析如下。
中频信号:
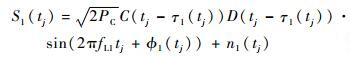 | (15) |
去载波后I和Q支路信号:
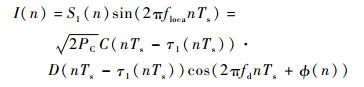 | (16) |
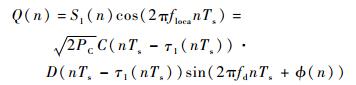 | (17) |
式中:floca为本地载波频率;Ts为采样周期:?为初始相位。
I和Q支路信号合并:
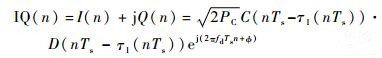 | (18) |
假设本地伪码与接收伪码同步时,则第n个PMF的输出为
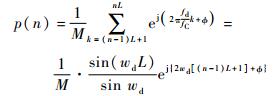 | (19) |
式中:wd=πfd/fC。
对这K个PMF分别进行NFFT点的FFT运算,可得FFT输出的归一化幅度响应:
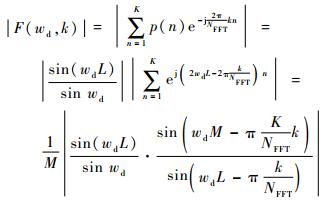 | (20) |
式中:F (wd, k) 可分为两部分:
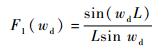 | (21) |
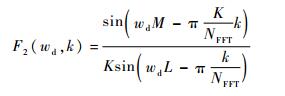 | (22) |
式中:F1(wd) 为PMF对整体幅频响应的影响;F2(wd, k) 为FFT运算对整体幅频响应增益的贡献。
为满足高动态下捕获,设置频率的捕获范围为20 kHz,FFT点数为256,令PMF的个数等于FFT点数为256,积分长度为12.8 ms,则总的相关运算为13 094.4,PMF的长度为51.15,由于PMF的长度要取整,因此取PMF的长度L=52,则M=13 312,NFFT=K=256,1/Tc=1 023 000(Tc为C/A码的码周期时间),采样频率为40 MHz,频率分辨率约为76.85 Hz。
如图 4所示为传统PMF+FFT归一化幅频响应图,从图中可知,PMF+FFT的带宽与仅有PMF结果的带宽相比增加了很多,即FFT对PMF的幅频在频率上起到了延伸的作用,使得PMF+FFT可以在高动态下正常工作。
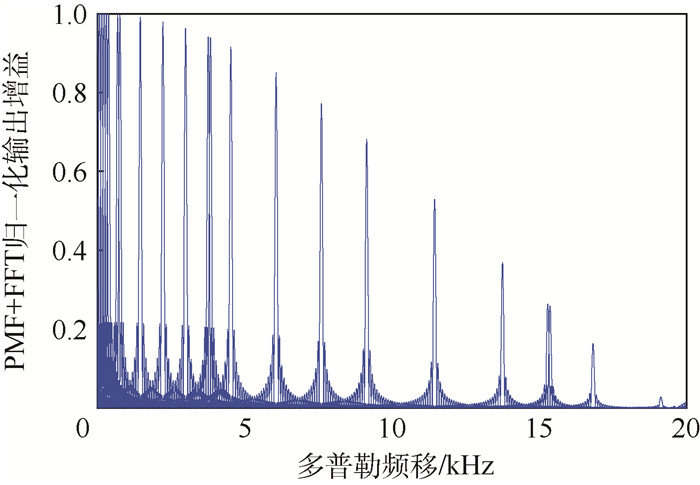 |
| 图 4 PMF+FFT归一化幅频响应 Fig. 4 Normalized PMF+FFT amplitude frequency response |
| 图选项 |
对PMF+FFT运算后的结果求其绝对值的最大值,该最大值所对应的即为捕获频带数和码相位值。
2.3 改进PMF+FFT 如图 5所示为PMF+FFT归一化幅频响应放大图,由图可知,当多普勒频率在2个FFT输出点之间时,该点频率所对应的幅值有明显的衰减,这种增益衰减称为扇贝损失[18],由FFT部分相位补偿不完全引起。由归一化PMF+FFT的幅频响应曲线可得,当多普勒频率落在第0个和第1个FFT输出点之间时,扇贝损失达到最大约为0.370 4。
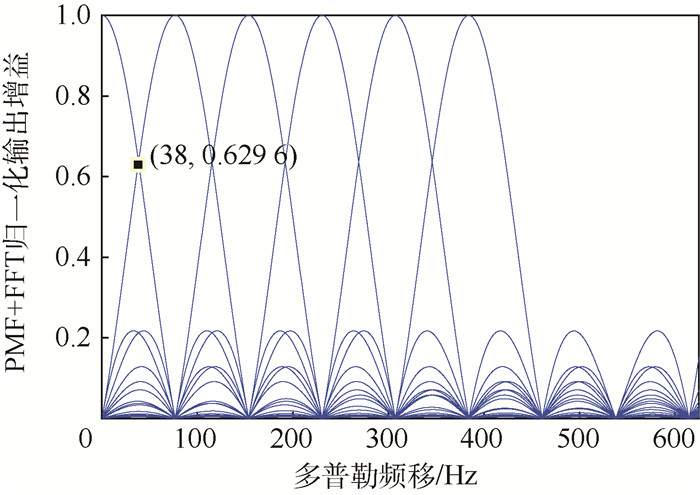 |
| 图 5 PMF+FFT归一化幅频响应放大图 Fig. 5 Enlarged view of normalized PMF+FFT amplitude frequency response |
| 图选项 |
扇贝损失会使得虚警率增加,捕获性能下降,因此针对PMF+FFT的改进主要是减少扇贝损失,本文采用加窗函数法来改善扇贝损失。
由图 5的幅频响应波形可知,每一个FFT点的响应曲线和矩形窗的幅频特性类似,但矩形窗的主瓣宽度较小,使得相邻FFT点之间的扇贝损失较大,因此可采用加窗函数来增加主瓣宽度,从而减小扇贝损失。本文以加汉宁窗为例:
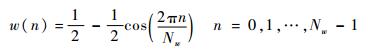 | (23) |
汉宁窗的频率响应幅度函数可表示如下:
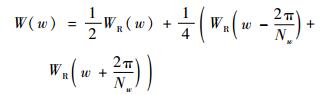 | (24) |
式中:WR(w) 是长为Nw的矩形窗的幅度特性。
针对PMF幅度随着多普勒频移增大而衰减的问题,对PMF也进行加窗处理,改善其低通特性。同样使用汉宁窗,为避免幅值衰减,对系统中参数均乘以2,因此PMF的输入数据进行加窗后的归一化频率响应为
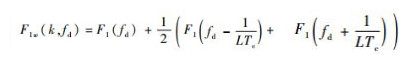 | (25) |
未加窗时F1(wd) 在fd=1/(LTc) 处增益为0,即主瓣宽度为19 673 Hz,如图 6所示为加窗后的归一化PMF幅频响应图,其主瓣宽度约为20 kHz,因此理论上捕获多普勒频率范围fd≤20 kHz。对PMF的输入数据进行加窗处理后,主瓣宽度明显加倍,且随着多普勒频率增大幅度衰减缓慢,因此加窗处理可提高在高动态下的捕获性能。
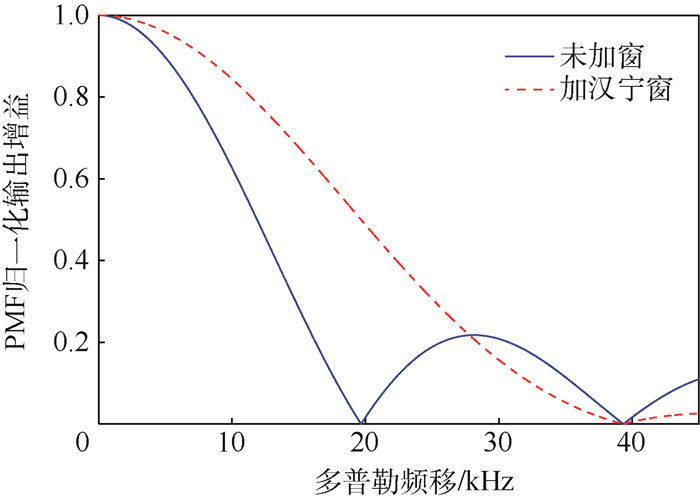 |
| 图 6 加窗后PMF归一化幅频响应 Fig. 6 Normalized PMF amplitude frequency response after window adding |
| 图选项 |
对于FFT模块,为减小扇贝损失,引入窗函数,加窗后的FFT模块的输出归一化幅度特性如下:
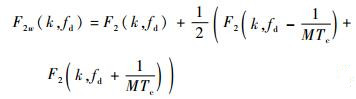 | (26) |
由式 (26) 可知对信号时域加窗可以通过对其频域进行线性运算实现。如图 7所示,只考虑FFT第0点输出,因为其他FFT点是第0点输出曲线的平移实现。
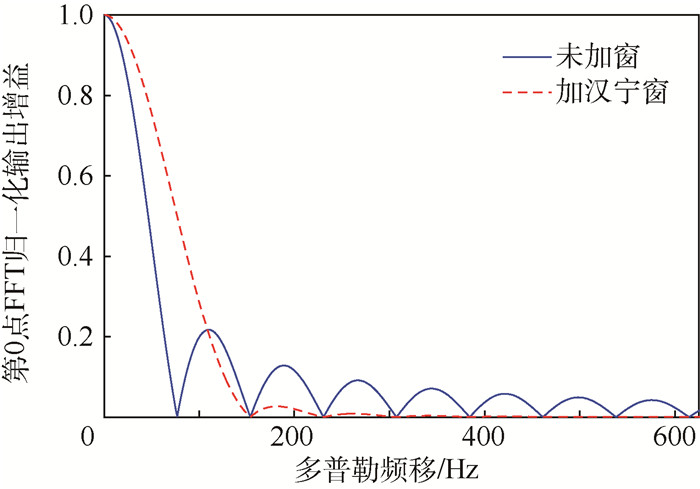 |
| 图 7 加窗后第0点FFT归一化幅频响应 Fig. 7 Normalized amplitude frequency response of the zero point of FFT after window adding |
| 图选项 |
如图 8所示为加窗后的FFT归一化幅频响应图,从图中可看出加窗处理可实现对信号频谱的平滑,增加了主瓣宽度,未加窗时第0点和第1点FFT的输出幅度曲线交点归一化幅度衰减了0.370 4,而加窗后交点归一化幅度值衰减了0.154 3,即加窗后相邻FFT点的输出幅度特性曲线的交点上移,从而可以减小扇贝损失。
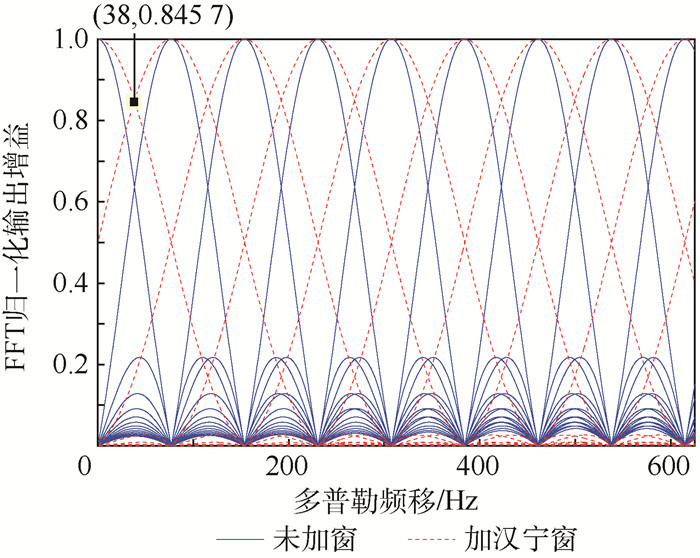 |
| 图 8 加窗后FFT归一化幅频响应 Fig. 8 Normalized FFT amplitude frequency response after window adding |
| 图选项 |
如图 9所示为同时对PMF和FFT加窗时的幅频响应与不加窗时的幅频响应的对比。综合考虑PMF加窗和FFT模块加窗,由仿真结果可知不仅减小了扇贝损失,也提高了系统在高动态下的捕获性能。
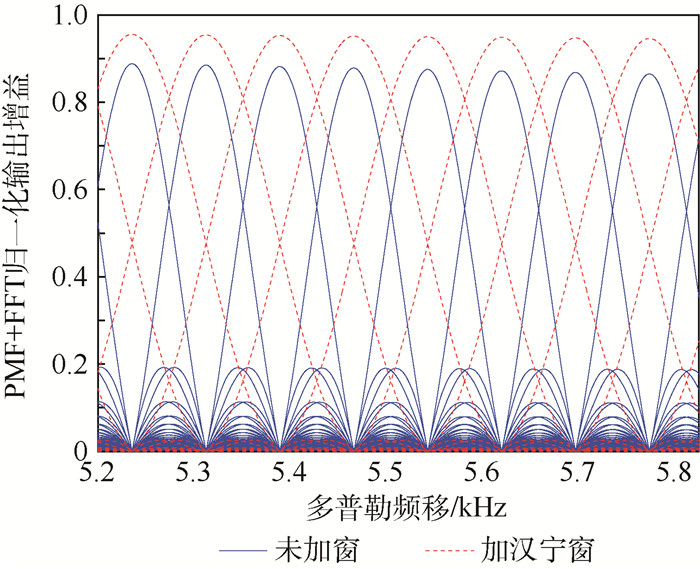 |
| 图 9 加窗后PMF+FFT归一化部分幅频响应 Fig. 9 Normalized PMF+FFT amplitude frequency response after window adding in part |
| 图选项 |
3 精捕实现 由于粗捕中频谱峰值检测存在约±80 Hz的频率误差,远远满足不了基于扩展卡尔曼的高动态跟踪精度的要求,因此必需进行频谱细化,复调制细化方法 (ZFFT) 和CZT是常用的2种频谱细化方法[19],文献[19]对比了2种方法的性能,得出对于单频率和谱线干涉不严重的多频率谐波成分,使用CZT细化分析,能得到高精度的频率、幅值和相位;而对于发生严重干涉现象的密集多频率谐波成分,ZFFT把干涉频率成分分离后进行校正也能获得高精度的参数,由于GPS信号中不存在严重多频干涉,因此本文选用CZT进行频谱细化。
3.1 CZT算法原理 CZT算法是采用螺线抽样进行Z变换,其只研究信号的任一频段,并对该频段密集抽样来提高分辨率,其可以研究非单位圆上的抽样值,CZT算法能准确计算Ns(Ns为输入信号序列的点数) 点DFT,且Ns为大的素数。CZT算法原理如下。
Ns点有限长序列,其Z变换为
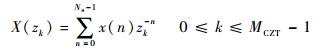 | (27) |
式中:zk=AW-k,如图 10所示A=A0ejθ0为采样轨迹的起点,A0为起点离原点的距离,θ0为起点与Re轴之间的角度,W=W0e-jφ0为相邻2个采样点之间的比例关系,W0控制采样轨迹的椭圆弧的方向,W0>1时轨迹趋向内圆,W0<1时轨迹趋向外圆,W0=1时在单位圆上采样,φ0为相邻2个采样点的相位差; MCZT为总的CZT采样点数。
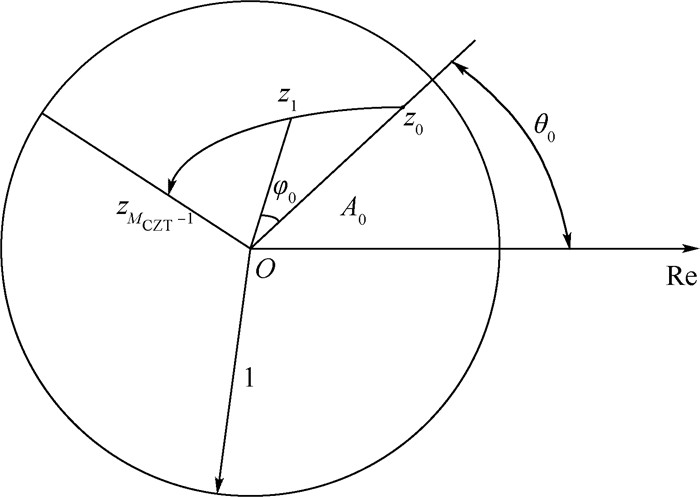 |
| 图 10 CZT取样示意图 Fig. 10 Schematic of CZT sampling |
| 图选项 |
3.2 CZT实现 1) 选择CZT实现的总点数Ltotal≥Ns+MCZT-1,且Ltotal=2m。
2) 形成Ltotal点序列g (n):
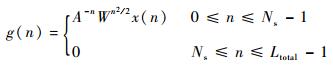 | (28) |
系数
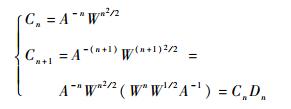 | (29) |
求其Ltotal点FFT:
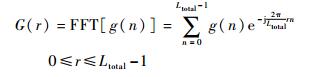 | (30) |
3) 形成Ltotal点序列h (n):
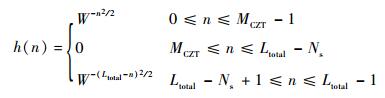 | (31) |
求其Ltotal点FFT:
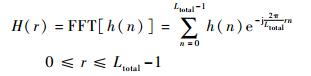 | (32) |
4) 求乘积:Q (r)=H (r) G (r)。
5) 求Ltotal点快速傅里叶逆变换 (IFFT) 的q (k):
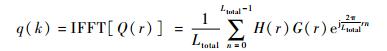 | (33) |
6) 求抽样点的Z变换:
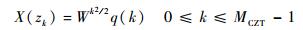 | (34) |
在粗捕获频率fcoaracq的基础上得到细化频率段的起点频率f1=fcoaracq-80和终点频率f2=fcoaracq+80,选取细化频段的频点数MCZT,MCZT越大细化精度
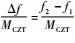
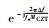
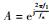
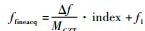
4 仿真实验及分析 4.1 高动态运动模拟 本实验模拟GPS中L1 C/A码所在频段信号,模拟高动态下接收机运动轨迹,图 11(a)~图 11(c)分别为速度、加速度和加加速度变化图,其中速度先呈上升趋势,初始速度为400 m/s,对应初始多普勒频率为2 100 Hz,仿真时间内速度最大为3 667 m/s,对于GPS L1频段,该速度对应的最大多普勒频率约为19.257 kHz,在本实验多普勒频率最大范围20 kHz以内;加速度在前3 s时一直保持100g,对应的多普勒频率变化率为5 146.372 Hz/s,加速度从3 s时由100g减小到-50g;加加速度可达到-150 g/s。
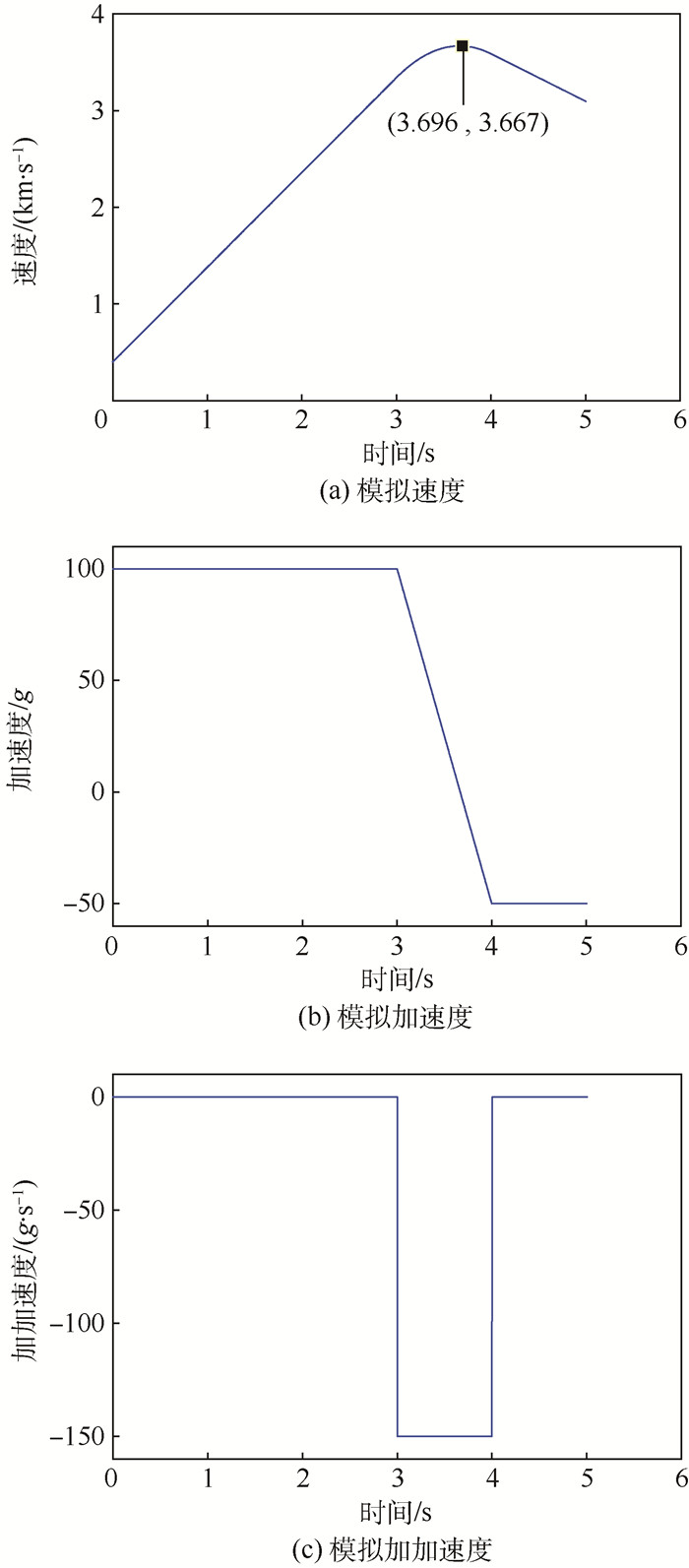 |
| 图 11 高动态下接收机运动轨迹 Fig. 11 Trajectories of receiver under high dynamic |
| 图选项 |
4.2 高动态捕获结果 本文分别仿真了基于FFT的并行码相位捕获方法和改进的PMF+FFT捕获算法,以及精捕CZT变换。读取10 ms数据进行捕获,则理论的捕获多普勒频率应为2 100+0.5×5 146.372×0.01=2 125.73 Hz。
如图 12所示,采用基于FFT的并行码相位捕获方法,设置频率的捕获范围为20 kHz,频率步进为1 000 Hz,最终捕获多普勒频率为2 000 Hz,误差为126 Hz左右,可见基于FFT的并行码相位捕获方法捕获精度不高。
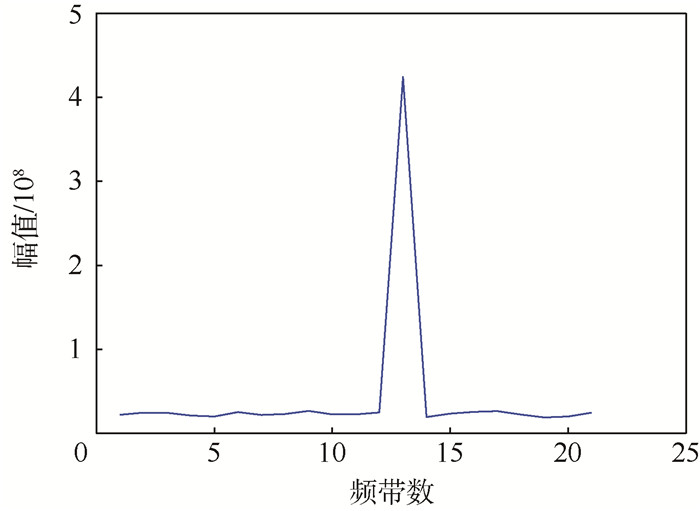 |
| 图 12 并行码相位捕获后的频谱 Fig. 12 Spectrum after parallel code phase acquisition |
| 图选项 |
如图 13和图 14所示,采用本文提出的改进PMF+FFT捕获方法,峰值明显,通过门限判决取最大值可得到对应信号的码相位偏移和多普勒频移,捕获的码相位偏移无误,捕获的多普勒频率约为2 075 Hz,误差在频率分辨率76.85 Hz之内。
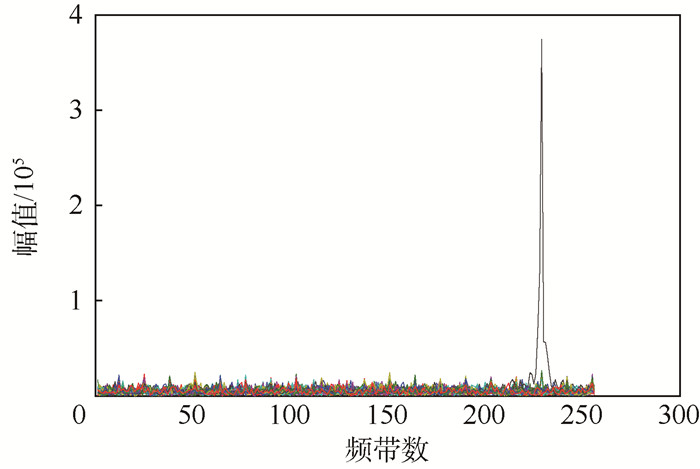 |
| 图 13 改进的PMF+FFT捕获多普勒频率结果 Fig. 13 Doppler frequency result of improved PMF+FFT acquisition |
| 图选项 |
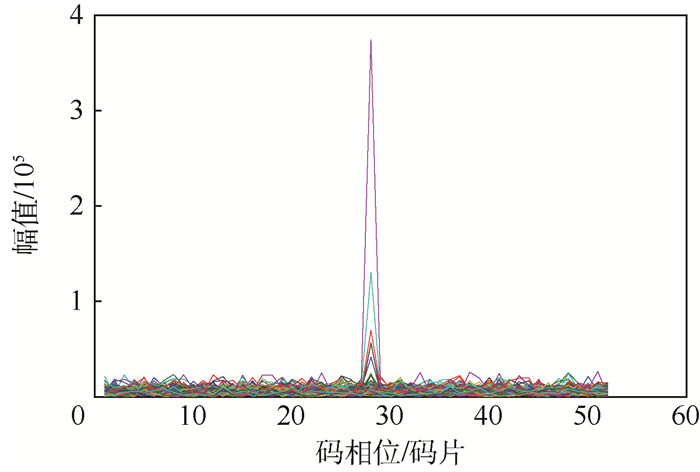 |
| 图 14 改进的PMF+FFT捕获码相位结果 Fig. 14 Code phase result of improved PMF+FFT acquisition |
| 图选项 |
如图 15所示为精捕CZT变换后的多普勒频谱图,在粗捕的多普勒频移基础上极大地缩小捕获范围,选取CZT变换点数为128,则经过精捕后得到的多普勒频率约为2 125 Hz,与理论捕获频率值误差在1 Hz以内。
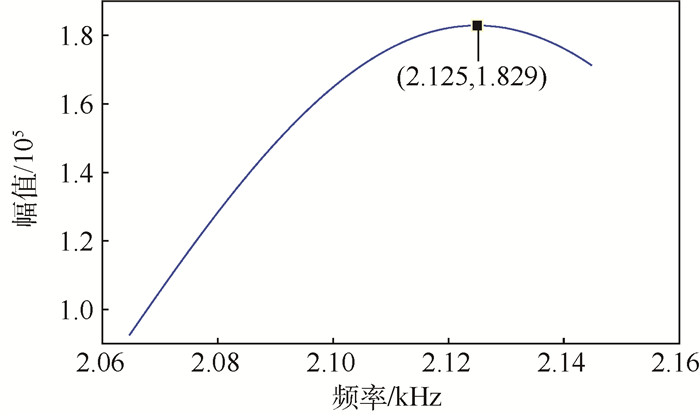 |
| 图 15 精捕CZT变换后的频谱 Fig. 15 Spectrum after fine acquisition by CZT |
| 图选项 |
5 结论 1) 实现了高动态数字中频信号模拟产生, 可设置任意加速度和加加速度的动态运动。
2) 仿真实现了改进的PMF+FFT粗捕获方法,结果表明加窗后的扇贝损失减小为原来的一半,大大缩短了捕获时间和提高了捕获性能。
3) 仿真实现了精捕获CZT变换,仿真结果表明在加速度为100g时能实现快速捕获且捕获精度在10 Hz以内,为后续的高动态跟踪奠定了良好的基础。
为使本文提出的高动态下粗捕获和精捕获算法能更好地适用于真实的动态环境下,仍需要后续使用GNSS导航仿真器GSS8000输出模拟真实的高动态GPS信号和射频前端输出高动态GPS中频信号。
参考文献
| [1] | 胡琼. 高动态及微弱GPS信号的捕获算法研究[D]. 上海: 上海交通大学, 2013: 16-30. HU Q.Research on the acquisition algorithm of high dynamic and weak GPS signal[D].Shanghai:Shanghai Jiao Tong University, 2013:16-30(in Chinese). |
| [2] | 孙函子. 高动态GPS接收机基带信号处理算法研究[D]. 南昌: 华东交通大学, 2010: 35-40. SUN H Z.High dynamic GPS receiver base band signal processing algorithm research[D].Nanchang:East China Jiaotong University, 2010:35-40(in Chinese). |
| [3] | LI Y, XI X L.Combining FFT and circular convolution method for high dynamic GPS signal acquisition[C]//20078th International Conference on Electronic Measurement and Instruments.Piscataway, NJ:IEEE Press, 2007:2159-2163. |
| [4] | 倪光华. 高动态环境下GPS C/A码信号的捕获与跟踪算法研究[D]. 西安: 西安电子科技大学, 2008: 45-49. NI G H.Research on acquisition and tracking algorithm of GPS C/A signal under high dynamic environment[D].Xi'an:Xidian University, 2008:45-49(in Chinese). |
| [5] | 周三文, 黄龙, 卢满宏. FFT在高动态信号捕获中的应用[J].飞行器测控学报, 2005, 24(2): 61–64. ZHOU S W, HUANG L, LU M H. Acquisition of high dynamic spread spectrum signals with FFT[J].Journal of Spacecraft TT & C Technology, 2005, 24(2): 61–64.(in Chinese) |
| [6] | 王仕成, 杨东方, 刘志国, 等. 一种高动态GPS软件接收机方案研究[J].宇航学报, 2009, 30(3): 1079–1085. WANG S C, YANG D F, LIU Z G, et al. Research on high dynamic GPS software receiver[J].Journal of Astronautics, 2009, 30(3): 1079–1085.(in Chinese) |
| [7] | 谢钢. GPS原理与接收机设计[M].北京: 电子工业出版社, 2009: 30-65. XIE G. Principles of GPS and receiver design[M].Beijing: Publishing House of Electronics Industry, 2009: 30-65.(in Chinese) |
| [8] | ELLIOT D K. Understanding GPS:Principles and applications[M].Norwood: Artech House Publisher, 1996: 50-70. |
| [9] | 齐巍, 常青, 张其善, 等. 高动态信号模拟器中的多普勒模拟算法[J].航空学报, 2008, 29(5): 1252–1257. QI W, CHANG Q, ZHANG Q S, et al. Arithmetic of Doppler simulation in high dynamic signal simulator[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1252–1257.(in Chinese) |
| [10] | 李恺冰. 高动态GPS信号捕获算法研究及仿真实现[D]. 哈尔滨: 哈尔滨理工大学, 2014: 19-23. LI K B.Research and simulation realization of high dynamic GPS signal capture algorithm[D].Harbin:Harbin University of Science and Technology, 2014:19-23(in Chinese). |
| [11] | CHANSARKAR M M, GARIN L.Acquisition of GPS signals at very low signal to noise ratio[C]//Processing of ION NTM 2000.Manassas:the Institute of Navigation, 2005:731-737. |
| [12] | EEROLA V.Rapid parallel GPS signal acquisition[C]//Proceedings of ION GPS 2000.Manassas:The Institute of Navigation, 2000:810-812. |
| [13] | NUNES F D, LEI J M N.A new fast code/frequency acquisition algorithm for GPS C/A signals[C]//Vehicular Technology Conference, IEEE VTC.Piscataway, NJ:IEEE Press, 2003, 766-770. |
| [14] | 黄云青. 高动态GNSS信号快速捕获算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2014: 30-37. HUANG Y Q.Research on the fast acquisition algorithm of high dynamic GNSS signal[D].Harbin:Harbin Institute of Technology, 2014:30-37(in Chinese). |
| [15] | LIN D M.Comparison of acquisition methods for software GPS receiver[C]//Proceedings of ION GPS 2003.Manassas:The Institute of Navigation, 2003:71-79. |
| [16] | ZHENG Y Z, ZHANG Y X.An improved segmented match filters with FFT approach for GNSS signal acquisition[C]//20102nd International Conference on Computer Technology and Development of ICCTD.Piscataway, NJ:IEEE Press, 2010:425-428. |
| [17] | 罗和平, 邱蕾, 曾祥新. GPS软件接收机捕获方法研究[J].大地测量与地球动力学, 2011, 31(1): 147–151. LUO H P, QIU L, ZENG X X. Acquisition algorithm for GPS software receiver[J].Journal of Geodesy and Geodynamics, 2011, 31(1): 147–151.(in Chinese) |
| [18] | LIN Z H, SHUAI H G, YONG H.Improved fast Fourier transform processing on fast acquisition algorithms for GPS signals[C]//Proceeding of 9th International Conference on Electronic Measurement & Instruments.Piscataway, NJ:IEEE Press, 2009:4221-4224. |
| [19] | 丁康, 潘成颢, 李巍华. ZFFT与Chirp-Z变换细化选带的频谱分析对比[J].振动与冲击, 2006, 25(6): 9–12. DING K, PAN C H, LI W H. Spectrum analysis comparison between ZFFT and Chirp-Z transform[J].Journal of Vibration and Shock, 2006, 25(6): 9–12.(in Chinese) |
