超奈奎斯特(FTN)传输技术是一种高频谱效率的传输方式，相较于传统信号可以用更高的速率传递信息，适用于频谱资源有限的系统，有望在5G通信中投入使用。1975年，Mazo^[1]提出了FTN信号传输模型，并且理论上证明了使用二进制相移键控(BPSK)调制和sinc函数脉冲成型时，FTN信号传输速率可以在传统正交信号的基础上加速25%，同时保持信号码元最小欧氏距离不变，理论误码性能不受影响。Anderson等^[2]在此基础上证明若使用滚降系数为30%的升余弦函数成型脉冲代替sinc函数成型脉冲，在码元最小欧氏距离不变条件下传输速率最多可增加42%。但是在实际应用时，复杂度有限的接收机不能完全消除FTN信号中无限长度码间串扰给系统误码率(BER)带来的损失。因此，设计FTN接收机时需要综合考虑系统误码率和复杂度这2个相互制衡的因素。
目前针对FTN信号有不同的均衡算法。Anderson和Prlja等^[3-6]提出了Ungerboeck模型下^[7-10]基于最大后验概率检测的M-BCJR算法。在M-BCJR算法中，前向量度和后向量度被用于搜索后验概率最大的路径。基于最大后验概率的算法可以在很大程度上消除码间串扰对误码率的影响，然而由于需要在篱状图上同时搜索出前向路径和后向路径，接收机的运算量大。韩国Baek等^[11]针对FTN信号码间串扰的特性提出了基于矩阵分解的部分判决反馈均衡算法。FTN信号的均衡还可以用预编码的方式实现^[12-13]。基于矩阵分解的算法运算复杂度较低，但系统的误码率受成型脉冲升余弦滚降系数的影响。
软输出维特比算法(SOVA)^[14]是复杂度介于BCJR和矩阵分解之间的一种算法，采用了残余码间串扰消除技术^[15]后，可以得到非常接近无码间串扰的正交信号的误码率。本文基于SOVA算法提出针对FTN信号的低复杂度算法，通过设置一个中止标准，动态地调整回溯比较次数，同时统计不影响误码率的最小回溯深度分布，设定回溯路径长度经验值。实际工程应用中，算法根据统计经验值裁剪回溯路径长度。本文算法可降低回溯过程的比较运算次数，也可以减少接收机所需的寄存器数目和延时。
1 系统模型 经过星座映射和脉冲成型的FTN信号为

(1)

式中:y(t)为第t时刻接收端采样获得的信号；L为传输码元总长度; a_n为第n时刻发送端传输的码元，使用BPSK调制，a_n的取值是1或-1;h(t-nτT)为对应第n时刻码元的成型脉冲，其中T代表码元周期, τ在0至1之间取值，代表FTN信号的加速系数。在奈奎斯特正交条件得到满足时，τ=1，此时不同时刻的信号是正交的。即第n时刻的信号和第k时刻的信号满足：

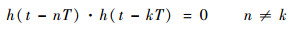(2)

而在FTN传输条件下，τ < 1。此时奈奎斯特第一定律中的正交条件不再满足，不同时刻的码元不可避免地发生了码间串扰，成为FTN信号。FTN信号相对奈奎斯特正交信号传输加速1/τ倍。经过加性高斯白噪声信道后，接收端信号为

(3)

式中：n(t)为加性高斯白噪声，经过接收端匹配滤波后的信号为

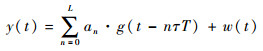(4)

式中:g(t)=h(t)?h^*(-t)，为升余弦成型脉冲; w(t)=n (t)?h^*(-t), 为经过匹配滤波后的噪声。令t=nτT，信号表达式为

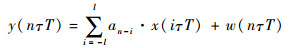(5)

式中：x(iτT)为在FTN信号中由成型脉冲混叠带来的第i阶码间串扰系数；l为维特比算法考虑的码间串扰长度。
2 低复杂度FTN信号接收算法 2.1 SOVA算法 用J_n表示第n时刻状态的累积路径量度，FTN信号的路径量度公式为^[16]

(6)

进入每个节点的2条路径都需要进行比较和选择，其中量度较大的路径被保留，称为“幸存路径”，量度较小的路径称为“竞争路径”。每一条幸存路径都对应有一条竞争路径。
SOVA算法需要判断各个时刻码元的对数似然比(LLR)。在初始化时，设篱状图上每个时刻码元的对数似然比为无穷大。在运行时，记录各状态的路径量度差值。进入一个状态的2条路径的量度分别为J₁(t, S)和J₂(t, S)，其中J₁属于幸存路径，J₂属于竞争路径，则J₁(t, S) > J₂(t, S)。2条路径量度差值为Δ(t, S)=J₁(t, S)-J₂(t, S)。幸存路径和竞争路径的译码结果分别是u_i⁽¹⁾和u_i⁽²⁾。在t时刻对数似然比的值为

(7)

式中：δ为SOVA算法在篱状图上的回溯深度，δ=6(l+1)。
SOVA算法的复杂度是O(SLδ)，因此每时刻状态数S、传输码元总长度L和回溯深度δ是影响算法复杂度的3个主要因素。减少SOVA算法考虑的码间串扰长度会降低最大似然路径的判决精度。传输码元总长度不由接收机决定。所以在不增加误码率的前提下减少算法的回溯深度对减少接收机复杂度十分重要。
2.2 本文提出的算法 在FTN接收机中，第t时刻的幸存路径在第t′时刻的状态为

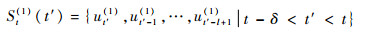(8)

第t时刻的竞争路径在第t′时刻的状态为

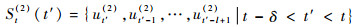(9)

FTN信号在幸存路径和竞争路径上的状态均由连续l位码元的译码结果确定，若{u_i⁽¹⁾=u_i⁽²⁾|?i?[t′-l+1, t′]}，则S_t⁽¹⁾(t′)=S_t⁽²⁾(t′)，即认为幸存路径和竞争路径已经合并，作为中止比较操作和对数似然比更新的条件。由于?t, S_t⁽¹⁾(t)=S_t⁽²⁾(t)，可得

(10)

即t时刻的幸存路径和竞争路径在t-1到t-l+1时刻会给出相同的判决结果，不需要比较。本文提出的算法对于t时刻的状态直接从t-l时刻的路径判决值开始回溯，回溯比较次数K和比较需要的回溯深度δ′的关系为：K=δ′-l+1。
算法步骤表示如下：
1) 确定t时刻的幸存路径量度J₁(t)和竞争路径量度J₂(t)，计算第t时刻的路径量度差值Δ_t=J₁(t)-J₂(t)。
2) 从t′=t-l时刻开始，沿幸存路径和竞争路径向前回溯，如果2条路径判决结果不同，即u_t⁽¹⁾(t′)≠u_t⁽²⁾(t′)，则进行更新操作：LLR(t′)=min{Δ_t′, Δ_t}。
3) 判断幸存路径和竞争路径是否连续l次判决都给出同样的结果，即{u_i⁽¹⁾=u_i⁽²⁾|?i?[t′, t′+l-1]}。
4) 如果步骤3) 满足，结束本轮幸存路径和竞争路径的回溯，释放竞争路径占用的寄存空间，此时回溯比较次数记为K；否则继续执行步骤2), 直到两条路径回溯深度到达δ。
在SOVA算法和本文提出的回溯比较次数可调算法(下文记作modified-SOVA-1算法)中，幸存路径和竞争路径要经过逐位的比较过程以更新对数似然比。但本文提出的算法通过步骤3) 在幸存路径和竞争路径满足回溯中止条件时提前结束回溯过程，减小了比较和似然比更新操作次数。
在硬件实现时回溯路径长度决定所需寄存器数目。因此本文在回溯比较次数可调算法的基础上提出直接截短回溯深度算法(下文记作modified-SOVA-2算法)。预设概率门限ε，根据统计出的每一个时刻比较次数K(对应需要的回溯深度为δ′)的统计分布，归纳出一个固定的回溯深度经验值，满足P(δ′≤)≥1-ε。算法将回溯深度由δ直接截短为。modified-SOVA-2算法可以减少回溯比较次数和查找表规模，既降低运算量也节省存储资源，同时降低译码延时，便于硬件应用。
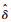
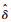
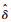
3 性能分析与仿真 3.1 算法复杂度分析 基于最小均方误差估计(MMSE)和矩阵QR分解的部分判决反馈均衡(DFE)算法、BCJR算法、SOVA算法和本文提出的基于SOVA算法的低复杂度接收算法(modified-SOVA-1和modified-SOVA-2) 均可用于FTN信号的均衡。DFE算法需要N²+N(N+1)/2+N次乘法运算，N代表DFE算法的矩阵块的规模。由于矩阵的规模N小于FTN信号码元总长度L，所以DFE算法拥有较低的复杂度，但是DFE算法误码率受到成型脉冲升余弦系数影响。BCJR算法需要计算每个时刻每个状态的前向量度和后向量度，至少需要6LS次乘法运算，复杂度为SOVA算法的3倍。SOVA算法的误码率低于DFE算法，复杂度低于BCJR算法；modified-SOVA算法的误码率相对SOVA没有恶化，而复杂度有进一步降低。算法回溯过程的复杂度取决于回溯深度平均值δ′和回溯比较次数平均值K。本节统计了FTN信号在使用modified-SOVA-1算法时回溯比较次数分布规律。理论上FTN信号人为引入的码间串扰的长度是无限的，l取值过小会影响接收端的误码率；l取值过大则系统复杂度指数上升，为了折衷误码率和复杂度，在仿真中取l=4。由于l=4，幸存路径和竞争路径出现连续4个相同的结果时才能结束回溯过程，比较次数至少为5，对应回溯深度为8。l=4时SOVA算法的回溯深度δ=30。本节仿真使用的传输码元总长度L=5×10⁵。表 1为SNR=3 dB时, τ=9/10，5/6的FTN比较次数和回溯深度分布。
表 1 SNR=3 dB时, 不同参数τ的FTN信号比较次数和回溯深度分布 Table 1 Backtracking comparison number and depth distribution for FTN signal with coefficient τ when SNR=3 dB

K	τ=9/10		τ=5/6
	δ′	δ′占比/%	δ′	δ′占比/%
5	8	89.43	8	81.57
6	9	2.76	9	4.86
7	10	2.66	10	4.48
8	11	2.36	11	3.73
9	12	2.03	12	2.73
10	13	0.30	13	0.95
11	14	0.20	14	0.65
12	15	0.12	15	0.43
13	16	0.08	16	0.25
14	17	0.02	17	0.16
15	18	0.01	18	0.09
16	19	0.01	19	0.05
17	20	0.01	20	0.03
18			21	0.02
19			22	0.01
20			23	0.01

表选项






图 1分别为使用modified-SOVA-1算法时，参数τ=9/10和τ=5/6(相对奈奎斯特正交信号分别加速10%和20%)的FTN信号在不同信道比条件下传输，回溯比较次数的统计结果。在2种情况下，FTN信号回溯深度和比较次数均集中于δ′≤13和K≤10的部分。其中K=5、δ′=8, 占比均超过了80%，而K > 10、δ′ > 13出现的概率不足5%。加速10%的FTN信号平均回溯比较次数K=5.28(对应回溯深度δ′=8.28)，加速20%的FTN信号平均回溯比较次数为K=5.534 9(对应回溯深度δ′=8.534 9)。由图 1可知，比较次数的平均值K随着信噪比的提高而减小，趋近于K=5。

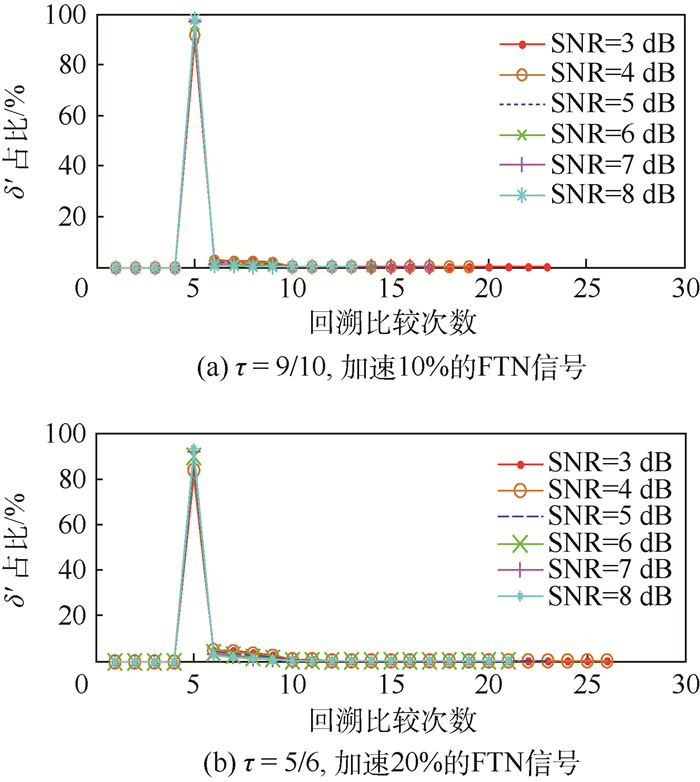图 1 FTN信号在不同信噪比条件下modified-SOVA-1算法回溯比较次数分布 Fig. 1 Backtracking comparison number distribution for FTNsignal under different SNRs by modified-SOVA-1 algorithm

图选项

表 2为SOVA算法和modified-SOVA-2算法在回溯过程中的比较操作次数。在信噪比为3 dB时，加速10%的FTN信号的回溯比较次数降为SOVA的17.6%，加速20%的FTN信号的回溯比较次数降为SOVA的18.4%。大信噪比条件下FTN信号回溯过程比较次数最多可降至SOVA算法的1/6。
表 2 SOVA和modified-SOVA-2算法的回溯比较次数 Table 2 Backtracking comparison number in SOVA and modified-SOVA-2 algorithms

算法	回溯比较次数
SOVA	LSδ
modified-SOVA-2	LS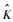

表选项






modofied-SOVA-2算法根据modified-SOVA-1算法对回溯比较次数分布的统计结果，截短回溯路径长度至新的经验值。算法回溯比较操作次数由LSδ降为LS，回溯路径所需寄存器个数由Sδ降为S，延时由δ降为。由表 1，可以看到超过90%的回溯比较次数小于10，因此modified-SOVA-2算法可将定为5~10之间，此时回溯比较次数降为原先的1/6~1/3，回溯路径所需寄存器资源降为原先的26%~43%，延时由30个码元降为8~13个码元。
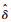
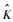
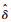
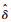
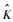
3.2 算法误码率分析
3.2.1 modified-SOVA-1算法误码率 图 2分别为参数为τ=9/10和τ=5/6的FTN信号在使用BPSK调制和滚降系数α=0.1的平方根升余弦成型脉冲，并经过加性高斯白噪声信道时，不同均衡算法下的误码率。图中各算法曲线为10次仿真所得误码率结果的平均值。

图 2 FTN信号在不同算法下的误码率 Fig. 2 BERs for FTN signal by different algorithms

图选项

图 2中，VA表示硬输出维特比算法，QR-DFE代表基于QR分解的判决均衡反馈算法。可以看出在图 2中，回溯比较次数经过调整的modified-SOVA-1算法的误码率曲线均与SOVA算法的误码率曲线重合，表明降低回溯比较次数没有恶化本文算法的误码率。

3.2.2 modified-SOVA-2算法误码率 表 1中显示的modified-SOVA-1算法中每个时刻实际回溯比较次数大多分布在10次以下，对应所需的回溯路径长度不超过13，在硬件实现时可以直接对回溯路径长度进行截短。图 3分别给出了参数为τ=9/10和τ=5/6的FTN信号在使用BPSK调制和滚降系数α=0.1的平方根升余弦成型脉冲，并经过加性高斯白噪声信道，使用modified-SOVA-2算法，在不同回溯路径长度下的误码率。图中不同长度的截短回溯路径条件下的误码率曲线为进行10次仿真后误码率结果的平均值。

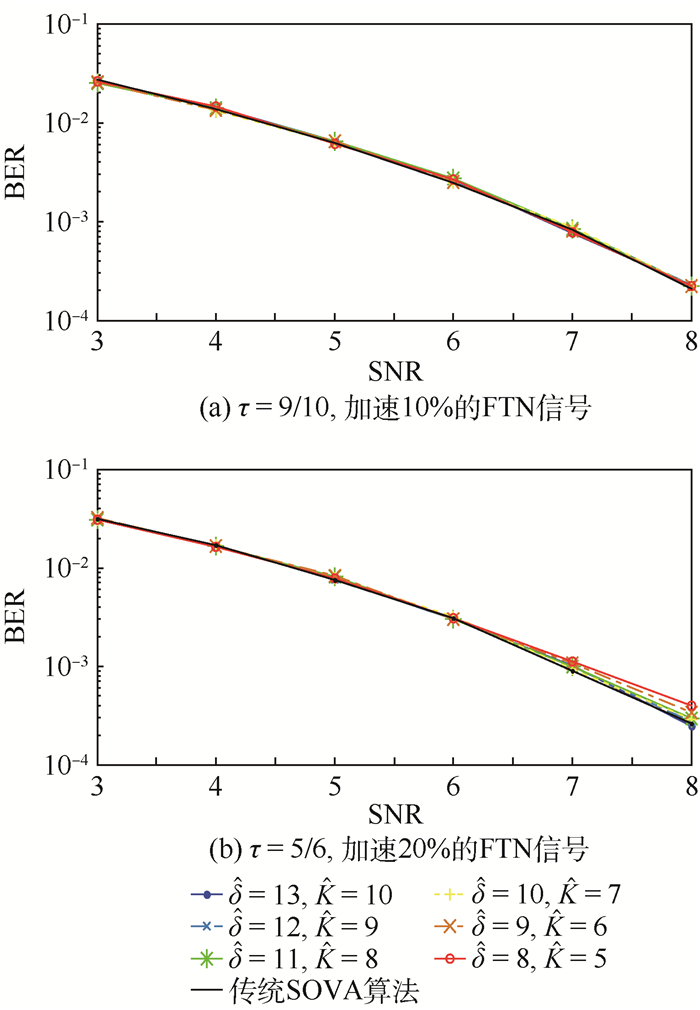图 3 FTN信号在不同回溯路径长度/比较次数下的误码率 Fig. 3 BERs for FTN signal under different backtracking lengths/numbers of comparison

图选项

从图 3中可以看到，在小信道比条件下，经过截短的回溯路径长度对FTN信号均衡误码率几乎没有影响；在大信道比条件下，随着截短后回溯路径长度的增加，modified-SOVA-2算法误码率结果和SOVA算法的误码率结果逐渐接近。对于加速10%的FTN信号，截短回溯路径长度不小于8，回溯比较次数不小于5时modified-SOVA-2算法误码率和SOVA算法相同。取=8, =5，回溯过程比较次数和回溯路径所需寄存器资源分别降为SOVA算法的17%和27%，延时由30个码元降为8个码元。对于加速20%的FTN信号，截短回溯路径长度不小于10，回溯比较次数不小于7时modified-SOVA-2算法误码率和SOVA算法相同。取=10, =7，回溯过程比较次数和回溯路径所需寄存器资源分别降为SOVA算法的23%和33%，延时由30个码元降为10个码元。因此modified-SOVA-2算法在降低算法比较次数的同时减少了存储空间资源消耗和延时。
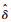
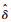
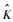
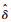
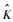
4 结论 1) 本文针对FTN信号提出了回溯比较次数可调算法(modified-SOVA-1)，统计了FTN信号在篱状图中的回溯深度比例，以此基础设计回溯中止条件，降低接收机比较次数。
2) 在此基础上提出的直接截短回溯深度算法(modified-SOVA-2)，在FTN信号相对加速10%和20%时将回溯过程比较次数降低至原先的17%和23%，同时减少了所需寄存器数目和延时。

参考文献

[1]	MAZO J E. Faster-than-Nyquist signaling[J].Bell Labs Tecnical Journal, 1975, 54(8): 1451–1462.
[2]	ANDERSON J B, RUSEK F, OWALL V. Faster-than-Nyquist signaling[J].Proceedings of the IEEE, 2013, 101(8): 1817–1830.DOI:10.1109/JPROC.2012.2233451
[3]	PRLJA A, ANDERSON J B, RUSEK F.Receivers for faster-than-Nyquist signaling with and without turbo equalization[C]//IEEE International Symposium on International Theory.Piscataway, NJ:IEEE Press, 2008:464-468.
[4]	ANDERSON J B, PRLJA A, RUSEK F.New reduced state space BCJR algorithms for the ISI channel[C]//IEEE International Symposium on Information Theory.Piscataway, NJ:IEEE Press, 2009:889-893.
[5]	ANDERSON J B, PRLJA A.Turbo equalization and an M-BCJR algorithm for strongly narrowband intersymbol interference[C]//International Symposium on Information Theory and its Applications.Piscataway, NJ:IEEE Press, 2010:261-266.
[6]	PRLJA A, ANDERSON J B. Reduced-complexity receivers for strongly narrowband intersymbol interference introduced by faster-than-Nyquist signaling[J].IEEE Transactions on Communications, 2012, 60(9): 2591–2601.DOI:10.1109/TCOMM.2012.070912.110296
[7]	RUSEK F, COLAVOLPE G, SUNDBERG C E W. 40 years with the Ungerboeck model:A look at its potentialities[J].IEEE Signal Processing Magazine, 2015, 32(3): 156–161.DOI:10.1109/MSP.2014.2374221
[8]	RUSEK F, LONCAR M, PRLJA A.A comparison of Ungerboeck and Forney models for reduced-complexity ISI equalization[C]//IEEE Global Telecommunications Conference.Piscataway, NJ:IEEE Press, 2007:1431-1436.
[9]	FORNEY G D. Maximum likelihood sequence estimation of digital sequences in the presence of intersymbol interference[J].IEEE Transactions on Information Theory, 1972, 18(3): 363–378.DOI:10.1109/TIT.1972.1054829
[10]	LONCAR M, RUSEK F. On reduced-complexity equalization based on Ungerboeck and forney observation models[J].IEEE Transactions on Signal Processing, 2008, 56(8): 3784–3789.DOI:10.1109/TSP.2008.920142
[11]	BAEK M S, HUR N H, LIM H.Novel interference cancellation technique based on matrix computation for FTN communication system[C]//IEEE Military Communications Conference.Piscataway, NJ:IEEE Press, 2014:830-834.
[12]	RINGH E.Low complexity algorithm for faster-than-Nyquist signaling:Using coding to avoid an NP-hard problem[D]. Stockholm:Royal Institute of Technology, 2013.http://www.academia.edu/10561060/A_doubly_distributed_genetic_algorithm_for_network_coding
[13]	NIE S Y, GUO M X, SHEN Y H.Precoding based on matrix decomposition for faster-than-Nyquist signaling[C]//5th International Conference on Electronics Information and Emergency Communication.Piscataway, NJ:IEEE Press, 2015:194-197.
[14]	HAGENAUER J, HOEHER P.A Viterbi algorithm with soft decision outputs and its applications[C]//IEEE Global Telecommunication Conference and Exhibition.Piscataway, NJ:IEEE Press, 1989:1680-1686.
[15]	LIVERIS A, GEORGHIADES C. Exploiting faster-than-Nyquist signaling[J].IEEE Transactions on Communications, 2003, 51(9): 1502–1511.DOI:10.1109/TCOMM.2003.816943
[16]	UNGERBOECK G. Adaptive maximum-likelihood receiver for carrier-modulated data-transmission systems[J].IEEE Transactions on Communications, 1974, 22(5): 624–636.DOI:10.1109/TCOM.1974.1092267