目前对于线缆耦合问题,主要从如下方面进行考虑和解决:① 设计预测,即针对实际使用中的各种线缆类型和线缆结构,分别研究建立其耦合模型 (如平直线束[3-5]、双绞线[6-8]、屏蔽层[9-11]等),从而实现对线缆耦合效应的设计和预测。② 安装规范,即对线缆系统的设计和安装提出相应的规范和要求,从而避免因人为原因导致的屏蔽失效或效能下降[12-13]。③ 实物测试,即通过对实际系统进行测试获取其电磁兼容特性,必要时设定相应的门限值要求,例如GJB 151B-2013[14]中的CS、RS类试验。
上述方法在实际使用中取得了良好的效果,但同样存在局限性:① 3种方法通常针对特定布线场景和外加场源的特性进行考虑,难以处理实际问题的多样性与随机性。例如,线缆设计预测时通常考虑的是远场辐射的均匀平面波;安装规范通常采用的是特性实验条件下测得的参考量值;实物测试或采用均匀平面波辐射,或采用注入法对外场进行等效。然而线缆布线路径具有很强的随机性,且布线中经历的场分布状态同样是复杂和未知的,因此很难保证设定的场景能够覆盖线缆实际使用中遇到的情况。② 3种方法均发生于线缆相关电子系统工作之前,并不能够实时反映系统真实工作状态下的线缆耦合情况。例如,当线缆在使用过程中遭到损伤或状态变化时,很难及时获知其当前耦合状态。
因此,本文提出一种利用线缆束中的非功能线缆作为监测线,在不影响设备正常工作的前提下,对功能线缆耦合到的干扰信号状态进行实时监测的方法。通过这种方法,可以实时跟踪线缆在实际使用中的耦合状态,避免了出现预料之外的外加场状态或者线缆本身状态的变化所可能导致的耦合问题。同时,监测系统的另一重要意义在于:其所采集的线缆耦合数据为线缆耦合相关地面试验的完善提供了丰富的样本,从而为其他研究工作提供有力支持。
1 实时监测方法原理与基本假设 机载线缆结构通常为在屏蔽层包裹下的由多根相同的平直线或者双绞线构成的线束。在外加场存在的条件下,线缆可能耦合到电磁干扰信号。在耦合量值较高时,干扰信号与功能信号叠加会导致功能信号波形的畸变,从而影响系统的正常工作。
由于影响线缆耦合的外场特性与布线路径具有很强的多样性与随机性,线缆耦合的准确预测十分困难。然而,同一线缆束中的2条线通常具有完全相同的结构参数,同时其外场分布和路径也是基本相同的,因此二者几乎具有完全相同的耦合特性[3]。这就意味着,可以通过从一条线 (监测线) 的耦合推算另一条线 (被测线) 耦合。这是本文所建立模型的基本假设。
另外,为了简化模型计算,本文作出其他2条假设,说明如下:
1) 单根被测线与监测线间建立的电流关系可推广至实际中多根被测线同时存在的情况。多线与单线相比,所增加的影响在于其他线的存在可能影响所研究的单线的传输线特征阻抗,但一方面这种影响量值较低;另一方面在本文中对单线特性进行测定时其他线是同时存在的,测得的参数中已计入其他线的影响。因此,这种假设是可以成立的。
2) 被测线终端负载为正实数,即为纯电阻。对于线缆中的成对线,本文方法测得的为其共模耦合量值,此时其等效阻抗通常接近于开路。而对于线缆中以屏蔽层为回路的单线,则其终端负载通常为开路或匹配状态。无论何种情况,终端负载均可近似用实数来描述。而虽有可能存在寄生电感电容,但其量值很难达到与特征阻抗比拟的程度,对本文方法影响很小。
基于上述假设,本文以单监测线和单被测线构成的线缆系统为例建立了其端口间电流关系。第2节推导中忽略了监测线与被测线同时存在所带来的耦合效应的影响。通过第3节建立的方法,该效应可以在线缆参数测试的过程中得到修正。
2 监测线-被测线端口电流数学关系 对于相同的监测线与被测线,若两线对应终端分别具有相同的负载,则监测线两端信号将与被测线完全相同。然而实际问题中,线束中可能存在多个需要监测的线缆对象,而各线的终端负载状态并不完全一样,或者存在未知的情况,难以将监测线终端调整到与被测线相同的状态。因此,在推算过程中必须针对不同终端负载下的耦合情况进行考虑。本文通过如下3步,建立了监测线-被测线端口电流数学关系,并将其转化为硬件可实现的信号流图形式。
2.1 不同负载条件下二端口网络电流的频域关系 本文选择线缆分析对象如图 1所示。假定监测线左右端口处的电流可知,分别为I10和I20,被测线左右端口处电流为I1x和I2x,则问题的关键在于得到由I10和I20推导I1x和I2x的数学关系。
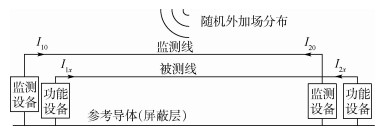 |
| 图 1 线缆耦合干扰实时监测方法原理 Fig. 1 Principle of real-time monitoring method of cable coupling interference |
| 图选项 |
由于监测线与被测线完全相同,因此可等效为相同的有源二端口网络,如图 2所示。
 |
| 图 2 监测/被测线缆系统二端口网络模型 Fig. 2 Two-port network model of monitored or monitoring cable system |
| 图选项 |
图 2中,被测线与监测线采用有源ABCD矩阵的形式表示如下:
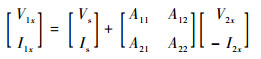 | (1a) |
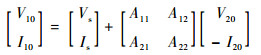 | (1b) |
式中:Vs和Is为由线缆耦合外加场所产生的等效源;V1x、V2x、I1x和I2x分别为被测线两端口处的电压和电流 (见图 2); 监测线两端口电压电流V10、V20、I10和I20满足同样的关系;Aij(i, j=1, 2) 为ABCD矩阵第i行第j列的元素。此处对二端口网络采用ABCD矩阵表示而不宜采用Z或Y矩阵,其原因在于:对于传输线系统,Z与Y矩阵元素在谐振频点可能出现极点,影响数值运算过程的稳定性。
为了保证两端监测设备的一致性,在监测设备设计中可令其输入阻抗为Z0。因此,监测线两终端负载均为Z0,被测线两端负载分别为Z1和Z2。因此,监测线左右端口处电压分别为V10=-I10Z0,V20=-I20Z0。代入式 (1b) 并通过推导可得I10、I20与Vs、Is关系如下:
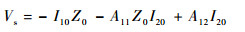 | (2a) |
 | (2b) |
待求量为被测线两端电流I1x、I2x,其终端负载分别为Z1和Z2,因此有V1x=-I1xZ1,V2x=-I2xZ2。代入式 (1a) 可得如下被测线终端参量关系:
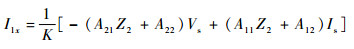 | (3a) |
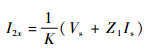 | (3b) |
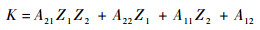 | (3c) |
将式 (2) 代入式 (3),可得以二端口网络参数表示的监测线-被测线终端电流关系如下:
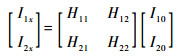 | (4) |
式中:
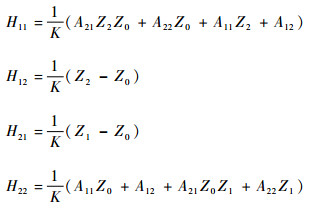 |
2.2 传输线的二端口网络频域模型 在式 (4) 中,若要由监测线终端电流推算被测线终端电流,二端口网络参量必须为已知。而实际使用中的线缆大多可以采用传输线理论模型[3]进行描述。一段线长为l的标准传输线ABCD矩阵如下:
 | (5) |
式中:β为波数,具有基本关系β=ω/v,ω为角频率,v为电磁波沿线传播的相速,v的量级与真空光速c=3×108 m/s相近,而由于介质层的存在,量值上v≤c;Zc为传输线特征阻抗,通常量级在几十至数百欧姆。Zc与v由线缆自身的内外径、介质的介电常数等参数决定,可通过测试获取 (详见第4节)。
将式 (5) 代入式 (4),可得由传输线特征参数描述的监测线-被测线终端电流关系为
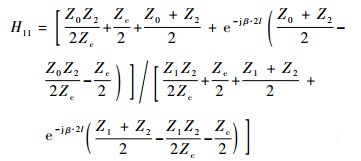 | (6a) |
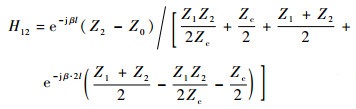 | (6b) |
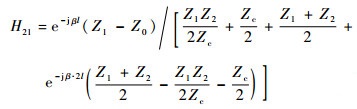 | (6c) |
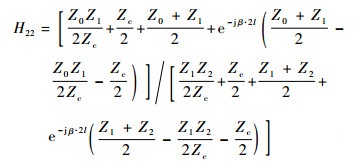 | (6d) |
2.3 端口电流关系的离散时间模型 式 (4) 和式 (6) 能够表征监测过程的频域数学关系,然而监测和被测信号本身均为时域信号,因此笔者希望能够将式 (6) 转化为离散时间模型[15],得出其信号流图,从而便于硬件实现。
根据式 (4),系统整体结构可表示为图 3。
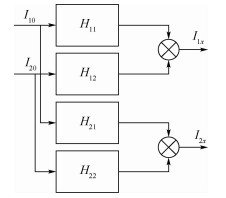 |
| 图 3 系统整体原理框图 Fig. 3 Principle diagram of whole system |
| 图选项 |
以H11子系统为例进行分析。根据H11表达式 (6a),令
 | (7a) |
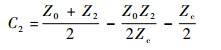 | (7b) |
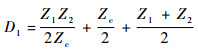 | (7c) |
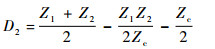 | (7d) |
因此,H11可表示为
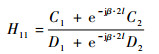 | (8) |
H11子系统框图如图 4所示 (以S1表示该系统的频域输出量,下文S2~S4同理)。
 |
| 图 4 H11子系统框图 Fig. 4 Block diagram for subsystem H11 |
| 图选项 |
由于Z0、Z1、Z2均为正实数 (纯电阻),则C1、C2、D1、D2为简单的实系数。由于e-jβ·2l(e-jω·2l/v) 项事实上代表大小为2l/v的时间延迟,其物理意义为信号从线一端发出后,到达另一端并反射回发出端所需要的时间。
在对系统进行时间离散的过程中,笔者希望时间延迟 (l/v和2l/v) 恰好为采样时间间隔ts的整数倍,然而由于实际线缆参数和可选择的晶振频率的限制,这一点很可能无法满足。对于不满足上述条件的延迟信号x(t-td),可将其表示为相邻两采样点处的插值。
假定td=Nts+tr(0≤tr < ts,N为整数),则y(t)=x(t-td)≈
 | (9) |
转化为离散时间关系如下:
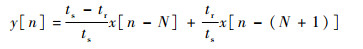 | (10) |
假定
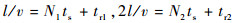
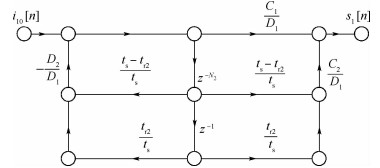 |
| 图 5 H11子系统信号流图 Fig. 5 Signal flow graph for subsystem H11 |
| 图选项 |
同理,对H12、H21 2个子系统也可得到其信号流图 (见图 6和图 7)。
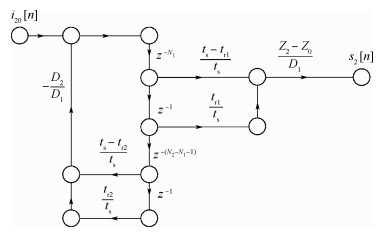 |
| 图 6 H12子系统信号流图 Fig. 6 Signal flow graph for subsystem H12 |
| 图选项 |
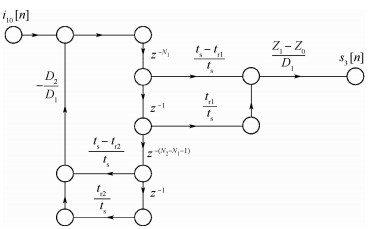 |
| 图 7 H21子系统信号流图 Fig. 7 Signal flow graph for subsystem H21 |
| 图选项 |
令
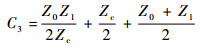 | (11a) |
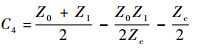 | (11b) |
则H22表示为
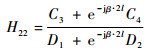 | (12) |
可以得到H22的信号流图 (见图 8)。
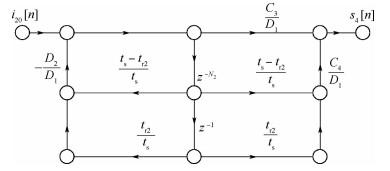 |
| 图 8 H22子系统信号流图 Fig. 8 Signal flow graph for subsystem H22 |
| 图选项 |
至此,可以得到系统可实现的离散时间模型,并以信号流图的形式给出,从而可以很方便地采用FPGA或DSP等通用数字处理芯片进行实现。
3 监测线-被测线间耦合效应修正 在第2节中,假定监测线与被测线之间不存在耦合效应,即在计算监测线 (被测线) 的网络矩阵参数时未考虑另一线的存在对矩阵量值的改变。因此,本节讨论考虑耦合效应情况下如何对方法进行修正的问题。
为便于数值运算,第2节中采用ABCD矩阵进行方法的描述。但在本节中,耦合效应更适合从阻抗矩阵 (Z矩阵) 出发进行讨论。考虑耦合效应,可将监测线与被测线视为完整的四端口网络,结合二者的对称性,构建Z矩阵形式的端口关系如下:
 | (13) |
式中:
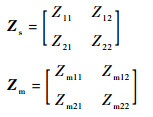 |
其中:Zs为监测线或被测线的自阻抗矩阵;Zm为两线间的互阻抗关系。
由式 (13) 可得到如下关系:
 | (14) |
从方程式 (14) 出发,结合负载的电流电压关系,即可推导得到所需的监测线-被测线电流关系。因此,从数学意义上,线缆系统的影响可完全体现在式 (14) 的Z矩阵关系中。而忽略耦合效应条件下,类似的关系应表示为
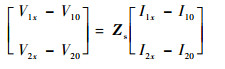 | (15) |
比较式 (14) 与式 (15),可以看出监测线-被测线间耦合的影响体现为需要在阻抗矩阵Zs的基础上减去一个耦合阻抗矩阵Zm。在物理上,这意味着需要用新的传输线系统替换原有的传输线系统。而且这种替换不仅对Z参数成立,对其他参数矩阵形式将同样成立。已知Zs代表单根监测线或被测线与地平面形成的传输线系统。而Zs-Zm同样可以找到明确的物理意义。
如图 9所示,在两线之间建立左右2个端口,其他连接方式不变。此时从原本的四端口网络的角度,存在I1x=-I10,I2x=-I20。且由于两线对称,可得到V1x=-V10,V2x=-V20。代入式 (13),可得
 |
| 图 9 修正特性参数测试所用的测试端口 Fig. 9 Port for measurement of modified characteristic parameters |
| 图选项 |
 | (16) |
进而可得
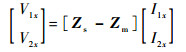 | (17) |
同时,对于图 9测试状态所标定的2个端口,其电压电流可表示为
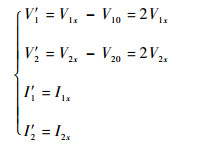 | (18) |
对图 9中的线缆系统,假定其阻抗矩阵为Zx,即存在
 | (19) |
将式 (18) 代入式 (19),并与式 (17) 比较可得Zs-Zm=Zx/2,因此Zs-Zm量值为图 9所示线缆系统特征阻抗的一半,其代表的物理意义是其中一条线与两线间的虚拟地平面间构成的传输线系统。只需测定图 9中两线构成的传输线系统的特征阻抗Z′c和相速v,然后取Z′c/2和v替换本节所有公式中的特征阻抗Zc和相速v,即可消除监测线-被测线间耦合效应所带来的影响。
值得注意的是,线间耦合效应的修正更多的体现在特征阻抗Zc上。对于相速v,理论上由于介质层的存在,线间耦合效应的确会改变其量值,但在实际中这种改变往往非常微小。在本文实验的精度下,相速v的变化几乎观测不到。
4 测试验证 为验证本文方法的有效性,搭建了线缆平台进行测试 (见图 10)。在该平台中,采用信号源注入激励模拟外加场,采用示波器模拟可能采用的监测终端设备。由于示波器采样率通常远高于实用中AD转换器及数字系统的处理速率,在数据处理中会将示波器采样数据进行减采样处理,以模拟实际监测装置的性能。
 |
| 图 10 四芯传输线系统验证模型 Fig. 10 Validation model of four-wire cable system |
| 图选项 |
图 10中平台所使用的线缆为四芯屏蔽线。在本测试中,屏蔽层作为参考地;1#线为信号注入线,可在屏蔽层内产生模拟干扰场;2#线模拟监测线,其左右终端外接51 Ω电阻 (市场上可买到的最接近50 Ω的贴片电阻),在进行测试时,示波器50 Ω内阻与之并联,因此线两端等效电阻为25.24 Ω;3#线模拟被测线,其两终端各串联100 Ω电阻后与示波器相连,因此等效电阻为150 Ω;4#线悬空不使用。线缆长度l=2 m。
对建模所用的传输线系统参数进行测试。首先截取一段1 m长的线缆样本,按第3节的方法将2#线 (监测线) 和3#线 (被测线) 的一端进行短路,然后在另一端口处利用阻抗分析仪测试其输入阻抗,得到幅度和相位结果如图 11所示。
 |
| 图 11 端口阻抗幅度和相位特性测试结果 Fig. 11 Measured results of port impedance magnitude and phase characteristics |
| 图选项 |
根据传输线理论,短路线输入阻抗公式为
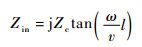 | (20) |
在极低频条件下,传输线输入阻抗可近似为
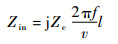 | (21) |
式中:f为频率。已知测试样本线长l=1 m,利用图 11(a)中幅度特性极低频段的斜率数据,可以得到
 | (22) |
同时,相位的第一零点 (即第一谐振点)f1符合如下关系:
 | (23) |
从图 11(b)中可读出f1=42.5 MHz,因此可求得v=1.7×108 m/s。结合式 (22) 可求得该系统的特征阻抗Z′c=104.55 Ω。因此,在建模分析应中采用参数为
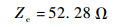 | (24a) |
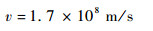 | (24b) |
此处若不采用图 9的测试方法,而是直接建立线终端对地端口的话,对应求得Zc=54.33 Ω,v=1.7×108 m/s。与式 (24) 相比,特征阻抗Zc有一定误差,但并不明显,因此可知线间耦合所带来的影响在本例中相对较小。
获取特征阻抗和相速参数后,按照图 10搭建验证线缆系统并进行测试。系统照片如图 12所示。
 |
| 图 12 验证系统实物图 Fig. 12 Photo of validation system |
| 图选项 |
选定信号源波形为1 V、10 MHz的方波,示波器直接测试得到监测线两端电压波形如图 13所示。
 |
| 图 13 监测线左右端口电压波形 Fig. 13 Voltage waveforms on left and right ports of monitoring wire |
| 图选项 |
由于本文方法的输入和输出变量均为端口电流,因此需要将监测线的电压波形转化为电流波形。本案例中,线缆长度l=2 m,因此线缆单程传输延迟时间l/v=11.765 ns。示波器采样率为20 GSa/s (Sa/s为采样率的单位,即每秒采集样本 (sample) 的数量),为模拟实际可能的硬件性能,通过数值减采样将其降低为100 MSa/s (对应采样时间间隔ts=10 ns)。然后按第2节所述方法可作出系统信号流图,采用MATLAB程序进行实现,最终计算出被测线终端电流波形。模型计算和实测结果对比如图 14所示。
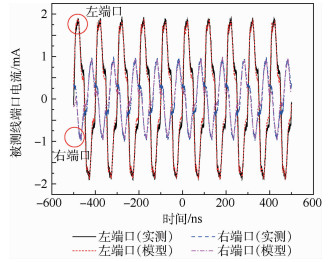 |
| 图 14 被测线左右端口电流波形 (实测与模型) Fig. 14 Current waveforms on left and right ports of monitoring wire (actual measurement and model) |
| 图选项 |
从图 14可以看出,采用本模型所获得的被测线左右端口电流波形与实测相比吻合良好,脉冲波形的峰值处预测误差最大值不超过6%(峰值误差/峰值高度)。通常情况下,该精度足以满足要求。
5 结论 1) 本文提出一种实时监测外界瞬态电磁信号的方法。主要思路是通过对多芯线缆中某一非功能线终端信号的监测,推算功能线终端的耦合情况。
2) 本文方法主要优势在于监测过程不影响设备正常工作,且具有实时性。
3) 通过对一条四芯屏蔽线的测试验证了本文方法的有效性和精度,同时证明监测线端口信号状态能够正确反映被测线耦合情况。
4) 针对加装监测系统可能带来的部分重量和成本的增加,可以将部分线缆束本身包含备用线,直接作为监测线使用;同时可以区分线缆链路的敏感程度,只对部分易受扰的线缆加装该监测系统。
参考文献
| [1] | 苏东林, 谢树果, 戴飞, 等.系统级电磁兼容性量化设计理论与方法[M].北京:国防工业出版社, 2015:125. SU D L, XIE S G, DAI F, et al.The theory and method of quantification design on system-level electromagnetic compatibility[M].Beijing:National Defense Industry Press, 2015:125(in Chinese). |
| [2] | PAUL C R.Introduction to electromagnetic compatibility[M].2nd ed. Hoboken, NJ:Wiley, 2006:503-557. |
| [3] | PAUL C R.Analysis of multiconductor transmission lines[M].2nd ed.New York:Wiley-IEEE, 2007:89-109. |
| [4] | WANG Y M, SU D L, CHEN W Q.Analysis of field-to-transmission line coupling in the airplane[C]//ISAPE 20088th International Symposium.Piscataway, NJ:IEEE Press, 2008:1052-1055. |
| [5] | LI B, WANG J J, SONG X W, et al.Equivalent circuit model of frequency-domain responses with external field[C]//2015 IEEE International Symposium on Electromagnetic Compatibility.Piscataway, NJ:IEEE Press, 2015:761-766. |
| [6] | PIGNARI S A, SPADACINI G. Plane-wave coupling to a twisted-wire pair above ground[J].IEEE Transactions on Electromagnetic Compatibility, 2011, 53(2): 508–523.DOI:10.1109/TEMC.2010.2061855 |
| [7] | JULLIEN C, BESNIER P, DUNAND M, et al. Advanced modeling of crosstalk between an unshielded twisted pair cable and an unshielded wire above a ground plane[J].IEEE Transactions on Electromagnetic Compatibility, 2013, 55(1): 183–194.DOI:10.1109/TEMC.2012.2206599 |
| [8] | SPADACINI G, PIGNARI S A. Numerical assessment of radiated susceptibility of twisted-wire pairs with random nonuniform twisting[J].IEEE Transactions on Electromagnetic Compatibility, 2013, 55(5): 956–964.DOI:10.1109/TEMC.2012.2235446 |
| [9] | 张莉. 同轴电缆屏蔽性能测量方法的比较[J].电线电缆, 2014(6): 21–23. ZHANG L. Comparison of coxial cable shielding effectiveness measurement methods[J].Electric Wire & Cable, 2014(6): 21–23.(in Chinese) |
| [10] | 齐磊, 崔翔, 谷雪松. 屏蔽电缆转移阻抗和转移导纳的宽频测量[J].电波科学学报, 2007, 22(4): 696–701. QI L, CUI X, GU X S. Wide-frequency measurement of transfer impedance and transfer admittance of shielded cable[J].Chinese Journal of Radio Science, 2007, 22(4): 696–701.(in Chinese) |
| [11] | IEC.Metallic communication cable test methods:CEI/IEC 62153-4-620066[S].Geneva:IEC, 2006. |
| [12] | Boeing Design Manual.Wiring design, assembly and installation:BDM-7124[S].Seattle:Boeing, 1991. |
| [13] | 陈穷, 蒋全兴, 周开基, 等. 电磁兼容性工程设计手册[M].北京: 国防工业出版社, 1993: 424-444. CHEN Q, JIANG Q X, ZHOU K J, et al. Electromagnetic compatibility engineering design manual[M].Beijing: National Defense Industry Press, 1993: 424-444.(in Chinese) |
| [14] | 中国人民解放军总装备部. 军用设备和分系统电磁发射和敏感度要求与测量: GJB 151B-2013[S]. 北京: 中国标准出版社, 2013. PLA General Equipment Department.Electromagnetic emission and susceptibility requirements and measurements for military equipment and subsystems:GJB 151B-2013[S].Beijing:Standards Press of China, 2013(in Chinese). |
| [15] | OPPENHEIM A V, SCHAFER R W, BUCK J R.Discrete-time signal processing[M].2nd ed.Upper Saddle River, NJ:Prentice Hall, 1998:340-438. |
