系统维修可大致分为事后维修和预防维修,随着传感器工业的发展,在传统的定时预防维修基础上又发展出了视情维修。视情维修是利用传感器、测试设备等,持续或非持续地获取系统状态,并根据系统实际情况来开展维修[5]。目前大多数视情维修研究主要面向单一部件系统,利用连续随机过程来建立系统可靠性模型,并充分利用检测信息合理安排维修策略[6-8]。对于多状态系统的可靠性分析与维修优化,大部分研究是面向多部件系统,且优化过程中通常不考虑系统检测,仅基于系统自身可靠性特性来建模分析系统在不同维修策略下的运行成本率,从而优化维修相关参数[9-15]。以上可知,视情维修优化的研究对象模型通常不是多状态系统,且多为单一部件系统,而多状态系统的维修优化通常不考虑系统检测。因此,考虑检测下的多部件多状态系统的维修优化研究具有较大意义。
一些多状态维修优化的研究虽然涉及了系统检测[16-22],但这些研究中大部分没有考虑系统检测误差,认为检测结果可完全代表系统状态,称为完美检测(perfect inspection);然而在实际中,由于设备误差、检测对象不完全,测量方式存在固有误差、数据分析延时、人为失误等原因,通常会导致检测不全面,或检测结果带有误差,称为非完美检测(imperfect inspection) [21]。文献[21]虽然考虑了非完美检测,但是研究对象为单一部件多状态系统。另外,其中一些文献仅考虑完美维修(perfect repair),即置换(维修后恢复如新),而未考虑非完美维修(imperfect repair)[20, 22] (非完美维修:维修后的部件状态介于全新状态和维修前旧状态之间[23])。
本文面向多部件多状态系统,采用随机滤波方法[24-26]有效融合可靠性模型和非完美检测数据,同时考虑非完美维修,在仿真环境中使用遗传算法(GA)实现检测和维修策略优化。
1 问题描述 考虑多部件多状态系统,系统可靠性随着时间推进逐渐发生退化。在系统运行时,故障发生前可采取预测性维修;系统故障时,采取事后维修。系统运行过程中采取周期性检测,检测数据从一定程度可反映出系统部件状态。维修、检测以及系统故障均会花费一定成本。最终目的是通过优化检测周期、系统维修时机以及维修时所采取的具体维修类型(置换或非完美维修),以降低系统长期运行成本率。
下文分别对多状态系统、可靠性模型、检测模型、维修与成本模型及维修策略模型分别进行阐述。
1.1 多状态系统描述 考虑一个由两部件组成的多状态并联系统,如图 1所示。
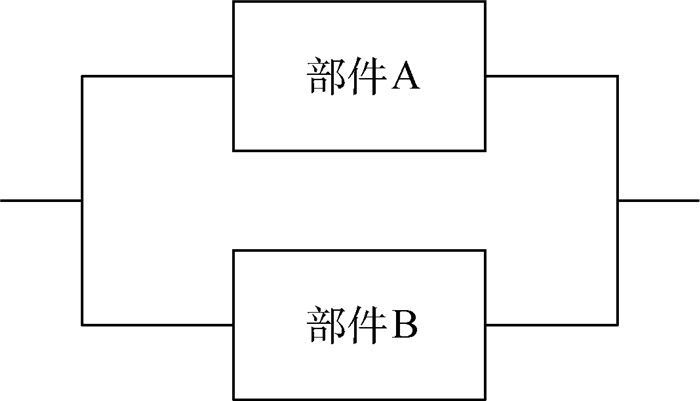 |
| 图 1 两部件并联系统 Fig. 1 Two-component parallel system |
| 图选项 |
该系统为广义系统,较为通用,具体可以代表制造系统、流网络(flow network)系统等。用一组有限离散变量1, 2, …,m表示系统中部件的状态。假定状态1代表部件全新状态,状态m代表彻底失效或故障,中间状态代表系统部分失效或性能退化。系统中的两部件互为备份,当某一部件发生故障时,系统由另一部件独立支撑仍可继续工作,但此时独立工作部件会承受更高的工作强度或受到故障部件所带来冲击伤害导致其退化加剧,具体表现为失效率增加,当两部件全部故障时系统发生灾难性故障,停止运行,工作人员立刻可知并对系统采取事后维修。系统运行过程中对系统采取非完美周期性检测,检测结果可反映部件状态,但是带有一定误差。
对于系统维修,分为系统故障后的事后维修以及故障前的预测性维修,维修对象为系统两部件,具体的维修类型分为非完美维修和置换。事后维修的维修方式为置换;预测性维修的维修方式为置换/非完美维修二选一。
事后维修属于非计划维修,除了置换部件的成本外,系统灾难性故障造成的效果十分恶劣,会造成较大损失,因此还需考虑其他损失带来的额外成本,称为惩罚成本。相对于事后维修,预测性维修可有效避免系统故障并且具有较好的经济性。本文总共考虑以下几类成本:① 检测成本;② 置换成本;③ 非完美维修成本;④ 惩罚成本。
关于系统模型的其他前提假设如下:
1) 本文考虑离散时间,时间间隔为Δt=100h,系统的退化、检测与维修均发生在离散时间点。
2) 初始时刻t=0,两部件为全新状态。
3) 两部件为相同部件,互为备份。
4) 状态空间1, 2, …, m中m=4。
5) 部件退化具有单向性,不存在维修时,部件从状态i仅可转移到状态j,其中j≥i。
6) 部件退化转移概率满足指数分布,失效率用λ(t)表示。考虑故障相关性,λ(t)与t时刻另一部件的故障次数k有关,当k不变时,失效率为常数。
7) 非完美维修后部件状态有所改善,失效率不变。
8) 采用周期检测,每隔时间T对部件A和部件B进行检测。
9) 系统维修所花费的时间与离散时间步长相比可以忽略,即认为维修不花费时间。
本文最终目的是通过系统检测与维护优化降低系统长期运行成本率。
1.2 系统可靠性模型 系统部件的状态转移为一离散马尔可夫链,示意图如图 2所示。
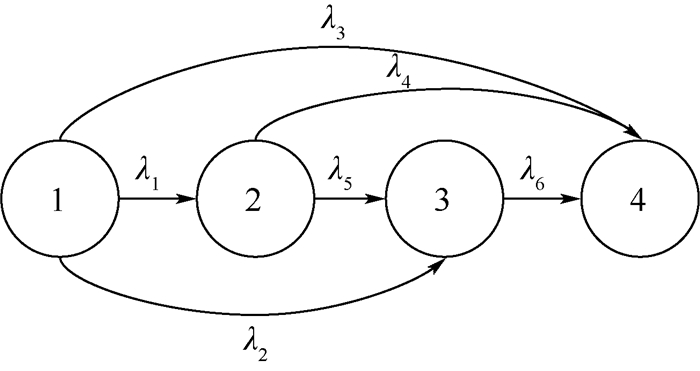 |
| 图 2 部件状态转移图 Fig. 2 Component state transfer diagram |
| 图选项 |
当部件处于状态i(i=1, 2, 3, 4) 时,下一时刻部件状态根据概率退化到状态j(j≥i)。图 2中λi代表了不同状态之间的转移率。假设相邻状态之间的转移率相同,即λ1=λ5=λ6;相隔状态之间转移率相同,即λ2=λ4;设λ=λ1+λ2+λ3,t时刻部件失效率为λi=λi(t),时刻t到下一时刻t+Δt的一步状态转移概率矩阵可表示为
 | (1) |
也可称Pij为退化矩阵,元素pij=pij(t)表示t时刻部件从状态S=i转移到状态S=j的一步转移概率:
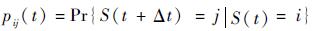 | (2) |
状态转移概率满足失效率λi的指数分布,当j < i时,pij=0,j≥i时,按照文献[27],转移概率如下。
从S=1转移到状态S=j的概率p1j:
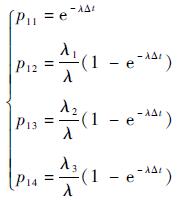 | (3) |
从S=2转移到状态S=j的概率p2j:
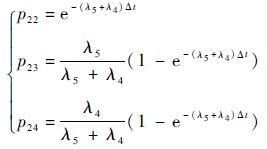 | (4) |
从S=3转移到状态S=j的概率p3j:
 | (5) |
以非齐次马尔可夫链建立系统退化仿真模型以及可靠性分析模型。t时刻部件的状态分布率用向量p(t)表示为
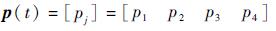 |
其中:元素pj=pj(t)表示t时刻部件处于状态j的概率,pj(t)=Pr{S(t)=j},S(t)从{1,2,3,4}中取值,部件的初始状态分布率为p0=[1 0 0 0],初始状态S(0)=1。t+Δt时刻部件状态分布率p(t+1) 可通过t时刻部件状态分布率p(t)和一步转移概率矩阵Pij(t)得到,具体为p(t+1)=p(t)·Pij(t),对状态分布率p(t+1) 采样便可得到系统状态S(t+1)。易知,若已知初始部件状态分布率p0和一步转移概率矩阵Pij(t),便可递推计算t > 0时部件的全部退化过程。
以上是单部件的可靠性模型。对于两部件并联系统,本文还考虑部件之间的故障相关性,即系统内某一部件故障会加速另一部件的退化。具体表现为:部件的失效率λa(t)与另一部件的故障次数k有关,其中λa(t)代表部件A中各状态之间的转移率λi(t)。
考虑故障相关后,t时刻部件A的失效率为
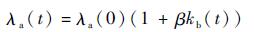 | (6) |
部件B类似,其中λa(0) 为t=0时刻(部件B未发生故障)部件A的初始失效率λi(0),部件A和部件B的初始失效率相同,设为λ0,即λ0=λa(0)=λb(0);kb(t)为时间为t时,距上一次部件A置换后部件B的故障次数(部件A置换后,失效率恢复为初始失效率λa(t)=λ0); 系数β反映故障相关性强度。可以看出,系统的退化过程实际上是非齐次马尔可夫链,部件的退化速率和另一部件的故障相关,在仿真部件退化时,需要首先根据部件故障计算失效率,之后进行状态转移。
1.3 系统检测模型 在二状态非完美检测中,存在漏警和虚警2类检测误差。本文把二状态系统非完美检测的模型扩展到多状态系统,得到了概率化后的多状态非完美检测的检测矩阵Zij:
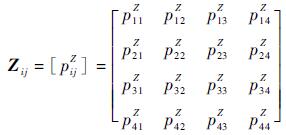 | (7) |
式中:元素pijZ代表部件状态S=j时,部件状态检测结果随机变量Z=j的条件概率,pijZ=Pr{Z=j|S=i}。
t时刻Z的分布率为
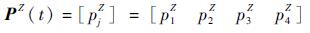 |
式中:元素pjZ为pjZ(t)=Pr{Z(t)=j}。
已知t时刻状态部件S(t),把S(t)写成状态分布率的形式P(t),检测结果Z的分布率可以通过PZ(t)=P(t)·Zij计算得到,之后从PZ(t)中采样便可得到t时刻的实际检测结果Z(t)。
1.4 系统维修与成本模型 系统维修采用预测性维修和事后维修。具体的维修方式分为完美维修(置换)和非完美维修,事后维修同时置换部件A和部件B,置换后的部件的失效率恢复为初始时刻失效率,状态恢复为全新状态,即n时刻的事后维修使得系统状态和失效率变为
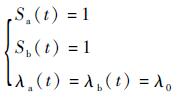 | (8) |
若对单个部件置换,例如只对部件A置换,那么部件A失效率恢复为初始时刻失效率,状态恢复成全新状态(部件B类似):
 | (9) |
式中:预测性维修是在系统故障前对系统维修,预测维修时,对部件采取置换或非完美维修,本文利用概率化方法对非完美维修建模[23],非完美维修后部件的失效率不变,状态以概率化的方式得到恢复,非完美维修的状态转移矩阵为
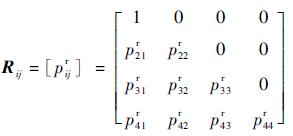 | (10) |
式中:元素pijr代表部件状态S=i时, 维修后状态随机变量Sr=j的条件概率,pijr=Pr{Sr=j|S=i},当j > i时,pijr=0。已知t时刻部件状态S(t),写成状态分布率P(t),利用
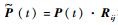
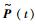
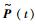

系统检测、维修以及发生故障时会花费一定成本。定义置换成本Cr、非完美维修成本Cim(Cim < Cr)、周期检测成本Cins、惩罚成本Cp以及预测性维修成本Ccbm,假设均为常数。每次检测花费成本Cins,事后维修的总成本为两部件置换成本加上故障带来的惩罚成本2Cr+Cp;预测性维修时系统未发生故障,因此成本Ccbm中没有惩罚成本Cp,Ccbm大小由部件A和部件B的具体维修形式决定。例如,采取部件A置换,部件B非完美维修时,预测性维修成本为Ccbm=Cim+Cr。
1.5 维修策略模型 系统在运行过程中不断发生状态退化,剩余寿命不断减少,因此以系统和部件的剩余寿命为可靠性指标,通过设置寿命阈值的方式触发维修。
首先定义剩余寿命和部件寿命。剩余寿命:部件从某时刻当前状态退化到故障所历经时间为剩余寿命?;部件寿命:当部件失效率λi不变时,从状态1退化到故障所历经时间为部件寿命l(λ),由于存在故障相关,随着故障的增多,部件失效率会递增,导致部件寿命递减,对部件预测性维修时,若部件寿命较大则采取非完美维修,过小时采取置换。
系统运行时的维修策略大致为:t时刻首先判断系统是否发生故障,发生故障则采取事后维修;若未发生故障,则估计部件的剩余寿命和部件寿命。由于是并联系统,两部件互为备份,系统的剩余寿命约为两部件剩余寿命中的较大者。当系统剩余寿命过小时,对系统采取预测性维修。维修时,需进一步对两部件分别判断所采取的维修类型(置换或非完美维修),判断的依据是部件的部件寿命,当部件寿命过小时采取置换,否则采取非完美维修。
图 3为系统维修策略的示意图,图中:?a和?b为部件A和部件B当前时刻的剩余寿命;la(λa)和lb(λb)分别是部件A和部件B在失效率分别为λa和λb时的部件寿命,部件寿命可理解为该部件在某失效率下,当状态S=1时的剩余寿命;ρ为系统剩余寿命阈值,用于触发预测性维修;η为部件寿命阈值,用来判别置换和非完美维修。
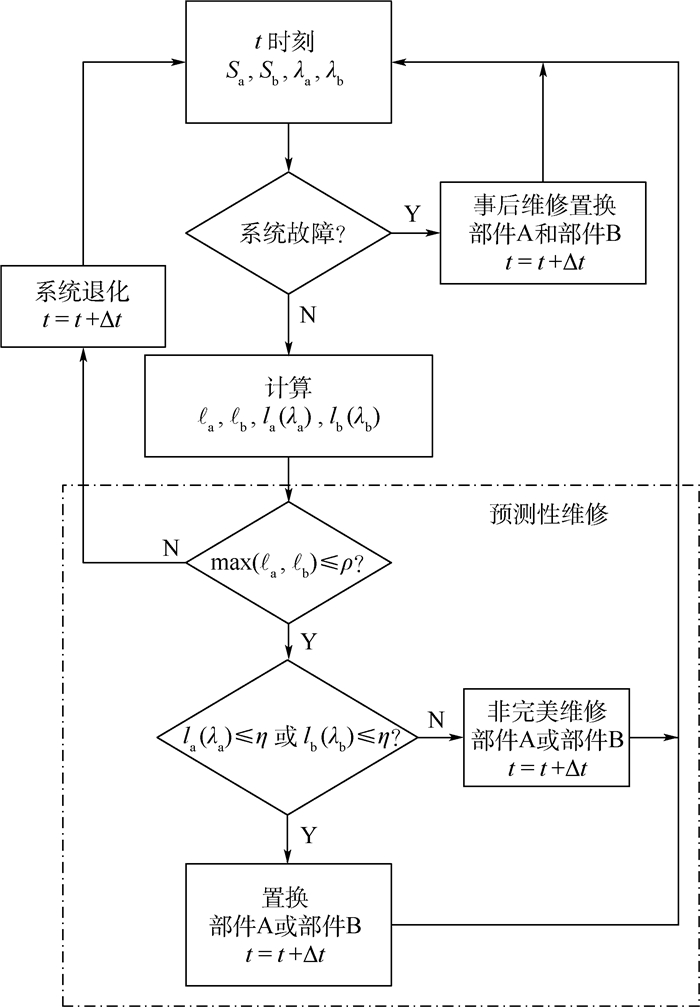 |
| 图 3 系统维修策略 Fig. 3 System repair policy |
| 图选项 |
系统维修优化是通过优化参数(T, ρ, η),使得系统的长期运行单位时间成本最小,其中T为检测周期。
2 系统的检测与维修优化方法 由于系统运行过程较为复杂,因此并没有采用解析方法实现优化,而是采用对系统运行过程建模仿真的方式,在较长一段时间内对系统运行过程进行仿真,不同的检测周期和维修相关阈值会仿真得到不同的成本率,通过蒙特卡罗方法,统计成本率均值,并以此作为目标函数,利用遗传算法迭代式对检测周期和维修策略寻优。
关于仿真建模,首先利用非齐次马尔可夫链建立实际系统退化模型,对实际系统的退化,检测和维修过程仿真,其中的仿真检测数据根据检测周期生成,除了实际系统仿真外,还建立了基于粒子滤波的分析模型,该方法可有效融合模型和数据,实现系统状态估计,继而得到系统的剩余寿命,并根据寿命阈值触发维修。
本文使用粒子滤波的原因是系统存在故障相关性和非完美特性,具有较强不确定性和非线性特性。另外,该方法较为通用,不仅适用于本文中的两部件并联系统,同样也适用于更多部件组成的系统。当系统部件较多时,虽然系统状态空间随着部件数量急剧变大,然而在进行粒子滤波过程中会滤除掉小概率情况(权重较低的粒子),相对于贝叶斯滤波(考虑状态空间中的全部状态)来说更加适合研究多部件系统。
2.1 系统退化仿真 系统退化时,由于存在故障相关性,退化模型为非齐次马尔可夫链。因此在仿真过程中,随着系统退化,每当系统单个部件发生故障,便对另一部件的失效率进行更新(维修中发生置换时,也更新失效率,即针对置换部件根据式(8) 或式(9) 更新被置换部件的失效率和状态)。
退化过程中的失效率更新方法如下:根据式(6),λa(t)可简单表示为λa(kb),系统状态退化是根据t时刻系统状态和失效率[Sa(t) Sb(t) λa(t) λb(t)]作为输入,计算得到下一时刻t+Δt的系统状态和失效率[Sa(t+Δt) Sb(t+Δt) λa(t+Δt) λb(t+Δt)]。计算过程如图 4所示。
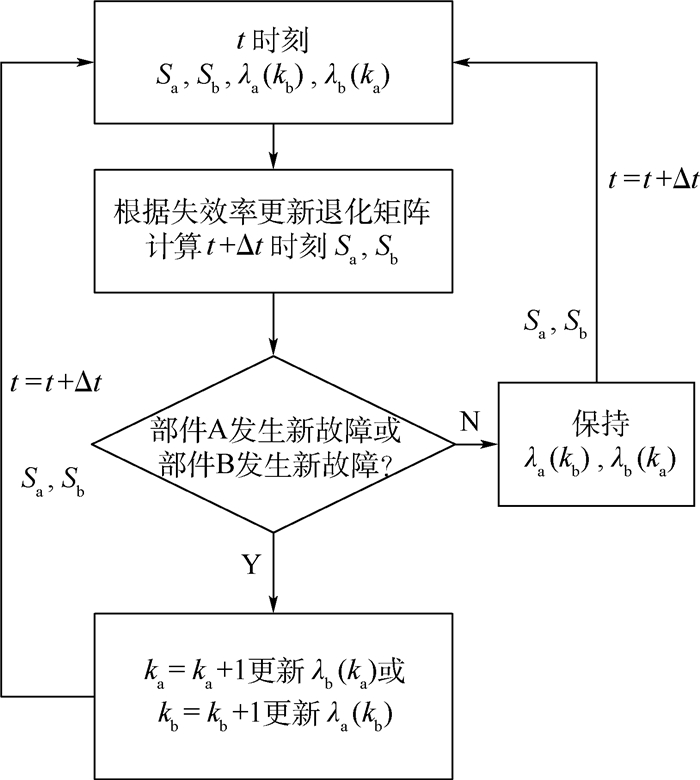 |
| 图 4 系统退化计算流程 Fig. 4 Flow of system degradation calculation |
| 图选项 |
即单个部件发生故障时,另一部件状态保持不变,但是失效率根据式(6) 更新,继而更新式(1) 中的退化矩阵,之后利用退化矩阵实现退化仿真。
2.2 利用检测数据更新寿命估计 预测性维修中的关键是利用检测信息以及系统自身的状态计算部件剩余寿命,由于系统具有故障相关性和非完美特性,系统行为具有高度的非线性和不确定性,非完美检测导致无法确切知道部件是否故障,也就无法确定部件的失效率,从而影响剩余寿命的计算。对于多部件系统,使用概率统计的解析方法计算剩余寿命会变得十分繁琐,本节阐述基于粒子滤波的剩余寿命计算方法。
2.3 粒子滤波 定义t时刻系统状态向量为Xt、观测向量为Zt,即对应于Xt的检测结果,t时刻内的观测序列为Zt={Z1 Z2 …Zt},那么系统状态更新模型和观测模型定义为
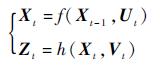 | (11) |
式中:f(·)为状态更新模型,Ut为系统噪声;h(·)为观测模型,Vt为观测噪声,用状态转移概率p(Xt|Xt-1)和观测概率P(Zt|Xt)表示f(·)和h(·),状态估计问题就转化成了计算后验概率P(Xt-1|Zt-1)。粒子滤波方法可以处理P(Xt-1|Zt-1)和P(Zt|Xt)是非线性的和高斯的情况。粒子滤波的核心思想是利用N个带权重的随机采样{Xt-1(i), wt-1(i)}i=1N逼近后验概率P(Xt-1|Zt-1),其中wt-1(i)为粒子Xt-1(i)的权重。利用贝叶斯迭代推理过程完成系统的动态求解[23],根据粒子滤波原理,t时刻权重wt(i)可表示为
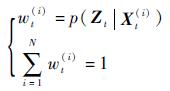 | (12) |
t时刻系统状态估计为
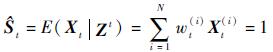 | (13) |
2.4 多状态并联系统剩余寿命计算 利用粒子滤波算法对前文提到的两部件并联系统进行剩余寿命预测。使用系统中两部件状态联合部件的失效率表达系统状态向量Xt,Xt=[Sa(t) Sb(t) λa(kb) λb(ka)];状态更新模型f(·)总共有3种形式,分别是状态退化、事后维修以及预测性维修,对于单个部件来说,状态更新包括状态退化,非完美维修以及置换,更新模型的选取由系统运行情况决定。状态退化用退化矩阵Pij表征,非完美维修用维修矩阵Pijr表征,置换就是把部件变为初始状态。观测模型h(·)包括非完美周期检测和系统总体状态——故障或非故障(由于系统发生故障时立刻可知,因此系统故障状态可分为作为观测信息)。
通过以下步骤计算剩余寿命:
1) 粒子群初始化。粒子群{X0(i)}i=1N中每个粒子为X0(i)=[1 1 λ0 λ0],所有粒子权值w0(i)为1/N。
2) 粒子采样。相当于预测过程,即根据更新模型f(·)对粒子群中的每个粒子从Xt(i)采样得到Xt+1(i)。
3) 权值计算。计算粒子样本与观测值的似然概率p(Zt|Xt(i))并更新粒子权值:
 | (14) |
对其归一化
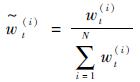 | (15) |
4) 重采样。根据有效粒子数Neff衡量粒子退化程度,当Neff小于设定门限时利用采样重要性重采样(Sampling Importance Resampling,SIR)方法得到N个新的粒子, 否则直接进入下一步。其中
 | (16) |
重采样具体流程可参考文献[24]。
5) 剩余寿命与部件寿命计算。输出一组带有权重的粒子{Xt(i), wt(i)}i=1N,利用其计算t时刻部件A和B的剩余寿命期望
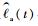
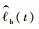

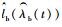
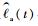
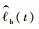
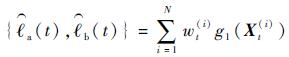 | (17) |
式中:g1(·)的作用是把系统状态X(i)t映射到部件A和B的剩余寿命。得到g1(·)的具体方法是提前利用蒙特卡罗方法通过大量仿真统计出两部件在不同状态、不同失效率条件下两部件的剩余寿命期望, 生成一个表格,以粒子中的Sa(t), Sb(t), λa(t), λb(t)作为输入便可直接查表得到
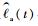
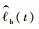
系统剩余寿命均值
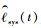
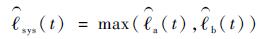 | (18) |
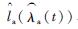
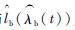
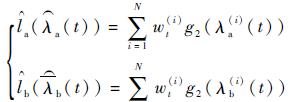 | (19) |
式中:g2(·)以失效率λ作为输入,输出结果是部件寿命。得到g2(·)的方法和得到g1(·)的方法类似,提前利用蒙特卡罗方法通过大量仿真统计出部件在不同失效率下的部件寿命,并生成表格。根据失效率通过查表便可得到相应部件寿命。表格中的失效率用式(6) 表示,另一部件的不同故障次数导致不同的失效率。
6) 迭代。t=t+1,重返步骤2)。
利用粒子滤波估计得到
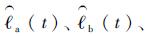
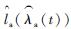
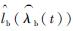
2.5 基于遗传算法的检测周期与维修策略优化 本文采用遗传算法实现系统维修策略寻优,目标是优化参数(T, ρ, η),使得系统长期运行成本率最低。遗传算法从一个由染色体组成的种群开始,染色体代表了待求问题的解,种群代表问题可能潜在的解集。基于遗传算法的寻优主要是通过迭代的方式,使得目标函数即适应度最强的解可以在多次迭代中存活下来,表现为基因的代代遗传。
遗传算法的整个流程涉及到对解的染色体编码、种群初始化、评价(计算解的适应度)、遗传配对以及终止条件,下面针对本文研究的问题阐述具体的方法。
1) 编码
对(T, ρ, η)采用15位二进制编码,1~5位代表η,5~10位代表ρ,11~15位代表T,数值范围是[1, 32]。
2) 种群初始化
遗传算法通过随机方式产生一组染色体作为初代种群。本文初始化的具体方式是随机产生12条染色体。
3) 适应度计算
对种群中的每条染色体计算适应度,为后续的遗传配对做准备。本文使用蒙特卡罗仿真结果计算适应度。对于一组特定的染色体(T, ρ, η),根据图 3的流程,使用粒子滤波计算部件剩余寿命
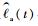
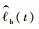
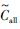
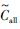
 | (20) |
成本期望越低说明解的适应度越高。可认为适应度反映了单位成本下系统运行的时长。
4) 遗传配对
计算完某代种群每条染色体的适应度后,通过遗传产生新一代种群。遗传过程中染色体经过配对(包括交叉和变异)以获得新的染色体。本文从上一代种群中选取2条适应度最高的染色体直接遗传到下一代作为2条新的染色体,剩下10条染色体通过交叉变异获得,最后对新一代所有12条染色体进行变异操作。
交叉首先需要选择2条染色体,然后通过交叉操作(基因交换)产生新的2条染色体。本文以上一代种群的适应度作为概率通过概率轮盘方式选取2条待交叉染色体。由于染色体位数较长,本文采用两点式交叉,首先在染色体的15位中随机产生2个交叉点,然后按随机产生的1、2、33个整数实现基因交换。随机数是1时对前面部分交叉,随机数是2时对中间部分交叉,随机数是3时对后面部分交叉,示意图如图 5所示。
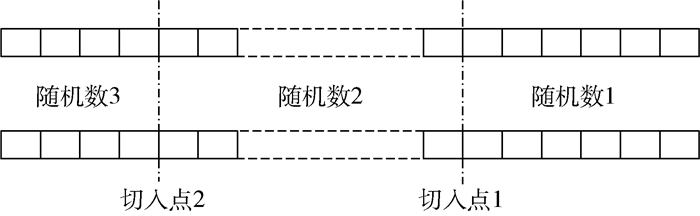 |
| 图 5 交叉操作 Fig. 5 Crossover operation |
| 图选项 |
通过5次交叉总共产生10条新的染色体,之后对该10条染色体进行变异操作。具体方式是:对于二进制染色体15位中的每一位,都有一定概率p发生变异——数值从0变为1或从1变为0。本文中设p=0.05。
变异后便完成了一代遗传,之后继续通过上述方法不断遗传产生新一代种群,直到达到终止条件。
5) 终止条件
本文采用2组条件作为终止条件,条件1:连续四代种群中适应度最高的染色体相同;条件2:遗传到达最大遗传代数(本文设定遗传代数为100)。当满足条件1或条件2中的任何一条时结束优化,并以最新一代最高适应度的染色体作为最终优化结果。
3 算例仿真 3.1 边界条件 设部件初始失效率λ0=0.001,λ1=0.95λ0,λ2=0.95(λ0-λ1),λ3=λ0-λ1-λ2;λ2=λ4,λ1=λ5=λ6;离散仿真时间步长Δt=100,考虑2组检测矩阵Zij(1)和Zij(2),Zij(1)检测误差较小,Zij(2)检测误差较大,分别如下:
 | (21) |
 | (22) |
维修矩阵Rij为
 | (23) |
式(6) 中的故障相关性强度β=0.2,成本参数:Cr=100,Cim=20,Cins=5,Cp=500。粒子滤波初始数量N=500,Neff的重采样门限为100。在用蒙特卡罗仿真系统行为时,设定仿真时长为1000,重复次数500次。
3.2 优化结果 使用遗传算法寻优,记录检测矩阵为Zij(2)时每一代的最大适应度,如图 6所示。
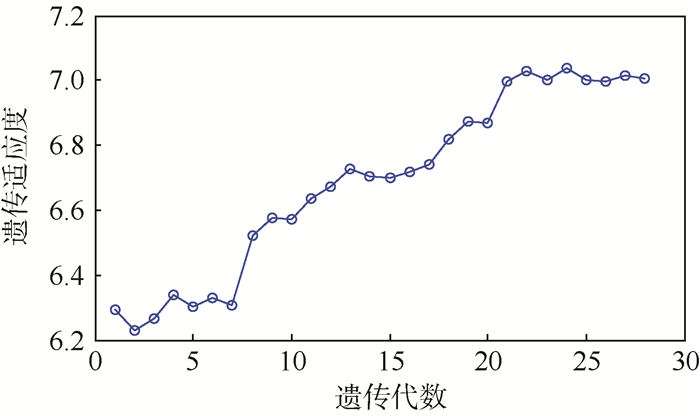 |
| 图 6 遗传算法优化中的各代最优适应度变化趋势 Fig. 6 Variation trend of the best fitness of each generation in GA optimization |
| 图选项 |
从图 6可以看出,虽然系统随机性造成了适应度变化并非严格单调,但是大体趋势是朝着更高适应度方向发展,在29代终止迭代,反映了遗传算法寻优的有效性。
分别考虑较小误差检测Zij(1)和较大误差检测Zij(2)情况下,对(T, ρ, η)寻优。为了反映检测误差的影响,另外采用忽略检测误差的传统方法对系统维修策略优化,即忽略检测误差,不使用随机滤波,把检测结果直接当作系统状态真值计算剩余寿命;优化内容为(T, ρ, n),n代表非完美维修次数,当次数大于n时对部件采取置换操作。优化对比结果如图 7所示,横坐标为系统运行的离散仿真时间,即仿真步数(例如,仿真时间为600时,实际时间为600Δt),纵坐标为系统运行的单位时间成本。
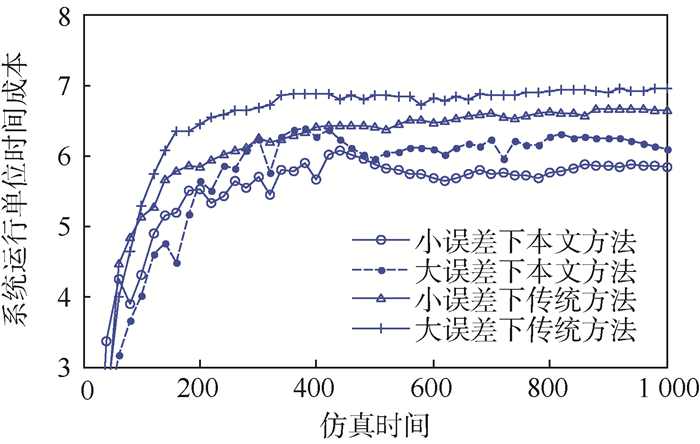 |
| 图 7 不同检测误差下的优化结果对比 Fig. 7 Comparison of optimization results under different inspection errors |
| 图选项 |
最终的优化参数结果为:小误差Zij(1)下(T, ρ, η)=(3, 4, 21);大误差Zij(2)下(T, ρ, η)=(21, 17, 24)。
从图 7中可以看出,使用粒子滤波后可以有效克服检测误差,与不考虑检测误差的传统方法相比,系统运行的单位时间成本更低,具有更好的经济性。对于不同程度的检测误差,该方法具有较好的鲁棒性。优化结果表明,检测误差较小时,检测周期较小,这使得寿命估计更加准确,因此寿命阈值较小;检测误差较大时,检测周期较大,寿命估计的不确定性较大,因此寿命阈值相对较宽。
4 结论 1) 使用蒙特卡罗仿真配合遗传算法可以同时对多状态系统的检测和维修进行优化,由于采用了仿真方法,因此可以充分保留系统行为的复杂性,更贴近实际系统。从优化结果可以看出,检测误差较小时,检测周期和维修相关寿命阈值较小;检测误差较大时,检测周期和维修相关寿命阈值较大。
2) 粒子滤波方法相当于同时利用系统行为模型(系统退化模型,系统维修模型)和检测数据,有效实现系统状态估计,继而实现寿命估计。该方法可克服系统中的故障相关性以及非完美特性带来的随机性和非线性特性;粒子滤波不仅适用于本文涉及的两部件系统,也适用于较多部件系统。
3) 遗传算法寻优时会出现小幅度波动,原因是蒙特卡罗仿真结果作为适应度具有一定随机性,但是适应度总体趋势变大,虽然不一定严格最优,但满足优化要求。
参考文献
| [1] | LAI M T, CHEN Y C. Optimal periodic replacement policy for a two-unit system with failure rate interaction[J].The International Journal of Advanced Manufacturing Technology, 2006, 29(3-4): 367–371.DOI:10.1007/s00170-004-2486-8 |
| [2] | 范江川, 刘子先. 基于故障相关与外部冲击的两部件系统机会维修研究[J].天津理工大学学报, 2014, 30(4): 1–5. FAN J C, LIU Z X. Opportunistic replacement policy for a two-unit system with failure interaction and external shocks[J].Journal of Tianjin University of Technology, 2014, 30(4): 1–5.(in Chinese) |
| [3] | 张卓琦, 吴甦, 李斌锋. 考虑故障相关的两部件系统机会维修策略[J].清华大学学报(自然科学版), 2012, 52(1): 122–127. ZHANG Z Q, WU S, LI B F. Opportunistic maintenance policy for a two-unit system with failure interactions[J].Journal of Tsinghua University(Science and Technology), 2012, 52(1): 122–127.(in Chinese) |
| [4] | LISNIANSKI A, FRENKEL I, DING Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M].New York: Springer Science & Business Media, 2010: 1-7. |
| [5] | JARDINE A K, LIN D, BANJEVIC D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J].Mechanical Systems and Signal Processing, 2006, 20(7): 1483–1510.DOI:10.1016/j.ymssp.2005.09.012 |
| [6] | GRALL A, BéRENGUER C, DIEULLE L. A condition-based maintenance policy for stochastically deteriorating systems[J].Reliability Engineering & System Safety, 2002, 76(2): 167–180. |
| [7] | WANG W, HUSSIN B, JEFFERIS T. A case study of condition based maintenance modelling based upon the oil analysis data of marine diesel engines using stochastic filtering[J].International Journal of Production Economics, 2012, 136(1): 84–92.DOI:10.1016/j.ijpe.2011.09.016 |
| [8] | YANG B S. An intelligent condition-based maintenance platform for rotating machinery[J].Expert Systems with Applications, 2012, 39(3): 2977–2988.DOI:10.1016/j.eswa.2011.08.159 |
| [9] | 成国庆, 李玲, 唐应辉. 多态退化串联可修系统的最优维修更换策略[J].系统工程理论与实践, 2012, 32(5): 1118–1123. CHENG G Q, LI L, TANG Y H. Optimal replacement policy for a deteriorating series repairable system with multi-state[J].Systems Engineering—Theory & Practice, 2012, 32(5): 1118–1123.DOI:10.12011/1000-6788(2012)5-1118(in Chinese) |
| [10] | 胡康. 基于Markov过程的多状态可维修系统可靠性建模与仿真[D]. 赣州: 江西理工大学, 2013: 10-13. HU K.Reliability modeling and simulation of multi-state repairable system based on Markov process[D]. Ganzhou:Jiangxi University of Science and Technology, 2013:10-13(in Chinese). |
| [11] | 尹晓伟, 钱文学, 谢里阳. 基于贝叶斯网络的多状态系统可靠性建模与评估[J].机械工程学报, 2009, 45(2): 206–212. YIN X W, QIAN W X, XIE L Y. Multi-state system reliability modeling and assessment based on Bayesian networks[J].Journal of Mechanical Engineering, 2009, 45(2): 206–212.(in Chinese) |
| [12] | LEVITIN G, LISNIANSKI A. Optimization of imperfect preventive maintenance for multi-state systems[J].Reliability Engineering & System Safety, 2000, 67(2): 193–203. |
| [13] | SORO I W, NOURELFATH M, A?T-KADI D. Performance evaluation of multi-state degraded systems with minimal repairs and imperfect preventive maintenance[J].Reliability Engineering & System Safety, 2010, 95(2): 65–69. |
| [14] | LIU Y, HUANG H Z. Optimal replacement policy for multi-state system under imperfect maintenance[J].IEEE Transactions on Reliability, 2010, 59(3): 483–495.DOI:10.1109/TR.2010.2051242 |
| [15] | VLKV GVRLER, KAYA A. A maintenance policy for a system with multi-state components:An approximate solution[J].Reliability Engineering & System Safety, 2002, 76(2): 117–127. |
| [16] | HUANG C C, YUAN J. A two-stage preventive maintenance policy for a multi-state deterioration system[J].Reliability Engineering & System Safety, 2010, 95(11): 1255–1260. |
| [17] | GUO B, ZHOU W.Maintenance strategy for two-unit multi-state deteriorating systems concerned with failure interactions[C]//Prognostics and System Health Management Conference.Piscataway, NJ:IEEE Press, 2011:1-6. |
| [18] | TANG D, YU J, CHEN X, et al. An optimal condition-based maintenance policy for a degrading system subject to the competing risks of soft and hard failure[J].Computers & Industrial Engineering, 2015, 83. |
| [19] | LU Z, CHEN M, ZHOU D.Periodic inspection maintenance policy with a general repair for multi-state systems[C]//Chinese Automation Congress (CAC).Piscataway, NJ:IEEE Press, 2015:2116-2121. |
| [20] | MALEFAKI S, KOUTRAS V P, PLATIS A N.Optimizing the availability and the operational cost of a periodically inspected multi-state deteriorating system with condition based maintenance policies[C]//Availability, Reliability and Security (ARES).Piscataway, NJ:IEEE Press, 2014:403-411. |
| [21] | LE M D, TAN C M. Optimal maintenance strategy of deteriorating system under imperfect maintenance and inspection using mixed inspection scheduling[J].Reliability Engineering & System Safety, 2013, 113(1): 21–29. |
| [22] | MOGHADDASS R, ZUO M J.Condition-based replacement policy for a device using interval-censored inspection data[C]//Reliability and Maintainability Symposium (RAMS), 2013 Proceedings-Annual.Piscataway, NJ:IEEE Press, 2013:1-6. |
| [23] | BROWN M, PROSCHAN F. Imperfect repair[J].Journal of Applied Probability, 1983, 20(4): 851–859.DOI:10.1017/S0021900200024153 |
| [24] | MY?TYRI E, PULKKINEN U, SIMOLA K. Application of stochastic filtering for lifetime prediction[J].Reliability Engineering & System Safety, 2006, 91(2): 200–208. |
| [25] | CARR M J, WANG W. Modeling failure modes for residual life prediction using stochastic filtering theory[J].IEEE Transactions on Reliability, 2010, 59(2): 346–355.DOI:10.1109/TR.2010.2044607 |
| [26] | SI X S, WANG W, HU C H, et al. Remaining useful life estimation-a review on the statistical data driven approaches[J].European Journal of Operational Research, 2011, 213(1): 1–14.DOI:10.1016/j.ejor.2010.11.018 |
| [27] | CAI B, LIU Y, ZHANG Y, et al. Dynamic Bayesian networks based performance evaluation of subsea blowout preventers in presence of imperfect repair[J].Expert Systems with Applications, 2013, 40(18): 7544–7554.DOI:10.1016/j.eswa.2013.07.064 |
