结构稳健拓扑优化已引起了广大****的重视。文献[10]研究了随机不确定载荷和材料性能下的结构鲁棒拓扑优化。文献[11]对随机载荷下的桁架结构进行优化研究,通过等效成一个凸的极小-极大问题来求解该问题。文献[12]给出了载荷大小不确定条件下的结构柔度均值和方差的解析计算公式,并基于水平集方法实现了结构的稳健拓扑优化。文献[13]采用椭球模型对桁架结构进行了非概率稳健性优化。文献[14-15]提出了任意载荷不确定条件下的结构柔度均值和方差的数值计算方法,并基于密度法实现了结构的稳健拓扑优化。文献[16-17]分别研究了多工况条件下考虑载荷不确定性的结构稳健拓扑优化设计方法。
本文将研究载荷不确定性条件下的周期性结构稳健拓扑优化设计方法,其目标为最小化结构柔度均值和标准差的加权和,约束条件为体积和周期性。由于其简单高效且可以得到设计清晰的结构,本文将采用软删双向渐进结构优化 (Soft-kill BESO) 法[18-20]对周期性结构进行稳健性拓扑优化设计。
本文的主要架构如下:首先,建立周期性结构稳健拓扑优化模型;然后,推导了目标函数以及敏度数计算方法;最后,通过算例说明本方法的有效性以及优化结果的稳健性。
1 周期性结构 周期性结构是指整体结构由相同形式的子结构组成,即不同子结构相同位置上的单元保持一致元态的结构。以平面周期性结构的设计为例,为了在优化过程中考虑结构的周期性,需将设计区域分割成相同的子域。
如图 1所示,整个区域被分割成M=M1×M2个子域,M1和M2分别表示沿坐标轴x和y方向上的子域数,xs, t为二元态设计变量,本文表示单元 (s, t) 的密度,s和t分别为子域在整体结构中的位置以及该单元在子域中的位置,当该单元为实体单元时其值为1,否则为空单元时取xmin,其中xmin>0是为了避免优化求解过程中结构刚度阵奇异而赋予空单元的一个很小的正实数。
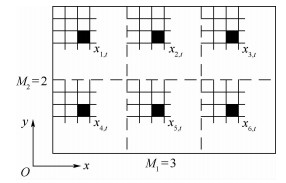 |
| 图 1 2D设计区域被分割成6个子域 Fig. 1 2D design domain with 6 unit cells |
| 图选项 |
2 材料插值技术 本文采用的Soft-kill BESO法进行结构拓扑优化设计。该方法在优化过程中将低效能材料单元赋予一个很小的数值,而不是直接删除。以下分析均以第s个子域为例进行表述。应用材料插值技术,每个单元的弹性模量为
 | (1) |
式中:E0为固体单元的弹性模量;p为惩罚因子。由于xs, t为二元态元素,可得
 | (2) |
3 不确定载荷的周期性结构稳健拓扑优化模型 考虑周期性的结构稳健拓扑优化设计模型可以表示为
 | (3a) |
 | (3b) |
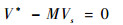 | (3c) |
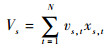 | (3d) |
 | (3e) |
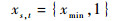 | (3f) |
式中:t=1, 2, …, N;s=1, 2, …, M;J为目标函数;μ(c) 与σ(c) 分别为结构柔度c的均值和标准差;正数α和β为权重系数,且α+β=1;K为结构刚度矩阵;f和u分别为作用力和位移向量;ω∈Θ表示载荷具有不确定性;Vs为第s个子域的总体积;vs, t为第s个子域的第t个单元的体积;V*为最终目标体积;N为每个子域的单元数; M为结构中子域的个数。
对于Soft-kill BESO法,二元态设计变量xs, t为单元的密度,当单元存在时为1,删除时为xmin。约束方程 (3e) 要求每个子域相同位置的单元状态相同,确保了结构设计结果具有周期性。
4 结构柔度均值和方差的计算[14-15] 对于任一不确定载荷,假设其大小hi和作用方向概率分布均已知。设f2i-1和f2i分别为该载荷的作用点沿x方向和沿y方向施加单位载荷时的结构整体载荷向量,且此时结构整体位移向量为u2i-1和u2i,则对于任意的n个不确定载荷
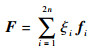 | (4) |
式中:ξi定义为
 | (5) |
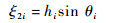 | (6) |
其中:θi为该载荷作用方向与x方向的夹角。
相应的结构位移为
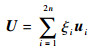 | (7) |
设m=2n,引入ξi的二阶和四阶中心距分别为
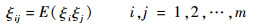 | (8) |
 | (9) |
则结构柔度的均值和方差分别为
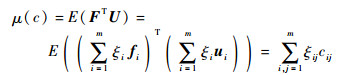 | (10) |
 | (11) |
式中:
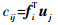
5 敏度数计算、过滤及周期性处理 5.1 敏度数的计算 单元敏度数在Soft-kill BESO法迭代过程中具有很重要的作用,每次迭代过程中根据单元敏度数的大小决定该单元是否删除或者添加。本文的优化目标是结构柔度均值和标准差的加权和,其对密度xs, t的导数为
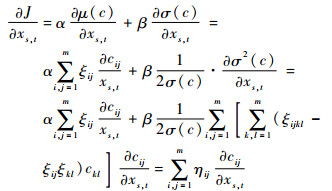 | (12) |
式中:
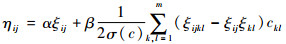
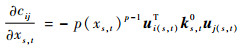 | (13) |
式中:ks, t0为固体时单元 (s, t) 的刚度阵;ui(s, t)和uj(s, t)分别为载荷fi和fj作用下单元 (s, t) 的位移向量。则单元 (s, t) 的敏度数为
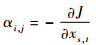 | (14) |
5.2敏度数过滤及周期性处理
为了克服拓扑优化中常存在的棋盘格、网格依赖性等现象,本文将用敏度过滤法对敏度数进行过滤。首先定义节点敏度数,其本身没有任何物理意义,只是节点相邻单元敏度数的平均值,其表达式为
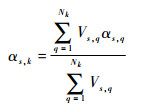 | (15) |
式中:Nk为与节点k相连的单元数;Vs, q为与节点k相连的单元q的体积。采用文献[2]中的过滤方法,可以得到过滤后的敏度数公式为
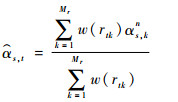 | (16) |
式中:Mr为过滤区域内包含的节点个数; w(rtk) 线性的权重因子,其定义为
 | (17) |
其中:rmin为指定的过滤半径,指定了节点的过滤区域;rtk为单元t的中心点到节点k的距离。
为了使收敛过程更加稳定,对敏度数进行更新。将敏度数的历史信息和当前迭代信息进行平均是一个比较有效的方法,即
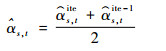 | (18) |
式中:ite代表当前迭代次数。
为了满足周期性要求,要求每个子域对应位置单元的敏度数一样大,单元删除与添加保持一致。任何子域中单元t的敏度数可以规划为所有子域单元相应第t单元柔度变化的平均值,即
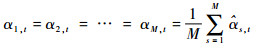 | (19) |
6 Soft-kill BESO法 Soft-kill BESO法主要根据单元敏度数信息对设计区域的单元进行删除或者添加。在每次单元删除或添加的迭代过程中,首先定义目标体积为
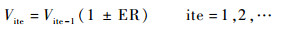 | (20) |
式中:ER为体积进化率,当体积达到约束值时就不再变化,随后的迭代过程的目标值即为约束值,即
 | (21) |
根据敏度数的大小及每次迭代的目标体积Vite,根据二分法依次移除或者添加相应的单元,具体方法见文献[20]。
7 本文方法流程 综合上述各部分的分析,可以给出载荷不确定下周期性结构稳健拓扑优化的具体过程如下:
1) 创建分析模型,施加约束边界和载荷条件。
2) 将设计区域划分为有限个周期单元,并初始化。
3) 进行有限元分析,并根据式 (14) 获得敏度数。
4) 通过式 (16) 和式 (18) 对敏度数进行过滤更新。
5) 通过式 (19) 实现周期性约束。
6) 利用第6节算法进行设计变量的更新。
7) 重复3)~6) 直到满足不等式 (22)。
 | (22) |
式中:τmax为允许的收敛误差;NN为考虑的迭代次数。
8 数值算例 针对本文算例,载荷大小不确定性对结构优化影响较小,因此,在算例分析时只考虑载荷方向不确定情况。本节以2个算例来说明本文方法有效性,并对载荷不确定性对周期性结构优化结果的影响进行分析总结。采用单位双线性正方形平面应力单元离散结构。材料特性为:弹性模量E=1 Pa,泊松比μ=0.3。优化过程中xmin=10-3,惩罚因子p=3,优化结束的准则为τ≤τmax=0.001。
8.1 双侧固定梁结构问题 双侧固定梁结构如图 2所示,设计域为80 m×40 m的长方形,左、右两侧均固定。中间施加一集中力F,大小为10 N,其作用方向与水平方向夹角服从均匀分布,区间为[-π/2-π/6, -π/2+π/6]。材料的许用体积为设计域的50%。
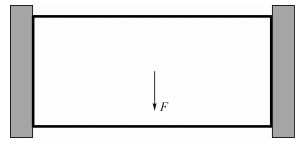 |
| 图 2 双侧固定梁结构的设计域 Fig. 2 Design domain for a bilateral clamped beam structure |
| 图选项 |
将整个设计区域离散为12 800(160×80) 个单元,并将均值和方差的权重系数α、β设置为0.5。对周期数为M=1×1、M=1×2、M=2×4的确定载荷情况、载荷方向不确定情况进行优化,优化结果如图 3和表 1所示。
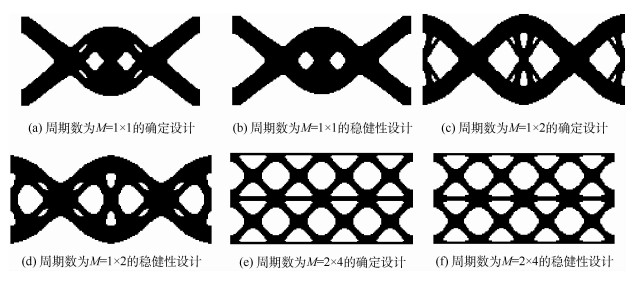 |
| 图 3 双侧固定梁拓扑优化得到的构型 Fig. 3 Layouts obtained from topology optimization of bilateral clamped beam |
| 图选项 |
表 1 双侧固定梁拓扑优化结果 Table 1 Topology optimization result of bilateral clamped beam
| J | |||||||
| 周期数 | 稳健性优化 | 确定性优化 | |||||
| 均值 | 标准差 | 目标函数 | 均值 | 标准差 | 目标函数 | ||
| M=1×1 | 525.62 | 11.98 | 268.80 | 529.72 | 7.84 | 268.78 | |
| M=1×2 | 601.58 | 1.78 | 301.68 | 615.17 | 17.70 | 316.44 | |
| M=2×4 | 862.01 | 35.40 | 448.71 | 884.58 | 33.04 | 458.81 | |
表选项
由图 3可知,优化结果边界清晰、周期性明显,说明本文方法是有效的。相对于确定优化,稳健性优化结构的材料更加集中于水平传力路线上,这样的最优结果增加了结构的水平承载能力。总之,在载荷存在方向不确定的情况下,稳健性优化得到的结构更加稳定,抵抗不确定性的能力更强。
图 4给出了周期数M=2×4的稳健性优化的收敛历史曲线。拓扑优化从满设计开始,去除率为2%,过滤半径取3。每次迭代去除2%的材料直到体积约束50%满足为止,然后体积保持常数,进行单元优化分布直到收敛条件满足为止。由图 4可知,体积分数和目标函数逐渐收敛且收敛过程迅速平稳,再次说明用该方法的有效性和稳定性。
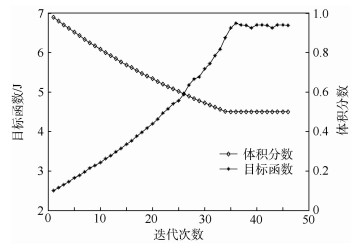 |
| 图 4 双侧固定梁拓扑优化迭代历史 Fig. 4 Iteration history of topology optimization of bilateral clamped beam |
| 图选项 |
8.2 米歇尔结构问题 如图 5所示,初始结构为480 m×160 m的矩形区域,两底端角点均简支,结构下端中心及距两侧各四分之一处分别作用一个竖直向下的不确定载荷P1、P2和P3。大小均为1 N,其作用方向均符合正态分布,方向的均值为θ=-π/2,标准差均为σ=π/6。材料的许用体积为设计域的40%。
 |
| 图 5 初始设计区域 Fig. 5 Primary design domain |
| 图选项 |
将整个设计区域离散为76 800(480×160) 单元,将均值和方差的权重系数α、β设置为0.5。对周期数为M=1×1, M=1×2, M=1×4的确定载荷情况、载荷方向不确定情况进行优化,优化结果如图 6所示。
 |
| 图 6 米歇尔结构拓扑优化得到的构型 Fig. 6 Layouts obtained from topology optimization of Michelle structure |
| 图选项 |
由图 6可知,优化结果边界清晰、周期性明显,说明本文方法是有效的。考虑载荷方向不确定性时与确定性时获得的结构构型相比变化明显:结构底端出现连接端点及载荷作用点的横杆,使得水平方向承载能力加强了,进而增加了结构整体的稳健性。
稳健优化结果和确定优化结果在载荷不确定下的目标值如表 2所示,可知确定性载荷条件下得到的结构在考虑载荷不确定性时的柔度均值、标准差和目标函数值均高于稳健优化得到的结果。因此,稳健优化的结构更加坚固和稳定,这证明了本文方法的有效性。
表 2 米歇尔结构拓扑优化结果 Table 2 Topology optimization result of Michelle structure
| J | |||||||
| 周期数 | 稳健性优化 | 确定性优化 | |||||
| 均值 | 标准差 | 目标函数 | 均值 | 标准差 | 目标函数 | ||
| M=1×1 | 92.43 | 10.46 | 51.45 | 141.66 | 67.41 | 104.54 | |
| M=1×2 | 120.52 | 14.87 | 67.70 | 359.52 | 235.67 | 297.60 | |
| M=1×4 | 139.89 | 20.44 | 80.17 | 265.13 | 132.34 | 198.74 | |
表选项
图 7给出了周期数为M=1×2稳健性优化的收敛历史曲线。拓扑优化从满设计开始,去除率为2%,过滤半径取4。每次迭代去除2%的材料直到体积约束40%满足为止,然后体积保持常数,进行单元优化分布直到收敛条件满足为止。由图可知,体积分数和目标函数逐渐收敛且收敛过程迅速平稳,说明该方法在本例中的应用是有效和稳定的。
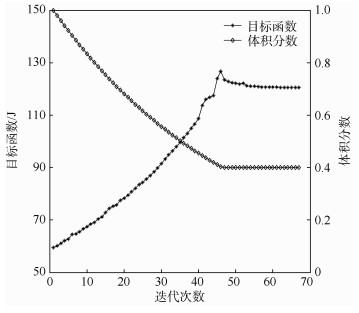 |
| 图 7 米歇尔结构迭代历史 Fig. 7 Iteration history of Michelle structure |
| 图选项 |
9 结论 本文研究了周期性约束下结构的稳健拓扑优化方法,针对线弹性体结构,基于概率方法提出了周期性结构稳健拓扑优化模型和求解方法。本文的主要贡献及结论:
1) 提出了弹性结构的周期性稳健拓扑优化模型。
2) 推导了周期性约束及载荷不确定条件下单元敏度数计算方法。
3) 应用数值算例验证了算法的稳定性和有效性。
4) 对不同约束条件下的算例研究表明:针对周期性结构,稳健性优化设计比确定性优化设计得到的结果更加稳定。
参考文献
| [1] | WADLEY H N G, FLECK N A, EVAN A G. Fabrication and structural performance of periodic cellular metal sandwich structures[J].Composites Science and Technology, 2003, 63(16): 2331–2343.DOI:10.1016/S0266-3538(03)00266-5 |
| [2] | HUANG, X D, XIE Y M. Optimal design of periodic structures using evolutionary topology optimization[J].Structural and Multidisciplinary Optimization, 2008, 36(6): 597–606.DOI:10.1007/s00158-007-0196-1 |
| [3] | 焦洪宇, 周奇才, 李文军, 等. 基于变密度法的周期性拓扑优化[J].机械工程学报, 2013, 49(13): 132–138. JIAO H Y, ZHOU Q C, LI W J, et al. Periodic topology optimization using variable density method[J].Journal of Mechanical Engineering, 2013, 49(13): 132–138.(in Chinese) |
| [4] | 荣见华, 廖莺, 赵志军, 等. 基于位移约束的类周期性连续体结构拓扑优化设计[J].应用力学学报, 2013, 30(6): 876–881. RONG J H, LIAO Y, ZHAO Z J, et al. Topology optimization of periodic-like structures with displacement constrains[J].Chinese Journal of Applied Mechanics, 2013, 30(6): 876–881.DOI:10.11776/cjam.30.06.B131(in Chinese) |
| [5] | 焦洪宇, 周奇才, 吴青龙, 等. 桥式起重机箱型主梁周期性拓扑优化设计[J].机械工程学报, 2014, 50(23): 134–139. JIAO H Y, ZHOU Q C, WU Q L, et al. Periodic topology optimization of the box-type girder of bridge crane[J].Journal of Mechanical Engineering, 2014, 50(23): 134–139.(in Chinese) |
| [6] | ZUO Z H, HUANG X D, YANG X Y. Comparing optimal material microstructures with optimal periodic structures[J].Computational Materials Science, 2013, 69(1): 137–147. |
| [7] | LUO Z, TONG L, KANG Z. A level set method for structural shape and topology optimization using radial basis functions[J].Computers and Structures, 2009, 87(7): 425–434. |
| [8] | GUEST J K, IGUSA T. Structural optimization under uncertain loads and nodal locations[J].Computer Methods in Applied Mechanics and Engineering, 2008, 198(1): 116–124.DOI:10.1016/j.cma.2008.04.009 |
| [9] | DUNNING P D, KIM H A, MULLINEUX G. Introducing loading uncertainty in topology optimization[J].AIAA Journal, 2011, 49(4): 760–768.DOI:10.2514/1.J050670 |
| [10] | CHEN S, CHEN W, LEE S. Level set based robust shape and topology optimization under random field uncertainties[J].Structural Multidisciplinary Optimization, 2010, 41(4): 507–524.DOI:10.1007/s00158-009-0449-2 |
| [11] | CHEN S, CHEN W. A new level-set based approach to shape and topology optimization under geometric uncertainty[J].Structural Multidisciplinary Optimization, 2011, 44(1): 1–18.DOI:10.1007/s00158-011-0660-9 |
| [12] | DUNNING P D, KIM H A. Robust topology optimization:Minimization of expected and variance of compliance[J].AIAA Journal, 2013, 51(11): 2656–2664.DOI:10.2514/1.J052183 |
| [13] | KANG Z, BAI S. On robust design optimization of truss structures with bounded uncertainties[J].Structural and Multidisciplinary Optimization, 2013, 47(5): 699–714.DOI:10.1007/s00158-012-0868-3 |
| [14] | 赵军鹏, 王春洁. 载荷不确定条件下的结构拓扑优化算法[J].北京航空航天大学学报, 2014, 40(7): 959–964. ZHAO J P, WANG C J. Algorithm of structural topology optimization under loading uncertainty[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 959–964.(in Chinese) |
| [15] | ZHAO J P, WANG C J. Robust topology optimization under loading uncertainty based on linear elastic theory and orthogonal diagonalization of symmetric matrices[J].Computer Methods in Applied Mechanics and Engineering, 2014, 273(2): 204–218. |
| [16] | 罗阳军, 亢战, 邓子辰. 多工况下结构鲁棒性拓扑优化设计[J].力学学报, 2011, 43(1): 227–234. LUO Y J, KANG Z, DENG Z C. Robust topology optimization design of structures with multiple load cases[J].Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 227–234.DOI:10.6052/0459-1879-2011-1-lxxb2010-147(in Chinese) |
| [17] | 付志方, 赵军鹏, 王春洁. 多工况线性结构稳健拓扑优化设计[J].力学学报, 2015, 47(4): 642–650. FU Z F, ZHAO J P, WANG C J. Robust topology optimization design of structures with multiple load cases[J].Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(4): 642–650.DOI:10.6052/0459-1879-15-072(in Chinese) |
| [18] | XIE Y M, ZUO Z H, HUANG X D, et al. Application of topological optimization technology to bridge design[J].Structural Engineering International, 2014, 24(2): 185–191.DOI:10.2749/101686614X13830790993366 |
| [19] | 刘丰睿, 赵丽滨, 韩邦成, 等. 磁悬浮控制力矩陀螺框架结构的拓扑优化设计[J].北京航空航天大学学报, 2010, 36(4): 455–458. LIU F R, ZHAO L B, HAN B C, et al. Topology optimization design of frame structure for magnetic suspension control moment gyroscope[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4): 455–458.(in Chinese) |
| [20] | HUANG X D, XIE Y M. Evolutionary topology optimization of continuum structures:Methods and applications[M].Chichester: John Wiley & Sons, 2010: 53-64. |
