文献[5-9]提出了着陆器的动力学分析方法,给出对软着陆性能影响较大的因素。文献[10]提出月球着陆缓冲器刚柔耦合模型的建模与分析方法。文献[11]运用响应面法,对单一工况下月球着陆器的软着陆性能进行了多目标优化。以上研究内容局限于着陆器单个性能指标或单一工况下多个性能指标的改进。相比于月球,其他星球的环境更加难以预测[12],着陆器各性能指标可能不在同一工况下达到最差,有必要在多组工况下,对着陆器多个性能指标进行优化。
本文建立了新型腿式着陆器的刚柔耦合动力学分析模型。探索着陆器最易翻倒、底面最易与星球表面岩石碰撞、主体承受最大碰撞力时对应的着陆工况。基于以上3组工况,以增强着陆器抗翻倒能力、降低着陆器主体底面与星球表面岩石碰撞的可能性、降低着陆器主体受力为目标进行优化设计。应用第二代非劣排序遗传算法 (NSGA-Ⅱ) 寻优,得到的优化结果明显提高了着陆器的软着陆性能。
1 着陆器刚柔耦合动力学模型 1.1 新型腿式着陆器构型 本文研究的新型着陆器包括主体结构和4套对称分布的着陆缓冲机构。主体在动力学分析中作为负载,着陆缓冲机构用于吸收着陆器着陆过程产生的冲击力,每套缓冲机构由主支柱、辅助支柱、足垫和外部缓冲件组成,如图 1所示。
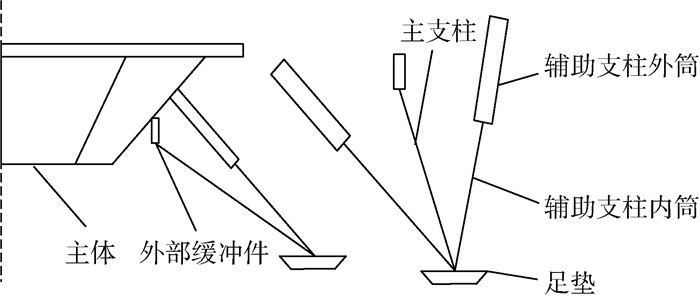 |
| 图 1 着陆缓冲机构 Fig. 1 Landing buffer mechanism |
| 图选项 |
主支柱起支撑作用;辅助支柱由内、外筒和缓冲元件组成,内、外筒之间存在缓冲元件,用于吸收压缩载荷;足垫用来增大着陆器与星球土壤的接触面积,防止着陆时着陆腿过度下陷;外部缓冲件与主体固连,当主支柱受到较大冲击力时,外部缓冲件间接受力,发生弯曲变形,进而产生缓冲弯矩,吸收冲击能量,防止主体受力过大。
1.2 着陆缓冲机构力学模型 辅助支柱内部的缓冲元件是着陆器着陆过程吸收冲击能量的主要结构,元件只能承受压缩载荷。在辅助支柱内外筒之间施加与内、外筒相对位移 (D) 有关的力 (FD) 代替缓冲元件的作用效果,辅助腿缓冲机构示意图及D与FD关系曲线如图 2所示。
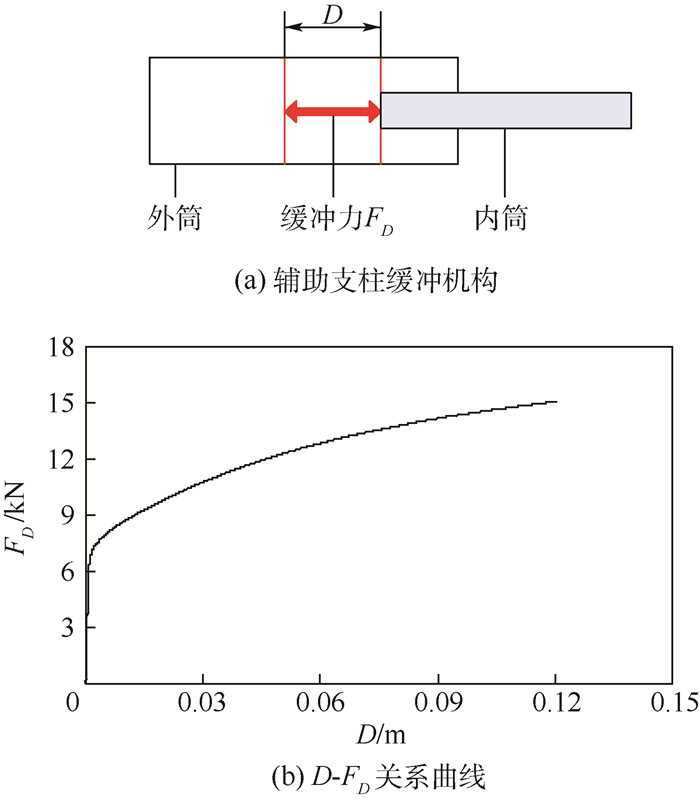 |
| 图 2 辅助支柱缓冲机构及力学特性 Fig. 2 Buffer mechanism and mechanical behavior of assistant pillar |
| 图选项 |
辅助支柱缓冲能力较强,外部缓冲件发生侧向弯曲的可能性很小。由于使用较多柔体构件导致动力学模型运算速度缓慢,使用如图 3方法对外部缓冲件进行刚体等效。
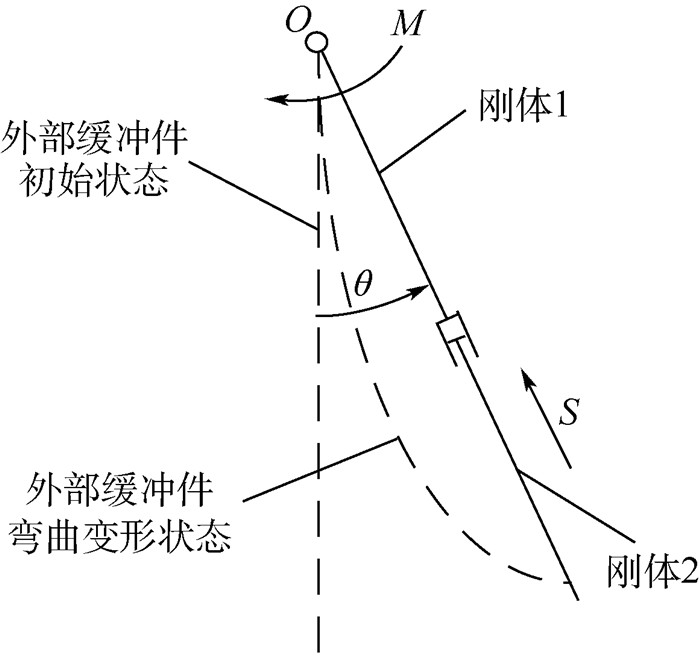 |
| 图 3 外部缓冲件等效方法 Fig. 3 Equivalent method of external buffer |
| 图选项 |
建立两段刚体模型,质量特性参照外部缓冲件柔体模型设置,刚体1绕转轴O转动,刚体2与刚体1只能沿轴线相对移动。刚体1转轴处施加与转角 (θ) 相关的转矩 (M),模拟外部缓冲件受弯时产生的缓冲弯矩;刚体2上施加与θ相关,沿刚体1轴线方向的运动 (S),模拟外部缓冲件自由端位置变化。在有限元软件中建立外部缓冲件模型,施加转矩,测得θ与M、θ与S关系曲线如图 4所示,输出数据文件,导入刚体模型。考虑等效模型质量、运动与力学特性均由有限元软件计算得到,即等效模型力学性能与柔体模型一致。
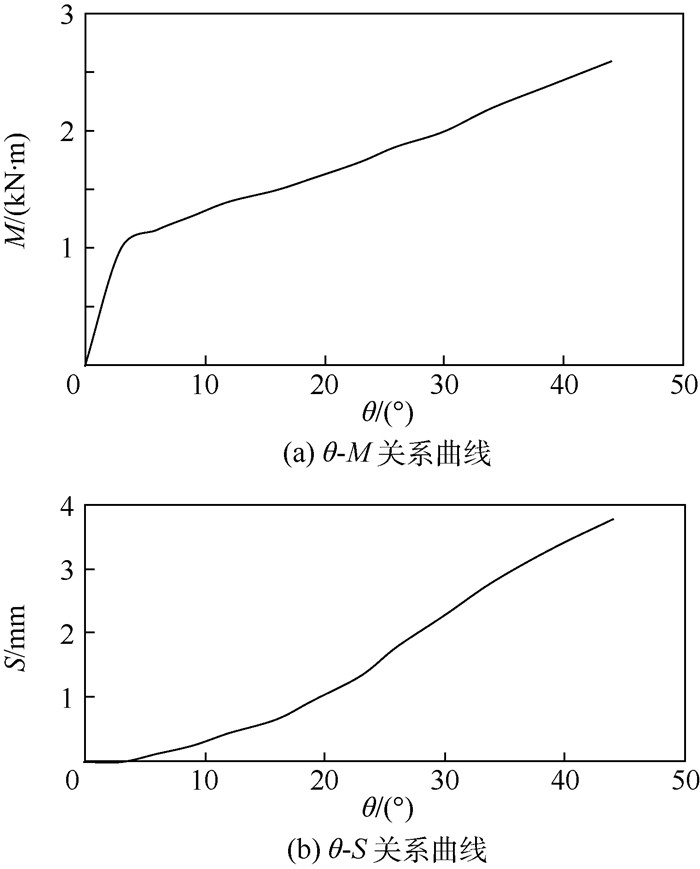 |
| 图 4 外部缓冲件力学特性 Fig. 4 Mechanical behavior of external buffer |
| 图选项 |
足垫触地时与星球表面的相互作用力分解为法向接触力Fn和切向摩擦力Ff,接触力Fn采用非线性阻尼弹簧碰撞方程描述:
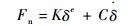 | (1) |
式中:K为接触刚度;δ为接触变形;e为非线性指数;C为阻尼系数。以上系数均与星球土壤特性密切相关。
摩擦力Ff采用库伦摩擦方程描述:
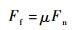 | (2) |
式中:μ为足垫与星球表面间的摩擦系数。
1.3 刚柔耦合动力学模型建模 刚柔耦合多体系统中,构件既存在大范围的刚体运动,也存在局部的弹性形变[10]。着陆器动力学模型中,足垫作为柔性构件可发生弹性形变,其余构件均为刚体构件。
采用有限元软件Patran建立足垫有限元模型,导入多体动力学分析软件ADAMS中作为柔体构件;采用ADAMS软件建立其余构件的刚体模型;应用ADAMS软件对着陆器着陆过程的动力学问题进行求解。
2 着陆器软着陆极限工况的确定 2.1 软着陆性能评判原则 根据着陆器安全着陆的性能指标,结合着陆器的构型,提出以下3种软着陆性能评判原则:
1) 着陆器在着陆过程中不发生翻倒,即着陆器质心距包含任意两足垫中心点的竖直翻倒墙平面的最小距离大于设计许用值[13]。
2) 着陆过程中辅助支柱外筒、外部缓冲件与主体连接点处的最大碰撞力不超过允许值,保证着陆器主体不会因为承受过大的碰撞力而受损。
3) 当着陆地点摩擦系数较小时,着陆器在着陆过程中,其着陆平台底面中心点距离星球表面的最小距离应大于预留间距值,避免着陆器底面与星球表面岩石发生碰撞而导致着陆器主体受损。
2.2 着陆工况参数 着陆工况的参数包括:式 (2) 中着陆器足垫与星球表面间的摩擦系数 (μ)、星球表面坡度 (α) 与凹坑分布情况 (n)、着陆器触地瞬间的竖直速度 (vx)、水平速度 (vz)、着陆偏航角 (θp)、着陆俯仰角 (θf) 以及着陆器整机质量 (m),如图 5所示。
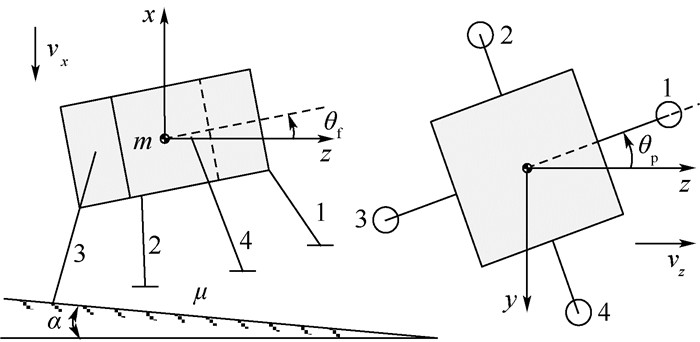 |
| 图 5 着陆工况的参数 Fig. 5 Parameters of landing condition |
| 图选项 |
着陆工况各参数的取值如表 1所示。
表 1 着陆工况各参数取值 Table 1 Value of parameters of landing condition
| 参数 | 取值 |
| μ | 0.3,0.8 |
| α/(°) | 7 |
| n | 0,1,2,3 |
| vx/(m·s-1) | 3.5 |
| vz/(m·s-1) | -1,+1 |
| θp/(°) | 0~45 |
| θf/(°) | -3,+3 |
| m/kg | 700,800 |
表选项
表 1中,n取0,1,2,3分别表示:着陆器没有着陆腿落入凹坑,2号与4号着陆腿落入坑中,1号与4号着陆腿落入坑中,1号、2号与4号着陆腿落入坑中;vz取正值表示水平速度方向背离坡面,负值表示水平速度朝向坡面;θf取正值表示着陆器俯仰角为仰角,负值表示俯仰角为俯角;遍历过程偏航角以1°为增量从0°增加至45°。将表 1中各参数取值进行组合,得到的着陆工况个数为2×1×4×1×2×46×2×2,即2 944种着陆工况。
2.3 软着陆极限工况参数取值 着陆器在特定工况下着陆,着陆过程中着陆器质心至翻倒墙距离取得最小值 (LT);或着陆过程中主体受碰撞力取得最大值 (FM);或着陆过程中着陆平台底面中心点至星球表面距离取得最小值 (LH),则称该工况为一种极限工况,对应的最值称为一种极限指标值。
基于2 944种着陆工况,通过仿真计算,得到3组极限工况及对应极限指标如表 2所示。
表 2 极限工况计算结果 Table 2 Calculation results of the worst landing condition
| 极限指标值 | μ | n | vz/(m·s-1) | θp/(°) | θf/(°) | m/kg |
| LT=1.11 mm | 0.8 | 2 | 1 | 9 | 3 | 700 |
| LH=734.23 mm | 0.3 | 3 | -1 | 0 | -3 | 800 |
| FM=27.22 kN | 0.8 | 3 | -1 | 0 | 3 | 800 |
表选项
根据表 2结果可知:着陆器质心距翻倒墙最小距离低于许用值 (30 mm),该情况认为着陆器已经翻倒;星球表面摩擦系数较小时,着陆平台底面中心点距星球表面最小距离低于预留间距值 (760 mm),着陆器极易与星球表面岩石碰撞;由于辅助支柱缓冲能力较强,主体所受的最大碰撞力位于主体与外部缓冲件连接处,接近允许值 (30 kN)。为了提升着陆器的软着陆性能,下文利用多目标优化方法对缓冲机构进行优化设计。
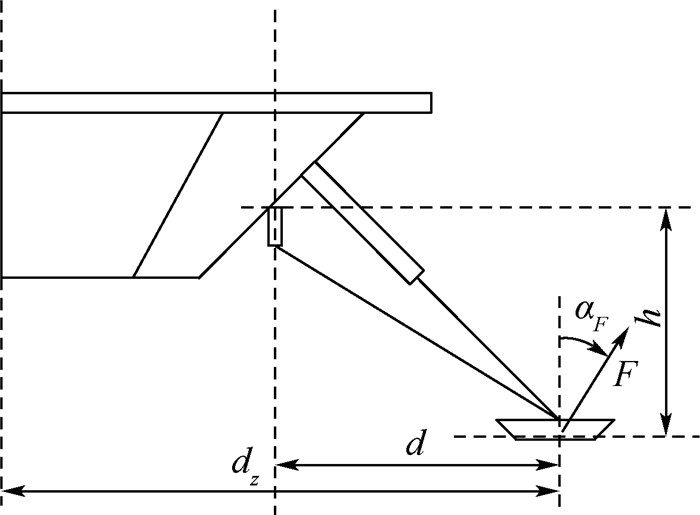
3 着陆器软着陆性能多目标优化 3.1 设计变量的选取 根据缓冲机构构型可知,增强外部缓冲件的缓冲力矩,可以提升着陆平台底面至星球表面距离的最小值,但主体受力可能超过许用值;增强辅助腿的缓冲力,可以提升着陆平台底面至星球表面距离的最小值,降低外部缓冲件与主体间的作用力,但缓冲性能降低导致着陆器更易翻倒;如图 6所示,增加足垫至着陆器中心轴线的距离 (dz),可使质心至翻倒墙初始距离增加,提升抗翻倒能力,但足垫受力点与外部缓冲件转轴水平距离 (d) 随之增加。根据力矩计算方程:
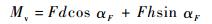 | (3) |
 |
| 图 6 着陆器性能分析 Fig. 6 Performance analysis of lander |
| 图选项 |
若着陆器足垫承受同样的冲击力 (F),足垫受力点与外部缓冲件转轴竖直距离h不变,冲击力与竖直方向夹角αF不变,d值增大,冲击转矩Mv增大,着陆腿向外扩张能力增强,进而导致着陆平台底面中心点至星球表面最小距离减小,着陆器底面更易与星球表面岩石相撞。
在着陆器主体结构与缓冲机构连接位置确定的情况下,同时避免着陆器竖直方向整体尺寸的增加,选取外部缓冲件缓冲转矩放大倍数 (kx)、辅助支柱缓冲力放大倍数 (kz)、足垫至着陆器中心轴线的距离 (dz) 作为设计变量进行多目标优化。
根据图 6可知,dz值增加导致着陆腿变长,着陆器整体尺寸随之增加。本文提到的缓冲元件提供的缓冲力与其尺寸成正比。为了保证着陆器整体尺寸不超出运载火箭可提供的最大安置空间,同时保证缓冲元件与着陆器其他结构不存在干涉,确定设计变量取值范围如表 3所示。
表 3 设计变量取值范围 Table 3 Value range of design variables
| 设计变量 | 取值范围 |
| kx | 1~2 |
| kz | 1~1.5 |
| dz/m | 1.37~1.45 |
表选项
3.2 软着陆性能多目标优化的实现 选取LT、LH、FM作为优化目标,约束LT、LH、FM满足2.3节给定的许用范围,结合设计变量的取值,建立数学模型如下:
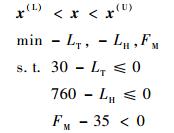 | (4) |
式中:x=(kx,kz,dz)T代表设计变量;x(L)与x(U)分别为设计变量的下界与上界。
本文采用NSGA-Ⅱ进行优化计算,算法基于帕累托最优理论,具有迭代次数少、寻优能力强等特点[14-15]。算法参数设置如表 4所示[11]。
表 4 优化参数取值[11] Table 4 Value of optimal parameters[11]
| 参数 | 种群规模 | 进化代数 | 交叉指数 | 变异指数 | 交叉概率 |
| 取值 | 12 | 20 | 10 | 20 | 0.9 |
表选项
综上所述,着陆器软着陆性能多目标优化具体流程如图 7所示。
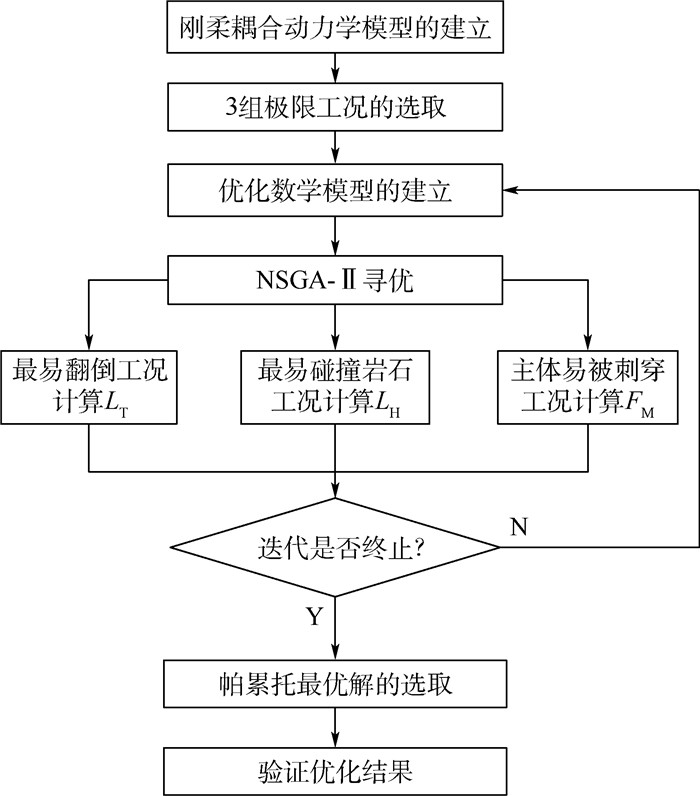 |
| 图 7 多目标优化流程图 Fig. 7 Flowchart of multi-objective optimization |
| 图选项 |
经过优化计算,得到帕累托最优解集如表 5所示。
表 5 帕累托最优解集 Table 5 Pareto optimal solution aggregate
| 编号 | kz | kx | dz/m | LH/mm | FM/kN | LT/mm |
| 1 | 1.46 | 1.07 | 1.45 | 757.91 | 24.07 | 413.92 |
| 2 | 1.46 | 1.23 | 1.45 | 757.97 | 26.31 | 416.59 |
| 3 | 1.49 | 1.13 | 1.44 | 761.38 | 25.57 | 378.00 |
| 4 | 1.49 | 1.03 | 1.43 | 763.07 | 23.36 | 349.08 |
| 5 | 1.49 | 1.05 | 1.41 | 765.81 | 23.95 | 258.71 |
| 6 | 1.49 | 1.22 | 1.42 | 764.49 | 27.31 | 306.33 |
| 7 | 1.49 | 1.08 | 1.43 | 762.92 | 24.07 | 352.49 |
| 8 | 1.49 | 1.04 | 1.43 | 762.57 | 23.50 | 360.83 |
| 9 | 1.49 | 1.03 | 1.42 | 764.15 | 23.46 | 311.13 |
| 10 | 1.48 | 1.19 | 1.43 | 761.46 | 25.72 | 365.11 |
表选项
根据图 6可知,dz值增加导致着陆腿变长,着陆器整体尺寸随之增加,为了减小着陆器整体尺寸,降低着陆器在运载火箭中的安置空间,选取帕累托解集中dz值最小的结果作为最优解,重新进行2 944次仿真计算,获得极限指标值与优化前结果对比如表 6所示。
表 6 优化前后性能对比 Table 6 Comparison of performance before and after optimization
| 对比项 | kx | kz | dz/m | LT/mm | LH/mm | FM/kN |
| 优化前 | 1 | 1 | 1.36 | 1.11 | 734.23 | 27.22 |
| 优化后 | 1.05 | 1.49 | 1.41 | 234.36 | 765.81 | 23.95 |
表选项
根据表 6可知,相比于初始设计,优化后的参数使LH增加4.2%,FM削弱12.1%,LT显著增加,着陆器在着陆过程中不再翻倒,软着陆性能获得明显提升。
4 结论 1) 建立了新型腿式着陆器刚柔耦合动力学分析模型,实现着陆器软着陆过程的仿真,提出新型着陆器软着陆性能评判原则。
2) 根据着陆工况各参数的取值,确定2 944种着陆工况,针对所有工况进行仿真计算,得到着陆器着陆过程中最易受损的3组恶劣工况。
3) 应用NSGA-Ⅱ算法,基于仿真得到的3组恶劣工况,对着陆器的软着陆性能进行多目标优化。优化后,着陆器在2 944种工况下着陆不存在翻倒现象,着陆平台底面中心点与星球表面的最小距离大于预留间距值,且主体受力得到明显地减弱。
参考文献
| [1] | 杨建中, 满剑锋, 曾福明, 等. "嫦娥三号"着陆缓冲机构的研究成果及其应用[J].航天返回与遥感, 2014, 35(6): 20–27. YANG J Z, MAN J F, ZENG F M, et al. Achievements and applications of landing gear for Chang'e-3 lander[J].Spacecraft Recovery & Remote Sensing, 2014, 35(6): 20–27.(in Chinese) |
| [2] | 李萌. 腿式着陆缓冲装置吸能特性及软着陆过程动力学仿真研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 1-10. LI M.Research on energy absorbers of legged-type lander and dynamic simulation on its soft landing process[D].Harbin:Harbin Institute of Technology, 2013:1-10(in Chinese). |
| [3] | 蒋万松, 黄伟, 沈祖炜, 等. 月球探测器软着陆动力学仿真[J].宇航学报, 2011, 32(3): 462–469. JIANG W S, HUANG W, SHEN Z W, et al. Soft landing dynamic simulation for lunar explorer[J].Journal of Astronautics, 2011, 32(3): 462–469.(in Chinese) |
| [4] | ADAM D S, MIGUEL S M, TOMMASO P R, et al. Mars science laboratory entry, descent, and landing system development challenges[J].Journal of Spacecraft and Rockets, 2014, 51(4): 994–1003.DOI:10.2514/1.A32866 |
| [5] | DING J Z, WANG C J.Fast modeling for lunar landing dynamics analysis:AIAA-2016-1191[R].Reston:AIAA, 2016. |
| [6] | 刘晓宇. 着陆器软着陆缓冲稳定性仿真分析[D]. 长沙: 湖南大学, 2013: 19-28. LIU X Y.Simulation analysis on soft landing's buffer and stability of lunar exploration[D].Changsha:Hunan University, 2013:19-28(in Chinese). |
| [7] | 陈金宝, 聂宏, 万峻麟. 深空探测着陆器数字化设计及着陆性能影响因素[J].航空学报, 2014, 35(2): 541–554. CHEN J B, NIE H, WAN J L. Digital design and landing performance influence factors of deep space lander[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 541–554.(in Chinese) |
| [8] | 罗昌杰, 邓宗全, 刘荣强, 等. 基于零力矩点理论的腿式着陆器着陆稳定性研究[J].机械工程学报, 2010, 46(9): 38–45. LUO C J, DENG Z Q, LIU R Q, et al. Landing stability investigation of legged-type spacecraft lander based on zero moment point theory[J].Journal of Mechanical Engineering, 2010, 46(9): 38–45.(in Chinese) |
| [9] | 罗松柏, 赵永嘉. 月球软着陆动力学分析与仿真[J].北京航空航天大学学报, 2012, 38(2): 185–190. LUO S B, ZHAO Y J. Dynamic analysis and simulation of soft-landing for lunar lander[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 185–190.(in Chinese) |
| [10] | 逯运通, 宋顺广, 王春洁. 基于刚柔耦合模型的月球着陆器动力学分析[J].北京航空航天大学学报, 2010, 36(11): 1348–1352. LU Y T, SONG S G, WANG C J. Dynamic analysis for lunar lander based on rigid-flexible coupled model[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(11): 1348–1352.(in Chinese) |
| [11] | 王家俊, 王春洁, 宋顺广. 基于响应面法的月球着陆器软着陆性能优化[J].北京航空航天大学学报, 2014, 40(5): 707–711. WANG J J, WANG C J, SONG S G. Performance optimization of lunar lander based on response surface methodology[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 707–711.(in Chinese) |
| [12] | BRIAN C S, MELISSA S, PETER I. Telecommunications performance during entry, descent, and landing of the Mars science laboratory[J].Journal of Spacecraft and Rockets, 2014, 51(4): 1237–1250.DOI:10.2514/1.A32790 |
| [13] | ZUPP G A, DOIRON H H.A mathematical procedure for predicting the touchdown dynamics of a soft-landing vehicle:NASA-TN-D-7045[R].Washington, D.C.:NASA, 1971. |
| [14] | MARLER R T, ARORA J S. Survey of multi-objective optimization methods for engineering[J].Structural and Multidisciplinary Optimization, 2004, 26(6): 369–395.DOI:10.1007/s00158-003-0368-6 |
| [15] | 黄晶晶, 郑龙席, 刘钢旗, 等. 双盘转子系统优化算法与试验[J].航空动力学报, 2016, 31(1): 65–71. HUANG J J, ZHENG L X, LIU G Q, et al. Optimization algorithm and experiment of two-disk rotor system[J].Journal of Aerospace Power, 2016, 31(1): 65–71.(in Chinese) |
