目前在筒壳结构屈曲、后屈曲研究方面,Jabareen[2-4]和Sheinman[2-3]对圆柱、圆锥壳结构的屈曲、后屈曲行为都做了大量的研究。其一,在动载荷下所得到结果能够得到完整的载荷-端部压缩位移曲线,柱/锥壳结构对初始几何缺陷是敏感的,随着缺陷幅值增大敏感度升高;其二,基于三维壳理论研究了柱/锥壳结构在轴压载荷作用下屈曲行为,对传统的特征值屈曲 (分支型屈曲) 考虑前屈曲非线性的影响,来预测结构的真实屈曲载荷和模态;其三,进行了带初始几何缺陷的柱/锥壳结构的后屈曲分析,分别研究了面内边界条件、初始几何缺陷的形状、大小以及结构半锥角对后屈曲行为的影响。
Goldfeld等[5-7]总结了基于经典的3种壳理论 (分别是Donnell的大挠度方程、Sanders的非线性薄壳理论以及Timoshenko的线弹稳定性理论) 下的分支点屈曲问题,得出层合柱壳的拉-弯耦合影响非常突出;研究了带加强筋柱/锥壳结构的线弹性屈曲和缺陷敏感度,其中包括加强筋的数目、布局位置和角度、层合圆柱壳在不同理论下的屈曲和后屈曲行为。在带加强筋柱/锥壳方面,集中研究了筋条的存在对屈曲载荷、屈曲模态和缺陷敏感度的影响,并由此提出通过带加强筋结构优化筒壳结构设计,提高抗失稳能力,以及分析了圆柱、圆锥壳结构对初始几何缺陷的敏感性。
Spagnoli和Chryssanthopoulos[8]分析了带加强筋薄墙柱/锥壳结构在轴压载荷的线弹性屈曲和非线性后屈曲,其对后屈曲的分析是在传统的线弹性特征值屈曲基础上,引入临界屈曲模态作为后屈曲分析的初始几何缺陷,并将线性分析得到的临界屈曲模态通过改变缺陷系数的大小,按不同幅值的几何缺陷加入后屈曲的参数化研究中。
李钟海等[9]利用有限元素法对平面布和单向带复合材料柱壳进行了压缩试验,研究了铺层方式对压缩性能的影响。阎崇年等[10]研究了含开口复合材料柱壳的压缩性能,分析了开口面积与开口高度对压缩性能的影响。王珂晟等[11]对含加强肋、加强环的复材料圆柱壳稳定性进行了研究,考虑了几何、材料非线性以及初始几何缺陷等因素。王毅等[12]采用奇异摄动法, 考虑非线性前屈曲、大扰动以及初始缺陷的影响,分析在两端固支条件下,各向异性的层合圆柱壳在轴压下的屈曲与后屈曲行为。Hilburger和Starnes[13]研究了矩形开口薄壁复合材料圆柱壳的受压屈曲行为,研究了开口加强结构的铺层方向、尺寸及厚度对圆柱壳压缩非线性响应的影响。
1 ABAQUS中Buckle、Riks法 特征值屈曲分析用于预测一个理想弹性结构的屈曲载荷、屈曲模态。经典特征值屈曲 (Buckle算法) 方程为
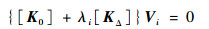 | (1) |
式中:K0为对应基础状态的刚度矩阵;KΔ为应力刚度矩阵;λi为特征值;Vi为屈曲模态向量。
应用Buckle算法进行线性特征值屈曲分析,屈曲载荷计算式为
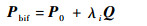 | (2) |
式中:P0为预加载荷,为初始常量载荷,在整个分析过程不变;Q为扰动载荷,此处取壳边缘单位载荷 (1 N/mm)。
特征值屈曲分析虽然能够快速求解结构的线性屈曲载荷和屈曲模态,对于处理几何、材料非线性稳定问题还得求助Riks法。一般的非线性问题常使用Newton-Raphson迭代法,Riks法引入“弧长”来衡量求解过程,其求解过程中载荷与位移都是未知量,使用弧长来推进求解过程,使得其能够很好解决结构下降段 (负刚度) 的跟踪问题。Riks法屈曲载荷计算式为
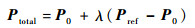 | (3) |
式中:Pref为给定参考载荷向量;λ为载荷比例系数,为Riks求解的结果。
本文采用线性屈曲分析——Buckle算法及含初始几何缺陷非线性后屈曲分析——Riks法进行研究。采用特征值屈曲模态的线性叠加引入初始几何缺陷, 缺陷幅值为ω=μh乘以“线性屈曲模态”,μ为初始几何缺陷系数,h为壳厚度,对于薄壳结构一般情况下取1%~10%壳厚度。
2 1/3柱壳试验 2.1 试验件 1/3含口盖柱壳 (120°) 试验件,外径257 mm,高608 mm,壳体周向30°与90°,高度196 mm与392 mm位置处,布置有宽10 mm,厚2 mm的筋条。试验时在柱壳两边前后各布置长588 mm、宽20 mm、厚8 mm的加强筋。在“井”字形筋条围成的矩形开口高170 mm、宽230 mm,背面用补片加强,补片中央的矩形开口高120 mm,宽180 mm,补片边缘和筋条边缘相接触。矩形口盖高170 mm、宽230 mm,通过10个直径为5 mm的螺钉与开口补强件连接。所有矩形开口处圆角半径为15 mm。实物如图 1所示。试验件采用树脂传递模塑 (Resin Transfer Moulding, RTM) 成型工艺制造,表 1、表 2中分别列出柱壳所用材料和力学性能及蒙皮、筋条、加强筋、补片和口盖的铺层方式。
 |
| 图 1 1/3含口盖柱壳实物图 Fig. 1 Practicality picture of 1/3 cylindrical shell with cover |
| 图选项 |
表 1 柱壳铺层复合材料的力学性能 Table 1 Mechanical properties of composite used in cylindrical shell
| 材料 | E11/GPa | E22/GPa | G12/GPa | μ12 | t/mm |
| 单向带T300/6808 | 117 | 8.00 | 3.00 | 0.300 | 0.160 |
| 0.125 | |||||
| 织物G814/6084 | 63.0 | 63.0 | 4.10 | 0.060 | 0.240 |
| ??注:E11—1方向弹性模量;E22—2方向弹性模量;G12—1-2平面内剪切模量;μ12—泊松比;t—单层厚度。 | |||||
表选项
表 2 柱壳不同位置的材料及铺层方式 Table 2 Materials and ply sequences of different parts on cylindrical shells
| 结构 | 材料 | 铺层方式 | 层数 |
| 蒙皮 | 单向带T300/6808 (0.160 mm) | [45/-45/02/90]S | 10 |
| 纵向筋条 | 单向带T300/6808 (0.125 mm) | [45/-45/02/45/-45/0/90]S | 16 |
| 横向筋条 | 单向带T300/6808 (0.125 mm) | [-45/45/902/-45/45/90/0]S | 16 |
| 两侧加强筋 | 单向带T300/6808 (0.125 mm) | [45/-45/02/45/-45/0/902/0/-45/45/02/-45/452/-45/02/45/-45/0/902/0/-45/45/02 /-45/45]S | 64 |
| 补片 | 织物G814/6084 | [011] | 11 |
| 口盖 | 织物G814/6084 | [011] | 11 |
表选项
2.2 压缩试验 含口盖试验件共3件,标为A、B、C,试验使用INSTRON 8802材料试验机逐级加载,载荷低于50 kN时,每级递增10 kN,高于50 kN时,每级递增5 kN,同时记录柱壳典型位置的应变以及加载载荷及位移。试验的压缩载荷-端部压缩位移曲线如图 2所示。3次试验过程中情况基本一致,在载荷水平达到60 kN附近时 (A 56 kN、B 56 kN、C 57 kN) 发生了初始屈曲现象,伴随第一次响亮的声响,此时结构已经发生了初始屈曲变形,图 3 (a) 为试验件C载荷57 kN初始屈曲时的模态图,在右下方出现了一个明显的凹坑;从载荷位移曲线可知结构在初始屈曲之前呈现线性压缩变形,之后发生了明显的非线性后屈曲行为,继续加载,不断有轻微的响声,最后在一声大响中结构压溃破坏,A、B和C的极限屈曲强度试验值分别为92.0、84.2和80.9 kN,平均极限屈曲载荷为85.7 kN, 相对于文献[1]中屈曲破坏载荷118.9 kN降低了许多,文献[14]中分析原因可能是边界加工不规整导致壳面受载不均匀,局部高载区导致结构提前进入屈曲状态,结构的初始几何缺陷导致2次试验结果相差很大。图 3 (b) 为试验件C的最终屈曲破坏图,模态转变为一种整体的屈曲行为,在口盖的4个边角上下方均出现了明显的凹坑。试验结果表明1/3复合材料含口盖柱壳在轴压载荷下是有后屈曲行为的,在初始屈曲到最终的压溃破坏的后屈曲现象很明显。
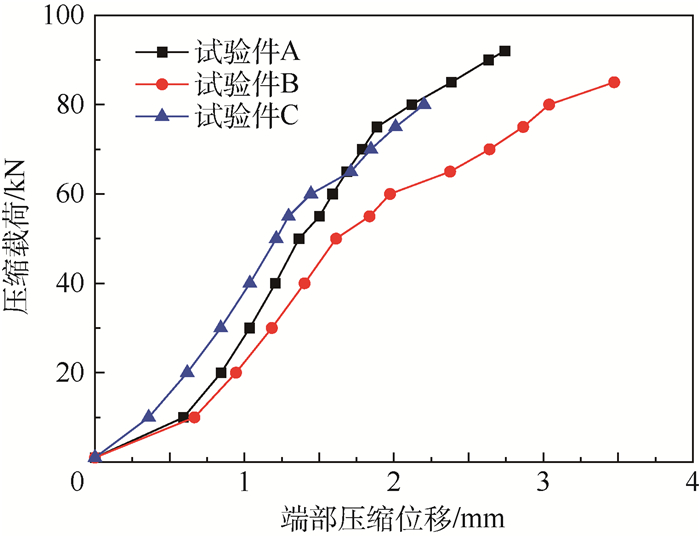 |
| 图 2 试验件压缩载荷-端部压缩位移曲线 Fig. 2 Compressive load-end shortening displacement curves of specimens |
| 图选项 |
 |
| 图 3 试验件C屈曲模态 Fig. 3 Buckling mode of specimen C |
| 图选项 |
试验同时采集了柱壳各典型部位的应变,应变布局如图 4所示,选取应变片10 (11)、19、20 (21) 模拟整个应变场,试验所获得的载荷-应变数据在第3.3节Riks法分析中给出。
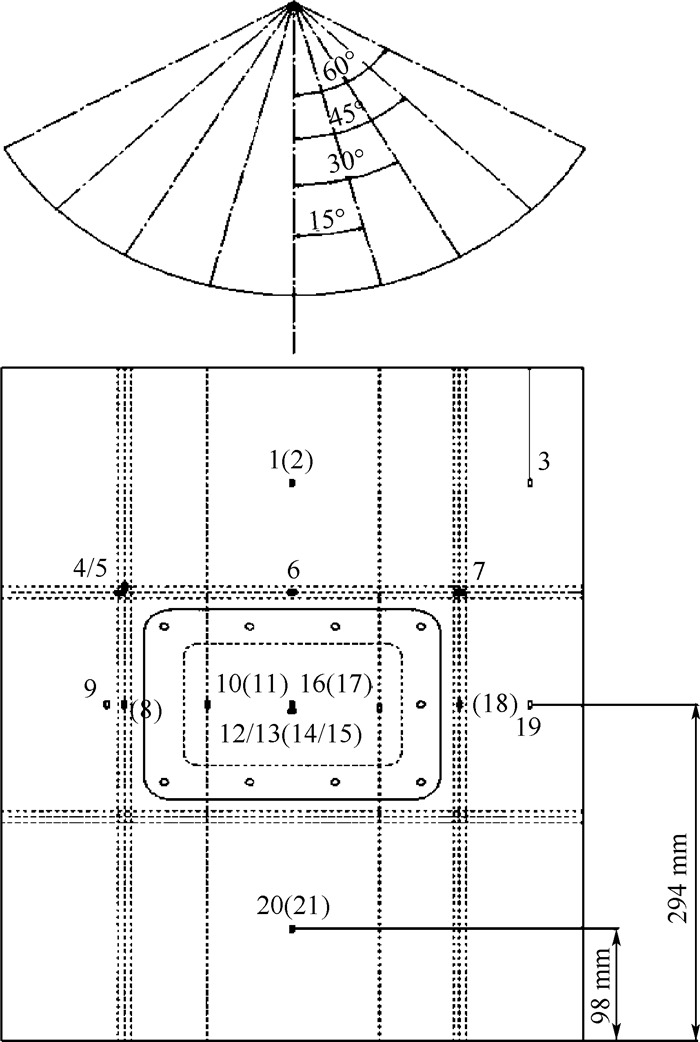 |
| 图 4 试验件应变布局 Fig. 4 Strain gauge layout of specimen |
| 图选项 |
3 1/3柱壳FEM分析 3.1 FEM模型 在柱坐标系RTZ下建立ABAQUS有限元模型 (FEM),选用S4R壳单元,柱壳高度方向为Z方向,向下为正,上端约束R、T方向位移,下端固支,两侧边为自由边界条件;含开口柱壳模型划分5408个单元,口盖划分482个单元。1/3含口盖复合材料柱壳FEM如图 5所示。
 |
| 图 5 1/3柱壳FEM Fig. 5 FEM of 1/3 cylindrical shell |
| 图选项 |
3.2 基于Buckle算法线性屈曲分析 对含口盖柱壳ABAQUS FEM进行了基于Buckle算法的线性特征值屈曲分析,在柱壳上端施加单位线载荷,边界条件上端约束周向和径向位移,下端固支,按式 (2) 计算所得线性屈曲载荷,含口盖柱壳临界 (第1阶) 屈曲载荷为137.9 kN, 对比文献[1]中计算结果133.3 kN, 误差约为3.3%,在可接受的范围内,并且屈曲模态基本一致,验证Buckle算法是有效的。含口盖第1阶到第5阶屈曲载荷十分接近,第2阶至第5阶载荷分别为138.2、141.6、141.7和143.8 kN,细微的载荷增量都会引起模态的阶跃,这种情况下,一系列间隔很近的特征值表明结构是缺陷敏感的,而对于缺陷敏感结构,特征值屈曲分析不能给出准确的屈曲载荷、屈曲模态预测;含口盖柱壳前4阶屈曲模态如图 6所示,第1阶、第2阶屈曲变形集中在壳的中下部位,第3、第4阶变形集中在壳中上部位,前4阶屈曲模态形状都很相似,主要表现为剪切变形,这主要是在理想情况下,复合材料铺层方式决定的结构整体刚度分布特点。
 |
| 图 6 Buckle算法所得屈曲模态 Fig. 6 Buckling mode obtained by Buckle algorithm |
| 图选项 |
3.3 基于Riks法FEM分析 非线性Riks法在分析屈曲问题时的最大优点是利用弧长增量来处理传统静力分析方法无法跨越极值点,追寻负刚度 (下降段) 阶段的载荷位移变化。真实结构不可能是理想完善,由于工艺水平或使用维修过程中难免会有损坏,考虑初始几何缺陷的非线性后屈曲研究对设计评估更加真实可靠。
在第3.2节线性特征值屈曲分析的基础上,进行了基于Riks法的含初始几何缺陷非线性后屈曲分析,以此方法来追踪结构的非线性平衡路径,主要的目标是获得结构的载荷-位移曲线,评估结构真实极限屈曲载荷和后屈曲行为,应用FEM和边界条件同线性分析方法一致。在建立Riks分析方法的同时通过inp文件修改模型的节点平移自由度,特征值屈曲分析所提取的屈曲模态作为初始几何缺陷。从试验与Riks法应变-压缩载荷曲线结果看 (如图 7所示),试验数据与Riks法分析所得数据吻合,验证模型和算法的有效性。图 8为基于Riks法含口盖柱壳压缩载荷-端部平均压缩位移曲线,以线性临界模态作为后屈曲分析初始几何缺陷,缺陷幅值为1%壳厚度,即μ=0.01,计算结果为:非线性分析的压缩载荷-端部平均压缩位移曲线能够得到若干个载荷极值点,其中上临界点屈曲载荷为118.6 kN (对应a=0.86), 下临界点屈曲载荷 (代表平衡状态中可能发生的最低载荷水平) 为93.8 kN (b=0.68), 后屈曲极限载荷为103.4 kN (c=0.75), 相比较线性临界屈曲载荷 (Fcr) 137.9 kN下降幅度很大,试验平均屈曲极限载荷85.7 kN,文献[1]中试验平均屈曲极限载荷118.9 kN,由于初始几何缺陷的存在,2次试验结果差别较大,下临界屈曲载荷与本文试验载荷相近,误差约为9.4%,上临界屈曲载荷与文献[1]试验结果相近,误差约为0.3%,Buckle线性屈曲载荷与本文试验结果误差高达60.9%,与文献[1]误差近16.0%,非线性分析所得载荷值更加贴近试验结果。由于试验前没有研究试验件的真实几何缺陷,试验件的边界不规整导致试验屈曲载荷降低很多,参考文献[1]中的试验载荷也可以得出:线性特征值屈曲分析所得的屈曲载荷较试验值偏离实际结果太高,尤其是在结构有初始几何缺陷的情况下所的结果更会偏离真实值,若以非线性Riks法为设计方法,考虑初始几何缺陷,在设计上更加真实可靠。另一方面,从屈曲模态图 9对比可得知,图 9 (a) 与图 9 (c) 为Buckle算法结果,图 9 (b) 与图 9 (d) 为Riks法结果,Riks法所得模态形状十分贴近试验屈曲模态 (图 3),都表现为口盖侧上下方位的凹坑形式,其中图 9 (b) 为引入线性临界屈曲模态作为初始几何缺陷,图 9 (d) 则引入4阶线性屈曲模态作为缺陷形式,缺陷系数均为0.01,不同的缺陷形状导致不同的非线性后屈曲变形。
 |
| 图 7 试验与Riks法应变-压缩载荷对比 Fig. 7 Comparison of strain-compressive load between test and Riks algorithm |
| 图选项 |
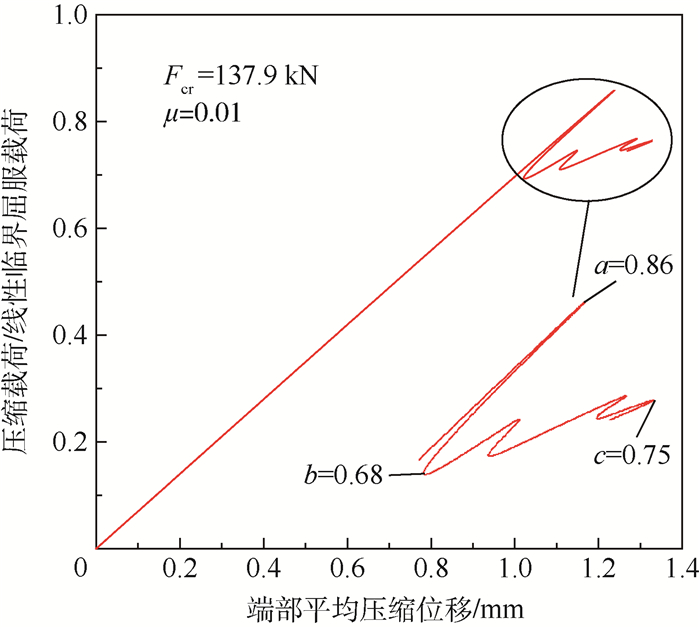 |
| 图 8 基于Riks法压缩载荷-端部平均压缩位移曲线 Fig. 8 Compressive load-average end shortening displacement curves based on Riks algorithm |
| 图选项 |
 |
| 图 9 基于Buckle和Riks法的不同模态变形 Fig. 9 Deformed shape of different modes based on Buckle and Riks algorithms |
| 图选项 |
根据Koiter理论,后屈曲初始阶段的性质可以由临界点的平衡状态是否稳定来判断。含口盖柱壳的压缩载荷-端部压缩位移曲线表明该结构能够获得稳定的后屈曲平衡路径,后屈曲极限强度能够达到103.4 kN,较下临界点屈曲载荷提高了约10.2%,结构在初始屈曲之后还有继续承载的能力。筋条的存在隔断了凹坑的周向和轴向扩展,限制屈曲变形在局部范围之内,Riks法擅于处理非线性和后屈曲一定阶段,但对于大变形压溃阶段可求助显式动力法。
3.4 含口盖柱壳几何缺陷敏感度分析 对薄壳结构在某种载荷条件下,在试验载荷远低于理论预测情况下发生的屈曲行为,可能的原因有:壳的厚度不均匀或者加载载荷不均匀以及不能保证精确的边界条件等,最新的研究表明, 初始几何缺陷是主要原因[15]。因此进行了初始几何缺陷敏感度分析,研究缺陷幅值对上临界屈曲载荷Fa的影响,缺陷模态仍选用Buckle算法线性临界模态,缺陷幅值由缺陷系数来控制,结果如图 10所示,随着缺陷幅值增大,上临界屈曲载荷降低,并且在1%~5%壳厚度区域载荷下降地最快,当几何缺陷增大到一定程度后,屈曲载荷变化趋于平缓。
 |
| 图 10 初始几何缺陷大小对上临界屈曲载荷影响 Fig. 10 Effect of initial geometric imperfection amplitude on up-critical buckling load |
| 图选项 |
4 结论 以1/3含口盖复合材料柱壳为研究对象,进行了线性特征值屈曲和含初始几何缺陷的非线性后屈曲分析, 并与试验结果进行了对比,在验证模型有效性的基础上,得出以下结论:
1) 含口盖柱壳线性Buckle算法所得屈曲载荷偏高,是一种理想化的分析,可作为结构稳定性分析初步评估;含初始几何缺陷的非线性Riks法屈曲载荷和屈曲模态更加贴近实际情况,在设计上非线性分析更加真实可靠。
2) Riks法计算结果表明1/3复合材料柱壳具有明显的后屈曲行为,非线性下临界载荷可作为屈曲设计载荷参考依据,后屈曲极限载荷相比下临界载荷能提高近10%,结构具有一定的后屈曲承载能力且后屈曲平衡路径是稳定的,结构设计上可以考虑这部分因素,提高结构利用效率。
3) 进行了初始几何缺陷的敏感性分析,表明含口盖柱壳结构对初始几何缺陷是非常敏感的,为了提高抗屈曲性能,应提高加工工艺质量,减少初始几何缺陷。
参考文献
| [1] | 范舟, 程小全, 李钟海, 等. 带口盖复合材料柱面壳压缩性能[J].北京航空航天大学学报, 2013, 39(1): 89–94.FAN Z, CHENG X Q, LI Z H, et al. Compressive behavior of composite cylinder shell[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(1): 89–94.(in Chinese) |
| [2] | JABAREEN M, SHEINMAN I. Buckling and sensitivity to imperfection of conical shells under dynamic step-loading[J].Journal of Applied Mechanics, 2007, 74(1): 74–80.DOI:10.1115/1.2178836 |
| [3] | SHEINMAN I, JABAREEN M. Postbuckling of laminated cylindrical shells in different formulations[J].AIAA Journal, 2005, 43(5): 1117–1123.DOI:10.2514/1.11557 |
| [4] | JABAREEN M. Rigorous buckling of laminated cylindrical shells[J].Thin-Walled Structures, 2009, 47(2): 233–240. |
| [5] | GOLDFELD Y. Elastic buckling and imperfection sensitivity of generally stiffened conical shells[J].AIAA Journal, 2007, 45(3): 721–729.DOI:10.2514/1.25830 |
| [6] | SHEINMAN I, GOLDFELD Y. Buckling of laminated cylindrical shells in terms of different theories and formulations[J].AIAA Journal, 2012, 39(9): 1773–1781. |
| [7] | SHEINMAN I, GOLDFELD Y. Shell theory accuracy with regard to initial postbuckling behavior of cylindrical shell[J].AIAA Journal, 2012, 42(2): 429–432. |
| [8] | SPAGNOLI A, CHRYSSANTHOPOULOS M K. Elastic buckling and postbuckling behaviour of widely-stiffened conical shells under axial compression[J].Engineering Structures, 1999, 21(9): 845–855. |
| [9] | 李钟海, 程小全, 汪源龙, 等. 复合材料柱面壳压缩性能分析[J].复合材料学报, 2011, 28(1): 206–210.LI Z H, CHENG X Q, WANG Y L, et al. Compressive properties analysis of composite cylindrical shells[J].Acta Materiae Compositae Sinica, 2011, 28(1): 206–210.(in Chinese) |
| [10] | 阎崇年, 范舟, 程小全, 等. 含开口复合材料柱面壳压缩性能[J].北京航空航天大学学报, 2012, 38(10): 920–924.YAN C N, FAN Z, CHENG X Q, et al. Compressive behavior of composite cylindrical shell with open hole[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10): 920–924.(in Chinese) |
| [11] | 王珂晟, 刘国强, 朱晓莹. 含初始缺陷的加强复合材料圆柱壳的非线性屈曲分析[J].机械设计与制造, 2004(2): 63–65.WANG K S, LIU G Q, ZHU X Y. Analysis on nonlinear buckling of reinforced laminated composite cylindrical shell with initial imperfection[J].Machinery Design and Manufacture, 2004(2): 63–65.(in Chinese) |
| [12] | 王毅, 罗永峰, 沈惠申. 各向异性复合材料圆柱薄壳轴压下的屈曲性能[J].同济大学学报, 2002, 30(6): 673–679.WANG Y, LUO Y F, SHEN H S. Post buckling analysis imperfect stiffened laminated cylindrical shell under axial compression[J].Journal of Tongji University, 2002, 30(6): 673–679.(in Chinese) |
| [13] | HILBURGER M W, STARNES J H JR. Buckling behavior of compression-loaded composite cylindrical shells with reinforced cutouts[J].International Journal of Non-Linear Mechanics, 2005, 40(7): 1005–1021. |
| [14] | 武鹏飞, 程小全, 张纪奎, 等. 开口及边界条件对复合材料三分之一柱面壳压缩屈曲性能的影响[J].复合材料学报, 2014, 31(6): 1525–1531.WU P F, CHENG X Q, ZHANG J K, et al. Effect of opening and boundary conditions on compressive buckling properties of composite one-third cylindrical shell[J].Acta Materiae Compositae Sinica, 2014, 31(6): 1525–1531.(in Chinese) |
| [15] | 杜启端. 现代薄壳非线性稳定性理论的发展和应用[J].强度与环境, 2002, 29(1): 41–51.DU Q R. The development and application of modern nonlinear stability theory of thin shell[J].Structure & Environment Engineering, 2002, 29(1): 41–51.(in Chinese) |
