但是针对编织复合材料紧固件的研究尚少,且对于板件的研究方法难以适用于紧固件的计算。其中,Mu等[17]建立了对碳/碳编织复合材料紧固件拉拔试验进行了分析,观察并得到了紧固件中存在层间滑移、碳布面内剪切破坏和纤维束拉断3种破坏模式,并建立紧固件有限元模型进行了对比。Guan等[18]基于试验观察发现碳/碳复合材料紧固件破坏区域为螺牙根部,并基于锥形短梁理论建立紧固件螺牙理论模型进行了验证。卢子兴等[19]基于三维Hashin失效准则对C/SiC编织复合材料紧固件拉拔试验进行了有限元模拟,得到了紧固件拉拔强度与螺牙有关几何参数的变化关系。
综合上述文献,在单胞研究过程中,单胞数值模型中划分出了纤维和基体区域。但是结构元件数值模型中没有划分出纤维和基体区域,而是统一采用等效计算后的弹性性能参数,并且一般采用跨尺度计算方法进行失效分析。该种方法通常适用于板件以及大型元件的研究,但是对于紧固件,由于其螺牙的尺寸与单胞的尺寸处于同一量级,因而需要对紧固件模型进行纤维和基体区域的划分以进行深入研究。
本文作者针对碳/碳缎纹编织复合材料紧固件,建立简化单胞结构组成的螺牙有限元模型模拟紧固件拉拔破坏过程,进行了紧固件拉拔试验,分析了试件破坏模式,验证了有限元模型的有效性。
1 试件基本属性 本文所研究的单螺牙紧固件(试验件)细观结构为缎纹编织,其单胞结构由8根经向纤维束和8根纬向纤维束交织成的纤维布、穿刺纤维束以及周围的基体组成,如图 1所示,该图中并未显示基体成分。单胞几何参数如表 1[16]所示。
 |
| 图 1 8枚缎纹编织复合材料单胞 Fig. 1 RVE of 8-harness satin weave composite |
| 图选项 |
表 1 缎纹编织复合材料单胞几何参数[16] Table 1 Geometric parameters of satin weave composite RVE[16]
| 几何参数 | 数值 |
| 单胞宽度/mm | 10.40 |
| 单胞厚度/mm | 0.46 |
| 经纬向纤维束宽度/mm | 0.60 |
| 经纬向纤维束高度/mm | 0.20 |
| 穿刺纤维束横截面直径/mm | 0.58 |
表选项
试验件如图 2所示,由螺钉和螺母构成,其中螺钉一端为单螺牙,另一端为多螺牙。试验件几何尺寸如表 2所示。螺钉加工方向如图 3所示,其中紧固件轴向方向平行于碳布。对比表 1和表 2的数据可以看出,紧固件部分细节尺寸,如螺牙间距和螺牙高度,与单胞的主要尺寸,如单胞厚度和穿刺纤维束横截面直径,差距不明显。在涉及螺牙计算时,由于纤维和基体材料属性差异而导致单胞内部应力分布不均匀的情况不能忽略。因而,在进行紧固件有限元模拟时,赋予统一的材料属性不能有效地反映螺牙的受载情况。
 |
| 图 2 缎纹编织碳/碳复合材料紧固件 Fig. 2 Satin weave carbon/carbon composite fastener |
| 图选项 |
表 2 缎纹编织碳/碳复合材料试验件尺寸 Table 2 Sizes of satin weave carbon/carbon composite specimen
| 几何尺寸 | 数值 |
| 螺牙间距/mm | 1.5 |
| 螺牙顶角/(°) | 60 |
| 螺牙高度/mm | 1.3 |
| 光杆直径/mm | 10 |
表选项
 |
| 图 3 缎纹编织碳/碳复合材料试验件加工方向示意图 Fig. 3 Schematic diagram of processing direction of satin weave carbon/carbon composite specimen |
| 图选项 |
本文研究对象基于碳/碳复合材料,其中T300碳纤维和无孔隙碳基体的材料属性如表 3[20]和表 4所示。
表 3 T300纤维材料力学性能[20] Table 3 Mechanical properties of T300 fiber[20]
| 性能参数 | 数值 |
| 纵向弹性模量Ef1/GPa | 230 |
| 横向弹性模量Ef2/GPa | 15 |
| 纵横剪切模量Gf12/GPa | 15 |
| 纵横主泊松比νf21 | 0.2 |
| 横向剪切模量Gf23/GPa | 7 |
| 横向泊松比νf23 | 0.07 |
| 纵向拉伸强度XfT/MPa | 2 500 |
| 纵向压缩强度XfC/MPa | 2 000 |
表选项
表 4 无孔隙碳基体材料力学性能 Table 4 Mechanical properties of pure carbon matrix
| 性能参数 | 数值 |
| 弹性模量Em/GPa[16] | 9.254 |
| 泊松比νm[16] | 0.23 |
| 剪切强度/MPa[15] | 37.6 |
表选项
2 试 验 由于目前对于编织复合材料还没有统一的试验规范和标准,试验方法参照纤维增强塑料拉伸性能试验方法ASTM D7332/D7332M-15a[21]进行。试验夹具和试验件装卡示意图如图 4所示,试验过程中上底板的向下移动导致中间两装卡板的背离运动,从而实现对试件的拉拔效果。试验采用时代试金WDW-200E微机控制电子式万能试验机(中国山东时代试金试验机有限公司)进行。将夹具放置于试验机压缩空间内,采用0.5 mm/min位移加载方式进行加载。当载荷越过最高值点并下降到90%左右时停止试验,如此保留试验件的初始损伤状态。
 |
| 图 4 紧固件拉拔试验夹具 Fig. 4 Fixture of fastener tensile test |
| 图选项 |
试验破坏载荷如表 5所示,载荷-位移曲线如图 5所示。图 6所示为载荷下降至最高值90%时试验件的破坏照片。
表 5 缎纹编织碳/碳复合材料单牙紧固件拉拔试验结果 Table 5 Results of satin weave carbon/carbon composite single thread fastener tensile test
| 试验名称 | 破坏载荷/N |
| 单牙螺钉拉拔 | 905.70 |
表选项
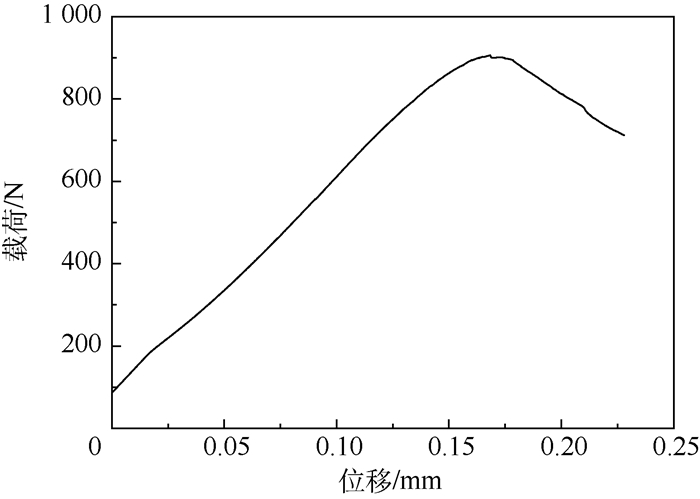 |
| 图 5 试验载荷-位移曲线 Fig. 5 Force-displacement curve of test |
| 图选项 |
 |
| 图 6 缎纹编织碳/碳复合材料单牙紧固件试验后照片 Fig. 6 Photographs of satin weave carbon/carbon composite single thread fastener after test |
| 图选项 |
3 数值模拟 3.1 数值模型的建立 本文基于ABAQUS商用有限元分析软件建立有限元模型,采用三维实体线性四面体单元C3D4。在建立缎纹编织单胞结构模型过程中,为兼顾有限元模型与真实情况的契合度以及有限元计算的可实现性,需要对缎纹编织碳布结构做出简化但仍保留穿刺纤维束以及碳布层间的基体。简化单胞结构有限元模型如图 7所示,其中绿色部分为碳布,白色部分为穿刺纤维束,红色部分为碳布层间基体。
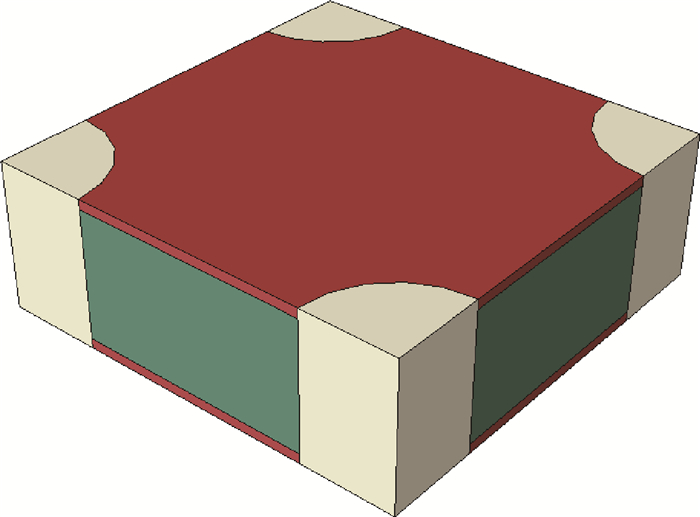 |
| 图 7 缎纹编织简化单胞有限元模型 Fig. 7 Finite element model of simplified satin weave RVE |
| 图选项 |
试验件破坏发生在单螺牙端,也即试验件的破坏载荷是由单螺牙的强度决定,本文以单螺牙为研究对象建立有限元模型进行研究。螺牙模型是由堆叠若干层的缎纹编织简化单胞结构中切取而成,螺母模型为统一材料属性,如图 8所示。图 9为螺牙与螺母装配后的有限元网格。
 |
| 图 8 螺牙及螺母有限元模型 Fig. 8 Finite element models of thread and nut |
| 图选项 |
 |
| 图 9 螺牙及螺母有限元网格 Fig. 9 Finite element grids of thread and nut |
| 图选项 |
3.2 材料属性及失效判断准则 螺牙有限元模型中,穿刺纤维束和层间基体分别为单一材料属性,见表 3和表 4。对于穿刺纤维束部分,失效判断采用最大应力准则:
 | (1) |
式中:σ11f为纤维束纵向正应力。对于基体部分,失效判断采用Mises应力准则:
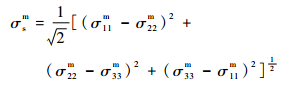 | (2) |
式中:σsm为基体屈服强度:σ11m、σ22m和σ33m分别为基体在3个方向的主应力。其中基体屈服强度约为剪切强度的2倍[15]。为保证结果精确同时确保有限元计算的可实现性,对于穿刺纤维束和层间基体部分,当组分材料发生损伤后,弹性参数分别折减至原来的1/1 000。
碳布部分实际仍为经纬向交叠纤维束和周围基体共同组成。碳布部分的材料属性需要采用混合率方法进行计算。碳布面内弹性模量和面内泊松比的计算过程可以参考文献[22]。将碳布单元划分为上、下两层,如图 10[22]所示,并做出假设:①上、下两部分在同一面内方向(方向1或方向2)的应变相等;②整个碳布单元中内应力保持平衡。
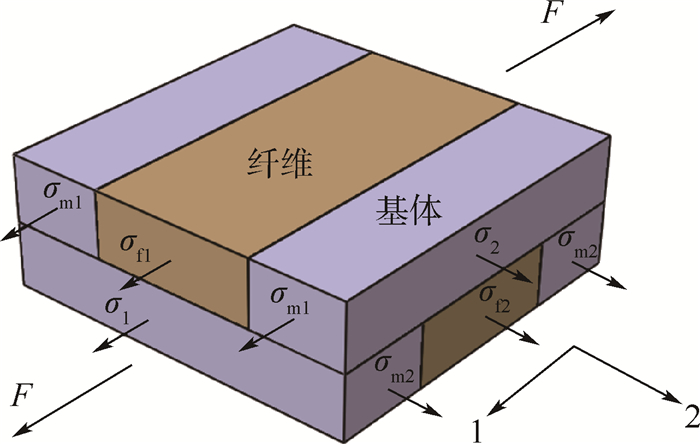 |
| F—碳布单元受力;σf1—上层纤维束1方向正应力;σf2—下层纤维束2方向正应力;σm1, σ1—上层和下层基体1方向正应力;σm2, σ2—下层和上层基体2方向正应力。 图 10 碳布单元受力状态[22] Fig. 10 Forced state of carbon cloth element[22] |
| 图选项 |
根据上述假设,可得
 | (3) |
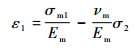 | (4) |
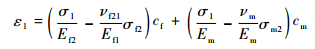 | (5) |
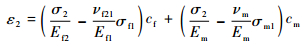 | (6) |
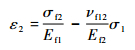 | (7) |
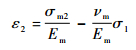 | (8) |
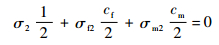 | (9) |
式中:ε1和ε2分别为1方向和2方向的应变;cf和cm分别是碳布单元中纤维束和基体的体积分数;νf12为纵横向次泊松比,且满足
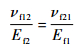 | (10) |
式(3)~式(9)可以整理为矩阵形式:
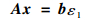 | (11) |
式中:
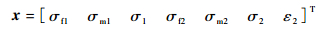 | (12) |
A和b均为只与材料参数和组分体积分数有关的常数矩阵和常数向量。
求解式(11)可得
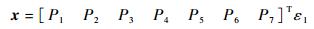 | (13) |
式中:P1, P2, …, P7均为只与材料参数和组分体积分数有关的常数。
则碳布有效面内弹性模量E1cloth和有效面内泊松比ν21cloth分别为
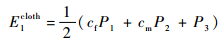 | (14) |
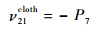 | (15) |
碳布离面弹性模量、剪切模量和离面泊松比的计算则采用混合率方法:
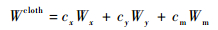 | (16) |
式中:Wcloth为所要计算的碳布等效弹性参数;Wx、Wy和Wm分别为纬向纤维束、经向纤维束和基体相应的弹性参数;cx和cy分别为纬向纤维束和经向纤维束在碳布单元中各自的体积分数。碳布弹性参数如表 6所示。
表 6 碳布有效力学性能 Table 6 Effective mechanical properties of carbon cloth
| 性能参数 | 数值 |
| 面内弹性模量/GPa | 58.4 |
| 面内泊松比 | 0.010 5 |
| 面内剪切模量/GPa | 5.41 |
| 离面弹性模量/GPa | 12.2 |
| 离面泊松比 | 0.18 |
| 离面剪切模量/GPa | 7.44 |
表选项
碳布的失效判断方法采用跨尺度计算,见文献[23]。跨尺度计算是建立宏观量与细观量的联系,将宏观量转化为细观量,通过细观的破坏准则进行宏观模型的失效判断。本文采用细观应力破坏准则,并建立宏观应力与细观应力之间的联系。宏观机械应力可以分解为6个方向应力分量的叠加。在单胞模型上分别施加6个方向的单位应力,计算得到纤维和基体上选定参考点的相应应力值,从而得到各参考点的应力放大系数矩阵。细观应力与宏观应力之间的关系表达式为
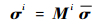 | (17) |
式中:σi为第i处参考点细观应力;Mi为第i处参考点机械应力放大系数矩阵;σ为所施加的宏观应力。计算得到第i处参考点的细观应力后,根据其所属的组分材料,分别采用上述纤维最大应力准则或基体Mises应力进行判断且当组分材料发生损伤后,需要对各自弹性参数折减至原来的1/1 000。对于碳布部分,需要将纤维或基体折减后的性能参数代入式(3)~式(15),重新计算折减后的碳布单元弹性参数。
螺母与螺钉实际采用相同的缎纹编织材料,由经向纤维束、纬向纤维束、穿刺纤维束和基体构成。本文并不涉及螺母螺牙的破坏研究且为保证螺钉螺牙各端面接触条件相同,因而须将螺母赋予各向同性材料属性,由于螺母碳布平面为主承载面,因而螺母弹性参数简化处理为整体单胞面内弹性参数。文献[16]已得到面内弹性模量,泊松比可根据碳布、穿刺纤维束和层间基体各自属性由混合率方法计算得到,见表 7。
表 7 螺母有效力学性能 Table 7 Effective mechanical properties of nut
| 性能参数 | 数值 |
| 螺母弹性模量/GPa[16] | 39.92 |
| 螺母泊松比 | 0.05 |
表选项
3.3 数值计算与结果 有限元计算过程中,螺母的上表面采用固支边界条件,螺钉的下横截面进行位移加载。
图 11所示为螺牙失效分布图,图 11(a)和图 11(b)分别为整体模型失效和层间基体失效分布图。
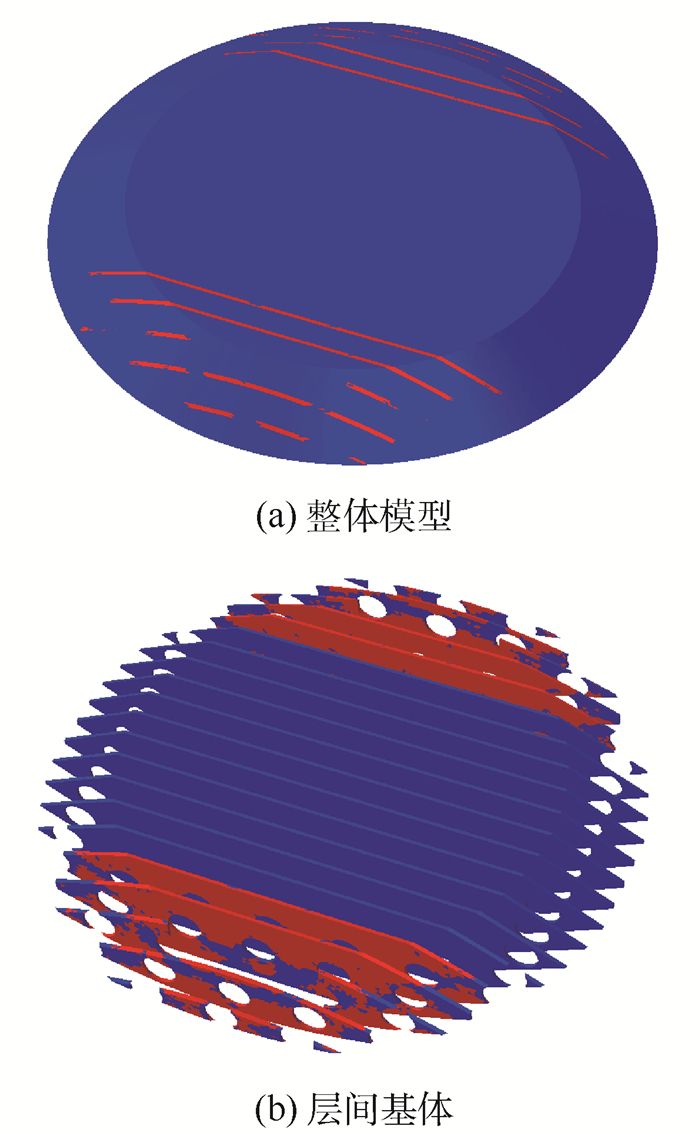 |
| 图 11 螺牙失效分布图 Fig. 11 Failure distribution of thread |
| 图选项 |
4 结果与讨论 图 12为试验和有限元方法(FEM)载荷-位移曲线,可以看出2条曲线的趋势相同。需要说明的是,有限元模型为单一螺牙,故计算位移为试件的局部变形,而试验位移包括整个试件的变形及试验机行程误差,二者存在量级差别。
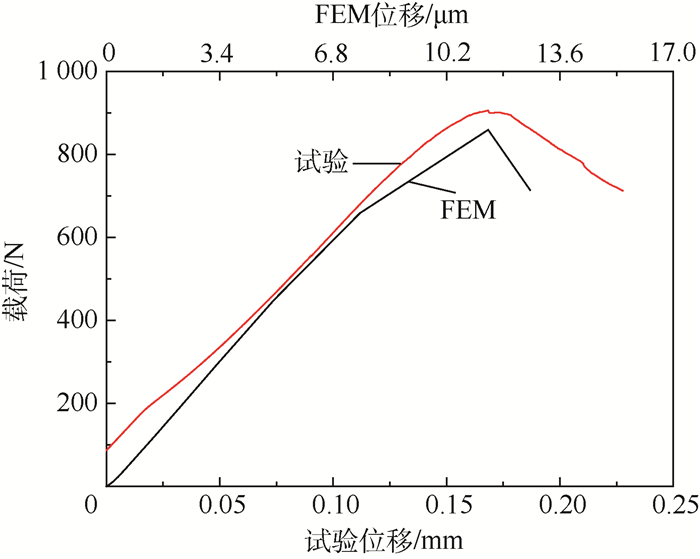 |
| 图 12 试验和有限元方法载荷-位移曲线 Fig. 12 Force-displacement curves of test and FEM |
| 图选项 |
表 8所示为试验和有限元方法破坏载荷的对比。从表 8可以看出,有限元方法破坏载荷与试验破坏载荷误差为5.17%,验证了有限元模型的有效性。
表 8 试验和有限元方法破坏载荷 Table 8 Damage forces of test and FEM
| 试验名称 | 破坏载荷 | ||
| 试验/N | FEM/N | 误差/% | |
| 单牙螺钉拉拔 | 905.70 | 858.86 | 5.17 |
表选项
从试验后照片图 6可以看出,螺牙并没有发生整体破坏。螺牙在穿刺纤维束垂直端面发生大面积剥落并露出穿刺纤维束横截面,而在穿刺纤维束平行端面仍残留有螺牙结构。有限元计算结果图 11显示,螺牙结构中碳布和穿刺纤维束并未发生破坏,在穿刺纤维束垂直端面层间基体发生大面积破坏。可以得出,初始损伤阶段试验件在穿刺纤维束垂直端面的螺牙剥落是由于该处层间基体失效引起。
5 结 论 1) 对缎纹编织碳/碳复合材料紧固件拉拔力学行为进行了数值模拟,建立了非统一材料属性宏观试件的有限元模型,并验证了其可行性。
2) 进行了缎纹编织碳/碳复合材料紧固件拉拔试验,观察并分析了其破坏模式。
3) 有限元计算破坏载荷与试验破坏载荷误差为5.17%,有限元计算破坏模式与试验破坏模式相符合,均为螺牙的不完全破坏,破坏区域发生在穿刺纤维束垂直端面。
参考文献
| [1] | 魏高峰, 孙晓强, 刘国永, 等. 三维编织复合材料几何建模及数值分析[J].固体力学学报, 2011, 32(Suppl.): 65–69.WEI G F, SUN X Q, LIU G Y, et al. Geometric model for three-dimensional braided composites and its numerical analysis[J].Chinese Journal of Solid Mechanics, 2011, 32(Suppl.): 65–69.(in Chinese) |
| [2] | 董伟锋, 肖军, 李勇, 等. 2.5维编织复合材料弹性性能的理论研究[J].南京航空航天大学学报, 2005, 37(5): 659–663.DONG W F, XIAO J, LI Y, et al. Theoretical study on elastic properties of 2.5D braided composites[J].Journal of Nanjing University of Aeronautics and Astronautics, 2005, 37(5): 659–663.(in Chinese) |
| [3] | 郑君, 温卫东, 崔海涛, 等. 2.5维机织结构复合材料的几何模型[J].复合材料学报, 2008, 25(2): 143–148.ZHENG J, WEN W D, CUI H T, et al. Geometric model of 2.5 dimensional woven structures[J].Acta Materiae Compositae Sinica, 2008, 25(2): 143–148.(in Chinese) |
| [4] | 曹海建, 钱坤, 盛东晓. 2.5维机织复合材料的几何结构模型与验证[J].纺织学报, 2009, 30(5): 58–62.CAO H J, QIAN K, SHENG D X. Geometry model and experimental verification of 2.5-D woven composites[J].Journal of Textile Research, 2009, 30(5): 58–62.(in Chinese) |
| [5] | 杨振宇, 俸翔, 苏洲, 等. 2.5D编织复合材料细观结构及弹性性能[J].宇航材料工艺, 2010(2): 67–71.YANG Z Y, FENG X, SU Z, et al. Meso-structure and elastic properties of 2.5D braided composites[J].Aerospace Materials and Technology, 2010(2): 67–71.(in Chinese) |
| [6] | 卢子兴, 冯志海, 寇长河, 等. 编织复合材料拉伸力学性能的研究[J].复合材料学报, 1999, 16(3): 129–134.LU Z X, FENG Z H, KOU C H, et al. Studies on tensile properties of braided structural composite materials[J].Acta Materiae Compositae Sinica, 1999, 16(3): 129–134.(in Chinese) |
| [7] | COX B N, DADKHAH M S, MORRIS W L. On the tensile failure of 3D woven composites[J].Composites Part A:Applied Science and Manufacturing, 1996, 27(4): 47–58. |
| [8] | CALLUS P J, MOURITZ A P, BANNISTER M K, et al. Tensile properties and failure mechanisms of 3D woven GRP composites[J].Composites Part A:Applied Science and Manufacturing, 1999, 30(12): 77–87. |
| [9] | BIGAUD D, HAMELIN P. Mechanical properties prediction of textile reinforced composite materials using a multiscale energetic approach[J].Composite Structures, 1997, 38(1-4): 361–371.DOI:10.1016/S0263-8223(97)00071-8 |
| [10] | 卢子兴, 刘振国, 麦汉超, 等. 三维编织复合材料强度的数值预报[J].北京航空航天大学学报, 2002, 28(5): 563–565.LU Z X, LIU Z G, MAI H C, et al. Numerical prediction of strength for 3D braided composites[J].Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(5): 563–565.(in Chinese) |
| [11] | ZENG T, WU L Z, GUO L C. A finite element model for failure analysis of 3D braided composites[J].Materials Science and Engineering:A, 2004, 366(1): 144–151.DOI:10.1016/j.msea.2003.09.054 |
| [12] | WAN Y M, WANG Y J, GU B H. Finite element prediction of the impact compressive properties of three-dimensional braided composites using multi-scale model[J].Composite Structures, 2015, 128: 381–394.DOI:10.1016/j.compstruct.2015.03.066 |
| [13] | LU Z X, ZHOU Y, YANG Z Y, et al. Multi-scale finite element analysis of 2.5D woven fabric composites under on-axis and off-axis tension[J].Computational Materials Science, 2013, 79: 485–494.DOI:10.1016/j.commatsci.2013.07.003 |
| [14] | YU X G, CUI J Z. The prediction on mechanical properties of 4-step braided composites via two-scale method[J].Composites Science and Technology, 2007, 67(3-4): 471–480.DOI:10.1016/j.compscitech.2006.08.028 |
| [15] | 袁辉.碳/碳复合材料刚度与强度预测模型研究[D].南京:南京航空航天大学,2009:23-50,113.YUAN H.Research on prediction models for stiffness and strength of C/C composites[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2009:23-50,113(in Chinese). |
| [16] | 阚晋.碳/碳复合材料微细观结构的表征及对有效性能的影响研究[D].哈尔滨:哈尔滨工业大学,2010:39,91-95.KAN J.Investigation on characterization of micro and meso structures and their influence on effective properties of carbon/carbon composites[D].Harbin:Harbin Institute of Technology,2010:39,91-95(in Chinese). |
| [17] | MU J W, GUAN Z D, BIAN T Y, et al. The experiment and numerical simulation of composite countersunk-head fasteners pull-through mechanical behavior[J].Applied Composite Materials, 2014, 21(5): 773–787.DOI:10.1007/s10443-013-9379-7 |
| [18] | GUAN Z D, MU J W, SU F, et al. Pull-through mechanical behavior of composite fastener threads[J].Applied Composite Materials, 2015, 22(3): 251–267.DOI:10.1007/s10443-014-9404-5 |
| [19] | 卢子兴, 廖强, 杨振宇, 等. C/SiC复合材料螺栓螺牙承载能力[J].复合材料学报, 2015, 32(1): 182–187.LU Z X, LIAO Q, YANG Z Y, et al. Load bearing capability pf thread teeth of C/SiC composite bolts[J].Acta Materiae Compositae Sinica, 2015, 32(1): 182–187.(in Chinese) |
| [20] | SODEN P D, HINTON M J, KADDOUR A S. Lamina properties,lay-up configurations and loading conditions for a range of fiber-reinforced composite laminates[J].Composites Science and Technology, 1998, 58(7): 1011–1022.DOI:10.1016/S0266-3538(98)00078-5 |
| [21] | American Society for Testing and Materials International.Standard test method for measuring the fastener pull-through resistance of a fiber-reinforced polymer matrix composite:ASTM D7332/D7332-15a[S].West Conshohocken,PA:American Society for Testing and Materials International,2007. |
| [22] | BIAN T Y,GUAN Z D,MU J W,et al.An analytical model for predicting the tension modulus and Poisson's ratio of satin weave composites[C/OL]//Proceedings of 20th International Conference on Composite Materials(ICCM).[S.l.]:International Committee on Composite Materials,2015[2015-05-18] http://www.iccm-central.org/Proceedings/ICCM20proceedings/papers/paper-P105-4.pdf. |
| [23] | 李星, 关志东, 刘璐, 等. 基于应变不变量失效理论的复合材料损伤模拟[J].北京航空航天大学学报, 2013, 39(2): 190–195.LI X, GUAN Z D, LIU L, et al. Damage simulation of composite materials based on strain invariant failure theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 190–195.(in Chinese) |
