目前,国内外****在复合材料铺层优化方面进行了大量研究。文献[1]提出一种改进模拟退火算法对复合材料层合板进行频率优化,设计变量为铺层角度和铺层数2种离散变量。文献[2]提出一种改进遗传算法来进行复合材料板的频率优化,设计变量为成对组合的铺层组。文献[3]在初步设计复合材料板结构和铺层方案的基础上,运用遗传算法实现复合材料板的多目标优化。文献[4]通过复合材料板参数优化和铺层顺序优选两步法实现了层合板频率优化。文献[5]通过一种从外层到内层的分层优化方法来进行复合材料板的频率优化。文献[6-7]则是通过对复合材料板的变刚度设计,来使复合材料结构更加高效。文献[8]设计铺层角度的同时,采用拓扑优化的思想,优化铺层材料在叠层材料中的分布。文献[9]提出了一种整数编码策略,以整数来表示铺层参数,并用遗传算法进行求解。文献[10]固定铺层厚度,以铺层角度作为设计变量来优化铺层顺序,采用蚁群算法求解。文献[11]对卫星承力筒复合材料结构进行了优化,以减重为目标,以固有频率和屈曲稳定性作为约束,保持铺层角度与铺层顺序不变,设计变量为每层铺层的厚度。以上研究是从铺层顺序、铺层角度和铺层厚度这些因素来进行优化,设计变量以离散变量为主,离散变量能有效地描述复合材料的铺层方式,但设计变量数会随着层数的增加而增加,因此计算量大,难以在实际工程中应用。
本文针对卫星天线复合材料框架的铺层优化问题,提出了一种复合材料铺层的两阶段优化方法。阶段Ⅰ目的是铺层顺序的优化,以框架的基频最大化作为优化目标。对于卫星天线框架,由于框架各梁的力学边界条件不同,因此每根梁的复合材料铺层均需单独作为设计变量,从而使得卫星天线框架铺层的优化问题的设计变量数上升。为了减少设计变量数量,本文将各离散变量映射成连续变量,从而阶段Ⅰ的优化问题由离散变量优化问题转换为连续变量优化问题,然后应用粒子群优化(PSO)算法求解。阶段Ⅱ目的是减少复合材料的铺层数,建立了多目标拓扑优化模型,优化目标为基频最大化与质量最小化,设计变量为各铺层相对于自身厚度的相对厚度,该相对厚度的取值为1或0,取1表示保留该铺层,取0表示去除该铺层,该阶段数学模型应用第2代非劣排序遗传算法(NSGA-Ⅱ)进行求解。最后基于该两阶段优化方法对某大型卫星天线框架的复合材料铺层进行优化设计,验证该方法的有效性。
1 复合材料框架的铺层优化设计问题 复合材料是一种各向异性严重不均匀的材料,尽管其纵向性能优秀,但是横向性能以及层间性能较差[12-13]。因此需要对复合材料参数进行设计,它包括:各单层的纤维方向(即铺层角度)、各单层的厚度和总体的排列顺序。在实际工程中,复合材料的优化问题通常是将每层的铺层角度作为设计变量,铺层角度一般由一组给定的角度组成,如{-45°, 0, 45°, 90°}。因此,复合材料的铺层优化是离散变量优化问题。
对于卫星天线复合材料材料框架的铺层优化,通常要求框架整体的基频高并且框架的质量低,因此框架的铺层优化为多目标优化。由于框架的铺层优化需同时考虑铺层顺序以及铺层数目,使得铺层优化问题的复杂度升高,因此,本文将复合材料框架的铺层优化分成2个阶段,以降低优化问题的复杂度。
1.1 阶段Ⅰ:铺层顺序优化设计 在优化阶段Ⅰ中,目的是得出一个初始的铺层方案,以天线框架的基频最大为目标,其数学模型为
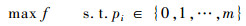 | (1) |
式中:f为天线框架的基频;pi为各铺层的角度,其中i∈{1, 2, …, n},n为各区域叠层复合材料的总铺层数;{0, 1, …, m}对应m+1种铺层角度。叠层复合材料的铺层顺序及角度用pi所构成的m+1进制数来表示,例如某区域所允许的铺层角度有4种,铺层方案为[0°/-45°/45°/90°],则该四进制表示形式为1023。
如式(1) 所示数学模型的设计变量数为n。随着天线框架结构的复杂性提高,各区域叠层复合材料的总铺层数n增高。为了方便计算,降低设计变量的个数,将该m+1进制数映射为连续的整型变量xj:
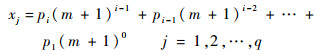 | (2) |
式中:q为划分的区域数;xj对应着第j个区域,则第j个区域的叠层复合材料的铺层形式可由一个实数变量来表示。设计变量数由n变为q,变量类型由离散变量转换为连续变量,xj的最大值为
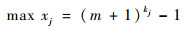 | (3) |
式中:kj为第j个区域的铺层数量。
综上,阶段Ⅰ数学模型由式(1) 变为
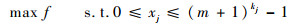 | (4) |
由于式(2) 的映射,阶段Ⅰ的优化问题从离散变量优化问题转换成了连续变量优化问题,因此可以结合现代优化算法求解。
本文采用PSO算法[14]对阶段Ⅰ数学模型进行求解。将式(4) 的xj作为粒子,搜索空间为q维,群体中的粒子在第t代的位置表示为一个q维向量,即xt=(x1t, x2t, …, xqt),粒子速度表示为vt=(v1t, v2t, …, vqt)。在粒子群的每次迭代中,粒子需要找到个体极值pbest和全局极值gbest,位置分别为pt=(p1t, p2t, …, pqt)和pgt=(pg1t, pg2t, …, pgqt)。则粒子的速度和位置的迭代格式可分别表示为
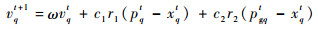 | (5) |
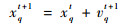 | (6) |
式中:ω为惯性系数;c1和c2为加速常数;r1和r2为在[0, 1]范围里服从均匀分布的2个独立随机数。
1.2 阶段Ⅱ:铺层的多目标拓扑优化 为了减小卫星天线框架整体质量,基于阶段Ⅰ所得的优化结果进行多目标拓扑优化,优化目标为框架的基频最大化及框架整体质量最小化。优化数学模型为
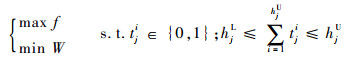 | (7) |
式中:W为天线的质量;hjU和hjL为第j个区域铺层数的上下边界;tji为第j个区域的第i铺层的相对厚度,tji取1表示保留该铺层,tji取0表示去除该铺层。
对于卫星天线复合材料框架的铺层多目标优化问题,各个目标间通常是相互冲突的,在减少铺层数目、降低质量的同时,框架刚度会下降,从而框架的基频也会降低。因此,给出该多目标优化的Pareto最优解集,供设计人员根据工程需要选择合适的解。Pareto最优解集由Pareto最优解构成,Pareto最优解定义为[15]:若对于多目标优化的可行域中的一点t*,不存在另一个可行点t′,使fq(t′)≤fq(t*),其中q=1, 2, …, k,并且至少有一个严格不等式成立,则称t*是多目标优化的一个Pareto最优解。
对于阶段Ⅱ的多目标拓扑优化数学模型,本文采用NSGA-Ⅱ[16]求解。将相对厚度tji所构成的序列作为父代。在群体的进化过程中,父代群体通过交叉变异操作得到新的子群体,并且与新的子群体合并。根据Pareto最优关系将个体按目标函数向量进行两两比较,将个体分成多个前沿层。当个体属于不同的Pareto层时,通过评价Pareto优越性来评定个体的优劣;当个体属于同一个Pareto层时,以聚集距离来评判个体的优劣。
1.3 两阶段优化方法的优化过程 综合以上内容可以给出复合材料框架铺层的两阶段优化方法,其流程如图 1所示。首先将铺层数定为条件允许的最大值,以四进制数的形式表示出各区域的铺层角度与铺层顺序;然后将四进制变量映射为连续变量,以映射所得到连续变量作为粒子,应用PSO算法进行各铺进行求解;在阶段Ⅰ得到的铺层序列基础上,对每个铺层引入相对厚度;以各铺层的相对厚度所构成的序列作为父代群体,采用NSGA-Ⅱ求解;最后得到Pareto最优解集。
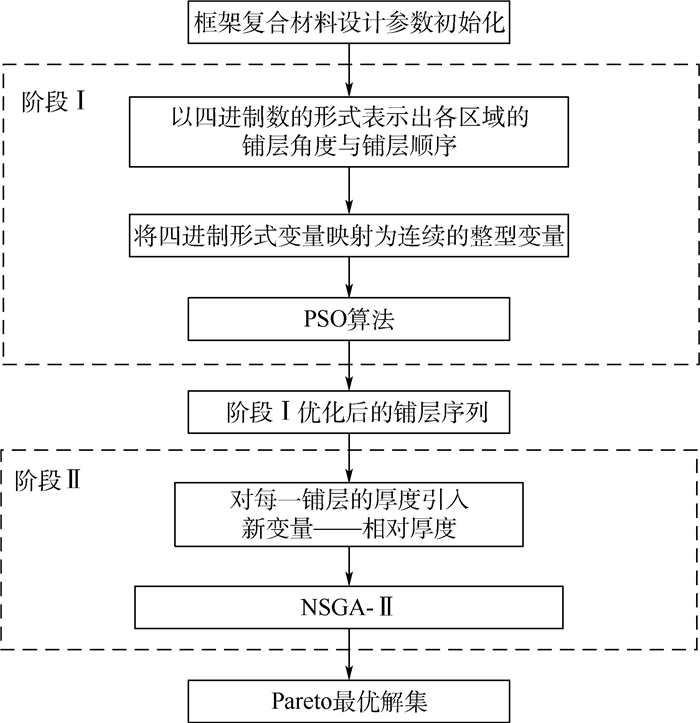 |
| 图 1 卫星天线复合材料框架铺层设计优化流程图 Fig. 1 Flowchart of layup design optimization of composite frame for satellite antenna |
| 图选项 |
2 应用实例 如图 2所示为某卫星天线复合材料框架。该框架的长边为矩形梁,两端短边为槽形梁,其余为工字梁,如图 3所示。各梁的铺层方式一致,均为[0°/45°/-45°/90°]重复铺叠,层数为32,每层厚度为0.125 mm,0°沿梁的长度方向,铺层材料为M40。框架的约束点位置如图 4所示,每个约束点均为六方向约束。对于本实例,基于Patran/Nastran软件建立了复合材料框架的模型,其响应分析方法为有限元法。该方案下的框架质量为38.37 kg,一阶频率为41.42 Hz。
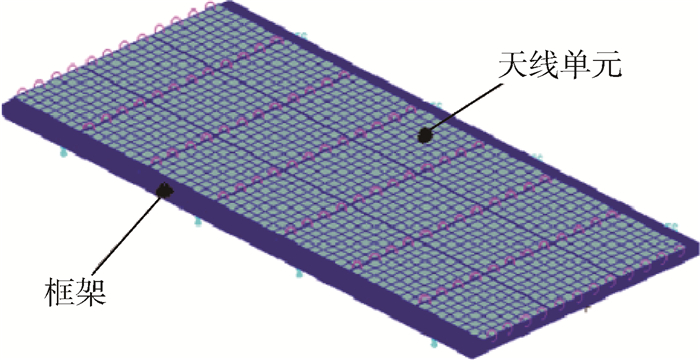 |
| 图 2 卫星天线装配图 Fig. 2 Assembly drawing of satellite antenna |
| 图选项 |
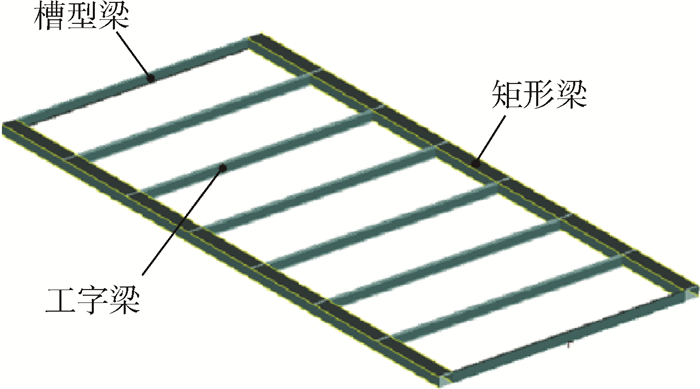 |
| 图 3 卫星天线框架 Fig. 3 Frame of satellite antenna |
| 图选项 |
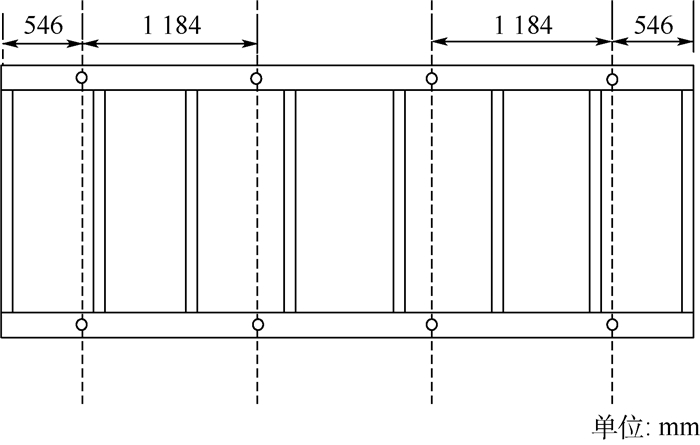 |
| 图 4 框架的8个约束点位置 Fig. 4 Position of eight constraint points of frame |
| 图选项 |
2.1 阶段Ⅰ的模型求解 在阶段Ⅰ中,m取3,{0, 1, 2, 3}对应铺层角度{-45°, 0°, 45°, 90°}。所允许的铺层最大层数为40,叠层复合材料为对称铺层的形式,因此,每个区域的铺层只需考虑对称的20层。
将框架材料铺层划分为3个区域,A区域为矩形梁(见图 5(a));B区域为工字梁(见图 5(b))和槽型梁(图 5(c))的上下表面;C区域为工字梁和槽型梁的竖直面。
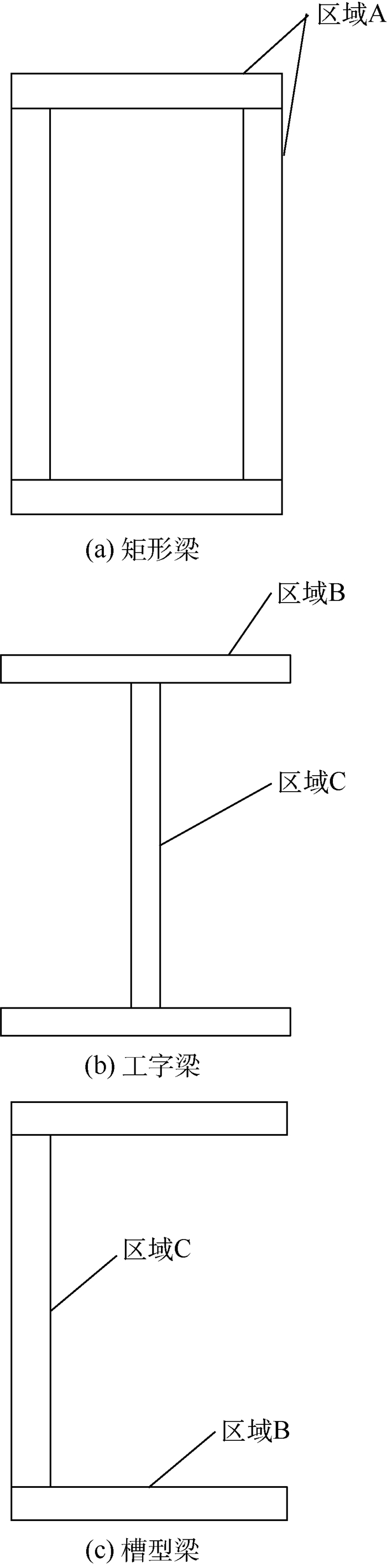 |
| 图 5 矩形梁、工字梁及槽型梁 Fig. 5 Rectangular beam, I-shape beam and U-shape beam |
| 图选项 |
A、B、C 3个区域的叠层复合材料的铺层形式可由3个实数变量来表示,如式(8) 所示。
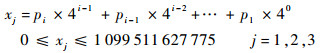 | (8) |
PSO算法的参数设置如表 1所示,其求解结果为x1=875 201 370 783、x2=366 537 432 406和x3=572 180 961 877,对应的铺层序列分别为[33122210101021033203]、[21111311111131111111]和[11112212012202301102]。A区域和C区域的各铺层角度分布较均匀,B区域的0°铺层数明显多于A区域和C区域的0°铺层数,说明框架B区域的沿梁的长度方向的铺层纤维对整体刚度的提高贡献大。
表 1 PSO参数设置 Table 1 Parameters setting of PSO
| 参数 | 最大迭代次数 | 粒子数 | 惯性权重 | 全局增量 | 粒子增量 | 最大搜索速度 |
| 数值 | 20 | 12 | 0.9 | 0.9 | 0.9 | 0.1 |
表选项
为了说明阶段Ⅰ的数学模型求解中采用由离散变量映射得到的实数变量比直接采用离散变量更有效率,应用PSO算法对离散变量下的数学模型进行求解,结果如表 2所示。比较可知,在迭代次数均为20的情况下,连续变量对应的求解结果优于离散变量对应的求解结果。
表 2 阶段Ⅰ求解结果 Table 2 Solving results of phase Ⅰ
| 变量类型 | x1(铺层序列) | x2(铺层序列) | x3(铺层序列) | 基频/Hz | 质量/kg | 迭代次数 |
| 连续变量 | [33122210101021033203] | [21111311111131111111] | [11112212012202301102] | 53.93 | 45.71 | 20 |
| 离散变量 | [21031003122122102102] | [13131113131112111110] | [13101011220213222221] | 52.49 | 45.71 | 20 |
表选项
2.2 阶段Ⅱ的模型求解 阶段Ⅱ算法设置如表 3所示,经过求解得到Pareto最优解集如表 4所示。其中方案19的基频的提升幅度在Pareto最优解集中最大,相对初始方案,基频提高了19.78%,质量降低了7.06%;方案20的质量的降低幅度在Pareto最优解集中最大,相对初始方案,基频提高了6.01%,质量降低了27.47%;方案10则属于一个折中的方案,相对初始方案,基频提高了16.29%,质量降低了22.10%。如果工程中需要基频显著提高,则可以选择方案19;如果需要以降低整体质量为主要目标,则可以选择方案20;如果对提高基频和降低质量的偏好一样,则选择折中的方案10。
表 3 NSGA-Ⅱ参数设置 Table 3 Parameters setting of NSGA-Ⅱ
| 参数 | 种群大小 | 迭代次数 | 交叉概率 | 交叉分布指数 | 变异分布指数 |
| 数值 | 12 | 30 | 0.9 | 10 | 20 |
表选项
表 4 阶段Ⅱ的Pareto最优解集 Table 4 Pareto optimal solution set of phase Ⅱ
| 方案 | ?区域A(铺层序列) | ?区域B(铺层序列) | ?区域C(铺层序列) | 基频/Hz | 质量/kg |
| 原始方案 | [1023102310231023] | [1023102310231023] | [1023102310231023] | 41.421 | 38.37 |
| 1 | [332210012032] | [1113111111111111] | [11221212030102] | 46.657 | 29.97 |
| 2 | [33221001020320] | [21113111111111111] | [112121203102] | 48.460 | 32.32 |
| 3 | [332201020323] | [11131111111111] | [112122031102] | 44.791 | 28.24 |
| 4 | [332210002032] | [1113111111111111] | [112121200102] | 46.479 | 29.06 |
| 5 | [332210002032] | [111311111111111] | [112121200102] | 45.816 | 28.65 |
| 6 | [3322100102032] | [111311111111111] | [112121200102] | 46.807 | 30.08 |
| 7 | [332210101020320] | [21113111111111111] | [112121203102] | 49.171 | 33.75 |
| 8 | [3322101010203203] | [1113111111111111] | [1121212031102] | 49.549 | 35.21 |
| 9 | [33221001020320] | [1113111111111111] | [112121200102] | 48.277 | 31.91 |
| 10 | [33220101021020] | [111131111111111111] | [112212010011] | 48.169 | 29.89 |
| 11 | [3322100102032] | [1113111111111111] | [112121200102] | 47.481 | 30.49 |
| 12 | [33221001020320] | [21113111111111111] | [11212120301102] | 48.761 | 33.22 |
| 13 | [3322100102032] | [21113111111111111] | [112121200102] | 47.748 | 30.90 |
| 14 | [332210002032] | [21113111111111111] | [112212120102] | 46.630 | 29.48 |
| 15 | [332210101020320] | [1113111111111111] | [121220301102] | 48.887 | 33.33 |
| 16 | [3322100102032] | [21113111111111111] | [1121212030102] | 47.799 | 31.35 |
| 17 | [33221001020320] | [21113111111111111] | [1121212001102] | 48.712 | 32.77 |
| 18 | [332210101020320] | [21113111111111111] | [1121212030102] | 49.326 | 34.20 |
| 19 | [3322101010203203] | [1113111111111111] | [11212120231102] | 49.613 | 35.66 |
| 20 | [332201020323] | [1113111111111] | [112220231102] | 43.912 | 27.83 |
表选项
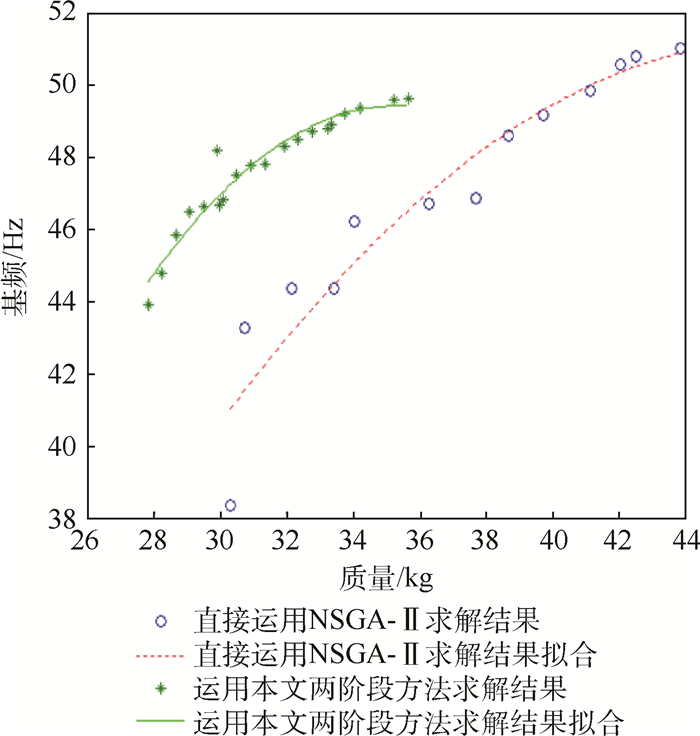
为了说明该两阶段优化方法能改善优化问题的复杂性,本文还结合NSGA-Ⅱ算法对A、B、C3个区域的铺层层数、铺层顺序同时进行了优化。在本例中,阶段Ⅰ迭代次数为20,阶段Ⅱ迭代次数为30,整个优化过程的总迭代次数为50,因此,在运用NSGA-Ⅱ算法对A、B、C 3个区域的铺层层数、铺层顺序同时进行优化时,NSGA-Ⅱ算法的迭代次数设置为50,其他参数均与表 3参数相同。将求解得到的Pareto前沿与运用本文的两阶段优化方法得到的Pareto前沿进行对比,如图 6所示,可知两阶段优化方法得到的Pareto前沿要优于直接结合NSGA-Ⅱ算法铺层层数、铺层顺序同时进行优化所得到的Pareto前沿。即相同质量下,两阶段方法得到的基频更高;相同基频下,两阶段方法得到的质量更低。
 |
| 图 6 Pareto前沿对比 Fig. 6 Comparison of Pareto frontiers |
| 图选项 |
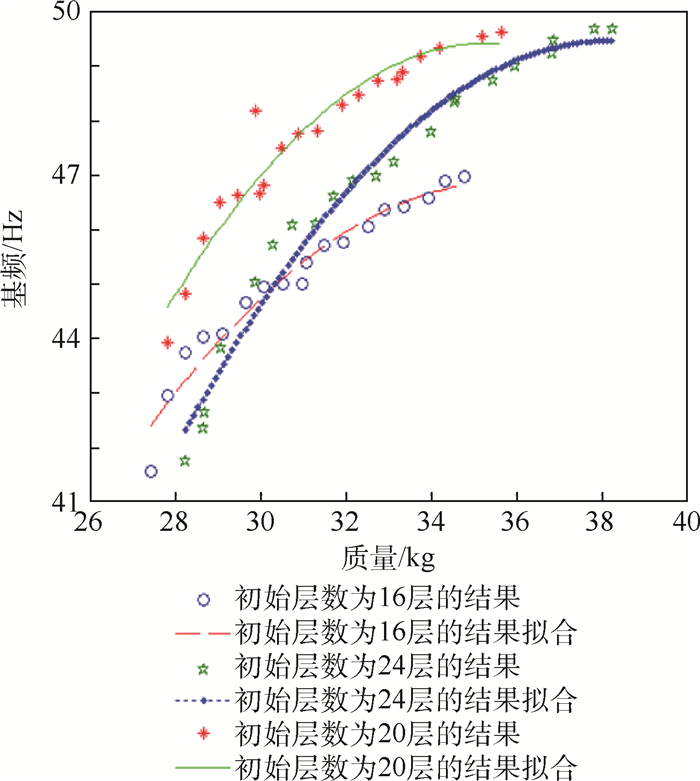
在本例中,阶段Ⅰ设置不同的初始铺层层数会为阶段Ⅱ的多目标拓扑优化提供不同的设计域,从而对优化结果会产生一定影响。将阶段Ⅰ中的初始层数改为16层和24层2种情况,PSO算法和阶段Ⅱ的NSGA-Ⅱ算法的参数保持不变,求解得到的Pareto前沿如图 7所示。
 |
| 图 7 不同初始层数下的Pareto前沿对比 Fig. 7 Comparison of Pareto frontiers for different initial layups |
| 图选项 |
由图 7所示的结果可知,阶段Ⅰ中的初始层数若设置偏大,则使设计域扩大,因此在同样的迭代次数下所得到的Pareto解集会劣于初始层数为20的情况;阶段Ⅰ中的初始层数若设置偏小,则使设计域缩小,因此可能导致更优解不在设计域内,此时得到的Pareto解集也会劣于初始层数为20的情况。综上所述,在运用两阶段优化方法对卫星天线复合材料框架的铺层进行优化时,阶段Ⅰ中的初始铺层数不宜给过大,通常取初始方案层数的125%左右即可,若要取更大层数,则应调整算法参数以得到更优的Pareto解集。
3 结论 1) 针对卫星天线复合材料框架的铺层优化问题,提出了综合应用粒子群优化算法与第2代非劣排序遗传算法的两阶段优化方法。运用该方法优化后的卫星天线复合材料框架的基频显著提高,质量显著降低, 说明了本文方法的有效性。
2) 通过将复合材料框架的各区域的铺层顺序及角度用多进制数来表示,再将多进制数映射为连续的整型变量,可以有效减少变量个数,简化框架的铺层优化数学模型。
3) 实例的优化结果表明,复合材料框架不同区域铺层的优化方案的铺层顺序与铺层层数差异均较大,因此,将框架各区域的铺层参数设置为不同的设计变量是必要的。
参考文献
| [1] | 孙士平, 张卫红. 基于改进模拟退火算法的复合材料层合板频率优化[J].复合材料学报, 2015, 32(3): 902–910. SUN S P, ZHANG W H. Frequency optimization of composite laminates using an improved simulated annealing algorithm[J].Acta Materiae Compositae Sinica, 2015, 32(3): 902–910.(in Chinese) |
| [2] | 晏飞, 李为吉. 基于改进遗传算法的复合材料层合板自振频率优化设计[J].机械科学与技术, 2000, 19(Suppl.): 91–96. YAN F, LI W J. Optimal design of composite laminates subject to natural frequency constraint using an improved genetic algorithm[J].Mechanical Science and Technology, 2000, 19(Suppl.): 91–96.(in Chinese) |
| [3] | 柯俊, 史文库, 钱琛, 等. 采用遗传算法的复合材料板簧多目标优化方法[J].西安交通大学学报, 2015, 49(8): 102–108. KE J, SHI W K, QIAN C, et al. A multiobjective optimization for composite leaf springs using genetic algorithm[J].Journal of Xi'an Jiaotong University, 2015, 49(8): 102–108.DOI:10.7652/xjtuxb201508017(in Chinese) |
| [4] | HONDA S, NARITA Y, SASAKI K. Discrete optimization for vibration design of composite plates by using lamination parameters[J].Advanced Composite Materials, 2009, 18(4): 297–314.DOI:10.1163/156855109X434739 |
| [5] | NARITA Y. Layerwise optimization for the maxi-mum fundamental frequency of laminated composite plates[J].Journal of Sound and Vibration, 2003, 263(5): 1005–1016.DOI:10.1016/S0022-460X(03)00270-0 |
| [6] | GHIASI H, FAYAZBAKHSH K, PASINI D, et al. Optimum stacking sequence design of composite materials Part Ⅱ:Variable stiffness design[J].Composite Structures, 2010, 93(1): 1–13.DOI:10.1016/j.compstruct.2010.06.001 |
| [7] | ABDALLA M M, SETOODEH S, GURDAL Z. Design of variable stiffness composite panels for maxi-mum fundamental frequency using lamination parameters[J].Composite Structures, 2007, 81(2): 283–291.DOI:10.1016/j.compstruct.2006.08.018 |
| [8] | STEGMAN J, LUND E. Discrete material optimization of general composite shell structures[J].International Journal for Numerical Methods in Engineering, 2005, 62(14): 2009–2027.DOI:10.1002/(ISSN)1097-0207 |
| [9] | 冯消冰, 黄海, 王伟. 基于遗传算法的大型风机复合材料叶片根部强度优化设计[J].复合材料学报, 2012, 29(5): 196–202. FENG X B, HUANG H, WANG W. Strength optimization of large wind turbine blade root on the genetic algorithm[J].Acta Materiae Compositae Sinica, 2012, 29(5): 196–202.(in Chinese) |
| [10] | 穆朋刚, 赵美英, 陈鹏飞, 等. 基于蚁群算法的复合材料层合板的铺层顺序优化[J].玻璃钢/复合材料, 2007, 11(6): 14–17. MU P G, ZHAO M Y, CHEN P F, et al. Ply stacking-sequence optimization of composite laminate plates by ant colony system[J].Fiber Reinforced Plastics/Composites, 2007, 11(6): 14–17.(in Chinese) |
| [11] | 顾元宪, 亢战, 赵国忠, 等. 卫星承力筒复合材料结构的优化设计[J].宇航学报, 2003, 24(1): 88–91. GU Y X, KANG Z, ZHAO G Z, et al. Optimal design of composite structure of satellite bearing cylinder[J].Journal of Astronautics, 2003, 24(1): 88–91.(in Chinese) |
| [12] | 陈烈民, 杨宝宁. 复合材料的力学分析[M].北京: 中国科学技术出版社, 2006: 98-101. CHEN L M, YANG B N. Mechanical analysis for composite materials[M].Beijing: Science and Technology of China Press, 2006: 98-101.(in Chinese) |
| [13] | 陈烈民. 航天器结构与机构[M].北京: 中国科学技术出版社, 2005: 102-103. CHEN L M. Spacecraft structures and mechanisms[M].Beijing: Science and Technology of China Press, 2005: 102-103.(in Chinese) |
| [14] | 唐俊. PSO算法原理及应用[J].计算机技术与发展, 2010, 20(2): 213–216. TANG J. Principle and application of PSO algorithm[J].Computer Technology and Development, 2010, 20(2): 213–216.(in Chinese) |
| [15] | MARLE R T, ARORA J S. Survey of multi-objective optimization methods for engineering[J].Structural and Multidisciplinary Optimization, 2004, 26(6): 369–395.DOI:10.1007/s00158-003-0368-6 |
| [16] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197.DOI:10.1109/4235.996017 |
