软体机器人的本体结构通常由弹性聚合物如橡胶、硅胶等构成[6],其驱动器是设计中的难点,须保证足够的柔顺性、输出力和行程。目前,通常采用的软体机器人驱动器有形状记忆合金(Shape Memory Alloy, SMA)、丝驱动机构(tendon-driven mechanisms)、电活性聚合物(ElectroActive Polymer, EAP)、人工气动肌肉(Pneumatic Artificial Muscle, PAM)等。Seok等[7]利用网格状SMA来模拟蚯蚓蠕动。Camarillo等[8]应用丝驱动于心脏导管中。Mattoli等[9]根据章鱼肌肉特性提出了基于EAP人工肌肉的仿生结构。Walker等[10]采用PAM模拟象鼻形态及其运动。哈佛大学Whitesides等[11]利用硅橡胶材料制造了可由气压快速驱动的Pneu-Net架构软体驱动器。在设计理论方面,Walker和Jones[12]在常曲率假设的基础上,利用改进的D-H模型和几何分析建立了适用于一类软体驱动器的运动学关系。Polygerinos等[13]针对线增强型软体气压驱动器提出了其分析模型,为软体驱动器确定性设计提供了方向。国内虽然对软体驱动器的研究起步较早,但目前工作仍缺乏系统性。如上海交通大学的马建旭等[14]提出了仿蚯蚓蠕动式微驱动器;哈尔滨工业大学的王振龙等[15]借鉴乌贼的肌肉性净水骨骼原理,提出并研制了嵌入SMA丝驱动的仿生柔性鳍单元。
上述软体驱动器中,SMA和EAP虽然控制效率高,但响应速度较慢,且输出力较小;丝驱动不能承受大负载,尤其是压缩载荷;而气压型驱动器由于其本体结构的柔顺性、轻质、快速响应及输出力大等优点具有良好的表现[16]。本文设计了一种可完成弯曲运动的新型软体气压驱动器,对其工作原理进行了阐述;基于弹性力学中虚功原理和几何方法建立其数学模型,对该软体驱动器在输入气压作用下的弯曲变形进行了分析。与文献[13]的分析过程相比,本文通过引入虚功原理使模型更加简洁、高效;同时建立了有限元模型,对驱动器的应力、应变等进行进一步观察;通过实验结果和仿真结果的对比,证明了理论模型和实际样机之间的一致性。
1 软体驱动器设计 该软体驱动器利用气压驱动力的偏心作用实现单自由度弯曲运动。圆柱形驱动器本体由高弹性硅胶材料(Ecoflex 00-50) 制成。如图 1所示,驱动器内部有一个偏心通道空腔,空腔截面形状为圆形。当腔道A充气时,其在气压的作用下伸长,而驱动器其余部分由于没有气压力的作用不会产生明显的伸长,所以软体驱动器将在y-z平面内沿y轴正方向弯曲。为了得到最大的弯曲效果,可以相对腔道A植入聚乙烯(PE)纤维线,并在驱动器2个端面将2根PE线相连。当空腔A充气伸长时,由于PE线的不可伸长性,平面B1B2C2C1可视作相对充气空腔的不可伸长面,气压作用完全转变为驱动器的弯曲运动。
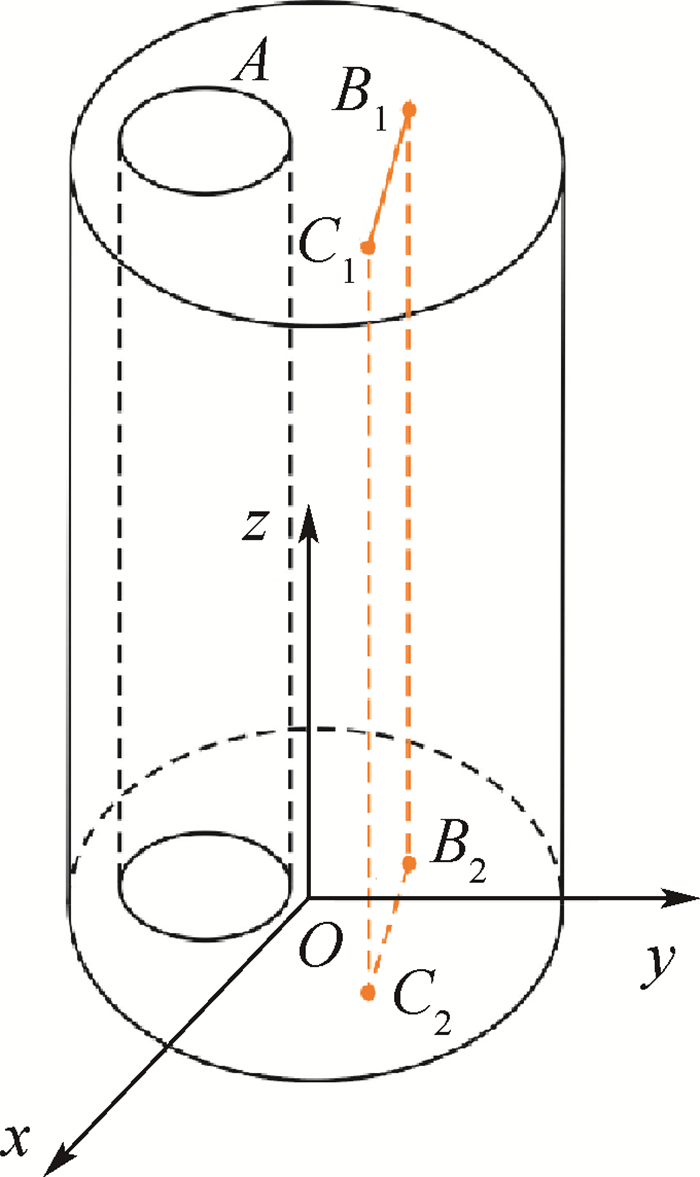 |
| 图 1 软体驱动器弯曲原理图 Fig. 1 Diagram of bending principle for soft actuator |
| 图选项 |
实际上,当气压充入封闭空腔时,如果没有任何限制,该空腔不仅会轴向伸长,同时也会发生径向膨胀。为了避免不必要的径向膨胀,在驱动器表面以螺旋方式缠绕PE线,如图 2所示。制作样机过程中,需注意绕线圈数的选择,圈数过多,在其他参数相同的情况下实现同样的弯曲需要提供更大的气压;圈数过少,驱动器在充入气压时线与线的间距间会产生不必要的径向膨胀,影响驱动器的弯曲性能,此处选择绕线圈数为28(驱动器本体长度80 mm)。为了避免模型由于绕线的影响产生扭转,采用双螺旋方式缠绕。为了避免缠绕线裸露在外,可在驱动器外部再覆盖一层相对驱动器本体材料较软的硅橡胶套。该软体驱动器的设计参数如表 1所示。
 |
| 图 2 软体驱动器结构示意图 Fig. 2 Schematic of soft actuator's structure |
| 图选项 |
表 1 软体驱动器设计参数 Table 1 Parameters for soft actuator design
| 参数 | 数值 |
| 长度l0/mm | 80 |
| 驱动器半径R0/mm | 6.5 |
| 空腔内径r0/mm | 1.5 |
| 空腔圆心偏离驱动器中心距离e1/mm | 3 |
| 不可伸长面与驱动器中心间距离e2/mm | 1.5 |
| 绕线圈数N | 28 |
| 绕线螺旋角/(°) | 5 |
| 质量/kg | 0.017 |
表选项
该软体驱动器所采用的结构简单可靠,易微型化,而且气压驱动反应速度快,具有较高的功率密度,同时也具有很好的抗疲劳性,在反复弯曲(106次弯曲)后仍能回复初始状态[11]。
2 软体驱动器建模 与传统的刚性驱动器不同,软体驱动器由于自身高度的柔顺性,因而不能直接利用刚体力学的方法进行分析。本文从基于弹性力学的数学模型和有限元模型两方面分析该软体驱动器的弯曲性能,不仅建立了输入气压与驱动器弯曲变形之间的关系,而且进一步观察了驱动器内部的相互作用。
2.1 数学模型 在考虑本体超弹性材料非线性和驱动器几何参数的基础上建立了该软体驱动器的数学模型。该模型基于以下前提假设[17]:
1) 硅橡胶材料近似不可压缩。
2) 驱动器在弯曲过程中几何形状均圆柱。
3) 驱动器在弯曲过程中均保持常曲率弯曲。
4) 绕线不可伸长,而且与驱动器外表面始终保持接触。
2.1.1 材料模型 该软体驱动器本体采用超弹性材料硅橡胶Ecoflex 00-50,由于超弹性材料在外力作用下材料特性和几何特性都呈非线性变化,所以为了描述硅橡胶材料的力学性能,通常采用应变能密度函数来表示。常用的函数有Neo-Hookean模型、Yeoh模型、Mooney-Rivlin模型等[18-19]。其中,Yeoh模型可以根据单轴拉伸试验的数据拟合其他不同的变形方式,如单轴压缩、剪切等,而且适合于模拟大变形,所以本文采用Yeoh模型建立材料应力与应变之间的非线性关系。应变能密度函数为
 |
式中:n为应变能密度函数的阶数;Ci为材料参数,材料参数的辨识和取值将在2.2节阐述;I1为Cauchy-Green应变张量的第1个不变量,即
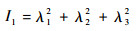 | (1) |
其中:λ1、λ2和λ3分别为轴向、径向和周向主拉伸比[13, 20]。
对于硅橡胶Ecoflex 00-50来说,利用两参数模型即可在一定范围内拟合其应力-应变特性[18],所以应变能密度为
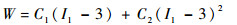 | (2) |
2.1.2 驱动器模型 对于该软体驱动器来说,当充入一定气压时,考虑壁的厚度,驱动器空腔在3个方向上的尺寸变化可用以下关系表示:
 | (3) |
式中:l0和r0分别为未发生变形时驱动器空腔中心轴线长度和半径;l和r分别为变形后空腔中心轴线长度和半径;t10和t30分别为未发生变形时驱动器空腔圆心与驱动器中心连线方向上的两侧厚度;t20和t40分别为未发生变形时与圆心连线方向垂直的两侧厚度;t1、t2、t3和t4分别为变形后与t10、t20、t30和t40对应的4个方向上的厚度。此处λ3近似用4个方向上厚度变化的平均值表示,如图 3所示。
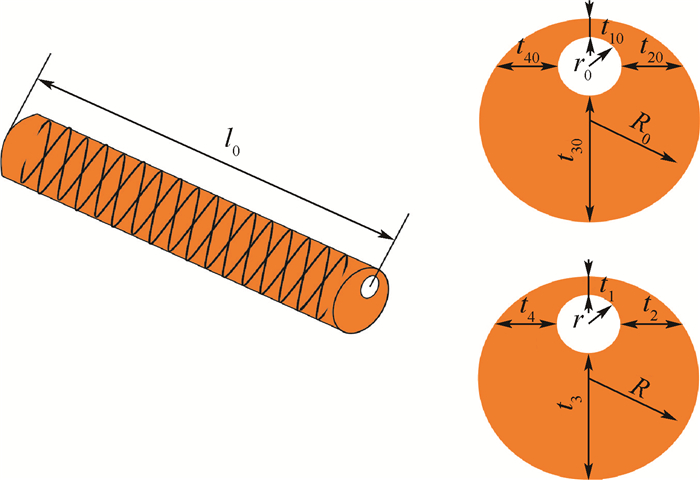 |
| 图 3 变形前后的驱动器尺寸 Fig. 3 Size of actuator before and after deformation |
| 图选项 |
驱动器充气时在平面内常曲率弯曲,如图 4所示,点O为驱动器末端圆心,由几何关系知
 | (4) |
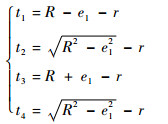 | (5) |
 |
| 图 4 弯曲驱动器的几何形状 Fig. 4 Geometry of bending actuator |
| 图选项 |
式中:θ为驱动器弯曲角;L和R分别为弯曲后驱动器中心轴线的长度和半径;e1为空腔圆心偏离驱动器中心的距离;e2为驱动器中心与不可伸长面间的距离。
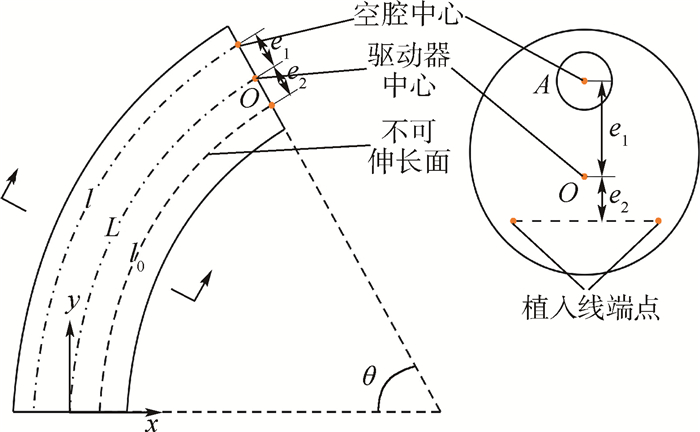
由于绕线不可伸长,驱动器几何形状参数间的关系可表示为
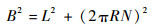 | (6) |
式中:B为缠绕线长;N为驱动器表面绕线圈数。如图 5所示。
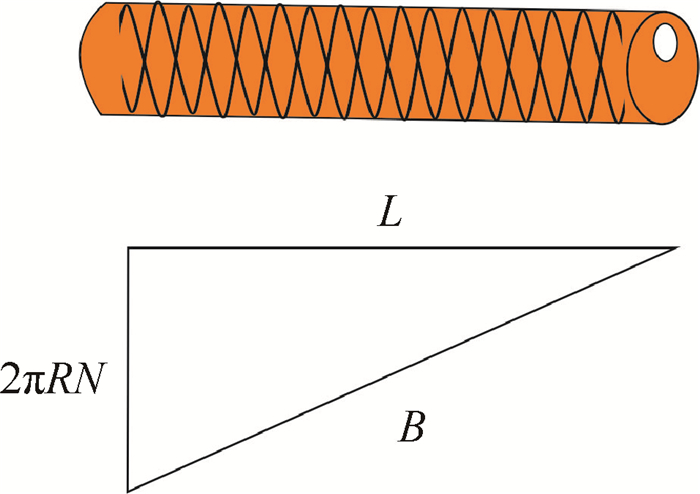 |
| 图 5 未变形驱动器几何形状 Fig. 5 Geometry of undeformed actuator |
| 图选项 |
当空腔充气发生变形后,内部气压所占体积Va与硅橡胶所占体积Vr分别为
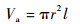 | (7) |
 | (8) |
由于硅橡胶的不可压缩性,即驱动器变形前后硅橡胶所占体积保持不变,可得
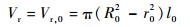 | (9) |
联立式(4)、式(6)、式(8) 和式(9) 可得
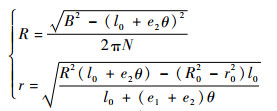 | (10) |
式(10) 对θ求导,可得
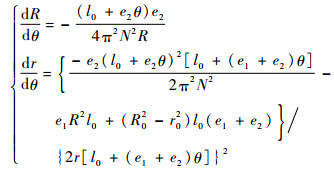 | (11) |
若未受到任何外力作用,则可以认为气压P所做的功完全转化为驱动器的弯曲变形。根据虚功原理,可知
 | (12) |
式(12) 可写为
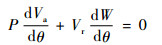 | (13) |
式(7) 对θ求导,可得
 | (14) |
联立式(1)~式(3),对θ求导得
 | (15) |
式中:
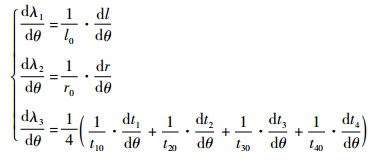 |
且由式(5) 易知
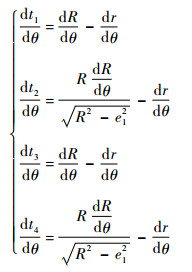 |
所以
 | (16) |
由式(10)、式(11) 和式(15) 知,r、dr/dθ和dW/dθ均可表示为只含有θ的函数,因而方程式(16) 中仅含未知数θ。所以在已知输入气压P的情况下,即可确定驱动器弯曲角θ。由式(16) 可知,气压P与弯曲角θ的关系受到驱动器几何参数R0、r0、l0、e1和e2的影响。根据式(16),图 6绘制了不同偏心距情况下(其他参数按表 1所示取值),气压P与弯曲角θ的关系。
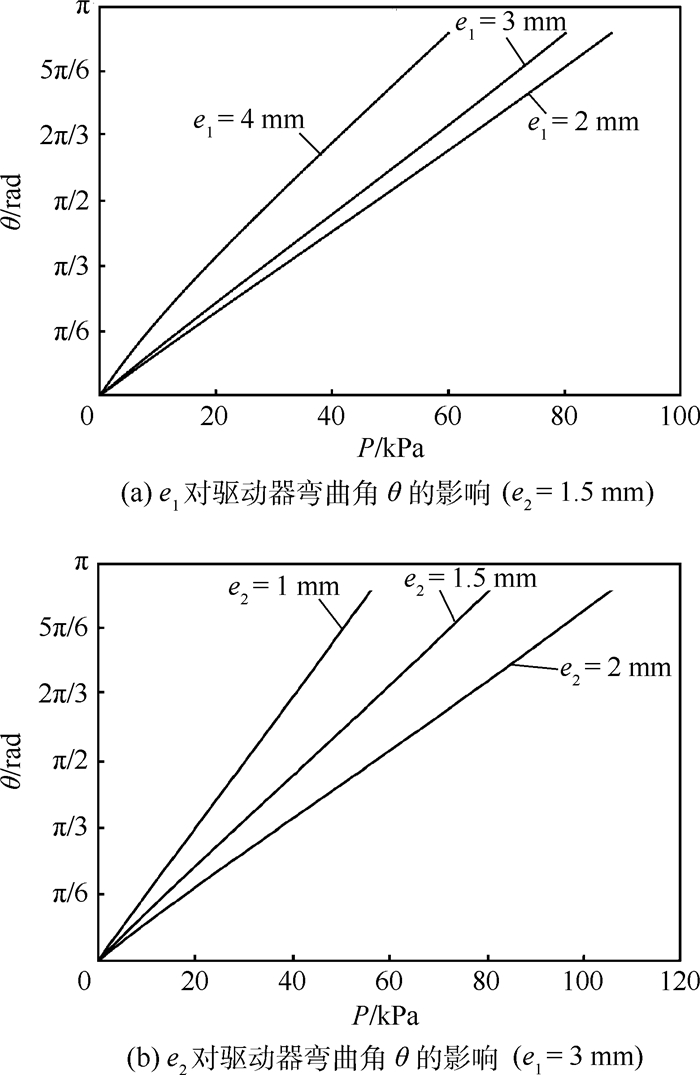 |
| 图 6 偏心距对驱动器弯曲角θ的影响 Fig. 6 Influence of eccentric distance on bending angle θ of actuator |
| 图选项 |
如图 6所示,在相同的气压下(其他参数均相同),随着e1增大或e2减小,该软体驱动器的弯曲角度增大。考虑到驱动器整体设计尺寸的约束及使用的气源压力范围(0~80 kPa),此处选择e1=3 mm,e2=1.5 mm,预期P=80 kPa时驱动器弯曲角度可以超过5π/6,后续实验结果也证明了该预测。
此时,由图 5中几何关系可以得到驱动器末端中心点位置坐标为
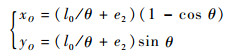 | (17) |
式中:xO和yO分别为此时驱动器末端圆心O点的x轴和y轴位置坐标。
因此,对于该软体驱动器来说,联立式(16) 和式(17),即可最终建立输入气压P与驱动器末端中心的位置坐标之间的关系。
2.2 有限元模型 对于实际软体驱动器来说,数学模型可以描述该驱动器对于充入气压的响应,而有限元模型则不仅能够直观地反应驱动器的非线性响应,而且能够将驱动器的位移以及内部应力、应变等可视化。
软体驱动器本体所使用的超弹性材料的Yeoh模型中,材料系数可以通过单轴拉伸和压缩试验确定。根据标准ASTM D638[21],将软体驱动器样机以500 mm/min进行拉伸试验,得到应力-应变数据曲线,应用最小二乘法拟合,即可得到模型中的未知参数。对于Ecoflex 00-50来说,材料参数:C1=0.10 MPa, C2=0.02 MPa;定义驱动器表面PE绕线为线弹性材料,其中弹性模量E=31 067 MPa,泊松比μ=0.36。
选择ABAQUS/Standard分析建立该软体驱动器的有限元模型,为了提高计算效率与有限元模型的收敛性,在模型中将驱动器硅橡胶部分设置为四面体二次杂交实体单元(C3D10H);将驱动器表面绕线设置为二次梁单元(B32);将实际样机中未充气的两空腔与植入的PE线组成的不可伸长面B1B2C2C1简化为材料属性线弹性的壳单元(STRI65),材料参数E=6 000 MPa,μ=0.2[13]。而且绕线和不可伸长面与硅橡胶弹性体部分的约束均为绑定约束。忽略重力和摩擦力等因素的影响,在ABAQUS中将压强作用于整个实际充入气压的空腔。驱动器变形结果如图 7所示,有限元模型与数学模型的对比将在3.2节论述。
 |
| 图 7 有限元模型中P=80 kPa下驱动器状态 Fig. 7 State of actuator in finite element model at P=80 kPa |
| 图选项 |
3 实验验证 3.1 实验平台搭建 由于该软体驱动器实现单自由度弯曲,所以只需考虑其在平面内的运动情况。驱动器基部固定,末端自由,初始位置与y轴对齐。实验平台如图 8所示。现阶段基于上述提及的软体机器人模型,采用开环控制方式,控制流程如图 9所示。上位机发送指令至Arduino板卡(UNO R3),输出PWM信号,再通过滤波电路调节输出直流电压,进而控制电气比例阀(SMC ITV 1051) 输出气压的大小来控制软体驱动器的弯曲。只需在上位机调节Arduino板卡PWM信号的占空比,即可控制驱动器的弯曲变形。同时,为了更精确地定位该软体驱动器的运动轨迹,采用3DGuidance trak-STAR (NDI Ascension)系统,可以同时记录4个传感器探头在空间中的位置,其精度为1.4 mm。该实验中,将2个传感器探头分别固定在驱动器基部与末端中心处,采集驱动器在0、20、40、60、80 kPa气压下的基部与末端中心点位置,并将其反馈至上位机。为了得到软体驱动器中心轴线末端运动轨迹,需对数据作如下处理:① 计算上述不同压力下末端点相对基点的位移;② 利用分段三次样条插值函数对末端点拟合得到驱动器末端运动轨迹。
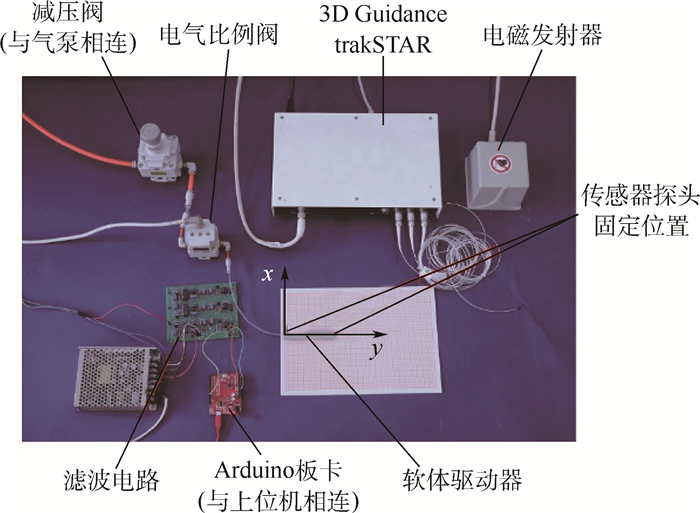 |
| 图 8 实验测量平台 Fig. 8 Experimental measurement platform |
| 图选项 |
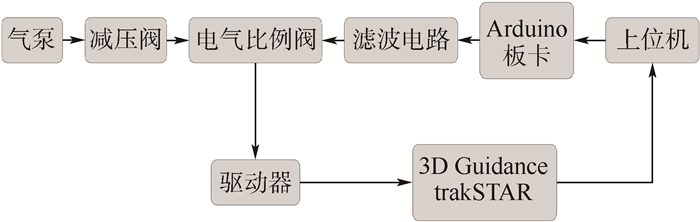 |
| 图 9 控制系统流程图 Fig. 9 Flowchart of control system |
| 图选项 |
3.2 实验数据分析 如图 10(a)所示,充气压力为80 kPa时,驱动器弯曲角度可以达到172°,符合图 6的预测。图 10(b)、图 10(c)为不同气压下数学模型、有限元模型和实验数据中驱动器中心轴线末端位移。为了验证数学模型的正确性,分别计算数学模型与有限元模型之间以及数学模型与实际样机之间的驱动器末端中心点的位移均方根误差e。
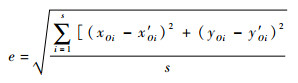 |
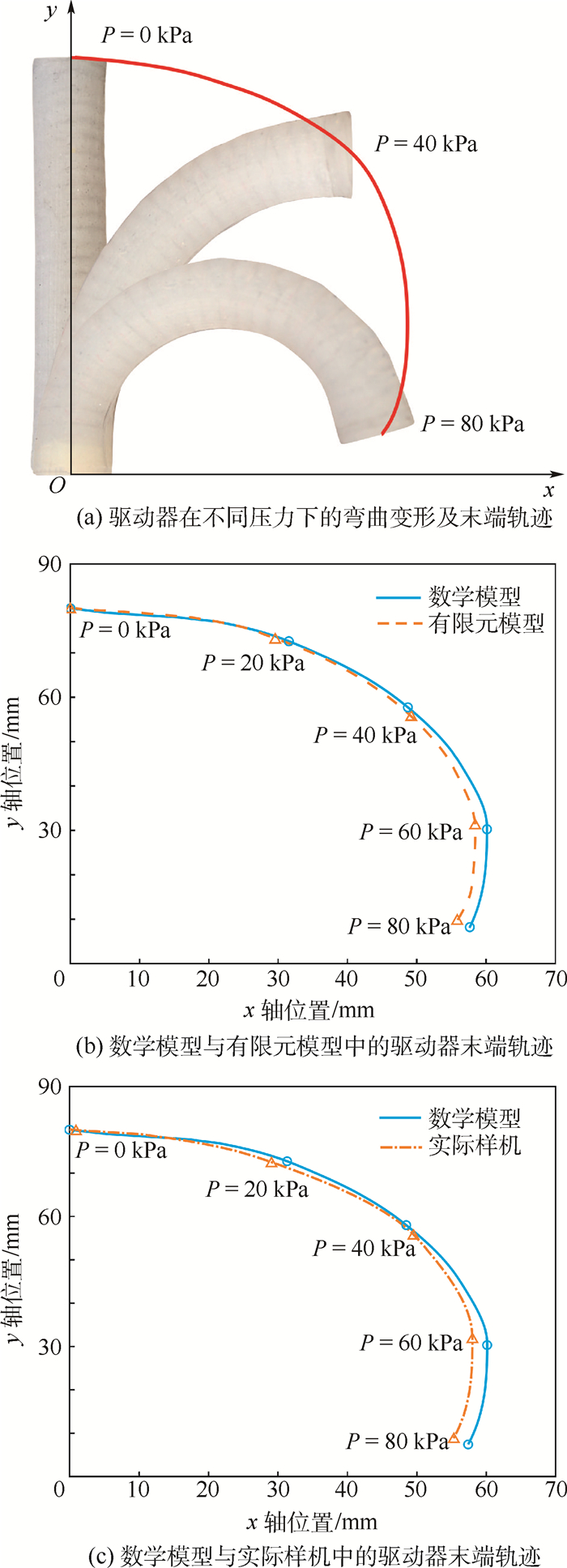 |
| 图 10 不同气压下软体驱动器末端位移 Fig. 10 Tip displacement of soft actuator in different pressure |
| 图选项 |
式中:xOi和yOi分别为输入气压P下数学模型中驱动器末端中心点的位置坐标;xOi′和yOi′分别为同一输入气压P下有限元模型或实验数据中驱动器末端中心点的位置坐标;s为测试次数。本文测试了5种不同压力下的末端中心点位置,所以s=5。可以得到数学模型与有限元模型之间均方根误差e3为2.96 mm(初始长度的3.7%),数学模型与实际样机之间均方根误差e4为3.56 mm(初始长度的4.45%),从而证明本文所提出的数学模型可以较好地模拟实际驱动器。造成上述误差的原因主要是由于驱动器样机在弯曲过程中其形状并不是严格符合常曲率假设,而且模型中材料参数的选取也可能存在一定的误差。
4 结论 1) 本文以所设计的新型软体驱动器样机为基础,利用虚功原理和几何方法建立了适用于该类型软体驱动器的数学模型,可用于预测软体驱动器在不同气压下的弯曲位置。
2) 借助有限元软件建立了有限元模型,不仅验证了数学模型的有效性,而且对驱动器的应力、应变等进行了观察,对将来进一步分析软体驱动器参数对弯曲性能的影响具有指导作用。
3) 通过仿真分析和原理样机实验验证了数学模型,并展示了其良好的弯曲能力。
4) 该软体驱动器具有良好的柔顺性、适应性与安全性,可用于驱动软体机器人在非结构环境中工作,如深腔探测、空间操作、医疗手术等。此外,在康复陪护、家政服务等具有较高安全性要求的场合,该驱动器及其驱动的机器人系统也有良好的应用潜力。
参考文献
| [1] | ROBINSON G, DAVIES J B C. Continuum robots-A state of the art [C]//1999 IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 1999, 4:2849-2854. |
| [2] | TRIVEDI D, RAHN C D, KIER W M, et al. Soft robotics:Biological inspiration, state of the art, and future research[J].Applied Bionics and Biomechanics, 2008, 5(3): 99–117.DOI:10.1155/2008/520417 |
| [3] | KIM S, LASCHI C, TRIMMER B. Soft robotics:A bioinspired evolution in robotics[J].Trends in Biotechnology, 2013, 31(5): 287–294.DOI:10.1016/j.tibtech.2013.03.002 |
| [4] | RUS D, TOLLEY M T. Design, fabrication and control of soft robots[J].Nature, 2015, 521(7553): 467–475.DOI:10.1038/nature14543 |
| [5] | 曹玉君, 尚建忠, 梁科山, 等. 软体机器人研究现状综述[J].机械工程学报, 2012, 48(3): 25–33. CAO Y J, SHANG J Z, LIANG K S, et al. Review of soft-bodied robots[J].Journal of Mechanical Engineering, 2012, 48(3): 25–33.(in Chinese) |
| [6] | ILIEVSKI F, MAZZEO A D, SHEPHERD R F, et al. Soft robotics for chemists[J].Angewandte Chemie International Edition, 2011, 50(8): 1890–1895.DOI:10.1002/anie.v50.8 |
| [7] | SEOK S, ONAL C D, CHO K J, et al. Meshworm:A peristaltic soft robot with antagonistic nickel titanium coil actuators[J].IEEE/ASME Transactions on Mechatronics, 2013, 18(5): 1485–1497.DOI:10.1109/TMECH.2012.2204070 |
| [8] | CAMARILLO D B, MILNE C F, CARLSON C R, et al. Mechanics modeling of tendon-driven continuum manipulators[J].IEEE Transactions on Robotics, 2008, 24(6): 1262–1273.DOI:10.1109/TRO.2008.2002311 |
| [9] | CIANCHETTI M, MATTOLI V, MAZZOLAI B, et al. A new design methodology of electrostrictive actuators for bio-inspired robotics[J].Sensors and Actuators B:Chemical, 2009, 142(1): 288–297.DOI:10.1016/j.snb.2009.08.039 |
| [10] | BARTOW A, KAPADIA A, WALKER I D.A novel continuum trunk robot based on contractor muscles[C]//Proceedings of the 12th WSEAS International Conference on Signal Processing, Robotics, and Automation.Cambridge:WSEAS Press, 2013:181-186. |
| [11] | MOSADEGH B, POLYGERINOS P, KEPLINGER C, et al. Pneumatic networks for soft robotics that actuate rapidly[J].Advanced Functional Materials, 2014, 24(15): 2163–2170.DOI:10.1002/adfm.v24.15 |
| [12] | JONES B A, WALKER I D. Kinematics for multisection continuum robots[J].IEEE Transactions on Robotics, 2006, 22(1): 43–55.DOI:10.1109/TRO.2005.861458 |
| [13] | POLYGERINOS P, WANG Z, OVERVELDE J T B, et al. Modeling of soft fiber-reinforced bending actuators[J].IEEE Transa-ctions on Robotics, 2015, 31(3): 778–789.DOI:10.1109/TRO.2015.2428504 |
| [14] | 马建旭, 李明东, 包志军, 等. 仿蚯蚓蠕动微机器人及控制系统[J].上海交通大学学报, 1999, 33(7): 855–857. MA J X, LI M D, BAO Z J, et al. Microperistaltic robot simulating earthworm and its control system[J].Journal of Shanghai Jiaotong University, 1999, 33(7): 855–857.(in Chinese) |
| [15] | 王振龙, 杭观荣, 李健, 等. 面向水下无声推进的形状记忆合金丝驱动柔性鳍单元[J].机械工程学报, 2009, 45(2): 126–131. WANG Z L, HANG G R, LI J, et al. Shape memory alloy wire actuated flexible biomimetic fin for quiet underwater propulsion[J].Journal of Mechanical Engineering, 2009, 45(2): 126–131.(in Chinese) |
| [16] | KANG R, BRANSON D T, ZHENG T, et al. Design, modeling and control of a pneumatically actuated manipulator inspired by biological continuum structures[J].Bioinspiration & Biomimetics, 2013, 8(3): 036008. |
| [17] | BISHOP-MOSER J, KRISHNAN G, KIM C, et al.Design of soft robotic actuators using fluid-filled fiber-reinforced elastomeric enclosures in parallel combinations [C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).Piscataway, NJ:IEEE Press, 2012:4264-4269. |
| [18] | YEOH O H. Some forms of the strain energy function for rubber[J].Rubber Chemistry and Technology, 1993, 66(5): 754–771.DOI:10.5254/1.3538343 |
| [19] | KOTHERA C S, JANGID M, SIROHI J, et al. Experimental characterization and static modeling of McKibben actuators[J].Journal of Mechanical Design, 2009, 131(9): 091010.DOI:10.1115/1.3158982 |
| [20] | 黄建龙, 解广娟, 刘正伟. 基于Mooney-Rivlin和Yeoh模型的超弹性橡胶材料有限元分析[J].橡胶工业, 2008, 55(8): 467–470. HUANG J L, XIE G J, LIU Z W. FEA of hyperelastic rubber material based on Mooney-Rivlin model and Yeoh model[J].China Rubber Industry, 2008, 55(8): 467–470.(in Chinese) |
| [21] | American Society for Testing and Materials.Standard test method for tensile properties of plastics:ASTM D638 [S].[S.l.]:ASTM, 2003. |
