灵敏度分析主要研究的是：模型的输出不确定性是如何分配到输入不确定性的^[1]。目前，灵敏度分析主要分为3类：局部灵敏度^[2-3]、区域灵敏度^[4-5]和全局灵敏度^[6]。全局灵敏度以其能够从全局的角度衡量随机输入变量对输出不确定性的影响而被广为应用。全局灵敏度分析的模型主要分为3类：非参模型^[7](相关系数模型)、基于方差的模型^[8-10]和矩独立模型^[11-13]。非参模型无法对非线性模型及输入变量的高阶交叉影响项提供充足的灵敏度信息。基于方差的全局灵敏度指标从输入输出函数关系的角度直接给出了输入变量对函数输出方差的贡献，其满足“全局性、可量化性及模型独立性”^[6]。Borgonovo^[12]指出基于方差的全局灵敏度能够反映输入变量对输出不确定性影响程度大小的前提是方差能够完全反映输出的不确定性信息。但方差仅是输出的二阶矩，是输出不确定性的一部分信息，其不能从输出整个分布的角度衡量输入变量的重要性信息，因此，提出了矩独立全局灵敏度指标，即利用无条件概率密度函数与条件概率密度函数的面积差异来衡量输入变量对输出不确定性的影响程度。其包含了输出不确定性的完整信息，而不依赖于输出的矩信息。在矩独立全局灵敏度指标的基础上，Cui等^[14]提出了可靠性全局灵敏度指标，其主要衡量的是输入变量的不确定性对结构系统失效概率影响的大小。Li等^[15]随后建立了可靠性全局灵敏度指标与方差全局灵敏度指标的关系。
目前该指标的计算分为两类：基于代理模型的方法^[15-16]和基于数字模拟的方法^[17]。在数字模拟法中，Wei等^[17]提出了单层Monte Carlo法(S-MCS)、重要抽样法及截断重要抽样法。S-MCS的本质仍是MCS的思想，对功能函数的形式没有限制，仅是将原始该指标计算的双层循环等价转换成单层循环，在一定程度上降低了计算量，但该方法的计算量仍与输入变量的维数线性相关。因此，一般利用该方法在大量样本情况下的解作为其他方法的参照解。重要抽样及截断重要抽样法是将抽样中心平移到设计点处，使得样本落入失效域的概率增加，以此来获得高的抽样效率和快的收敛速度。但由于文献[17]采用的是改进的一次二阶矩方法来寻找设计点，这使得对于非线性程度较大的情况，迭代算法受初始点的选取影响较大，且对于多设计点问题，改进的一次二阶矩方法可能会陷入局部最优，甚至不收敛^[18]。除此之外，Wei等^[17]所提的这3种方法的计算量均与输入变量的维数呈线性相关。因此，针对计算量与输入维数的相关性及重要抽样密度无法构造的情况，本文提出了基于密度权重^[19]、连续无重叠区间全方差公式的空间分割法来高效计算可靠性全局灵敏度指标。通过密度权重的方法在输入变量可能的取值区间内均匀地抽取样本点，利用空间分割策略^[20]，重复划分这一组样本来得到所有输入变量的可靠性全局灵敏度指标。该方法无需寻找设计点，并且计算量与输入维数无关，大大提高了样本的利用率。通过验证算例的计算结果，说明了本文方法在分析高度非线性及多设计点问题上的优越性。
1 可靠性全局灵敏度指标的定义 对于极限状态函数为Y=g(X)的结构可靠性模型，X=(X₁, X₂, …, X_n)为结构的随机输入变量，为从全局的角度分析输入变量对结构失效概率的影响程度，Cui等^[14]提出了可靠性全局灵敏度指标：

(1)

式中：E_Xi为X_i在其整个分布范围内取值时的期望算子；P_fY为结构的失效概率；P_fY|Xi为X_i固定在其分布中的某一名义值时的条件失效概率；f_Xi(x_i)为输入变量X_i的概率密度函数。根据失效概率定义可知：

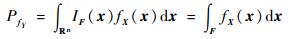(2)

式中：n为输入变量的维数；F={X:g(X)≤0}为由功能函数g(X)定义的失效域；f_X(x)为输入变量X的联合概率密度函数；I_F为失效域指示函数，定义为

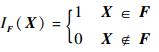(3)

Li等^[15]证明了δ_i^P的等价定义：

(4)

式中：V_Xi为X_i在整个分布范围取值时的方差算子；E_X-i为除X_i之外其余变量在其整个分布范围内取值时的期望算子。
Wei等^[17]通过添加这一常数项，使得可靠性全局灵敏度指标与基于方差的全局灵敏度指标在形式上完全统一，即

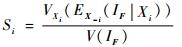(5)

通过S_i指标的排序可以确定对失效概率影响较大的输入变量，通过控制重要变量的不确定性来达到降低结构失效概率的目的。
2 基于密度权重和空间分割的S_i计算新方法 针对非线性程度较高的功能函数及多设计点问题，本文将利用密度权重法均匀地产生输入变量的样本，通过所证明的连续无重叠区间上的全方差公式加快空间分割方法的收敛速度。该方法无需寻找设计点，且计算量与输入变量的维数无关。下面将具体介绍该方法。
2.1 高效计算S_i的空间分割方法 由文献[20]可知：

(6)

式中：为X_i落在区间[a_k－1, a_k]上的概率，F_Xi(·)为随机输入变量X_i的累积分布函数；s为将X_i的取值范围[b₁, b₂]划分为连续无重叠区间A_k=[a_k－1, a_k](k=1, 2, …, s)的个数且，当，。基于式(6) 及全方差公式，可得式(5) 的近似计算式：

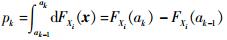
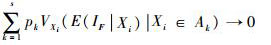
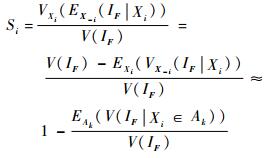(7)

式(7) 能够精确近似式(5) 的前提假设是，因此，区间划分得越密，理论上式(7) 对式(5) 的近似效果越好。但在实际计算当中，样本容量是有限的，那么就会使得在有限样本容量下式(7) 精确近似式(5) 的前提假设Δa→0与计算V(I_F|X_i∈A_k)需要较多样本之间会相互牵制。为缓解Δa→0与计算V(I_F|X_i∈A_k)所需样本较多的互相牵制，则希望将内层较难计算的方差项转换成较容易计算的均值项，为实现这一转换，下面证明连续不重叠区间上的全方差公式，即

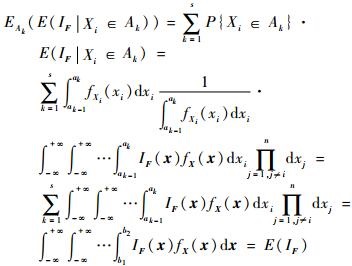(8)

在式(8) 证明的连续区间上的全期望公式的基础上，有

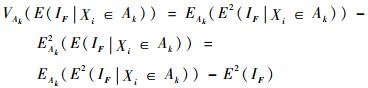(9)

(10)

将式(9) 与式(10) 相加得到如下连续区间上的全方差公式：

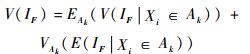(11)

基于式(11)，式(7) 有如下等价变形：

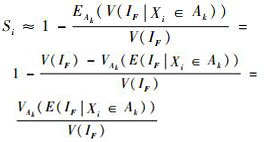(12)

由式(12) 可以看出，原式(7) 中内层的方差计算项等价转换成了均值计算项。在相同样本的情况下，均值E(I_F|X_i∈A_k)的计算较方差V(I_F|X_i∈A_k)的计算更精确，并且在样本容量N一定的情况下，Δa→0与s在数量上的增加是一致的，s的增加意味着计算V_Ak(·)的样本增加，从而估计V_Ak(·)的精度也是提高的。对于式(7)，在内层一阶矩E(I_F|X_i∈A_k)准确估计的样本基础上，二阶矩V(I_F|X_i∈A_k)的估计常常会出错，因为高阶矩的估计需要更多的样本，内层较多的样本会使得外层子区间的个数减少，从而使得Δa→0这一收敛条件在样本量较少的情况下很难保证，并且内层方差的错误估计，会直接导致该指标的估计错误。因此，在样本量相同的情况下，式(12) 较式(7) 更合理且高效。
为了解决非线性程度较高的极限状态函数及多设计点问题，本文将结合密度权重均匀地在输入变量取值区间内抽取样本点，避免寻找设计点。
2.2 基于密度权重抽样的空间分割方法 由文献[19]可知，式(2) 的失效概率可以等价表示为

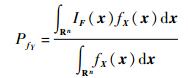(13)

在可靠性分析中，密度权重法对输入变量选择合适的取值区间，在其取值区间上采用均匀抽样，保证每个区域的点都尽可能地被抽取到，那么对于失效概率较小的情况，也可以得到较精确的解。在均匀抽取N组样本的情况下，失效概率可由式(14) 估计：

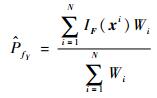(14)

式中：xⁱ为第i组样本；W_i=f_X(xⁱ)为样本xⁱ的密度权重。
基于式(14)，E(I_F|X_i∈A_k)可由式(15) 计算：

(15)

那么，E_Ak(E(I_F|X_i∈A_k))可由式(16) 计算得到

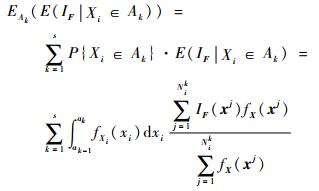(16)

式中:N_i^k为变量X_i的第k个子区间内包含的样本个数，且。因此，V_Ak(E(I_F|X_i∈A_k))有如下估计：

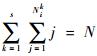
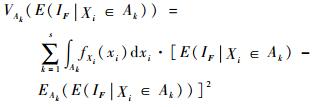(17)

对于V(I_F)，仍然可以利用这一组样本求得，先对V(I_F)等价变形得

(18)

由I_F的定义可知I_F²=I_F，且P_fY=E(I_F)，那么，式(18) 可由式(19) 计算：

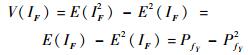(19)

式(19) 的样本估计式如下：

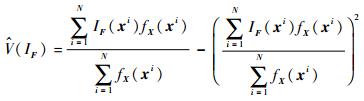(20)

通过式(15)~式(20) 的推导，本文给出了如何利用密度权重及空间分割来高效计算可靠性全局灵敏度指标的计算式。从该推导过程可以看出：
1) 本文方法仅需产生一组输入-输出样本通过对这一组样本的不同划分来近似得到所有输入变量的可靠性全局灵敏度指标。因此本文方法的计算量与输入变量的维数无关，而S-MCS方法的计算量与输入变量的维数呈线性相关，即(n+2)N^[17]。
2) 本文方法采用密度权重法等价地在输入变量的取值范围内均匀地抽样，使得抽取的样本以更高的可能性落入失效域，从而加快可靠性全局灵敏度指标计算的收敛速度。而S-MCS采用的是简单随机抽样，其根本依据是概率论中的大数定律，其需要大量的样本模拟才可能得到稳定的解。
2.3 可靠性全局灵敏度指标的计算流程 第1步??选择合适的输入变量取值区间。在选择每个输入变量取值区间时，文献[21]建议了2种方法：① 根据各个输入变量的边缘概率密度函数f_Xi(x_i)(i=1, 2, …, n)抽取一定量的样本，对样本排序，选出最大及最小值，作为该变量均匀采样区间的上下界；② 根据各个输入变量的累积分布函数F_Xi(x_i)(i=1, 2, …, n)确定均匀采样区间，即：假设均匀采样区间需包含变量X_i分布的(1－2α)%的数据，则变量X_i的均匀采样区间为[F_Xi^－1(α), F_Xi^－1(1－α)]，其中：α为分位数；1-α为置信度。
第2步??在第1步选择好的均匀采样区间内采用低偏差抽样^[22]来抽取N×n的样本矩阵A，即

(21)

第3步??依据式(3)，计算A样本矩阵对应的失效域指示值{I_F¹, I_F², …, I_F^N}及密度权重值{f_X(x¹), f_X(x²), …, f_X(xⁿ)}，I_F的方差可以通过式(20) 估计得到。
第4步??等样本数连续地将X_i的均匀采样样本空间划分为s个无重叠的子区间A_k=[a_k－1, a_k](k=1, 2, …, s)，来保证在每个子区间内样本的均匀性以满足密度权重法在每个子区间内成立的条件。计算每个子区间出现的概率，即

(22)

根据A_k找到与之相对应的I_F样本子集及对应的权重子集，即

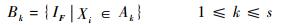(23)

(24)

那么E(I_F|X_i∈A_k)及E_Ak(E(I_F|X_i∈A_k))可由式(25) 估计得到:

(25)

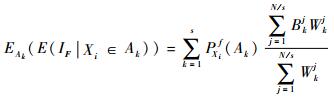(26)

第5步??估计条件期望的方差项：

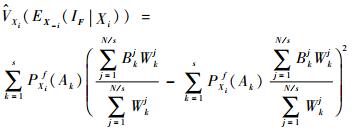(27)

因此，S_i估计如下：

(28)

本文所提的密度权重结合空间分割的思想，在计算S_i指标的过程中无需寻找设计点，并且仅需要一组样本就可以计算出所有变量的可靠性全局灵敏度指标，提高了样本的利用率，且计算量与输入维数无关。能够较好地解决非线性程度较高的极限状态函数及多设计点问题。
2.4 空间分割策略 利用式(12) 近似计算式(5) 的前提条件是Δa→0。但在实际处理中，Δa不能无限趋于0，因为若Δa无限趋于0，那么每个子区间内均值的计算会因为子区间内样本量较少而出错，内层均值的计算错误会直接导致最终结果的错误。然而内层样本也不能过大，内层样本过大会导致子区间的数目较少，较少的子区间数不尽不能保证收敛条件也会使得外层方差估计错误。因此，必须权衡内外层样本数的选择。
为加快计算的收敛速度，本文采用低偏差抽样中的Sobol序列^[22]。该低偏差抽样方法建议取2^k(k∈Z⁺)个样本。根据该原理，每个子区间内也应有2^k′(k′∈Z⁺)个样本，因此，区间分割情况也是有限的，即k种情况。若k为奇数，本文建议选择第(k+1)/2种的划分策略进行计算。若k为偶数，则选择在中间2种划分策略下估计值的平均作为该样本下的估计值。例如在128个总样本的情况下，其有7种划分方式，即每个子区间内可有2、4、8、16、32、64、128个样本，选择第4种划分，即每个子区间内包含16个样本的情况的计算结果作为S_i(i=1, 2, …, n)的估计值。在512个总样本的情况下，其有9种划分方式，选第5种即每个子区间内包含32个样本的情况下的计算结果作为S_i(i=1, 2, …, n)的估计值。可以看出随着样本数的增加，子区间内的样本数及子区间的个数同时都在增加，这样既保证了内外层矩的计算准确性，又保证了该方法的收敛条件，使得随着样本数的增加，估计值收敛于真实值。
3 算例分析 3.1 高度非线性算例(算例1) 非线性极限状态函数为g(X)=X₁⁴+2X₂⁴－20，其中X₁及X₂都服从均值为10、标准差为5的正态分布，计算结果如表 1所示。表 1中：D-MCS表示双层MCS法，其后括号内表示计算量；[]内数值表示100次重复计算的标准差；N/A表示无法计算出结果。从表 1中可以看出，在样本量小于等于2 048时，直接根据输入变量的密度函数进行抽样时，无法抽取到失效的样本点，从而使得S-MCS无法计算出可靠性全局灵敏度指标的值。而本文方法采用密度权重法在输入变量的取值区间内均匀地抽样，因此在样本量较少的情况下也可以抽取到失效点，从而在样本量较少的情况下也可以得到相应的可靠性全局灵敏度指标。并且，从表 1的可靠性全局灵敏度指标计算值及其100次重复计算结果的标准差上可以看出，本文方法不论在计算精度上还是指标计算的收敛速度上都高于文献[17]的S-MCS法。由于该功能函数的非线性程度较高，因此改进的一次二阶矩法无法寻找到设计点，这也使得文献[17]的重要抽样法不再适用，从而看出本文方法在处理高度非线性问题上的适用性及高效性。
表 1 算例1的计算结果 Table 1 Calculation results for example 1

样本量	Si
	X1		X2
	本文方法	S-MCS	本文方法	S-MCS
512	0.032 9[0.011 0]	N/A	0.043 4[0.013 5]	N/A
1 024	0.032 8[0.005 9]	N/A	0.043 7[0.005 6]	N/A
2 048	0.033 7[0.002 7]	N/A	0.044 6[0.004 3]	N/A
4 096	0.034 7[0.001 4]	0.029 0[0.013 4]	0.045 0[0.002 7]	0.043 0[0.024 1]
8 192	0.036 0[0.001 0]	0.030 5[0.007 1]	0.044 5[0.001 3]	0.039 6[0.009 1]
D-MCS(2×104×104)	0.036 2		0.044 7

表选项






3.2 多设计点算例(算例2) 对于极限状态函数:

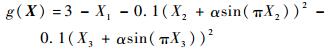(29)

其中:X_i(i=1, 2, 3)~N(0, 1)。图 1给出了α取不同值时的失效面。从图 1可以看出随着α的增加会出现多设计点的情况，且在α=0时功能函数的设计点是唯一的，在α=1时有明显的多设计点出现。表 2及表 3给出了在α=0时本文方法、文献[17]中的重要抽样法、S-MCS方法的计算结果。表 2中：IS表示重要抽样法；第1列括号外表示本文方法的计算量，括号内表示IS及S-MCS的计算量。从表 2中可以看出在样本量较少的情况下，S-MCS无法抽取到失效的样本点，从而无法得到可靠性全局灵敏度指标值。由于α=0时是单设计点问题，且功能函数退化成二次多项式形式，因此利用改进的一次二阶矩方法可以较好地寻找到设计点，但从表 2及表 3的计算结果中可以看出本文方法在计算精度及收敛速度上都高于重要抽样法，这是由于重要抽样法的计算量仍与输入变量的维数呈线性相关性，而本文方法的计算量与输入变量的维数无关。

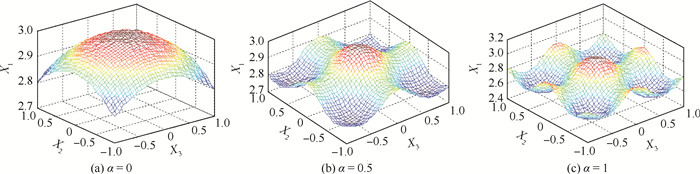图 1 α取不同值时算例2的失效面 Fig. 1 Failure surfaces of example 2 with different values of α

图选项

表 2 算例2中α=0的S_i计算结果 Table 2 Calculation results of S_i when α=0 for example 2

样本量	Si
	X1			X2			X3
	本文方法	IS	S-MCS	本文方法	IS	S-MCS	本文方法	IS	S-MCS
512(640)	0.612 0	0.624 0	N/A	0.003 5	0.001 8	N/A	0.003 4	0.002 3	N/A
1 024(1 280)	0.601 2	0.614 1	N/A	0.003 0	0.002 8	N/A	0.002 9	0.002 0	N/A
2 048(2 560)	0.656 2	0.616 1	0.624 0	0.002 6	0.002 1	0	0.002 7	0.002 1	-0.013 3
4 096(5 120)	0.621 1	0.612 0	0.621 7	0.002 7	0.001 9	0	0.002 7	0.002 8	0.003 3
8 192(10 240)	0.610 7	0.609 9	0.607 9	0.002 7	0.002 6	0.001 3	0.002 6	0.002 3	0.000 5
D-MCS(3×104×104)	0.611 21			0.002 7			0.002 7

表选项






表 3 算例2中α=0时100次S_i计算结果的标准差(SD) Table 3 Standard deviation (SD) of calculation results of S_i by 100 iterations when α=0 for example 2

样本量	SD
	X1			X2			X3
	本文方法	IS	S-MCS	本文方法	IS	S-MCS	本文方法	IS	S-MCS
512(640)	0.060 3	0.118 5	N/A	0.001 1	0.006 9	N/A	0.001 5	0.007 0	N/A
1 024(1 280)	0.043 2	0.077 4	N/A	0.000 5	0.009 8	N/A	0.000 6	0.005 0	N/A
2 048(2 560)	0.036 3	0.052 1	0.120 8	0.000 3	0.005 1	0	0.000 3	0.003 7	0.044 7
4 096(5 120)	0.024 0	0.038 2	0.039 1	0.000 2	0.002 8	0	0.000 2	0.007 1	0.002 8
8 192(1 0240)	0.014 6	0.023 1	0.018 2	0.000 1	0.005 2	0.001 3	0.000 1	0.003 7	0.001 2

表选项






表 4和表 5给出了α=1时本文方法、重要抽样法及S-MCS方法的计算结果。从图 1中明显地看出当α=1时出现了多设计点，因此改进的一次二阶矩方法在寻找设计点的过程中很可能陷入局部最优，无法解决多设计点问题，这也是表 4及表 5中，重要抽样方法计算精度差、计算收敛性低且跳跃的原因。S-MCS虽然在样本量较大的情况下可以得到较为精确的结果，但从表 4及表 5的计算结果可以看出本文方法无论在计算精度及收敛性方面都高于S-MCS方法。通过算例2的分析，可以看出本文方法在处理多设计点问题上的高效性及准确性。
表 4 算例2中α=1的S_i计算结果 Table 4 Calculation results of S_i when α=1 for example 2

样本量	Si
	X1			X2			X3
	本文方法	IS	S-MCS	本文方法	IS	S-MCS	本文方法	IS	S-MCS
512(640)	0.508 8	0.054 5	N/A	0.011 8	0.014 1	N/A	0.012 1	0.022 8	N/A
1 024(1 280)	0.532 4	0.324 7	0.535 7	0.010 4	0.009 2	0.010 0	0.010 6	0.017 7	0.010 0
2 048(2 560)	0.544 2	0.199 6	0.520 0	0.010 0	0.008 6	-0.012 0	0.009 9	0.011 2	0.014 7
4 096(5 120)	0.545 6	0.204 5	0.506 7	0.010 0	0.006 2	0.003 1	0.009 9	0.008 0	0.010 0
8 192(10 240)	0.548 0	0.300 8	0.485 3	0.009 6	0.006 2	0.009 6	0.009 6	0.007 8	0.011 1
D-MCS(3×104×104)	0.542 8			0.009 6			0.009 6

表选项






表 5 算例2中α=1时100次S_i计算结果的标准差 Table 5 Standard deviation of calculation results of S_i by 100 iterations when α=1 for example 2

样本量	SD
	X1			X2			X3
	本文方法	IS	S-MCS	本文方法	IS	S-MCS	本文方法	IS	S-MCS
512(640)	0.065 2	0.144 8	N/A	0.004 2	0.039 5	N/A	0.005 9	0.117 4	N/A
1 024(1 280)	0.049 8	2.668 8	0.264 9	0.002 2	0.019 6	0.010 0	0.002 7	0.062 3	0.010 0
2 048(2 560)	0.029 0	1.000 2	0.066 8	0.001 7	0.020 2	0.045 7	0.001 9	0.030 6	0.007 5
4 096(5 120)	0.021 9	0.534 0	0.022 2	0.001 1	0.008 4	0.002 7	0.001 4	0.015 7	0.002 0
8 192(10 240)	0.008 0	1.314 7	0.009 5	0.000 7	0.018 3	0.001 0	0.000 8	0.021 4	0.000 9

表选项






4 结论 1) 本文所证明的连续无重叠区间上的全方差公式，提高了可靠性全局灵敏度指标计算的收敛速度。
2) 本文方法仅需均匀地在输入变量可能的取值区间中抽取一组样本，通过对这组样本的不同划分同时估计出所有输入变量的可靠性全局灵敏度指标值，极大程度地提高了样本的利用率，使得计算量与输入变量的维数无关。
3) 本文方法无需寻找设计点，对于文献[17]无法解决的高度非线性极限状态函数及多设计点的情况，本文方法可以高效地解决。
4) 本文方法的估计值收敛于真实值的前提是，通过本文所提的空间分割策略，采用增加样本的方式，可以很好地保证这一前提。

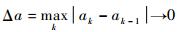
参考文献

[1]	SALTELLI A. Sensitivity analysis for importance assessment[J].Risk Analysis, 2002, 22(3): 579–590.DOI:10.1111/risk.2002.22.issue-3
[2]	BORGONOVO E, APOSTOLAKIS G E. A new importance measure for risk-informed decision-making[J].Reliability Engineering and System Safety, 2001, 72(2): 193–212.DOI:10.1016/S0951-8320(00)00108-3
[3]	BORGONOVO E, APOSTOLAKIS G E, TARANTOLA S, et al. Comparison of local and global sensitivity analysis techniques in probability safety assessment[J].Reliability Engineering and System Safety, 2003, 79(2): 175–185.DOI:10.1016/S0951-8320(02)00228-4
[4]	TARANTOLA S, KOPUSTINSKAS V, BOLADO-LAVIN R, et al. Sensitivity analysis using contribution to sample variance plot:Application to a water hammer model[J].Reliability Engineering and System Safety, 2012, 99(2): 62–73.
[5]	WEI P F, LU Z Z, RUAN W B, et al. Regional sensitivity analysis using revised mean and variance ratio functions[J].Reliability Engineering and System Safety, 2014, 121(1): 121–135.
[6]	SALTELLI A, RATTO M, ANDRES T, et al. Global sensitivity analysis[M].New York: John Wiley & Sons, 2008: 115-174.
[7]	SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J].Reliability Engineering and System Safety, 1990, 28(2): 229–253.DOI:10.1016/0951-8320(90)90065-U
[8]	ZHANG X F, PANDEY M D. An effective approximation for variance-based global sensitivity analysis[J].Reliability Engineering and System Safety, 2014, 121(4): 164–174.
[9]	WEI P, LU Z Z, SONG J W. A new variance-based global sensitivity analysis technique[J].Computation Physics Communication, 2013, 184(11): 2540–2551.DOI:10.1016/j.cpc.2013.07.006
[10]	DEMAN G, KONAKLI K, SUDRET B, et al. Using sparse polynomial chaos expansions for the global sensitivity analysis of groundwater lifetime expectancy in multi-layered hydrogeological model[J].Reliability Engineering and System Safety, 2016, 147: 156–169.DOI:10.1016/j.ress.2015.11.005
[11]	PIANOSI F, WAGENER T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions[J].Environmental Modelling & Software, 2015, 67: 1–11.
[12]	BORGONOVO E. A new uncertainty importance measure[J].Reliability Engineering and System Safety, 2007, 92(6): 771–784.DOI:10.1016/j.ress.2006.04.015
[13]	LIU Q, HOMMA T. A new importance measure for sensitivity analysis[J].Journal of Nuclear Science and Technology, 2010, 47(1): 53–61.DOI:10.1080/18811248.2010.9711927
[14]	CUI L J, LU Z Z, ZHAO X P. Moment-independent importance measure of basic random variable and its probability density evolution solution[J].Science China Technological Sciences, 2010, 53(4): 1138–1145.DOI:10.1007/s11431-009-0386-8
[15]	LI L Y, LU Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J].Structural Safety, 2012, 38: 40–47.DOI:10.1016/j.strusafe.2012.04.001
[16]	张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J].航空学报, 2014, 35(8): 2199–2206. ZHANG L G, LYU Z Z, CHEN J. An efficient method of failure probability-based moment-independent importance measure[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2199–2206.(in Chinese)
[17]	WEI P F, LU Z Z, HAO W R, et al. Efficient sampling methods for global reliability sensitivity analysis[J].Computation Physics Communication, 2012, 183(8): 1728–1743.DOI:10.1016/j.cpc.2012.03.014
[18]	DITLEVSEN O, MADSEN H O. Structural reliability methods[M].Chichester: Wiley, 1996: 102-109.
[19]	RASHKI M, MIRI M, MOGHADDAM M A. A new efficient simulation method to approximate the probability of failure and most probability point[J].Structural Safety, 2012, 39(4): 22–29.
[20]	ZHAI Q Q, YANG J, ZHAO Y. Space-partition method for the variance-based sensitivity analysis:Optimal partition scheme and comparative study[J].Reliability Engineering and System Safety, 2014, 131: 66–82.DOI:10.1016/j.ress.2014.06.013
[21]	吕召燕, 吕震宙, 李贵杰, 等. 基于密度权重的可靠性灵敏度分析方法[J].航空学报, 2014, 35(1): 179–186. LV Z Y, LV Z Z, LI G J, et al. Reliability sensitivity analysis method based on weight index of density[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 179–186.(in Chinese)
[22]	SOBOL I M. Uniformly distributed sequences with additional uniformity properties[J].USSR Computational Mathematics and Mathematical Physics, 1976, 16(5): 236–242.DOI:10.1016/0041-5553(76)90154-3