此外,由于大多数眼内手术机器人构型复杂,导致常用的动力学分析算法并不适用,需针对具体机器人模型进行动力学建模。机器人动力学模型的建立[9-11]主要采用2种动态数学模型,分别为牛顿-欧拉方程以及拉格朗日方程,其中拉格朗日方程不必求解关节内作用力,适用于具有RCM机构的眼内手术机器人。
国内外****对各种机器人进行了重力补偿的研究。文献[12]对具有弹性关节的机器人进行在线重力补偿的比例微分(PD)控制研究;文献[13]针对除冰机器人右臂提出了一种精确的在线重力补偿PD控制策略,并对其阶跃响应和动态跟踪特性进行分析;文献[14]建立了工程机器人动臂、前臂的动力学模型,并对其进行在线重力补偿,通过实验对机器人轨迹跟踪特性进行分析。
以上****的重力补偿研究多集中在工业机器人等非医疗领域,针对医疗机器人尤其是眼科手术机器人的相关研究较少。鉴于此,本文针对一种应用于视网膜静脉阻塞等眼内手术的机器人,根据D-H法建立了机器人坐标系,在构建机器人RCM机构等效模型的基础上,对其各构件质心瞬态位置进行分析;通过拉格朗日方程建立了该机器人系统的动力学模型;在此基础上,提出基于计算力矩法的重力补偿方法,并采用MATLAB/Simulink对重力补偿模型进行仿真,对比未重力补偿的独立PD控制模型,分析重力补偿策略的补偿效果,验证重力补偿模型的可行性。
1 坐标系建立 图 1所示为一种RCM机构的眼内手术机器人,该机器人共6个自由度,前三关节为3自由度SCARA机械臂,后三关节为3自由度RCM机构。采用D-H法[15]建立机器人各连杆坐标系Oixiyizi,如图 2所示,系统前三关节决定基坐标系O0x0y0z0下远程运动中心O点的位置,分别由绕z1轴的转动副、绕z2轴的转动副以及沿z3轴的移动副组成,2个转动副轴线z1与z2平行,移动副实现竖直运动。系统后三关节决定坐标系O3x3y3z3下末端器尖端Otop相对于O点的位置,且末端器轴线始终穿过远程运动中心O,后三关节分别由绕y3轴的转动副、绕y4轴的转动副以及沿z6轴的移动副组成。
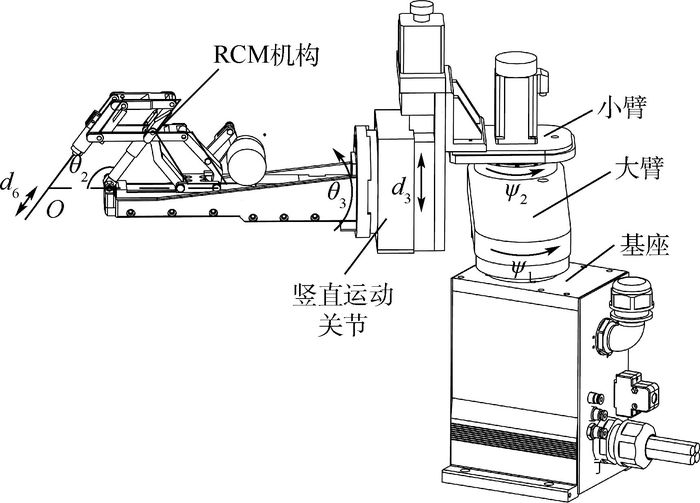 |
| 图 1 基于RCM机构的眼内手术机器人示意图 Fig. 1 Schematic diagram of intraocular surgery robotbased on RCM mechanism |
| 图选项 |
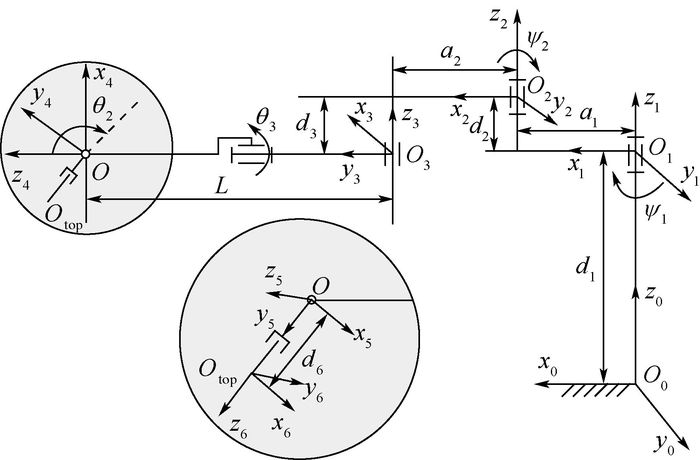 |
| 图 2 眼内手术机器人坐标系示意图 Fig. 2 Schematic diagram of coordinate system ofintraocular surgery robot |
| 图选项 |
设机器人系统中关节1高度为d1,长度为a1,关节2距离关节1高度d2,长度a2,关节3相对关节2高度为d3,远程运动中心O与关节3的距离不变,用L表示,关节6尖端Otop距远程运动中心O的距离为d6;根据D-H参数的定义,由图 2得到系统D-H参数如表 1所示。
表 1 机器人系统D-H参数 Table 1 D-H parameters of robot system
| i | 从zi-1到zi沿 xi-1距离ai-1 | 从zi-1到zi绕 xi-1角度αi-1 | 从xi-1到xi 沿zi距离di | 从xi-1到xi 绕zi角度θi |
| 1 | 0 | 0 | d1 | ψ1 |
| 2 | a1 | 0 | d2 | ψ2 |
| 3 | a2 | 0 | d3 | -90° |
| 4 | 0 | -90° | L | -90°+θ3 |
| 5 | 0 | -90° | 0 | θ2 |
| 6 | 0 | 0 | d6 | 0 |
表选项
图 2所示机器人坐标系不能够完全反映RCM机构的构成。图 3所示为机器人3自由度RCM机构简图,如图建立O′x′y′z′坐标系,其中li为各构件长度,分别将构件CD绕y′轴、构件HI绕y′轴与图 3各构件组成的平面机构绕x′轴的转动角度用θ1、θ2和θ3表示,构件AD移动距离用x1表示。分别将关节变量θ1、θ2、θ3以及x1作为机构的广义坐标。该RCM机构的自由度为3,有一广义坐标为被动,因此建立广义坐标间关系式,如式(1) 所示,已知θ1、θ2以及θ3 3个广义坐标可求出广义坐标x1,广义坐标x1速度与加速度由式(2) 得到。值得注意的是,广义坐标θ1、θ2、θ3为控制过程中的主动关节。
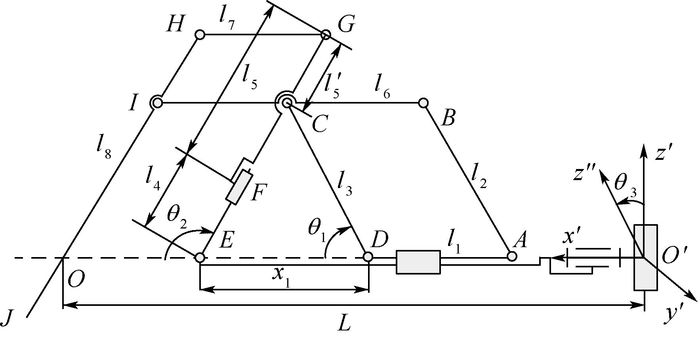 |
| 图 3 3自由度RCM机构简图 Fig. 3 Diagram of 3 degrees of freedom RCM mechanism |
| 图选项 |
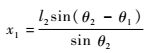 | (1) |
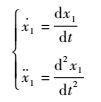 | (2) |
2 眼内手术机器人的动力学建模 眼内手术机器人在手术操作过程中需保证远程运动中心O固定,即在该过程中机器人前三关节保持固定,因此该机器人的动力学建模即为机器人后三关节RCM机构的动力学建模。由于RCM机构通常具有冗余约束[16],直接对其进行动力学分析有一定难度,因此有必要建立其等效模型。此外,需对等效模型的各构件质心位置进行分析,以便构建系统的动力学模型。
2.1 等效模型及各构件质心位置分析 由图 3可知,构件AB与构件CD运动规律一致,构件FG与构件HJ运动规律一致,因此建立等效模型,如图 4所示。图 3构件AB、BI、CD等效为图 4构件2,其长度为l2,其质量为3个构件总和;图 3中构件FG、GH、HJ等效为图 4中的构件4,其长度为l5-l5′,其质量为3个构件总和;构件2与构件4的质心矢径通过式(3) 得到。
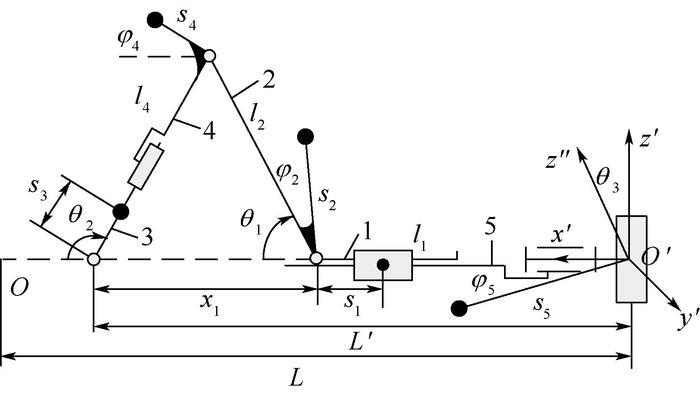 |
| si—各构件质心相对于转动关节的矢径的模;θi—关节变量;φi—与构件i质心矢径相对x′轴角度有关的参数。 图 4 等效后的RCM机构简图 Fig. 4 Equivalent diagram of RCM mechanism |
| 图选项 |
 | (3) |
式中:rs2、rs4分别为图 4中构件2、构件4的质心矢径;rAB等为图 3中对应构件的质心矢径;mAB等为对应构件的质量。
易知等效后的各构件矢径为广义坐标的函数,质心矢径rs2、rs4均可由矢径的模与矢径相对x′轴角度完全表示;推导所得质心矢径表达式较复杂,因此使用多项式拟合矢径函数,得到矢径的模与矢径相对x′轴角度关于广义坐标的等效函数。
对机器人系统RCM机构各构件质心位置分析,在图 4所示O′x′y′z′坐标系下各构件的质心位置函数表示为
 | (4) |
 | (5) |
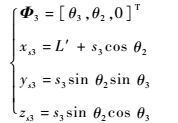 | (6) |
 | (7) |
 | (8) |
式中:Φi为构件i在O′x′y′z′坐标系下的角位移;xsi、ysi和zsi分别为构件i的质心在x′、y′和z′方向上的坐标表示。
2.2 动力学模型的建立 设机器人等效模型中各构件质心速度为vsi(i=1~5)。取图 4所示姿态为机器人各构件初始位置,O′x′y′面为系统零势能面,且不计机器人系统各构件间的摩擦。
根据2.1节所述眼内手术机器人各构件质心位置函数,建立机器人系统动力学模型。将式(4)~式(8) 对时间求导,得到构件i在广义坐标系下的角速度及质心速度,如式(9) 所示。
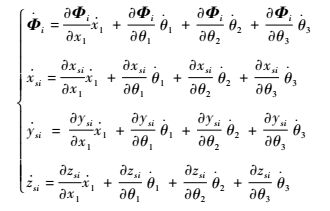 | (9) |
采用拉格朗日方程建立系统动力学模型:
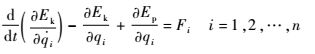 | (10) |
式中:Ek为系统动能;Ep为系统势能;qi为广义坐标;Fi为广义力,对应于驱动角θ1、θ2、θ3以及驱动位移x1的系统广义力,广义坐标为角位移时,Fi为力矩,广义坐标为线位移时,Fi为力;n为广义坐标数,该RCM机构中n为4。机器人系统的动能及势能分别为
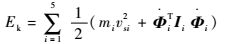 | (11) |
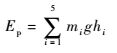 | (12) |
式中:Ii为构件i在O′x′y′z′坐标系下的惯性张量;mi为各构件质心质量;hi为各构件质心相对于零势能面的高度。质心速度vsi(i=1~5) 由式(13) 得到:
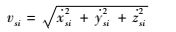 | (13) |
将各参数代入式(10),整理得到化简后的系统动力学方程为
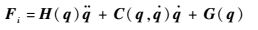 | (14) |
式中:

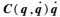
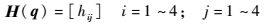 | (15) |
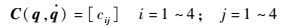 | (16) |
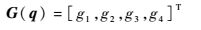 | (17) |
经推导,得
 | (18) |
 | (19) |
 | (20) |
式中:J′j(j=1~8) 分别为图 3中各构件质心相对于y′轴的转动惯量;JTotal为图 4机器人初始状态各构件相对于x′轴的转动惯量总和。
由式(14) 可知,已知各连杆位置、速度、加速度曲线即可求得对应的各驱动关节力矩曲线,即机器人逆动力学表示。值得注意的是,式(14) 所述动力学方程具有4个广义坐标,分别为θ1、θ2、θ3和x1,其中θ1、θ2和θ3为驱动关节变量,将式(1) 和式(2) 代入式(14) 所述动力学方程,得到关于θ1、θ2与θ3的动力学方程,其中F1、F2和F3分别对应θ1、θ2和θ3的3个广义坐标产生的广义力。
3 眼内手术机器人的重力补偿方法 根据第2节推导的动力学模型,可知动力学方程中重力项对于系统驱动力或力矩的影响较为明显。通常采用的具有固定重力补偿的PD控制,该控制方法虽然可有效补偿重力项,但必须事先得知各驱动关节的期望位置,不能实时跟踪关节轨迹,同时该方法忽略了各关节变量之间的耦合。针对以上重力补偿方法的缺陷,设计一种可在线重力补偿的计算力矩法[17]。该重力补偿方法不仅可实时地获取重力项并补偿,并且可以对期望的关节变量轨迹曲线进行跟踪。
该控制方案的基本思路为,在内控制回路中引入非线性补偿,且机器人的重力项包括在该非线性补偿中,使得机器人系统变为易于控制的线性定常系统,该控制方案的结构框图如图 5所示,引入控制为
 |
| 图 5 重力补偿模型结构框图 Fig. 5 Structure diagram of gravity compensation model |
| 图选项 |
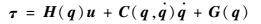 | (21) |
机器人系统的受控方程为
 | (22) |
H(q)可逆,且假定获得的机器人各参数名义值足够精确,可忽略模型中各矩阵与机器人实际矩阵的误差,经过化简,受控方程等价于如下定常系统:
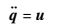 | (23) |
将该定常系统引入PD控制:
 | (24) |
式中:Kd与Kp为正定矩阵,由Kd与Kp的正定性可知
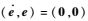
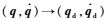
4 MATLAB重力补偿仿真及结果分析 眼内手术机器人参数如下:机器人各构件采用均质铝合金材料,密度为2.7 kg/m3,各构件长度l2=60 mm,L′=294 mm,各构件矢径的模为s1=25 mm,s2=35.058 3 mm,s3=21.747 mm,s5=137.885 mm,m1=0.142 kg,m2=0.078 kg,m3=0.036 kg,m4=0.28 kg,m5=1.32 kg,φ4=39.96°,φ5=5.173°。设机器人系统各关节变量初始位置为q=[44.05°, 135°, 0°],3 s后到达期望位置[40°, 120°, 45°],则该眼内手术机器人RCM机构的关节变量期望轨迹可用如下函数表示:
 | (25) |
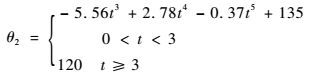 | (26) |
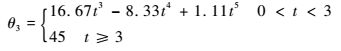 | (27) |
重力补偿模型参数矩阵Kd=diag(4.5, 3.8, 8.5),Kp=diag(0.028 8, 0.0388 8, 0.26),仿真时间为5 s,对于给定的关节变量变化曲线,采用拉格朗日逆动力学,得到采样周期内各关节变量驱动力矩变化曲线,如图 6所示,可知驱动力矩曲线变化平缓,且没有突变;稳定时刻各关节的驱动力矩即为各关节变量对应的重力项,大小分别为0.104 3、-0.046 5和-0.036 1 N·m。
 |
| 图 6 机器人系统驱动力矩变化曲线 Fig. 6 Driving torque variation curves of robot system |
| 图选项 |
为分析重力补偿策略的效果,设定一对照模型与重力补偿模型进行对比,对照模型为不采用重力补偿的独立PD控制模型,该模型结构框图如图 7所示。采用MATLAB/Simulink对上述2种模型进行仿真,得到采样周期内各关节变量的响应曲线。
 |
| 图 7 独立PD控制模型结构框图 Fig. 7 Structure diagram of independent PD control model |
| 图选项 |
独立PD控制模型的响应曲线如图 8所示,其参数矩阵的选取与重力补偿模型参数矩阵一致。分析可知,未采用重力补偿时,响应曲线达到稳定值后存在稳态误差,其大小受重力项的影响,稳态误差分别为-3.621 7°,1.195 9°,0.138 9°。值得注意的是,图 8所示独立PD控制模型各关节的驱动角均从0°开始变化,且前2个关节在仿真初期与期望曲线差距较大,这是由于该模型不能完成对连续时变轨迹的跟踪任务,对前两关节设定的从非零初始条件出发的轨迹无法实现全程跟踪。
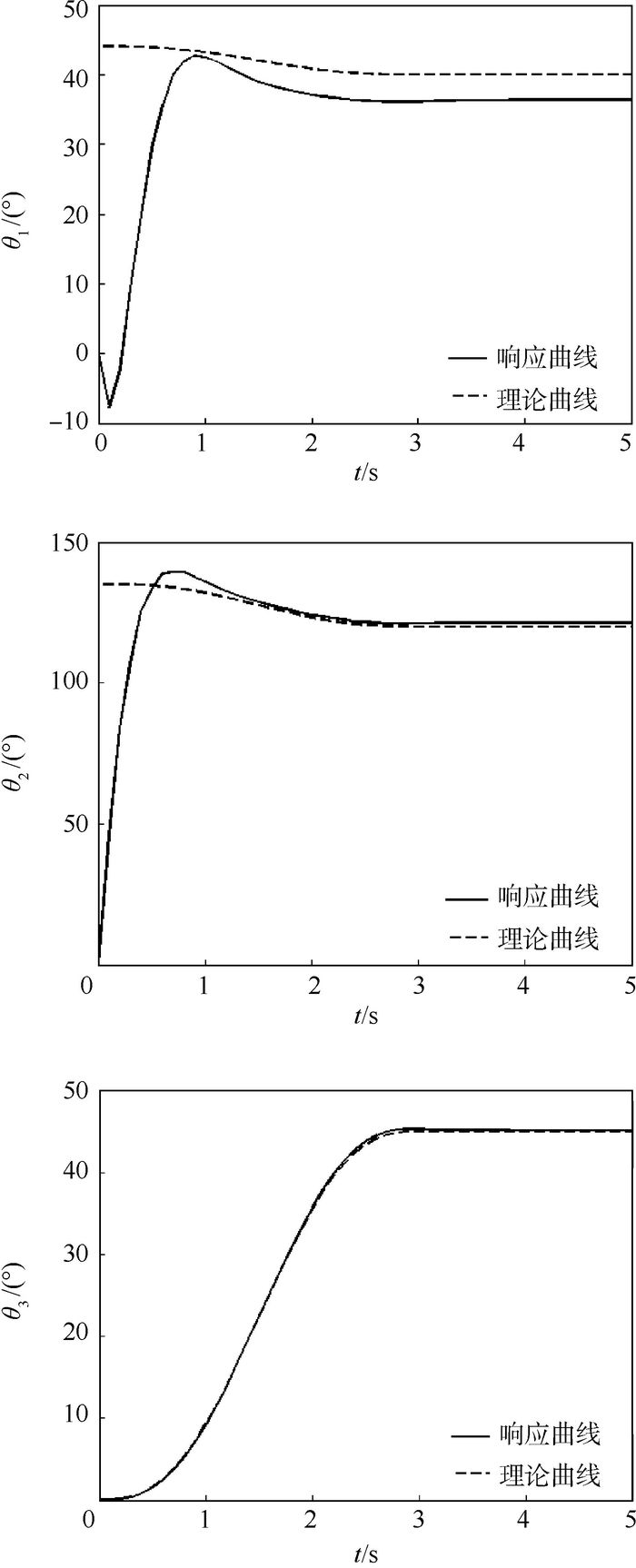 |
| 图 8 独立PD控制模型响应曲线 Fig. 8 Response curves of independent PD control model |
| 图选项 |
图 9为采用第3节所述在线重力补偿的计算力矩法模型的响应曲线,由图可知响应曲线变化平稳,且有较好的跟踪特性,模型的稳态误差为零。对比图 8与图 9,分别取±2%与±5%作为响应曲线的误差带,则各关节变量响应曲线调节时间如表 2所示。
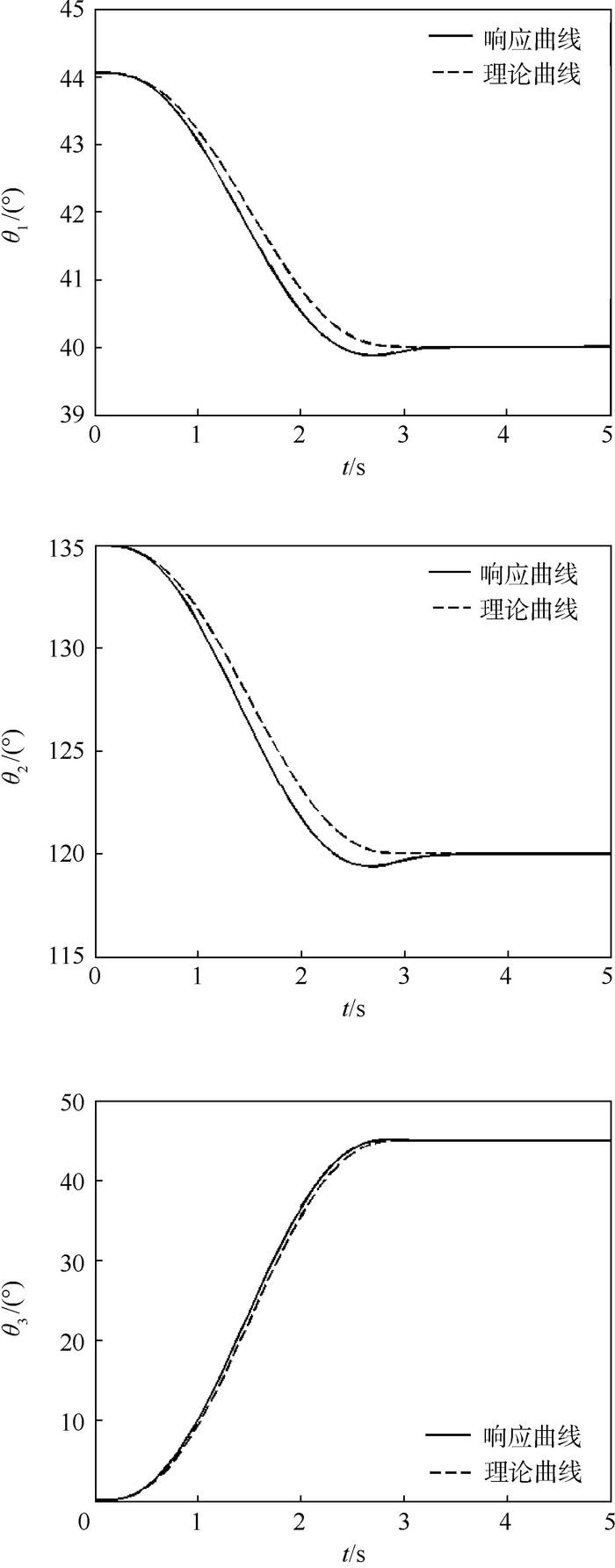 |
| 图 9 基于计算力矩法的重力补偿模型响应曲线 Fig. 9 Response curves of gravity compensation model based on computed torque method |
| 图选项 |
表 2 各关节响应曲线的调节时间 Table 2 Adjusting time of response curve of each joint
| 误差带 | 关节变量 | 调节时间/s | |
| 计算力矩法 | PD控制模型 | ||
| ±2% | θ1 | 1.9 | 2.0 |
| θ2 | 1.9 | 2.1 | |
| θ3 | 2.4 | 2.6 | |
| ±5% | θ1 | 1.4 | 1.7 |
| θ2 | 1.5 | 1.6 | |
| θ3 | 2.3 | 2.4 | |
表选项
由图 8、图 9及表 2可知,相对于未重力补偿的独立PD控制模型,重力补偿模型响应曲线的调节时间较小,响应速度相比较有一定优势,且模型可有效补偿系统的重力项,因此重力补偿模型相对于独立PD控制模型具有明显优势。
图 10所示为采用重力补偿模型各关节变量期望曲线与响应曲线的差值变化,由图可知,关节变量θ1在t=1.9s达到最大误差0.337 8°,关节变量θ2在t=1.9 s达到最大误差1.453 3°,关节变量θ3在t=1.8 s达到最大误差-1.134 2°。分析可知,从t=0 s开始,各关节响应位置与期望位置重合,随仿真时间变化,响应位置与期望位置误差变大,分别于t=1.9 s,t=1.9 s与t=1.8 s达到峰值并逐渐减小,且误差均不超过1.5°;因此该重力补偿模型的补偿精度高,具有良好跟踪特性,该模型有较高的可行性。
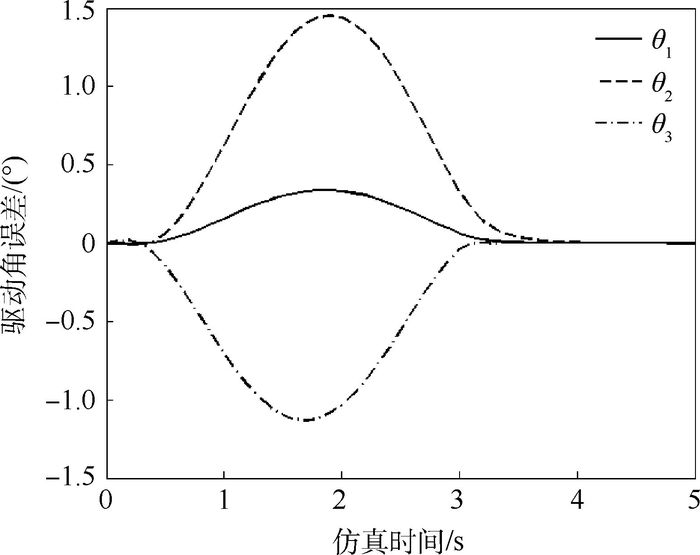 |
| 图 10 重力补偿模型期望曲线与响应曲线的差值 Fig. 10 Difference between expected curves and response curves of gravity compensation model |
| 图选项 |
5 结论 1) 本文给出一种基于RCM机构的眼内手术机器人的动力学模型,以便对机器人系统进行力矩控制。
2) 通过与未重力补偿的独立PD控制模型进行比较,证明重力补偿模型可有效补偿系统的重力项,且响应速度有一定优势。
3) 通过分析重力补偿模型期望曲线与响应曲线的差值变化,验证重力补偿模型的重力补偿精度高,具有良好的跟踪特性,该模型有较高的可行性。
参考文献
| [1] | WEI W, GOLDMAN R, SIMAAN N, et al.Design and theoretical evaluation of micro-surgical manipulators for orbital manipulation and intraocular dexterity[C]//2007 IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2007:3389-3395. |
| [2] | 肖晶晶, 杨洋, 沈丽君, 等. 视网膜血管搭桥手术机器人系统的研究[J].机器人, 2014, 36(3): 293–299. XIAO J J, YANG Y, SHEN L J, et al. A robotic system for retinal vascular bypass surgery[J].Journal of Robotics, 2014, 36(3): 293–299.(in Chinese) |
| [3] | BECKER B C.Vision-based control of a handheld micromanipulator for robot-assisted retinal surgery[D].Pittsburgh:Carnegie Mellon University, 2012. |
| [4] | 裴旭, 于靖军, 毕树生, 等. 一维远程运动中心机构的型综合[J].机械工程学报, 2009, 45(2): 144–148. PEI X, YU J J, BI S S, et al. Type synthesis for one-dimensional remote-center-of motion mechanisms[J].Journal of Mechanical Engineering, 2009, 45(2): 144–148.(in Chinese) |
| [5] | 黄龙, 杨洋, 苏鹏, 等. 1R1T远程运动中心机构的型综合[J].机械工程学报, 2015, 51(13): 131–136. HUANG L, YANG Y, SU P, et al. Type synthesis of 1R1T remote center of motion mechanisms[J].Journal of Mechanical Engineering, 2015, 51(13): 131–136.(in Chinese) |
| [6] | GIJBELS A, WOUTERS N, STALMANS P, et al.Design and realisation of a novel robotic manipulator for retinal surgery[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS), 2013.Piscataway, NJ:IEEE Press, 2013:3598-3603. |
| [7] | GIJBELS A, VANDER POORTEN E B, STALMANS P, et al.Design of a teleoperated robotic system for retinal surgery[C]//2014 IEEE International Conference on Robotics and Automation (ICRA).Piscataway, NJ:IEEE Press, 2014:2357-2363. |
| [8] | 肖晶晶, 杨洋, 李大寨, 等. 眼科显微手术机器人研究进展及关键技术分析[J].机械工程学报, 2013, 49(1): 15–22. XIAO J J, YANG Y, LI D Z, et al. Advances and key techniques of ophthalmic microsurgical robots[J].Journal of Mechanical Engineering, 2013, 49(1): 15–22.(in Chinese) |
| [9] | 蔡自兴. 机器人学基础[M].北京: 机械工业出版社, 2009: 6. CAI Z X. Fundamentals of robotics[M].Beijing: China Machine Press, 2009: 6.(in Chinese) |
| [10] | LIU X, LI H, WANG J, et al. Dynamics analysis of flexible space robot with joint friction[J].Aerospace Science and Technology, 2015, 47: 164–176.DOI:10.1016/j.ast.2015.09.030 |
| [11] | 刘善增, 余跃庆, 刘庆波, 等. 3-R RC并联机器人动力学分析[J].机械工程学报, 2009, 45(5): 220–224. LIU S Z, YU Y Q, LIU Q B, et al. Dynamic analysis of 3-R RC parallel manipulator[J].Journal of Mechanical Engineering, 2009, 45(5): 220–224.(in Chinese) |
| [12] | DE LUCA A, SICILIANO B, ZOLLO L. PD control with on-line gravity compensation for robots with elastic joints:Theory and experiments[J].Automatica, 2005, 41(10): 1809–1819.DOI:10.1016/j.automatica.2005.05.009 |
| [13] | 龚捷, 鲍金锋, 衣冠超, 等. 基于计算力矩法的装载机工作装置轨迹控制[J].机械工程学报, 2010, 46(13): 141–146. GONG J, BAO J F, YI G C, et al. Trajectory-following control for manipulator of wheel loaders based on computed torque[J].Journal of Mechanical Engineering, 2010, 46(13): 141–146.(in Chinese) |
| [14] | 唐新星, 侯敬巍, 倪涛, 等. 在线重力补偿下工程机器人自主作业轨迹跟踪性能分析[J].农业工程学报, 2013, 29(3): 30–37. TANG X X, HOU J W, NI T, et al. Analysis on autonomous task trajectory tracking performance of construction robot with online gravity compensation[J].Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(3): 30–37.(in Chinese) |
| [15] | CRAIG J J. Introduction to robotics:Mechanics and control[M].Upper Saddle River: Pearson Prentice Hall, 2005: 62-100. |
| [16] | 宗光华, 裴旭, 于靖军, 等. 双平行四杆型远程运动中心机构的设计[J].机械工程学报, 2007, 43(12): 103–108. ZONG G H, PEI X, YU J J, et al. Design of double parallelogram remote-center-of-motion mechanisms[J].Chinese Journal of Mechanical Engineering, 2007, 43(12): 103–108.DOI:10.3321/j.issn:0577-6686.2007.12.020(in Chinese) |
| [17] | 霍伟. 机器人动力学与控制[M].北京: 高等教育出版社, 2005: 124-140. HUO W. Robot dynamics and control[M].Beijing: Higher Education Press, 2005: 124-140.(in Chinese) |
