导弹在长期贮存过程中要经历仓库储存、运输、值班等一系列任务，期间会受到各种环境因素的影响，在这些环境因素中，尤其以力学环境的影响最大^[1]。运输振动作为导弹在贮存过程中遇到的主要力学环境，由于其振动频率低、振幅大，长期作用会对导弹造成疲劳累积损伤，影响导弹的性能。因此，积极有效地开展振动试验是提高导弹可靠性、延长导弹寿命的主要手段。
作为振动试验的基础和输入，振动谱记录了振动载荷等级及其作用时间，是振动试验的重要组成部分。理想条件下，振动谱的设计应基于产品实际使用条件下的激励数据，然而由于振动具有随机性，随机路面激励很难通过测量得到，所以目前国内在开展导弹振动试验中所采用的振动谱，大都基于监测到的部分响应数据，参照一定的标准进行编谱。例如，郭强玲^[2]针对空空导弹在使用过程中承受的挂飞振动，分别采用GJB 150.16—1986^[3]、GJB 899A—2009^[4]以及美军标MIL-STD-810^[5]，探讨了导弹耐久振动试验条件的确定方法。张绍伟和龚庆祥^[6]在阐述了对导弹进行全弹振动环境应力筛选必要性的基础上，参照GJB 1032—90^[7]，依次确定了振动试验振动谱的谱型、量值、时间及方向。陈万创和李爱国^[8]、张策等^[9]依据GJB 899A—2009^[4]和GJB 150—86^[10]，分别设计出空空导弹和防空导弹的综合环境可靠性试验振动剖面，计算出相应振动量值。刘凯^[11]在讨论空空导弹自由飞振动条件制定方法时指出，按GJB 150—86^[10]进行的振动试验不可能精确模拟实际试件的使用环境条件，它只能偏保守地反映使用环境的主要特征或损坏能力，提出采用基于实测数据和频段划分的统计方法，但最终仍采用国军标所提供的平谱或梯形谱来对得到的数据综合谱进行规范。
针对基于标准的振动谱设计方法与导弹实际振动环境差距大，以及随机路面激励难以测量等问题，本文采用逆虚拟激励法对导弹运输过程的振动谱进行设计，在随机路面激励未知的条件下，由测得的导弹振动响应谱来反求激励谱，并以该激励谱作为振动谱设计依据，使得最终得到的振动谱能够反映导弹的实际使用环境条件，增加了振动试验结果可信性和说服力，对于提高导弹可靠性及环境适应性具有一定参考意义。
1 逆虚拟激励法基本原理 逆虚拟激励法是林家浩等^[12-13]为解决路面或轨道表面不平度的功率谱难以识别和模拟而提出的，他们将虚拟激励法逆向推广，用来求解随机载荷的反问题(随机载荷识别问题)，亦即从测量得到的随机响应，逆推随机载荷，将平稳随机振动的计算转化为简谐振动计算，从而为随机载荷的识别开辟了一条有效的途径^[14]。一系列实验与理论研究^[15-19]表明，逆虚拟激励法不但易于实施，计算成本低，而且识别精度高，抗噪声能力强，具有良好的应用前景，其基本原理如下。
在频域中求解平稳随机响应的公式为

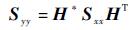(1)

式中：S_yy为已知的n×n阶响应功率谱密度(Power Spectral Density, PSD)矩阵；S_xx为待求的m×m阶激励功率谱密度矩阵；H为n×m阶频率响应矩阵；n和m分别为响应和激励自由度；上标*和T分别表示矩阵的共轭和转置。
根据虚拟激励法，将S_yy作如下分解：

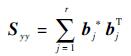(2)

式中：r为矩阵S_yy的秩。
构造虚拟简谐响应为

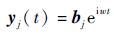(3)

引起该虚拟响应的虚拟激励为

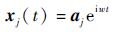(4)

由激励响应关系知

(5)

则

(6)

式中：上标+表示矩阵的广义逆。
由式(1)~式(6) 求得激励功率谱矩阵为

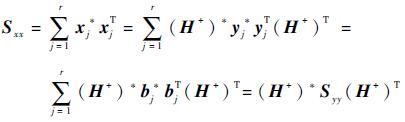(7)

2 导弹-悬架系统四自由度振动模型 为简化问题作如下假设：① 导弹运输车沿纵向中心线左右对称，并作匀速直线运动；② 将导弹视为密度均匀、阻尼不计的圆柱体，与运输车悬架直接连接；③ 悬架弹簧与平衡杆视为相互独立的元件，并忽略平衡杆的转动惯量；④ 忽略轮胎阻尼及路面以外的其他振源^[20]。
对于等级较低的路面，其表面不平度整体上分布比较均匀，路面对于左右车轮的激励基本相同，并基于假设①，故将左右轮的激励简化为一个信号。
基于以上假设，建立了导弹-悬架系统四自由度振动模型，如图 1所示。图中：m₁、m₂和m₃分别为导弹及前后轮胎的质量；I₁为导弹绕质心O的转动惯量；k₁、k₂、k₃和k₄分别为前后悬架与前后轮胎的等效刚度；c₁和c₂分别为前后悬架的阻尼强度；l₁和l₂为前后悬架离导弹质心的距离；z₁和θ₁分别为导弹质心的垂直位移和导弹质心绕y轴的转角；z₂和z₃分别为前后轮胎的垂直位移；q₁和q₂分别为前后轮路面激励。

图 1 导弹-悬架系统四自由度振动模型 Fig. 1 Four-degree-of-freedom vibration model of missile-suspension system

图选项

根据上述振动模型可以得到系统动力学方程为

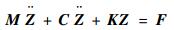(8)

式中：M、C和K分别为系统质量矩阵、阻尼矩阵和刚度矩阵；Z为系统激励位移向量；F为激励向量。



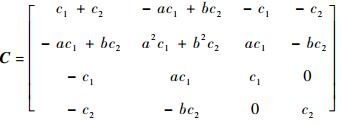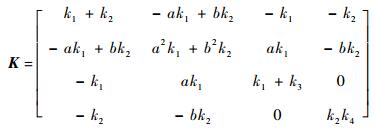3 基于逆虚拟激励法的振动谱识别算法 3.1 数据预处理 在振动响应数据采集过程中，得到的是离散时域位移响应数据Z₁(t)：

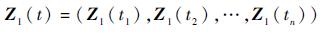(9)

式中：Z₁(t)属于平稳随机过程；Z₁(t_n)表示t_n时刻的系统响应值。
Z₁(t)的自相关函数为

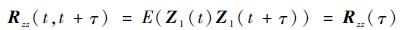(10)

通过Fourier变换将R_zz转化为频域的功率谱密度：

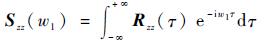(11)

另外，若采集到的不是系统位移响应，而是系统振动加速度时，可采用式(12) 进行转换：

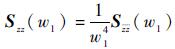(12)

式中：为加速度功率谱矩阵。
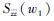
3.2 振动谱识别模型 假定导弹在运输过程中路面整体是水平的，在足够长的一段直线距离内，路面竖向不平度视为一个空间平稳随机过程^[21]，故导弹振动属于平稳随机过程，且前后车轮所受激励完全相干，因此系统激励功率谱矩阵可分解^[12]为

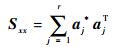(13)

则可构造虚拟激励为

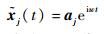(14)

将式(14) 代入式(8)，得系统虚拟响应为

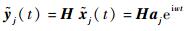(15)

式中：H=[－w²M+iwC+K]^－1为系统的频率响应矩阵。
对响应功率谱矩阵按式(2) 进行分解。
导弹在公路运输过程中响应功率谱矩阵可以通过测量得到，则根据式(2) 构造虚拟简谐响应为

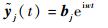(16)

又由式(15) 知，则

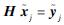
(17)

综上所述，可以求出激励功率谱矩阵为

(18)

为验证算法准确性，引入识别误差

(19)

由于功率谱矩阵必定为非负的Hermite矩阵，因此对于式(2) 的求解，可以采用特征值分解法^[22]。

(20)

式中：λ为特征值；φ为相应的特征向量；φ^H表示共轭转置。
3.3 振动谱设计流程 根据上述理论推导，可以得到基于逆虚拟激励法的导弹振动谱设计步骤，具体如下：
1) 根据式(15) 建立导弹-悬架系统动力学方程，计算频率响应矩阵H。
2) 对实测得到的导弹时域振动响应数据进行预处理，按式(10)~式(12) 计算得到系统位移响应功率谱矩阵S_yy。
3) 将响应功率谱矩阵S_yy按式(2) 进行分解，构造如式(16) 的虚拟简谐响应。
4) 根据式(17) 计算各虚拟激励，并按式(18) 第2个等式计算激励谱矩阵。
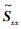
5) 采用一定的功率谱处理方法，求得激励谱矩阵上限曲线，设计出导弹运输振动试验谱。
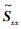
4 实验仿真 4.1 仿真流程 为简化计算，仿真过程中以运输车前后轮及导弹质心垂直位移作为响应输入，忽略导弹绕质心的转动。
首先计算系统阻尼，通过模态试验，对系统前后轮施加q₁、q₂正弦激励，将加速度传感器采集得到导弹运输车前后轮及导弹质心的时域振动响应数据，代入式(8) 计算，可以得到系统前后悬架阻尼。
外在激励q₁、q₂完全相干，只存在一个相位差ζ，故给定如下外在激励：

式中：A为外在激励振幅; ζ=w_o(l₁+l₂)/v；w_o为激励频率；v为车速。
然后采用文献[14]中的虚拟激励法计算出运输车前后轮及导弹质心垂直位移功率谱，将其作为实测的系统响应功率谱；最后采用逆虚拟激励法反求系统激励功率谱、，利用式(20) 与给定激励功率谱S_q1、S_q2进行对比，验证算法准确性。仿真参数如表 1所示。
表 1 仿真参数 Table 1 Simulation parameters

变量	m1/kg	m2/kg	m3/kg	k1/(kN·m-1)	k2/(kN·m-1)	k3/(kN·m-1)	k4/(kN·m-1)	c1/(Ns·m-1)	c2/(Ns·m-1)	l1/m	l2/m	A/m	wo/(rad·s-1)	v/(m·s-1)
数值	1 000	40	45	18	24	190	220	350	600	3	2	20	30	50

表选项






4.2 仿真结果分析 对系统进行模态分析，计算得到系统一阶、二阶、三阶固有频率分别为58、112、167Hz，并由虚拟激励法计算得到运输车前后轮及导弹质心垂直位移功率谱密度，如图 2所示。

图 2 运输车前后轮及导弹质心垂直位移PSD Fig. 2 Vertical displacement PSD of front-rear wheels of vehicle and missile centroid

图选项

1) 零噪声识别误差分析。零噪声条件下，采用逆虚拟激励法，由上述响应功率谱反求得到运输车前后轮所受激励谱，并与给定激励谱进行对比，如图 3和图 4所示。可知，前轮识别得到的功率谱在低频段误差较小，中高频段( > 100Hz)由于系统共振误差出现一定波动，Error=2.39%；后轮识别得到的功率谱与实际功率谱基本吻合，Error=1.96%。由此可见，根据逆虚拟激励法，由系统响应反求系统激励的方法是可行的，具有较高精度。

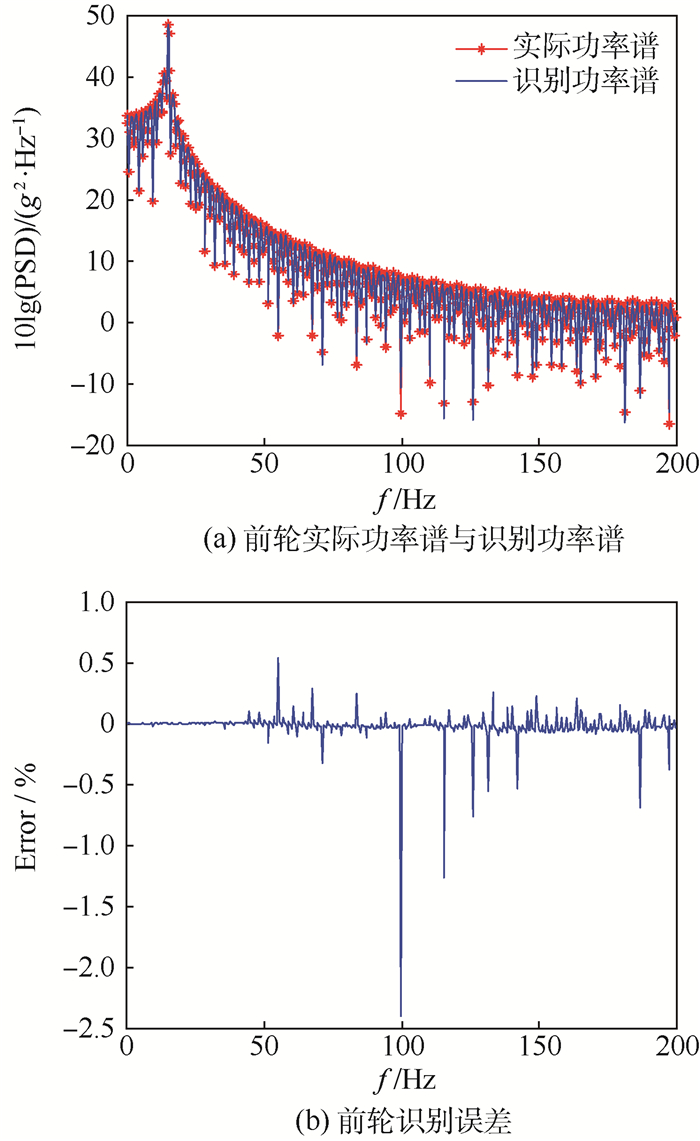图 3 前轮识别功率谱密度及误差曲线 Fig. 3 Identified PSD and identification error curves of front wheels

图选项

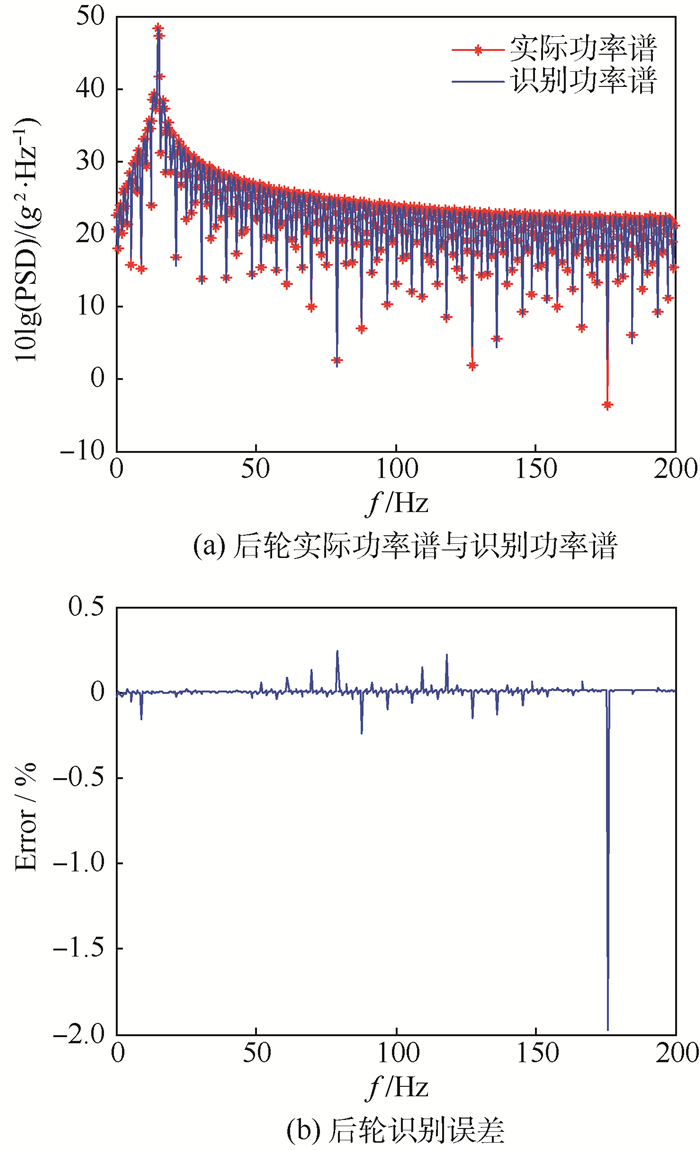图 4 后轮识别功率谱密度及误差曲线 Fig. 4 Identified PSD and identification error curves of rear wheels

图选项

2) 加入30%响应噪声识别误差分析。以前轮为例，利用MATLAB中“randn”命令，在系统响应数据中加入30%的高斯白噪声，得到前轮识别功率谱及其误差曲线，如图 5所示。可知，在低频段识别精度较高，中高频段( > 80Hz)由于高频噪声影响误差较大，Error=3.21%，证明该方法具有一定抗噪能力。

图 5 30%噪声条件下前轮识别功率谱密度及误差曲线 Fig. 5 Identified PSD and identification error curves of front wheels under condition of 30% noise

图选项

3) 小阻尼条件下识别误差分析。以前轮为例，分别取原系统阻尼c₁、c₂的60%及30%，利用逆虚拟激励法求得前轮激励功率谱及误差曲线，如图 6和图 7所示。可知，系统阻尼降为原来的60%时，功率谱识别误差Error=2.48%，30%时Error=4.49%。由此可见，降低系统阻尼后，功率谱识别精度有所降低，尤其在系统固有频率附近，误差较大。这是由于较小的阻尼导致系统刚度矩阵在固有频率附近出现病态，可通过增加测点数量和提高响应数据精度的方法克服。

图 6 60%系统阻尼前轮识别功率谱密度及误差曲线 Fig. 6 Identified PSD and identification error curves of front wheels under condition of 60% system damping

图选项

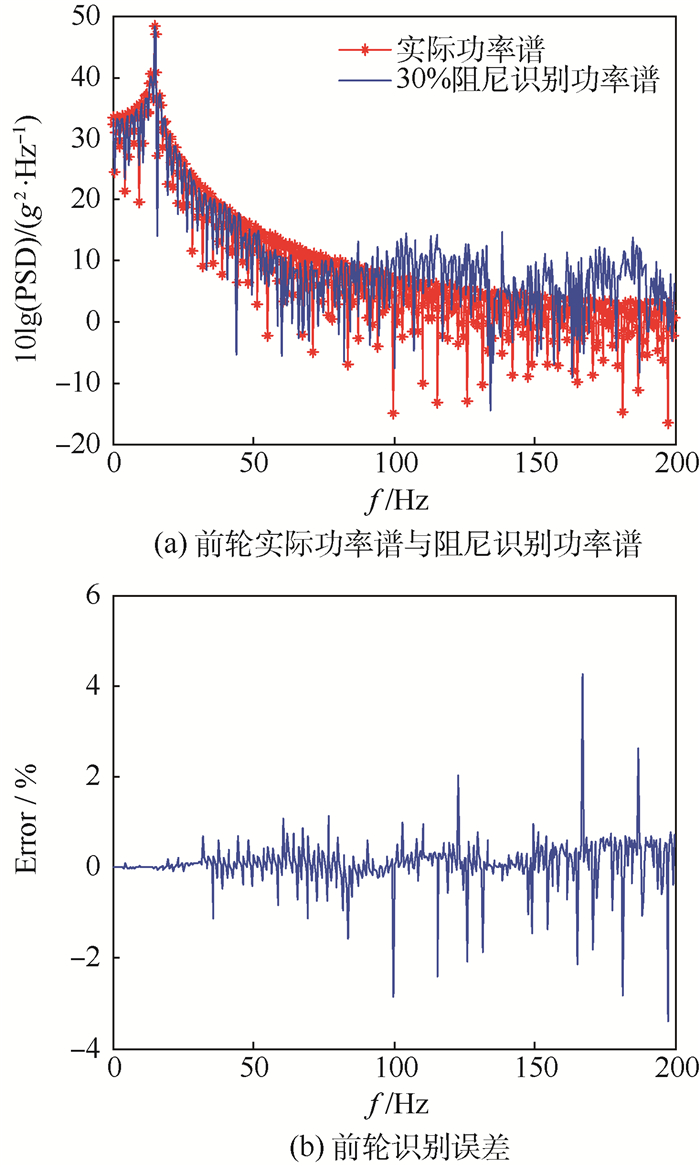图 7 30%系统阻尼前轮识别功率谱密度及误差曲线 Fig. 7 Identified PSD and identification error curves of front wheels under condition of 30% system damping

图选项

5 结论 逆虚拟激励法经过不断研究与改进，在航空、车辆、土木工程等领域得到了广泛的应用，但在导弹振动环境试验方面的应用较为少见。针对目前导弹振动试验谱设计存在的不足，主要完成了以下工作：
1) 根据导弹公路运输特点，建立了导弹-悬架四自由度振动模型。
2) 基于逆虚拟激励法求得导弹运输过程路面激励谱，给出了导弹运输振动谱设计流程。
3) 讨论了噪声及阻尼对振动谱精度的影响，通过仿真验证了本文算法具有一定抗噪能力和较好的鲁棒性。
此外，本文主要讨论了导弹垂直方向的振动情况，忽略了导弹另外2个方向的振动，下一步的工作主要针对以上问题展开研究，进一步完善导弹振动谱设计算法，提高编谱精度。

参考文献

[1]	李晓松. 随机载荷识别技术在导弹振动试验中的应用研究[D]. 南京: 南京航空航天大学, 2011: 1. LI X S.Application research on stochastic loads identification for missile vibration test[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2011:1(in Chinese).
[2]	郭强玲. 空空导弹振动试验条件确定方法[J].航空标准化与质量, 2006(3): 34–37. GUO Q L. Determined method of the vibration test conditions of air to air missile[J].Aeronautic Standardization and Quality, 2006(3): 34–37.(in Chinese)
[3]	中国人民解放军总装备部.军用装备实验室环境试验方法:GJB 150.16—1986[S].北京:中国人民解放军总装备部军标出版发行部, 1986. The Chinese People's Liberation Army General Armaments Department.Military equipment laboratory test method:GJB 150.16—1986[S].Beijing:The Chinese People's Liberation Army General Armaments Department Military Standard Publication Distribution Department, 1986(in Chinese).
[4]	中国人民解放军总装备部.可靠性鉴定和验收试验:GJB 899A—2009[S].北京:中国人民解放军总装备部军标出版发行部, 2009. The Chinese People's Liberation Army General Armaments Department.Reliability evaluation and acceptance test:GJB 899A—2009[S].Beijing:The Chinese People's Liberation Army General Armaments Department Military Standard Publication Distribution Department, 2009(in Chinese).
[5]	Department of the Air Force.Air and ground equipment of environment test method:MIL-STD-810[S].New York:United States Department of Defense, 1962.
[6]	张绍伟, 龚庆祥. 导弹全弹振动环境应力筛选方案研究[J].飞航导弹, 2003(3): 24–26. ZHANG S W, GONG Q X. Research on vibration environment stress screening of whole missile[J].Winged Missiles Journal, 2003(3): 24–26.(in Chinese)
[7]	中国人民解放军总装备部.电子产品环境应力筛选方法:GJB 1032—90 [S].北京:中国人民解放军总装备部军标出版发行部, 1991. The Chinese People's Liberation Army General Armaments Department.Electronic products environmental stress screening methods:GJB 1032—90 [S].Beijing:The Chinese People's Liberation Army General Armaments Department Military Standard Publication Distribution Department, 1991(in Chinese).
[8]	陈万创, 李爱国. 空空导弹综合环境可靠性试验剖面研究[J].上海航天, 2005, 1(4): 41–44. CHEN W C, LI A G. Research on air to air missile combined environment reliability test profile[J].Aerospace Shanghai, 2005, 1(4): 41–44.(in Chinese)
[9]	张策, 王冬, 刘艳, 等. 防空导弹的综合环境可靠性试验剖面研究[J].装备环境工程, 2006, 3(5): 48–52. ZHANG C, WANG D, LIU Y, et al. Antiaircraft missile combined environment reliability test profile research[J].Equipment Environmental Engineering, 2006, 3(5): 48–52.(in Chinese)
[10]	中国人民解放军总装备部.军用设备环境试验方法:GJB 150—86[S].北京:中国人民解放军总装备部军标出版发行部, 1986. The Chinese People's Liberation Army General Armaments Department.Military equipment environment test method:GJB 150—86[S].Beijing:The Chinese People's Liberation Army General Armaments Department Military Standard Publication Distribution Department, 1986(in Chinese).
[11]	刘凯. 基于实测数据的空空导弹自由飞振动条件制定方法研究[J].装备环境工程, 2014, 11(5): 114–118. LIU K. Study on the method of making free flight vibration profile for air-to-air missile based on measured data[J].Equipment Environmental Engineering, 2014, 11(5): 114–118.(in Chinese)
[12]	林家浩, 智浩, 郭杏林. 平稳随机振动载荷识别的逆虚拟激励法(一)[J].计算力学学报, 1998, 15(2): 127–136. LIN J H, ZHI H, GUO X L. Inverse pseudo excitation method for loading identification of stationary random vibration(1)[J].Chinese Journal of Computational Mechanics, 1998, 15(2): 127–136.(in Chinese)
[13]	LIN J H, GUO X L, ZHI H, et al. Computer simulation of structural random loading identification[J].Computers & Structures, 2001, 79(4): 375–387.
[14]	赵岩, 张亚辉, 林家浩. 车辆随机振动功率谱分析的虚拟激励法概述[J].应用数学和力学, 2013, 34(2): 107–116. ZHAO Y, ZHANG Y H, LIN J H. Summary on the pseudo-excitation method for vehicle random vibration PSD analysis[J].Applied Mathematics and Mechanics, 2013, 34(2): 107–116.(in Chinese)
[15]	CAPRANI C C. Application of the pseudo-excitation method to assessment of walking variability on footbridge vibration[J].Computers & Structures, 2014, 132(1): 43–54.
[16]	侯秀慧, 邓子辰, 黄立新, 等. 桥梁结构移动平稳随机载荷识别的新方法[J].计算力学学报, 2009, 26(5): 659–663. HOU X H, DENG Z C, HUANG L X, et al. A new method for the identification of a stationary random load moving on bridge structure[J].Chinese Journal of Computational Mechanics, 2009, 26(5): 659–663.(in Chinese)
[17]	ZHANG J, ZHAO Y, ZHANG Y H, et al. Identification of the power spectral density of vertical track irregularities based on inverse pseudo-excitation method and symplectic mathematical method[J].Inverse Problems in Science & Engineering, 2014, 22(2): 334–350.
[18]	LV Z H, LI K, CHEN K M, et al. Grinding load identification of an Horomill using inverse pseudo excitation method[J].Advanced Materials Research, 2012, 496(2): 243–246.
[19]	ZHANG Y W, ZHAO Y, ZHANG Y H, et al. Riding comfort optimization of railway trains based on pseudo-excitation method and symplectic method[J].Journal of Sound & Vibration, 2013, 332(21): 5255–5270.
[20]	秦玉英, 李杰, 田国红, 等. 基于虚拟激励法的载货汽车随机振动仿真[J].拖拉机与农用运输车, 2011, 38(1): 89–92. QIN Y Y, LI J, TIAN G H, et al. Truck random vibration simulation based on pseudo-excitation method[J].Tractor & Farm Transporter, 2011, 38(1): 89–92.(in Chinese)
[21]	林家浩, 钟万勰. 辛数学·精细积分·随机振动及应用[M].合肥: 中国科学技术大学出版社, 2008. LIN J H, ZHONG W X. Precise integration, random vibration and application[M].Hefei: Press of University of Science and Technology of China, 2008.(in Chinese)
[22]	张丽萍, 郭立新. 基于逆虚拟激励法的随机路面谱的识别方法[J].东北大学学报, 2012, 33(2): 258–261. ZHANG L P, GUO L X. Identification of random road spectrum based on inverse pseudo-excitation method[J].Journal of Northeastern University, 2012, 33(2): 258–261.(in Chinese)