EMD最早由Huang等[1]提出,是一种数据驱动的自适应多尺度算法, 能够将原始数据逐级分解为不同尺度的内蕴模态函数(Intrinsic Mode Function, IMF)和一个单调光滑的余量,其摆脱了传统时频分析方法本质上对平稳数据处理方法的依赖,不再依赖具体的基函数。基于上述优势,EMD已经在一维信号和二维图像的分析与处理中得到了广泛应用,如图像融合和增强[2]、图像压缩[3]、图像去噪[4]等。
近年来, EMD算法在三维几何模型处理中也逐渐得到关注。Qin等[5]首先在曲面参数化的帮助下, 将三维曲面的坐标函数转化为二维平面信号, 然后用传统的二维EMD算法进行分解, 但全局网格参数化限制了其应用范围。Wang等[6]通过求解狄利克雷边界条件的双调和场得到三角形网格上信号的上下包络, 实现了三维网格上EMD分解算法,避免了曲面参数化问题, 扩大了EMD在数字几何处理中的使用范围。进一步,Hu等[7]以平均曲率作为EMD的输入信号,能够更加准确地提取三角形网格上的不同尺度特征。为实现三角形网格上EMD的快速计算,Wang等[8]利用空间填充曲线方法将三角形网格上的信号转换为一维信号,利用经典的一维EMD算法对输入信号进行分解。
原始的EMD算法存在过光滑的局限, 使得现有推广EMD算法在图形图像处理中无法很好地保持数据自身的特征。基于EMD的思想, Suber等[9]提出边缘保持的多尺度图像分解, 核心思想是把局部极大值点和局部极小值点之间的振荡作为细节。在三维几何处理中,受Suber等[9]的启发,Wang等[6]通过薄板样条插值计算三维几何信号的包络,直接将一维EMD推广到三维几何曲面上,该算法进一步通过构建各向异性的拉普拉斯算子,进行特征保持的EMD多尺度分解,但该特征保持的插值算法不够鲁棒,同时也无法处理开曲面。Hu等[7]引入平均曲率作为EMD的输入信号,并以提取到的特征点作为约束进行特征保持的数据平滑和去噪。类似的,在提取到特征点后,Wang等[8]通过将特征信号与输入信号分离,提出了一种分而治之的EMD分解框架。
相对于三角形网格数据,点云数据缺乏固有的拓扑连接关系,并且易受噪声、离群点等因素的影响,直接将EMD应用到散乱点云数据还存在很多困难和挑战。为此,本文在已有相关工作的基础上,将EMD推广到三维散乱点云数据处理中, 以扩大EMD在三维数字几何处理中的应用范围。由于点云EMD存在过光滑的局限性,无法保持点云数据中点云EMD存在过光滑的局限性,无法保持点云数据中存在的显著特征,为此在特征点提取的基础上实现了特征保持的点云EMD。算法首先以点云数据的拉普拉斯矩阵坐标和向量的内积作为输入信号, 提取输入信号的极值点作为插值点计算信号的上下包络。然后为实现特征保持的EMD信号分解,通过检测点云数据特征点,并在计算信号上下包络的过程中作为约束,克服传统EMD算法无法保持特征的局限。最后由原始信号减去上下包络的均值得到IMF和余量。通过迭代处理余量得到多个IMF和余量,基于多个IMF和余量的组合与拉普拉斯矩阵重建新的点云数据,由滤波器设计实现了点云数据平滑和增强。实验结果表明, 本文算法有效地将EMD推广到三维散乱点云数据中, 扩大EMD在三维几何中的应用范围,在点云数据平滑和增强方面取得了很好的效果。图 1所示为八面体点云模型特征保持的点云EMD示意图, 图 1(a)为无噪声的原始模型及其对应的输入信号, 图 1(b)为5%高斯噪声的模型和对应的输入信号, 图 1(c)~图 1(d)分别为经典的点云EMD和特征保持的点云EMD的输出结果信号及其由余量重建结果。
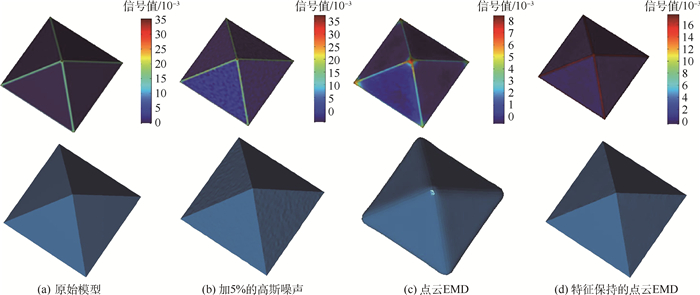 |
| 图 1 八面体点云模型的EMD Fig. 1 EMD of octahedral point cloud model |
| 图选项 |
1 点云EMD 给定点云数据P={p1, p2, …, pn}, pi=(xi, yi, zi)∈R3以及定义在点云数据上的信号g,EMD可以将输入信号g分解为有限个IMF和余量,并表示为
 | (1) |
式中:Dk为分解得到的IMFs;rN为对应的余量。
1.1 输入信号的定义 点云EMD的输入信号需要既能描述点云数据的几何形状,也能展现几何特征。点云数据的拉普拉斯矩阵可以度量点云数据潜在曲面的局部偏差,并且描述潜在曲面局部形状信息。本文利用点云数据的拉普拉斯矩阵与法向的内积作为点云数据EMD算法的输入信号。
点云数据的拉普拉斯矩阵可以利用文献[10-11]中的方法进行构建。对于点集P中的一点pi, pi与其邻居点pj间的权重为
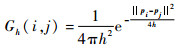 | (2) |
式中:h为控制影响的区域。
由此可以构建n×n的拉普拉斯矩阵L为
 | (3) |
式中:Ai为pi处[12]定义的维诺图权重, 可以粗略估计为pi点在流形曲面上局部维诺图的面积, 在构造拉普拉斯矩阵的过程中, 一个重要的参数是邻居点个数的选取。对于受噪声影响较大的模型, 为了使算法更加鲁棒, 邻居点个数可以适当地设置大一些。经过大量实验表明,邻居点个数选取在15~35之间可以得到较好的实验结果。
点云EMD的输入信号定义为拉普拉斯矩阵坐标L与法向N的内积:
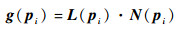 | (4) |
式中:点云法向可由文献[13]中的算法估计得到, 该输入信号具有旋转不变性和平移不变性, 可以被用作点云EMD算法的输入信号。
1.2 点云EMD分解流程 EMD存在过光滑的局限, 利用文献[7]中信号分解的方法将EMD直接应用到点云数据处理中无法保持数据固有的特征信息,如图 1(c)所示重建得到的八面体点云模型中存在特征边过度平滑的问题。因此, 在点云数据EMD分解过程中需要额外的工作来实现特征保持。为此,本文将通过显式检测特征点的方式,将特征点作为约束应用到信号上下包络计算中,实现特征保持的点云EMD。信号g是由式(4) 定义的输入信号, 特征保持的点云EMD可以表示为式(1) 的形式。本文默认的分解次数为3。
受Suber等[9]保持边缘多尺度图像分解的启发, 本文从输入信号中迭代提取点云模型的细节, 将特征保持的分解结果保留在余量中。
特征保持的点云EMD算法步骤如下:
输入??点云数据信号g。
输出??分解得到的N个IMFs:Dk(k=1, 2, …, N)和对应的余量rN。
Step 1??设置初始余量r0=g和IMF的初始索引k=1。
Step 2??提取细节。
1) 计算rk-1的全部极值点。
2) 在特征点G的约束下由极值点插值求得上下包络Urk-1和Drk-1, 然后求得平均包络mk-1=(Urk-1+Drk-1)/2。
3) 提取第k个细节Dk=rk-1-mk-1和第k个余量rk=mk-1。
Step 3??如果k的个数达到N, 结束此分解过程。否则,k=k+1,继续Step 1。
1.2.1 点云特征点提取 为了实现点云数据特征保持的EMD, 一项重要的工作是点云数据的特征点提取。由于点云数据缺乏固有的拓扑连接关系, 并且扫描得到的点云数据经常受到噪声的影响,所以本文采用具有良好抗噪能力的点云特征点提取方法[14]。图 2给出了此方法在八面体、立方体、Fandisk点云模型的特征点提取结果。
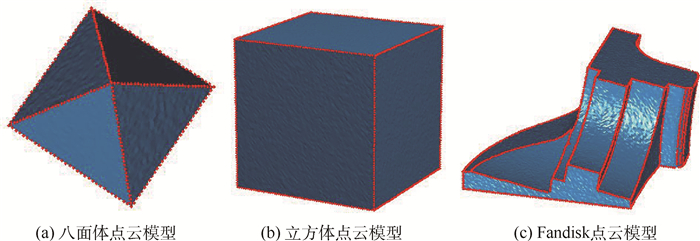 |
| 图 2 点云特征点提取结果 Fig. 2 Feature point extraction results of point clouds |
| 图选项 |
1.2.2 信号极值点的定义 为了获得信号中足够多的极值点,引入参数t,定义极值点如下:对于pi∈P, 在第k层的分解中, 如果g(pi)满足如下条件:
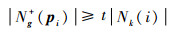 | (5) |
则这个点被定义为极大值点。其中Ng+(pi)表示为
 | (6) |
式中:|·|为集合元素的个数;t∈[0, 1]为调节极值点个数的参数;Nk(i)为pi点的邻近点。类似地, 可以定义极小值点。如果t非常小, 则会包含更多的极值点,本文中t的默认值为0.8。
提取出来的特征点可能包含在极值点中, 为了避免由局部极值点得到的上下包络的均值在提取细节过程中产生模糊效应, 需要将特征点从极值点中剔除,得到极值点索引集合为C。
1.2.3 计算包络的插值方法 对于给定的插值点和相应的信号值{(pi, g(pi)), i∈C},本文采用双调和插值的方法计算信号的上下包络。为了实现特征保持的信号分解,基于提取到的特征点构建各向异性的拉普拉斯矩阵[15-16],同时将特征点集G={s1, s2, …, sm}作为软约束加入到点云数据重建中。具体地, 在极值点?(pi)=g(pi), i∈C的约束下, 最小化式(7) 的能量函数来求解插值函数?=(?(p1), ?(p2), …, ?(pn))。
 | (7) |
式中:λ为特征点位置的权重因子, 默认值为0.1;L′为基于以下元素定义的各向异性拉普拉斯矩阵:
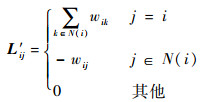 | (8) |
其中:wij的选取分2种情况。对于非特征点
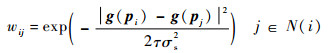 | (9) |
对于特征点
 | (10) |
式中:σs为信号g在pi点k近邻的局部标准方差;τ为用来控制特征保持强度的参数, τ的值越小, 特征保持的越强, 本文的默认值为0.6。
式(7) 的能量函数可以写为如下形式:
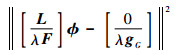 | (11) |
式中:gG为点云数据的特征点集合G的信号值;F为由以下元素组成的m×m矩阵:
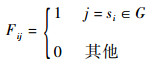 |
式(11) 是一个线性最小二乘优化问题, 等价于如下(n+m)×n线性系统:
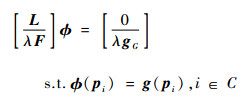 | (12) |
此线性系统可以用文献[17]中提到的直接消去法求解,将式(12) 对应的已知插值点消去,未知的插值函数值可以通过计算重新得到的线性系统求解。
1.3 点云数据的重建 通过对分解后的IMF和余量处理后,将得到新的几何信号g′,对应新的点云数据P′,可以通过以原来点的位置P作为约束,利用最小二乘法最小化如下能量函数重建得到:
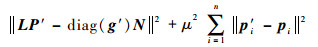 | (13) |
此能量函数可以转化为
 | (14) |
此公式对应的2n×n的线性系统AP′=b为
 | (15) |
式中:μ为原始点位置的权重因子, 本文中的默认值为0.1。此线性系统可以用乔里斯基分解求解(ATA)P′=ATb。
图 3为Dragon点云模型特征保持的EMD结果。图 3(a)为原始模型及其对应的输入信号, 图 3(b)~图 3(e)分别给出了3个IMF和余量重建的结果及其对应的信号值。由EMD结果可以看出此模型的不同尺度特征。
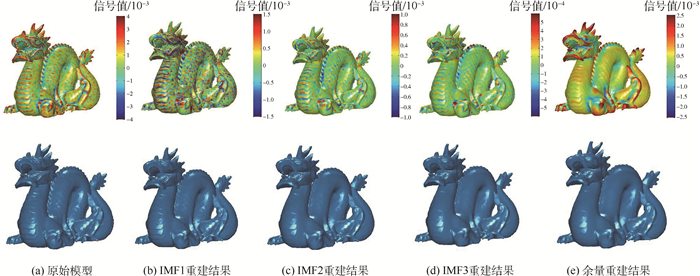 |
| 图 3 Dragon点云模型的多尺度分解结果 Fig. 3 Multi-scale decomposition results of Dragon point clouds model |
| 图选项 |
2 点云数据平滑与增强 点云EMD将输入信号分解为不同尺度特征, 可以用于不同的应用中,本文基于滤波器设计,实现了点云数据平滑和增强。
2.1 滤波器的设计 点云EMD的各种应用可以通过构建不同的滤波器来实现。滤波器设计可以由EMD得到的IMF和余量的组合实现。
 | (16) |
式中:η(k)用来控制不同的滤波器操作。比如平滑可以使用低通滤波器,高通滤波器可以用来数据的增强。在实验中,IMF的个数默认设置为3。
2.2 点云数据平滑 基于点云数据的EMD,通过设计滤波器,实现点云数据的平滑。由于噪声通常包含在前几个IMF中,设置低通滤波器,过滤掉信号中高频的部分,保留低频的部分,从而实现噪声的去除。对于点云数据的平滑, 使用低通滤波器即特征保持的点云EMD得到的余量进行点云数据的重建, 为了避免在提取细节的过程中尖锐边缘和角点变的模糊, 点云数据中的特征点事先用现有的方法提取出来,并且为了更好地重建平滑的点云模型,用法向加权平均更新了法向。
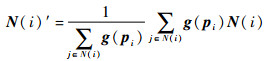 | (17) |
图 4和图 5为用低通滤波器系数(0, 0, 0) 得到的平滑结果。对于图 4(a)和图 4(c)的噪声模型,可以实现平滑,并且对于真实的点云数据模型,图 5(a)和图 5(c)也能实现较好的平滑效果。
 |
| 图 4 Dodecahandle和Venubody模型的平滑结果 Fig. 4 Smoothing results of Dodecahandle and Venubody models |
| 图选项 |
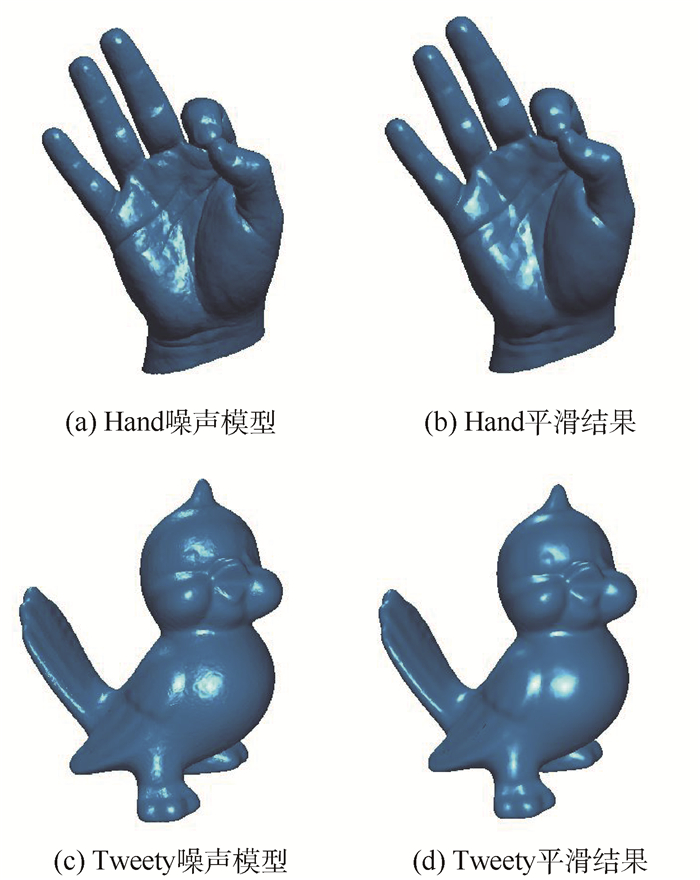 |
| 图 5 Hand和Tweety模型的平滑结果 Fig. 5 Smoothing results of Hand and Tweety models |
| 图选项 |
为了验证本文算法的有效性, 图 6和图 7给出了带有特征的点云数据平滑结果,并与局部最优投影(WLOP)方法[18]、边缘保持重采样(EAR)方法[19]、最小二乘(MLS)方法[20]进行了比较。图 6(b)和图 6(c)分别为使用Huang等[18]和文献[19]代码得到的结果。图 6(d)为由软件MeshLab得到的结果。由实验结果可以看到,这些方法均可以去除噪声,但是WLOP方法在尖锐边缘周围有很大的间隙, 为了克服此局限性, EAR使用了上采样的方法。尽管EAR方法在一定程度上解决了尖锐边缘的问题, 但是尖锐特征还是不能得到很好的保持。MLS方法在特征点区域的周围产生了过平滑的现象。与这些方法相对比, 本文算法能得到较好的平滑结果并且有效地保持了特征。
 |
| 图 6 立方体模型的对比结果 Fig. 6 Comparison results of cube model |
| 图选项 |
 |
| 图 7 Fandisk模型的对比结果 Fig. 7 Comparison results of Fandisk model |
| 图选项 |
图 7的Fandisk模型进一步验证了本文算法平滑和保持特征的有效性。模型为加了5%平均点云间距离的高斯噪声, 图 7(b)~图 7(d)分别为利用WLOP、EAR、MLS方法得到的结果。这些方法中尖锐特征均存在不同程度的平滑, 而本文算法可以得到较为满意的结果, 在平滑的同时保持了特征, 尤其是位于扇形区域较弱的特征。
2.3 点云数据增强 基于点云数据的EMD,通过滤波器的设计,实现了点云数据的增强。由于高频细节通常包含在前几个IMF中,可以通过增强前几个IMF来实现几何细节的增强。图 8给出了Max Planck和Dog模型的平滑和增强结果。图 8(a)图 8(d)为用系数(0, 0, 0) 重建的结果, 可以看出细节特征被平滑掉;图 8(b)和图 8(e)是用系数(1, 1, 1) 重建出来的原始模型;图 8(c)和图 8(f)为使用系数(3, 1, 1) 得到的增强结果, 可以看出细节特征被显著增强。
 |
| 图 8 Max Planck和Dog模型的平滑和增强结果 Fig. 8 Smoothing and enhancing results of Max Planck and Dog models |
| 图选项 |
2.4 参数设置和时间统计 本文涉及的参数均在相应的部分进行了说明。本文代码是在MATLAB 2013a中实现的。运行代码的电脑处理器是Inter(R) Core (TM) i7-4790 CPU @ 3.60 GHz, 内存16.0 GB。代码运行的时间主要由拉普拉斯矩阵构建、EMD分解的时间构成。表 1列出了本文中涉及到的实验模型的模型点数P、构建拉普拉斯矩阵选定的邻居点个数NB、IMF个数nIMF的参数设置情况以及运行中花费的构建拉普拉斯矩阵时间tL、EMD时间tEMD、总时间tTOTAL。
表 1 各模型参数设置及运行时间统计 Table 1 Parameter setting and running time statistics for each model
| 模型 | P | NB | nIMF | 运行时间/s | ||
| tL | tEMD | tTOTAL | ||||
| 八面体 | 4 098 | 15 | 3 | 3.835 | 5.425 | 9.670 |
| Dragon | 50 000 | 25 | 3 | 46.439 | 74.245 | 124.770 |
| Dodecahandle | 38 390 | 15 | 3 | 34.358 | 52.278 | 89.298 |
| Venubody | 11 362 | 15 | 3 | 10.502 | 15.229 | 26.529 |
| Hand | 20 002 | 15 | 3 | 18.076 | 27.015 | 46.500 |
| Tweety | 93 047 | 15 | 3 | 85.297 | 136.972 | 229.845 |
| 立方体 | 24 578 | 15 | 3 | 22.526 | 34.611 | 59.771 |
| Fandisk | 27 827 | 15 | 3 | 25.787 | 38.875 | 67.315 |
| Max Planck | 49 132 | 25 | 3 | 43.872 | 70.614 | 119.321 |
| Dog | 101 108 | 25 | 3 | 91.739 | 152.658 | 253.532 |
表选项
3 结论 本文将EMD应用到点云数据中, 实现了特征保持的点云EMD。
1) 以点云模型的拉普拉斯矩阵坐标与法向的内积作为EMD的输入信号,将输入信号进行多尺度分解。
2) 基于分解出来的IMF和余量的组合,通过滤波器设计实现了点云数据平滑和增强,扩大了EMD在三维数字几何处理中的应用范围,为计算机辅助设计与逆向工程提供新的数据处理工具。
3) 通过将本文算法和现有的特征保持的算法进行对比,验证了本文提出的特征保持点云EMD算法的有效性。
尽管本文给出了特征保持的点云EMD算法, 但是在进行特征保持的过程中, 需要显式提取特征点, 如果点云模型中含有大量的噪声, 特征点提取不准确, 则在进行特征保持的信号分解时,特征信息仍然会存在模糊、保持不好的情况。为了解决这个问题, 拟通过隐式定义特征来实现特征保持, 这将是笔者接下来的研究方向。
参考文献
| [1] | HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society of London A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995.DOI:10.1098/rspa.1998.0193 |
| [2] | 郑有志, 覃征. 基于二维经验模态分解的医学图像融合算法[J].软件学报, 2009, 20(5): 1096–1105. ZHENG Y Z, TAN Z. Medical images fusion algorithm based on dimensional empirical mode decomposition[J].Journal of Software, 2009, 20(5): 1096–1105.(in Chinese) |
| [3] | 徐琼, 李峰, 吕回. 二维EMD分解的数字图像压缩[J].计算机工程与应用, 2009, 45(5): 180–182. XU Q, LI F, LV H. Digital image compression of dimensional EMD decomposition[J].Computer Engineering and Applications, 2009, 45(5): 180–182.(in Chinese) |
| [4] | 郭耸, 顾国昌, 李常有, 等. 利用EMD的自适应图像去噪[J].计算机工程与应用, 2013, 49(8): 12–16. GUO S, GU G C, LI C Y, et al. Adaptive image denoising based on EMD[J].Computer Engineering and Applications, 2013, 49(8): 12–16.(in Chinese) |
| [5] | QIN X, CHEN X, ZHANG S, et al.EMD based fairing algorithm for mesh surface[C]//11th IEEE International Conference on Computer-Aided Design and Computer Graphics, 2009.Piscataway, NJ:IEEE Press, 2009:606-609. |
| [6] | WANG H, SU Z, CAO J, et al. Empirical mode decomposition on surfaces[J].Graphical Models, 2012, 74(4): 173–183.DOI:10.1016/j.gmod.2012.04.005 |
| [7] | HU J P, WANG X C, QIN H. Improved, feature-centric EMD for 3D surface modeling and processing[J].Graphical Models, 2014, 76(5): 340–354.DOI:10.1016/j.gmod.2014.03.006 |
| [8] | WANG X C, HU J P, ZHANG D B, et al. Efficient EMD and Hilbert spectra computation for 3D geometry processing and analysis via space-filling curve[J].The Visual Computer, 2015, 31(6): 1135–1145. |
| [9] | SUBER K, SOLER C, DURAND F. Edge-preserving multiscale image decomposition based on local extrema[J].ACM Transactions on Graphics, 2009, 28(5): 1–9. |
| [10] | LUO C, ISSAM S, WANG Y. Approximating gradients for meshes and point clouds via diffusion metric[J].Computer Graphics Forum, 2009, 28(5): 1497–1508.DOI:10.1111/cgf.2009.28.issue-5 |
| [11] | BELKIN M, SUN J, WANG Y.Constructing Laplace operator from point clouds in Rd[C]//ACM-SIAM Symposium on Discrete Algorithms.New York:SIAM, 2009:1031-1040. |
| [12] | LUO C, SUN J, WANG Y.Integral estimation from point cloud in d-dimensional space:A geometric view[C]//Proceedings of the 25th Annual Symposium on Computational Geometry.New York:ACM, 2009:116-124. |
| [13] | LIU J, CAO J, LIU X, et al. Mendable consistent orientation of point clouds[J].Computer-Aided Design, 2014, 55(3): 26–36. |
| [14] | 王小超, 刘秀平, 李宝军, 等. 基于局部重建的点云特征点提取[J].计算机辅助设计与图形学学报, 2013, 25(5): 659–665. WANG X C, LIU X P, LI B J, et al. Feature point extraction from point clouds based local reconstruction[J].Journal of Computer-Aided Design & Computer Graphics, 2013, 25(5): 659–665.(in Chinese) |
| [15] | FLEISHMAN S, DRORI I, COHEN-OR D. Bilateral mesh denoising[J].ACM Transactions on Graphics, 2003, 22(3): 950–953.DOI:10.1145/882262 |
| [16] | LEVIN A, LISCHINSKI D, WEISS Y. Colorization using optimization[J].ACM Transactions on Graphics, 2004, 23(3): 689–694.DOI:10.1145/1015706 |
| [17] | FLOATER M, HORMANN K.Parameterization of triangulations and unorganized points [M]//ISKE A, QUAK E, FLOATER M S.Tutorials on multiresolution in geometric modelling.Berlin:Springer, 2002:287-316. |
| [18] | HUANG H, LI D, ZHANG H, et al. Consolidation of unorganized point clouds for surface reconstruction[J].ACM Transactions on Graphics, 2009, 28(5): 89–97. |
| [19] | HUANG H, WU S, GONG M, et al. Edge-aware point set resampling[J].ACM Transactions on Graphics, 2013, 32(1): 60–61. |
| [20] | GUENNEBAUD G, GROSS M. Algebraic point set surfaces[J].ACM Transactions on Graphics, 2007, 26(3): 1–9.DOI:10.1145/1276377 |
