国内外专家****对光伏发电系统在局部阴影条件下光伏阵列的建模及GMPPT方法进行了大量研究。文献[7]建立单二极管参数的太阳电池功率方程,提出恒压跟踪方法进行最大功率点跟踪(MPPT),并且分析模型中串联电阻、并联电阻及二极管参数对恒压跟踪方法的影响;文献[8]建立光伏阵列的高维数学模型,提出了易于分布式实现的、适合于任意阴影条件的光伏阵列输出特性快速计算机仿真算法;文献[9]构建遮蔽条件下传统算法、智能算法以及群优化算法等多种MPPT算法,分析各种方法的优势和使用局限;文献[10]提出采用傅里叶函数并使用曲线拟合的方法对阴影条件下光伏阵列进行非机理建模,能对不同功率等级、不同精度要求的光伏阵列进行建模;文献[11]在光照在局部阴影条件下,利用人工神经网络,达到MPPT的目的,实验效果良好;文献[12]提出新型的分布式MPPT光伏系统结构,保证在不同光照条件下每块光伏板都可以工作在各自的最大功率点;文献[13-15]均是基于粒子群算法,通过在结构和参数调整改进粒子群优化(PSO)算法,简化算法结构,保证收敛速度,实现动态和静态环境下GMPPT,提高多峰值MPPT的速度和精度;文献[16]从概率论角度出发,提出基于蒙特卡罗的光伏多峰MPPT控制算法,其收敛速度与准确性不受光伏曲线形状的影响;文献[17]根据局部阴影条件下的光伏阵列分段函数输出特性曲线,建立S函数模型,提出免疫细菌觅食算法,实现大容量光伏阵列GMPPT。
分析以上研究过程局限性,并结合其研究成果,本文从研究局部阴影条件下光伏发电系统出力特征演化角度出发:首先,建立局部阴影条件下光伏组件的数学模型,确定为其多峰值优化问题,深入剖析常规寻优算法失效的原因;然后,根据优化策略及多峰现象,提出引入量子行为的粒子群优化(QPSO)算法,以增加粒子多样性,提高跳出局部最优能力,加快搜索速度,有效地完成GMPPT功能;最后,利用算例分析,并与标准PSO算法对比,说明量子行为的粒子群优先算法更适于解决局部遮挡条件下的光伏MPPT问题,有效地提高光伏利用率及发电效率。
1 局部阴影条件下的光伏阵列模型与GMPPT实现电路 1.1 局部阴影条件下的光伏阵列模型 图 1为典型的光伏(PV)阵列结构图,尺寸为n×m,即每一串有n块光伏组件,再并联m串。串联单元需配置旁路二极管Ds,以消除在局部阴影条件下,个别光伏组件的“热区效应”,提高阴影时的电流畅通;同时,为了防止并联支路之间形成环流而引起的电能到送,一般串联防逆二极管Dp后再并联。
 |
| 图 1 光伏阵列结构 Fig. 1 Structure of photovoltaic array |
| 图选项 |
在局部阴影条件下,光伏阵列的电压-电流(U-I)、电压-功率(U-P)曲线受旁路二极管和阻塞二极管的影响较大,出现多阶多峰的现象[18]。下面将以带旁路二极管的光伏组件模型为基础,得到局部阴影条件下的含旁路二极管的光伏组件工程数学模型表达式:
 | (1) |
式中:

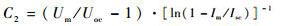
1.2 光伏阵列GMPPT的电路实现 目前常用于光伏发电系统中进行MPPT的电路是Boost电路,Boost电路具有直流升压的能力,在进行MPPT的同时能够减少光伏阵列组串个数,有效地提高其利用率,降低发电成本[19]。
Boost电路的原理图如图 2所示。Boost电路由开关管Q1、电感L,电容C组成。Boost电路的作用是将电压UPV升压到Uc,UPV为光伏阵列的输出电压,Uc为Boost电路的输出电压。
 |
| 图 2 Boost电路原理 Fig. 2 Principle of Boost circuit |
| 图选项 |
在连续导电模式下,电路工作模式根据开关管状态分为2个阶段。在开关管Q1导通期间,电感电流IL线性上升,电感处于储能状态,负载所需能量来源于电容;在开关管Q1关断期间,由于电感电流不能突变,电感电流通过二极管向电容和负载释放能量。根据电感伏秒平衡特性和电容安秒平衡特性,可以推出:
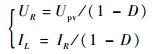 | (2) |
式中:UR为负载电压;IR为负载电流;D为Boost电路的占空比。。
从Boost的输入端看,即光伏电池输出端,利用戴维南等效原理,解得Boost电路等效阻抗为
 | (3) |
结合电路理论及式(3) 形式可看出,光照、温度一定的前提下,光伏电池的输出电压、电流以及功率可以由Boost的占空比D决定。换而言之,MPPT算法即对变量D的寻优过程。
2 局部阴影条件下的GMPPT算法实现 2.1 局部阴影条件下常规方法失效分析 以本文模拟的3种光照条件的U-I和U-P曲线为例,如图 3所示,说明局部阴影条件下常规方法GMPPT失效原因。
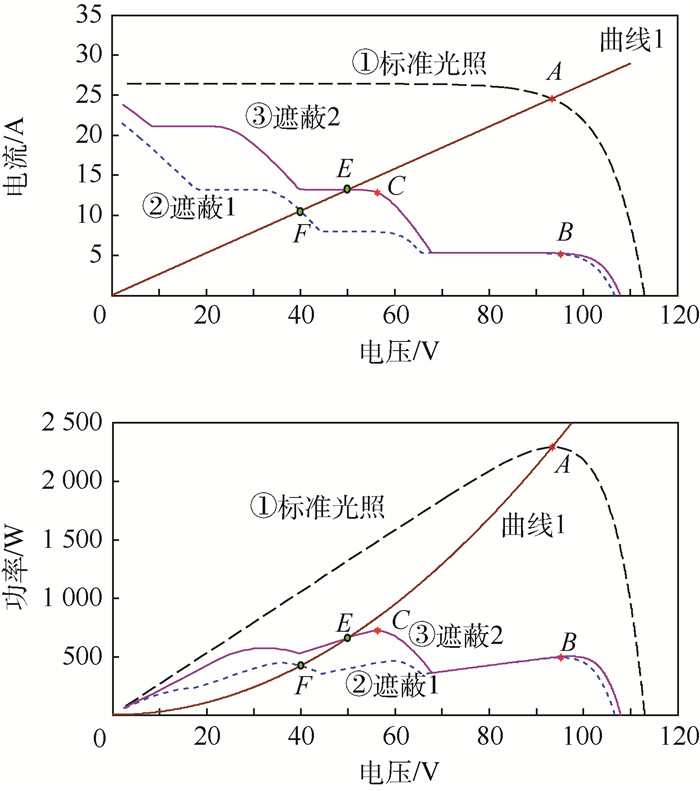 |
| 图 3 不同光照条件下,光伏输出U-I和U-P曲线 Fig. 3 Photovoltaic output U-I and U-P curves under different illumination conditions |
| 图选项 |
选择3块光伏电池板串联,模拟3种光伏电池工况,即标准光照、遮蔽情况1和遮蔽情况2(以下简称为“遮蔽1”和“遮蔽2”),并采用相同结构和光照条件并联两路,构成3×3光伏阵列,具体光照条件如表 1所示。为模拟复杂遮蔽工况,设置每一块板采用均分的2路光照模式,设置为G11、G12、G21、G22、G31、G32。光照变化顺序为标准光照条件,在0.5 s发生遮蔽1,在1.1 s发生遮蔽2。
表 1 不同工况下光照强度 Table 1 Illumination intensity under different conditions
| 光照模式 | 光照强度/(W·m-2) | ||
| 标准光照 | 遮蔽1 | 遮蔽2 | |
| G11 | 1 000 | 1 000 | 1 000 |
| G12 | 1 000 | 1 000 | 1 000 |
| G21 | 1 000 | 500 | 800 |
| G22 | 1 000 | 300 | 500 |
| G31 | 1 000 | 200 | 200 |
| G32 | 1 000 | 200 | 200 |
表选项
图 3中曲线1表示在标准光照条件下,MPPT点所对应的等效电阻负载特性U-I和U-P曲线图。A为标准光照条件下的最大功率点,B为遮蔽1下的最大功率点,C为遮蔽2的最大功率点。
1) 当光照条件由标准光照条件变为遮蔽2时,对应功率点将从A变换到E,此时若采用传统优化算法,如观察扰动法、爬山法等,可以寻优找到此光照条件下的最大功率点C。
2) 当光照条件由标准光照条件变为遮蔽1时,对应的功率点将从A变化到F,若此时采用传统的寻优算法,难以跟踪到最大功率点B。
故采用经典寻优算法难以解决局部阴影下的GMPPT问题,即多峰问题。传统的寻优算法很容易失效,利用全局搜索能力强的优化算法,是解决该问题的主要手段。
2.2 基于δ势阱的量子粒子群算法 根据2.1节的分析结论可知,遮蔽条件下光伏GMPPT问题,传统经典的优化算法无法满足复杂遮蔽的工况要求,故需要建立简单易实现、全局搜索能力强、防止搜索早熟的优化算法完成。GMPPT问题描述如式(4) 所示。
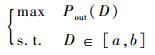 | (4) |
式中:Pout(D)表示占空比为D时,光伏电池系统的输出功率;a为D的下限;b为D的上限。
基于δ势阱的量子粒子群优化(QPSO)算法[20],是一种引入量子行为改进粒子群算法,算法参数少易于实现,量子粒子进化过程具有强不确定性,粒子以某种概率出现在可行空间的任意位置,并通过量子粒子平均位置进行演化过程,大大提高算法的全局搜索能力,有效地抑制早熟现象,符合遮蔽条件下光伏GMPPT问题需求,算法流程如图 4所示,具体实现如下:
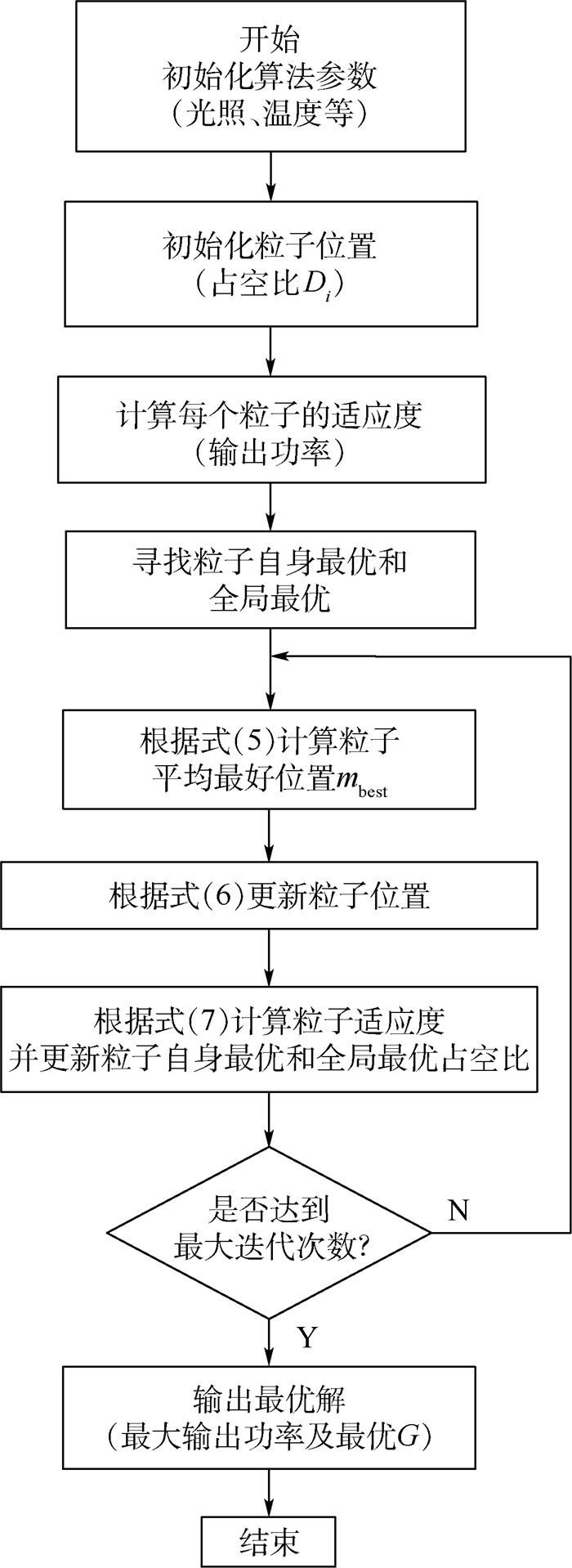 |
| 图 4 基于δ势阱的QPSO算法流程图 Fig. 4 Flowchart of QPSO algorithm based on δ-potential well |
| 图选项 |
Step 1??令迭代次数g=0,初始化参数及粒子群中每一个粒子所代表的当前占空比Di(0),并记录粒子的最优位置Pi(0)= Di(0) 和全局最优占空比Gi(0)。
Step 2??根据式(5) 计算粒子群中平均最优占空比为
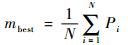 | (5) |
式中:N为粒子数。
Step 3??根据式(6),更新每一个粒子所代表的占空比Di(g)。
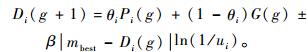 | (6) |
式中:ui和θi为第i个粒子更新产生的2个随机数;β为收缩-扩张系数。随机数θi决定第i个粒子向自身历史最优值和全局最优值运动的权重。随机数ui决定了粒子向平均最优位置运动的幅度,正负号表示运动方向,同样亦为随机产生。2个随机数以及随机正负号大大增加了粒子在空间中运动的多样性。β是QPSO算法中唯一控制参数,决定了每一个粒子收敛于统一最优解的快慢。
Step 4??计算更新后的粒子适应度(即光伏电池输出功率值),利用式(5) 更新每一个粒子自身历史最优占空比Pi(g)以及当前全局最优占空比G(g)。
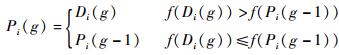 | (7) |
Step 5??分析搜索结果是否满足截止条件,若满足转入Step 6,否则令g=g+1再转入Step 2(本文设置最大迭代次数为截止条件)。
Step 6??输出最优占空比G, 终止寻优过程。
3 算例分析 为验证上述算法,本文基于MATLAB/SIMSCAPE平台中的Solar Cell单元搭建光伏电池板,每一块光伏电池板采用72个Solar Cell串联,每8个并联一个旁路二极管,即36个Solar Cell接受1种光照条件,每块光伏板参数如表 2所示,Pm为最大功率。
表 2 单块光伏电池板参数 Table 2 Parameters of single photovoltaic cell panel
| 参数 | 数值 |
| Uoc/V | 37.67 |
| Isc/A | 8.81 |
| Pm/W | 254.9 |
| Um/V | 31.8 |
| Im/A | 8.18 |
表选项
3.1 仿真工况及参数说明 Boost电路参数及算法参数如表 3所示。
表 3 Boost电路及算法参数 Table 3 Boost circuit and algorithm parameters
| 参数 | 数值 |
| 负载电阻R/Ω | 200 |
| 粒子数N | 5 |
| 迭代次数Gmax | 20 |
| 收缩-扩张系数β | 1.2 |
| 自变量范围[Dmin, Dmax] | [0, 1] |
表选项
3.2 算例结果及分析 分别利用QPSO算法和标准PSO算法进行GMPPT实验20次,在遮蔽1下,2种算法的5个粒子运动轨迹如图 5所示,搜索结果如图 6、图 7及表 4所示,GMPPT效果如图 8所示。
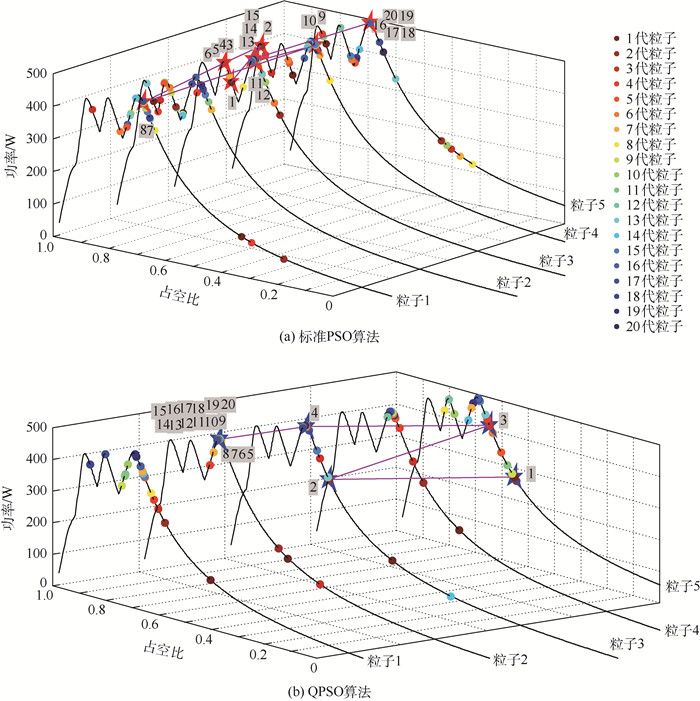 |
| 图 5 标准PSO和QPSO算法在遮蔽1下的搜索轨迹对比 Fig. 5 Comparison of search trajectories between standard PSO and QPSO algorithms under shaded 1 |
| 图选项 |
 |
| 图 6 QPSO和标准PSO算法在遮蔽1下的搜索结果对比 Fig. 6 Comparison of search results between QPSO and standard PSO algorithms under shaded 1 |
| 图选项 |
 |
| 图 7 QPSO和标准PSO算法在遮蔽1下的全局最优值曲线对比 Fig. 7 Comparison of global optimum curves between QPSO and standard PSO algorithms under shaded 1 |
| 图选项 |
表 4 收敛准确率σ对照 Table 4 Comparison of convergence accuracy rate σ
| 算法 | σ/% | ||
| 标准光照 | 遮蔽1 | 遮蔽2 | |
| QPSO | 100 | 95 | 100 |
| 标准PSO | 100 | 80 | 90 |
表选项
 |
| 图 8 QPSO和标准PSO算法GMPPT效果图 Fig. 8 Effect pictures of GMPPT by QPSO and standard PSO algorithms |
| 图选项 |
为定量比较2种算法,本文定义指标收敛百分比σ,用以衡量GMPPT寻优算法优劣情况。
定义1??本文定义优化算法最优值与真实最优值的百分比,称之为收敛精度ξ。
定义2??N0次实验中,若收敛精度ξ大于给定阈值η(本文设置η=99%)次数为n,称n与N0的比值用百分比表示为收敛准确率σ。
图 5所示为标准PSO与QPSO算法搜索轨迹对比,随机选取5个粒子进行运动轨迹分析,从图 5中可以看出,基于δ势阱的QPSO算法中5个粒子在保证在自变量范围内大范围变化同时,最终均收敛至全局最大点,保证粒子的一致性。在保证粒子收敛的前提下,QPSO算法保证了算法的多样性,有效防止早熟现象发生。
从图 6和表 4中可以看出,基于δ势阱的QPSO算法的收敛准确率高于标准PSO算法。根据图 6的收敛曲线可以看出,基于δ势阱的QPSO算法的收敛速度更快。故从搜索快速性和准确性方面均体现出QPSO算法的优越性。
从图 8中可以看出,不论单峰问题(标准光照条件)还是多峰问题(遮蔽1和2),相较于标准PSO算法,QPSO均可以更快地收敛至全局最优解,实现MPPT的要求;根据图 8(d)的稳态值可以看出其精度亦在标准PSO算法以上。QPSO算法在进行GMPPT时,快速的动态过程与高跟踪精度的稳态过程,有效地提高光伏利用率,避免能源浪费。
4 结论 本文针对局部阴影条件下,光伏电池GMPPT问题展开研究,首先, 通过分析局部阴影对目前常用的GMPPT算法的影响,分析其失效原因;然后,构建全局搜索能力强的QPSO算法,实现GMPPT,得到结论如下:
1) 光伏局部阴影条件下的GMPPT问题,是典型的多峰值寻优问题。需采用全局搜索能力强的优化算法,如群智能优化算法。
2) 引入量子行为的改进粒子群算法,可以很好地解决上述多峰问题,寻优准确程性、快速性以及多样性均优于标准粒子群算法,适用于解决局部阴影下的GMPPT问题。
3) 本文提出的QPSO算法,参数少,搜索快,全局搜索能力强,防早熟效果明显,适用于GMPPT实现。
参考文献
| [1] | 王成山, 王守相. 分布式发电供能系统若干问题研究[J].电力系统自动化, 2008, 32(20): 1–4. WANG C S, WANG S X. Study on some key problem related to distributed generation systems[J].Automation of Electric Power Systems, 2008, 32(20): 1–4.DOI:10.3321/j.issn:1000-1026.2008.20.001(in Chinese) |
| [2] | 雷金勇, 谢俊, 甘德强. 分布式发电供能系统能量优化及节能减排效益分析[J].电力系统自动化, 2009, 33(23): 29–36. LEI J Y, XIE J, GAN D Q. Optimization of distributed energy system and benefit analysis of energy saving and emission reduction[J].Automation of Electric Power Systems, 2009, 33(23): 29–36.DOI:10.7500/AEPS200906182(in Chinese) |
| [3] | 钱科军, 袁越, 石晓丹, 等. 分布式发电的环境效益分析[J].中国电机工程学报, 2008, 28(29): 11–15. QIAN K J, YUAN Y, SHI X D, et al. Environmental benefits analysis of distributed generation[J].Proceedings of the CSEE, 2008, 28(29): 11–15.DOI:10.3321/j.issn:0258-8013.2008.29.003(in Chinese) |
| [4] | 王丰, 吴新科, LEEF C. 嵌入式智能光伏模块的最大功率输出统一控制[J].中国电机工程学报, 2013, 33(21): 81–89. WANG F, WU X K, LEE F C. Application of unified output MPPT control in DMPPT PV systems[J].Proceedings of the CSEE, 2013, 33(21): 81–89.(in Chinese) |
| [5] | 刘晓艳, 祁新梅, 郑寿森, 等. 局部阴影条件下光伏阵列的建模与分析[J].电网技术, 2010, 34(11): 192–197. LIU X Y, QI X M, ZHENG S S, et al. Model and analysis of photovoltaic array under partial shading[J].Power System Technology, 2010, 34(11): 192–197.(in Chinese) |
| [6] | 吴春华, 周笛青, 李智华, 等. 光伏组件热斑诊断及模糊优化控制方法[J].中国电机工程学报, 2013, 33(36): 50–61. WU C H, ZHOU D Q, LI Z H, et al. Hot spot detection and fuzzy optimization control method of PV module[J].Proceedings of the CSEE, 2013, 33(36): 50–61.(in Chinese) |
| [7] | 张忠政, 程晓舫. 太阳电池最大功率恒压跟踪研究[J].中国电机工程学报, 2014, 34(26): 4521–4527. ZHANG Z Z, CHENG X F. Constant voltage tracking research adopted in solar cell maximum power[J].Proceedings of the CSEE, 2014, 34(26): 4521–4527.(in Chinese) |
| [8] | 戚军, 张晓峰, 张有兵, 等. 考虑阴影影响的光伏阵列仿真算法研究[J].中国电机工程学报, 2012, 32(32): 131–138. QI J, ZHANG X F, ZHANG Y B, et al. Study on simulation algorithm of PV array considering shade effect[J].Proceedings of the CSEE, 2012, 32(32): 131–138.(in Chinese) |
| [9] | AHMED J, SALAMN Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems[J].Renewable and Sustainable Energy Reviews, 2015, 47: 933–953.DOI:10.1016/j.rser.2015.03.080 |
| [10] | 孙黎霞, 李云峰, 郑丹丹, 等. 局部阴影下光伏阵列非机理建模[J].电网技术, 2015, 39(5): 1186–1191. SUN L X, LI Y F, ZHENG D D, et al. Non-mechanism modeling of photovoltaic array under partial shade[J].Power System Technology, 2015, 39(5): 1186–1191.(in Chinese) |
| [11] | RIZZO S A, SCELLBA G. ANN based MPPT method for rapidly variable shading conditions[J].Applied Energy, 2015, 145: 124–132.DOI:10.1016/j.apenergy.2015.01.077 |
| [12] | 王丰, 孔鹏举, LEEF C, 等. 基于分布式最大功率跟踪的光伏系统输出特性分析[J].电工技术学报, 2015, 30(24): 127–134. WANG F, KONG P J, LEE F C, et al. Output characteristic analysis of distributed maximum power point tracking PV system[J].Transactions of China Electrotechnical Society, 2015, 30(24): 127–134.DOI:10.3969/j.issn.1000-6753.2015.24.017(in Chinese) |
| [13] | 李善寿, 张兴, 张鸿恺, 等. 基于功率闭环控制与PSO算法的全局MPPT方法[J].中国电机工程学报, 2014, 34(28): 4809–4816. LI S S, ZHANG X, ZHANG H K, et al. Global MPPT method based on power closed-loop control and PSO algorithm[J].Proceedings of the CSEE, 2014, 34(28): 4809–4816.(in Chinese) |
| [14] | 张永革, 石季英, 张文, 等. 复杂遮阴条件下光伏系统MPPT控制改进PSO算法仿真研究[J].中国电机工程学报, 2014, 34(S1): 39–46. ZHANG Y G, SHI J Y, ZHANG W, et al. Research of improved PSO in MPPT control of PV systems under complex shading condition[J].Proceedings of the CSEE, 2014, 34(S1): 39–46.(in Chinese) |
| [15] | 祝青, 张兴, 李善寿, 等. 一种基于功率闭环的动态多峰值最大功率点跟踪算法研究与测试[J].中国电机工程学报, 2016, 36(5): 1218–1227. ZHU Q, ZHANG X, LI S S, et al. Researches and tests of a dynamic multi-peak maximum power point tracking algorithm based on power loop[J].Proceedings of the CSEE, 2016, 36(5): 1218–1227.(in Chinese) |
| [16] | 唐磊, 曾成碧, 苗虹, 等. 基于蒙特卡洛的光伏多峰最大功率跟踪控制[J].电工技术学报, 2015, 30(1): 170–176. TANG L, ZENG C B, MIAO H, et al. A novel maximum power point tracking scheme for PV systems under partially shaded conditions based on Monte Carlo algorithm[J].Transactions of China Electrotechnical Society, 2015, 30(1): 170–176.(in Chinese) |
| [17] | 张明锐, 蒋利明, 孙华, 等. 基于免疫细菌觅食算法的大容量光伏阵列GMPPT算法[J].中国电机工程学报, 2016, 36(1): 104–111. ZHANG M R, JIANG L M, SUN H, et al. Large-capacity photovoltaic array's GMPPT technology based on the immune bacterial foraging optimization algorithm[J].Proceedings of the CSEE, 2016, 36(1): 104–111.(in Chinese) |
| [18] | 田琦, 赵争鸣, 邓夷, 等. 光伏电池反向模型仿真分析及实验研究[J].中国电机工程学报, 2011, 31(23): 121–128. TIAN Q, ZHAO Z M, DENG Y, et al. Simulation and experimental study about reverse model of photovoltaic cells[J].Proceedings of the CSEE, 2011, 31(23): 121–128.(in Chinese) |
| [19] | BALATO M, VITELLI M.A hybrid MPPT technique based on the fast estimate of the maximum power voltages in PV applications[C]//2013 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER).Piscataway, NJ:IEEE Press, 2013:1-7. |
| [20] | SUN J, FENG B, XU W B.Particle swam optimization with particles having quantum behavior[C]//Congress on Evolutionary Computation, 2004.Piscataway, NJ:IEEE Press, 2004:325-331. |
