现有文献对最优机动问题进行了研究。文献[3]在假设导弹类型和状态(位置、速度和加速度)已知的条件下,求出了战机最优机动问题的闭环解;文献[4]提出了一种基于影响图(influence diagram)的飞机最优机动模型; 文献[5]将影像图和博弈论相结合,提出了“一对一”情形下飞机的机动优化方法。文献[6]对无人机规避来袭导弹的最优机动问题进行了研究,在假设导弹状态已知的条件下,在距离和角度的离散点上确立了最佳机动时机和机动方向。
对最佳ECM的研究,一般使用博弈论相关理论或者将之转换为线性规划问题。文献[7]采用了博弈论的方法对单部雷达在检测阶段的自适应干扰问题进行了研究;文献[8]研究了“追-逃”问题中最佳ECM的使用方法;文献[9]提出了使用线性规划的方法对“多部干扰机干扰多部雷达”情形下的干扰资源分配问题进行了求解。
以上文献对飞机的最优机动和最佳ECM使用问题分别进行了研究,实际上,战机为了提高生存能力,一般都是将机动和ECM结合起来使用。文献[10]将战机对抗导弹问题定义为导弹对抗措施优化(Missile Countermeasures Optimization,MCO)问题,采用遗传规划(Genetic Programming,GP)的方法,对导弹类型和状态不确定条件下的最佳机动和ECM结合问题进行了研究;文献[2]介绍了一种用于战机飞行员的决策辅助系统(Decision Support System,DSS),该系统将作战经验使用Prolog语言转换为计算机语言,并使用贝叶斯网络(Bayesian Network,BN)对“机动+ECM”进行自适应决策。
目前的研究均集中在单独的武器对抗阶段或者单独的传感器对抗阶段,没有考虑武器对抗和传感器对抗的相互影响。例如,导弹的发射依赖于雷达等传感器对目标的发现和跟踪,导弹对目标的命中也依赖于传感器对目标的信息获取。飞机进行战术机动或者实施ECM的目的是为了提高飞机生存力,文献[11]对飞机生存力的定义和评估方法进行了全面的阐述,文献[12]对无源干扰条件下的飞机生存力进行了建模,文献[13]建立了有源干扰条件下飞机生存力模型,文献[14]对飞机在不同航路下的飞机生存力进行了研究,并提出了在威胁位置不确定条件下的飞机生存力评估方法。
这些研究为评估不同条件下的飞机生存力提供了很好的参考,但是建立的生存力模型均是静态的,没有考虑不同阶段进行不同战术机动和ECM的生存力优化问题。实际上,在不同作战阶段使用不同的机动和ECM对飞机生存力的影响是不同的,需要根据整个作战过程进行研究。本文对战机在面-空导弹(Surface-to-Air Missile,SAM)威胁下的对抗措施优化方法进行研究,旨在建立一种能够根据作战环境和阶段自适应选择对抗措施的模型和算法,从而为飞行员提供决策辅助或者直接用于无人作战飞机中。
1 问题描述 考虑如图 1所示的典型作战场景:装备有自卫电子对抗设备的战机对目标实施打击,但是必须经过目标周围的SAM阵地,图 1中虚线表示战机执行任务的航线。本文研究战机按照该航线飞行、在不同阶段实施不同对抗措施的生存力优化问题。SAM阵地按照功能可以分为以下3个区域。
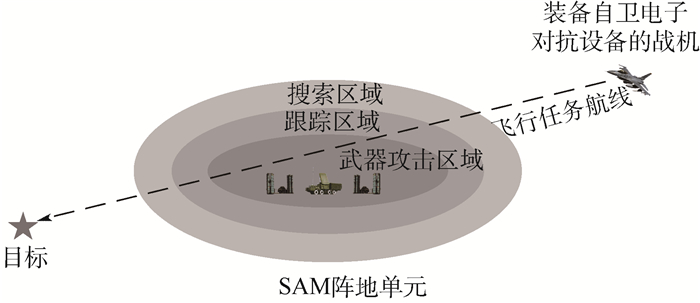 |
| 图 1 典型的对地突防作战场景 Fig. 1 Typical air-to-ground penetration scenario |
| 图选项 |
1) 搜索区域:表示目标指示雷达可以发现目标的区域。
2) 跟踪区域:表示制导雷达可以对目标实施跟踪的区域。
3) 武器攻击区域:表示在此区域导弹可以发射并以一定的概率击中目标。
图 1中飞机的战术决策不同,作战区域的相对大小还会发生改变,这也是通过战术决策优化飞机生存力的依据。
对作战场景作如下假设:① SAM阵地每次只发射一枚导弹,导弹的中制导阶段由制导雷达提供目标信息,末制导阶段目标信息由导引头提供;② 飞机按照既定航路飞行,即飞机不可以通过改变航路的方式规避威胁,机动也不改变既定航路;③ SAM制导雷达为多功能雷达(Multi-Function Radar,MFR)[15],可以同时工作在多种模式(如搜索、跟踪、制导等)以应对多个目标;④ 战机携带的自卫电子对抗设备包括电子干扰机和箔条、红外投放器,暂不考虑支援干扰机(Stand-Off Jamming,SOJ)的作用。
2 飞机生存力优化模型 假设飞机分别在t0, t1, …, tn, …等离散时刻点进行战术决策,可选择的战术包括机动、ECM或者两者的组合[10],将可供选择的战术记为有限数量的战术集合A,ai(i=1, 2,…,N)为A中的某一项战术,即ai∈A。ai的效果与当前飞机所处的状态有关,例如,如果该时刻敌方雷达对飞机实施距离跟踪,有效的干扰方法是距离波门拖引或者距离假目标干扰[16];如果敌方导弹雷达导引头已经锁定目标,应该在释投放箔条弹的同时进行与导引头视场角垂直的切向机动[2]。飞机在tn时刻所处的状态记为s(tn),每个时刻的战术决策模型如图 2所示。
 |
| 图 2 战术决策模型 Fig. 2 Strategic decision-making model |
| 图选项 |
如图 2所示,s(tn)在a(tn)作用下向s(tn+1)转移是一个概率事件,用P(s(tn+1)|s(tn), a(tn))表示此概率,不同行动下此概率并不相同。文献[14]定义了飞机所处的5种作战状态,并且根据SAM的作战流程指出各状态之间的转移概率满足Markov特性,即
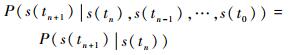 | (1) |
定义生存密度函数λ(t)用于求解各个状态之间的转移概率:
 | (2) |
但是文献[14]没有考虑不同行动下生存密度函数的不同,即当ai≠aj(ai∈A,aj∈A)时,一般有
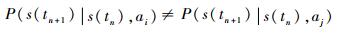 | (3) |
同时,对于现代MFR而言,仅仅使用搜索和跟踪2种状态并不能完全描述雷达的多种工作模式。飞机的战术决策问题,可以归结为根据tn时刻飞机所处的状态s(tn),选择最佳行动a(tn)的问题,这是一个典型的不确定条件下的序贯决策问题。决策的目的是为了使飞机的生存力最大化,飞机的生存力可以用一定准则下飞机所处的某个状态进行表征。
Markov决策过程(Markov Decision Process,MDP)为该序贯决策问题的求解提供了方法,相比影响图等其他方法,MDP在多级动态决策方面表达式更为简洁, 求解也更为方便[17],这也使得MDP理论在很多方面得到了应用[18]。本文用MDP理论对飞机的作战决策问题进行求解。
3 对抗措施优化模型 3.1 MDP的基本要素 根据定义[17],MDP可以由如下五元组进行表示:
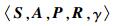 | (4) |
其中:S表示状态集,即战机在不同作战阶段敌方雷达或者导弹的状态,是对威胁环境的一种划分;A表示行动集,即可供战机选择的机动、ECM及其组合形式;P(s(tn+1)|s(tn), a(tn))(P∈P,P为状态转移概率组成的矩阵)表示tn时刻采取行动a(tn)(记为a)时,状态从s(tn)(记为s)转移到状态s(tn+1)(记为s′)的概率,反映了各种对抗措施的不确定性;R(s′|s, a)(R∈R)表示在状态s时采取行动a获得的报酬(或者付出的代价);γ表示对未来期望报酬的折扣。战机对抗导弹MDP模型中的各要素定义如下:
1) 状态集S。定义S={s1, s2, …, sM},本文采用文献[19]中定义的8种雷达状态,并将其拓展到武器系统发射之后的阶段,共13种状态,即M=13。各状态的具体定义如表 1所示。
表 1 状态集及其元素 Table 1 State set and its elements
| 编号 | 状态名称及缩写 |
| s1 | Search |
| s2 | Acquisition (ACQ) |
| s3 | Non-Adaptive Track (NAT) |
| s4 | Range Resolution 1 (RR1) |
| s5 | Range Resolution 2 (RR2) |
| s6 | Range Resolution 3 (RR3) |
| s7 | Track Maintenance (TM) |
| s8 | Passive Track (PT) |
| s9 | Missile Launching (ML) |
| s10 | Mid-Course Guidance (MCG) |
| s11 | Terminal Guidance (TG) |
| s12 | Miss the target (Miss) |
| s13 | Hit the target (Hit) |
表选项
各状态可以由机载传感器,如电子支援措施(Electronic Support Measure,ESM)、导弹逼近告警器(Missile Approaching Warning,MAW)等根据截获的信号进行估计。
2) 行动集A。行动集包括单独的ECM、单独的战术机动以及机动和ECM的组合,单独的ECM用A1表示,单独的机动的用A2表示,机动与ECM的组合用A3表示。本文采用NASA提出的7种最常用的空战机动方式[20]以及文献[16]中提到的几种ECM,行动集合如表 2所示。
表 2 行动集及其元素 Table 2 Action set and its elements
| 行动集 | 状态相关的行动 | 行动名称 |
| A1 | a1→s1, s2, s10 | Multi False Target (MFT) |
| a2→s1~s7, s10 | Noise Jamming (NJ) | |
| a3→s4 | Range False Target 1 (RFT1) | |
| a4→s5 | Range False Target 2 (RFT2) | |
| a5→s6 | Range False Target 3 (RFT3) | |
| a6→s3 | Range-Gate Pull-Off (RGPO) | |
| a7→s7, s10 | Velocity-Range-Gate Pull-Off (VRGPO) | |
| a8→s11 | Flares+Chaffs | |
| a9→s8 | No Jamming (NoJ) | |
| A2 | a10→s1 | No Maneuvering (NoM) |
| a11→s7 | Maximum Acceleration (MA) | |
| a12→s7 | Maximum Deceleration (MD) | |
| a13→s10, s11 | Maximum Overload Pull-Up (MOPU) | |
| a14→s10, s11 | Maximum Overload Dive (MOD) | |
| a15→s10, s11 | Maximum Overload Left Turn (MOLT) | |
| a16→s10, s11 | Maximum Overload Right Turn (MORT) | |
| A3 | a17→s2, s7 | MOPU/MOD/MOLT/MORT+MFT |
| a18→s7, s10 | MOPU/MOD/MOLT/MORT+VRGPO | |
| a19→s10, s11 | MA/MD+Chaffs+Flares | |
| a20→s11 | MOPU/MOD/MOLT/MORT+Chaffs+Flares |
表选项
各种行动是针对特定状态设计的,表 2中也列举除了各行动与状态的对应关系。A中还包括2种特殊的行动,即a9和a10,这2种行动表示飞机不采取任何ECM和战术机动,A1中的行动也是在a10条件下实施的。实际上,文献[14]中对不同航路飞机生存力的评估就是在这一行动下进行的,可以认为文献[14]是本文的一个特例。
3) 状态转移概率矩阵P。状态实际上反映了环境对飞机的威胁程度[14-15],例如,雷达处于跟踪状态要比雷达处于搜索状态对飞机威胁性更大,使用战术机动以及ECM的目的是为了使战机尽量多地停留在低威胁等级的状态中。状态转移矩阵反映了各行动结果的不确定性,各状态的转移如图 3所示。
 |
| 图 3 状态及其转移情况 Fig. 3 States and their transitions |
| 图选项 |
图 3中实线表示2个状态之间的转移概率不为0,箭头表示状态转移的方向。虚线表示如果第1枚导弹脱靶,SAM可能继续重新搜索目标开始发射第2枚导弹。此外,雷达只有在干扰存在的条件下才有向s8(PT)状态转移的可能。状态转移分为以下3种情况:① 停留在当前状态;② 向威胁等级更高的状态转移;③ 向威胁等级低的状态转移。
从SAM的作战过程可知[21],s1~s13,威胁等级依次增大,但是由于被动跟踪只有目标的角度信息,所以认为PT的威胁等级与NAT相同,同时,3种距离分辨(RR1、RR2、RR3)的威胁等级相同,s12(Miss)的威胁等级与s1(Search)相同。
图 3中,s1为起始状态,威胁等级最低;如果进入s13(Hit),则以概率1停留在此状态,而此状态威胁等级最高。战术决策的目的就是要使飞机尽可能少地进入s13,或者使飞机尽可能多地停留在s1。为了评估不同行动的效果,用a9和a10条件下的状态转移概率为基准,以各行动与a9和a10条件下相比该基准概率的变化量作为各行动的效果评估指标,对a∈A:
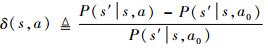 | (5) |
式中:a0=a9+a10,表示既不做机动,也不实施ECM;s′的威胁等级(记为υ(s′))低于s的威胁等级(记为υ(s));如果δ(s, a′) > δ(s, a),则表示对于状态s,a′比a的效果要好。
对?a∈A,各状态的转移概率满足:
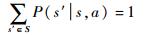 | (6) |
P需要经过相关的试验获取数据,然后经过增强学习(Reinforcement Learning,RL)算法进行确定[17]。但是由于相关试验非常困难甚至不可能,所以一般只能通过理论分析和仿真实验产生的数据代替实际数据[2],然后再对P进行学习。
4) 报酬函数R。报酬函数是确定最佳行动的准则,因为无论战术机动还是ECM,其目的都是让飞机尽量在低威胁等级的状态上,所以,对于?a∈A,定义报酬函数如下:
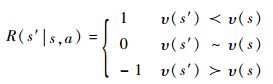 | (7) |
式中:υ(s′)?υ(s)表示s′的威胁等级低于s的威胁等级;υ(s′)~υ(s)表示s′威胁等级与s的威胁等级相等;υ(s′)?υ(s)表示s′的威胁等级高于s的威胁等级。另外,令R(s13|s11, a)=-10表示导弹命中目标是最不希望的结果。
建立MDP模型是为了求解每个阶段飞机的最佳决策,所有状态对应的行动称之为策略,将之记为π,所有的策略组成的集合记为Π,则
 | (8) |
为了寻找最佳策略,本文采用无限阶段折扣准则[17],将R(s′|s, a)简记为rt,则在某一初始状态下总的报酬函数为
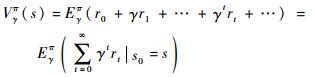 | (9) |
式中:V(s)为值函数,表示某一初始状态s0下总的报酬函数;E(·)表示期望运算符。最佳决策可以表示为
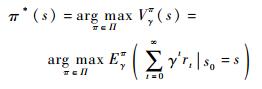 | (10) |
最佳策略的存在性及唯一性证明参见文献[17-18]。
5) 折扣因子γ。γ用来平衡当前报酬与未来报酬的关系,γ越大,表示未来报酬所占的比重也越大,一般0 < γ < 1。无论是机动还是ECM,效果并不能立即显现[22],所以需要考虑一段时间以后该行动的影响。
3.2 MDP的求解算法 MDP的求解方法分为值迭代法和策略迭代法,策略迭代法效率较高,故本文采用策略迭代法,求解步骤如下[17]。
初始化:π0∈∏
n←0
重复:
对于?s∈S, 求解:
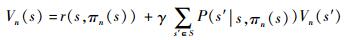 |
对于?s∈S,求解:
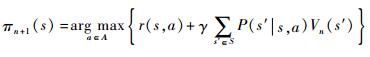 |
n←n+1
直到πn=πn+1
返回Vn, πn+1
如果求得最佳决策π*,则可以根据π*确定任意状态对应的最佳行动,即对于?s∈S,最佳的行动为
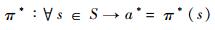 | (11) |
4 仿真实例 4.1 仿真参数设置 现有文献已对部分P(s′|s, a)进行了理论分析和仿真实验。本文研究在该概率已知的条件下,如何对各项措施进行优化。首先对P假设如下:
1) 在a0条件下,图 3中各实线部分表示的转移概率是平均分布的。
2) 各状态对应的行动使得该状态向高威胁等级状态转移概率降低δ(s, a),此时停留在此状态以及向低威胁等级状态转移的概率依然满足平均分布。例如,在a0条件下
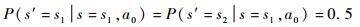 |
设δ(s1, a1)=50%,则
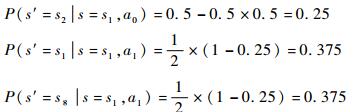 |
其他行动下各状态转移概率的确定方法与此相同,根据表 2,将各行动分为“专用”(单个行动只针对单一状态)和“通用”(单个行动对应多个状态)2类,假设专用行动的δ(s, a)为60%,通用行动的δ(s, a)为25%;γ=0.90;图 3中虚线表示的P(s1|s12, a)(对任意a∈A)设为0.50。
4.2 MDP策略下状态的转移 在确定了P、R和γ后,使用策略迭代法对MDP模型进行求解,得到的最佳策略如图 4所示。
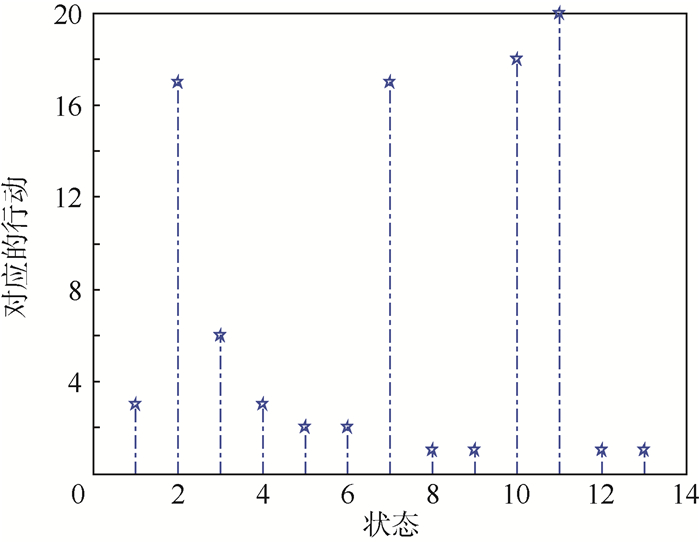 |
| 图 4 最佳策略下各状态与行动的对应关系 Fig. 4 Relationship between states and actions under optimal policy |
| 图选项 |
图 4以及本文其他部分,状态和行动对应的编号分别与表 1和表 2所示的状态和行动对应。设初始状态为s1,经20步各状态的转移情况如图 5所示。图 5分别表示2次实验中命中目标和未命中目标2种情况。
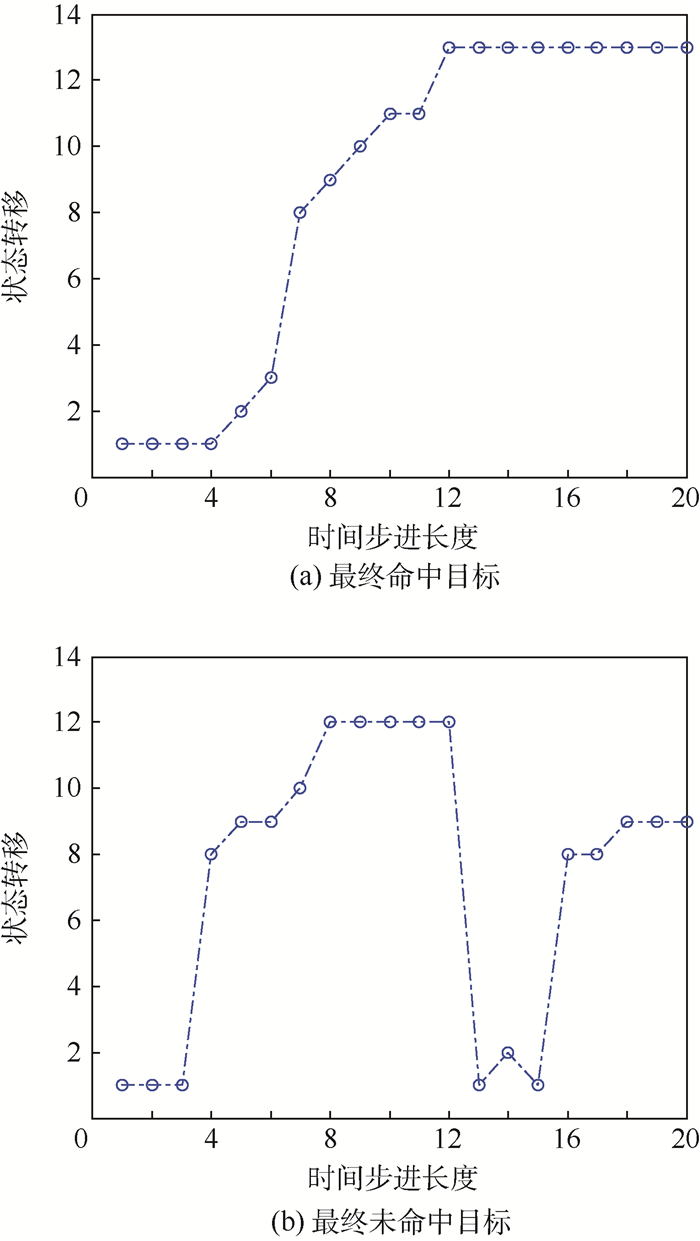 |
| 图 5 单次实验作战状态的转移情况 Fig. 5 Fighting state transition in one trial |
| 图选项 |
用一定时间内达到s13(即飞机被导弹命中)和停留在s1的次数表征不同策略下飞机的生存力,对图 5中的转移实验重复1000次,得到各状态的平均占有率如图 6所示。
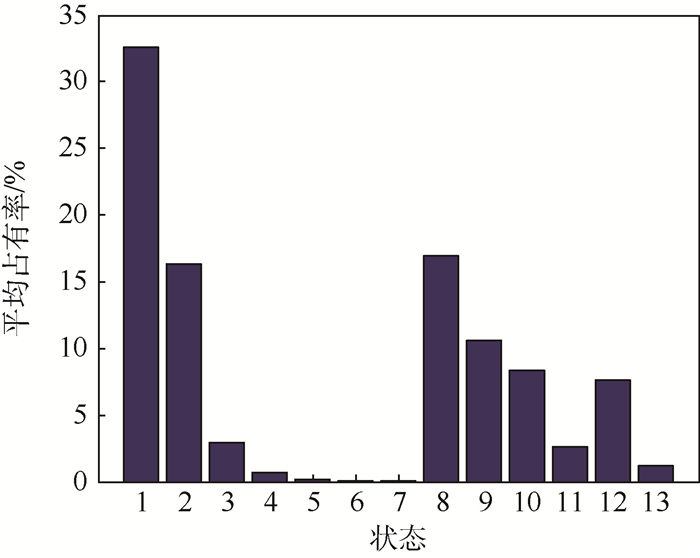 |
| 图 6 有限时间内各状态的平均占有率 Fig. 6 Average occupancy rate for all states in finite time steps |
| 图选项 |
由图 6可知,20步转移时搜索状态(s1)的平均占有率为32.8%,命中状态(s13)的平均占有率为1.14%。其中,s8的平均占有率为17.2%,实际上反映了由于敌方雷达抗干扰措施的存在,使用ECM可能面临的风险(使敌方雷达转入被动跟踪,从而发射导弹)。
图 1中,飞机分为进入敌SAM阵地和(如果未被击中)离开SAM阵地2个过程,这反映作战决策的初始状态不同,不同初始状态下s1和s13的平均占有率如图 7所示。
 |
| 图 7 不同初始状态下s1和s13的平均占有率 Fig. 7 Average occupancy rate of s1 and s13 under different initial states |
| 图选项 |
由图 7可知,不同的初始状态下s1和s13的平均占有率并不相同,而且随着初始状态威胁等级的升高,s1的平均占有率逐渐降低, 而s13的平均占有率逐渐升高,且初始状态为s11(导弹处于末制导阶段)时最终的命中概率最大。同时,如果第1枚导弹脱靶,则此时的命中概率相比处于s1时的命中概率要低。
4.3 不同策略下飞机生存力的比较 在相同的P、R以及初始状态条件下,对以下几种策略同MDP策略下的飞机生存力进行比较:
1) 固定策略(fixed policy):即a(tn+1)=a(tn)(n=0,1, …)。
2) 随机策略(random policy):在整个飞行过程中,飞机以等概率随机选取其中的一种对抗措施。
3) 贪婪策略(greedy policy):又称为单步最优策略,即
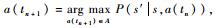
4) MDP策略(MDP policy):即按照式(11) 确定的每个状态对应的行动。根据式(9) 可知贪婪策略可以看作是MDP策略中γ=0的特例。
设固定策略中a(tn+1)=a(tn)=a2(n=1, 2, …)。单次实验中不同策略下的状态转移情况和对应的行动如图 8和图 9所示。
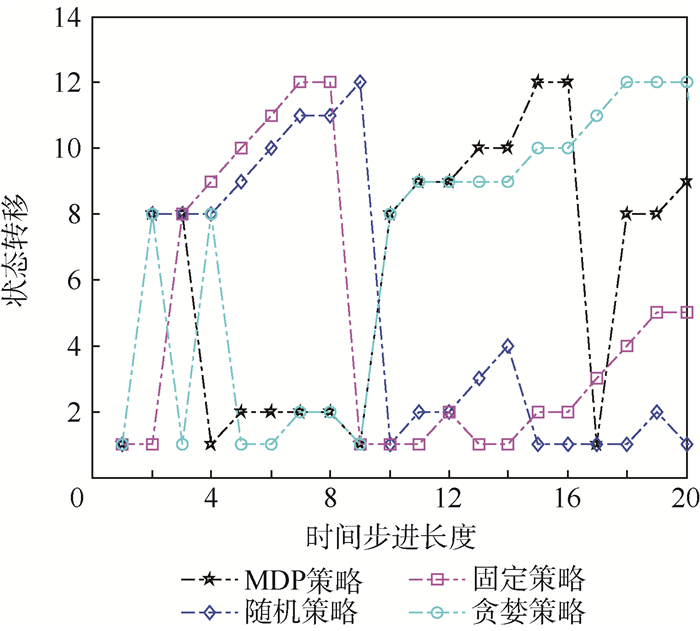 |
| 图 8 不同策略下的状态转移情况 Fig. 8 State transition under different policies |
| 图选项 |
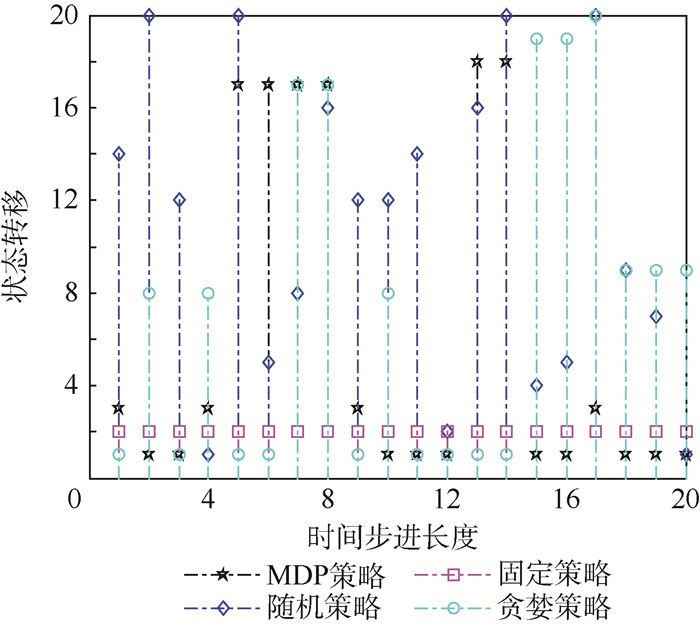 |
| 图 9 不同策略下的行动 Fig. 9 Actions under different policies |
| 图选项 |
由图 8和图 9可知,某些状态下随机策略和贪婪策略与MDP策略下的行动可能是一致的。为了比较不同策略下飞机的生存力,用稳态时飞机到达s13和s1的期望来表示生存力的大小。对图 8和图 9进行1 000次Monte Carlo实验,得到各策略下s13和s1的平均占有率,如图 10和图 11所示。
 |
| 图 10 不同策略下s13的平均占有率(γ=0.90) Fig. 10 Average occupancy rate of s13 under different policies (γ=0.90) |
| 图选项 |
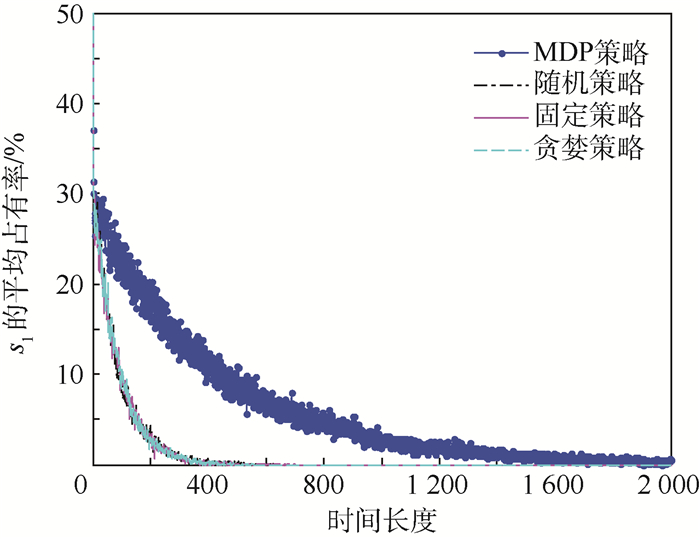 |
| 图 11 不同策略下s1的平均占有率 Fig. 11 Average occupancy rate of s1 under different policies |
| 图选项 |
由图 10和图 11可知,经过约2000步以后,所有策略下s13的平均占有率均收敛到100%,同时s1的平均占有率均收敛到0,对于其他初始状态也可以得到类似的结论。这表明,随着时间的推移,飞机的生存力逐渐下降,这与文献[14]的结论类似。但是,MDP策略下s1和s13的收敛速度更慢,这表明使用MDP策略可以使飞机在相同时间内处于更安全的状态,MDP策略可以有效地提高飞机生存力。同时,图 10和图 11表明,虽然同样利用了一定的先验信息(使用了状态转移矩阵P),在个别状态下使用的行动甚至相同,但是贪婪策略并没有体现出该先验信息的作用,或者说从长期来看,贪婪策略与随机策略和固定策略一样,这表明单个阶段的优化不能有效提高飞机的生存力。
5 结论 1) 通过对作战阶段进行划分,用状态来表征不同作战阶段对飞机的威胁程度,将飞机对抗导弹的措施优化问题转化为不确定条件下的序贯决策问题,从而将整个作战过程中战术机动和ECM等对抗措施的优化问题统一到一个框架下进行解决,同时考虑了作战过程中传感器与武器系统的相互作用。
2) 不同的战术对抗措施是针对特定的作战阶段(状态)的,而且各措施的效果并不能立即观测得到,MDP同时考虑了对抗措施的不确定性和未来状态转移对当前决策的影响,求解得到的最佳决策易于实施,同时适用于飞机进入敌方SAM阵地和退出战斗2个过程。
3) 单步最优策略没有考虑传感器与武器的相互作用,并不能提高飞机的生存力。除了对单个阶段各措施的转移概率进行分析外,还需从整个作战阶段出发对单个阶段的措施进行优化。
4) 不同策略下飞机的生存力并不相同,且生存力是时间的递减函数,如果时间有限且相同,MDP策略下飞机的生存能力最大。
参考文献
| [1] | ERLANDSSON T, NIKLASSON L. An air-to-ground combat survivability model[J].Journal of Defense Modeling and Simulation, Application, Methodology, Technology, 2013, 12(3): 1–15. |
| [2] | RANDLEFF L R.Decision support system for fighter pilots[D].Kongens Lyngby:Technical University of Denmark, 2007. |
| [3] | ZARCHAN P. Tactical and strategic missile guidance[M].6th edReston: AIAA, 2012: 33-58. |
| [4] | VIRTANEN K, RAIVIO T. Decision theoretical approach to pilot simulation[J].Journal of Aircraft, 1999, 36(4): 18–27. |
| [5] | VIRTANEN K, KARELAHTI J, RAIVIO T. Modeling air combat by a moving horizon influence diagram game[J].Journal of Guidance, and Dynamics, 2006, 29(5): 1080–1091.DOI:10.2514/1.17168 |
| [6] | YOMCHINDA T.A study of autonomous evasive planar-maneuver against proportional-navigation guidance missiles for unmanned aircraft[C]//2015 Asian Conference on Defense Technology.Piscataway, NJ:IEEE Press, 2015. |
| [7] | BACHMANN D J, EVANS R J, MORAN B. Game theoretic analysis of adaptive radar jamming[J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1081–1100.DOI:10.1109/TAES.2011.5751244 |
| [8] | BROOKS R R, PANG J E, GRIFFIN C. Game and information theory analysis of electronic countermeasures in pursuit-evasive games[J].IEEE Transactions on Systems, Man and Cybernetics-Part A:Systems and Humans, 2008, 38(6): 1281–1294.DOI:10.1109/TSMCA.2008.2003970 |
| [9] | 沈阳, 陈永光, 李修和. 基于0-1规划的雷达干扰资源优化分配研究[J].兵工学报, 2007, 28(5): 528–532. SHEN Y, CHEN Y G, LI X H. Research on optimal distribution of radar jamming resource based on zero-one programming[J].Acta Armamentarii, 2007, 28(5): 528–532.(in Chinese) |
| [10] | MOORE F W. A methodology for missile countermeasures optimization under uncertainty[J].Evolutionary Computation, 2002, 10(2): 129–149.DOI:10.1162/106365602320169820 |
| [11] | BALL R E. The fundamentals of aircraft combat survivability analysis and design[M].2nd ed.Reston: AIAA, 2003: 445-602. |
| [12] | 杨哲, 李曙林, 周莉. 机载自卫压制干扰和箔条干扰下飞机生存力研究[J].北京理工大学学报, 2013, 33(4): 375–379. YANG Z, LI S L, ZHOU L. Study of aircraft survivability under the conditions of self-defense jamming and chaff jamming[J].Transactions on Beijing Institute of Technology, 2013, 33(4): 375–379.(in Chinese) |
| [13] | 宋海方, 肖明清, 吴华, 等. 不同机载电子干扰条件下的飞机敏感性模型[J].航空学报, 2015, 36(11): 3630–3639. SONG H F, XIAO M Q, WU H, et al. Genetic model of aircraft susceptibility to different airborne electronic countermeasures[J].Acta Aeronautica et Astroautica Sinica, 2015, 36(11): 3630–3639.(in Chinese) |
| [14] | ERLANDSSON T, NIKLASSON L. Automatic evaluation of air mission routes with respect to combat survival[J].Information Fusion, 2014, 20(1): 88–98. |
| [15] | HASAN S M, GUITOUNI A. Variable dwell time task scheduling for multifunction radar[J].IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 463–472.DOI:10.1109/TASE.2013.2285014 |
| [16] | MARTINO A D. 现代电子战系统导论[M]. 姜道安, 等, 译. 北京: 电子工业出版社, 2014: 5-18. MARTINO A D.Introduction to modern EW systems[M].JIANG D A, et al, translated.Beijing:Publishing House of Electronic Industry, 2014:5-18(in Chinese). |
| [17] | SIGAUD O, BUFFET O. Markov decision processes in artificial intelligence:MDPs, beyond MDPs and applications[M].New York: John Wiley & Sons, 2010: 1-63. |
| [18] | RUSSELL S J, NORVIG P. Artificial intelligence:A modern approach[M].3rd edBeijing: Tsinghua University Press, 2011: 645-684. |
| [19] | VISNEVSKI N, KRISHNAMURTHY V, WANG A, et al. Syntactic modeling and signal processing of multifunction radars:A stochastic context-free grammar approach[J].Proceeding of IEEE, 2007, 95(5): 1000–1025.DOI:10.1109/JPROC.2007.893252 |
| [20] | 傅莉, 谢福怀, 孟光磊, 等. 基于滚动时域的无人机空战决策专家系统[J].北京航空航天大学学报, 2015, 41(11): 1994–1999. FU L, XIE F H, MENG G L, et al. An UAV air-combat decision expert system based on receding horizon control[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 1994–1999.(in Chinese) |
| [21] | 娄寿春. 面空导弹武器系统分析[M].北京: 国防工业出版社, 2013: 50-132. LOU S C. Surface-to-air missile weapon system analysis[M].Beijing: National Defense Industry Press, 2013: 50-132.(in Chinese) |
| [22] | BANDIERA F, FARINA A, ORLANDO D, et al. Detection algorithms to discriminate between radar targets and ECM signals[J].IEEE Transactions on Signal Processing, 2010, 58(12): 5984–5993.DOI:10.1109/TSP.2010.2077283 |
