当前研究中,针对LFM信号提出了众多的移频干扰样式,例如脉间分段移频干扰[3]、线性函数移频干扰[4]、分段线性函数移频干扰[4]、随机移频干扰[5]、N阶频谱扩展-压缩 (SSC) 盲移频干扰[6]等。这些干扰样式都是针对固定移频干扰易被雷达识别的缺陷,提出相应的改进措施,达到了较好的干扰效果。但是与之相反的是,移频干扰对抗技术的发展表现出一定的滞后性,文献[2]提出利用移频干扰信号中心频率的变化,补偿移频所引起的距离偏差,从而得到目标的真实距离,但是只适用于对抗固定移频干扰,并且文献[7]针对这一缺陷提出了频偏特征的隐藏技术,进一步提高了干扰对抗的难度,文献[8]提出构建过完备原子库,利用稀疏分解实现对移频干扰的抑制,但是当干扰与回波信号在时间上重叠时,该方法无法重构回波信号,并且由于改进的多次移频干扰在频移原子中的非稀疏性,也导致该方法失效。
多次移频干扰用于自卫式干扰时,干扰信号与回波信号在时域、频域和空域均无法分辨,对抗干扰造成了极大的困扰。盲源分离技术能够直接从观测信号中提取出原始的信号分量,对于在电子对抗中提取干扰和回波参数有着重要的意义。对于盲源分离应用于欺骗干扰的抑制,文献[9]和文献[10]分别提出改进的复值非高斯最大方法和改进的基于峭度的自然梯度方法来对抗频谱弥散干扰,但是都需要雷达是具有多通道接收能力的阵列雷达。对于常规单脉冲雷达,文献[11]提出利用干扰和回波在和差通道中的混合信号作为两路混叠信号进行盲源分离,并利用干扰和回波在微多普勒特征上的差异实现干扰鉴别,该方法实际上也是利用雷达具有多个接收通道的特性,但是对于自卫式干扰,由于干扰和回波从同一方向进入,该方法失去效果。文献[12]针对单天线雷达的欺骗干扰,提出利用相邻脉冲的回波和干扰信号构成两路混叠信号,之后利用分段盲分离的方法实现对回波和干扰的分离,但是该方法需要利用回波和干扰的脉压峰值来确定干扰和回波的混合部分的起止时刻,仅能对抗单个时间延迟干扰。
现有的常规雷达在对抗多次移频自卫式干扰时,由于干扰和回波从同一方向进入,相当于仅有一个接收通道对回波进行接收。本文针对这一情况,根据目标回波和干扰极化特性的差异,利用雷达的正交极化辅助通道扩展接收通道,并利用最大信噪比盲源分离方法实现对干扰信号和回波信号的分离,并根据分离结果与参考信号匹配滤波的差异,实现对干扰的抑制和对回波参数的提取。
1 信号模型及可分离性分析 1.1 雷达接收信号模型 雷达发射线性调频信号,用r(t) 表示,t为时间,主瓣自卫式干扰信号为多次移频干扰,用j(t) 表示,即有
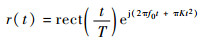 | (1) |
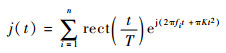 | (2) |
式中:f0为雷达信号的中心频率;B=KT为信号的带宽,K为信号的调频斜率,T为信号的脉冲宽度;n为干扰信号中移频分量的个数;fi为第i个干扰分量的中心频率。
雷达辅助天线通常用于相干旁瓣相消 (CSLC),外军的一些高性能雷达均采用了该技术,诸如美国“爱国者”雷达有5个辅助阵, “宙斯盾”雷达有6个辅助阵。在旁瓣对消 (SLC) 系统中,为了消除主辅通道交叉极化响应不匹配的影响,辅助天线通常采用垂直和水平2种辅助天线以便对消掉干扰信号的垂直和水平分量[13],这里利用与主天线极化方式正交的辅助天线接收信号构建第2路混叠信号。
在雷达接收天线端口处,目标回波信号和干扰信号可分别表示为
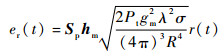 | (3) |
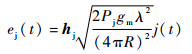 | (4) |
式中:Sp为目标的极化散射矩阵;hm为雷达主天线的极化矢量;Pt为雷达发射信号的峰值功率;gm为雷达主天线增益;λ为雷达工作波长;σ为目标的雷达散射截面积 (RCS);R为目标所在距离;hj为干扰机发射天线的极化矢量;Pj为干扰功率。进入主天线的接收电压信号可表示为
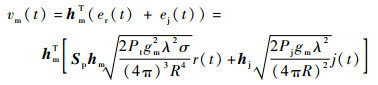 | (5) |
同样设辅助天线增益ga,交叉极化辅助天线的极化矢量为ha,那么进入辅助天线的接收电压信号可表示为
 | (6) |
进入雷达主辅接收通道的信号可表示为
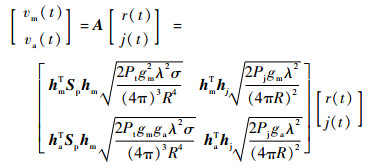 | (7) |
表示成矩阵形式,即为Y=AS。
1.2 信号的可分离性分析 本节将分析回波信号和干扰信号的可分离性。
对于盲源分离而言,通常需要满足:① 源信号之间相互统计独立;② 混合矩阵为列满秩矩阵;③ 源信号中有不多于一个高斯分布的源信号[14]。
1) 由于回波信号和干扰信号是由2个相互独立的物理过程所产生,因而两者是统计独立的。
2) 对于干扰机而言,为了避免极化失配所引起的极端损耗,通常将干扰机天线极化设计为斜极化或者圆极化,由于干扰信号的极化状态主要由干扰天线的极化状态确定,其极化状态相对稳定,而目标通常具有较为复杂的外形,其极化散射矩阵随着视角的变化而变化,即在接收天线端口处,回波信号和干扰信号具有不同的极化状态,又由于辅助通道采用正交极化,因而混合矩阵A为列满秩矩阵。
3) 干扰信号和回波信号均为具有一定脉内调制特征的信号,为非高斯信号,并且由于干扰从主瓣进入,干扰的功率远高于通道噪声,因而可忽略通道噪声。
综上所述,利用交叉极化辅助通道扩展接收通道后,所构成的两路混叠信号满足盲源分离的要求,可应用盲源分离方法进行回波和干扰的分离。
设雷达发射峰值功率为40 kW,主天线增益为30 dB,辅助天线增益为ga=10 dB,雷达工作波长为10 cm,雷达主天线极化为水平极化,hm=
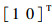
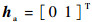
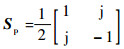
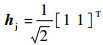
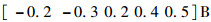
主通道接收的目标回波和干扰信号的波形如图 1所示。
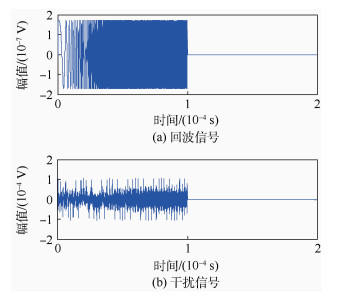 |
| 图 1 主通道接收回波和干扰信号波形 Fig. 1 Waveform of echo and jamming signals in main channel |
| 图选项 |
对主通道的混叠信号进行脉冲压缩处理,并以回波信号的输出峰值做归一化处理,可得干扰效果如图 2所示。
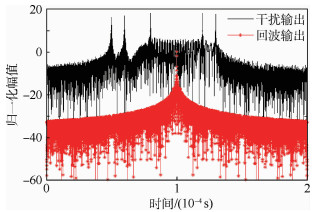 |
| 图 2 主通道接收信号脉冲压缩输出 Fig. 2 Pulse compression output of signals in main channel |
| 图选项 |
从图 2中可以发现,移频干扰信号经过脉冲压缩后,在真实回波附近形成了多个假目标,这些假目标密集分布在目标所在距离单元附近,并且其强度远高于回波信号的脉冲压缩输出,使雷达无法检测到真实目标。
2 回波和干扰信号的分离 基于盲源分离的抗干扰方法只是通过方法的处理将干扰和回波信号分别输出,并且由于盲源分离方法固有的排序不确定性,因而对于盲源分离的结果还需要进行鉴别,从而确定干扰信号和回波信号。因此基于盲源分离的干扰抑制方法应当包含3个部分的内容,即信号预处理、盲源分离和干扰鉴别。
盲源分离的目标是估计一个分离矩阵W,使得
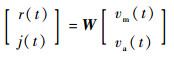 | (8) |
即X=WY。
要想估计分离矩阵,必须建立一个以W为变量的目标函数M(W),根据目标函数求得分离矩阵的最佳估计W。
2.1 信号预处理 在对信号进行盲源分离之前,需要对信号进行预处理,预处理包括零均值化处理和白化处理。零均值化处理就是将观测信号减去其算数平均值,得到零均值的观测向量。白化处理就是消除观测信号各分量之间的相关性。
根据移频干扰的原理,移频干扰信号与回波信号存在频谱上的重叠部分,从盲源分离的角度来看,相当于观测信号的2个分量之间存在相关性,因此必须对观测信号进行白化处理。
白化处理的过程是根据观测信号计算一个矩阵Q,使得变换后的观测向量Y′=QY的自相关矩阵为一个单位阵,即
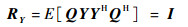 | (9) |
式中:E[·]为变量的算术平均。
这里直接引用文献[11]的结果,得到白化矩阵为
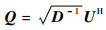
2.2 基于最大信噪比盲源分离的干扰抑制方法 最大信噪比盲源分离方法以源信号与估计信号的误差作为噪声信号,构建目标函数为[15]
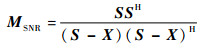 | (10) |
由于源信号是未知的,因此用源信号的滑动平均S代替S,则式 (10) 变为
 | (11) |
式中:
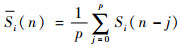
将X=WY, S=WY代入式 (11),可得
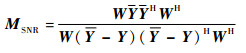 | (12) |
令
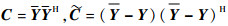
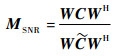 | (13) |
式 (13) 对W求偏导可得
 | (14) |
式 (14) 的零点即为信噪比函数的极值点,由此可求得分离矩阵的方程为
 | (15) |
对式 (15) 进行求解,即可得到分离矩阵的估计W。根据已有的研究[16],可知式 (15) 的解W是矩阵
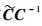
主通道和辅助通道接收的信号经过混叠后,其波形如图 3所示。
 |
| 图 3 主通道和辅助通道的混叠信号 Fig. 3 Mixed signals in main channel and auxiliary channel |
| 图选项 |
取滑动平均阶数p=50,则利用最大信噪比盲源分离方法的分离结果如图 4所示。
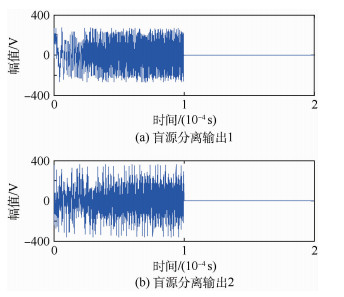 |
| 图 4 盲源分离方法的分离结果 Fig. 4 Separation results of BSS method |
| 图选项 |
经过盲源分离处理后,输出两路分离后的信号,这两路信号分别表示干扰和回波的分离结果,将两路信号分别与参考信号进行匹配滤波处理,其输出如图 5所示。
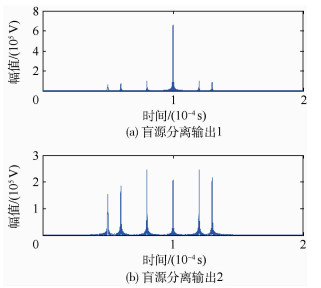 |
| 图 5 分离结果的脉冲压缩输出 Fig. 5 Pulse compression output of separation results |
| 图选项 |
从匹配滤波的结果可以发现,经过盲源分离处理,输出的两路信号能够分别反映回波和干扰的特征,其中第1个信号 (见图 5(a)) 表示分离出来的回波信号的脉冲压缩输出,第2个信号 (见图 5(b)) 表示分离出来的干扰信号的脉冲压缩输出。
3 对干扰鉴别和抑制 多次移频干扰信号经过脉冲压缩后,会形成多个峰值输出,而目标回波则只有一个输出峰值。根据盲源分离的原理,分离的结果应当是使分离出来的信号中,某一分量占据主要成分,尽可能地降低另一分量所占成分。从图 5可以发现,经过盲源分离处理后,分离出来的回波脉冲输出中,仍然存在干扰的分量输出,这些干扰分量与回波的强度为同一数量级,这对于弱信号的检测是不利的,因此必须采取消除干扰分量的影响。
由于干扰信号与回波信号的频谱存在较大的重叠部分,即两者有着较强的相关性,因而对干扰信号分离结果做脉冲压缩后,脉压结果中,除了能够显示构成干扰的5个分量外,还存在一个由回波所引起的分量输出。但是相对于盲源分离之前,回波信号完全被淹没的情况,此时干扰和回波脉压输出已经可以分别进行检测。
根据移频干扰的原理,移频干扰所产生的假目标信号的中心频率与回波信号的中心频率相差 (fi-f0)/2,并且脉压后的干扰信号输出峰值与回波信号输出峰值所在时刻相差
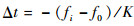
因此方法的基本流程为:
步骤1?提取主极化通道和交叉极化辅助通道的两路混叠信号,构成观测信号。
步骤2?对观测信号进行零均值处理和白化处理。
步骤3?计算观测信号的滑动平均,计算矩阵
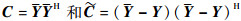
步骤4?计算矩阵

步骤5?将W代入X=WY,得到分离结果。
步骤6?利用参考信号对分离结果进行脉压处理。
步骤7?根据输出结果确定回波和干扰。
步骤8?根据干扰的参数,分别对干扰分量进行频率补偿。
在2.2节中,忽略了通道噪声,实际中,干扰机在形成干扰信号的过程中,由于器件的影响,会引入噪声,尤其是合成干扰信号后,需要经过射频放大装置和天线将干扰信号辐射出去,在此过程中,噪声也会相应地放大。此外,干扰机也可在形成的移频干扰信号中加入噪声,此时相当于噪声+移频复合干扰。假设噪声为零均值高斯噪声,那么当干噪比不同时,盲源分离输出信号的脉压结果如图 6所示。
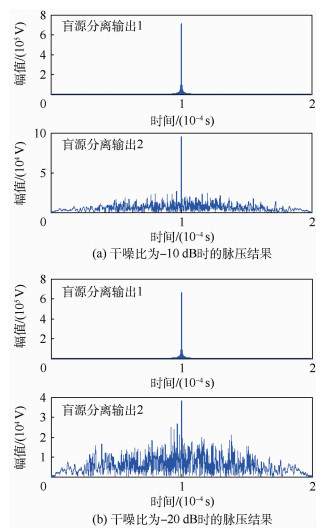 |
| 图 6 干扰机内噪声对盲源分离结果的影响 Fig. 6 Effects of noise in jammer on BSS results |
| 图选项 |
从图 6可以发现,干扰信号中加入噪声后,相对于无噪声时的情况,目标峰值附近仍存在一些假目标输出峰值的情况,分离出来的回波信号的脉压输出仅有一个峰值,表明加入噪声后,降低了干扰和回波之间的相关性,进一步降低了回波分量中的干扰成分。但是加入噪声后,分离出来的干扰信号中,已经很难看到移频分量,从盲源分离的角度来说,加入噪声后,对干扰信号的提取是失败的,即噪声影响到了盲源分离的性能。但是从抗干扰的角度来说,由于回波信号具有较为明显的特征,因而加入噪声后,仍可从盲源分离的结果提取回波信号,从而保证雷达的正常工作。
4 结论 针对移频干扰对LFM脉冲压缩雷达的影响,本文提出了一种基于极化通道扩展和盲源分离结合的干扰对抗方法,主要结论如下:
1) 建立了主瓣干扰条件下,主通道和交叉极化辅助通道的接收信号模型,讨论了干扰和回波信号的可分离性。
2) 研究了基于最大信噪比盲源分离和频率补偿的干扰抑制方法,实现了干扰信号和回波信号的分离,并根据移频干扰的原理,通过频率补偿实现对目标距离信息的正确估计。
3) 通过理论分析和仿真实验可知,该方法具有较好的抗干扰效果,在主瓣干信比为20 dB时,仍可实现对目标距离信息的提取。
本文所提出的方法对于进一步研究移频干扰的对抗方法具有重要的参考意义。但是实际应用环境中,仍然存在许多未知的影响,因而对该方法在实际对抗主瓣干扰中的应用,还需要做进一步的研究。
参考文献
| [1] | 黄翀鹏, 王剑, 徐保国. 线性调频脉冲的移频干扰性能研究[J].系统工程与电子技术, 2013, 35(5): 935–939. HUANG C P, WANG J, XU B G. Performance of shift frequency jamming against LFM signal pulse[J].Systems Engineering and Electronics, 2013, 35(5): 935–939.(in Chinese) |
| [2] | 刘忠, 陈登伟, 谢晓霞, 等. LFM脉冲压缩雷达抗移频干扰的方法研究[J].现代雷达, 2006, 28(11): 84–86. LIU Z, CHEN D W, XIE X X, et al. A countering technique for LFM PC radar against shift frequency jamming[J].Modern Radar, 2006, 28(11): 84–86.DOI:10.3969/j.issn.1004-7859.2006.11.024(in Chinese) |
| [3] | 吴晓芳, 邢世其, 王雪松, 等. 对合成孔径雷达的脉间分段移频干扰[J].航天电子对抗, 2010, 26(1): 53–57. WU X F, XING S Q, WANG X S, et al. Interpulse subsection shift-frequency jamming to SAR[J].Aerospace Electronic Warfare, 2010, 26(1): 53–57.(in Chinese) |
| [4] | 顾成虎, 曲丽娜. LFM脉冲压缩雷达的移频干扰技术研究[J].哈尔滨商业大学学报 (自然科学版), 2015, 31(3): 350–353. GU C H, QU L N. Study on frequency-shifting jamming to LFM pulse compression radar[J].Journal of Harbin University of Commerce (Natural Sciences Edition), 2015, 31(3): 350–353.(in Chinese) |
| [5] | 周政, 唐宏, 张永顺. LFM脉压雷达的随机移频干扰研究[J].现代防御技术, 2010, 38(1): 103–106. ZHOU Z, TANG H, ZHANG Y S. Randomly shift frequency jamming to LFM pulse compression radar[J].Modern Defence Technology, 2010, 38(1): 103–106.(in Chinese) |
| [6] | 王玉军, 赵国庆. 对LFM雷达的N阶SSC盲移频干扰方法[J].电路与系统学报, 2011, 16(4): 70–74. WANG Y J, ZHAO G Q. Blind Nth-order SSC shift-frequency jamming to LFM radar[J].Journal of Circuits and Systems, 2011, 16(4): 70–74.(in Chinese) |
| [7] | 王玉军, 朱丽莉, 蒋磊. LFM雷达移频干扰特征的消隐方法研究[J].雷达学报, 2012, 1(4): 420–425. WANG Y J, ZHU L L, JIANG L. The study on characteristic blanking technique in frequency shifting jamming for LFM radar[J].Journal of Radars, 2012, 1(4): 420–425.(in Chinese) |
| [8] | 冯有前, 余付平, 高大化, 等. 稀疏分解在雷达移频干扰抑制方面的应用研究[J].计算机工程与应用, 2012, 48(6): 129–130. FENG Y Q, YU F P, GAO D H, et al. Research on radar shift-frequency jamming suppression based on sparse decomposition[J].Computer Engineering and Applications, 2012, 48(6): 129–130.(in Chinese) |
| [9] | 尹洪伟, 李国林, 路翠华. 一种基于复值盲分离的欺骗干扰抑制方法[J].上海交通大学学报, 2015, 49(10): 1564–1569. YIN H W, LI G L, LU C H. An algorithm of deception jamming suppression based on complex-value blind source separation[J].Journal of Shanghai Jiao Tong University, 2015, 49(10): 1564–1569.(in Chinese) |
| [10] | 李飞, 李国林, 粘朋雷. 基于盲源分离的雷达信号欺骗干扰抑制[J].海军航空工程学院学报, 2015, 30(5): 424–428. LI F, LI G L, NIAN P L. Radar signal deception jamming suppressing based on blind source separation[J].Journal of Naval Aeronautical and Astronautical University, 2015, 30(5): 424–428.DOI:10.7682/j.issn.1673-1522.2015.05.005(in Chinese) |
| [11] | 王小静, 罗双才. 一种基于慢时域盲分离的欺骗干扰抑制方法[J].电子信息对抗技术, 2013, 28(2): 42–46. WANG X J, LUO S C. An approach to the deception jamming suppression based on blind signal separation in slow-time domain[J].Electronic Information Warfare Technology, 2013, 28(2): 42–46.(in Chinese) |
| [12] | 罗双才, 唐斌. 一种基于盲分离的欺骗干扰抑制方法[J].电子与信息学报, 2011, 33(12): 2801–2806. LUO S C, TANG B. An algorithm of deception jamming suppression based on blind signal separation[J].Journal of Electronics & Information Technology, 2011, 33(12): 2801–2806.(in Chinese) |
| [13] | SCHLEHER D C. Electronic warfare in the information age[M].New York: Artech House, 1999: 271-273. |
| [14] | 刘琚, 孙建德, 许宏吉. 盲信号处理理论与应用[M].北京: 科学出版社, 2013: 10-12. LIU J, SUN J D, XU H J. Blind signal processing theory and application[M].Beijing: Science Press, 2013: 10-12.(in Chinese) |
| [15] | 高剑茹, 高宝成. 基于最大信噪比的盲源分离方法的修正与比较[J].电脑与信息技术, 2009, 17(1): 19–21. GAO J R, GAO B C. Revision and comparison of blind source separation algorithm based on maximum signal noise ratio[J].Computer and Information Technology, 2009, 17(1): 19–21.(in Chinese) |
| [16] | BORGA M. Learning multidimensional signal processing[M].Linkoping: Linkoping University, 1998: 60-61. |
