雷达对抗中，基于数字射频存储器 (DRFM) 的转发式欺骗干扰，能够对雷达探测信号进行瞬时截获和精确复制，使雷达产生多个逼真假目标，给信号检测和目标跟踪带来巨大挑战。
针对DRFM假目标干扰，文献[1-2]通过发射一组相关性能优良的信号集，利用转发式欺骗干扰与目标回波的相对时延实现干扰信号抑制，但无法处理干扰与回波在同一脉冲重复周期内的混合信号。文献[3]研究了目标回波和转发式欺骗干扰在幅度起伏、高阶统计量、双谱特征上的差异，但相关特征量计算复杂度高，且提取较为困难。文献[4-5]研究了网络化雷达场景下，通过位置、速度、角度数据融合及各站雷达回波幅度的相关性检测等手段，实现假目标剔除。当假目标数量较多时，相关算法计算复杂度高，难以满足探测跟踪的实时性要求。
2006年，Antonik等^[6]提出了频率分集阵列 (FDA) 的概念，引起了广泛关注。FDA雷达通过在传统相控阵雷达各阵元中引入微小频差，使空间波束指向随距离变化而发生变化，实现了波束的空间扫描，同时，其距离独立性和角度自动扫描的性质使频率分集可用于鉴别和抑制干扰，在多径抑制及假目标干扰方面具有较大潜力^[6-8]。近年来，国内外****针对FDA体制的波束扫描特性开展了大量研究，文献[9]讨论了FDA的波束特性及应用前景，指出了FDA体制仍需解决的几项问题；文献[10-11]对FDA空间波束扫描特性进行了理论分析，得到了FDA阵列波束指向与引入频差间的对应关系；文献[12]讨论了FDA体制在多输入多输出 (MIMO) 中的应用，给出了FDA-MIMO雷达的波束控制及波束形成算法；文献[13-15]讨论了FDA体制在角度及距离参数估计方面的主要特点，指出了FDA在目标参数估计方面较传统相控阵精度较高；文献[16]提出了可用于转发式欺骗干扰抑制的FDA-MIMO模型，但仅对发射信号为单频信号的状态进行了讨论，且未提及相邻阵元相位差的提取方法。
针对以上问题，本文提出了基于FDA的假目标干扰抑制方法，通过提取雷达接收信号在不同阵元间的相位差或空间角频率，实现目标回波与假目标的区分与鉴别，理论推导与仿真结果表明，该方法能有效对抗各类DRFM假目标干扰。
1 FDA信号模型 目前，得到普遍讨论的FDA主要为均匀线性阵列 (ULA) FDA，结构如图 1所示。各阵元发射信号可表示为

图 1 ULA FDA结构示意图 Fig. 1 Structure diagram of ULA FDA

图选项

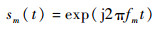(1)

式中：t为自脉冲起始时刻起脉冲传播经历的时间；各阵元发射频率为

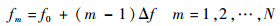(2)

式中：f₀、Δf和N分别为载频、阵元间频差和阵元总数。
设在空间中某位置{R, θ}处有一目标，阵元m的发射信号，经目标反射且重新被阵元m接收的接收信号为

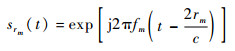(3)

式中：r_m=R-mdsin θ，d为阵元间距；c为光速。由此，接收端两相邻阵元接收信号的相位差为

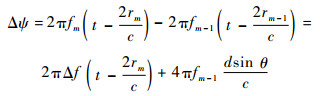(4)

FDA中，要求f₀≥NΔf ^[9]，此时：

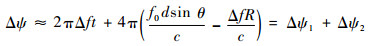(5)

当Δf=0时，FDA阵列转换为传统相控阵模式。该相位差由两部分组成，Δψ₁=2πΔft为两相邻阵元初始信号因脉宽产生的相位差，该相位差是时变的，为传播过程中，因为频差及波程差造成的相位差，该相位差与距离、角度呈线性关系。实际计算时，Δψ₁可根据发射信号脉宽及频率间隔进行补偿，本文只考虑Δψ₂，即传播过程引起的相位差。
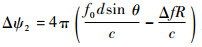
线性调频 (LFM) 信号是一种大时宽带宽积信号，具有低截获、较好的多普勒容忍度等良好特性，在当前武器装备中应用最为广泛，本文主要针对LFM信号展开研究。目前，DRFM干扰机针对LFM信号实施转发式欺骗干扰，往往通过复制雷达信号，并附加一定时延实现，为达到速度欺骗及假目标前移等效果，还会添加一定频移^[17]。设各阵元发射信号相互正交，目标接收各阵元发射信号的混合信号，统一进行复制并附加时延后，在距离r_j上产生一假目标，由于未进行相位调制，转发的信号与真实目标回波信号基本一致，即假目标信号在相邻阵元间的相位差与式 (5) 相同，此时：

(6)

从式 (6) 看出，假目标在相邻阵元间产生的相位差与距离、角度是“失配”的，可利用其进行假目标鉴别与抑制。
2 FDA-MIMO假目标鉴别模型 利用FDA进行假目标鉴别的前提是相邻阵元间的相位差能够被检测和提取。若相邻阵元发射信号的波形相同，则阵元接收的回波信号是所有阵元回波的混合信号，原有的相位关系会被破坏。因此，要实现相位差的鉴别，不同阵元需发射正交波形，即工作于MIMO模式以实现各自收发的目的。
2.1 回波信号的各阵元间相位差 设FDA-MIMO雷达含N个阵元，阵元1和阵元n的接收信号可分别表示为

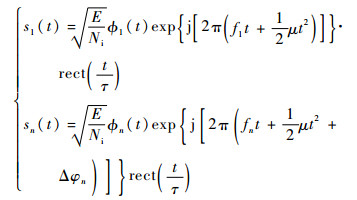(7)

式中：为接收端信噪比，E为接受的雷达信号能量，N_i为噪声信号能量；τ为发射信号脉宽；μ为调频斜率；Φ_n(t) 为相位调制项，以保证各阵元间发射的信号相互正交，即

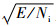
(8)

式中：根据匹配滤波相关理论，其对相位的影响在匹配滤波后会被消除，因此本文不考虑正交调制对相位差造成的影响。由式 (5) 可得，回波信号匹配滤波前在相邻阵元间的相位差和各发射信号起始点因波程差引起的固有相位差分别为

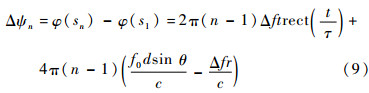(9)

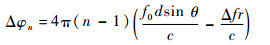(10)

匹配滤波后，各阵元输出信号为^[18]

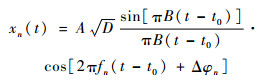(11)

式中：A为信号的幅度放大系数；B=μτ为LFM信号带宽；D=Bτ为LFM信号的时宽带宽积；t₀为匹配滤波器固有时延。则匹配滤波后，各阵元输出信号的相位差为

(12)

在尖峰输出时刻 (t=t₀)，各阵元输出相位差Δψ_n=Δφ_n。
2.2 转发式欺骗干扰信号的各阵元间相位差 对转发式欺骗干扰，设DRFM干扰机能成功检测并精确复制各阵元发射信号，以间歇采样信号为例 (重复采样信号可看作多个间歇采样信号的叠加)，DRFM干扰机对第n个阵元发射信号的采样信号和复制转发信号可分别表示为

(13)

式中：p(t) 为取样函数；δ为冲激函数；τ′为采样脉宽；T_s为重复周期。匹配滤波前，各阵元的相位差为

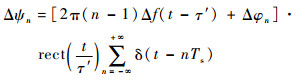(14)

该信号经匹配滤波后的时域函数为^[17]

(15)

式中：f_s=1/T_s为采样频率；y_n为包络调制项，则到匹配滤波后，干扰信号在各阵元输出相位差为

(16)

在干扰信号输出的峰值点 (t=t₀+τ′)：

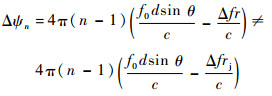(17)

因此，干扰信号在相邻阵元间产生的相位差与按式 (5) 计算的理论相位差并不匹配。

2.2.1 移频给相位差带来的影响 针对LFM信号的复制转发干扰通常结合移频共同使用，设移频量为ζ，则移频干扰信号的匹配滤波输出为^[17]

(18)

移频干扰信号匹配滤波后为一单频振荡信号，尖峰输出时刻为，则移频干信号在各阵元输出的相位差依然可用式 (15) 表示，在尖峰输出时刻，其相位差为

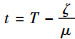
(19)

可见，移频的添加并未改变相位差的变化规律，但改变了干扰信号的峰值输出时刻，也相应改变了峰值输出时刻对应的相位差。

2.2.2 上下变频各相位差带来的影响 干扰机截获、复制雷达信号，以及雷达接收机发射、接收信号，都要进行上下变频。本节讨论上下变频对相位差的影响。
1) 干扰机上下变频对相位差的影响
因为各阵元发射信号频率间隔较小，干扰机会用同一本振对各阵元发射信号进行上下变频，设干扰机接收阵元n的发射信号为

(20)

干扰机本振为f_δ，设下变频时本振信号为

(21)

则下变频后中频信号为

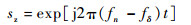(22)

设干扰机对发射信号的复制转发造成的延时为τ，此时本振信号为

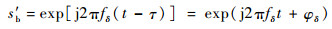(23)

经上变频后的信号为

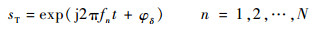(24)

即上下变频会使转发信号引入一个相位调制，但该调制对所有阵元信号是相同的，在求取相位差时会将该调制项直接抵消掉，即干扰机的上下变频不会对相位差鉴别带来影响。
2) 雷达上下变频对相位差的影响
各阵元发射信号频率间隔的相关信息对雷达发射、接收机是已知的，雷达对各阵元发射信号的上下变频可通过2种方式进行，一种是雷达使用同一本振对所有阵元信号进行上下变频，此时，变频引入的相位调制对所有阵元是一致的，不会影响阵元间相位差。而若雷达每个阵元通道都使用对应的本振进行上下变频，变频引入的相位调制则与各阵元发射频率有关，该相位调制会减弱各阵元间接收信号的相位差异，给相位差信息的提取带来困难。此时，可采用相位法测多普勒频率时，变频相位差的补偿算法进行相位补偿。本文假设雷达方使用同一本振对各阵元信号进行变频。
2.3 混合信号中各阵元的相位差 重复采样信号可看成多个间歇采样过程的混合，在干扰情况下，雷达接收端接收的是干扰与回波的混合信号，因此，需讨论混合信号各阵元间相位差与各分量信号的关系。假设某输出信号包含2路输出复信号s₁和s₂，相位分别为φ₁和φ₂，实部分别表示为a₁和a₂，则s₁和s₂可分别表示为

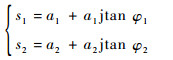(25)

则混合信号s=s₁+s₂的相位为

当φ₁和φ₂比较接近时，φ可近似表示为

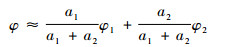(26)

即2路信号线性混合后的相位为原2路信号在相位域的“能量质心”。
对接收机接收的混合信号 (同时包含干扰与回波)，为达到欺骗效果，往往要求输出假目标与真实目标分布在不同距离单元内。真实目标所在距离上的信号为回波峰值与假目标副瓣信号叠加的混合信号，相位差以回波信号为主；而在假目标对应距离上的信号为回波副瓣与干扰信号峰值叠加的混合信号，相位差主要以假目标产生的相位差为主。
2.4 空间角频率的计算及测量 基于空间角频率的假目标鉴别方法与基于相差的鉴别方法思想基本一致，信号的空间角频率可通过阵元间相差直接计算得出，根据空间角频率的定义^[16]，各阵元接收信号在尖峰输出时刻的理论空间角频率为

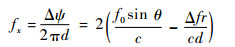(27)

而对距离欺骗干扰产生的假目标，实际的空间角频率为

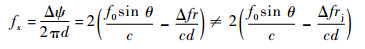(28)

实际应用中，空间角频率可通过截取各阵元同一时间的输出信号，直接进行快速傅里叶变换 (FFT) 处理测量得出，FFT处理后的频率分辨精度由阵元总数及频率间隔确定，阵元总数越多、频率间隔越大，FFT的频率分辨精度越高。
综上分析，可得出FDA-脉压雷达进行假目标鉴别的具体流程如下：
1) 相位差鉴别方法
① 利用单脉冲测角法，得到目标所在的精确方位θ_n。
② 根据匹配滤波输出，读出各输出峰值对应的距离r_n。
③ 利用式 (3)，求解各峰值输出点在各阵元间的理论相位差Δφ_n。
④ 根据IQ双通道输出，直接求取各峰值输出点的实际输出相位，求解各阵元的实际相位差Δψ_n。
⑤ 设置门限ε，若，则判定为真目标，相反，则判定为假目标。
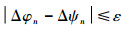
2) 空间角频率鉴别方法
① 根据相位差法中的步骤① 和步骤②，读出各峰值对应的角度、距离{θ_n, r_n}。
② 利用式 (27)，计算各峰值对应的理论空间角频率f_xn。
③ 取峰值输出时刻各阵元的输出信号，直接进行FFT处理，求得实际的空间角频率f′_xn。
④ 设置门限ε，若，则判定为真目标，相反，则判定为假目标。
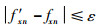
3 仿真分析 3.1 相位差法仿真 仿真数据：FDA-MIMO含2个阵元，雷达中频频率为20 MHz，带宽5 MHz，各阵元频差为1 kHz，脉宽100 μs，目标与雷达距离30 km，方位角为π/6。未释放干扰时，各对应距离上两阵元匹配滤波输出信号的相位差如图 2所示。

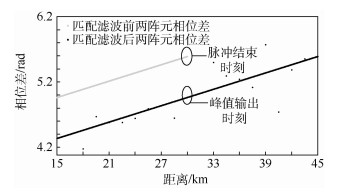图 2 回波信号在两阵元间的相位差 Fig. 2 Phase difference between two array elements of echo signal

图选项

3.1.1 间歇采样干扰信号仿真 目标利用DRFM干扰机释放间歇采样式干扰，干扰幅度为回波3倍，信号每采样10 μs转发1次，共转发5次，实验分2组，一组无移频，一组含1 MHz的正向移频，释放干扰时，2组干扰信号与回波信号的匹配滤波输出如图 3所示。

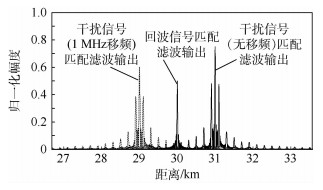图 3 间歇采样干扰信号与回波信号的匹配滤波输出 Fig. 3 Matched filtering output of interrupted-sampling jamming and echo signals

图选项

从图 3可看出，干扰信号在回波信号所在距离单元外产生了假目标，附加移频时，假目标产生位置发生前移。当接收端接收干扰与回波的混合信号时，两阵元相位差如图 4所示。

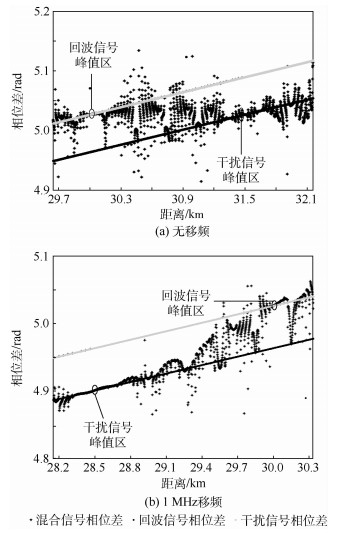图 4 回波信号、间歇采样干扰信号 (无移频和1 MHz移频) 与混合信号匹配滤波输出的阵元间相位差 Fig. 4 Matched filtering output's phase difference of echo signals, interrupted-sampling jamming signals (without any frequency shift and with 1 MHz frequency shift) and mixed signals

图选项

由图 4看出，回波信号的相位差与干扰信号的相位差随时间的变化趋势一致，但干扰附加了一定时延，峰值产生位置发生了偏移。在回波信号峰值点，混合信号相位与回波信号相位基本一致，而在干扰信号峰值点，混合信号相位与干扰信号基本一致。不同干信比 (JSR) 下，干扰信号1(不含移频)、干扰信号2(含1 MHz移频)、回波信号、混合信号1(回波与干扰1)、混合信号2(回波与干扰2) 相位差如表 1所示。
表 1 不同干信比下回波信号、间歇采样干扰信号及混合信号在两阵元间的相位差 Table 1 Phase difference between two array elements of echo, interrupted-sampling jamming and mixed signals under different JSRs

信号类型	峰值指示距离/km	目标类型	各距离相位差理论值/rad	不同干信比下相位差测量值/rad
				JSR=6 dB	JSR=9 dB	JSR=12 dB	JSR=20 dB
回波	30.0	真	5.026	5.026	5.026	5.026	5.026
干扰1	31.5	假	4.960	5.026	5.026	5.026	5.026
干扰2	28.5	假	5.089	4.901	4.909	4.909	4.909
混合1	30.0	真	5.026	5.026	5.026	5.026	5.026
混合1	31.5	假	4.960	5.026	5.026	5.026	5.026
混合2	30.0	真	5.026	5.026	5.026	5.026	5.026
混合2	28.5	假	5.089	4.909	4.901	4.901	4.901

表选项






从表 1看出，混合信号中，真实目标对应距离上，实测相差与理论相差基本一致，而假目标对应距离上，实测相差与理论相差存在0.1~0.2 rad的偏差，且该偏差对干信比不敏感。

3.1.2 重复采样干扰信号仿真 目标释放重复采样式干扰，干扰幅度为回波幅度的3倍，释放干扰时，信号采样长度5 μs，重复发送3次，共采样5次。实验分两组，一组无移频，一组含1 MHz正向移频。此时，重复采样信号可以看成3个间歇采样信号的合成信号 (各间歇采样信号采样周期20 μs，采5 μs，发5 μs，但均有一定时延，分量信号1采样之后直接转发，分量信号2为采样之后延时5 μs转发，分量信号3为延时10 μs转发)。两组干扰信号与回波信号的匹配滤波输出如图 5所示。

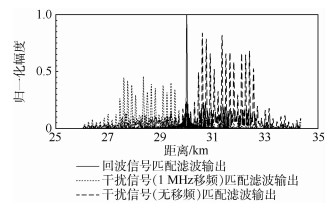图 5 重复采样干扰信号与回波信号的匹配滤波输出 Fig. 5 Matched filtering output of repeated-sampling jamming and echo signals

图选项

由图 5可看出，重复采样信号在真实目标周围产生了一定数量的假目标群 (主假目标个数与重复转发次数一致)。雷达接收重复干扰信号与回波信号的混合信号，回波信号、干扰信号、混合信号的相位差关系如图 6所示。

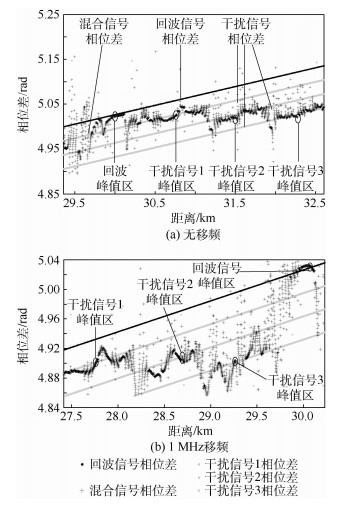图 6 回波信号、重复采样干扰信号 (无移频和1 MHz移频) 与混合信号匹配滤波输出的阵元间相位差 Fig. 6 Matched filtering output's phase difference of echo signals, repeated-sampling jamming signals (without any frequency shift and with 1 MHz frequency shift) and mixed signals

图选项

由图 6看出，在真实目标对应距离上，混合信号相位差与回波信号基本一致，而在各假目标
对应距离上，混合信号相位差与重复采样信号各分量信号基本一致，不同干信比下，回波信号、干扰信号1(无移频)、干扰信号2(1 MHz移频)、混合信号1(回波与干扰1)、混合信号2(回波与干扰2) 的相位差如表 2和图 7所示 (图 7中，实线代表无移频干扰信号，虚线代表含移频干扰信号)。

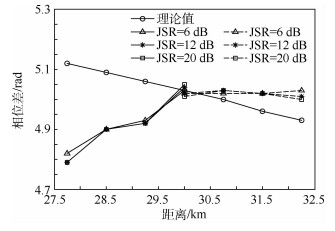图 7 不同干信比下，混合信号各峰值相位差与理论相位差对比 Fig. 7 Comparison between peak's phase difference of mixed signal and theoretic phase difference under different JSRs

图选项

表 2 不同干信比下回波信号、重复采样干扰信号及混合信号在两阵元间的相位差 Table 2 Phase difference between two array elements of echo, repeated-sampling jamming and mixed signals under different JSRs

信号类型	峰值指示距离/km	目标类型	各距离相位差理论值/rad	不同干信比下相位差测量值/rad
				JSR=6 dB	JSR=9 dB	JSR=12 dB	JSR=20 dB
回波	30.00	真	5.026	5.026	5.026	5.026	5.026
混合1	30.00	真	5.026	5.022	5.021	5.021	5.021
混合1	30.75	假	5.000	5.020	5.020	5.030	5.030
混合1	31.50	假	4.960	5.020	5.020	5.020	5.020
混合1	32.25	假	4.930	5.030	5.040	5.010	5.000
混合2	30.00	真	5.026	5.028	5.033	5.034	5.039
混合2	27.75	假	5.120	4.820	4.790	4.790	4.790
混合2	28.50	假	5.090	4.900	4.900	4.900	4.900
混合2	29.25	假	5.060	4.930	4.920	4.920	4.920

表选项






由表 2和图 7可看出，在真实目标位置处，混合信号相位差与理论相位差基本一致 (偏差随干信比增大而增大)，在假目标位置处，混合信号相位差与理论相位差存在一定差异，对无移频干扰信号，差距在0.1 rad左右，对含移频干扰信号，差距在0.15~0.40 rad之间，且相位误差对干信比不敏感。
3.2 空间角频率法仿真 仿真数据：设FDA-MIMO雷达含128个阵元 (方便FFT处理)，阵元间频差1 kHz，阵元间距0.15 cm，脉宽100 μs，目标与雷达距离30 km，方位角为π/6。间歇采样干扰参数设置与相位差法设置一致，回波与干扰信号尖峰输出时刻的理论空间角频率可通过式 (27) 计算得出，通过FFT处理测得混合信号各峰值输出时刻的空间角频率如图 8所示 (x和y分别为点的横纵坐标值)。

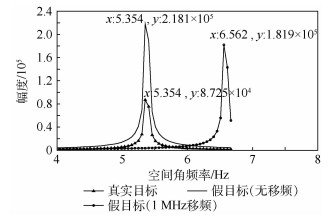图 8 回波与间歇采样干扰信号的空间角频率测量值 Fig. 8 Measured spatial frequency of echo and interrupted-sampling jamming signals

图选项

由图 8可看出，各信号均有恒定的空间角频率，混合信号各峰值输出点对应距离、理论空间角频率与实际空间角频率如表 3所示。
表 3 回波与间歇采样干扰信号的空间角频率 Table 3 Spatial frequency of echo and interrupted-sampling jamming signals

信号类型	峰值指示 距离/km	理论空间 角频率/Hz	实际空间 角频率/Hz
回波	30.0	5.34	5.354
干扰1	31.5	5.26	5.354
干扰2	28.5	5.40	6.562
注：干扰1不含移频，干扰2含1 MHz移频。

表选项






由表 3可知，除去FFT频率分辨力引起的测频误差，回波的实际角频率与理论角频率基本一致，而干扰1、干扰2实际角频率与理论角频率均存在一定差异，特别是添加移频后，角频率差异较大，可用于假目标干扰鉴别。
对重复转发式欺骗干扰，参数设置与相位差法一致，通过FFT处理测得混合信号各峰值输出时刻的空间角频率如图 9所示。

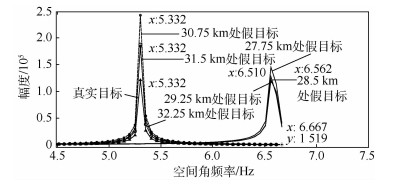图 9 回波与重复采样干扰信号的空间角频率测量值 Fig. 9 Measured spatial frequency of echo and repeated-sampling jamming signals

图选项

由图 9可知，各种干扰与回波的混合信号，在各峰值输出时刻均有恒定的空间角频率。各峰值输出点对应距离、理论空间角频率与实际空间角频率如表 4所示。
表 4 回波与重复采样干扰信号的空间角频率 Table 4 Measured spatial frequency of echo and repeated-sampling jamming signals

信号类型	峰值指示距离/km	理论空间角频率/Hz	实际空间角频率/Hz
回波	30.00	5.336	5.332
干扰1	30.75	5.300	5.332
干扰1	31.50	5.270	5.332
干扰1	32.25	5.220	5.332
干扰2	27.75	5.430	6.562
干扰2	28.50	5.400	6.510
干扰2	29.25	5.370	6.510
注：干扰1不含移频，干扰2含1 MHz移频。

表选项






由表 4可知，除去FFT频率分辨力引起的测频误差，回波的实际角频率与理论角频率基本一致，而干扰1、干扰2引起的多个假目标实际角频率与理论角频率均存在一定差异，可用于假目标干扰鉴别。
4 结论 本文基于FDA体制，提出了一种假目标干扰鉴别方法，理论推导及仿真结果表明：
1) FDA雷达中，回波信号在相邻阵元间的相位差与目标真实距离及角度呈线性关系。
2) 间歇采样、重复采样、移频等多种干扰信号产生的假目标，在FDA雷达相邻阵元间产生的相位差 (空间角频率) 与理论相位差 (空间角频率) 存在明显差异。
3) 干扰与回波信号的混合，不影响接收端相位差信息 (空间角频率信息) 的提取。
4) 干扰与回波的混合信号中，各峰值距离上相位差信息的提取精度对干信比不敏感。
综上结论，FDA雷达能够通过提取相邻阵元间的相位差 (空间角频率) 信息，实现对多种假目标干扰信号的鉴别及剔除。

参考文献

[1]	AKHTAR J.An ECCM scheme for orthogonal independent range-focusing of real and false targets[C]//Proceedings of IEEE National Radar Conference.Piscataway, NJ:IEEE Press, 2007:17-20.
[2]	SCHUERGER J, GARMATYUK D.Performance of random OFDM radar signals in deception jamming scenarios[C]//2009 IEEE Radar Conference.Piscataway, NJ:IEEE Press, 2009:221-226.
[3]	田晓. 雷达有源欺骗干扰综合感知方法研究[D]. 成都: 电子科技大学, 2013. TIAN X.Study on the methods of radar active deception jamming integrated sensing[D].Chengdu:University of Electronic Science and Technology, 2013(in Chinese).
[4]	LI J X.Signal feature analysis and experimental verification of radar deception jamming[C]//2011 IEEE CIE International Conference.Piscataway, NJ:IEEE Press, 2011:131-136.
[5]	ZHAO S S, ZHANG L R, ZHOU Y, et al. Signal fusion-based algorithms to discriminate between radar targets and deception jamming in distributed multiple radar architectures[J].IEEE Sensors Journal, 2015, 15(11): 6697–6706.DOI:10.1109/JSEN.2015.2440769
[6]	ANTONIK P, WICKS M C, GRIFFITHS H D, et al.Multi-mission multi-mode waveform diversity[C]//Proceedings of the IEEE Conference on Radar.Piscataway, NJ:IEEE Press 2006:215-217.
[7]	ANTONIK P.An investigation of a frequency diverse array[D].London:University College London, 2009:3-4.
[8]	SAMMARTINO P F, BACKER C J, GRIFFITHS H D. Frequency diverse MIMO techniques for radar[J].IEEE Transactions on Aerospace and Electronic System, 2013, 49(1): 201–222.DOI:10.1109/TAES.2013.6404099
[9]	WANG W Q. Frequency diverse array antenna:New opportunities[J].IEEE Antennas and Propagation Magazine, 2015, 57(2): 145–152.DOI:10.1109/MAP.2015.2414692
[10]	XU J W, LIAO G S, ZHU S Q.Receive beamforming of frequency diverse array radar systems[C]//Proceedings of the 31st URSI General Assembly and Scientific Symposium (URSIGASS).Piscataway, NJ:IEEE Press, 2014:1-5.
[11]	WANG W Q, SO H C. Transmit subaperturing for range and angle estimation in frequency diverse array radar[J].IEEE Transactions on Signal Processing, 2014, 62(8): 2000–2011.DOI:10.1109/TSP.2014.2305638
[12]	WANG W Q. Phased-MIMO radar with frequency diversity for range-dependent beamforming[J].IEEE Sensors Journal, 2013, 13(4): 1320–1328.DOI:10.1109/JSEN.2012.2232909
[13]	XIANG L H, LI P C, GONG Z M. Frequency diverse array radar for target range-angle estimation[J].The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2016, 35(3): 7–17.
[14]	XU J W, LIAO G S, ZHU S Q. Joint range and angle estimation using MIMO radar with frequency diverse array[J].IEEE Transactions on Signal Processing, 2015, 63(13): 3396–3410.DOI:10.1109/TSP.2015.2422680
[15]	HIGGINS T, BLUNT S D.Analysis of range-angle coupled beamforming with frequency-diverse chirps[C]//2009 International Waveform Diversity and Design Conference (WD&D).Piscataway, NJ:IEEE Press, 2009:140-144.
[16]	XU J W, LIAO G S, ZHU S Q, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J].Journal of Signal Processing, 2015(113): 9–17.
[17]	WANG X S, XIAO S P, FENG D J, et al. Modeling and simulation of modern radar and electronic warfare systems[M].Beijing: Publishing House of Electronic Industy, 2010: 139-143.
[18]	赵树杰. 雷达信号处理技术[M].北京: 清华大学出版社, 2010: 140-150. ZHAO S J. The technology of radar signal processing[M].Beijing: Tsinghua University Press, 2010: 140-150.(in Chinese)