目标跟踪领域对系统真实模式和变化参数的估计是典型的非线性、非高斯随机混合系统估计。混合系统是将系统动态分解为一定数量的运动学模型，其中每个模型的状态向量由差分或者微分方程描述。混合系统估计包含了系统对目标真实离散运动模式的估计，又包含了对目标连续状态分量的估计^[1]。由于目标机动通常是随机发生，并且机动大小未知，所以很难用单个确定的运动学模型来描述混合系统的真实运动状态。由Blom和Bar-Shalom^[2]提出的交互式多模型(Interacting Multiple Model，IMM)算法因其具有极高费效比，被广泛用于解决混合系统的估计问题。经过数十年的发展，IMM算法已经成为目标跟踪领域中的主流算法^[3-4]。
传统的IMM算法每个模型匹配的是卡尔曼滤波器(Kalman Filter, KF)或者扩展卡尔曼滤波器(Extended Kalman Filter, EKF)。KF针对线性系统，并且过程噪声和量测噪声为高斯白噪声，而EKF仅适用于弱非线性系统中滤波误差很小的情况，否则滤波初期估计误差协方差下降太快会导致滤波器不稳定甚至发散^[5]。为了满足机动目标跟踪的高精度和实时性等要求，需要根据模型的非线性、非高斯、机动性能等特性来选择适当的滤波算法。针对机动目标模型的状态方程或(和)量测方程非线性、过程噪声或(和)量测噪声非高斯的问题，Gordon等^[6]提出了粒子滤波(Particle Filter，PF)算法。
标准交互式多模型粒子滤波(Interacting Multiple Model Particle Filter，IMMPF)算法是将IMM算法和PF算法的优点结合的一种算法，其可以在非线性、非高斯随机混合系统中获得较高的估计精度^[7-10]。但PF算法存在粒子退化问题，粒子退化是指在经过有限次递推滤波后，某些粒子的权值会趋近1，而其他粒子的权值会趋近0，这样会有很大一部分采样粒子被丢弃，导致估计后验概率密度函数无法接近真实后验概率密度函数，估计精度降低。针对粒子退化问题，很多****提出了重采样方法，例如系统重采样、分层重采样、残差重采样等^[11-14]。重采样是指利用粒子更新权值信息重新获得采样粒子，利用新的支撑点集来近似真实状态后验概率密度函数。上述重采样方法会带来新的问题，即样本多样性匮乏，最严重的情况是最新的采样粒子集合中全部是一个大权值采样点的子代。标准IMMPF算法重采样过程仍然使用传统的单个模型重采样思想，仅利用本模型中的粒子和权值信息来重新获得粒子集合，而没有利用其他模型在滤波过程中获得的粒子和权值信息，样本多样性匮乏现象仍然存在。更重要的是，模型集中与目标真实模式失配的模型经过一次递推滤波后，有大量粒子的权值很小甚至为0，虽然可以通过模型更新概率来调整失配模型的所占比重，但是失配模型的粒子集合无法近似真实状态后验概率密度函数，如果目标频繁的发生机动，系统会有较大峰值误差。
本文利用各个模型中的粒子更新权值、模型更新概率和马尔可夫转移概率矩阵等信息，对每个模型中权值较小的粒子进行调整，保留需要删除粒子的部分信息，融合本模型和其他模型中拥有较大权值的粒子信息，从而将每个模型中权值较小的粒子替换成新的采样粒子，达到粒子集合中粒子多样化的目的，使系统可以获得更高的估计精度和更小的峰值误差。
1 目标跟踪建模 目标跟踪领域里，通常将机动目标的动态建模为一阶马尔可夫跳跃非线性混合系统(Jump Markov Nonlinear Hybrid System，JMNHS)。

(1)

式中：x(k)为k时刻状态向量，状态向量维数为n_x；f为状态函数；m_k^j∈M为k时刻匹配系统真实模式的第j个系统模型，j=1, 2, …, r，M为模型集合；g(m_k^j)为噪声增益矩阵；z(k)为量测向量，量测向量维数为n_z；h为系统量测函数；w(m_k^j)为基于模型m_k^j的过程噪声；v(m_k^j)为基于模型m_k^j的量测噪声；prob(m_k^j|m_k－1ⁱ)为马尔可夫转移概率，简写为π_ij；k为时刻。
定义z_1:k={z₁, z₂, …, z_k}为系统量测序列，则混合系统式(1) 的估计结果为

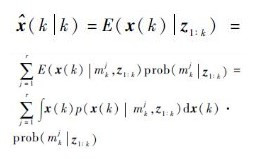(2)

式中：prob(m_k^j|z_1:k)为k时刻模型更新概率，本文用u^j(k)表示；p(x(k)|m_k^j, z_1:k)为第j个模型的状态后验概率密度函数，本文用p^j(x(k)|z_1:k)表示。p^j(x(k)|z_1:k)由以下贝叶斯步骤获得：
1) 预测

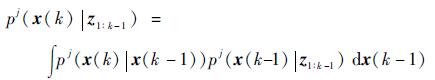(3)

式中：p^j(x(k)|x(k－1))为状态转移概率密度函数。
2) 更新

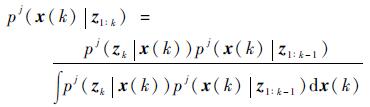(4)

式中：p^j(z_k |x(k))为似然函数，而分母中积分量只有在状态方程和量测方程是线性高斯的条件下才可以利用KF算法获得。对于非线性、非高斯系统，可以通过Monte Carlo仿真获得其近似状态后验概率密度函数，利用随机抽样方法，从p^j(x(k)|z_1:k)中抽取N个独立同分布的粒子{x_l^j(k); l=1, 2, …, N}，则式(4) 中后验概率密度函数p^j(x(k)|z_1:k)可以利用采样粒子近似表示。

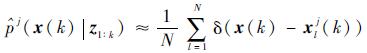(5)

式中：δ(x(k)－x_l^j(k))为狄拉克函数。
2 IMMPF及其改进算法 下面介绍标准IMMPF算法k－1→k的具体滤波步骤：
1) 输入交互阶段
混合概率：

(6)

式中：为归一化因子。
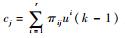
混合交互：

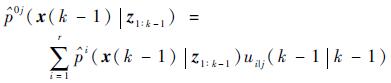(7)

2) 滤波阶段
式(7) 中抽取N个采样粒{x_l^j(k－1), w_l^j(k－1)}，表示第j个模型的第l个粒子及权重，其中，w_l^j(k－1)=1/N，l=1, 2, …, N，j=1, 2, …, r，多模型粒子总数为N_r。基于标准PF算法，选取状态转移概率密度函数p(x_l^j(k)|x_l^j(k－1))为重要性密度函数。进行如下粒子滤波步骤：
预测粒子：

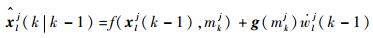(8)

式中：为从过程噪声w(m_k^j)采样的样本。
量测预测：

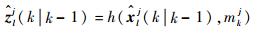(9)

量测残差：

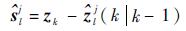(10)

残差均值：

(11)

粒子残差协方差：

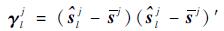(12)

粒子似然函数：

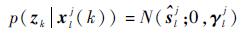(13)

式中：N(·)表示正态分布。
模型j残差协方差：

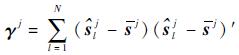(14)

模型j似然函数：

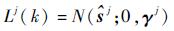(15)

模型j概率更新：

(16)

粒子权值更新：

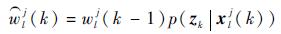(17)

粒子权值归一化：

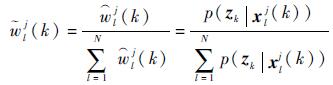(18)

重采样:设

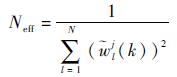(19)

表示有效样本数。设定一个采样门限N_th, 当N_eff < N_th时，则进行重采样，得到新的粒子集合及对应权值{x_l^j(k), w_l^j(k)=1/N}。
模型j状态估计：

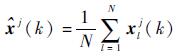(20)

3) 输出融合阶段

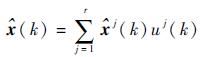(21)

下面介绍交互式多模型粒子滤波优化重采样(Interacting Multiple Model Particle Filter Optimization Resampling，IMMPFOR)算法的理论基础。
定理1??设有N个来自概率密度函数p(x)的随机变量x的采样点，随机变量x的维数为n_x，则任意采样点邻域内采样点间的平均距离^[15]为

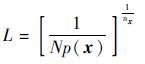(22)

IMMPFOR算法中，在获得量测信息后，利用标准IMMPF算法重采样方法，将每个模型粒子分为2个集合，称为复制组和抛弃组。将需要复制的大权值粒子放入复制组，将需要抛弃的小权值粒子放入抛弃组。根据式(22)，抛弃组中的粒子替换为新粒子：

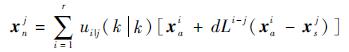(23)

式中：x_n^j为第j个模型新的采样粒子；x_aⁱ为第i个模型中复制组中的粒子；d为步长系数，其存在的目的是为了消除x_aⁱ－x_s^j的欧氏距离带来的影响；x_s^j为第j个模型抛弃组中的粒子；L^i－j为第i个模型复制组中的粒子到第j个模型抛弃组中的粒子合适步长。在获得各个模型的混合概率u_i|j(k|k)后，将每个模型中抛弃组中的粒子x_s^j替换为新粒子x_n^j，x_n^j包含了第j个模型需要复制的大权值粒子信息和第j个模型与其他模型交互后的大权值粒子信息。设每个模型采样粒子数目为N，模型数量为r，状态向量维数为n_x，复制组中采样点邻域空间在整个粒子空间的分布概率为w_l^j(k)′。在标准IMMPF算法中，量测更新后获得的各个模型粒子集合及其权值在本模型内确定，而与其他模型无关。如何确定不同模型之间步长L中的概率密度p(x)成为问题所在。通过模型概率u^j(k)，将各个模型独立的粒子集合合并为一个大的粒子集合，即将所有模型的粒子整体做归一化处理，这样每个粒子的权值w_l^j(k)′是整个粒子空间的分布概率。具体实现如下：

(24)

则被抛弃点到该采样点的合适步长为

(25)

IMMPFOR算法步骤如下：
1) 根据式(7) 获得N_r个采样粒子。
2) 根据式(8)~式(13) 逐点计算对应的状态转移函数p(x_l^j(k)|x_l^j(k－1))及似然函数p(z_k|x_l^j(k))。
3) 根据式(14)~式(16) 和式(6) 计算各个模型更新概率u^j(k)、模型混合概率u_i|j(k|k)。
4) 根据式(17) 计算粒子的更新权值。
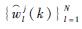
5) 根据式(18) 计算粒子归一化权值。
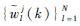
6) 根据粒子归一化权值大小将每个模型中的粒子分到复制组和抛弃组中。
7) 根据式(23)~式(25)，将每个模型抛弃组中的粒子替换为新的采样粒子，最终得到各个模型的粒子集合{x_l^j(k), w_l^j(k)=1/N}。
8) 由式(20)、式(21) 得到状态估计。
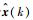
3 目标跟踪仿真分析 本文通过一个典型的目标跟踪场景对IMMPFOR算法进行仿真。使用3种目标运动模型，分别为常速度(Constant Velocity, CV)模型、协同转弯(Coordinate Turn, CT)模型和常加速度(Constant Acceleration, CA)模型。目标状态向量包含x轴和y轴位置、速度、加速度x(k)=[R_x(k), V_x(k), a_x(k), R_y(k), V_y(k), a_y(k)]^T。
1) CV模型。设T为采样时间间隔，则状态转移矩阵为

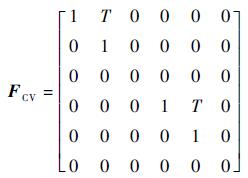过程噪声增益矩阵为

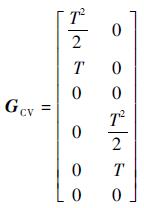2) CT模型。设w为转弯角速度，则状态转移矩阵为

过程噪声增益矩阵为

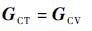3) CA模型。状态转移矩阵为

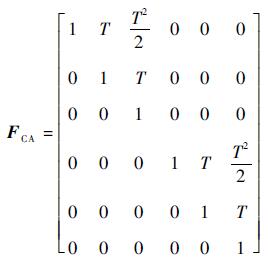过程噪声增益矩阵为

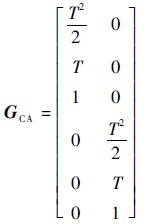过程噪声协方差为

目标量测向量包含量测距离、多普勒速度和方位角z(k)=[h₁, h₂, h₃]^T。

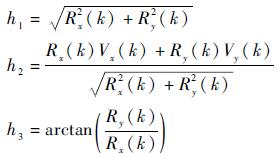观测噪声协方差阵为

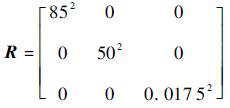设定3个模型的初始模型概率为1/3，马尔可夫转移概率矩阵为

目标初始状态为[60 000 m, －172 m/s, 0, 40 000 m, 200 m/s, 0]^T。
设定每个模型采样粒子数量N=500，采样时间间隔为T=1 s。本文通过100次Monte Carlo仿真来分析IMMPFOR算法与标准IMMPF算法性能。
定义位置均方根误差(Root Mean Square Error，RMSE)为

式中：MC=100为Monte Carlo次数；和R_{x, i}分别为第i次Monte Carlo仿真时x轴方向估计位置和真实位置。
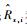
位置均方根误差的峰值和均值见表 1, 目标真实运动轨迹和估计轨迹如图 1所示。
表 1 位置均方根误差峰值和均值(N=500) Table 1 Peak and average of root mean square error in distance (N=500)

算法	RMSE/m
	峰值	均值
IMMPF	910.1	420.7
IMMPFOR	552.4	312.3

表选项

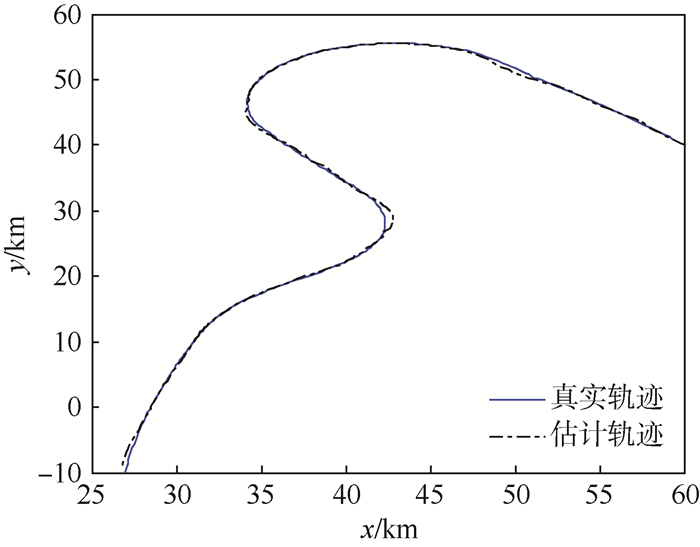图 1 机动目标真实轨迹和估计轨迹 Fig. 1 True and estimated trajectory of maneuvering target

图选项

由图 2可以看出，目标在发生机动时，例如目标做左右转弯运动时，100 s和200 s附近处使用标准IMMPF算法会产生较大的估计误差。同样的，标准IMMPF估计结果(实线)在100 s和200 s处产生较大的峰值误差，而本文提出的IMMPFOR算法(点线)较标准IMMPF算法有更小的峰值误差，整体估计性能更优。主要是因为通过线性优化重采样后，失配模型中的粒子包含了其他模型的信息。匹配模型和失配模型都拥有近似系统真实模式的粒子信息，即每个模型的状态后验概率密度函数更加近似于系统真实的状态后验概率密度函数，目标真实模式发生切换时，系统的估计精度仍然很高，均方根误差曲线收敛性更强。图 3为x轴、y轴方向的位置均方根误差曲线。图 4为x轴、y轴方向的速度均方根误差曲线。仿真结果表明，经过优化重采样，可以使系统的整体估计精度获得提升。图 5为N=2 000时的位置和速度均方根误差曲线，与图 2相比，估计结果更优，说明提高多模型粒子数目可以改善系统估计性能。

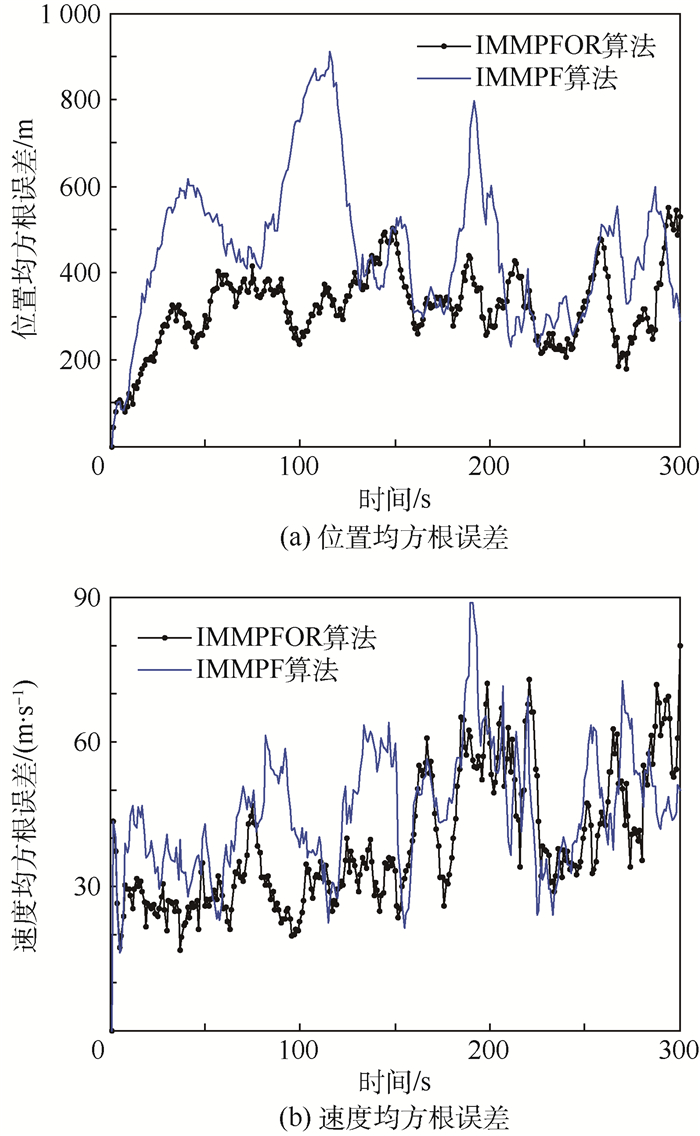图 2 位置和速度均方根误差曲线 Fig. 2 Curves of root mean square error in position and velocity

图选项

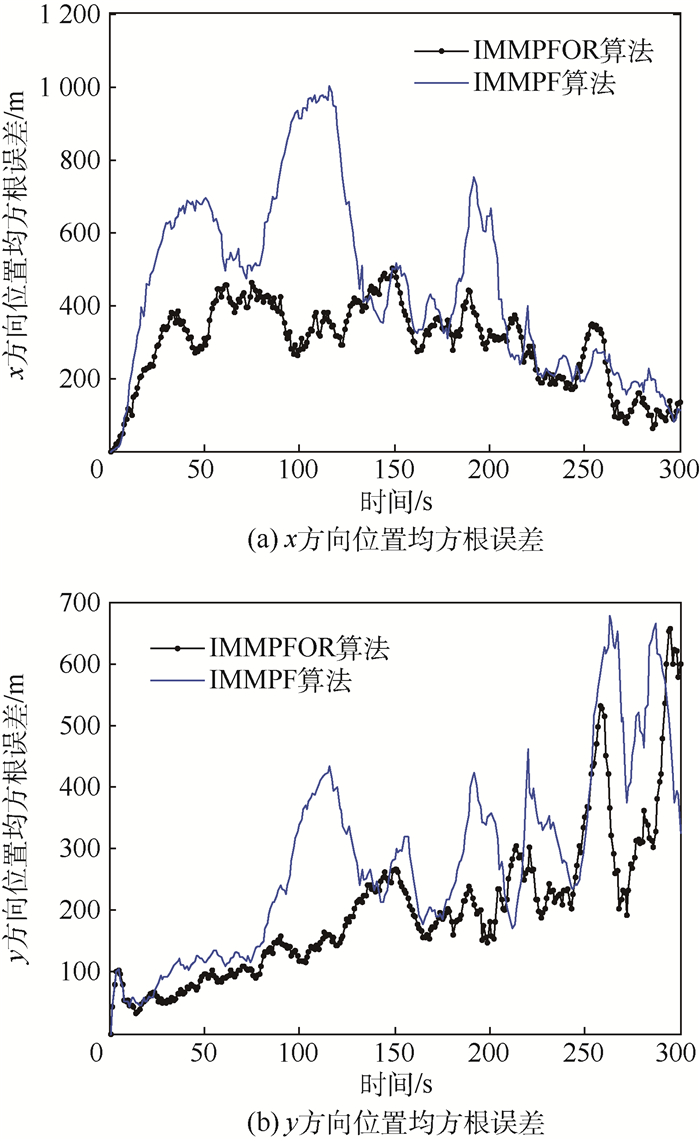图 3 x方向和y方向位置均方根误差曲线 Fig. 3 Curves of root mean square error in x and y position

图选项

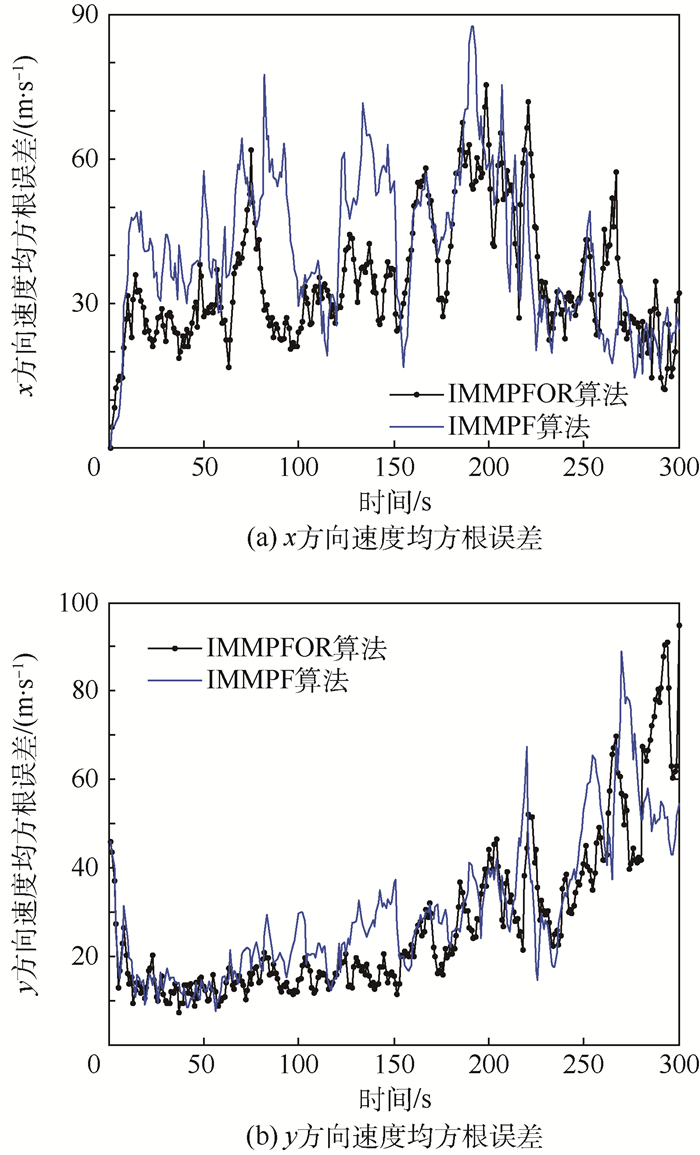图 4 x方向和y方向速度均方根误差曲线 Fig. 4 Curves of root mean square error in x and y velocity

图选项

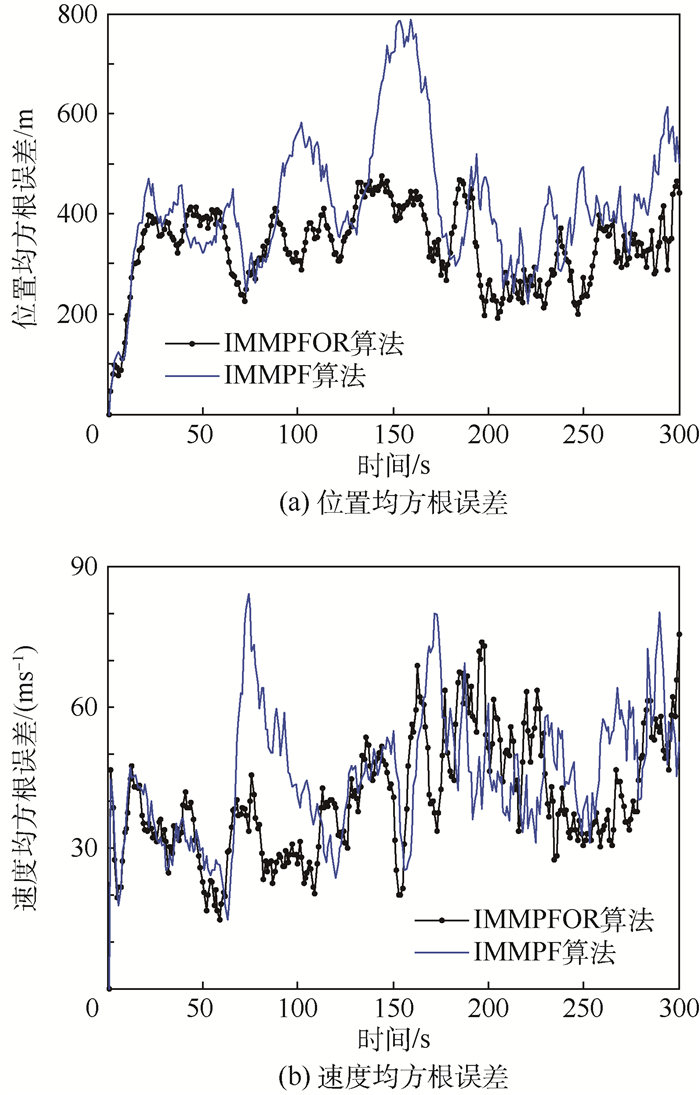图 5 N=2 000时位置和速度均方根误差曲线 Fig. 5 Curves of root mean square error in position and velocity at N=2 000

图选项

4 结论 1) 本文采用线性优化方法，将每个模型中的小权值粒子替换为新的粒子。
2) 优化后的新粒子充分利用了每个模型的先验信息和量测信息，各个模型特别是失配模型的粒子集合包含了其他模型的粒子信息。
3) 通过目标跟踪的仿真结果证明，IMMPFOR算法与标准IMMPF算法相比会获得更高的估计精度和更小的峰值误差。

参考文献

[1]	SEAH C E, HWANG I. State estimation for stochastic linear hybrid systems with continuous state dependent transitions: An IMM approach[J].IEEE Transactions on Aerospace & Electronics Systems, 2009, 45(1): 376–392.
[2]	BLOM H A P, BAR-SHALOM Y. The interacting multiple model algorithm for systems with Markovian switching coefficients[J].IEEE Transactions on Automatic Control, 1988, 33(8): 780–783.DOI:10.1109/9.1299
[3]	VIVONE G, BRACA P, HORSTMANN J.Variable structure interacting multiple model algorithm for ship tracking using HF surface wave radar data[C]// Oceans-2015.Piscataway, NJ:IEEE Press, 2015:1-8.
[4]	ZHOU W, LIU M. Robust interacting multiple model algorithms based on multi-sensor fusion criteria[J].International Journal of Systems Science, 2016, 47(1): 92–106.DOI:10.1080/00207721.2015.1029566
[5]	朱志宇. 粒子滤波算法及其应用[M].北京: 科学出版社, 2010. ZHU Z Y. Particle filter algorithm and its application[M].Beijing: Science Press, 2010.(in Chinese)
[6]	GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEEE Proceedings F-Radar & Signal Processing, 1993, 140(2): 107–113.
[7]	BOERS Y, DRIESSEN J N. Interacting multiple model particle filter[J].IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(5): 344–349.DOI:10.1049/ip-rsn:20030741
[8]	王晓, 韩崇昭. 基于混合采样的多模型机动目标跟踪算法[J].自动化学报, 2013, 39(7): 1152–1156. WANG X, HAN C Z. A multiple model particle filter for maneuvering target tracking based on composite sampling[J].Acta Automatica Sinica, 2013, 39(7): 1152–1156.(in Chinese)
[9]	王伟, 余玉揆. 多点测试的多模型机动目标跟踪算法[J].自动化学报, 2015, 41(6): 1201–1212. WANG W, YU Y K. Multi-try and multi-model particle filter for maneuvering target tracking[J].Acta Automatica Sinica, 2015, 41(6): 1201–1212.(in Chinese)
[10]	MCGINNITY S, IRWIN G W. Multiple model bootstrap filter for maneuvering target tracking[J].IEEE Transactions on Aerospace & Electronics Systems, 2000, 36(3): 1006–1012.
[11]	VAN DER MERWE R, DOUCET A, DE FREITAS N, et al. The unscented particle filter[J].Advances in Neural Information Processing Systems, 2000, 13: 584–590.
[12]	MUSSO C, OUDJANE N, LE GRAND F.Improving regularized particle filters[M]//DOUCET A, DE FREITAS N, GORDON N.Sequential Monte Carlo method in practice.New York:Springer-Verlag, 2001:247-271.
[13]	TANIZAKI H.Nonlinear filters based on Taylor series expansion [M]// TANIZAKI H.Nonlinear filters:Estimation and applications.Berlin:Springer, 1993, 25(6):81-88.
[14]	LIU J S, CHEN R. Sequential Monte Carlo methods for dynamic systems[J].Journal of the American Statistical Association, 1998, 93(443): 1032–1044.DOI:10.1080/01621459.1998.10473765
[15]	邹国辉, 敬忠良, 胡洪涛. 基于优化组合重采样的粒子滤波算法[J].上海交通大学学报, 2006, 40(7): 1135–1139. ZOU G H, JING Z L, HU H T. A particle filter algorithm based on optimizing combination resampling[J].Journal of Shanghai Jiaotong University, 2006, 40(7): 1135–1139.(in Chinese)