伴随控制理论技术的发展,AFS控制律设计方法经历了经典控制理论和现代控制理论阶段。目前,理论研究以现代控制理论方法为主,并呈现出方法多样化、多种方法融合的特点。其中,线性二次型高斯(LQG)方法是气动弹性主动控制备受关注的一种方法,在20世纪90年代,曾广泛地得到研究与讨论[2-4]。LQG方法使用最优滤波器做状态估计,可以在控制过程中考虑控制输入与受控对象输出中的随机噪声干扰,该特点非常适用于气动弹性AFS和阵风减缓问题[4-5]。但是,LQG控制律的高阶次以及控制效果对模型精度的依赖,使其工程应用受到限制。国内外大量研究致力于改善LQG方法的工程适用性[2-5]。
近年来,滑模控制(SMC)方法出现在气动弹性研究领域,并逐渐引起关注。国际上,Na等[6-7]尝试使用滑模观测器做状态估计,实现气动弹性主动控制,并与LQG方法对比取得较满意的结果。有关滑模控制气动弹性应用的最新进展见文献[8]。国内方面,西北工业大学张惠媛、史忠科[9]将滑模变结构控制方法用于飞机抛物响应控制,较早地把这种方法用于气动弹性相关学科。笔者在前期工作中讨论了SMC方法应用于二维机翼AFS的控制机理[10-11],并使用Utkin滑模观测器实现了二维机翼的AFS[12]。这些研究表明,SMC方法适用于气动弹性主动控制,且该方法具有较强的鲁棒性[6-12]。特别是基于滑模观测器的方法,同LQG方法一样可以在控制设计中考虑随机噪声干扰,具有应用前景。但是这类观测器的常规设计过程较为繁琐,需多次坐标变换将受控对象方程转换为标准型[13]。当模型阶次较高时,有时难以设计出观测器参数。现有研究多见于二维机翼对象,暂未见用于三维真实机翼。
非定常气动力求解技术是气动弹性研究的基础。国内外关于SMC方法的气动弹性应用研究多以二维机翼为对象,其中非定常气动力多采用简化的准定常气动力理论或西奥道森频域气动力[6-14]。当对象扩展到三维机翼时,简化的气动力方法不再适用,非定常气动力理论发展了时域和频域2类方法。时域求解基于CFD技术,理论精度高,但计算耗时长,目前尚不适用于对实时性要求高的AFS控制和工程应用。以偶极子格网法为代表的频域非定常气动力方法兴起于20世纪60~70年代,因其效率高、工程适用性强,迅速在亚声速非定常气动力工程计算和气动弹性应用方面占据了主导地位。2003年,美国****Yurkovich[15]发表了一篇关于非定常气动力的重要综述,其中认为偶极子格网法仍将是未来若干年气动弹性领域亚声速非定常气动力工程应用的主流。
本文以二次型最优控制方法和滑模观测器为基础,借鉴Na等[6-7]的思路,尝试新的滑模观测器设计流程和控制律设计方法。首先,利用二次型最优控制LQG方法设计状态反馈矩阵和观测器增益;然后,对比LQG方法与滑模观测器方法的控制框图,提出该观测器新的设计流程;最后,利用气动弹性系统的物理背景,对控制律进行分析与处理,使该方法理论上可以用于实践。本文的非定常气动力采用经典的偶极子格网法,结合有理函数拟合技术将其拓展至时域,从而能够将SMC方法的AFS应用推广至三维真实机翼模型,更具有一般性和工程意义。
1 模型描述 1.1 模型动力学特性 以某机翼风洞试验模型为对象(见图 1),研究其AFS控制律设计方法。该模型具有2个后缘控制面,分别由2个相同规格电机驱动。机翼为双梁结构,前、后梁共布置3个加速度传感器。该模型曾用于阵风响应减缓风洞试验研究[16]。
 |
| 图 1 某机翼风洞试验模型结构示意图 Fig. 1 Schematic of wind-tunnel test model of a wing |
| 图选项 |
建立机翼的结构动力学有限元模型,由梁单元模拟机翼主梁刚度特性,集中质量单元模拟模型的质量分布。经地面振动试验校核与调试,用于颤振分析的模型前6阶弹性模态(除去面内模态)频率如表 1所示。
表 1 动力学模型模态列表(翼根固支约束) Table 1 List of vibration modes of dynamic model (cantilever restriction)
| 序号 | 模态名称 | 模态频率/Hz | 试验值/Hz |
| 1 | 一阶弯曲 | 1.61 | |
| 2 | 二阶弯曲 | 6.21 | 6.19 |
| 3 | 一阶扭转 | 14.75 | 14.85 |
| 4 | 三阶弯曲 | 16.48 | 16.65 |
| 5 | 四阶弯曲 | 27.60 | 27.91 |
| 6 | 二阶扭转 | 33.71 |
表选项
1.2 运动方程建立 气动弹性系统无阻尼一般运动方程为[14]
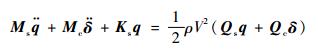 | (1) |
式中:M、K和Q分别为质量矩阵、刚度矩阵和广义非定常气动力矩阵;q和δ分别为广义自由度坐标向量和舵偏自由度向量;ρ为气流密度;V为空气来流速度;下标s表示与结构自由度相关,c表示与控制自由度相关。
采用偶极子格网法计算频域非定常气动力,由最小状态法有理函数拟合(滞后根取正)可得[14, 17]
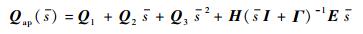 | (2) |
式中:Qap为气动力有理函数拟合矩阵;Γ为气动力滞后根对角阵;H、E和Qi(i=1, 2, 3) 为拟合系数矩阵;I为单位矩阵;s为无量纲的拉氏变量。
取加速度过载为输出,输出方程为
 | (3) |
式中:nz为z向加速度过载向量;g为重力加速度;Φ为模态矩阵。
联立式(1)~式(3),可得
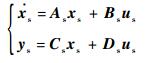 | (4) |
式中:x为状态变量;矩阵A、B、C和D为系数矩阵;u为系统输入;y为系统输出。
取δ为舵偏角向量,xa为气动力增广向量,则有
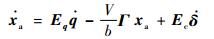 | (5) |
式中:b为参考半弦长。
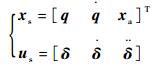 |
电机的动态特性由三阶传递函数模拟,参数经测定,具体形式如下:
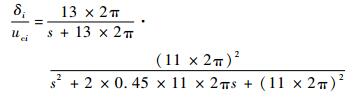 |
式中:uci为电机输入。
将电机动态特性的三阶传递函数表示为状态空间方程的形式:
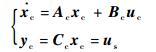 | (6) |
将式(4) 与式(6) 联立,得到广义受控对象:
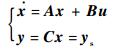 | (7) |
式中:
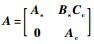
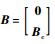
2 理论方法 2.1 线性二次型最优控制 考虑受控对象的状态空间一般运动方程为
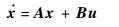 | (8) |
线性二次最优控制,即系统状态方程是线性的,指标函数J是状态变量和控制变量二次型积分。
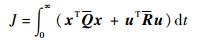 | (9) |
式中:Q和R为加权阵。
最优控制设计要寻找一个状态反馈控制律:
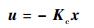 | (10) |
式中:Kc为反馈增益阵。
式(10) 使式(9) 性能指标最优化[15]。线性二次调节问题对上述最优控制有唯一解,归结为代数黎卡提方程求解。
 | (11) |
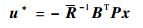 | (12) |
式中:u*为最优控制律;P为黎卡提方程的解。
状态反馈控制的实现依赖于系统状态变量是可测量的。而气动弹性系统状态变量通常为广义坐标,不具有明确的物理含义。因此,最优控制的实现需要状态观测器。
LQG方法使用最优滤波器做状态估计,可以考虑随机噪声干扰。考虑具有随机性的系统:
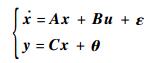 | (13) |
式中:ε和θ为不相关、零均值白噪声向量,且有
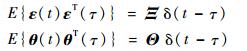 |
其中:Ξ为与ε对应的白噪声矩阵;Θ为与θ对应的白噪声矩阵;δ(t)为dirac函数。
最优滤波器的一般形式为
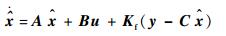 | (14) |
式中:Kf为滤波器增益矩阵;
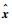
最优滤波器设计亦归结为黎卡提方程求解:
 | (15) |
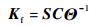 | (16) |
式中:S为最优滤波器的黎卡提方程的解。
由分离原理,LQG问题可分离为最优状态反馈设计和最优状态滤波估计问题[18],最终框图如图 2所示。
 |
| 图 2 LQG方法的估计器实现框图 Fig. 2 Realization block diagram of estimator of LQG method |
| 图选项 |
2.2 滑模观测器 本文使用的观测器是由Walcott与?ak提出的一种具有SMC特点的状态观测器[13],其状态估计误差满足滑模运动渐近稳定性,观测器的输入具有SMC的开关特性。该观测器的一般形式为
 | (17) |
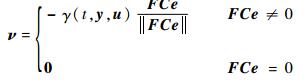 | (18) |
式中:G为使矩阵A0=A-GC具有稳定特征值的增益矩阵;P为满足A0的Lyapunov方程的矩阵;F为满足式(19) 约束的矩阵;ν为滑模观测器的控制切换输入;e=
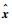
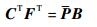 | (19) |
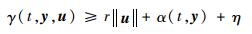 | (20) |
式中:r为可知标量;α为可知函数;η为正标量。
假设式(13) 中的随机白噪声向量满足式(21),则
 | (21) |
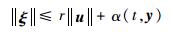 | (22) |
因随机白噪声有界,故满足式(22) 的r与α存在。
该观测器常规设计的难点与关键在于G、P矩阵的确定,并且要求满足式(19) 约束的F矩阵存在。文献[13]提供了算法与说明,但其参数矩阵计算非常繁琐,需多次坐标变换。对比式(17) 与式(14) 不难发现,该滑模观测器与最优滤波器相比增加了滑模控制切换输入项。当v=0时,式(17) 将退化为式(14),形式上与最优滤波器兼容。因此,这里提出一种简化的设计流程:
1) 对式(13) 的一般运动方程设计最优滤波器,并令滤波器增益Kf为滑模观测器的G矩阵。
2) 寻找满足矩阵A0=A-GC的Lyapunov方程的Lyapunov矩阵对(P, Q0)。
 | (23) |
3) 利用式(19) 约束条件,以P、B矩阵的乘积代替滑模观测器中的F、C矩阵乘积项。
该设计流程不需受控对象方程坐标变换,参数矩阵的求解可应用成熟的商业软件,便于实现。但是需注意,该流程理论上无法保证F矩阵存在。由于F、C矩阵以乘积的形式出现,得到的控制系统实际为半输出反馈、半状态反馈。下文将利用气动弹性的物理背景对控制系统加以处理,使半状态反馈部分的系统状态变量可测。按照上述流程与思路,得到半输出反馈、半状态反馈滑模控制器的闭环系统如图 3所示。
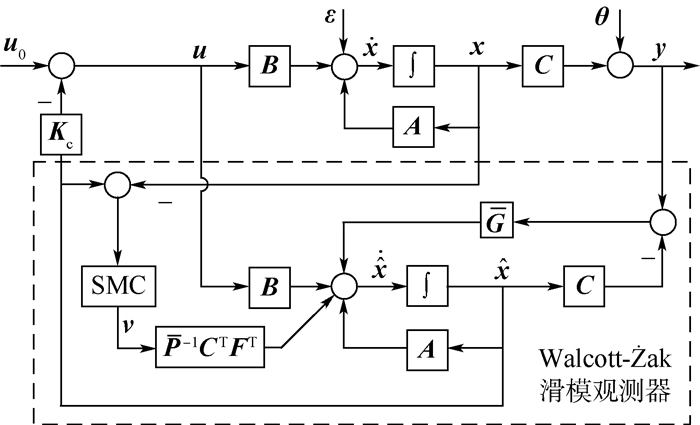 |
| 图 3 滑模观测器方法的估计器实现框图(半输出反馈) Fig. 3 Realization block diagram of estimator of sliding mode observer (half output feedback) |
| 图选项 |
3 数值仿真 以式(9) 为目标的最优控制问题中,加权矩阵Q、R的选取对设计结果有一定影响。Q反映了对系统状态响应的约束,R反映了对控制输入能量的约束(具体到本文对象,R与舵偏幅值相关)。以控制舵偏输入满足常规舵偏量级为原则,本文的Q、R参考值调试选取如下:
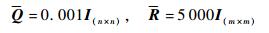 |
式中:n与m对应于x与u的维数。在本文的滑模观测器中,标量函数γ需要确定,其取值应满足式(20) 约束。为简化设计,本文γ取为常值0.5。
3.1 无噪声干扰时的控制效果 系统开环颤振速度为37 m/s,在42 m/s速度状态进行AFS设计与仿真,临界稳定速度提高量约13.5%。如图 2、图 3所示构造闭环系统模型,在系统输入端u0处施加图 4所示脉冲激励。不考虑噪声干扰,时域仿真结果如图 5~图 7所示。
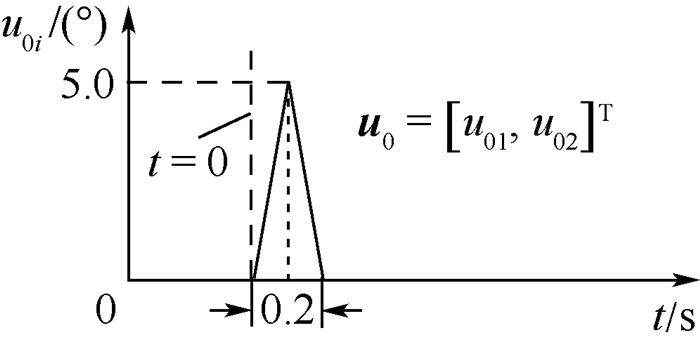 |
| 图 4 舵偏指令的三角脉冲激励 Fig. 4 Flap deflection command excited by delta impulse |
| 图选项 |
 |
| 图 5 无控状态开环系统输出响应 Fig. 5 Open-loop output responses of system without control |
| 图选项 |
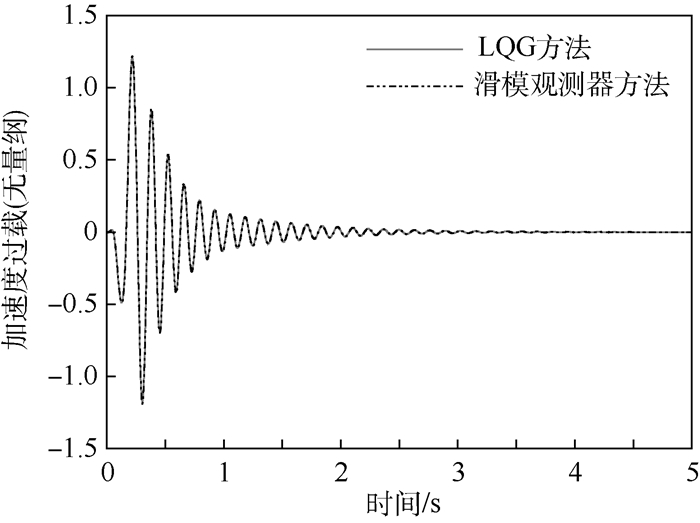 |
| 图 6 有控状态闭环系统输出响应(1#传感器) Fig. 6 Closed-loop output responses of system with control (Sensor No.1) |
| 图选项 |
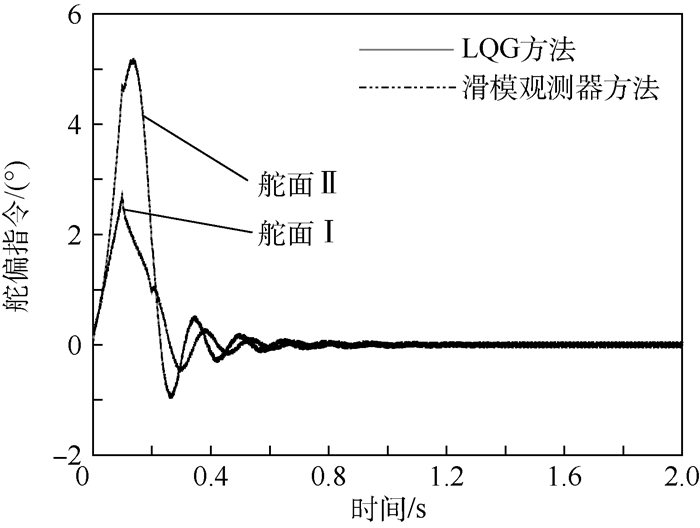 |
| 图 7 有控状态的舵偏指令时间历程 Fig. 7 Time histories of flap deflection command with control |
| 图选项 |
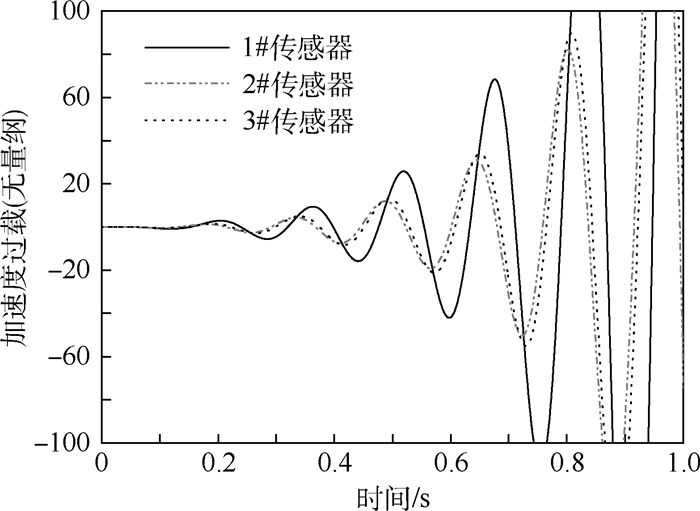
从仿真结果来看,开环系统在脉冲激励输入下振荡发散,是不稳定的。接入AFS控制系统,闭环系统稳定,2种方法均有效果。并且在无噪声干扰时,LQG方法与滑模观测器方法设计的控制律得到几乎相同的时域响应。
3.2 随机噪声扰动下的控制效果对比 在系统控制输入指令中加入式(21) 形式的状态变量随机噪声干扰ε。其中,ξ取为均匀分布、随机白噪声向量,扰动幅度±0.3°。计算有噪声干扰情况下的闭环时域响应。仿真速度状态仍取为42 m/s(高于颤振速度13.5%)。
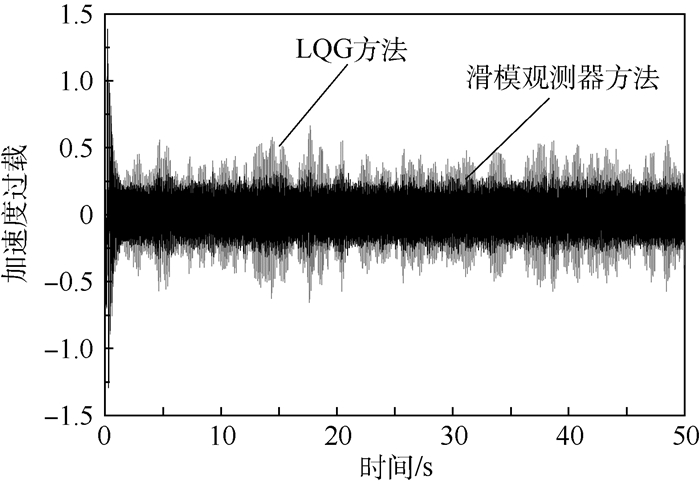
图 8结果表明,状态变量有噪声干扰时,2种方法的AFS控制系统均使系统稳定。滑模观测器方法的系统响应幅值明显小于LQG方法,表现出更好的抗噪能力。图 9给出外侧舵面的时间响应历程,2种方法的控制舵偏幅度相当,没有明显差异。但细致观察某一时间段,滑模观测器方法的控制输入中带有滑模观测器产生的高频信号,这是滑模观测器方法与LQG方法的主要不同。
 |
| 图 8 输入指令有噪声干扰时的闭环响应(1#传感器) Fig. 8 Closed-loop responses of system with noise disturbance in input commands (Sensor No.1) |
| 图选项 |
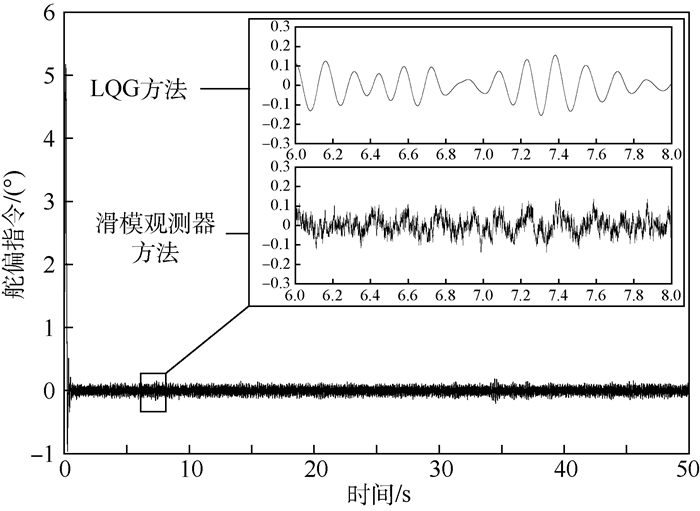 |
| 图 9 输入指令有噪声干扰时的舵偏指令时间历程(舵面Ⅱ) Fig. 9 Time histories of flap deflection command with noise disturbance in input commands (FlapⅡ) |
| 图选项 |
3.3 控制系统分析与全输出反馈 3.2节数值仿真结果表明,图 3所示基于滑模观测器的控制系统比LQG方法具有更好的抗噪能力。但是,半输出反馈、半状态反馈的控制系统仍然需要状态变量作为控制器输入,暂无法用于实际。有必要对控制系统做改进,使其输入全部可测量。
滑模观测器式(18) 的控制切换可以表示为
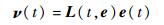 | (24) |
式中:L(t, e)为控制切换的系数矩阵函数。
式(24) 为非线性关系,但每个时刻滑模切换指令v仍可看作状态估计误差e的线性组合。可以认为ν由与e相关的各阶分量组成。定义某个时域区间各阶状态变量对滑模切换指令的贡献量为
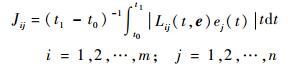 | (25) |
式中:Lij为矩阵L中的元素;ej为状态估计误差分量。指标Jij实际上反映了各阶状态分量在滑模控制指令中所占有的比重,计算结果见图 10。
 |
| 图 10 各阶状态变量对滑模观测器输入指令贡献量 Fig. 10 Contributions of different-order state variables to input commands of sliding mode observer |
| 图选项 |
计算结果可见,各状态变量对滑模观测器输入指令的贡献量不同,第18阶、20阶状态变量是舵面Ⅰ滑模指令的主项;第19阶、21阶状态变量是舵面Ⅱ滑模指令的主项。这几阶状态变量恰具有明确的物理含义(第17~20阶状态变量分别对应于舵面Ⅰ和舵面Ⅱ的角速度、舵面Ⅰ和舵面Ⅱ的角加速度),因而是可以测量的。由此可将图 3控制律结构近似改写为全输出反馈形式,见图 11。
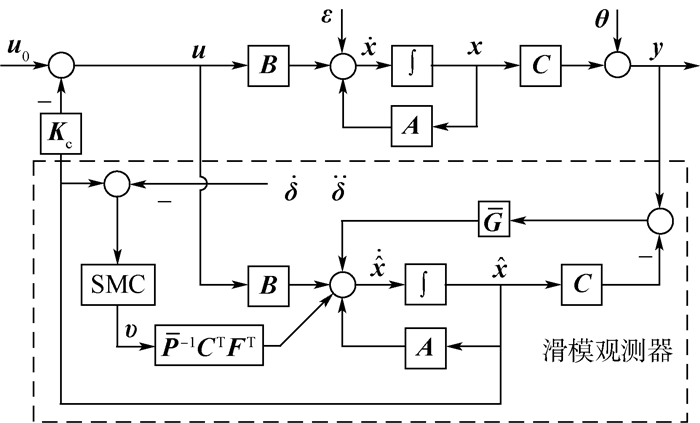 |
| 图 11 滑模观测器方法的全输出反馈实现 Fig. 11 Full output feedback realization of sliding mode observer |
| 图选项 |
采用全输出反馈形式滑模观测器控制结构,在系统控制舵偏指令输入端加入-0.3°~+0.3°噪声信号,同时在系统输出端加入-0.2 g~+0.2 g噪声信号。系统时域响应对比如图 12所示(系统输入、输出信号均有噪声)。可见,滑模观测器控制仍然有效,且动态响应的平稳性优于LQG方法。
 |
| 图 12 全输出反馈控制下的输入、输出均有噪声时域响应对比(1#传感器) Fig. 12 Comparison of time domain responses of system with noise disturbance in both inputs and outputs under full output feedback control (Sensor No.1) |
| 图选项 |
本文数值仿真迭代均采用0.001 s时间步长,模拟闭环物理系统1 kHz采样率情形。该采样率对于目前的PCB传感器使用带宽而言是可以物理实现的。由于控制指令输入端已考虑舵机系统的动态特性,若不计数据传输过程中的系统延时,闭环系统的实时性主要取决于控制指令解算的实时性。基于当前的计算机硬件求解速度,参考以往同类型气动弹性试验测控系统的物理实现经验[16],试验条件下使控制指令解算速度满足采样率跟随性要求是可行的。
4 结论 1) 改进的滑模观测器设计流程简单,方法有效,可实现三维机翼的AFS控制律设计。
2) 无噪声干扰时,该滑模观测器控制将退化为LQG的效果;有噪声干扰时,该方法在抵抗输入、输出噪声方面与LQG方法相比具有优势。
3) 利用气动弹性物理背景,可使滑模观测器具有全输出反馈形式,从而理论上可以实现。
参考文献
| [1] | THOMPSON G O, KASS G J. Active flutter suppression-An emerging technology[J].Journal of Aircraft, 1972, 9(3): 230–235.DOI:10.2514/3.58962 |
| [2] | MUKHOPADHYAY V.Flutter suppression digital control law design and testing for the AFW wind-tunnel model:AIAA-1992-2095[R].Reston:AIAA, 1992. |
| [3] | NISSIM E. Reduction of aerodynamic augmented states in active flutter suppression systems[J].Journal of Aircraft, 1991, 28(1): 82–93.DOI:10.2514/3.45995 |
| [4] | MAHESH J K, STONE C R, GARRARD W L, et al. Control law synthesis for flutter suppression using linear quadratic Gaussian theory[J].Journal of Guidance, Control, and Dynamics, 1981, 4(4): 415–422.DOI:10.2514/3.56094 |
| [5] | 吴志刚, 杨超. 主动气动弹性机的颤振主动抑制与阵风减缓研究[J].机械强度, 2003, 25(1): 32–35. WU Z G, YANG C. Investigation on active flutter suppression and gust alleviation for an active aeroelastic wing[J].Journal of Mechanical Strength, 2003, 25(1): 32–35.(in Chinese) |
| [6] | NA S, LIBRESCU L, MARZOCCA P, et al.Aeroelastic response of flapped wing systems using robust estimation methodology:AIAA-2004-1673[R].Reston:AIAA, 2004. |
| [7] | KIM K W, LEE B, NA S, et al.Comparative analysis of control performances applied to a 3-DOFs nonlinear supersonic lifting surface:AIAA-2008-1724[R].Reston:AIAA, 2008. |
| [8] | LEE K W, SINGH S N. Robust higher-order sliding-mode finite-time control of aeroelastic systems[J].Journal of Guidance, Control, and Dynamics, 2014, 37(5): 1664–1670.DOI:10.2514/1.G000456 |
| [9] | ZHANG H Y, SHI Z K. Variable structure control of catastrophic course in airdropping heavy cargo[J].Chinese Journal of Aeronautics, 2009, 22(5): 520–527.DOI:10.1016/S1000-9361(08)60135-1 |
| [10] | 宋晨, 吴志刚, 杨超. 二元机翼滑模变结构控制颤振主动抑制[J].北京航空航天大学学报, 2010, 36(11): 1400–1403. SONG C, WU Z G, YANG C. Sliding mode variable structure control of flutter suppression for a two-dimensional wing[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(11): 1400–1403.(in Chinese) |
| [11] | YANG C, SONG C, WU Z G, et al. Application of output feedback sliding mode control to active flutter suppression of two-dimensional airfoil[J].Science China:Technological Sciences, 2010, 53(5): 1338–1348.DOI:10.1007/s11431-010-0099-z |
| [12] | SONG C, WU Z G, YANG C.Active flutter suppression of a two-dimensional airfoil based on sliding mode control method[C]//The 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, 2010. |
| [13] | EDWARDS C, SPURGEON S K. Sliding mode control:Theory and applications[M].London: Taylor & Francis, 1998. |
| [14] | 杨超, 吴志刚, 万志强, 等. 飞行器气动弹性原理[M].北京: 北京航空航天大学出版社, 2011. YANG C, WU Z G, WAN Z Q, et al. Principles of aeroelasticity for air vehicles[M].Beijing: Beihang University Press, 2011.(in Chinese) |
| [15] | YURKOVICH R. Status of unsteady aerodynamic prediction for flutter of high-performance aircraft[J].Journal of Aircraft, 2003, 40(5): 832–842.DOI:10.2514/2.6874 |
| [16] | 陈磊, 吴志刚, 杨超, 等. 多控制面机翼阵风减缓主动控制与风洞试验验证[J].航空学报, 2009, 30(12): 2250–2256. CHEN L, WU Z G, YANG C, et al. Active control and wind tunnel test verification of multi-control surface wing for gust alleviation[J].Acta Aeronoutica et Astronautica Sinica, 2009, 30(12): 2250–2256.DOI:10.3321/j.issn:1000-6893.2009.12.002(in Chinese) |
| [17] | 宋晨, 杨超, 吴志刚. 3种气动弹性状态空间建模方法的对比[J].航空学报, 2007, 28(Sup.): S81–S86. SONG C, YANG C, WU Z G. Comparison of three aeroelastic state-space modeling methods[J].Acta Aeronoutica et Astronautica Sinica, 2007, 28(Sup.): S81–S86.(in Chinese) |
| [18] | 吴敏, 桂卫华, 何勇. 现代鲁棒控制[M].2版长沙: 中南大学出版社, 2006. WU M, GUI W H, HE Y. Modern robust control[M].2nd edChangsha: Central South University Press, 2006.(in Chinese) |
