作为主动流动控制技术的一种,微射流(MJ)主要是流体通过微型喷口喷出并与来流耦合而实现流动控制的一种方法,由于喷口直径较小,通常不大于1 mm,因此被称为微射流。Ryszard等最早提出了利用定常MJ与超声速来流作用产生的流向涡实现对SWBLI的控制,结果表明采用MJ控制减小了分离区尺寸,削弱了激波振荡幅度[1-3]。Ali等利用粒子成像测速(PIV)和背景导向纹影技术就不同注入压比(MJ注入总压/来流总压)下直径为0.4 mm的MJ与超声速来流作用特性进行了研究,他们认为MJ与来流作用产生的斜激波倾角与注入压比呈线性关系,且间距较小的MJ分布会削弱所产生的流向涡强度[4-7]。在此基础上,他们又对MJ作用下马赫数为2的来流在24°压缩拐角引发的SWBLI进行了实验研究,当注入压比增加至3时可以将其在分离区造成的壁面压强波动最大削减约50%[8-9]。Verma等则进一步研究了90°垂直注入MJ与45°倾斜注入MJ分别对SWBLI的影响情况,认为对壁面压强波动起到相同的抑制效果时,垂直注入MJ需要的注入总压更小,更具优势[10-11]。另外,Souverein和Debiève通过实验说明了展向倾斜45°、直径为0.8 mm的MJ对SWBLI引发的分离有抑制作用,并给出了MJ作用下分离区示意图[12-13]。除以上基础研究以外,Young等则把MJ运用到了超声速进气道的流动控制中,认为在将流量为进气道流量1.5%的射流被布置在正激波分叉区内后总压恢复提升了3.5%,畸变指数下降了35%[14]。这些研究都在一定程度上验证了MJ的流动控制潜力,但是其控制机理尚不明晰。比如,现有研究表明,超临界MJ会对超声速来流形成阻挡作用并与之耦合产生流向涡对,而改变注入压比又会影响MJ与来流的相互作用程度,最终造成控制效果各有不同。但不同注入压比MJ对主流如何起到的控制作用,下游流场又是如何变化?这些问题在已有的研究中很难找到。
鉴于MJ在流动控制领域的广阔应用前景及其控制机理尚不明确的研究现状,本文以压缩拐角作为流场模型,对不同注入压比MJ作用下的超声速流场进行了数值模拟,研究MJ在不同注入压比下对边界层的控制作用以及对拐角附近激波的控制作用,并在控制机理上进行了探索性研究。
1 计算模型、数值方法及算例验证 1.1 计算模型和数值方法 计算模型为常规压缩拐角模型,如图 1(a)所示,其中X方向为流向,Z方向为展向,各尺寸已在图中标出。如图 1(b)所示,MJ轴线位于(-50,0,-5) mm处,喷嘴出口与壁面齐平,喷射方向垂直于来流。MJ为收缩型喷管,形状尺寸如图 1(c)所示,喷嘴出口直径D为1 mm。边界条件如图 1(a)、图 1 (b)所示。来流参数及边界层厚度见表 1,各方案MJ入口参数及出口平均马赫数见表 2,其中各方案中MJ均为欠膨胀状态。利用注入压力与来流总压的比值将注入压力进行无量纲化,即得到注入压比。
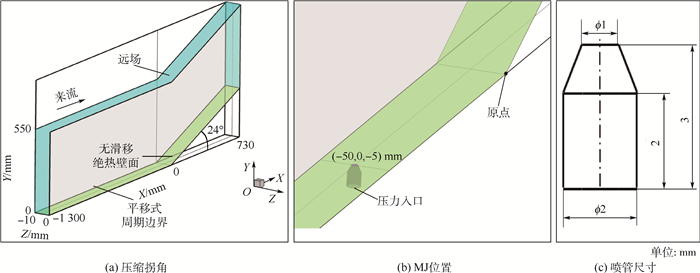 |
| 图 1 计算模型 Fig. 1 Calculation model |
| 图选项 |
表 1 来流参数及边界层厚度 Table 1 Incoming flow parameters and boundary layer thickness
| 参数 | 来流总压/kPa | 来流总温/K | 来流马赫数 | 单位雷诺数/(107 m-1) | 边界层厚度/mm |
| 数值 | 680 | 265 | 2.9 | 6.5 | 15.4 |
表选项
表 2 各方案MJ入口参数及出口平均马赫数 Table 2 Inlet parameters and average outlet Mach number of MJ in different schemes
| 方案 | 入口总压/kPa | 注入压比 | 入口总温/K | 出口平均马赫数 |
| No control | 265 | |||
| Case 1 | 78 | 0.11 | 265 | 0.84 |
| Case 2 | 108 | 0.16 | 265 | 0.86 |
| Case 3 | 308 | 0.45 | 265 | 0.86 |
| Case 4 | 408 | 0.60 | 265 | 0.86 |
| Case 5 | 680 | 1 | 265 | 0.86 |
| ??注:No control为未加MJ方案。 | ||||
表选项
所有计算方案均采用布局形式一致的结构网格,如图 2所示。MJ采用O-Block划分方式。为了获得MJ周围和拐角区域的流动细节,近壁面、MJ附近、拐角处采用网格加密。本文通过Fluent软件对雷诺平均Navier-Stokes方程进行数值模拟,湍流模型为Realizable k-ε,此外,黏性底层的求解对SWBLI流场结构模拟至关重要,为提高其准确性,这里采用Enhanced Wall Treatment壁面函数。此壁面函数要求y+≈1才可确保对黏性底层进行求解,为保证此值,将第1层节点布置在距离壁面0.001 mm处。y+≈1会在近壁面引入大长宽比网格而不利于计算收敛,所以在求解过程中采用CAFSM(Convergence Acceleration For Stretches Meshes)方法改善这种状况并加速收敛速度。鉴于此方法对初场要求较高,因此计算前利用多重网格初始化(FMG)技术以满足其要求。
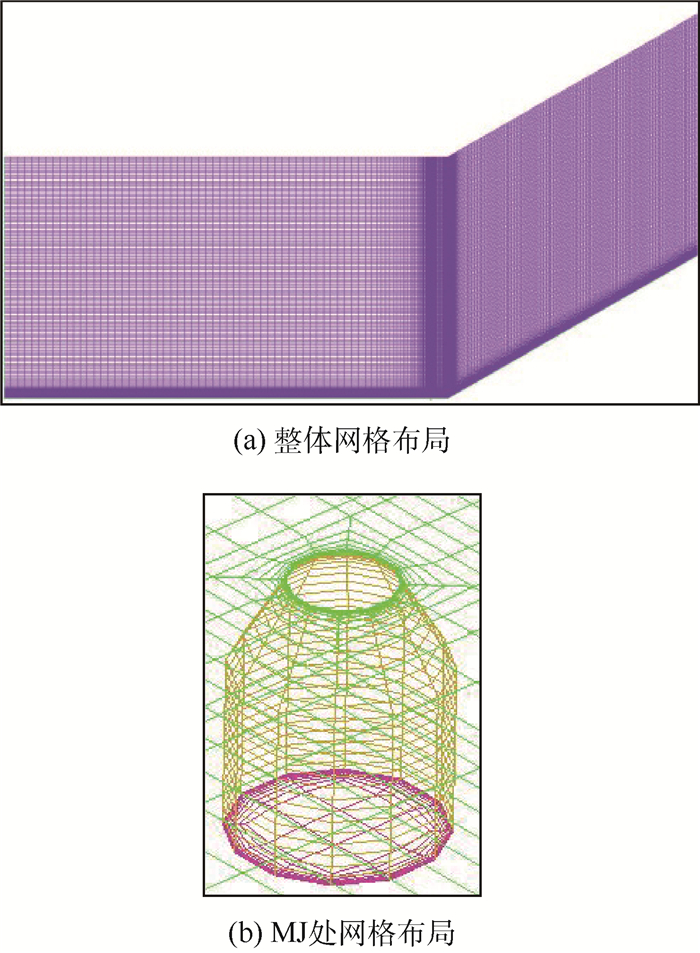 |
| 图 2 网格布局 Fig. 2 Grid layout |
| 图选项 |
1.2 算例验证 文献[15]对压缩拐角流场进行了详细的实验研究,实验模型如图 3所示,此模型与本文计算模型相近,并且其实验数据具有一定代表性,所以选取此实验进行算例验证。为排除网格数量的影响,验证时分别对数量约为0.6×106、1.0×106、1.6×106的网格进行了计算,计算方法以及网格布置方式均与本文相同。得到的壁面压强分布以及未受扰动位置处边界层流向速度分布与文献[15]提供的实验数据的对比情况如图 4所示(图中δ、P∞、U∞分别为实验中边界层厚度、来流静压及来流速度),图示表明网格数为1.0×106、1.6×106的计算结果基本相近且与实验数据吻合较好。通过对比证明了本文计算方法及网格布置方式的可靠性,为节省计算资源,网格总数设置约为1.0×106。
 |
| 图 3 实验模型[15] Fig. 3 Experimental model[15] |
| 图选项 |
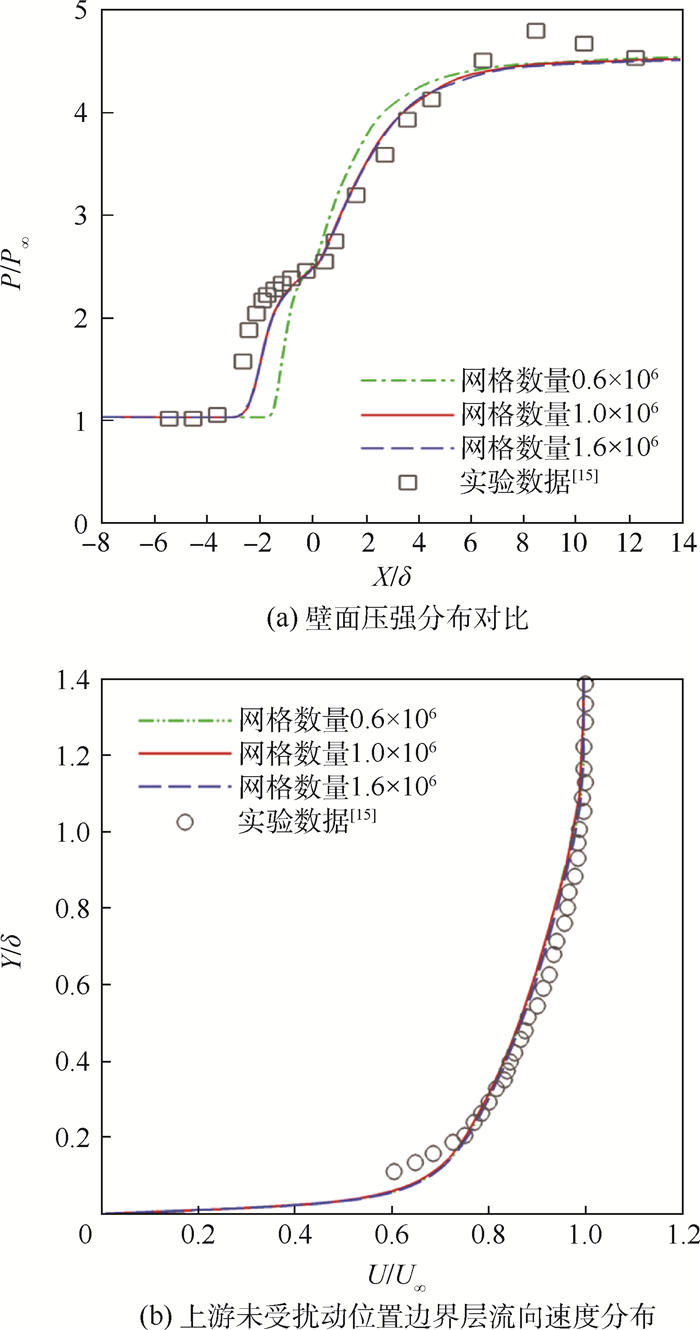 |
| 图 4 模拟结果与实验数据[15]对比 Fig. 4 Comparison between simulation results and experimental data[15] |
| 图选项 |
2 计算结果及其分析 2.1 不同方案MJ周围流场分析 图 5为不同方案MJ展向中心平面马赫数云图。坐标均用喷嘴出口直径D进行无量纲化。如图所示,MJ对横向来流产生阻挡形成一道弓形激波,弓形激波作用下使迎风区近壁面发生流动分离1。随着注入压比的增加,弓形激波强度、分离程度均有所增强,如图 5(a)~ 图 5(e)中流线变化所示。射流流出喷口发生膨胀,并终止于桶状激波及马赫盘,膨胀随注入压比的增加而更加强烈,如图 5(a)~ 图 5(e)马赫数云图所示。此外,射流与来流之间形成了明显的边界,由于注入压比最大、出口膨胀程度最剧烈,所以图 5(e)中Case 5相对其他方案造成的边界与壁面的距离都要大。MJ下游背风区的低压特性会造成此处近壁面产生流动分离2,如图 5(a)~ 图 5(e)流线所示,注入压比的增加会使此分离加剧。
 |
| 图 5 不同方案MJ展向中心平面马赫数云图 Fig. 5 Mach number contours of different schemes at spanwise center surface near MJ |
| 图选项 |
上述分析可知:高压注入MJ会造成更强的阻挡特性、更加剧烈的射流膨胀及更大程度的流动分离(如图 5(e)中分离1、分离2)。
此外,MJ与来流耦合作用还会产生复杂的三维涡结构,图 6给出了MJ与横向来流作用产生的三维涡结构(各方案均会产生同样涡结构,这里以Case 4计算结果为代表),其中X=-40D平面的涡量标度Ω′=Ω/1 000,Ω为实际涡量值。涡结构由以下3对涡组成:近壁面流动遇射流阻挡形成的马蹄涡对;射流与来流剪切掺混形成的正反向旋转流向涡对(Counter Rotating Vortex Pair,CVP);在CVP与壁面之间由于剪切作用产生的二次涡对。CVP由于其涡强度、作用范围相对其他涡对较大,所以是对来流造成影响的主要作用者。沿图 6中X轴正方向观察,正涡量涡为顺时针旋转,负涡量涡为逆时针旋转。
 |
| 图 6 三维涡结构示意图 Fig. 6 Sketch map of three-dimensional vortex structure |
| 图选项 |
以上给出了MJ与来流作用产生的三维涡结构示意图并分析得到CVP是影响主流流动的主要作用者,虽然各方案MJ与来流作用均会产生CVP,但其强度、作用范围会因注入压比的不同而发生明显变化。图 7为MJ下游X=-40D处各方案涡量云图,由图 7(a)~ 图 7(e)所示,流动关于展向中部呈现了高度的对称特性。CVP涡核之间是上洗区域,涡核两侧为下洗区域。除这些共性外,注入压比的增加会增大CVP的搅动范围,产生此变化的原因在于CVP的产生主要依靠MJ与来流在边界处(即图 5中的边界)的剪切掺混作用,而注入压比的增加扩大了边界范围,这就导致涡的搅动范围增加。为辨识各方案产生的CVP强度,取图 7(a)~ 图 7(e)中最大涡量Ωmax,并将其列入表 3中(由于对称性,表中仅列出正涡量)。由表中数据可知,CVP强度未随着注入压比的增加而增强,Case 4中强度最大。但Case 5中由于MJ造成的强弓形激波导致来流速度损失过大无法与其形成强耦合作用而减弱了CVP强度。
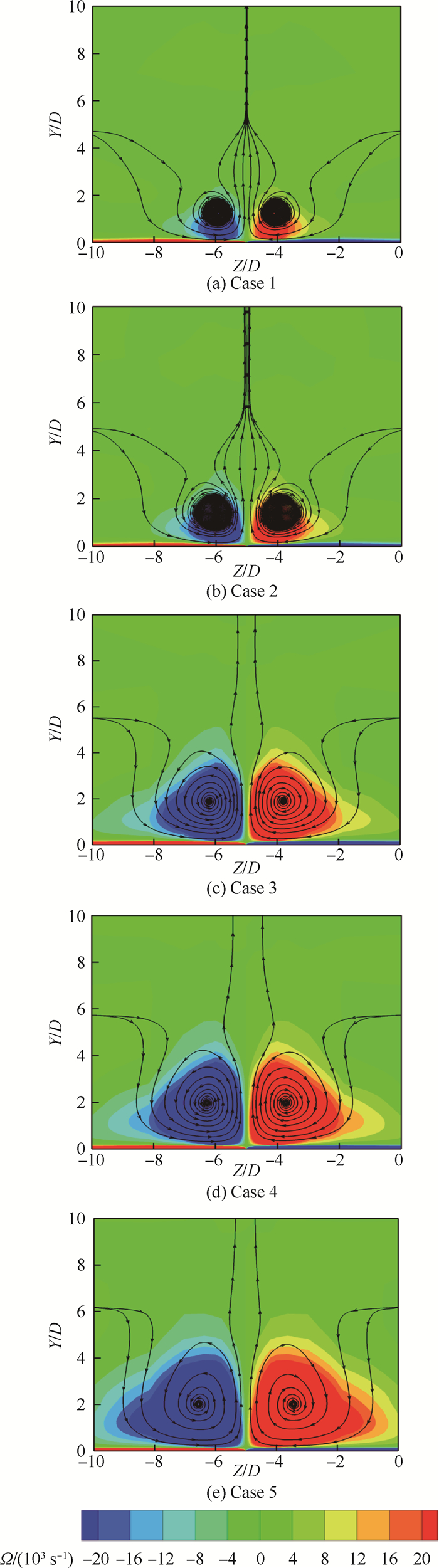 |
| 图 7 X=-40D处不同方案涡量云图 Fig. 7 Vorticity contours of different schemes at X=-40D |
| 图选项 |
表 3 不同方案X=-40D处最大涡量 Table 3 Maximum vorticity of different schemes at X=-40D
| 方案 | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
| Ωmax/(104 s-1) | 3.89 | 5.56 | 11.97 | 12.31 | 9.90 |
表选项
通过给出MJ与来流作用产生的三维涡结构示意图以及对不同方案产生的CVP特性分析可知:CVP是影响主流流动的主要作用者,且随注入压比的增加其搅动范围会增大,Case 4中产生的CVP强度最大。
2.2 各方案MJ下游流场特性变化及MJ控制机理 CVP沿流向运动过程中,其特性会发生改变。此变化在各方案中均会呈现,这里以Case 4为代表对其进行定性描述。CVP特性沿流向变化如图 8所示,图中给出了X=-40D, -35D, -30D, -25D 4处截面涡量云图。由图中涡量及流线所示:随流向位置远离MJ,涡强度衰减、涡核与壁面的距离增加、涡核间距增加。
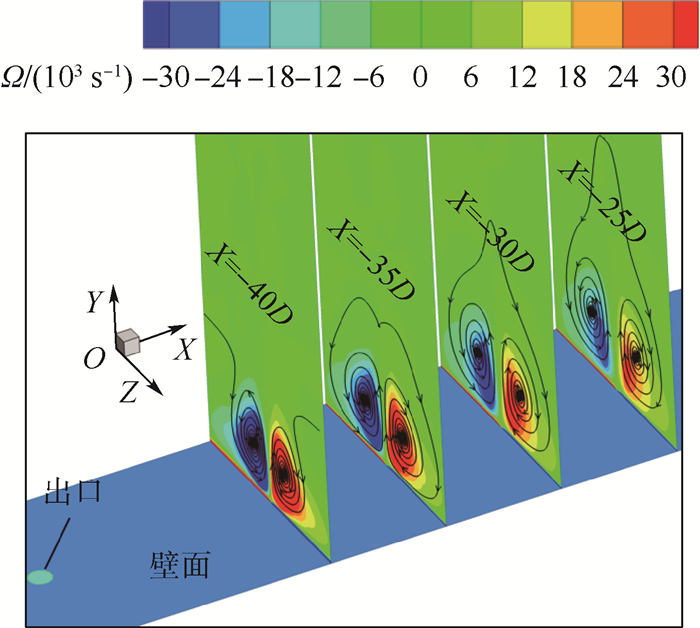 |
| 图 8 Case 4中CVP流向变化特性 Fig. 8 Streamwise variation feature of CVP in Case 4 |
| 图选项 |
上述特性势必会因为注入能量的不同而在量值上产生差异。图 9就从涡强度、涡与壁面距离、涡核间距3个角度出发定量地给出了不同方案中CVP沿流向发展变化的程度。由图 9(a)所示,各方案产生的CVP沿流向运动时,都会产生涡量耗散,相对X=-40D处,在X=-25D位置Case 1~5的耗散程度依次为:82%、78%、75%、73%、72%。以上数据说明,高注入压比MJ产生的CVP沿流向衰减程度要弱。虽然Case 5衰减程度最小,但由于起初产生的CVP强度并非最大,所以衰减后最大涡量依旧稍低于Case 3及Case 4。此外,图 9(b)、图 9(c)给出了CVP涡核位置(用Y、Z方向速度为0位置代表)在Y方向的变化及Z方向的间距变化。由图中数据,Case 1~5中涡核与壁面的距离依次增加了62%、33%、17%、17%、32%,涡核间距依次增加了45%、51%、49%、44%、36%,并未呈现规律性变化,但高注入压比方案产生的CVP相对低注入压比方案产生的CVP,其涡核与壁面的距离以及涡核间距S在下游各流向位置均较大,从而可以卷入更高能量的流体到边界层底部,并扩大CVP在展向的作用范围。
 |
| 图 9 不同方案CVP流向变化特性 Fig. 9 CVP variation feature of different schemes in streamwise direction |
| 图选项 |
MJ作用下,壁面剪切力沿流向又是如何变化,如图 10所示。图 10(a)、图 10(b)和图 10(c)分别给出了不同方案在X=-35D、X=-30D、X=-25D处的展向壁面剪切系数Cf分布,其中纵坐标C′f=Cf×103,Cf为实际值。由图 10所示,壁面剪切系数关于展向中部对称,同CVP的分布一致。此外,在图 10(a)、图 10(b)、图 10(c)中均可以发现随注入压比的增加,展向两侧附近的壁面剪切系数也随之增大,而且随流向位置靠近下游拐角处,展向两边缘处的壁面剪切系数相对No control方案增量越大。前述已知Case 5产生的CVP并非最强,但其搅动范围最大,而且沿流向运动会逐渐远离壁面并向展向两侧移动,所以在CVP下洗作用下会带入远离壁面处的更高能量流体到边界层底部近壁面和展向边缘,以至于其激活能力相对较好。虽然MJ对靠近展向两侧的流动有不同程度的激活能力,但由于靠近展向中部MJ阻挡作用较强,所以在靠近展向中部(如图 10(a)、图 10(b)中位于-5.5D~-4.5D处)造成了负面影响。随流向位置逐渐靠近拐角,MJ阻挡作用变弱,负面影响呈弱化趋势。
 |
| 图 10 展向壁面剪切系数分布 Fig. 10 Shear coefficient distribution at spanwise wall surface |
| 图选项 |
以上分析已知在CVP下洗作用下,靠近展向两侧处的壁面剪切系数值均有增加,但边界层的变化如何,如图 11所示。图 11给出了Z=-1D处在X=-35D、X=-30D、X=-25D 3个流向位置的流向速度分布(如图 11(a)~图 11(c)所示)以及对应的近壁面框中放大图(如图 11(d)~图 11(f)所示)。由图 11(a)~ 图 11(c)所示,由于MJ对来流的阻挡作用,边界层在Y=1D以上位置不再饱满,在边界层底部近壁面(Y=1D以下位置)却出现了相反的趋势:流向速度分布变得更加饱满且随注入压比的增加其程度增强,如图 11(d)~ 图 11(f)所示,另外,随流向位置靠近拐角分离区,MJ作用下的边界层底部近壁面处的速度分布相对No control方案的饱满程度会随之变大,这一点与展向壁面剪切系数值沿流向的变化趋势一致。边界层底部的变化主要与MJ产生的CVP的强度、搅动范围、衰减程度等几大因素有关,高压注入方案(如Case 4、Case 5) 在以上因素中均占据了优势,所以对近壁面流动的激活效果较好。Case 4产生的CVP虽最强,但搅动范围相对Case 5较小,所以激活能力稍弱于Case 5。
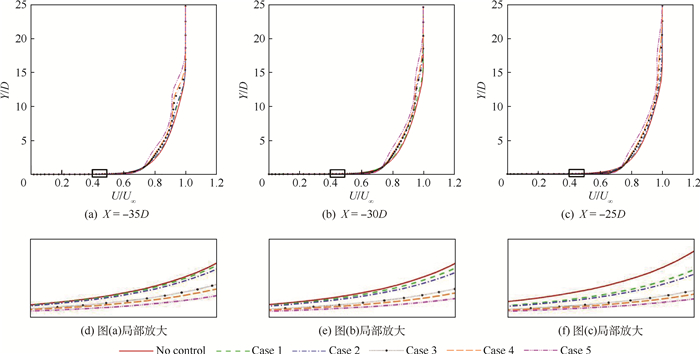 |
| 图 11 Z=-1D处流向速度分布 Fig. 11 Streamwise velocity distribution at Z=-1D |
| 图选项 |
综合以上对流场沿流向变化的分析:Case 5产生的CVP对靠近展向两侧的边界层近壁面流动有相对较强的激活作用;Case 4产生的CVP在到达拐角分离区之前,其强度相对其他方案一直最大。
2.3 各方案MJ作用下压缩拐角附近流场特性变化及MJ控制机理 上述分析已知不同方案MJ与来流作用下会使其下游边界层发生变化,这种变化势必会对拐角附近流动产生影响。图 12为沿Y轴负方向俯视的壁面剪切系数云图。云图中忽略了大于0的部分以便对分离区进行辨识。图 12(a)中给出了未加控制时的分离位置及再附位置。MJ作用下,分离区被有效抑制,特别是在图 12(e)中Case 4中MJ对分离区面积削弱程度最大,在其作用下分离位置最靠近下游,削弱幅度近70%。前文分析已知随注入压比的增加,MJ对靠近展向两侧的边界层底部低能流体有更好的激活作用,这可以提高边界层抵抗逆压梯度的能力而不易分离,所以控制效果集中体现在展向两侧,且在高压方案中表现明显,如图 12(d)~图 12(f)所示。但Case 5中MJ造成边界层在Y=1D以上位置不饱满程度相对较大且在其下游背风区造成的分离2(如图 5(e))也最大,这会使分离2与拐角分离区更加靠近,从而导致两处分离有相连趋势,所以在Case 5控制下分离位置要稍靠前(如图 12(e)、图 12(f)对比所示)。
 |
| 图 12 压缩拐角附近壁面剪切系数云图 Fig. 12 Shear coefficient contours at wall surface around compression corner |
| 图选项 |
图 13给出了展向中部面压力系数云图,其中压力系数Cp=(Ps-P∞)/(0.5ρU∞2), 其中:Ps为静压;ρ为空气密度。由图 13(a)所示,拐角处形成的λ形激波由分离激波和一系列压缩波构成的再附激波组成,二者相交处为激波交汇点。除拐角处激波外,MJ与来流作用还会产生弓形激波和膨胀波,如图 13(b)所示。加入控制后图中λ形激波有明显变化:分离区减小导致分离激波向下游移动、再附激波向上游移动、交汇点与壁面的距离减小。压比增加到0.45以后交汇点与壁面距离不再发生改变,如图 13(d)~图 13(f)所示,这是因为这3种方案对于分离区的改变程度相近导致的,交汇点最多下降了约37%。另外,如图 13(a)~ 图 13(f)所示,上游同一位置的流线经过分离激波发生较大偏折,最后在再附激波作用下逐渐与斜坡平行。相对图 13(a),加入控制后拐角处分离漩涡在CVP上洗作用下不再闭合,流体被抬起直接流向下游,对拐角处的分离流动起到了改善作用。
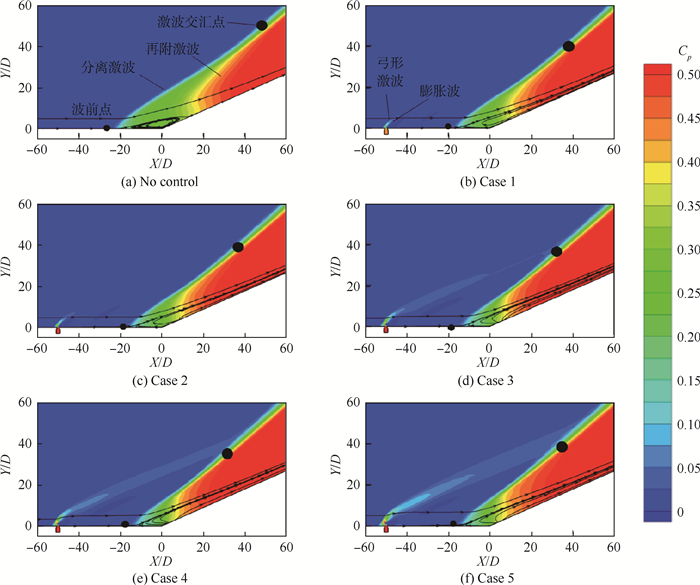 |
| 图 13 展向中部面压力系数云图 Fig. 13 Pressure coefficient contours at spanwise center surface |
| 图选项 |
图 14为拐角附近壁面展向中部的压力系数分布曲线。由图所示,拐角上游压力系数因为分离激波作用陡升,所以在压力系数上升起始段斜率最大。取斜率最大线段终点(即图 14中黑点标识位置)作为分离激波波后点,取分离激波脚前一点为波前点(如图 13(a)所示)。各方案曲线距离较近,为清晰辨识波后压强,将分离激波前后压强及压强比列入表 4,由表中数据可知分离激波强度在Case 5控制下最大被削弱了13%,Case 4中削弱能力与其相近,为12%。MJ作用下会减小来流速度,且减小程度随注入压比的增加而增大,所以增加注入压比可以进一步削弱分离激波强度。分离区域减小会使再附激波向上游移动,由此导致了斜坡壁面压力系数在MJ作用下会有所升高,但最终均恢复到未加控制时的值。
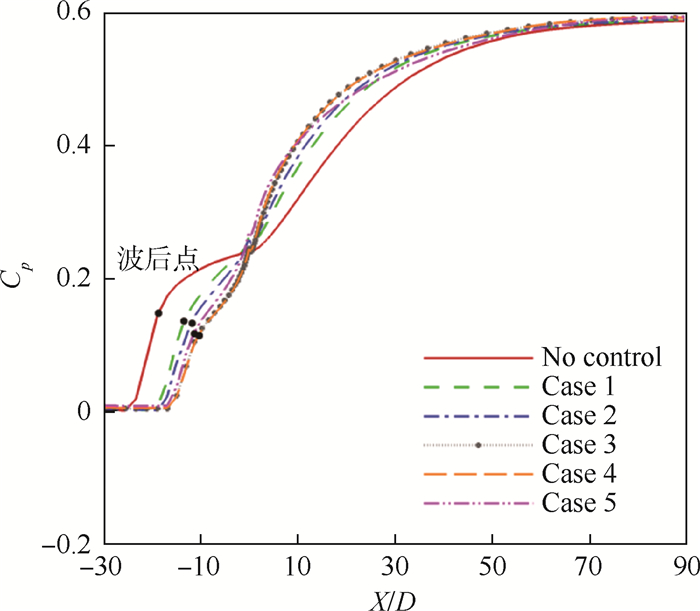 |
| 图 14 压缩拐角附近壁面中心线的压力系数分布曲线 Fig. 14 Pressure coefficient distribution curves at center line of wall surface around compression corner |
| 图选项 |
表 4 分离激波前后压强 Table 4 Pressure before and after separation of shock wave
| 方案 | 波前压强/kPa | 波后压强/kPa | 波后压强/波前压强 |
| No control | 21.7 | 40.2 | 1.85 |
| Case 1 | 21.7 | 38.7 | 1.78 |
| Case 2 | 21.7 | 38.3 | 1.76 |
| Case 3 | 22.0 | 35.9 | 1.63 |
| Case 4 | 22.1 | 35.9 | 1.62 |
| Case 5 | 22.6 | 36.3 | 1.61 |
表选项
以上分析证明了MJ对超声速压缩拐角流场的流动有改善作用,而且Case 4对拐角附近的分离抑制程度最大,近70%,Case 5对分离激波强度削弱最多,近13%。权衡2种方案带来的控制效果及所需能量,Case 4为最优方案。
3 结论 本文针对展向间距为10倍出口直径、不同压比垂直注入MJ作用下的24°超声速压缩拐角流场进行了数值研究,并得到以下结论:
1) MJ与来流耦合产生的CVP是影响来流的主导者,随注入压比的增加,其搅动范围会扩大,注入压比为0.60的方案产生的CVP强度最大。
2) CVP沿流向运动时,涡核会逐渐远离壁面,涡核间距会增加,其强度会衰减,衰减程度随注入压比的增加而减小。MJ阻挡作用下会减小来流速度,进而削弱分离激波强度,削弱程度随注入压比的增加而变大。在靠近展向两侧位置处,边界层近壁面流体被CVP下洗作用带入的高能流体激活,而且随注入压比的增加,被激活程度随之增大。
3) MJ对压缩拐角附近流动有明显改善作用,λ形激波交汇点与壁面的距离随注入压比的增加而逐渐减小,直至注入压比为0.45时不再改变,最大被降低了约37%。注入压比为0.60时拐角附近的分离抑制程度最大,近70%,注入压比为1时分离激波强度被削弱最多,近13%。权衡各方案控制效果及所需能量,注入压比为0.60的方案控制效果最优。
参考文献
| [1] | PIOTR D, RYSZARD S.Shock wave-boundary layer interaction control by streamwise vortices[C]//Proceedings of XXI ICTAM, 2004. |
| [2] | RYSZARD S. Shock wave induced separation control by streamwise vortices[J].Journal of Thermal Science, 2005, 14(3): 249–254.DOI:10.1007/s11630-005-0009-z |
| [3] | RYSZARD S, PAWEL F, JAN S, et al.Shock wave-boundary layer interaction control by air-jet streamwise vortices[C]//Proceedings of the 8th International Symposium on Experimental and Computational Aerothermodynamics of Internal Flows, 2007:1-7. |
| [4] | KUMAR R, BOTU A, ALI M Y, et al.Virtual shock shaping using microjet arrays[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston:AIAA, 2010:1-8. |
| [5] | ALI M Y, AHMED K A, KUMAR R, et al.Flowfield characteristics of oblique shocks generated using microjet arrays[C]//AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Reston:AIAA, 2011, 6(3):1-15. |
| [6] | KUMAR R, ALI M Y, ALVI F S, et al. Generation and control of oblique shocks using microjets[J].AIAA Journal, 2011, 49(12): 2751–2759.DOI:10.2514/1.J051148 |
| [7] | ALI M Y, ALVI F S.Three-dimensional flowfield of microjets in supersonic crossflow[C]//43rd AIAA Fluid Dynamics Conference.Reston:AIAA, 2013. |
| [8] | ALI M Y, ALVI F S, MANISANKAR C, et al.Studies on the control of shock wave-boundary layer interaction using steady microactuators[C]//41st AIAA Fluid Dynamics Conference and Exhibit.Reston:AIAA, 2011. |
| [9] | ALI M Y, ALVI F S, KUMAR R, et al. Studies on the influence of steady microactuators on shock-wave/boundary-layer interaction[J].AIAA Journal, 2013, 51(12): 2753–2762.DOI:10.2514/1.J052201 |
| [10] | VERMA S B, MANISANKAR C. Shockwave/boundary-layer interaction control on a compression ramp using steady microjets[J].AIAA Journal, 2012, 50(12): 2753–2764.DOI:10.2514/1.J051577 |
| [11] | VERMA S B, MANISANKAR C, AKSHARA P. Control of shock-wave boundary layer interaction using steady micro-jets[J].Shock Waves, 2015, 25(5): 535–543.DOI:10.1007/s00193-014-0508-5 |
| [12] | SOUVEREIN L J, DEBIéVE J F. Effect of air jet vortex generators on a shock wave boundary layer interaction[J].Experiments Fluids, 2010, 49(5): 1053–1064.DOI:10.1007/s00348-010-0854-8 |
| [13] | SOUVEREIN L J, DEBIéVE J F. Effect on a shock wave boundary layer interaction of air jet vortex generators[J].Progress in Flight Physics, 2012, 3: 141–156. |
| [14] | YOUNG D D, JENKINS S A, MILLER D N.An investigation of active flowfield control for inlet shock/boundary layer interaction[C]//AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Reston:AIAA, 2013:1660-1670. |
| [15] | MATTHEW J R, PATRICK B, CHRISTOPHER W, et al. Experimental study of a Mach 3 compression ramp interaction at Reθ=2400[J].AIAA Journal, 2009, 47(2): 373–385.DOI:10.2514/1.38248 |
